SUMMARY
Excitation is balanced by inhibition to cortical neurons across a wide range of conditions. To understand how this relationship is maintained, we broadly suppressed the activity of parvalbumin-expressing (PV+) inhibitory neurons and asked how this affected the balance of excitation and inhibition throughout auditory cortex. Activating Archaerhodopsin in PV+ neurons effectively suppressed them in layer 4. However, the resulting increase in excitation outweighed Arch suppression and produced a net increase in PV+ activity in downstream layers. Consequently, suppressing PV+ neurons did not reduce inhibition to principle neurons (PNs) but instead resulted in a tightly coordinated increase in both excitation and inhibition. The increase in inhibition constrained the magnitude of PN spiking responses to the increase in excitation and produced nonlinear changes in spike tuning. Excitatory-inhibitory rebalancing is mediated by strong PN-PV+ connectivity within and between layers and is likely engaged during normal cortical operation to ensure balance in downstream neurons.
INTRODUCTION
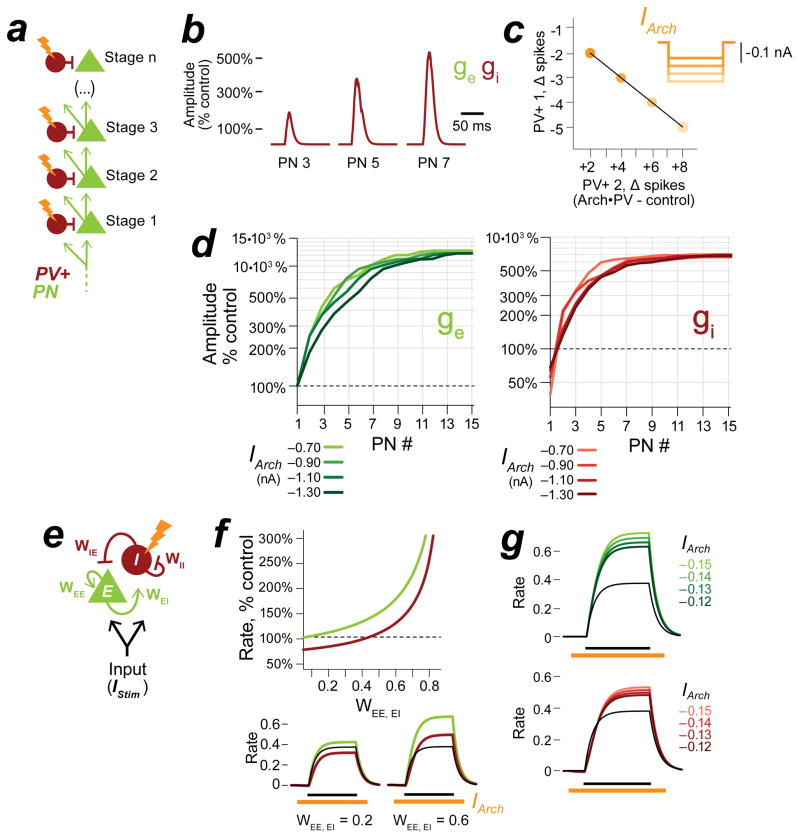
Synaptic inhibition orchestrates spontaneous and sensory-driven activity in the mammalian cortex. Inhibitory interneurons are tightly integrated with the excitatory network, and can be classified by their morphological and molecular features (Pfeffer et al., 2013; Xu et al., 2009; Yoshimura and Callaway, 2005). Recent years have seen major progress in linking these features to specific functions. The best understood and most numerous of these interneurons are parvalbumin-expressing (PV+) neurons, which form powerful inhibitory synapses on the perisomatic compartments of excitatory principal neurons (PNs). PV+ cells and PNs receive common excitatory input. Consequently, PV+ cells provide proportional inhibition to PNs, which has a divisive effect on the PN spiking response to excitatory input (Isaacson and Scanziani, 2011; Swadlow, 2002; Xue et al., 2014). This effect is well-described by classic models of feedforward inhibition (Figure 1a–c) (Ayaz and Chance, 2009; Pouille et al., 2009; Pouille and Scanziani, 2001) and has been recently demonstrated in vivo. In mouse visual cortex, for example, optogenetically suppressing PV+ activity in L2/3 produces a multiplicative increase in PN spiking responses without altering their orientation tuning (Atallah et al., 2012; Wilson et al., 2012).
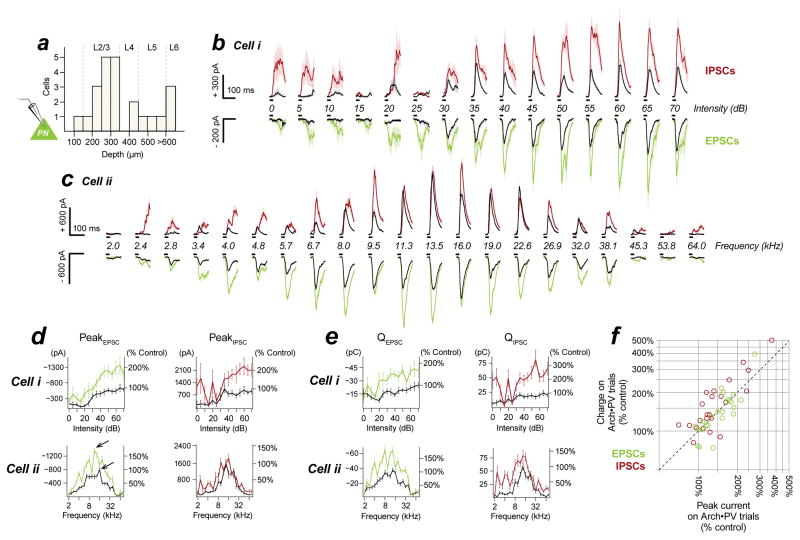
Figure 1. Suppressing PV+ inhibitory neurons increases PN spiking responses throughout the depth of cortex.
a–c, In the classic model of feedforward inhibition, suppressing PV+ activity (a) causes a reduction of synaptic inhibition (b, red traces) without affecting synaptic excitation (b, green traces) in recorded PNs. This multiplicatively increases PN spiking without altering tuning (c). Black: control, orange: Arch•PV (illumination). Panel b is a conductance-based integrate and fire model, panels a and c are cartoons. d, PV-Cre expression in a cross to a tdTomato reporter line. Colocalization of native tdTomato fluorescence (red) and PV antibody label (green). 96% of tdTomato-expressing cells expressed PV (n=638 cells; 4 sections, 1 mouse). Section thickness, 30 μm; scale bar, 100 μm. e, Coronal section through auditory cortex showing the colocalization of membrane-bound Arch-GFP (green) and PV antibody labeling (red). 95% of labeled cells expressed Arch-GFP (n=624 cells, 9 sections, 3 mice). Section thickness 30 μm; scale bar, 100 μm. f, Schematic of experimental setup. We recorded from PNs in all layers of cortex (n=85 PNs, extracellular and intracellular recordings). Laser illumination (532 nm) is represented in orange in all figures. g, Depth distribution of presumed PN recordings obtained using the blind patch technique. h, PNs in all layers showed an increase in trial-averaged firing rate on Arch•PV trials. Points show the median response across best stimuli in the Arch•PV and control conditions; error bars show IQR. “Best stimuli” for each cell were the stimuli that evoked spiking responses in the 75th percentile on control trials, i.e. the most effective 1/4th of the stimulus array (WN or CF tones, 0–70 dB).
PV+ cells are embedded in an interconnected network, in which PNs and PV+ cells excite and inhibit their neighbors (Cruikshank et al., 2010; Kubota et al., 2016; Moore and Wehr, 2013). Can we extrapolate from the direct postsynaptic effect of PV+ inhibition to understand their function at the network level? PV+ neurons are powerfully positioned to regulate the output of excitatory circuits and provide a natural control point for regulating local spiking activity. PV+ excitability is influenced by numerous modulatory signals (Marín, 2012), and recent studies in sensory cortex have identified PV+ cells as key intermediates in a disinhibitory circuit motif for associative learning (Kepecs and Fishell, 2014; Letzkus et al., 2011; Pi et al., 2013). Understanding how changes in PV+ activity affect the larger excitatory network will be essential in understanding how these circuits shape sensory processing. However, attempts to extend the classic feedforward inhibition model to predict PV+-PN interactions on a larger scale have been largely unsuccessful. Broadly suppressing PV+ activity does not result in a uniform increase in PN response gain, as might be expected from the canonical feedforward model, but instead produces variable and unpredictable changes in the responses of individual PNs. Similarly, broadly activating PV+ neurons produces diverse mixtures of subtractive and divisive changes in spiking that indicate more complicated nonlinear effects (Aizenberg et al., 2015; Douglas and Martin, 2009; El-Boustani and Sur, 2014; Kato et al., 2017; Kumar et al., 2013; Lee et al., 2014; Lee et al., 2012; Phillips and Hasenstaub, 2016; Seybold et al., 2015; Wilson et al., 2012; Zhu et al., 2015). Why is this? It is likely that manipulating PV+ activity affects not only inhibitory input to PNs, but also excitatory input. Because PNs are densely interconnected, any change in PN spiking would be expected to produce widespread changes in excitatory input to connected neurons. To further complicate matters, this would also be expected to alter synaptic input to PV+ cells themselves, because PNs are their main source of excitation (Levy and Reyes, 2012; Oswald et al., 2009; Runyan and Sur, 2013). This line of reasoning prompts a more general question: how does an inhibitory imbalance propagate through the cortical network, and what mechanisms, if any, are in place to correct it? One way to disentangle these effects would be to directly measure changes in synaptic excitation and inhibition in downstream PNs.
To understand how changes in inhibitory activity affect synaptic input to downstream neurons, we obtained voltage clamp recordings from PNs while optogenetically suppressing PV+ activity in mice that expressed archaerhodopsin (Arch) in PV+ cells in all cortical layers. We found that cortical circuits can correct an excitatory-inhibitory imbalance in a matter of milliseconds and that PV+ suppression had distinct consequences for downstream neurons at different positions in the circuit. Although Arch was expressed in PV+ neurons in all layers, illumination suppressed PV+ spiking only in thalamorecipient layer 4 (L4). The suppression of PV+ activity in L4 led to an increase in excitatory drive to neurons downstream of L4, which outweighed the suppressive effect of Arch and produced a net increase in PV+ spiking. Consequently, PV+ suppression produced a coordinated increase in both excitation and inhibition to PNs. We observed a similar increase in PV+ activity when we restricted Arch expression to a focal region in L2/3. In these experiments, the suppression of PV+ activity within the Arch expression site produced an increase in spiking in neighboring L2/3 PV+ neurons. For PNs, the increase in excitation enhanced the trial-to-trial reliability of sound-evoked spikes, but the concurrent increase in inhibition constrained the number of spikes that could be fired on individual trials. PNs with unreliable spiking responses therefore showed a linear increase in trial-averaged responses, whereas PNs that spiked reliably reached a saturation point on laser trials and exhibited nonlinear changes in frequency-intensity tuning. We show that this phenomenon — which we refer to as excitatory-inhibitory “rebalancing” — is a robust feature of networks with multiple stages of feedforward inhibition or reciprocal PN-PV+ connectivity, providing a link between the network-wide response to PV+ suppression and current models of PV+ function.
RESULTS
We examined the effects of suppressing PV+ activity in transgenic mice that we generated by crossing a Cre-dependent Arch-GFP line (Madisen et al., 2012) to a Pvalb-IRES-Cre line (Hippenmeyer et al., 2005). The specificity of expression in the Pvalb-IRES-Cre driver line has been verified in cortex (Atallah et al., 2012; Kuhlman and Huang, 2008; Runyan and Sur, 2013). We confirmed the expression pattern in auditory cortex in a cross to a tdTomato reporter line (Madisen et al., 2012; Moore and Wehr, 2013). In tdTomato/Pvalb-Cre mice, 97% of tdTomato-expressing cells stained positively for Pvalb and 96% of Pvalb+ cells expressed tdTomato (Figure 1d; n=638 cells, 4 sections from 1 mouse). In Arch-GFP/Pvalb-Cre mice, approximately 95% of Pvalb+ cells expressed Arch-GFP (Figure 1e; n=624 cells, 9 sections from 3 mice). Intracellular recordings confirmed that illumination generated hyperpolarizing currents and suppressed spiking responses in PV+ neurons both in vitro and in vivo (Figure S1).
PV+ suppression increases both excitation and inhibition to PNs
To learn how PV+ suppression affected PN spiking responses, we used the blind patch technique to obtain extracellular and intracellular recordings from presumed principle neurons (PNs) in L2–6 (Figure 1f–h). We compared the spiking response to sounds presented alone (“control”) to the spiking response to sounds embedded in a 150 ms laser pulse (“Arch•PV”), on interleaved trials. The minimal model of divisive inhibition predicts that suppressing PV+ activity should decrease inhibition to PNs and thereby increase their spiking output (Figure 1a–c). Consistent with this prediction, we found that illumination produced an increase in trial-averaged firing rates of PNs in all cortical layers. The firing rates of individual neurons increased to 260±120% of their firing rates on control trials (median±IRQ for n=85 PNs, depths 100–720 μm). The magnitude of the change in firing rate did not depend on recording depth (Spearman correlation, n.s. p=0.21, ρ=0.025).
To learn whether the increase in PN spiking activity was due to a decrease in inhibition, an increase in excitation, or a combination of both, we obtained voltage-clamp recordings from PNs in L2–6 (Figure 2a, n=23 recordings with channel blockers in the internal solution, depths 147–780 μm). We measured changes in excitatory and inhibitory postsynaptic currents (EPSCs and IPSCs) at the soma by clamping the voltage at the reversal potential for inhibition and excitation, respectively. PNs in all layers showed a dramatic increase in sound-evoked EPSCs on Arch•PV trials, consistent with strong PN↔PN connectivity and the increase in PN spiking activity that we observed in our extracellular recordings. Unexpectedly, we found that in most cases this increase in excitation was accompanied by an increase in inhibition. Figure 2b–c shows the change in sound-evoked EPSCs and IPSCs for two example PNs. Both cells showed a robust increase in the amplitude of sound-evoked EPSCs on Arch•PV trials – as did nearly all recorded PNs (Skillings-Mack, p<0.05 for 20/23 cells). Both cells also showed a significant increase in IPSC amplitude, as did most PNs (Skillings-Mack, p<0.05 for 15/23 cells). In no cells did we observe a significant decrease in inhibition. Illumination produced no significant change in either EPSC or IPSC amplitudes in 3/23 cells, which are not included in the following analyses. To examine the overall magnitude of these changes, we compared the amplitudes of the maximum current response in the control and Arch•PV conditions (arrows in Figure 2d). On Arch•PV trials, the maximum EPSC amplitude was 152±32% of the largest response on control trials (median±IQR for n=20 cells showing a significant change in EPSCs). IPSC amplitudes increased by a similar amount, to 132±27% of the peak response on control trials (median±IQR for n=15 cells showing a significant change in IPSCs). The effect of illumination was very strong at the level of individual PNs, with a median effect size (d) of 0.7±0.3 for changes in EPSC amplitudes (n=20 cells) and 0.8±0.2 for changes in IPSC amplitudes (n=15 cells). This was not due to a difference in input resistance, which did not change with laser illumination (see STAR Methods for details).
Figure 2. PV+ suppression increases excitation and inhibition to PNs.
a, We recorded from cells in all layers (n=23 cells recorded in voltage-clamp). Depths binned at 50 μm. b–c, Sound-evoked EPSCs and IPSCs for two example PNs. Black, control trials; red/green, Arch•PV trials, mean±SEM. Upper red/black traces are IPSCs (inhibition); lower green/black traces are EPSCs (excitation). Sound presentation indicated by black bars. The amplitude of excitatory and inhibitory synaptic currents increased on Arch•PV trials. This was true for most neurons (for EPSCs, 20/23 cells; IPSCs, 15/23 cells). In no cells did we observe a significant decrease in inhibition. Stimuli: (a) 25 ms WN from 0–70 dB (5 dB steps), 15±2 paired repetitions; (b) 25 ms tones from 2–80 kHz (5 frequencies/octave) at 60 dB, 11±2 paired repetitions. Note separate scales for EPSCs and IPSCs.d–e, Changes in peak current (d) and synaptic charge (e) for the example cells in panels b–c; EPSCs at left, IPSCs at right. Raw values are expressed as a percentage of the maximum control response. Arrows in (d) show the maximum response evoked by a single stimulus in the control and Arch•PV conditions. f, Summary of changes in peak current amplitudes and synaptic charge (n=23 neurons; IPSCs in red, EPSCs in green). Values are normalized to the maximum trial-averaged response, across stimuli, on control trials (see arrows for the example in panel d).
An increase in peak current amplitude could be due to an increase in the number of spikes fired by presynaptic neurons, or due to more tightly-synchronized spiking activity without an increase in overall spike numbers. To distinguish between these possibilities, we measured the time integral of the postsynaptic current (total charge, QE and QI), which scales with the number of presynaptic spikes, independent of their timing (Figure 2e–f and Figure S2). Excitatory and inhibitory charge increased by approximately the same factor as peak current amplitudes: QE increased by 139±33% (median±IQR, n=20 cells), and QI by 168±39% (median±IQR, n=15 cells). The rapid and reversible increase in both peak amplitude and charge suggest that the increase in sound-evoked currents was caused by an increase in the spiking responses of excitatory and inhibitory neurons, presynaptic to the recorded PNs.
Excitatory-inhibitory balance and timing are preserved
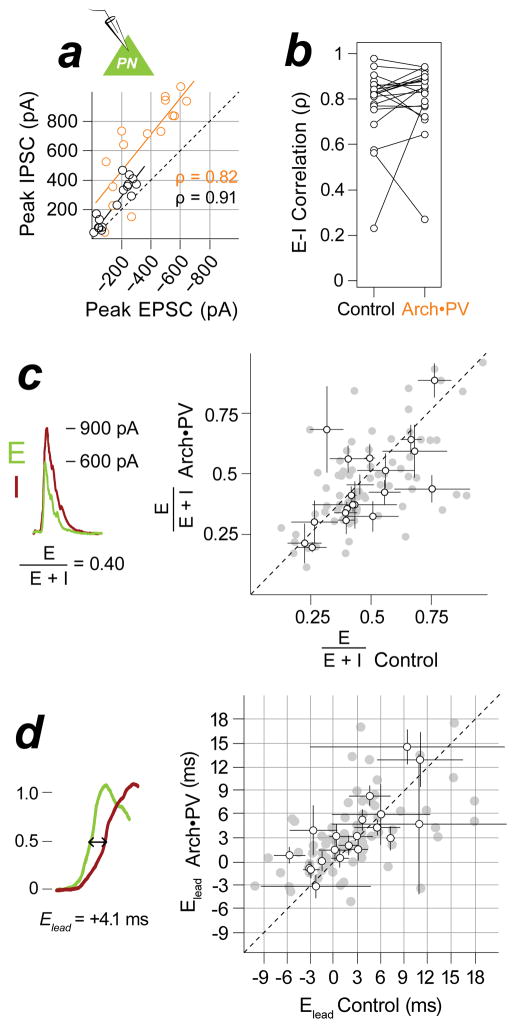
Excitation and inhibition both increased in magnitude on Arch•PV trials, but were they still balanced? Excitatory-inhibitory (E-I) “balance” can refer either to the co-tuning of excitation and inhibition across a wide range of stimuli (similar receptive field shape), or to their amplitude ratio for individual stimuli. We tested for changes in both measures of E-I balance. Note that “balance” in either of these senses is not meant to imply equality or instability. To quantify co-tuning we computed the rank correlation coefficient (ρ) between excitatory and inhibitory responses to an array of frequencies or intensities (Figure 3a–b). EPSC and IPSC amplitudes were highly correlated across stimuli on control trials, indicating strong co-tuning. On Arch•PV trials, the amplitude of the responses increased substantially, yet excitation and inhibition remained co-tuned (ρ: control 0.82±0.05, Arch•PV 0.86±0.06; signed-rank, n.s. p=0.35, d=0.17, n=20 cells). Although one-fourth of these cells did not show a significant increase in IPSCs, excitation and inhibition remained correlated on Arch•PV trials because the tuning of EPSCs did not change. Measures of E-I correlation (such as ρ) compare receptive field shape but not the relative amplitude of excitatory and inhibitory input, and thus would not reveal a disproportionate increase in excitation relative to inhibition, or vice versa. To test for changes in E-I balance in this latter sense, we measured the ratio of excitation to inhibition for each frequency or sound level in the stimulus array — computed as , which ranges from 0 (pure inhibition) to 1 (pure excitation) and has a value of 0.5 when E-I magnitudes are equal. There was no change in E-I ratio on Arch•PV trials (Figure 3c; : control 0.43±0.08, Arch•PV 0.42±0.12; signed-rank, n.s. p=0.19, d=0.09, n=20 cells) and hence no evident trend toward a greater increase in excitation versus inhibition. Thus E-I balance was well-preserved on Arch•PV trials — both in the co-tuning of E-I receptive fields, and the E-I amplitude ratio for responses to individual stimuli. Finally, we asked whether illumination altered the relative timing of synaptic input (Elead, Figure 3d). Sensory stimuli evoke a stereotyped E-I sequence in cortical PNs, in which inhibition follows excitation with a 2–3 ms delay (Pouille and Scanziani, 2001; Wehr and Zador, 2003). This delay period was unchanged on Arch•PV trials (Elead: control 2.1±3.9 ms, Arch•PV 3.1±2.2 ms; signed-rank, n.s. p=0.26, d=0.18, n=20 cells).
Figure 3. Excitatory-inhibitory balance and timing are preserved.
a, E-I co-tuning. EPSC and IPSC responses to tones for example cell in Figure 2c, means across trials. Control, black; Arch•PV, orange. EPSC and IPSC amplitudes were highly correlated across stimuli on control trials (Spearman’s ρ=0.91, p<0.05). The amplitude of evoked currents approximately doubled on Arch•PV trials but EPSCs and IPSCs remained co-tuned (ρ=0.82, p<0.05). b, Group data for E-I correlation (ρ), for n=20 cells showing a significant change in excitatory input on Arch•PV trials. c, E-I ratio. Left: We computed the ratio E/(E+I) from the peak amplitude of trial-averaged currents, as illustrated. Right: Comparison of amplitude ratios on control and Arch•PV trials, n=20 cells. Grey points: E/(E+I) for best stimuli (75th percentile), black points: median±IQR across best stimuli for each cell. d, E-I delay. Left: We computed the excitatory lead time Elead from trial-averaged currents, as illustrated: Elead = inhibitory latency minus excitatory latency, measured at half maximum. Right: Grey points: Elead for best stimuli, black points: median±IQR across best stimuli for each cell, n=20 cells.
In summary, we found that broadly suppressing PV+ activity did not reduce inhibition to PNs, but instead produced a tightly coordinated increase in both excitation and inhibition, in which all major features of E-I interactions — amplitude ratio, relative timing, and co-tuning — were preserved. These changes were specifically due to PV+ suppression in auditory cortex, because direct illumination of thalamic nuclei had no impact on spiking activity in either thalamus or cortex (Figure S3). The fact that we did not observe reduced inhibition on Arch•PV trials could not be explained by insufficient expression or activation of Arch, because intracellular recordings from PV+ cells showed robust and reliable photosuppression in vitro and in vivo (Figure S1).
PN-PV+ circuits mediate excitatory-inhibitory rebalancing
What mechanism is responsible for “rebalancing” excitation and inhibition to PNs? Homeostatic plasticity is an unlikely explanation because the increase in synaptic currents was both rapid and reversible. Although homeostatic mechanisms have been shown to compensate for chronic disruptions in E-I balance (for example, by adjusting neuronal excitability or the efficacy of synaptic transmission), the time course of these changes ranges from minutes to days (Turrigiano, 2011; Xue et al., 2014). Here, laser illumination preceded sound onset by only 50 ms, and interleaved laser and control trials were separated by less than 1 s. Given the millisecond onset and reversibility of these effects, we hypothesized that the increase in postsynaptic currents was caused by a transient increase in presynaptic spiking activity.
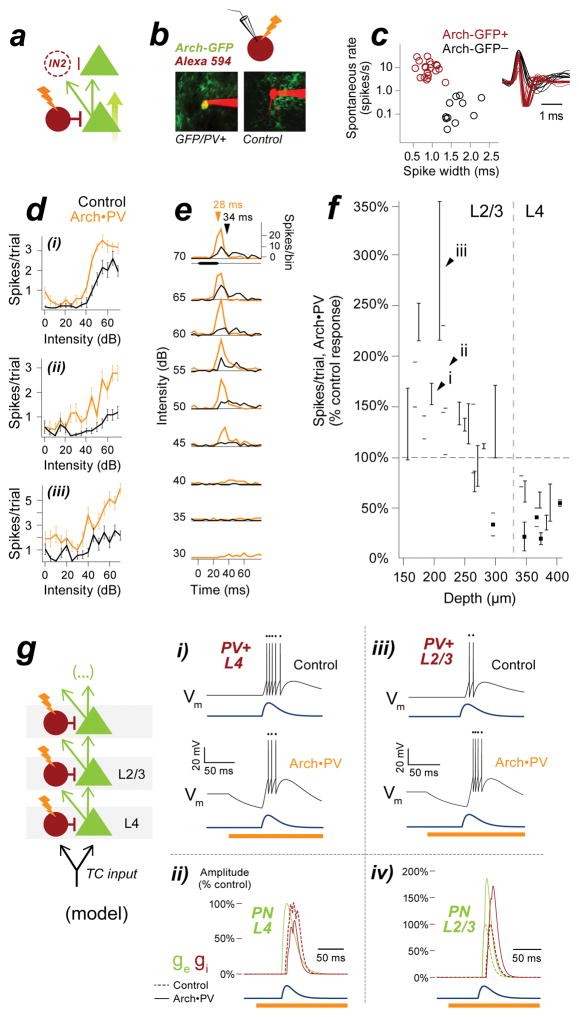
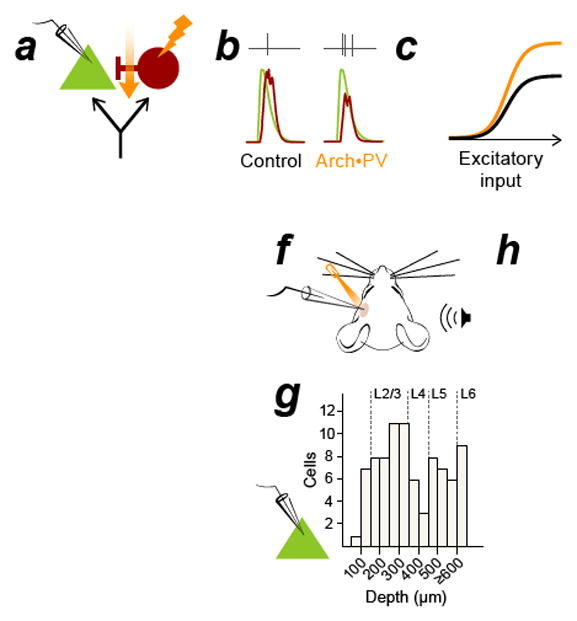
These changes could not be explained by the minimal inhibitory circuit shown in Figure 1a, which predicted neither the increase in excitation nor the increase in inhibition that we observed in PNs. The simplest addition to the circuit that could account for these effects was a feedforward projection to a second identical layer of neurons (Figure 4a). In this candidate circuit, the disinhibition of the first PN would result in an increase in excitation to the second layer of neurons. In this account, the disinhibited PN in the first layer of the circuit would be the source of the increased EPSCs seen in our voltage-clamp recordings. The increase in excitation to the inhibitory neuron in the second layer of the circuit would explain the increase in IPSCs. What inhibitory cell type could be mediating this effect? PV-negative cells such as SOM or VIP neurons are one possibility (Karnani et al., 2014; Pfeffer et al., 2013; Xu et al., 2009). Alternatively, the additional inhibition could originate from PV+ neurons themselves. PV+ neurons are known to receive strong excitatory input from cortical PNs, both across and within layers (Levy and Reyes, 2012; Yoshimura and Callaway, 2005). If these connections were strong enough, the increase in excitatory spiking activity could conceivably outweigh the suppressive effect of Arch and produce a net increase in PV+ activity. To test this idea, we targeted cell-attached extracellular recordings to PV+ cells in L2/3 and L4 using 2-photon microscopy. Recorded cells were filled with red fluorescent dye (Alexa 594), which allowed us to unambiguously distinguish Arch-GFP-expressing PV+ neurons from PN controls (Figure 4b). All GFP-expressing cells were fast-spiking neurons, which were well-separated from PNs in terms of their extracellular spike waveforms and high spontaneous firing rates (Figure 4c; spike width: GFP-negative cells (n=11) 1.61±0.26 ms, GFP-positive cells (n=21) 0.86±0.14 ms; rank-sum, p<0.001, d=1.0; spontaneous firing rate: GFP-negative cells 0.1±0.8 Hz, GFP-positive cells 9.5±4.5 Hz; rank-sum, p<0.001, d=1.0).
Figure 4. Laser illumination increases spiking in Arch-expressing PV+ neurons in L2/3.
a, Possible sources of increased inhibition to PNs. PV+ suppression disinhibits PN1 and increases excitatory input to downstream neurons PN2 and IN2. This unidentified inhibitory neuron IN2 could represent a distinct PV-negative inhibitory cell type, or potentially PV+ neurons themselves. PV+ neurons could provide increased inhibition to PNs if the increase in excitatory drive was strong enough to overcome the suppressive effect of Arch. b, To test this idea, we targeted extracellular recordings to PV+ cells in L2/3 and L4 using 2-photon microscopy. Left: PV+ neurons expressed membrane-bound Arch-GFP; right: PV- controls did not. Cells filled gradually with red Alexa dye over the course of the recording, or with current pulses at termination. c, Extracellular spike width and spontaneous firing rate for n=21 Arch-GFP-positive PV+ cells (red) and n=11 Arch-GFP-negative PN controls (black) collected in the same penetrations. Inset shows peak-aligned waveforms computed from 100 spikes. d, Example L2/3 PV+ neurons showing increased spike count on Arch•PV+ trials. Stimuli, WN at 0–70 dB; values are mean±SEM of 20 repetitions. See Figure S1 for example cells in L4. e, Spike times for example cell 4dii, pooled across all repetitions of the stimulus. Arrows, median spike time at 70 dB. f, Percent change in spike count plotted against recording depth for PV+ neurons in L2/3 and L4. Note the transition from suppression to enhancement near the L3–L4 boundary. Open circles, 2-photon targeted recordings (n=21 PV+ neurons); black squares, blind-patch recordings from Figure S1 (n=5 PV+ neurons). Black arrowheads correspond to example cells in 4d. Values are median, IQR across best stimuli (75th percentile). g, Integrate-and-fire model of a circuit with 2 layers of feedforward inhibition, representing cortical layers 2/3 and 4. When a hyperpolarizing current is applied to both PV+ neurons (IArch = −0.5 nA), PV+ activity is suppressed in the first layer (gi) but enhanced in the second layer (giii). E-I balance is disrupted in the first PN (gii), but the increase in PV+ activity “rebalances” synaptic input to the second PN (giv). Blue: excitatory input to the first layer of the model.
We found that illumination had the opposite effect on the activity of PV+ neurons in layers 4 and 2/3 (Figure 4d–f). In agreement with our intracellular recordings (Figure S1), Arch activation suppressed the spiking responses of PV+ cells in L4 to 55±15% of control values (median±IQR, n=11 PV+ cells at depths ≥300 μm). In contrast, PV+ cells located in L2/3 showed a net increase in spiking on Arch•PV trials — in L2/3, PV+ spike counts increased to 133±25% of control values. The same cells showed a 5.0±2.7 ms decrease in median spike latency, a hallmark of increased excitatory drive (median±IQR, n=15 Arch+/PV+ cells at depths 0–300 μm). The increased spiking seen in L2/3 PV+ cells was not due to ineffective activation of the opsin, because illumination suppressed spiking in L4 PV+ cells recorded in the same animals. At the group level, PV+ cells showed a transition from suppression to enhancement at the L3–L4 boundary. The difference in the response to laser illumination (suppression vs. enhancement) for cells in L4 versus L2/3 was highly significant (Fisher’s exact test, p<0.001).
To gain further insight into the seemingly paradoxical effect of Arch on L2/3 PV+ cells, we implemented our two-layer circuit as an integrate-and-fire model (Figure 4g). When we applied a hyperpolarizing current to PV+ cells in both layers, the response of the PV+ cell in the first layer (PV+L4) was suppressed, which increased the response of its target PN. In the second layer, the increase in excitatory drive outweighed the suppressive effect of Arch and produced a net increase in the response of PV+L2/3, which resulted in a coordinated increase in excitation and inhibition to the second PN. This rebalancing occurred for a wide range of values for the simulated Arch hyperpolarization, including the values we measured directly from PV+ cells in vitro (Figure S4).
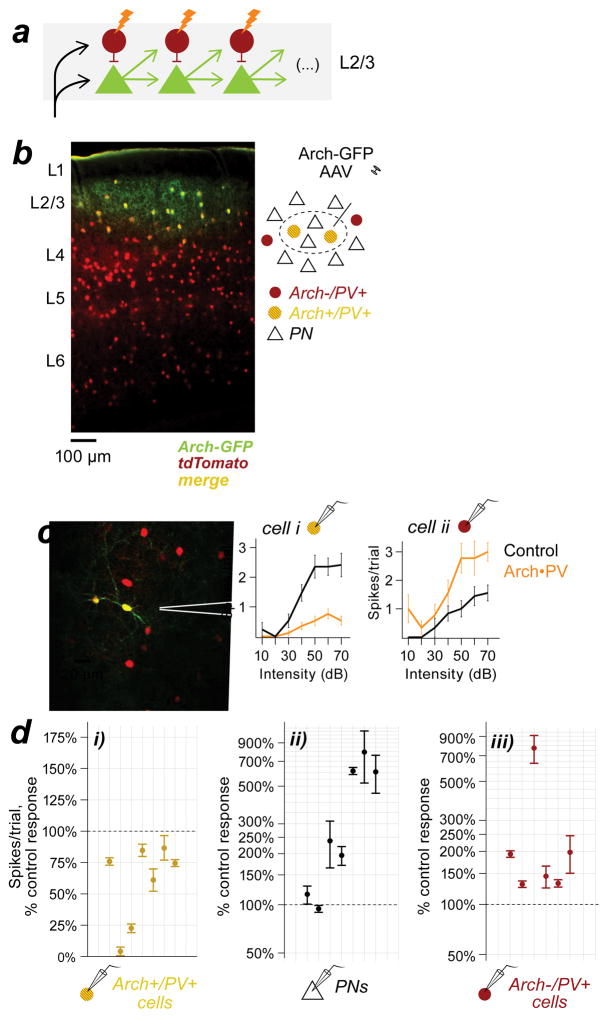
An increase in excitatory drive could be mediated not only by PN→PV+ connections between cortical layers, but also by horizontal connections within layers (Figure 5a). Although an increase in excitation from L4 would be sufficient to explain the increased spiking we observed in L2/3 PV+ cells, we wondered whether the disinhibition of PNs within L2/3 might also contribute to the effect. Because PN spiking responses increased in both L2/3 and L4 (Figure 1e–f), this experiment could not distinguish translaminar from intralaminar excitatory input to L2/3 PV cells. To test whether PV+ suppression could increase PV+ activity solely via horizontal L2/3 connections, we restricted Arch expression to PV+ neurons in L2/3 by injecting a small volume of Cre-dependent Arch-GFP virus into auditory cortex in PV-Cre/tdTomato mice. In these mice, PV+ cells in all layers expressed the tdTomato reporter, but only infected PV+ cells in L2/3 within several hundred microns of the injection site expressed Arch-GFP (Figure 5b and Figure S5). In this way, we eliminated any change in excitatory input originating from PNs in other cortical layers. We found that Arch-positive PV+ cells within the expression site were suppressed by illumination (Figure 5c–d). PV+ spiking responses were reduced to 74±25% of control values (median±IQR, n=6 Arch+/PV+ cells), producing a 238±239% increase in the spiking responses of neighboring PNs (n=7 cells in L2/3). To learn how the increase in PN activity affected PV+ responses in the surrounding cortex, we targeted recordings to Arch-negative PV+ cells at the edge of the expression site in the same animals (n=5 mice). Arch-negative PV+ cells responded to the change in PN activity with a strong increase in spiking (169±33% of control response, n=7 Arch-/PV+ cells). The opposing effect of Arch activation on PV+ cells is shown by the example recordings in Figure 5c, where the suppression of the Arch-positive PV+ cell is accompanied by a net increase in spiking in its Arch-negative neighbor. To control for potential differences related to the method of expression in these experiments, we used the viral strategy to express Arch in PV+ cells in all layers, to match the expression pattern in our transgenic mice. When Arch was virally expressed in PV+ neurons in all layers, illumination increased spiking in L2/3 Arch-positive PV+ cells (Figure S5). This result shows that the increased activity we observed in Arch-expressing neurons was not related to the method of expression, but rather to the spatial scale of the manipulation. In other words, the increase in PV+ activity was a general consequence of suppressing PV+ neurons at an earlier stage in the cortical circuit.
Figure 5. Focal suppression of PV+ neurons in L2/3 increases PV+ activity in the same layer.
a, Feed-forward circuit shown in 4g, re-oriented to show the predicted effects of PV+ suppression within a layer. b, Coronal section from a PV-Cre/tdTomato mouse injected with cre-dependent Arch-GFP AAV. All PV+ neurons expressed tdTomato (red) but only infected PV+ cells in L2/3 expressed Arch-GFP (green). Section thickness, 50 μm; scale bar, 100 μm. Inset: cartoon of the Arch expression site (dashed ellipse). c, Example recordings from neighboring L2/3 PV+ cells at the edge of the expression site. Left: Both neurons expressed tdTomato (red); cell i also expressed Arch-GFP (green). Right: Trial-averaged spike counts on control and Arch•PV trials. The Arch-positive PV+ cell (i) was suppressed on laser trials, whereas the Arch-negative PV+ cell (ii) showed increased spiking responses. d, Sound-evoked spiking responses on Arch•PV trials, as a percentage of the control response. Group data from n=5 mice. di, Arch-positive PV+ cells were suppressed on laser trials (n=6 recordings). dii, Neighboring PNs (n=7) showed increased responses on laser trials. diii, Arch-negative PV+ cells at the edge of the expression site (n=7) showed increased responses on laser trials. Points show the median change across best stimuli; error bars, IQR. Stimuli: WN, 0–70 dB.
Together these experiments show that an acute reduction in PV+ inhibition results in a near-instantaneous increase in the activity of downstream PV+ cells, and that this effect is mediated by excitatory PN↔PV+ connections both within and between cortical layers. Although we did not record from PV+ cells in the deeper cortical layers, they would be expected to show a similar increase in activity on Arch•PV trials, because like PV+ cells in L2/3, PV+ cells in L5–6 receive strong excitatory input from cortical PNs via extra- and intralaminar projections (Levy and Reyes, 2012; Oswald et al., 2009). These results do not rule out the involvement of other inhibitory cell types. Nevertheless, PV+ cells are likely to be the primary source of the increased inhibition in our voltage clamp recordings, because they are uniquely equipped to generate fast and powerful inhibition in PNs. Indeed, one of the key insights provided by the simple model in Figure 4g is that no separate interneuron type needs to be invoked to explain the rebalancing of excitation and inhibition.
Network models for excitatory-inhibitory rebalancing
Our findings thus far are summarized by a network model with multiple stages of feedforward inhibition (Figure 6a) which we refer to as the Cascaded Feed-Forward network (CFF). The network contains an arbitrary number of “stages” which can represent either neurons in different cortical layers (as in Figure 4g) or connected cells within the same layer (as in Figure 5a). In the CFF, suppressing PV+ activity disrupted the balance of excitation and inhibition to the PN in the first stage of the network. In all subsequent stages, the increase in excitatory input to PNs was countered by a compensatory increase in inhibition (Figure 6b–d).
Figure 6. Network models for excitatory-inhibitory rebalancing.
a, Cascaded Feed Forward (CFF) network model. b, Excitatory and inhibitory input to PNs in stages 3, 5, 7 with PV+ suppression (IArch=−0.50 nA). Excitatory conductance, ge (green); inhibitory conductance, gi (red). c, The increase in inhibition is not suppressed by stronger Arch currents. Plot shows the change in spiking for PV+ cells in layers 1 and 2 with increasing suppression (IArch = −0.6 to −1.8 nA). d, Excitatory and inhibitory input to PNs with increasing suppression, stages 1–15. With stronger suppression, synaptic inputs increase in magnitude but remain balanced. e, Inhibition Stabilized Network (ISN) model. The ISN consists of a pool of interconnected excitatory (E) and inhibitory neurons (I) with weighted connections WEE, WEI, WIE, WII. The average firing rates of the pools are represented as continuous variables, rE and rI. See STAR Methods for details. When recurrent connectivity is strong (all weights = 1.0), a brief stimulus IStim elicits a balanced excitatory and inhibitory response (a single black line in 6f–g). f, In f–g, a suppressive current IArch is applied to the inhibitory pool. The strength of recurrent excitation (WEE, EI) is varied, all other parameters are fixed (IStim = 0.5, duration 800 ms, IArc h = −0.13, duration 1200 ms). Top: Plot of the excitatory and inhibitory response (peak firing rate) for increasing values of WEE, EI. Bottom: Example traces. When excitatory connections are weak (WEE, EI = 0.2), IArch suppresses the inhibitory response below control levels. When excitatory connections are strong (WEE, EI = 0.6), the increase in excitatory input to the inhibitory pool outweighs the suppressive current and produces a net increase in the inhibitory response. Control response is shown in black, Arch•PV response is shown in red and green. g, Excitatory and inhibitory rates with increasing suppression; WEE, EI = 0.75.
In addition to feedforward projections, cortical circuits also contain considerable recurrent connectivity. We therefore asked whether a simple recurrent E-I circuit would exhibit rebalancing. We turned to a well-studied class of recurrent E-I models in which the average firing rates across pools of neurons are represented as continuous variables (Ahmadian et al., 2013; Ozeki et al., 2009; Tsodyks et al., 1997; Wilson and Cowan, 1972). In this model, which we refer to as the Inhibition-Stabilized Network (ISN, Figure 6e–g), external input elicits a balanced E-I response. When we applied a hyperpolarizing Arch current to the inhibitory population, inhibitory activity was briefly suppressed but then increased rapidly in response to an increase in excitatory activity. We explored this behavior further by varying the strength of the excitatory connections WEE and WEI with all other parameters held constant. We found that we could only suppress inhibitory activity effectively when excitatory connections were very weak. As excitatory connections became stronger, positive feedback from the excitatory population overwhelmed the suppressive effect of Arch and led to progressively greater increases in inhibition. To unify these two models, note that increasing the strength of the excitatory connections in the ISN is analogous to increasing the number of feed-forward layers in the CFF.
Together, these models show that any network with strong E-I connectivity will quickly compensate for an inhibitory imbalance with a change in inhibitory activity. Both models were robust to changes in parameters, including the magnitude of the suppressive Arch current. In fact, increasing the strength of the suppressive Arch current produced even greater increases in PV+ spiking, because the initial disinhibitory effect on PNs was stronger.
Coordinated changes in excitation and inhibition influence the timing and tuning of PN spikes
Broadly suppressing PV+ activity has variable effects on PN spiking that do not conform to the predictions of purely divisive or subtractive models of inhibition (Seybold et al., 2015). To see whether E-I rebalancing could account for these extracellular effects, we examined the membrane potential and spiking responses of PNs in both anesthetized and awake mice. PNs showed a wide range of changes in tuning on Arch•PV trials with no identifiable trends across layers, in agreement with previous reports (Aizenberg et al., 2015; Seybold et al., 2015; Zhu et al., 2015).
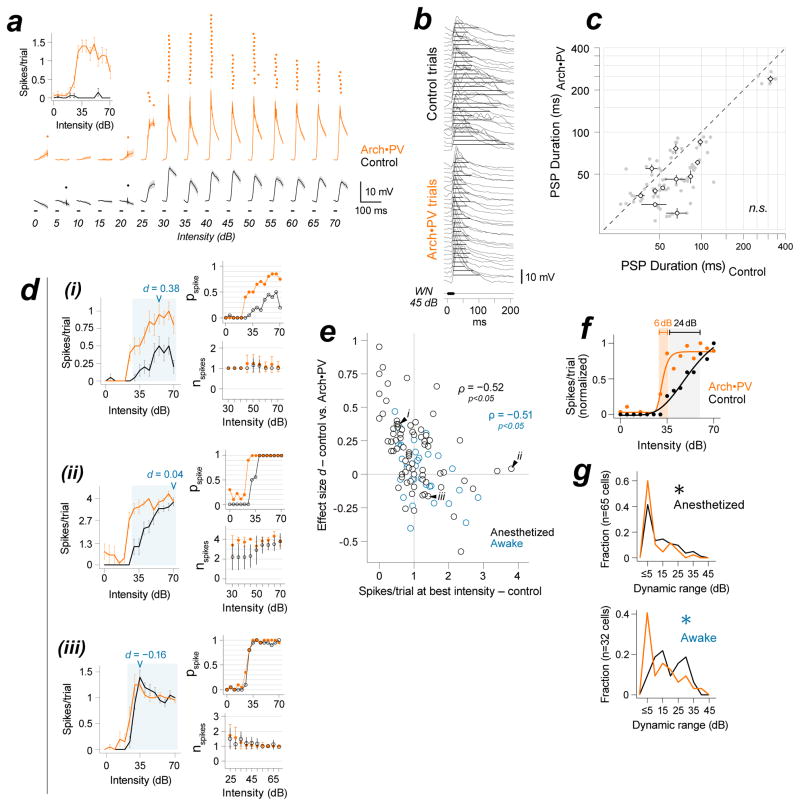
Nearly all of this variability stemmed from two well-characterized nonlinearities in the conversion of synaptic input to spiking output. The first was spike threshold. For example, the neuron shown in Figure 7a fired very few spikes on control trials because the membrane potential rarely exceeded spike threshold. The same cell spiked with high reliability on Arch•PV trials, revealing its receptive field. Most PNs showed increased spiking to non-preferred tones and low intensity sounds on Arch•PV trials, but neurons like the example in Figure 7a (whose receptive field was almost completely subthreshold on control trials and suprathreshold on laser trials) were relatively uncommon, comprising only ~10% of our PN sample. Most PNs also showed an increase in the speed of the membrane potential response on Arch•PV trials, which resulted in a ~5 ms decrease in spike latency (Figure S6). This is a remarkably large difference for auditory cortex, which is exquisitely sensitive to spike timing and where differences as little as 3 ms are relevant to behavior (Yang et al., 2008).
Figure 7. Nonlinearities in the process of spike generation shape tuning on Arch•PV trials.
a, Spike threshold. Spike rasters and trial-averaged membrane potential traces for an example PN (20 repetitions). Inset: spike count; mean±SEM, all trials. Subthreshold PSPs were completely masked by spike threshold on control trials. b, PSP duration for an example PN (stimulus, 45 dB WN). Duration was measured at half-maximal amplitude of the control response (black lines). Spikes removed for visibility. c, Temporal limit on response duration. PSP duration, n=12 PNs. Filled grey circles: duration of responses to best stimuli (50th percentile); open circles: median±IQR across best stimuli for each cell. d, Three example cells illustrate changes in response reliability (pspike) and spike number (nspike). We defined pspike as the probability that a sound-evoked response contained at least one spike, and nspike as the number of spikes fired on responses that contained at least one spike. Left panels in i–iii: Trial-averaged spike counts for a CF tone at increasing intensities, 0–70 dB (mean±SEM). Arrowheads, effect size (d) for changes in spike count at best intensity. Right panels: Same data, partitioned into pspike (top) and nspike (bottom). nspike is shown for the subset of intensities that evoked spikes, shaded blue in the left plot; error bars, SD. di, In general, PNs with low-probability spiking responses (pspike ≪1.0 on control trials) showed a multiplicative increase in the trial-averaged response. This was due to an increase in trial-to-trial reliability (pspike), rather than the number of spikes fired on a single trial (nspike); note that this cell responded with at most 1 spike in both conditions. dii, PNs with near-saturated responses at the highest intensities (here, where nspike~=4) showed a disproportional increase in response to weak stimuli. Note the change at 25–45 dB where pspike<1.0, nspike<4 on control trials. However, due to the temporal constraint on the response (panels b–c) there was almost no change in the spiking response to preferred stimuli (60–70 dB; nspike did not exceed 4). diii, Finally, PNs with steep and saturating spiking responses on control trials showed almost no change in spiking on Arch•PV trials. In this example, response reliability saturates at pspike=1.0, nspike=1. e, Control response at best intensity vs. laser effect size d. Anesthetized, black (n=73 cells); awake, blue (n=33 cells). Due to the limit on spike numbers, there was a strong negative correlation between the magnitude of the trial-averaged control response and the effect of illumination. ρ, Spearman’s rank correlation. Black arrows, example cells shown in panel d. f, Dynamic range. IRFs were normalized to a maximum of 1 and fit with a generalized logistic function for sigmoidal curves (see STAR Methods for details). The dynamic range was computed from the fit to the data, Δ dB from 20–80% of the maximum response. g, Dynamic range was reduced across the population on Arch•PV trials, in both anesthetized (top) and awake (bottom) mice. Asterisk indicates significance at the group level (rank-sum; see text).
The second non-linearity was the upper limit on synaptic integration that arises from the brief delay between excitation and inhibition. This delay limits the duration of the membrane potential response in cortical neurons, and is thought to be responsible for the saturation of spiking output in response to strong sensory stimuli (Ayaz and Chance, 2009; Pouille et al., 2009; Wehr and Zador, 2003). Naively, one might expect that suppressing inhibition would prolong response duration and increase the number of spikes fired. Instead, many cells showed a net decrease in the duration of sound-evoked PSPs on Arch•PV trials (Figure 7b–c; PSP duration at half-maximum: control 66±21 ms, Arch•PV 47±16 ms; signed-rank, p=0.009, d=0.36, n=12 cells). The fact that PSP duration was reduced or unchanged is consistent with our finding that the brief delay between excitation and inhibition was preserved on Arch•PV trials. This imposed a ceiling on PN spiking responses, so although PNs spiked earlier and more reliably on Arch•PV trials, the total number of spikes fired on a single trial rarely exceeded the normal maximum for a given neuron. Consequently, PNs with unreliable spiking responses showed greater changes than cells with high reliability on control trials (Figure 7d). For the example cell in Figure 7di, response reliability (pspike) increased dramatically on Arch•PV trials, while the number of spikes fired on a single spiking trial (nspike) remained constant. For this neuron, which had low response reliability on control trials, the increase in trial-to-trial reliability resulted in a linear increase in the trial-averaged response across the full range of sound intensities. In contrast, cells with highly-reliable spiking responses at high sound intensities (Figure 7dii) showed a disproportionate increase in the response to low intensity sounds. Finally, neurons with highly-reliable spiking responses across the full range of intensities (Figure 7diii) showed almost no change in spiking on Arch•PV trials. At the group level, PNs showed no change in the maximal spiking response to individual stimuli (Supplemental Table 1), as well as a strong negative correlation between a neuron’s response on control trials and the change in its response on Arch•PV trials (Figure 7e; anesthetized recordings (n=65 cells), Spearman’s ρ=−0.52, p<0.001; awake recordings (n=33 cells), ρ=−0.51, p<0.005). Because PN responses typically fall between 0–1 spikes/trial in auditory cortex (DeWeese et al., 2003; Hromadka et al., 2008), effect size was also negatively correlated with response probability (p spike vs. effect size d: anesthetized recordings (n=65 cells), ρ=−0.61, p<0.001; awake recordings (n=33 cells), ρ=−0.50, p<0.005). To investigate the time course of this effect, we varied the relative timing of laser onset and sound onset (Figure S7). We found that when the laser onset occurred within a brief window around sound onset, PN spiking responses were increased and prolonged, consistent with suppressed inhibition (and with the minimal inhibitory circuit in Figure 1a). The duration of this window was 37 ms, suggesting that rebalancing occurs within about 40 ms. To verify that these effects were network-level consequences of manipulating PV cell activity, rather than a pH-dependent effect of Arch (a proton pump) on transmitter release (Mahn et al., 2016), we expressed Halorhodopsin (a chloride pump) in PV cells in all layers and found that illumination produced the same rebalancing effects with Halorhodopsin as it did with Arch (Figure S8).
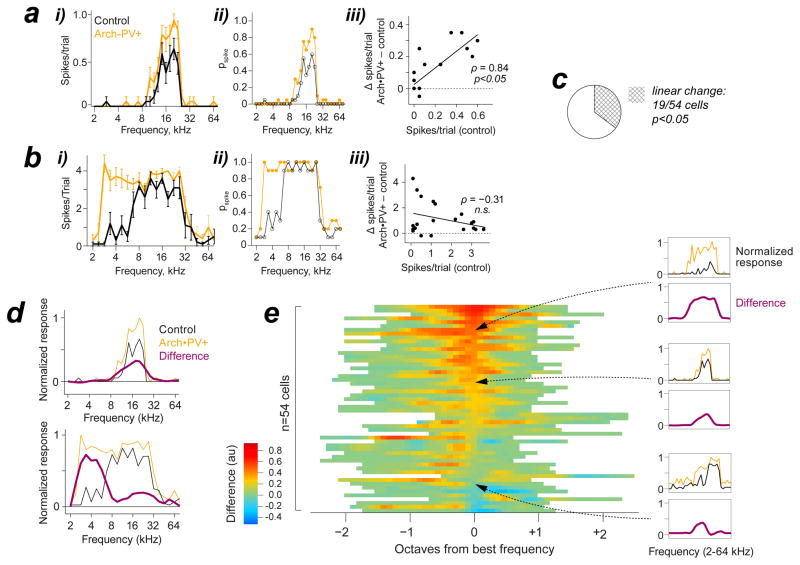
The computational trade-off of this ceiling effect was a loss of stimulus information (Figure 7f–g). For example, the intensity-response function (IRF) of the PN in Figure 7f became much steeper on Arch•PV trials, which reduced the range of intensities that could be represented by a change in spiking output. The dynamic range (Δ dB) of our PN sample was reduced by roughly half on Arch•PV trials, in both awake and anesthetized animals (dynamic range: anesthetized recordings (n=65 cells), control 10±8 dB, Arch•PV 5±5 dB; rank-sum, p=0.01, d=0.25; awake recordings (n=33 cells), control 18±8 dB, Arch•PV 12±9 dB; rank-sum, p=0.03, d=0.25). This was accompanied by a significant loss of stimulus-specific information (Butts, 2003; Montgomery and Wehr, 2010) (median loss at best intensity, anesthetized recordings (n=65 cells): −0.10±0.16 bits; signed-rank, p<0.001, d=0.15; awake recordings (n=33 cells): −0.14±0.13 bits; signed-rank, p<0.001, d=0.456). Frequency tuning was also altered by this ceiling effect. For cells with low spike reliability, responses simply scaled up without changing the shape of the frequency tuning curve (FTC). However, cells with highly reliable spiking to at least some stimuli showed substantial changes in FTC shape, typically a flattening around the preferred frequency. Previous studies have yielded conflicting results as to whether manipulating PV+ activity produces linear (multiplicative or additive) or nonlinear changes in PN spike tuning, which would have distinct implications for PV+ function if they were specifically caused by an increase or decrease in PV+-mediated inhibition (Atallah et al., 2012; Lee et al., 2012; Seybold et al., 2015; Zhu et al., 2015). To quantify changes in frequency tuning in these terms, we compared the control response to each tone with the change on Arch•PV trials, for individual PNs (Figure 8a–c). The example neuron shown in Figure 8a showed the largest changes near best frequency, due to an increase in trial-to-trial reliability. Hence, the increase was proportional to the control response, and there was a significant linear relationship between them (Pearson’s ρ = 0.84, p<0.0001). In contrast, the neuron in Figure 8b showed no change at preferred frequencies, where response reliability was maximal on control trials. Instead, this neuron showed a dramatic increase at lower frequencies that rarely elicited spikes on control trials. For this cell, the increase in the response in the Arch•PV condition was uncorrelated with the control response (Pearson’s ρ = −0.31, n.s. p=0.92). Although the majority of PNs exhibited a significant increase in spiking on Arch•PV trials (Skillings-Mack; p<0.05 for 42/54 cells), only 19/54 cells (35%) showed linear changes in tuning (Figure 8c). To visualize changes in FTC shape across our PN sample, we normalized the control and Arch•PV curves to the maximum response on Arch•PV trials, and then subtracted them (Figure 8d). For the first example cell, the resulting “difference curve” was greatest at best frequency. In contrast, the difference curve for the second example cell peaked roughly two octaves below best frequency. Figure 8e shows the difference curves for all PNs. Cells are sorted by the difference at best frequency to underscore the range of effects on spike tuning. For the majority of PNs, the balanced increase in excitation and inhibition saturated the spiking response and distorted the shape of the spike tuning curve. Together these results show how the range of linear and nonlinear effects of PV+ manipulations that have been previously reported stem from increased response reliability constrained by spike threshold and the synaptic integration window. Thus coordinated changes in excitation and inhibition produce diverse, yet predictable, changes in the spiking activity of individual neurons.
Figure 8. Changes in PN frequency tuning.
a, Example of a linear increase in the spiking response. i: Trial-averaged spike count, 20 stimulus repetitions in each condition. Spiking responses increased on Arch•PV trials, but the shape of the frequency tuning curve was preserved. ii: The increase in trial-averaged spike count was completely accounted for by increased trial-to-trial reliability (pspike). iii: Control response to each tone, vs. the change in the response on Arch•PV trials. The increase was proportional to the control response, showing linearity (ρ: Pearson’s linear correlation). Stimuli, 2–80 kHz at 6 frequencies/octave, intensity 35 dB. Baseline spike rates were not subtracted. b, Nonlinear example. This neuron showed little change in the response to preferred frequencies (~8–16 kHz), where pspike~1, but showed a dramatic increase at lower frequencies, where the control response was weak. Here, the increase was not correlated with the control response to tones. Stimuli, 2–80 kHz at 4 frequencies/octave, 70 dB. c, We evaluated the linearity of the change in frequency tuning for n=54 cells recorded in anesthetized mice, as in a-b. Stimulus, 2–80 kHz at 6 frequencies/octave, +20 dB above the intensity threshold of the neuron. Only 19/54 PNs showed a linear increase in spiking on Arch•PV trials (35% of our sample). d, To visualize the changes in tuning curve shape, we normalized the control (black) and Arch•PV curves (orange) to the maximum response on Arch•PV trials, and then subtracted them. The resulting “difference curve” (purple) was smoothed at ½ octave. Examples correspond to the neurons in panels a and b. e, Difference curves for all n=54 PNs. Cells are sorted by the difference at best frequency. Three examples are shown at right.
DISCUSSION
In this study we used Arch to suppress the activity of PV+ inhibitory neurons on a broad scale and asked how this affected the balance of excitation and inhibition throughout auditory cortex. We found that illumination suppressed PV+ neurons in thalamorecipient L4. However, downstream of L4, the resulting increase in excitatory activity outweighed Arch suppression and produced a net increase in PV+ activity. Thus the net effect of suppressing PV+ activity was not reduced inhibition but rather a coordinated increase in both excitation and inhibition to PNs, in which all major features of excitatory-inhibitory balance were preserved. In recent years the focus of interneuron research has shifted from synaptic interactions between single neurons to how these populations shape activity at the network level. However, the complexity of cortical circuits has made it difficult to link our understanding of inhibitory function at these two levels. We show that the seemingly-paradoxical effect of suppressing PV+ activity is predicted by a network model with multiple stages of feedforward inhibition, and likewise by a recurrent network model where excitatory and inhibitory neurons are represented as population-averaged firing rates. In both cases, suppressing PV+ inhibition produced a robust increase in PV+ activity, regardless of the magnitude of the simulated Arch current. Stronger suppression produced an even greater increase in the inhibitory response, which further suggests that the effects we observed were not a consequence of weak expression or ineffective activation of the opsin. Together these models illustrate the common principle that underlies rebalancing: any network with strong excitatory→inhibitory connectivity will rapidly compensate for a decrease in inhibition with an increase in inhibitory activity.
Dense and unbiased PN-PV+ connectivity is present in all areas of cortex (Packer and Yuste, 2011), which is thought to underlie the broad tuning of PV+ neurons for certain sensory features (Hofer et al., 2011; Moore and Wehr, 2013; Scholl et al., 2015), but the computational value of untuned inhibition has remained unclear. Our results suggest an important function for this nonselective connectivity pattern: local pooling allows PV+ cells to provide inhibition that scales dynamically in proportion to the overall level of excitatory activity within the region. The speed of this response (~40 ms) complements the time course of homeostatic processes that are engaged by a chronic disruption in E-I balance (Marín, 2012; Turrigiano, 2011; Xue et al., 2014).
Cortical activity is constantly in flux, yet excitatory and inhibitory input to individual neurons is persistently matched in both magnitude and time. It therefore seems likely that the circuits that mediate rebalancing are engaged frequently in the course of normal cortical processing. Computations that involve shifts in E-I balance at one stage of the network — such as push-pull interactions in V1 simple cells or A1 binaural cells (Froemke et al., 2007; Hirsch et al., 1998; Kyweriga et al., 2014) — would be expected to elicit rebalancing, to ensure that excitation and inhibition would be balanced in downstream neurons. Could other inhibitory cells provide a similar function? A recent study (Kato et al., 2017) showed that suppressing somatostatin-expressing neurons paradoxically increases spontaneous excitation and inhibition to PNs, but at a slower time course (peaking 100–200 ms after laser onset). This suggests that a similar mechanism could be at play for somatostatin-expressing interneurons, but the more gradual time course indicates that they are unlikely to play a role in the rapid rebalancing that we describe for PV+ cells.
Experimentally, we found that changes in sound-evoked activity scaled smoothly with laser power (Figure S8), which suggests that the response to natural changes in PV+ activity would be smaller but otherwise identical to those we observed. Recent studies suggest that PV+ cells play a key role in disinhibitory circuits that modulate the output of PNs under specific behavioral conditions (Karnani et al., 2016; Kepecs and Fishell, 2014; Letzkus et al., 2011). The circuit we describe allows for flexible disinhibition while preventing local E-I imbalances from propagating to the rest of the network. PV+ neurons may thus serve dual roles in cortical circuits, both as control points for disinhibitory regulation, and checkpoints to prevent disinhibition from propagating between nodes of the network. Predictive coding theory offers another interesting perspective on the computational role of balanced inhibition. Because PV+ cells pool the available excitatory input in the local network, their activity can be said to represent a prediction of the excitatory input that a postsynaptic PN will receive (Rao and Ballard, 1999). Inhibition that is matched to this anticipated input eliminates redundant spiking responses that can be successfully predicted from network activity, leading to flexible and efficient coding (Olshausen and Field, 1996).
These findings provide a useful framework for interpreting the effects of manipulating inhibitory activity in cortex. Two results in particular have important implications for future studies. First, we show that widespread changes in PV+ activity can have profoundly different consequences for different PNs, depending on their relative position in the cortical circuit. This effect is shown by the CFF model, where PV+ suppression decreases inhibition to the PN in the first stage of the network, but has the opposite effect on inhibition in all subsequent stages. This accounts for what first appeared to be a conflict between our findings and those of a similar study (Atallah et al., 2012) in which the authors used Arch to suppress PV+ neurons in L2/3 of mouse visual cortex. In their experiments, Arch had the expected effect on PV+ activity — laser illumination suppressed the spiking responses of Arch+/PV+ cells and reduced inhibition to L2/3 PNs, as occurs in the first stage of the CFF network. When we replicated this experiment in auditory cortex, we likewise found that when Arch expression was restricted to a focal region in L2/3, PV+ neurons were effectively suppressed. To understand how this affected downstream neurons, we targeted recordings to Arch-negative PV+ neurons at the edges of the expression site and found that these neurons responded with a net increase in spiking, as seen in subsequent stages of the CFF. The key difference between these experiments was the spatial extent of the manipulation, rather than the expression method (Figure S5). This shows that horizontal (intralaminar) PN→PV+ connectivity can drive increased inhibitory activity, much like excitatory projections from other cortical layers (translaminar input). Consistent with this finding, Atallah et al. reported that a small subset of PV+ cells (<10%) were paradoxically activated rather than suppressed by illumination. Together these experiments show that the net effect of suppressing inhibitory activity depends on a neuron’s position in the circuit, relative to the manipulation. In experiments that rely specifically on suppression of inhibition, it will be important to verify that the manipulation has the expected outcome at the synaptic level.
Second, we found that E-I rebalancing had a variable impact on the tuning of PNs. While some of this variability could be due to the fact that PV+ cells are a heterogenous population (Moore and Wehr, 2013; Runyan and Sur, 2013), it is important to note that these effects were primarily driven by nonlinearities in the process of spike generation rather than a change in the balance of synaptic input. The increase in sound-evoked excitation drove PNs to spike earlier and more reliably on Arch•PV trials, but because inhibition increased proportionately, the window for integrating excitatory input remained brief (2–3 ms) and imposed a strict ceiling on the number of spikes fired. It is important to note that we could not have inferred this mechanism from a comparison of PN spiking responses on laser and control trials. Indeed, these results exemplify one of the major challenges in making functional inferences about a neural population based only on changes in extracellular activity (Kumar et al., 2013; Otchy et al., 2015; Seybold et al., 2015). Nevertheless, these experiments show that optogenetic manipulations in cortical circuits can be highly informative, provided that one is aware of the potential for strong secondary effects like the ones described here.
STAR Methods
CONTACT FOR REAGENTS AND RESOURCE SHARING
Requests should be addressed to the Lead Contact, Michael Wehr (wehr@uoregon.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
All procedures were in accordance with the National Institutes of Health guidelines, as approved by the University of Oregon and Oregon Health and Science University Animal Care and Use Committees. We used male and female mice, aged 2–4 months. Transgenic Arch+/PV+ mice were heterozygous for Pvalb-Cre (JAX Stock No. 008069) and Arch-GFP (JAX Stock No. 012735). Arch-GFP was virally expressed in mice that were heterozygous for Pvalb-Cre and Ai9-tdTomato (JAX No. 007909). Researchers were not blind to genotype and analyses were not randomized for experimental animals. Intracellular voltage-clamp and current-clamp recordings (n=40 cells total) and extracellular loose cell-attached recordings (n=73 cells total) were obtained using the blind patch technique in 64 transgenic mice. Two-photon targeted recordings (n=52 cells total) were obtained in 8 transgenic and 11 virus-injected mice. Slice recordings (n=38 cells) were obtained in cortical sections from 3 transgenic mice. Single-unit recordings in awake animals were obtained in 7 transgenic and 6 virus-injected mice with implanted tetrodes.
METHOD DETAILS
Surgical Procedures
Acute preparation
Mice were anesthetized with a ketamine cocktail (in mg/kg: 120 ketamine, 0.24 medetomidine, 3 acepromazine). The head was fixed using a custom apparatus that clamped the palate and both orbits, leaving the ears unobstructed. A craniotomy was performed over the left auditory cortex. For blind recordings, the dura was removed and the cortical surface was covered with a thin layer of 4% agarose (thickness <1 mm). Body temperature was maintained at 37°C throughout the experiment.
Tetrode and fiber implantation
Surgical anesthesia was maintained with isoflurane (1.25–2.0%), and dexamethasone (0.1 mg/kg) and atropine (0.03 mg/kg) were administered pre-surgically to reduce inflammation and respiratory irregularities. We implanted an eight-tetrode recording array dorsal to auditory cortex (left hemisphere; AP 2.3 mm relative to bregma, ML 4.5 mm, depth 0.5 mm below the dura). The array was mounted on a custom microdrive. Tetrodes were made of 18 μm tungsten wire (25 μm coated; California Fine Wire) and housed in a 23 ga. stainless steel guide cannula. An optical fiber (diameter 0.2 mm) was implanted immediately adjacent to the tetrode array, 15° from the vertical. We administered ketoprofen (4.0 mg/kg) post-operatively to minimize discomfort. Mice were housed individually following the surgery and were allowed ≥7 days for recovery. Tetrodes were then incrementally advanced into auditory cortex over several days. At the end of the recording period, the brains were extracted and post-fixed in a 4% PFA solution. Brain sections (thickness 100 μm) were examined to confirm the path of the array through auditory cortex, based on the location of the tetrode tracks relative to proximal structures as previously described (Weible et al., 2014a).
Viral injections
Mice expressing Pvalb-Cre and tdTomato were injected with virus AAV2/9.flex.CBA.Arch-GFP.W.SV40 (Addgene #22222) 12±2 days prior to recording. To express Arch in all layers of auditory cortex, the needle was passed through a 1 mm2 cranial window (AP −2.8 mm, ML 4.2 mm), 0° from the vertical axis, to a depth of 0.7–0 .8 mm from the dura. To limit Arch expression to L2/3, the needle was passed through a 1 mm2 window immediately ventral to the cranial ridge over auditory cortex (AP −2.8mm, ML 5.0 mm), 35° from the vertical axis, to a depth of 0.4–0.5 mm from the dura. Injections were made with a 500 nL Hamilton syringe with a 32 ga. needle at a rate of 5 nL/min (volume 50–100 nL, titre ~4.7×1011 GC/ml). The needle was maintained at depth for 5 minutes following the injection. The needle was then slowly retracted and a thin layer of Vaseline was applied over the craniotomy. The skull was covered with a layer of Grip Cement (Dentsply, Milford, DE) and Ketoprofen (4.0 mg/kg) was administered post-operatively to minimize discomfort. PV+ cells had normal spontaneous and sound-evoked spike rates in the absence of laser illumination, and we found no significant differences between PV+ cells recorded in transgenic and virus-injected mice in these measures.
The injection procedure was identical for experiments with halorhodopsin (AAV-EF1a-DIO-eNpHR3.0-EYFP, Addgene #26966) except that virus was injected at two locations to allow for tetrode recordings within auditory cortex. The two injections were made through the same cranial window with the syringe angled 10° toward a midpoint along the AP axis (AP −2.4 & −3.5 mm, ML 4.5 mm, depth 1.2 mm). Injections were made at a rate of 50 nL/min (volume 600 nL/site, titre ~4×1012 GC/mL) and the syringe was maintained at depth for 5 minutes before removal.
Immunohistochemistry
Animals were perfused transcardially with a 4% PFA solution. Brains were postfixed overnight and cryoprotected in 30% sucrose. Thaw-mounted sections (thickness 30 μm) were blocked in 10% normal goat serum with 0.3% Triton in PBS for 3 hours. Sections were incubated overnight in mouse anti-parvalbumin (1:4000; Millipore MAB1572). The sections were incubated for 4 hours in Alexa Fluor 546 goat anti-mouse (Pvalb-Cre/Arch-GFP, Figure 1e; 1:400, Invitrogen A11003) or Alexa Fluor 488 goat anti-mouse (Pvalb-Cre/tdTomato, Figure 1d; 1:400, Invitrogen A21121), and then coverslipped with anti-fade mounting medium. To quantify the specificity of expression, cells were identified in separate fluorescent channels and subsequently scored for colocalization. Intensities were equalized before overlaying the images.
Recording Procedures and Stimuli
Recordings were performed in a double-walled sound isolation chamber. Sounds were delivered from a free-field speaker facing the contralateral ear. Acoustic stimuli were 25 ms pure tones or white noise (WN), with 3 ms 10–90% cosine-squared ramps. The speaker was calibrated within ±1 dB of the target intensity with a B&K ¼” microphone positioned where the ear would be, without the animal present.
Arch was activated using a 532 nm (green) laser coupled to an optical fiber (diameter 0.8 mm). Light was gated with a custom TTL-controlled shutter. The fiber tip was positioned 1–2 mm above the cortical surface using a micromanipulator. The laser was calibrated at the beginning of each experiment to deliver 30±5 mW total power from the fiber tip, for a calculated irradiance of ~2–4 mW/mm2 at depth of 1 mm (Madisen et al., 2012). We observed effects of illumination in PNs throughout the depth of cortex (recording depths ~100–950 μm), but no change in thalamic responses (Figure S3). Importantly, changes in auditory cortical activity were not due to illumination of the retina or neighboring cortical areas, because the laser ceased to have an effect if the center of the beam was moved more than ~0.5 mm from the recording site.
Auditory stimuli were presented in pseudorandom order on alternating “control” (laser off) and “Arch•PV” (laser on) trials, such that each stimulus was repeated an equal number of times in the two conditions. On Arch•PV trials, the stimulus was embedded in a continuous pulse of green light. The pulse began 50 ms prior to sound onset and lasted for a total of 150 ms. We used a fixed interstimulus interval (ISI) of 850 ms between the offset of the sound and the onset of the next stimulus event (either light pulse or sound alone). In a subset of cells, we tested a range of laser pulse parameters (e.g. longer or shorter pulse duration, pre-sound period, and/or ISI, by several hundred milliseconds). The effects of different pulse parameters were not discernibly different within cells (data not shown).
For each animal we obtained a coarse map of auditory cortex based on the tuning of the local field potential in the middle layers (200–400 μm). We saw no evidence of C57BL/6J age-related hearing loss in 2–4 month old animals: all mice had normal sound thresholds and tonotopy and had sites tuned to 40 kHz and higher. The cells included in our analysis were obtained in well-tuned regions of auditory cortex. Based on the tonotopic gradient, most of these neurons were located in A1, although a small fraction may have been in the contiguous well-tuned areas A2 or AAF (Guo et al., 2012). We determined the characteristic frequency (CF) and sound threshold for each neuron using a coarse frequency-intensity tuning curve (2–80 kHz at 4 frequencies/octave, 10–70 dB in 20 dB steps, 10 repetitions) followed by a custom tone array centered on our initial estimate of CF (typically 6 frequencies/octave, 10 dB intensity increments, ≥10 repetitions) in the absence of the laser. We then recorded a light-interleaved intensity-response function (IRF) (CF tones and WN, 0–70 dB in 5 dB steps, 20 paired repetitions), followed by a light-interleaved frequency tuning curve (FTC) (2–80 kHz tones presented at a single intensity, +20 dB above sound threshold; 6 frequencies/octave, 20 paired repetitions). We used the CF IRF (control) to determine the threshold of the neuron, which we defined as the lowest of three or more consecutive intensities that elicited a response above spontaneous baseline (mean + 2 SEM). We measured spontaneous spiking activity in the 100 ms prior to sound onset on control trials. Depending on recording duration, for some cells only a subset of these stimulus arrays were presented.
Blind patch recordings
Loose cell-attached and whole-cell recordings were obtained using standard blind patch techniques (DeWeese et al., 2003; Wehr and Zador, 2003). Signals were amplified with an Axopatch 200B amplifier and digitized at 10 kHz. The electrode traveled orthogonal to the cortical surface. Subpial recording depths were determined from micromanipulator travel. The cortical surface (depth 0 μm) was identified by the change in resistance when the electrode tip passed through the pia. The reversal in polarity of the sound-evoked local field potential at the L1–L2 boundary (~100 μm) (Christianson et al., 2011) served as an additional reference point, which we verified upon entering and withdrawing from each penetration. For extracellular cell-attached recordings (75 cells, depths 100–720 μm), patch pipettes contained an internal solution of 0.9% saline.
For voltage-clamp (whole-cell) recordings, patch pipettes (2–4 MΩ) contained a cesium-based internal solution (in mM: 140 Cs-gluconate, 10 HEPES, 2 MgCl2, 0.05 CaCl2, 4 MgATP, 0.4 NaGTP, 10 Na2 Phosphocreatine, 10 BAPTA, 4 TEA, 6 QX-314; pH 7.25, 290 mOsm) with a calculated reversal potential of −85 mV for Cl− conductances. Holding potentials were stepped (1 s ramp) to the reversal potential for excitatory currents (−3±11 mV) and inhibitory currents (−85±6mV); we determined the exact reversal potential online after obtaining a stable whole-cell configuration. Voltage pulses (10 mV, 10 pulses) were delivered on each voltage step to monitor series and input resistance. We did not use online series resistance compensation. To detect changes in input resistance due to laser illumination alone, we compared the median input resistance in the 50 ms prior to sound onset, with and without laser illumination. Differences in input resistance were small (on the order of ±1 MOhm for individual neurons) and there were no significant group-level differences at either holding potential (signed-rank test, n=23 recordings; EPSC holding potentials, n.s. p=0.72, d=0.02; IPSC holding potentials, n.s. p=0.98, d=0.02signed-rank). The cells included in this report showed sound-evoked currents >100 pA in magnitude at both holding potentials on control trials. The median series resistance across the duration of the recording was 30±17 MΩ, input resistance 88±31 MΩ (n=23 cells). Holding potentials were corrected offline for series error and a liquid junction potential of 12 mV.
For current-clamp (whole-cell) recordings, patch pipettes contained a potassium-based internal solution (in mM: 120 K-gluconate, 10 HEPES, 2 MgCl2, 0.05 CaCl2, 4 MgATP, 10 Na2 Phosphocreatine, 10 BAPTA; pH 7.25, 290 mOsm). The resting membrane potential across the duration of the recording was −67±9 mV (n=12 cells). Laser illumination alone did not have a significant effect on the resting membrane potential of PNs.
Two-photon targeted recordings
Two-photon targeted patching was performed with a movable objective microscope (Sutter Instruments) with a 16x/0.8NA objective (Nikon), coupled to a Mai-Tai HP Ti:Sapphire pulsed laser (Spectra Physics; ≤80 mW power). Images were acquired with ScanImage software (Pologruto et al., 2003).
The animal’s head was angled so that the microscope was focused on the surface of auditory cortex and subpial recording depths were determined from the z step of the objective. Recordings were performed in a small sound-attenuating chamber. Sounds were delivered from a free-field speaker facing the contralateral ear, which was calibrated at the beginning of the experiment as described above. The electrode penetrated cortex at 25° from horizontal. The optical fiber was aligned to the same angle using an independent micromanipulator. The fiber tip was positioned between the objective and the cortical surface, with the beam centered on the recording site.
Cell-attached recordings (n=32 cells total, depths 157–389 μm) were obtained with 4–6 MΩ patch pipettes containing Alexa 594 (50 μM; Molecular Probes) in the potassium-based internal solution used for current-clamp recordings. PV+ cells were targeted based on the expression of the Arch-GFP fusion protein (Figure 4) and/or tdTomato (Figure 5). Recorded neurons filled slowly with dye over the course of the recording, or with brief current pulses afterwards. We obtained “control” recordings from GFP-/tdTomato-PNs in the same animals using the shadow-patching technique (Kitamura et al., 2008), which were typically located within 100 μm of recorded PV+ cells. Control PNs showed significant changes in spiking activity on laser trials, similar to those described in Figures 7–8 (data not shown).
Tetrode recordings
For tetrode recordings, mice were loosely restrained in a perforated plastic tube (inner diameter 35 mm, tube thickness 1.5 mm) affixed to a flat base, with the head fixed in a forward-facing position. An open slot along the top provided access to the recording array and optical fiber. The fiber (diameter 0.2 mm) was calibrated to 10 mW total power at the tip; we have found that this intensity reliably illuminates within, but not beyond, auditory cortex (Weible et al., 2014b). Tetrode signals were acquired with 32-channel RHD2000 hardware (Intan Technologies) and Open Ephys software (www.open-ephys.org). Signals were band-pass filtered at 0.6–6 kHz and digitized at 30 kHz. A minimum threshold of 50 μV was used for collection of spiking activity. Single-unit spike sorting was performed off-line manually using the spike sorting packages Simple_Clust (J. Voigts, MIT) and MClust (A.D. Redish, Univ. of Minnesota).
We assessed the tuning of recording sites using a coarse frequency-intensity tuning curve as described above. If the site was not tuned or no well-isolated neurons were present, the array was advanced 45–90 μm and the mouse was returned to its home cage for ≥2 hours. Otherwise, we recorded responses to a light-interleaved CF and/or WN IRF (0–70 dB; CF estimated from the coarse tuning curve). We recorded a sample of 50 well-isolated neurons on tetrodes with well-tuned LFPs; of these, 33 neurons met our inclusion criteria of responding above spontaneous baseline for at least half of intensities presented. At the end of the awake recording session, mice were removed from the tube and anesthetized with the ketamine cocktail used for acute recordings. The mouse was then placed on a heating pad in the same orientation relative to the speaker, and we recorded responses to the same set of stimuli to verify that effects of illumination were comparable to those we observed in our single-neuron recordings in the acute preparation. At the end of the recording session, the array was advanced ~90 μm and the animal was returned to its home cage. We reconstructed the paths of the tetrodes through auditory cortex post-mortem using standard histological techniques (Weible et al., 2014b).
Slice recordings
Animals were anesthetized with isoflurane and decapitated. The brain was rapidly extracted into ice-cold cutting artificial cerebral spinal fluid solution (ACSF) containing (in mM): 90 N-methyl-D-Glucamine,110 HCl, 20 HEPES, 25 NaHCO3, 25 glucose, 3 KCl, 1.1 NaH2PO4, 0.5 CaCl2, 10 MgCl2, 3 pyruvic acid, 10 ascorbic acid, bubbled with 95% O2 / 5% CO2 (Karnani et al., 2016). Coronal sections containing auditory cortex were cut at 300 μm thickness with a vibratome (VT1200S, Leica) in ice-cold cutting ACSF. Immediately after cutting, slices were incubated in 37°C cutting ACSF for 5–15 min, then transferred to 37°C recording ACSF for 45 min, followed by storage at room temperature in recording ACSF. Recording ACSF contained (in mM): 130 NaCl, 2.1 KCl, 1.2 KH2PO4, 3 Na-HEPES, 10 glucose, 20 NaHCO3, 2 Na-pyruvate, 2 CaCl2, 1 MgSO4, 0.4 Na-ascorbate, bubbled with 5% CO2 / 95% O2 (300–305 mOsm). Slices were transferred to submerged recording chamber and superfused with room temperature ACSF at 3 ml/min. In all experiments, synaptic responses were blocked by bath application of 5 μM NBQX (AMPAR antagonist) and 5 μM SR-95531 (GABAAR antagonist). Slices were viewed using infrared Dodt contrast and a 60X water-immersion objective (LUMPlanFL, Olympus) and camera (IR-1000, Dage-MTI) on a fixed stage microscope (Axioskop 2 FS Plus, Zeiss). PV+ cells were identified by their GFP fluorescence. All cells recorded were filled with 10 μM Alexa Fluor 594 hydrazide sodium salt (A10438, Molecular Probes) in order to verify their morphology. Pipettes were pulled from thin-walled borosilicate glass capillaries (1.2 mm OD, WPI) to a tip resistance of 5–8 MΩ. The internal pipette solution contained (in mM): 113 K-gluconate, 9 HEPES, 4.5 MgCl2, 0.1 EGTA, 14 Tris-phosphocreatine, 4 Na2-ATP, 0.3 Tris-GFP, with osmolality adjusted to ~ 290 mOsm with sucrose and pH adjusted to pH 7.3 with KOH. Reported voltages are corrected for a −10 mV liquid junction potential. Whole-cell recordings were amplified (10X), low-pass filtered (10 kHz Bessel, Multiclamp 700B, Molecular Devices) and digitized using pClamp software (50 kHz, Digidata 1550, Molecular Devices). Series resistance was compensated with correction 20–40% and prediction 60–70%, bandwidth 2–2.5 kHz. Cells were voltage-clamped at −70 mV. Arch was activated using full-field green LED light delivered through the objective using a TRITC filter set. Light irradiance was 0.95 mW/mm2 at the surface of the slice.
Network Models
Recurrent network model
We used a model described in detail previously (Ahmadian et al., 2013). Briefly, the network consisted of pools of interconnected excitatory neurons (E) and inhibitory neurons (I), whose average firing rates were represented as continuous variables rE and rI. The firing rate of the excitatory pool was described by rE = g(WEE•rE − WIE•rI + Istim), where WEE and WIE are positive numbers representing the strength of connections E→E and I→E, and g(x) is a non-saturating power law g(x) = 3x3. Here, the positive input to the network (IStim) was a current step with magnitude +0.5, duration 800 ms. The inhibitory pool received an additional current IArch to mimic the suppressive effects of Arch, but was otherwise identical: rI = g(WEI•rE − WII•rI + Istim + IArch). The current IArch began 200 ms before the onset of the stimulus, and ended 200 ms after it (total duration 1200 ms, magnitude −0.13, except as indicated in Figure 6g). The only parameter that we varied was a single value for both excitatory weights WEE and WEI. Weights WII, WIE were fixed at 1.
Feedforward network model
PV+ cells and PNs were modeled as identical integrate-and-fire neurons (passive properties: C=750 pF, grest=20 nS (50 MΩ), Erest=−65 mV,τ, τm =37.5 ms). Excitatory and inhibitory synaptic inputs were modeled as conductances, ge and gi; excitatory battery=0 mV, inhibitory battery=−80 mV. A spike was emitted when the membrane potential reached a fixed threshold +20 mV above rest, and the membrane potential was reset to its resting value. The membrane potential V(t) of each cell was determined by the equation:
Excitatory input to the first stage of the network (ge to PN 1 and PV+ 1) was an alpha function with exponent a=0.1, total conductance 0.2 nS, half-width at half-height (HWHH) 24.3 ms. In subsequent layers, PNs received excitatory input from the PN in the previous layer (ge), and inhibitory input from the PV+ cell in the same layer (gi). PV+ cells received the same excitatory input as the PN, and no inhibitory input. On Arch•PV trials, PV+ cells received a step current IArch (beginning 50 ms prior to external input) with a starting value of −0.5 nA to mimic the ~15–20 mV hyperpolarization seen in our intracellular recordings (Figure S1). Increasing the strength of the hyperpolarizing current did not change the behavior of the model (−0.6 to −1.8 nA, Figure 6c–d). To convert spiking responses into postsynaptic conductances, presynaptic spike times (from the previous layer) were convolved with an alpha function (exponent a=0.2, 0.1 nS total conductance, HWHH 1.2 ms). Inhibitory rebalancing was robust to changes in model parameters across orders of magnitude. Specifically, we varied C from 0.1–1 nF, grest from 5–50 MΩ, alpha function exponents from 0.05–0.5, and total conductance from 0.02–0.27 nS. We observed rebalancing in all cases except those in which total conductance was too small (<0.05 nS) for spiking activity to propagate through the network. Changes in the strength of feedforward input or passive membrane properties affected the timing and magnitude of model neuron responses, but had no effect on the qualitative behavior of the model.
QUANTIFICATION AND STATISTICAL ANALYSIS
Data Analysis
Synaptic currents
Synaptic currents were computed by subtracting the holding current measured in the 50 ms window prior to sound onset. Many PNs showed an increase in the frequency of spontaneous synaptic events during illumination (before sound onset). To isolate changes in sound-evoked currents, we culled trials with spontaneous fluctuations overlapping with sound onset. Trials were excluded if the synaptic current crossed a threshold value in the 20 ms leading up to sound onset. Because the level of spontaneous activity varied across PNs, we determined the threshold for exclusion on a cell-by-cell basis using an automated procedure. The threshold value was determined from control trials, and applied to both control and Arch•PV trials. To determine threshold, we measured the peak current in the 300 ms window after sound onset, for all sound stimuli and repetitions, and then used the 10th percentile of this distribution as the exclusion threshold (in pA). We found that this choice of signal-to-noise ratio optimally discriminated between sound-evoked and spontaneous currents. The threshold was computed separately for each holding potential. Within individual cells, a similar fraction of EPSC and IPSC trials were excluded in both the laser and control conditions. In other words, the frequency of spontaneous EPSCs and IPSCs was approximately equal under control conditions, and increased by about the same amount on Arch•PV trials.
After this culling procedure, 9±5 repetitions of each stimulus remained in each laser condition, at each of two holding potentials (16±9% of control trials discarded; 24±11% of laser trials discarded; n=23 cells). Including all trials did not change the significance of any of our results, but led to an overestimate of the change in sound-evoked current in some cells. Culled trials were excluded from further analyses. Peak amplitude and integrated charge (Figure 2d–f, 3a) were calculated for individual trials. E-I timing and ratio (Figure 3c,d) were computed from the trial-averaged currents. For comparisons at the group level, we used the median value across the “best stimuli” for each cell, where best stimuli were defined as the 75% that evoked the largest summed responses on control trials (EPSC+IPSC amplitudes). Using other values, e.g. the single best stimulus or the median across all stimuli, did not change the results.
Membrane potential
Consistent with the increase in spontaneous EPSCs and IPSCs, most neurons showed a modest increase in spontaneous PSPs in response to laser illumination alone. To isolate changes in sound-evoked potentials, we culled trials with spontaneous fluctuations overlapping with sound onset. The process was similar to that described above for currents. A trial was excluded if the membrane potential exceeded a threshold value in a 30 ms window centered on sound onset. The threshold value (in mV) was set as the 15th percentile of the distribution of peak values in the 300 ms window after sound onset. We removed spikes for this step, as described in an earlier report (Scholl et al., 2008). After culling, we retained 34±8 trials for each stimulus, in each of the two laser conditions (5±3% of control trials discarded; 9±5% of laser trials discarded; n=12 cells). Including all trials did not change the significance of our results.
For our spike latency analysis (Figure S6), we computed the inflection point (to) and slope of sound-evoked PSPs in the 100 ms period after sound onset. We limited our analysis to trials with PSPs ≥10 mV to ensure robust estimates of inflection point and slope. Including all trials did not change the significance of our results. We measured the inflection point to at the intersection of two best-fit lines: one to the first 0–25 ms of the response, and a second to the rising phase from +2 to +10 mV above resting membrane potential. We measured the slope of the response (ΔmV/Δms) from to to +10 mV. Varying these values over a reasonable range (0–15 mV) did not affect the significance of our results. We measured the duration of the response above a fixed threshold, equal to the half-maximum amplitude of the control PSP (averaged across trials).
Spiking responses
Extracellular spike width (Figure 4c) was computed from the average of 100 spikes as described previously (Moore and Wehr, 2013). Spikes were extracted from the high-pass (300 Hz) filtered trace using a fixed voltage threshold ≥1 mV. Sound-evoked spikes were analyzed in the 100 ms period after sound onset. “Best stimuli” were determined from the control response (spikes/trial). Occasionally, we encountered neurons that rarely spiked on control trials (less than approximately 0.2 spikes/trial for any stimulus), but spiked reliably on Arch•PV trials (similar to the cell in Figure 7a; n=8/73 PNs). The intensity response functions (IRFs) for these cells were not included in the spike latency or dynamic range analysis (Figures 7 and S5) because there was no control response to compare. Instead, we used the spiking response on Arch•PV trials to compute best stimulus for these cells.
To compute dynamic range (Figure 7f–g) we separately normalized the control and Arch•PV IRFs for each neuron and fit each curve with a generalized logistic function for sigmoidal curves. If the response could not be fit in one or both experimental conditions (corrected RMSE>0.5 spikes), then that cell was excluded from the dynamic range analysis (8/73 cells recorded in anesthetized animals, 4/33 cells recorded in awake animals). We computed the dynamic range from the fit as the decibel range over which the response rose from 20% to 80% of maximum. The fits described the control and Arch•PV IRFs equally well (corrected RMSE: Arch•PV 0.18±0.07, control 0.20±0.10; rank-sum, n.s. p=0.42, n=94 cells in total). We computed shuffle-corrected stimulus-specific information at best intensity (as determined on control trials) as described previously (Montgomery and Wehr, 2010).
These procedures were identical for PV+ neurons, with the following exceptions. Because fast-spiking PV+ cells have high spontaneous firing rates (Figure 4c) we analyzed sound-evoked spiking in a variable window (rather than a fixed window of 100 ms as we did for PNs). This window was selected using an automated procedure to capture sound-evoked spikes in both conditions: a Gaussian curve was fit to the distribution of all post-stimulus spike times across all control and Arch•PV trials, and the window duration was given by the 90th percentile of this distribution (≤100 ms). This did not affect the significance of our results (i.e. compared to a fixed 100 ms window) but did a better job of discriminating sound-evoked from spontaneous spiking for individual cells. Similarly, because of high spontaneous rates in PV+ cells, we used the median spike time as a measure of response latency instead of the timing of the first spike.
Statistics
Spike counts, currents, and voltage traces are plotted as mean ± SEM, unless otherwise indicated in the figure legends. We used the non-parametric Wilcoxon rank-sum test for statistical comparisons at the group level (across cells), because the data were rarely both normally distributed (Shapiro-Wilk test) and of equal variance (Levene’s test). Accordingly, we report the median ± symmetric interquartile range (IQR) as measures of central tendency in the text. All tests are two-tailed, unless otherwise indicated in the text. We used the non-parametric measure of effect size d (Cliff’s delta) (Cliff, 1993), which is a measure of the separation between two distributions — ranging from 0 (indistinguishable distributions) to ±1 (completely separable distributions); we report the absolute value of d except in Figure 7e and S8c. To test for significant effects within cells (i.e., across trials, stimuli, and laser condition) we used the Skillings-Mack test, a non-parametric alternative to the ANOVA (Skillings and Mack, 1981). See Table S2 for a list of statistical tests reported in the main text.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Mouse anti-parvalbumin | Millipore | Catalog # MAB1572 |
| Alexa Fluor 546 goat anti-mouse | Invitrogen | Catalog # A11003 |
| Alexa Fluor 488 goat anti-mouse | Invitrogen | Catalog # A21121 |
| Bacterial and Virus Strains | ||
| AAV-FLEX-Arch-GFP | Addgene | Addgene plasmid # 22222 |
| Addgene 26,966 | UNC Vector Core | Addgene plasmid # 26966 |
| Biological Samples | ||
| Chemicals, Peptides, and Recombinant Proteins | ||
| Critical Commercial Assays | ||
| Deposited Data | ||
| Experimental Models: Cell Lines | ||
| Experimental Models: Organisms/Strains | ||
| Pvalb-Cre (mouse) | Jackson Laboratory | Catalog # 008069, RRID IMSR_JAX:008069 |
| Arch-GFP (mouse) | Jackson Laboratory | Catalog # 012735, RRID IMSR_JAX:012735 |
| Ai9-tdTomato (mouse) | Jackson Laboratory | Catalog # 007909, RRID IMSR_JAX:007909 |
| Oligonucleotides | ||
| Recombinant DNA | ||
| Software and Algorithms | ||
| ScanImage | Vidrio Technologies (Pologruto et al., 2003) | http://scanimage.vidriotechnologies.com |
| Open Ephys | Open-ephys | www.open-ephys.org |
| Simple_Clust | J. Voigts, MIT | https://github.com/open-ephys/simpleclust |
| Mclust | A.D. Redish, Univ. of Minnesota | http://redishlab.neuroscience.umn.edu/MClust/MClust.html |
| Other | ||
Supplementary Material
Table S2: Included as a separate file: Table_S2.xlsx “Table S2 (related to STAR Methods) – Summary of statistical tests reported in the main text”
Acknowledgments
We thank Cris Niell and Joe Wekselblatt for help with 2-photon microscopy. This work was supported by NIH R01DC015828, NIH DC014878, and NIH R01DC004450.
Footnotes
AUTHOR CONTRIBUTIONS
A.K.M. designed, conducted, and analyzed experiments.
A.K.M. and M.W. designed and analyzed experiments and models, and wrote the paper.
A.P.W. conducted tetrode experiments.
T.S.B., M.W., & L.O.T. designed, conducted and analyzed in vitro experiments and helped write the paper.
DECLARATION OF INTERESTS
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ahmadian Y, Rubin DB, Miller KD. Analysis of the stabilized supralinear network. Neural Comput. 2013;25:1994–2037. doi: 10.1162/NECO_a_00472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahrens S, Jaramillo S, Yu K, Ghosh S, Hwang GR, Paik R, Lai C, He M, Huang ZJ, Li B. ErbB4 regulation of a thalamic reticular nucleus circuit for sensory selection. Nature neuroscience. 2015;18:104–111. doi: 10.1038/nn.3897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aizenberg M, Mwilambwe-Tshilobo L, Briguglio JJ, Natan RG, Geffen MN. Bidirectional Regulation of Innate and Learned Behaviors That Rely on Frequency Discrimination by Cortical Inhibitory Neurons. PLoS Biol. 2015;13:e1002308. doi: 10.1371/journal.pbio.1002308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson LA, Christianson GB, Linden JF. Mouse auditory cortex differs from visual and somatosensory cortices in the laminar distribution of cytochrome oxidase and acetylcholinesterase. Brain Res. 2009;1252:130–142. doi: 10.1016/j.brainres.2008.11.037. [DOI] [PubMed] [Google Scholar]
- Anderson LA, Linden JF. Physiological differences between histologically defined subdivisions in the mouse auditory thalamus. Hearing research. 2011;274:48–60. doi: 10.1016/j.heares.2010.12.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atallah BV, Bruns W, Carandini M, Scanziani M. Parvalbumin-expressing interneurons linearly transform cortical responses to visual stimuli. Neuron. 2012;73:159–170. doi: 10.1016/j.neuron.2011.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayaz A, Chance FS. Gain modulation of neuronal responses by subtractive and divisive mechanisms of inhibition. J Neurophysiol. 2009;101:958–968. doi: 10.1152/jn.90547.2008. [DOI] [PubMed] [Google Scholar]
- Butts DA. How much information is associated with a particular stimulus? Network. 2003;14:177–187. [PubMed] [Google Scholar]
- Christianson GB, Sahani M, Linden JF. Depth-dependent temporal response properties in core auditory cortex. J Neurosci. 2011;31:12837–12848. doi: 10.1523/JNEUROSCI.2863-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cliff N. Dominance statistics: Ordinal analyses to answer ordinal questions. Psychological Bulletin. 1993;114:494–509. [Google Scholar]
- Cruikshank SJ, Urabe H, Nurmikko AV, Connors BW. Pathway-specific feedforward circuits between thalamus and neocortex revealed by selective optical stimulation of axons. Neuron. 2010;65:230–245. doi: 10.1016/j.neuron.2009.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeWeese MR, Wehr M, Zador AM. Binary spiking in auditory cortex. J Neurosci. 2003;23:7940–7949. doi: 10.1523/JNEUROSCI.23-21-07940.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas RJ, Martin KA. Inhibition in cortical circuits. Curr Biol. 2009;19:R398–402. doi: 10.1016/j.cub.2009.03.003. [DOI] [PubMed] [Google Scholar]
- El-Boustani S, Sur M. Response-dependent dynamics of cell-specific inhibition in cortical networks in vivo. Nat Commun. 2014;5:5689. doi: 10.1038/ncomms6689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Froemke RC, Merzenich MM, Schreiner CE. A synaptic memory trace for cortical receptive field plasticity. Nature. 2007;450:425–429. doi: 10.1038/nature06289. [DOI] [PubMed] [Google Scholar]
- Guo W, Chambers AR, Darrow KN, Hancock KE, Shinn-Cunningham BG, Polley DB. Robustness of cortical topography across fields, laminae, anesthetic states, and neurophysiological signal types. J Neurosci. 2012;32:9159–9172. doi: 10.1523/JNEUROSCI.0065-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hippenmeyer S, Vrieseling E, Sigrist M, Portmann T, Laengle C, Ladle DR, Arber S. A developmental switch in the response of DRG neurons to ETS transcription factor signaling. PLoS Biol. 2005;3:e159. doi: 10.1371/journal.pbio.0030159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirsch JA, Alonso JM, Reid RC, Martinez LM. Synaptic integration in striate cortical simple cells. J Neurosci. 1998;18:9517–9528. doi: 10.1523/JNEUROSCI.18-22-09517.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofer SB, Ko H, Pichler B, Vogelstein J, Ros H, Zeng H, Lein E, Lesica NA, Mrsic-Flogel TD. Differential connectivity and response dynamics of excitatory and inhibitory neurons in visual cortex. Nat Neurosci. 2011;14:1045–1052. doi: 10.1038/nn.2876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hromadka T, Deweese MR, Zador AM. Sparse representation of sounds in the unanesthetized auditory cortex. PLoS Biol. 2008;6:e16. doi: 10.1371/journal.pbio.0060016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isaacson JS, Scanziani M. How inhibition shapes cortical activity. Neuron. 2011;72:231–243. doi: 10.1016/j.neuron.2011.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karnani MM, Agetsuma M, Yuste R. A blanket of inhibition: functional inferences from dense inhibitory connectivity. Curr Opin Neurobiol. 2014;26:96–102. doi: 10.1016/j.conb.2013.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karnani MM, Jackson J, Ayzenshtat I, Tucciarone J, Manoocheri K, Snider WG, Yuste R. Cooperative Subnetworks of Molecularly Similar Interneurons in Mouse Neocortex. Neuron. 2016;90:86–100. doi: 10.1016/j.neuron.2016.02.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato HK, Asinof SK, Isaacson JS. Network-Level Control of Frequency Tuning in Auditory Cortex. Neuron. 2017;95:412–423. e414. doi: 10.1016/j.neuron.2017.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepecs A, Fishell G. Interneuron cell types are fit to function. Nature. 2014;505:318–326. doi: 10.1038/nature12983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitamura K, Judkewitz B, Kano M, Denk W, Häusser M. Targeted patch-clamp recordings and single-cell electroporation of unlabeled neurons in vivo. Nat Methods. 2008;5:61–67. doi: 10.1038/nmeth1150. [DOI] [PubMed] [Google Scholar]
- Kubota Y, Karube F, Nomura M, Kawaguchi Y. The Diversity of Cortical Inhibitory Synapses. Front Neural Circuits. 2016;10:27. doi: 10.3389/fncir.2016.00027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhlman SJ, Huang ZJ. High-resolution labeling and functional manipulation of specific neuron types in mouse brain by Cre-activated viral gene expression. PLoS One. 2008;3:e2005. doi: 10.1371/journal.pone.0002005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar A, Vlachos I, Aertsen A, Boucsein C. Challenges of understanding brain function by selective modulation of neuronal subpopulations. Trends Neurosci. 2013;36:579–586. doi: 10.1016/j.tins.2013.06.005. [DOI] [PubMed] [Google Scholar]
- Kyweriga M, Stewart W, Cahill C, Wehr M. Synaptic mechanisms underlying interaural level difference selectivity in rat auditory cortex. J Neurophysiol. 2014;112:2561–2571. doi: 10.1152/jn.00389.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Kwan AC, Dan Y. Interneuron subtypes and orientation tuning. Nature. 2014;508:E1–2. doi: 10.1038/nature13128. [DOI] [PubMed] [Google Scholar]
- Lee SH, Kwan AC, Zhang S, Phoumthipphavong V, Flannery JG, Masmanidis SC, Taniguchi H, Huang ZJ, Zhang F, Boyden ES, et al. Activation of specific interneurons improves V1 feature selectivity and visual perception. Nature. 2012;488:379–383. doi: 10.1038/nature11312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Letzkus JJ, Wolff SB, Meyer EM, Tovote P, Courtin J, Herry C, Luthi A. A disinhibitory microcircuit for associative fear learning in the auditory cortex. Nature. 2011;480:331–335. doi: 10.1038/nature10674. [DOI] [PubMed] [Google Scholar]
- Levy RB, Reyes AD. Spatial profile of excitatory and inhibitory synaptic connectivity in mouse primary auditory cortex. J Neurosci. 2012;32:5609–5619. doi: 10.1523/JNEUROSCI.5158-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madisen L, Mao T, Koch H, Zhuo JM, Berenyi A, Fujisawa S, Hsu YW, Garcia AJ, 3rd, Gu X, Zanella S, et al. A toolbox of Cre-dependent optogenetic transgenic mice for light-induced activation and silencing. Nat Neurosci. 2012;15:793–802. doi: 10.1038/nn.3078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahn M, Prigge M, Ron S, Levy R, Yizhar O. Biophysical constraints of optogenetic inhibition at presynaptic terminals. Nature Neuroscience. 2016;19:554. doi: 10.1038/nn.4266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marín O. Interneuron dysfunction in psychiatric disorders. Nat Rev Neurosci. 2012;13:107–120. doi: 10.1038/nrn3155. [DOI] [PubMed] [Google Scholar]
- Montgomery N, Wehr M. Auditory cortical neurons convey maximal stimulus-specific information at their best frequency. J Neurosci. 2010;30:13362–13366. doi: 10.1523/JNEUROSCI.2899-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore AK, Wehr M. Parvalbumin-expressing inhibitory interneurons in auditory cortex are well-tuned for frequency. J Neurosci. 2013;33:13713–13723. doi: 10.1523/JNEUROSCI.0663-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. 1996;381:607–609. doi: 10.1038/381607a0. [DOI] [PubMed] [Google Scholar]
- Oswald AM, Doiron B, Rinzel J, Reyes AD. Spatial profile and differential recruitment of GABAB modulate oscillatory activity in auditory cortex. J Neurosci. 2009;29:10321–10334. doi: 10.1523/JNEUROSCI.1703-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otchy TM, Wolff SB, Rhee JY, Pehlevan C, Kawai R, Kempf A, Gobes SM, Ölveczky BP. Acute off-target effects of neural circuit manipulations. Nature. 2015;528:358–363. doi: 10.1038/nature16442. [DOI] [PubMed] [Google Scholar]
- Ozeki H, Finn IM, Schaffer ES, Miller KD, Ferster D. Inhibitory stabilization of the cortical network underlies visual surround suppression. Neuron. 2009;62:578–592. doi: 10.1016/j.neuron.2009.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Packer AM, Yuste R. Dense, Unspecific Connectivity of Neocortical Parvalbumin-Positive Interneurons: A Canonical Microcircuit for Inhibition? The Journal of Neuroscience. 2011;31:13260. doi: 10.1523/JNEUROSCI.3131-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeffer CK, Xue M, He M, Huang ZJ, Scanziani M. Inhibition of inhibition in visual cortex: the logic of connections between molecularly distinct interneurons. Nat Neurosci. 2013;16:1068–1076. doi: 10.1038/nn.3446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips EA, Hasenstaub AR. Asymmetric effects of activating and inactivating cortical interneurons. Elife. 2016:5. doi: 10.7554/eLife.18383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pi HJ, Hangya B, Kvitsiani D, Sanders JI, Huang ZJ, Kepecs A. Cortical interneurons that specialize in disinhibitory control. Nature. 2013 doi: 10.1038/nature12676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinault D. The thalamic reticular nucleus: structure, function and concept. Brain Research Reviews. 2004;46:1–31. doi: 10.1016/j.brainresrev.2004.04.008. [DOI] [PubMed] [Google Scholar]
- Pologruto TA, Sabatini BL, Svoboda K. ScanImage: flexible software for operating laser scanning microscopes. Biomed Eng Online. 2003;2:13. doi: 10.1186/1475-925X-2-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouille F, Marin-Burgin A, Adesnik H, Atallah BV, Scanziani M. Input normalization by global feedforward inhibition expands cortical dynamic range. Nat Neurosci. 2009;12:1577–1585. doi: 10.1038/nn.2441. [DOI] [PubMed] [Google Scholar]
- Pouille F, Scanziani M. Enforcement of temporal fidelity in pyramidal cells by somatic feed-forward inhibition. Science. 2001;293:1159–1163. doi: 10.1126/science.1060342. [DOI] [PubMed] [Google Scholar]
- Rao RP, Ballard DH. Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat Neurosci. 1999;2:79–87. doi: 10.1038/4580. [DOI] [PubMed] [Google Scholar]
- Runyan CA, Sur M. Response selectivity is correlated to dendritic structure in parvalbumin-expressing inhibitory neurons in visual cortex. J Neurosci. 2013;33:11724–11733. doi: 10.1523/JNEUROSCI.2196-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholl B, Gao X, Wehr M. Level dependence of contextual modulation in auditory cortex. J Neurophysiol. 2008;99:1616–1627. doi: 10.1152/jn.01172.2007. [DOI] [PubMed] [Google Scholar]
- Scholl B, Pattadkal JJ, Dilly GA, Priebe NJ, Zemelman BV. Local Integration Accounts for Weak Selectivity of Mouse Neocortical Parvalbumin Interneurons. Neuron. 2015;87:424–436. doi: 10.1016/j.neuron.2015.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seybold BA, Phillips EA, Schreiner CE, Hasenstaub AR. Inhibitory Actions Unified by Network Integration. Neuron. 2015;87:1181–1192. doi: 10.1016/j.neuron.2015.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skillings JH, Mack GA. On the Use of a Friedman-Type Statistic in Balanced and Unbalanced Block Designs. Technometrics, Taylor & Francis, Ltd; 1981. pp. 171–177. [Google Scholar]
- Swadlow HA. Fast-spike interneurons and feedforward inhibition in awake sensory neocortex. Cereb Cortex. 2002;13:25–32. doi: 10.1093/cercor/13.1.25. [DOI] [PubMed] [Google Scholar]
- Tsodyks MV, Skaggs WE, Sejnowski TJ, McNaughton BL. Paradoxical effects of external modulation of inhibitory interneurons. J Neurosci. 1997;17:4382–4388. doi: 10.1523/JNEUROSCI.17-11-04382.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turrigiano G. Too many cooks? Intrinsic and synaptic homeostatic mechanisms in cortical circuit refinement. Annu Rev Neurosci. 2011;34:89–103. doi: 10.1146/annurev-neuro-060909-153238. [DOI] [PubMed] [Google Scholar]
- Wehr M, Zador AM. Balanced inhibition underlies tuning and sharpens spike timing in auditory cortex. Nature. 2003;426:442–446. doi: 10.1038/nature02116. [DOI] [PubMed] [Google Scholar]
- Weible AP, Liu C, Niell CM, Wehr M. Auditory cortex is required for fear potentiation of gap detection. J Neurosci. 2014a;34:15437–15445. doi: 10.1523/JNEUROSCI.3408-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weible AP, Moore AK, Liu C, DeBlander L, Wu H, Kentros C, Wehr M. Perceptual gap detection is mediated by gap termination responses in auditory cortex. Curr Biol. 2014b;24:1447–1455. doi: 10.1016/j.cub.2014.05.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson NR, Runyan CA, Wang FL, Sur M. Division and subtraction by distinct cortical inhibitory networks in vivo. Nature. 2012;488:343–348. doi: 10.1038/nature11347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu X, Roby KD, Callaway EM. Immunochemical characterization of inhibitory mouse cortical neurons: three chemically distinct classes of inhibitory cells. J Comp Neurol. 2009;518:389–404. doi: 10.1002/cne.22229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue M, Atallah BV, Scanziani M. Equalizing excitation-inhibition ratios across visual cortical neurons. Nature. 2014;511:596–600. doi: 10.1038/nature13321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y, DeWeese MR, Otazu GH, Zador AM. Millisecond-scale differences in neural activity in auditory cortex can drive decisions. Nat Neurosci. 2008;11:1262–1263. doi: 10.1038/nn.2211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshimura Y, Callaway EM. Fine-scale specificity of cortical networks depends on inhibitory cell type and connectivity. Nat Neurosci. 2005;8:1552–1559. doi: 10.1038/nn1565. [DOI] [PubMed] [Google Scholar]
- Zhu Y, Qiao W, Liu K, Zhong H, Yao H. Control of response reliability by parvalbumin-expressing interneurons in visual cortex. Nat Commun. 2015;6:6802. doi: 10.1038/ncomms7802. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S2: Included as a separate file: Table_S2.xlsx “Table S2 (related to STAR Methods) – Summary of statistical tests reported in the main text”