Approaching Ultimate Intrinsic SAR in RF shimming using high-permittivity materials at 7 Tesla

Abstract

Purpose

To evaluate the effect of integrated high-permittivity materials (HPMs) on excitation homogeneity and global SAR for transmit arrays at 7 Tesla.

Methods

A rapid electrodynamic simulation framework was employed to calculate L-curves associated with excitation of a uniform 2D profile in a dielectric sphere. We used Ultimate Intrinsic SAR as an absolute performance reference to compare different transmit arrays in the presence and absence of a layer of HPM. We investigated the optimal permittivity for the HPM as a function of its thickness, the sample size, and the number of array elements.

Results

Adding a layer of HPM can improve the performance of a 24-element array to match that of a 48-element array without HPM, whereas a 48-element array with HPM can perform as well as a 64-element array without HPM. Optimal relative permittivity values changed based on sample and coil geometry, but were always within a range obtainable with readily available materials (ε_r =100–200).

Conclusions

Integration of HPMs could be a practical method to improve RF shimming performance, alternative to increasing the number of coils. The proposed simulation framework could be used to explore the design of novel transmit arrays for head imaging at ultra-high field strength.

INTRODUCTION

Magnetic resonance (MR) imaging at ultra-high (≥ 7T) static magnetic field strength (B₀) can provide higher signal-to-noise ratio (SNR) compared to clinical scanners that operate at lower field strength [1–4], potentially improving clinical and investigative power [5–8]. However, the shortening of the wavelength in tissues at higher field strengths results in inhomogeneity of the radiofrequency (RF) transmit (B₁⁺) and receive (B₁⁻) fields, which limits the diagnostic utility of the MR images [3, 9–13]. B₁⁺ inhomogeneity can be addressed by using transmit arrays and applying RF shimming or parallel transmission techniques [14–19]. Although these techniques can be optimized to also reduce global Specific Absorption Rate (SAR), which increases approximately as the square of B₀ [20, 21], they present an additional safety concern, since constructive interferences between the electric fields from multiple transmit coils can result in amplifications of local SAR that may be difficult to predict [17, 22].

Local and global SAR depend on the pulse sequence design, the RF pulse shape, amplitude, and duration, the particular transmit approach (e.g., parallel transmission), and the RF coil design. For a given excitation, the SAR varies based on the coil structure and its position relative to the excitation plane. In order to accurately evaluate this dependence, Guerin et al. [23] developed an L-curves [24] optimization approach for parallel transmission. In this method, the constraint on excitation fidelity for a given parallel transmit excitation is slowly relaxed, and the minimal possible SAR generated by the resulting series of excitations is plotted as a function of the RMSE with respect to the desired excitation profile. This procedure can then be repeated for different excitation plane positions, parallel transmit techniques, or coil designs. L-curves therefore enable the comparison of a variety of parallel transmit pulse designs for a given set of coil geometries and desired excitations [25].

However, the L-curves method only measures relative coil performance. Lattanzi et al. [26, 27] introduced the Ultimate Intrinsic SAR (UISAR), which is the theoretically smallest global SAR for a desired excitation profile in a given sample, as an absolute reference for coil design optimization for RF shimming or parallel transmission. Since UISAR varies based on the homogeneity requirements of the pulse design, the relationship between UISAR and the corresponding excitation homogeneity (i.e., the L-curve for the ideal transmit array) can be used as an absolute reference against which to compare L-curves of actual coil designs.

High-permittivity, low-conductivity materials (HPMs) placed between RF coils and the subject have been proposed as a method for varying the spatial distribution of the B₁⁺ field, independent of RF shimming or parallel transmission, to improve field homogeneity [28–30] or enhance SNR in targeted regions [31–33]. The use of HPMs in combination with RF coils has also been shown to reduce overall required input RF power in transmission [30, 32, 34, 35] and improve coil sensitivity at a variety of field strengths in reception [29, 30, 35], both in experiments and numerical simulations.

In this work we explored how the performance of transmit head arrays could be affected by using HPMs to fill the space between the coils and the sample. In fact, transmit-receive arrays are generally designed so that the coil elements are at a distance greater than or equal to 1 cm from the subject, separated by low-conductivity material, such as plastic and air, placed between the conductive elements and the imaging subject to avoid exposure to the strong electric fields directly surrounding capacitors. Utilizing an L-curve analysis and UISAR as a reference, we investigated the optimal placement, thickness, and relative permittivity of HPMs in order to approach the highest possible RF shimming performance.

METHODS

Ultimate Intrinsic SAR and array global SAR calculations

UISAR and the global SAR of finite arrays of circular coils surrounding a uniform spherical sample were calculated with the dyadic Green’s function (DGF) simulation framework [26]. In particular, we used a recent extension of this formalism [36, 37], which enables full-wave electrodynamic simulations in multi-layered spherical geometries [38]. In DGF, a complete basis of current modes is defined on a closed surface at a distance from the sample, and used as a hypothetical infinite coil array to calculate UISAR. Realistic loop coils can be modeled as weighted combination of the same basis set [Figure 1]. To ensure convergence of the UISAR calculations, we employed a total of 8712 current modes, including both divergence-free and curl-free current types.

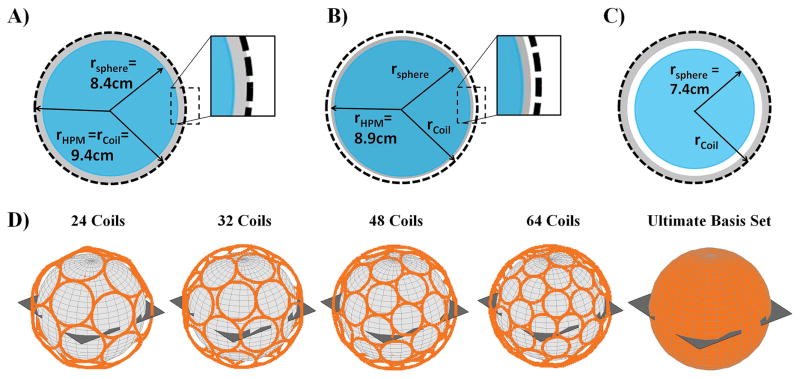
Figure 1.

Various geometrical configurations used for the simulations. (A,B,C) Schematic representations of the homogeneous spherical phantom (blue, r_sphere), the spherical surface where the current distribution of the transmit elements is defined (black dashes, r_coil), and the layer of High Permittivity Material (grey, r_HPM), is shown for three cases. The fully-filled (A) and half-filled (B) cases used to determine the optimal relative permittivity have set sphere and coil radii. Reduction of the phantom size (r_sphere) while the distributed transmit elements and layer of HPM remain fixed is shown as the third case (C), with the smallest phantom size displayed. The simulated transmit array geometries (D), positioned at r_coil and fully encircling the phantom and HPM, are shown, together with the excitation plane through the center of the sample.

We calculated UISAR and array global SAR for an excitation designed to achieve a uniform flip angle (FA) on a transverse plane through the center of a homogeneous sphere with an 84 mm radius, and electrical properties of average brain tissue (ε_r = 63, σ = 0.46 S/m) [39] at 297 MHz, the Larmor frequency of protons at 7 Tesla. The target excitation profile was predefined with uniform phase and amplitude. The surface current distribution was defined 10 mm above the surface of the sphere, and the excitation plane had a resolution of 24 × 24 voxels [Figure 1A].

Integration of High-Permittivity Materials

To investigate the effect of integrating a continuous layer of HPM into the structure of a transmit array, we defined three test cases: the space (10 mm) between the current distribution and the sample filled completely with air, completely with HPM [Figure 1A], and half with HPM and half with air [Figure 1B]. The HPM was assumed to have vanishing conductivity (σ = 0 S/m) in all cases, whereas different relative permittivity values (1 < ε_r < 300) were investigated. Sample size and electrical properties, as well as the radius at which the current distribution was defined (r = 94 mm), remained constant in all cases.

For all three cases, we calculated UISAR and global SAR for four transmit array geometries with 24, 32, 48, and 64 coils [Figure 1D]. All transmit arrays were made of identical loop coils and arranged in tightly-packed configurations, tiled as closely as possible based on the number of elements [40]. Since coil distance to the sample was kept constant for all configurations, an increase in the total number of coil elements corresponded to a decrease in individual element size. Two additional coil designs, with 16 and 128 coils, were analyzed only for the case without the HPM layer. The effect of sample size was then investigated by varying the sample radius while maintaining a constant coil size and HPM layer. The thickness of the HPM, as well as the relative position of coil and HPM with respect to the center of the sample, was held constant, resulting in an increasing layer of air between the HPM and the sample with the reduction of sample size [Figure 1C].

RF shimming algorithm and generation of L-Curves

We employed an RF shimming algorithm that minimizes global SAR for a given target excitation profile [27]. In particular, the algorithm is defined as the following constrained minimization problem:

$$\begin{array}{ll}\text{minimize}\hfill & ({\mathbf{\alpha }}^{\mathrm{H}}\mathbf{\Phi }\mathbf{\alpha })\hfill \\ \text{subject}\text{to}\hfill & \mathbf{S}\mathit{\alpha }=\mathbf{\mu }\hfill \end{array}$$ (1)

The quadratic function α^HΦα is the global SAR, in which α is a vector whose elements include the complex RF shimming modulation coefficients (amplitude and phase) for each coil, the superscript ^H indicates a conjugate transpose, and Φ is the electric field covariance matrix:

$${\mathbf{\Phi }}_{l,l^{\prime }}=\int \mathrm{\sigma }{\mathbf{E}}_l·{{\mathbf{E}}_{l^{\prime }}}^{\ast }\text{dv},$$ (2)

where l and l′ are the coil indices, and σ is the electric conductivity. The other term in Eq. (1) describes profile fidelity, where μ is the target excitation profile, specified as the magnitude and phase of the flip angle distribution across the field of view, and S is a matrix containing the complex-valued B₁⁺ of each coil at all voxels positions. The optimal set of coefficients that satisfies Eq. (1) is given by:

$$\mathbf{\alpha }={\mathbf{\Phi }}^{-1}{\mathbf{S}}^{\mathrm{H}}{(\mathbf{S}\mathbf{\Phi }{\mathbf{S}}^{\mathrm{H}})}^{-1}\mathbf{\mu }.$$ (3)

We added a regularization procedure to control the tradeoff between maximization of profile fidelity and minimization of global SAR. This was implemented by adjusting the tolerance in the SVD-based inversion of (SΦS^H) [27], which allows the constraint on profile fidelity in the least squares problem (Eq. (1)) to be relaxed. This simple procedure is nearly equivalent to addition of a standard Tikhonov regularization term, with the scaling of the effective regularization parameter controlling the desired tradeoff.

Excitation profile fidelity was measured as the root mean squared error (RMSE) between the target and achieved excitation profile. L-curves describing absolute array performance were generated for each transmit array by plotting the global SAR achieved by RF shimming (first term in Eq. (1)), normalized by the corresponding UISAR, as a function of the RMSE of the achieved excitation profile over various degrees of regularization [23, 24]. Relative permittivity of the HPM was varied between 1 (i.e., air) and 300 (e.g., Barium titanate/water slurry [41]) and the optimal value for each coil setup was determined by finding the L-curve closest to the origin of the axes.

To ensure that the results found from this methodology would be generalizable to phase-relaxed RF shimming, the simulated B₁⁺ and E fields from the above evaluations were imported into a basic iterative RF shimming algorithm [42]. Small variations in phase and amplitude of each coil were considered iteratively, optimizing for both the resulting RMSE of the amplitude of the excitation and the global SAR, until a new optimal excitation was reached. Excitation phase was not considered in the RMSE evaluation. A variety of starting points for the algorithm were used to ensure that a global minimum was reached, including the uniform excitation produced by the DGF-constrained RF shimming algorithm. This method was repeated for all HPM cases for the 48-channel array to evaluate the effect of RF shimming methodology on the optimal relative permittivity value.

RESULTS

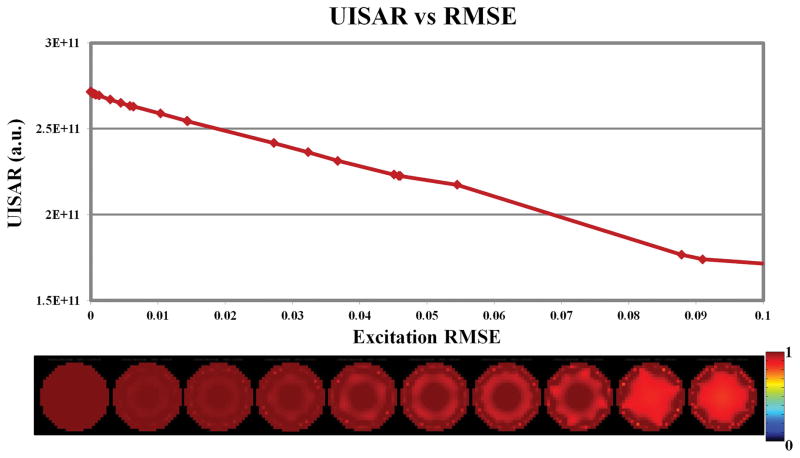
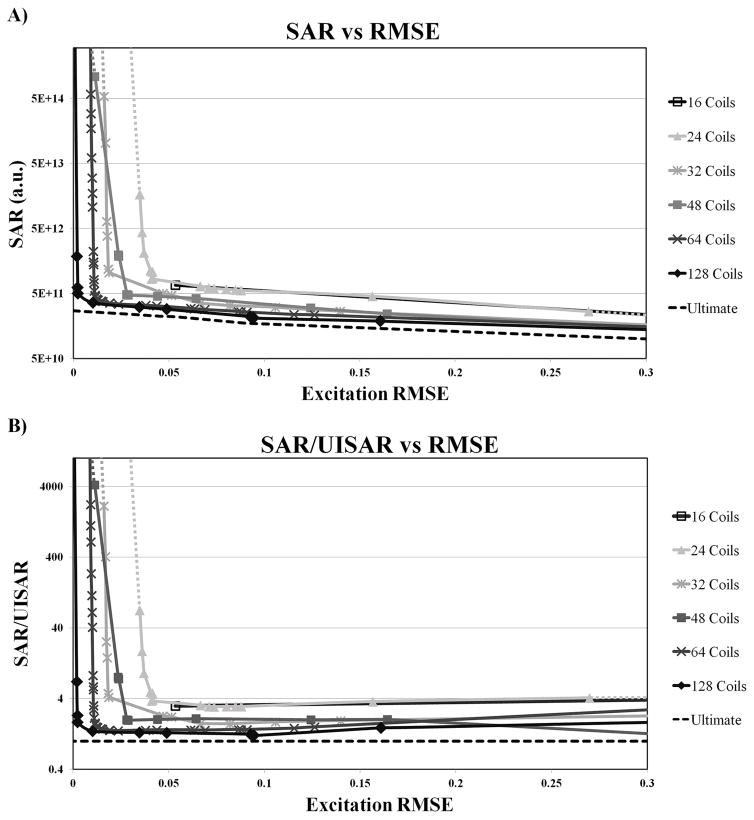
UISAR monotonically decreased as the constraint on transmit homogeneity was relaxed, i.e., when the RMSE of the excited profile increased [Figure 2]. The layer of HPM had no effect on the UISAR, regardless of relative permittivity, because the UISAR depends on the best possible field distribution in the sample within the constraints of the Maxwell equations. Figure 3A shows the typical L-curve relationship between excitation RMSE and SAR for different transmit arrays, for the case without HPM between the coils and the sphere. Figure 3B presents the corresponding normalized L-curves showing absolute array performance. The normalized L-curves moved closer to the origin of the axes for an increasing number of coil elements, indicating that larger arrays can approach UISAR. In particular, for an almost perfect excitation (RMSE = 0.05), global SAR decreased by more than half, from 3.7 times the UISAR to 1.4 times the UISAR, using 64 vs. 24 array elements. The L-curves varied in shape for each array configuration, based on the number of array elements crossing or neighboring the transverse plane, since these were the coils contributing the most to the excitation of the target FA profile. An example of this is shown in Figure 3A by the crossing of the L-curves corresponding to the 32- and 48-element arrays.

Figure 2.

Ultimate intrinsic SAR, displayed in arbitrary units, for a SAR-optimized RF shimming excitation in a transverse FOV through the center of a homogeneous sphere, as a function of excitation profile fidelity. Loosening the transmit homogeneity constraint allows for decreasing SAR requirements. A subset of the simulated RF shimming excitation profiles, with different degrees of homogeneity, are shown at the bottom.

Figure 3.

L-curves showing global SAR as a function of the root mean squared error (RMSE) of the excitation profile for transmit coil arrays with various numbers of elements. A) Global SAR (arbitrary units) as a function of RMSE. B) SAR values normalized by the UISAR as a function of RMSE. Dashed lines pointing toward infinite SAR indicate projected performance for coil designs that do not have enough degrees of freedom to achieve a near-perfect excitation. No HPM layer was used for these cases.

For the case with HPM completely filling the space between the coils and the surface of the sample, coil performance improved as relative permittivity of the HPM was increased up to an optimal value, after which it began to worsen. Figure 4 depicts this evaluation for a 48-channel coil; 24- and 32-channel coil analyses are included in supplemental material [Supporting Figure S1]. For each array, we identified an optimal relative permittivity based on the L-curve closest to the origin. For the 24-, 32-, and 48-element arrays, the optimal relative permittivity values for the simulated geometry were 175, 150, and 100, respectively, suggesting that a larger total number of transmit elements and smaller individual transmit elements reach maximum performance with lower relative permittivity. Using these optimal relative permittivity values, global SAR for a fixed excitation profile (RMSE = 0.05) decreased by 57.2%, 67.6%, and 78.0% with respect to the case without HPM, for the three arrays, respectively. When the number of coils was very large, as in the case of the 64-element array, negligible performance improvement was observed with the addition of HPM of any relative permittivity value (results not shown).

Figure 4.

L-curves with high permittivity material filling the space beneath a 48-loop array. Increasing the relative permittivity values improves coil performance (solid lines) up to an optimum permittivity (green line). Increasing the relative permittivity beyond the optimal value degrades coil performance (dashed lines). Using the optimal permittivity for the HPM improves array performance considerably compared to the case without HPM. Numerical values in legends indicate relative permittivity of the HPM.

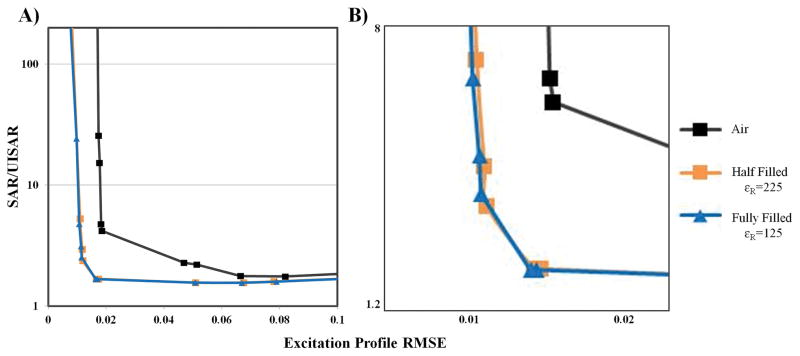
When the space between the coil and the phantom was only half filled with HPM [Figure 1B], the same overall trend as for the fully filled case was found for the L-curves. However, the optimal relative permittivity for the half filled case was approximately twice the corresponding value for the fully filled case. For example, for the 32-element array, the optimum ε_r = 225 for the half filled case corresponded to ε_r = 125 for the fully filled case, resulting in almost identical L-curves [Figure 5].

Figure 5.

Comparison, for a 32-element transmit array, of the case in which the entire space between the phantom and the coil is filled with HPM (Fully Filled), and the case in which only one half of this available space is filled (Half Filled). The optimal permittivity value was used for each case. A) L-curves for the two cases as well as the case with no HPM. B) A zoomed view highlighting similarities between the Fully Filled and Half Filled cases with appropriate adjusted optimum permittivity.

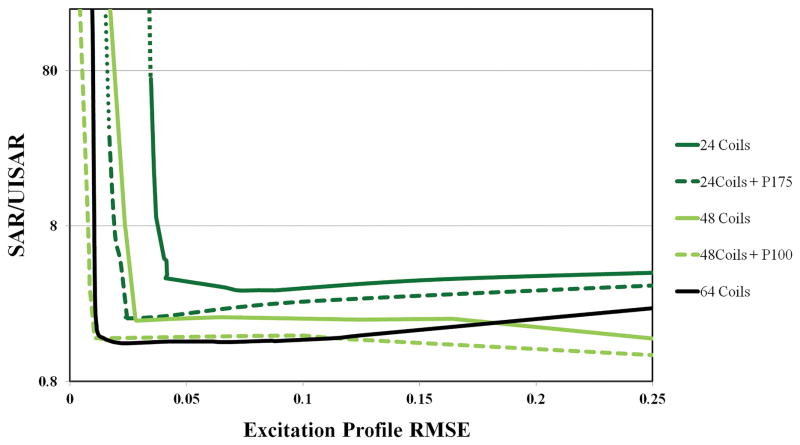
Figure 6 compares the performance of 24- and 48-element arrays, with and without a layer of HPM with optimal relative permittivity, with respect to the L-curve of a 64-element array without HPM. The results show that the performance improvement associated with the use of HPMs can exceed that provided by adding more transmit elements in the array. In fact, when the space between the coils and a head-size sphere was filled with the optimal HPM, the performance of a 24-element array slightly exceeded that of a 48-element array without HPM, whereas the performance of a 48-element array with the optimal HPM was as good as that of a 64-element array without HPM.

Figure 6.

L-curves for 24-, 48-, and 64-element arrays without HPM are compared to the performance improvements provided by fully filling the space between the coil and the phantom with HPM. Optimal relative permittivity values were used for the 24-element (ε_r = 175) and 48-element (ε_r = 100) array. Performance of 24 coils with optimal relative permittivity is similar to performance of 48 coils without HPM. Performance of 48 coils with optimal relative permittivity is similar to performance of 64 coils without HPM.

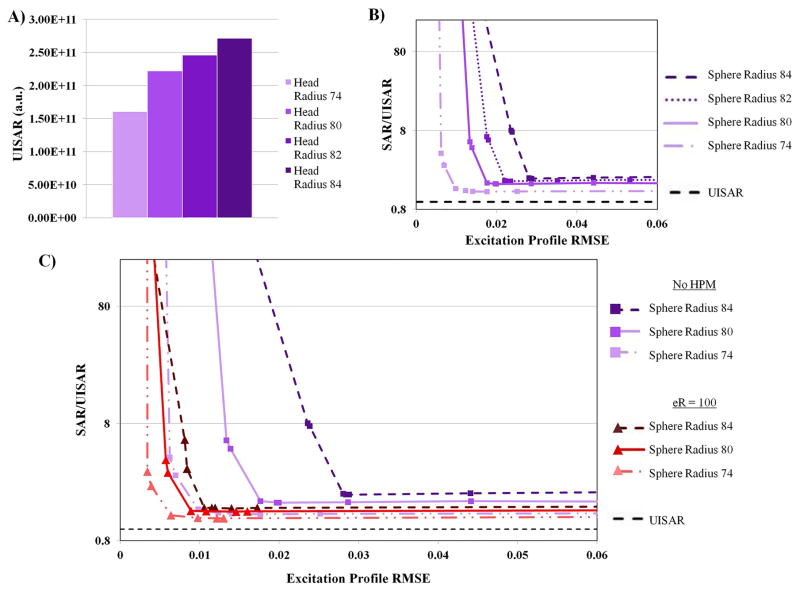
As shown in Figure 5, a layer of air between the sample and the coil and/or HPM affects optimal relative permittivity. Therefore, in a practical case, for which the coil and HPM geometries are fixed, it is important to know the effect of sample size on the optimal dielectric constant of the HPM. In order to model this effect, the diameter of the sphere was varied inside a 48-element array geometry, while the thickness of the HPM and the distance of the coil from the center of the sphere were kept constant [Figure 1C]. For a given profile RMSE, UISAR decreased with smaller sample size, with a 10 mm decrease in sample radius corresponding to a 40% decrease in UISAR for a near-perfect excitation [Figure 7A]. The absolute performance of the 48-element array with no added HPM improved for smaller sample sizes, as shown by the L-curve analysis [Figure 7B]. For a profile RMSE of 0.05, a 10 mm reduction of the sample radius (74 mm vs 84 mm) resulted in a reduction in global SAR from 2.03 to 1.36 times the UISAR. The optimal relative permittivity for the HPM layer increased as sample size became smaller for all simulated arrays (results not shown), with optimal ε_r = 100, 100, 125, and 150, for 84mm, 82mm, 80mm, and 74mm sample sizes, respectively. Note that relative permittivity values were only tested in increments of 25 for these cases. When the optimal relative permittivity was set to 100, a performance improvement was seen for all sample sizes with respect to the case with no HPM [Figure 7C], though the improvements made for the smallest sample sizes were not as significant.

Figure 7.

Effect of phantom size on normalized L-curve performance. Coil size, HPM thickness and position were kept constant for all cases. UISAR, depicted in arbitrary units determined by the simulation method, decreases for decreasing sphere sizes (A), and this trend also appears in the L-curves for a 48-element array (B). When the optimal relative permittivity for the largest sphere size is chosen, all sphere sizes continue to show substantial improvement over the case without HPM (C).

Table 1 shows the results of the RF shimming methodology analysis. For all cases the iterative phase-relaxed RF shimming algorithm resulted in both a reduced RMSE of the excitation profile and a reduced global SAR, however the reductions in both cases were very small. The algorithm did not produce a reduced RMSE of the excitation profile if the phase component was considered. In all cases, the starting point provided by the phase-constrained RF shim resulted in the shortest path to the global minima. The phase-relaxed RF shimming method did not change the overall trends found for the optimal relative permittivity. Average improvement for the RMSE of the amplitude was 1.61%, whereas the resulting SAR decreased by only 2.7% on average.

Table 1.

Comparison of RF Shimming Methods for a 48-element Array with HPM: Global SAR for the phase variable case normalized by the UISAR for the phase-constrained case at the RMSE reached. Optimal relative permittivity (*) does not change with the phase variable shimming method, and SAR/UISAR and RMSE trends appear unchanged.

	Phase Constrained		Phase Variable
εR	SAR/UISAR	RMSE	SAR/UISAR	RMSE
1	1.87725E+15	0.054402	1.84143E+15	0.052239
50	1.18203E+15	0.051043	1.16777E+15	0.050245
75	5.59597E+14	0.050302	5.47761E+14	0.049628
*100	2.17741E+14	0.049977	2.09344E+14	0.049361
125	9.68836E+13	0.049821	9.20353E+13	0.04932
150	7.89397E+13	0.049738	7.64111E+13	0.049174

DISCUSSION

We have used a semi-analytical framework to perform a systematic, analytically-based evaluation of the effect of including HPMs in the space between a coil array and a spherical sample. The distance between the coils and the sample was as small as 1 cm, as this represents the typical gap placed between an actual transmit array and a subject. We evaluated array performance for variations in HPM configuration, number of coils, and sample size, assessing the optimal value for the relative permittivity in each case. The use of the UISAR as a reference in the L-curve analysis allowed us to optimize coil design relative to an absolute performance benchmark.

Our results showed that the inclusion of a layer of HPM, with optimized electrical properties, can yield both lower SAR and improved transmit homogeneity for a given transmit array. This performance benefit was seen for all coil cases tested, but arrays with a smaller number of coils showed a larger performance improvement with respect to the UISAR. Additionally, we showed (Table 1) that this improvement, and the optimization of a single HPM for each coil configuration, was not an artifact of the phase-constrained RF-shimming algorithm, and could be generalized to more practical, phase-relaxed RF shimming cases.

In this study, coils were distributed evenly around the sphere for each array [40], leading to a different distribution of the coils with respect to the excitation plane for each case. This may have contributed to the shape differences in the L-curves of different array geometries, since the coils near the excitation plane had the largest RF shimming coefficients. With this choice of coil arrangement we expect that analyzing optimal relative permittivity using a volumetric excitation would produce similar trends, though the RF shimming algorithm used in this work is not suitable for such analysis. Since the array elements were distributed evenly around the sphere, the number of coils near the excitation plane varied depending on the size of the array, such that for arrays with a low number of elements (8 or 16 elements), exact coil positions became a confounding variable in the L-curve analysis. For the 24 coil packing only 10 coils crossed the excitation plane, while in the 32 coil packing only 18 coils surrounded the excitation plane. This suggests that similar results might be observed by arranging 8- or 16-channel transmit arrays, which are more common options in current MR system, around the excitation plane.

The optimal relative permittivity for the HPM decreased with an increasing number of coils. While UISAR, calculated using a hypothetical infinite array for which the surface current distribution was unconstrained, did not change after adding a layer of lossless HPM, global SAR of a finite arrays of loops varied based on the relative permittivity of the HPM. We observed that for a small number of coils, a relatively high permittivity was needed to maximize array performance, whereas the optimal permittivity value decreased for an increasing number of coils. We hypothesize that the mechanism behind this trend is directly related to displacement currents in the HPM, which is proportional to the relative permittivity. As the number of coils becomes infinitely large, the current can flow in a more unconstrained manner on the coil-surface surrounding the sample. On the other hand, as the number of coils decreases, current is confined to a smaller number of discrete current pathways, and thereby departs from the distributed nature of the pattern that is optimal for excitation. As a result, stronger displacement currents, which are more distributed by nature, are needed to approach the desired excitation, and therefore the optimal permittivity is higher. This can also explain the limited performance improvement in the cases with more than 64 channels. In these densely packed arrays, the current paths along coil conductors are well distributed over an almost continuous conductive surface, so the net current distribution more closely resembles the ideal current patterns associated with UISAR [26]. Therefore, since these coils already approach the performance limits, the addition of high permittivity materials does not generate significant improvements in coil performance. It should also be noted that we simulated an ideal HPM layer with zero conductivity. As a result the presence of the high permittivity layer did not introduce additional losses. However, in practice all HPMs have non-zero, although low, conductivity [43], which should be considered when optimizing the design of actual arrays with integrated HPM.

The optimal relative permittivity and the thickness of the HPM showed a near inversely linear relationship. That is, when the thickness of the HPM is halved, the optimal relative permittivity is almost doubled. This relationship also suggests that displacement currents, which increase linearly with both thickness and relative permittivity, are responsible for the performance benefit seen with the addition of the HPM [Figure 5,7].

When evaluating the optimal dielectric material to use for a real-life coil construction, it is important to contemplate the SAR implications associated with variable subject size. In general, it is expected that the largest subject is the most at risk of exceeding SAR limits. If we fail to optimize for the case leading to the highest overall SAR, we can jeopardize the safety of the HPM-integrated-coil. It is therefore desirable that the optimal permittivity for the worst-case scenario, that of the largest phantom size, prevents performance loss with different phantoms. As illustrated in Figure 7, it is possible to find an optimal HPM that can improve performance for a wide range of sample sizes by optimizing for the largest sample size.

Our finding that the optimal relative permittivity value depends on the HPM thickness allows for flexibility in coil design. For example, when the thickness is set by the particular coil geometry, we can determine a target dielectric value. Conversely, when the realizable relative permittivity is limited by available materials, we can accommodate a different HPM thickness in our design in order to optimize performance.

The analysis we performed here to optimize the relative permittivity for integrated HPMs in coil structural design was limited by the fact that the RF shimming algorithm constrained both the amplitude and phase of the target excitation. In practice, RF shimming approaches that do not constrain the excitation phase are generally used, as they enable lower global SAR minima for given target profiles [44, 45]. However, if the constraint on the excitation phase is removed, the SAR minimization problem becomes non linear and it is no longer guaranteed to arrive at a global optimum. Therefore, it would not be possible to reliably calculate the UISAR. An alternative approach to calculate UISAR for a more realistic target profile phase distribution may exist, but it is beyond the scope of this work. Nevertheless, we showed that for a finite transmit array a phase-relaxed RF shimming approach yields similar results to the phase-constrained case. Furthermore, we showed that the trends found when optimizing relative permittivity based on coil design were not dramatically affected by the constraint on the phase in the RF shimming algorithm. This analysis was limited in SAR normalization by a lack of UISAR results for a phase-relaxed shimming case, so all SAR results were normalized based on the UISAR for the phase-constrained case. The unchanged optimal relative permittivity in the phase-relaxed shim case suggests that the optimal relative permittivity may be more dependent on coil structure relative to the HPM and the excitation plane position than on the RF shimming method. While these results are currently limited to RF shimming, they could also be extended to other approaches, such as fully parallel transmission. Our UISAR optimization algorithm is based on the minimization of global SAR. While further analysis of HPM optimization under a local SAR constraint could provide additional insight for coil design, calculation of ultimate intrinsic local SAR is still an open problem. A first attempt has been presented by Guerin et al. [46], although their preliminary results did not converge to a single ultimate local SAR distribution.

In conclusion, this work suggests that the use of HPM is a practical way to improve RF shimming performance, as an alternative to increasing the number of coils in the transmit array. The use of a fast electrodynamic simulation framework may aid a coil designer to quickly explore the HPM parameter space within their specific engineering design constraints in order to improve coil performance.

Supplementary Material

Supp FigS1

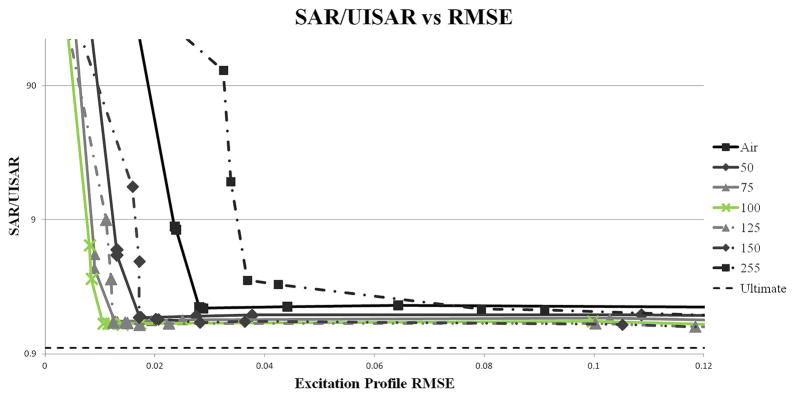
Supporting Figure S1: Optimization of high permittivity material for 24- and 32-channel coil arrays, top and bottom, respectively. Increasing the relative permittivity values (solid lines) improves coil performance up to an optimum permittivity, shown in green with “x” markers. Increasing the relative permittivity beyond the optimal value degrades coil performance (dashed-dot lines indicated with +). Using the optimal permittivity for the HPM improves array performance considerably compared to the case without HPM. Numerical values in legends indicate relative permittivity of the HPM. Dashed lines indicate approximation of L-curve not visible using current RF shimming algorithm.