Abstract
Purpose
Detection of endogenous metabolites using multiplexed editing substantially improves the efficiency of edited MRS. Multiplexed editing – performing more than one edited experiment in a single acquisition – requires a tailored, robust approach for correction of frequency and phase offsets. Here, a novel method for frequency-and-phase correction (FPC) based on spectral registration (SR) is presented and compared against previously presented approaches.
Methods
One simulated dataset and forty GABA-/GSH-edited HERMES datasets acquired in vivo at three imaging centers were used to test four FPC approaches: no correction (NC); SR; SR with post hoc choline-creatine alignment (SR+CC); and multi-step FPC (msFPC). The performance of each routine for the simulated dataset was assessed by comparing the estimated frequency/phase offsets against the known values, while the performance for the in vivo data was assessed quantitatively by calculation of an alignment quality metric based on choline subtraction artifacts.
Results
The msFPC approach returned corrections that were closest to the true values for the simulated dataset. Alignment quality scores were on average worst for NC and best for msFPC in both the GABA- and GSH-edited spectra in the in vivo data.
Conclusion
msFPC results in improved correction of frequency/phase errors in multiplexed GABA-/GSH-edited MRS experiments. The optimal FPC strategy is experiment-specific, and may even be dataset-specific.
Keywords: frequency/phase correction, GABA, GSH, HERMES, MRS, spectral registration
Introduction
Proton magnetic resonance spectroscopy (1H MRS) is a noninvasive technique for detecting the NMR signals of metabolites in vivo. Localized 1H MRS can be implemented in a single- (1) or multi-voxel fashion (2,3), and has broad applications in clinical and basic science (4–6). Detection of lower-concentration metabolites such as γ-aminobutyric acid (GABA) and glutathione (GSH) is more challenging given their inherently weak signals and overlap with higher-concentration metabolites. A common approach for unambiguously detecting these metabolites is J-difference editing, usually applied as the MEGA-PRESS experiment (7). Conventional J-difference editing involves two sets of sub-experiments: one in which frequency-selective editing pulses refocus the evolution of J-coupled resonances of a target metabolite (the ON scan) and another in which these pulses are applied off-resonance (the OFF scan) (8,9). Subtracting the ON and OFF scans results in a difference-edited spectrum, where the signal of the target metabolite is resolved and the signals of any metabolites that are unaffected by the editing pulses are removed. With the development of double editing (10) and Hadamard encoding and reconstruction of MEGA-edited spectroscopy (HERMES) for multiplexed editing (11–14), it is now possible to simultaneously edit multiple metabolites in a single acquisition with equivalent data quality as two separate MEGA-PRESS acquisitions.
J-difference editing involves subtracting out larger signals to reveal smaller underlying signals. Changes in center frequency during the acquisition, that can occur due to heating/cooling of scanner hardware elements and participant head motion, lead to subtraction artifacts in the difference spectra as a result of the subtraction of misaligned peaks (15,16). Thus, there is a strong requirement for robust and accurate alignment of data, especially since editing of lower-concentration metabolites requires relatively long measurement times (~10 min) to build up sufficient signal-to-noise.
A variety of retrospective approaches to correct for frequency and phase instabilities have been proposed. Given the presence of a residual water signal, it is possible to correct for frequency offsets by, for instance, performing a circular shift of spectra in the frequency-domain to align the maxima of the water peak (17). If an interleaved water navigator is acquired, the metabolite data can be phase-corrected by deconvolution (18). Alternatively, modeling of an endogenous metabolite signal, in particular creatine (Cr), can correct for both frequency and phase errors (16,19). Recently, Near et al. (20) introduced spectral registration, a time-domain method that employs nonlinear regression to align individual free induction decays (FIDs) to a reference FID. For edited data, alignment approaches have included adaptive spectral registration in the frequency domain (21), basis-set-driven correction (22), power minimization in the difference spectrum (23) and frequency-domain correlation (24). In general, frequency-and-phase correction (FPC) for editing is more challenging than for non-edited acquisitions because the signal characteristics of ON and OFF scans are different. Successful correction requires an algorithm that is not misled by these editing-derived differences, and one which correctly accounts for shot-to-shot instabilities. Thus, strategies that are successful for GABA editing (16,19), which impacts the N-acetylaspartate signal, are not necessarily successful for GSH editing (21), which impacts the residual water signal. The case of multiplexed editing is additionally challenging, requiring the alignment of at least four different sets of signals. Saleh et al. (12) used an ad hoc method to align GABA-/GSH-edited HERMES data whereby all FIDs were first aligned using spectral registration and then the GSH-edited data were further aligned in the frequency domain to reduce choline (Cho) subtraction artifacts, the Cho signal being neither directly impacted by editing pulses nor overlapped by edited signals. Subsequent testing of this method across larger datasets has revealed a lack of robustness, however.
In this paper, a novel method for FPC of HERMES data is presented. This approach is an extension of spectral registration (20) but one which is specifically tailored to multiplexed editing of GABA and GSH. The performance of this new FPC routine was tested on simulated data and 40 in vivo datasets, and compared against methods described previously. The aim was to demonstrate that the new tailored FPC routine is robust for multiplexed edited MRS.
Methods
Simulated Data
A simulated HERMES (12) dataset of 320 FIDs was generated in FID-A (25) using ideal excitation/refocusing pulses and shaped editing pulses. Briefly, the HERMES experiment involves four sub-experiments (A, B, C and D) in which editing pulses are applied to: both GABA (1.9 ppm) and GSH (4.56 ppm) (A: ONGABA, ONGSH); GABA only (B: ONGABA, OFFGSH); GSH only (C: OFFGABA, ONGSH); or neither (D: OFFGABA, OFFGSH). GABA- and GSH-edited difference (DIFF) spectra are reconstructed based on the principle of orthogonality of a Hadamard matrix. Acquisition parameters were: TE = 80 ms; 20-ms Gaussian editing pulses; 2048 discrete data points; 2 kHz spectral width. Fourteen metabolites were included in the simulated dataset, plus eight macromolecule resonances and a residual water signal, with signal intensities and lineshapes modeling in vivo values. Gaussian noise was added to each FID (approximating in vivo signal-to-noise ratios (SNR)). Known shot-to-shot frequency/phase offsets were added as previously described (20). Frequency offsets consisted of a linear trend with a total drift of 5 Hz over the course of the entire experiment, superposed with normally distributed random shot-to-shot frequency offsets with a standard deviation of 1 Hz. Similarly, phase offsets consisted of a linear trend with a total of −1 degree of drift, superposed with normally distributed random shot-to-shot phase offsets with a standard deviation of 6 degrees. Finally, to simulate the effect of a “jump” in frequency/phase offsets due to participant head motion, the frequency/phase offset functions were then each superposed with step functions with amplitudes of 5 Hz and 20 degrees, respectively, with the step randomly chosen to occur at the 264th average. FPC, as described further below, was implemented within Gannet (26). Additional data processing steps included 3-Hz exponential line-broadening, zero-filling to 32k points and removal of the residual water signal using a Hankel singular value decomposition filter (27).
In Vivo Data
Forty GABA-/GSH-edited HERMES datasets were acquired on 3T Philips scanners (Philips Healthcare, The Netherlands) at three imaging centers (Kennedy Krieger Institute, Cincinnati Children’s Hospital, University of Sheffield). Data were acquired from voxels in the medial parietal lobe, with dimensions ranging from 3 × 3 × 3 cm3 to 3.6 × 3.6 × 3.6 cm3. Other acquisition parameters matched the simulated data, except TR = 2000 ms (see Saleh et al. (12) for further experimental details). Interleaved water referencing (28) was employed to minimize linear B0 field drift during data acquisition. Scans were performed with local institutional review board approval and informed consent. Gannet was used for FPC and data processing in the same way as the simulated dataset.
FPC Approaches
Preliminary investigations involved testing a large number of algorithms for FPC, including various time- and frequency-domain methods. For the sake of clarity, in this paper we present the most successful of these methods, and compare it to: no correction; spectral registration, the most widely used method for GABA-edited MRS; and the method previously proposed for HERMES of GABA and GSH (12), spectral registration with post hoc Cho-Cr alignment.
No Correction
Datasets were first processed with no correction (NC) of frequency/phase offsets, serving as a baseline for qualitatively and quantitatively assessing the performance of the FPC approaches, as detailed below.
Spectral Registration
Spectral registration (SR) is an efficient and robust method for correcting frequency/phase offsets in the time domain (20). Each mth FID Sm(t) is fitted to a reference FID R(t) by simultaneous adjustment of its frequency, f (in Hz), and phase, ϕ (in degrees), using nonlinear least-squares minimization. This is formulated as
| [1] |
where
| [2] |
Typically, R(t) is chosen to be the first FID acquired in the scan. In certain cases, however, significant amounts of frequency and/or phase offset that occur later in the scan will lead the nonlinear least-squares minimization algorithm to converge on a false solution or to fail outright, and it is important to select a reference that is central to the dataset as a whole (21). In this paper, a “complex median” was calculated; that is, the median of the M × N × 2 data matrix along the m-dimension, where M is the total number of FIDs, N is the number of data points and 2 denotes the real and imaginary components. This creates a 1 × N × 2 “median FID” reference that has a frequency and phase offset close to the median of frequency/phase offsets of the raw FIDs. This method is similar to a previously described algorithm for signal artifact reduction (29). Minimization of Eq. [1] was performed using nonlinear regression using nlinfit in MATLAB (The MathWorks Inc., Natick, MA). The real and imaginary components of Sm(t) and R(t) were concatenated into one-dimensional real-valued vectors to obtain real-valued frequency and phase parameter estimates.
Excluding the later, noise signal portion of the FIDs in the nonlinear regression substantially increases computational efficiency, so only the first n points of the FIDs were used for registration. The value n was calculated for each dataset based on an SNR threshold of 3. Signal was calculated from the magnitude-average of the GSH-OFF FIDs (i.e., sub-experiments B and D). Noise was estimated from the average standard deviation of the real signal in the last quarter of each of these FIDs.
Outlier removal of individual FIDs was performed by first deriving the mean squared error (MSE) of each mth nonlinear regression computation and then converting the values into standardized z-scores:
| [3] |
| [4] |
where 2n is the number of data points in each concatenated FID. The bar denotes the mean and σ denotes the standard deviation (across the M FIDs). The criterion to reject FIDs was met if zMSE,m < −3 or zMSE,m > 3, which equates to a rejection criterion of ±3 standard deviations (19,30).
The FIDs were then Fourier-transformed into the frequency domain. Alignment to true frequency/phase offset was performed by fitting a two-Lorentzian model with frequency and phase parameters to the Cho-Cr signals of the sum of all the spectra (SUM spectrum) and accordingly correcting the residual global frequency/phase offset of each spectrum.
Spectral Registration with Post Hoc Cho-Cr Alignment
Saleh et al. (12) proposed an FPC approach described as spectral registration with post hoc Cho-Cr alignment (SR+CC). All FIDs of the HERMES data were first aligned using the SR pipeline as described above and then the averaged GSH-ON and GSH-OFF spectra were aligned in the frequency domain. The Cho-Cr signals were shifted in frequency and phase until the standard deviation of the Cho subtraction artifact was minimized. This approach was shown to improve alignment of the GSH-edited spectra, as SR alone resulted in good alignment for the reconstructed GABA-edited spectra in the 10 datasets of that study.
Multi-Step FPC
Our mixed experience of applying the SR+CC method beyond the limited dataset acquired in the original paper motivated the current investigation, and ultimately led to a new multi-step FPC (msFPC) method. First, the FIDs in a given dataset were segregated into the four sub-experiment sets inherent to HERMES: Si,m(t), where i ∈ {A, B, C, D}. Within each set, frequency/phase offsets were estimated using SR as described above using four “median FID” references Ri(t) generated from each sub-experiment set, but corrections were not yet applied. The SNR algorithm for selecting the value n was performed separately for each sub-experiment set. Cauchy probability density functions (PDFs) were fitted to the distributions of frequency/phase offset estimates for each sub-experiment set. A Cauchy PDF is expressed as
| [5] |
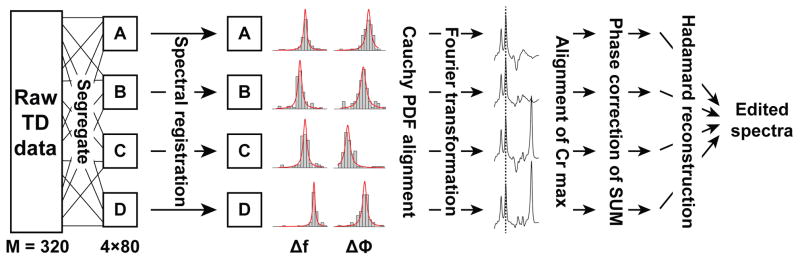
where s and l are the scale and location parameters of the function, respectively, and are determined by maximum likelihood estimation. The estimated location parameters, which correspond to the centers of the distributions, were then subtracted from the frequency/phase offset estimates for each respective sub-experiment set of FIDs to derive the corrections that were then applied to the raw data. This approach aligns the FIDs of the four sub-experiments to one another. Use of a Cauchy PDF is advantageous given that it is insensitive to outliers and therefore robust in cases of abrupt and significant frequency/phase offset. Finally, residual frequency misalignment was corrected by conducting a frequency-domain shift of the real spectra to align the Cr signal maxima. Residual zero-order phase correction was performed by model fitting of the Cho-Cr signals of the SUM spectrum as described above. A schematic of the msFPC pipeline is displayed in Figure 1. Individual FIDs were rejected as above except z-scores zMSE,m were calculated within each sub-experiment set.
FIG. 1.
Schematic of the multi-step frequency-and-phase correction (msFPC) pipeline. A, B, C and D represent each of the four HERMES editing sub-experiments (see text for details). TD = time domain; PDF = probability density function.
Alignment Quality
For the simulated data, the true frequency/phase offsets are known so it was possible to assess the performance of each FPC approach by calculating a normalized root sum square error metric Qrsse:
| [6] |
where py,m is either the estimated or true frequency offset, Δf, or phase offset, Δϕ, of the mth FID. A score of 1 indicates perfect alignment, a value less than 0 indicates worse alignment and a value of 0 indicates no correction. Outcomes were displayed as modified Bland-Altman plots (31).
To assess quantitatively the alignment quality for the in vivo data, an alignment quality metric based on the Cho subtraction artifact around 3.2 ppm in both the GABA- and GSH-edited DIFF spectra was developed. Specifically, the alignment quality metric Qy was calculated as:
| [7] |
| [8] |
where σ(SAy) is the standard deviation of the Cho subtraction artifact between 3.175 and 3.285 ppm pre- or post-alignment, σ(εy) is the standard deviation of the linearly detrended noise signal between 10 and 11 ppm and med denotes the median across the group. The standard deviations of noise are subtracted from the numerators and denominators in Eqs. [7] and [8] to adjust for the fact that the spectral noise represents a theoretical ceiling of alignment quality (or a floor for subtraction artifacts). Normalization to the pre-alignment Cho-subtraction-artifact median results in the median of Qpre scores being 0. A median Qpost score greater than 0 would indicate that the given FPC approach improved alignment whereas a median less than 0 would indicate worse alignment. A median Qpost score of 1 suggests that the algorithm has removed the Cho subtraction artifact, leaving only noise.
Results
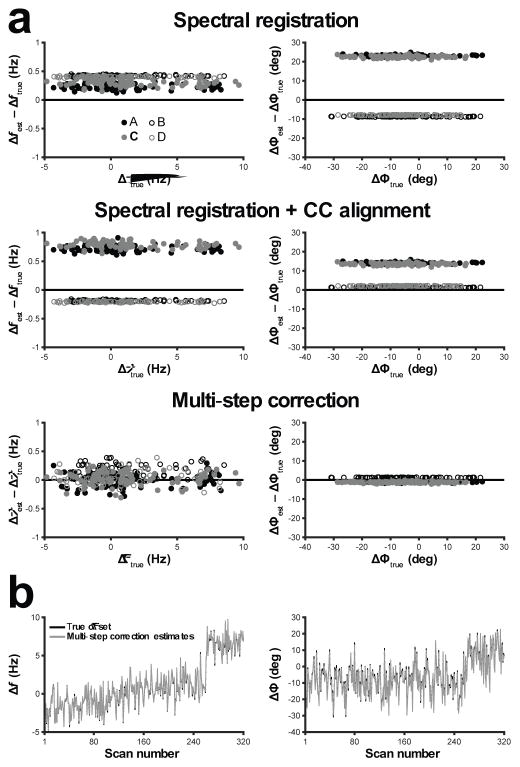
The Qrsse,p scores derived from correction of the simulated dataset were highest for the msFPC approach (frequency: 0.96; phase: 0.90). For SR, these scores were 0.90 (frequency) and −0.37 (phase); for SR+CC, these were 0.84 (frequency) and 0.22 (phase). Bland-Altman-like plots, visually displaying the accuracy and biases of each approach with respect to frequency and phase correction, are presented in Figure 2a. SR and SR+CC resulted in poorer accuracy and clear biases in estimation of the true frequency (Δf) and phase (Δϕ) offsets. The mean differences between the estimated and true frequency and phase offsets were 0.34 Hz and 7.13 degrees for SR, respectively, and 0.27 Hz and 7.63 degrees for SR+CC, respectively. For msFPC, the mean differences were 0.06 Hz and −0.64 degrees, respectively, demonstrating substantially better accuracy and lower bias when applying this method. It is clear that the algorithms responded differently to the GSH-ON (filled circles) and GSH-OFF (open circles) sub-experiments, resulting in clustering of similar points. The occurrence of these systematic biases is the essence of the challenge of FPC for edited experiments. Figure 2b shows the true frequency and phase offsets of the simulated dataset overlaid by the estimated offsets derived by msFPC.
FIG. 2.
a: Modified Bland-Altman plots showing the accuracy and bias of each FPC approach with respect to estimation of frequency (left column) and phase (right column) offsets in the simulated HERMES dataset. The errors in estimated frequency/phase offsets (Δfest − Δftrue, Δϕest − Δϕtrue) are plotted against the true offsets (Δftrue, Δϕtrue). Filled/open circles correspond to GSH ON/OFF scans; black/gray circles correspond to GABA ON/OFF scans. b: The true frequency (left) and phase (right) offsets (black line) overlaid by the offsets estimated by the multi-step FPC approach (grey line) for each simulated FID.
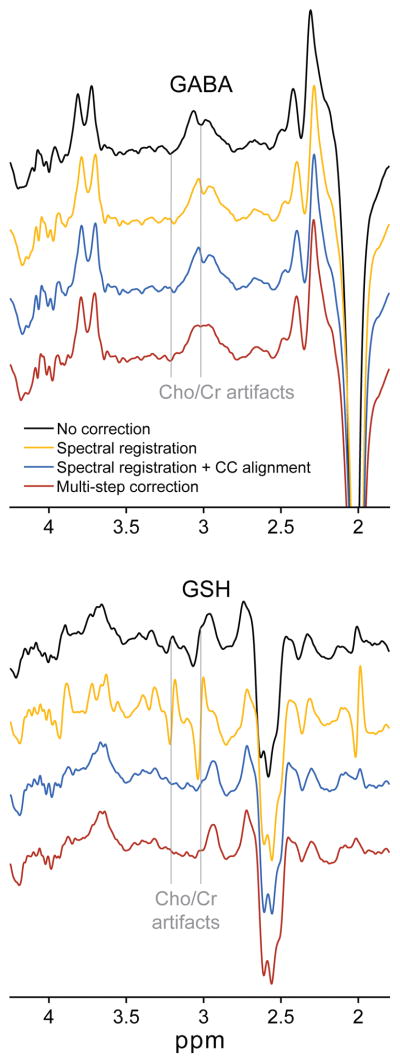
Example GABA-/GSH-edited DIFF spectra aligned using each FPC approach are shown in Figure 3. In this example, Cr subtraction artifacts are visible in the GABA DIFF spectrum when NC, SR and SR+CC approaches were used, but removed with the msFPC approach. The GSH DIFF spectrum shows observable Cho subtraction artifacts for the NC and, in particular, the SR routines. The poor alignment of the GSH-edited data but good alignment of the GABA-edited data when using SR reproduces findings previously reported by Saleh et al. (12). Median Qpost scores for the GABA-edited spectra were −0.15 (SR), −0.15 (SR+CC) and 0.69 (msFPC). For the GSH-edited spectra, these were −20.27 (SR), −1.38 (SR+CC) and −0.18 (msFPC). msFPC showed a clear advantage in frequency/phase alignment over the other routines.
FIG. 3.
Example GABA- (top) and GSH- (bottom) edited DIFF spectra from one dataset frequency- and phase-corrected using each of the four FPC approaches. The two grey vertical lines show the location of Cho/Cr subtraction artifacts in the spectra. Cr subtraction artifacts are clearly seen in the GABA DIFF spectra, while Cho subtraction artifacts are clearly seen in the GSH DIFF spectra. Black = no correction; gold = spectral registration; blue = spectral registration with post hoc Cho-Cr alignment; red = multi-step FPC.
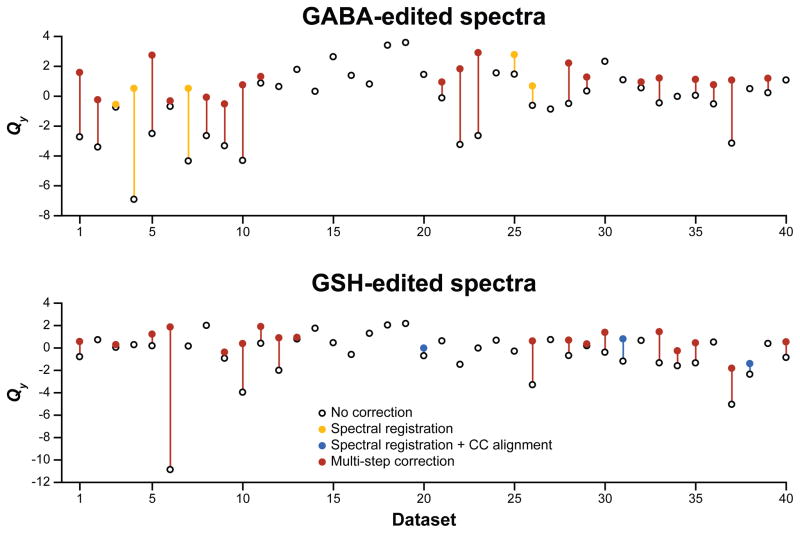
However, it was clear that the different algorithms performed better on different datasets. Figure 4 plots the Qpre scores for each in vivo dataset for both edited spectra as open circles and the best post-alignment score Qpost as a second colored circle (but only for when there was an improvement in alignment). In 8 of 40 datasets, subtraction artifacts were not reduced by any of the three FPC strategies in both the GABA and GSH DIFF spectra. An additional 18 datasets showed no improvement in either the GABA or the GSH DIFF spectra: these unimproved datasets had relatively good alignment without intervention. Five GABA DIFF spectra were most improved by SR and three GSH DIFF spectra were most improved by SR+CC. A clear benefit of having a quantitative metric of alignment quality is that cases where FPC leads to diminished data quality can be avoided, and it is even possible to select the FPC method to be used in each case based on an outcome score (i.e., the best of all tested FPC approaches). The median of these outcome-driven alignment quality scores was 1.07 for the GABA-edited spectra (reaching the expected noise ceiling) and 0.58 for the GSH-edited spectra.
FIG. 4.
Best alignment quality scores (Qy) for each in vivo HERMES dataset for the GABA- (top row) and GSH- (bottom row) edited DIFF spectra. The alignment quality score for each dataset with no correction is displayed as an open circle. Additionally, on a dataset-by-dataset basis, the outcome of the most successful FPC approach (i.e., the largest increase in Qy) is plotted as a filled, colored circle. Where none of the FPC approaches resulted in a reduction in Cho subtraction artifacts, only the pre-corrected Qy score is shown. White = no correction; gold = spectral registration; blue = spectral registration with post hoc Cho-Cr alignment; red = multi-step FPC.
Interestingly, the msFPC algorithm is faster to run than either the SR or SR+CC algorithms, presumably because the spectral registration step aligns like-with-like and the minimization associated with that is computationally less demanding. For a given HERMES dataset as described here (320 averages), typical alignment times were: ~20 s (SR); ~20 s (SR+CC); and ~8 s (msFPC).
Discussion
The results from this work suggest that a multi-step approach to correction of frequency and phase errors in multiplexed edited MRS data is robust and quantitatively better than the current conventional or ad hoc SR-based approaches. They also suggest that the performance of the various algorithms varies from dataset to dataset, and that outcome-based selection of optimal FPC strategy leads to dramatic improvements.
Recent developments in FPC of edited data (21–24) demonstrate the need for algorithms that can robustly handle editing-derived differences in spectral signals. Multiplexed editing presents a particular challenge for FPC, as it requires alignment of four or more, rather than two, subspectra and generates more than one DIFF spectrum in which subtraction artifacts can be revealed. The msFPC routine approaches the problem by treating each edited sub-experiment separately. It then relies on probabilistic procedures to align spectra from each sub-experiment to each other. The use of a “complex median” reference not only ensures better solutions to the least-squares minimization in SR but also results in shifting the frequencies and phases of each FID to a near-central position across the dataset. Although not investigated in this study, it is possible that a median reference could overcome issues of unstable water signals, which can hamper the performance of SR (20). Additional alignment of the probability distributions of the frequency/phase offsets by estimation of Cauchy PDFs further improves the probabilistic alignment, a fairly novel approach in MRS data processing.
Although msFPC performed better than SR and SR+CC overall, the median alignment quality score for the GSH-edited spectra did not rise above 0, indicating no net improvement over performing no correction. Twenty-one of the forty datasets were improved by msFPC. The average pre-alignment quality score of the nineteen datasets that were not improved by msFPC was very high (0.63), indicating that approximately 50% of the GSH-edited spectra did not “need” FPC. The Bland-Altman plots of FPC accuracy for the simulated dataset indicate that msFPC did perform reasonably well, but applying a correction with small errors can have a negative impact on high-quality in vivo data.
The specific implementation of msFPC described here has been shown to be relatively successful in correcting frequency and phase errors in multiplexed edited data. However, there are some limitations to this method. Firstly, it is likely that as multiplexed editing schemes become more complex, aspects of the msFPC pipeline will need to be accordingly modified or optimized. For instance, in this paper the Cho-Cr signals were used for residual frequency and phase alignment, given that they were not saturated by the editing pulses in any of the HERMES sub-experiments. This may not be the case in other possible editing schemes and so a tailored approach would be needed for residual alignment of frequency/phase offsets. Secondly, accurate estimation of the center of the probability density of estimated frequency/phase offsets through use of a Cauchy function will be hampered in cases where there are fewer FIDs in each HERMES sub-experiment set than acquired in the in vivo data here. Thirdly, the Bland-Altman plots revealed that a minor bias still remained in the correction of phase offsets. This was specific to sub-experiment B (GABA-ON, GSH-OFF). It is not clear at which stage in the msFPC pipeline this bias was introduced but it was relatively small, differing from the offsets estimated for the other three sub-experiments by ~2 degrees. Finally, it should be noted that accurate estimation of the Cho subtraction artifact can be difficult in cases where the residual signal is close in magnitude to the noise signal. Additionally, the standard-deviation-based alignment quality metric can be impacted by a non-constant baseline. This metric can effectively guide algorithm selection when one algorithm is performing badly. In cases where multiple algorithms perform well, the metric will provide less discriminative accuracy, particularly in high-quality in vivo data where further improvements in alignment are subtle. However, since the aim is to select an algorithm that performs well, rather than to select the best algorithm, this is a minor concern.
An outcome-driven approach was briefly explored in this paper, whereby the alignment quality metric for the in vivo data was used to choose the optimal FPC approach from among the four possible methods. While not the main objective of our study, we propose the possibility of using “competitive” FPC, where a series of FPC routines are employed and the best outcome selected on a dataset-by-dataset basis. Indeed, previous studies that have compared conventional SR with either SR-based variants or non-SR-based methods have shown that one method may perform better than, or just as well as, another in certain cases (32), such as when SNR is low (20,23,24) or when the dominant signal in the spectrum is unstable (20). One could even argue that the prime advantage of the msFPC approach is that it exploits the strengths of several of the previously described FPC algorithms. More advanced algorithms, particularly those tailored to more complex multiplexed editing experiments, may work best if they are designed with this premise in mind. While there is a time cost from competitive FPC, in terms of carrying out multiple FPC routines on the same dataset, processing times are not prohibitive (~16 s per dataset per FPC routine), so it would be practicable to compare four approaches (plus NC). Selecting a different FPC algorithm for each dataset is perhaps an unconventional approach, and it is reasonable to be concerned that it might introduce bias. However, since the aim of FPC is to shift each dataset closer to the “perfectly aligned” ideal, we believe that selecting an optimal FPC approach for each dataset reduces, rather than introduces, bias associated with imperfect alignment.
Conclusions
In conclusion, a multi-step spectral registration-based FPC approach has been shown to robustly correct frequency/phase offsets of multiplexed GABA-/GSH-edited MRS data, and competitive FPC based on outcome-driven algorithm selection outperforms any single current method.
Acknowledgments
This work was supported by NIH grants R01 EB016089, R01 EB023963, R01 MH106564, R01 NS096207, P41 EB015909 and R01 ES0277224. NAJP receives salary support from NIH grant K99 MH107719. IDW acknowledges support from the Wellcome Trust and NIHR Sheffield Biomedical Research Centre.
References
- 1.Yahya A. Metabolite detection by proton magnetic resonance spectroscopy using PRESS. Prog Nucl Magn Reson Spectrosc. 2009;55:183–198. doi: 10.1016/j.pnmrs.2009.04.001. [DOI] [Google Scholar]
- 2.Barker PB, Lin DDM. In vivo proton MR spectroscopy of the human brain. Prog Nucl Magn Reson Spectrosc. 2006;49:99–128. doi: 10.1016/j.pnmrs.2006.06.002. [DOI] [Google Scholar]
- 3.Posse S, Otazo R, Dager SR, Alger J. MR spectroscopic imaging: Principles and recent advances. J Magn Reson Imaging. 2013;37:1301–1325. doi: 10.1002/jmri.23945. [DOI] [PubMed] [Google Scholar]
- 4.Öz G, Alger JR, Barker PB, et al. Clinical Proton MR Spectroscopy in Central Nervous System Disorders. Radiology. 2014;270:658–679. doi: 10.1148/radiol.13130531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Duncan NW, Wiebking C, Muñoz-Torres Z, Northoff G. How to investigate neuro-biochemical relationships on a regional level in humans? Methodological considerations for combining functional with biochemical imaging. J Neurosci Methods. 2014;221:183–188. doi: 10.1016/j.jneumeth.2013.10.011. [DOI] [PubMed] [Google Scholar]
- 6.Ross AJ, Sachdev PS. Magnetic resonance spectroscopy in cognitive research. Brain Res Rev. 2004;44:83–102. doi: 10.1016/j.brainresrev.2003.11.001. [DOI] [PubMed] [Google Scholar]
- 7.Mescher M, Merkle H, Kirsch J, Garwood M, Gruetter R. Simultaneous in vivo spectral editing and water suppression. NMR Biomed. 1998;11:266–272. doi: 10.1002/(SICI)1099-1492(199810)11:6<266::AID-NBM530>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- 8.Harris AD, Saleh MG, Edden RAE. Edited 1H magnetic resonance spectroscopy in vivo: Methods and metabolites. Magn Reson Med. 2017;77:1377–1389. doi: 10.1002/mrm.26619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bogner W, Hangel G, Esmaeili M, Andronesi OC. 1D-spectral editing and 2D multispectral in vivo 1H-MRS and 1H-MRSI - Methods and applications. Anal Biochem. 2017;529:48–64. doi: 10.1016/j.ab.2016.12.020. [DOI] [PubMed] [Google Scholar]
- 10.Terpstra M, Marjanska M, Henry PG, Tkáč I, Gruetter R. Detection of an antioxidant profile in the human brain in vivo via double editing with MEGA-PRESS. Magn Reson Med. 2006;56:1192–1199. doi: 10.1002/mrm.21086. [DOI] [PubMed] [Google Scholar]
- 11.Chan KL, Puts NAJ, Schär M, Barker PB, Edden RAE. HERMES: Hadamard encoding and reconstruction of MEGA-edited spectroscopy. Magn Reson Med. 2016;76:11–19. doi: 10.1002/mrm.26233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Saleh MG, Oeltzschner G, Chan KL, Puts NAJ, Mikkelsen M, Schär M, Harris AD, Edden RAE. Simultaneous edited MRS of GABA and glutathione. Neuroimage. 2016;142:576–582. doi: 10.1016/j.neuroimage.2016.07.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chan KL, Oeltzschner G, Schär M, Barker PB, Edden RAE. Spatial Hadamard encoding of J-edited spectroscopy using slice-selective editing pulses. NMR Biomed. 2017;30:e3688. doi: 10.1002/nbm.3688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chan KL, Saleh MG, Oeltzschner G, Barker PB, Edden RAE. Simultaneous measurement of Aspartate, NAA, and NAAG using HERMES spectral editing at 3 Tesla. Neuroimage. 2017;155:587–593. doi: 10.1016/j.neuroimage.2017.04.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Harris AD, Glaubitz B, Near J, John Evans C, Puts NAJ, Schmidt-Wilcke T, Tegenthoff M, Barker PB, Edden RAE. Impact of frequency drift on gamma-aminobutyric acid-edited MR spectroscopy. Magn Reson Med. 2014;72:941–8. doi: 10.1002/mrm.25009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Evans CJ, Puts NAJ, Robson SE, Boy F, McGonigle DJ, Sumner P, Singh KD, Edden RAE. Subtraction artifacts and frequency (mis-)alignment in J-difference GABA editing. J Magn Reson Imaging. 2013;38:970–975. doi: 10.1002/jmri.23923. [DOI] [PubMed] [Google Scholar]
- 17.Helms G, Piringer A. Restoration of motion-related signal loss and line-shape deterioration of proton MR spectra using the residual water as intrinsic reference. Magn Reson Med. 2001;46:395–400. doi: 10.1002/mrm.1203. [DOI] [PubMed] [Google Scholar]
- 18.Thiel T, Czisch M, Elbel GK, Hennig J. Phase coherent averaging in magnetic resonance spectroscopy using interleaved navigator scans: Compensation of motion artifacts and magnetic field instabilities. Magn Reson Med. 2002;47:1077–1082. doi: 10.1002/mrm.10174. [DOI] [PubMed] [Google Scholar]
- 19.Waddell KW, Avison MJ, Joers JM, Gore JC. A practical guide to robust detection of GABA in human brain by J-difference spectroscopy at 3 T using a standard volume coil. Magn Reson Imaging. 2007;25:1032–1038. doi: 10.1016/j.mri.2006.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Near J, Edden R, Evans CJ, Paquin R, Harris A, Jezzard P. Frequency and phase drift correction of magnetic resonance spectroscopy data by spectral registration in the time domain. Magn Reson Med. 2015;73:44–50. doi: 10.1002/mrm.25094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.An L, Zhang Y, Thomasson DM, Latour LL, Baker EH, Shen J, Warach S. Measurement of glutathione in normal volunteers and stroke patients at 3T using J-difference spectroscopy with minimized subtraction errors. J Magn Reson Imaging. 2009;30:263–270. doi: 10.1002/jmri.21832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.van der Veen JW, Marenco S, Berman KF, Shen J. Retrospective correction of frequency drift in spectral editing: The GABA editing example. NMR Biomed. 2017;30:e3725. doi: 10.1002/nbm.3725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cleve M, Krämer M, Gussew A, Reichenbach JR. Difference optimization: Automatic correction of relative frequency and phase for mean non-edited and edited GABA 1 H MEGA-PRESS spectra. J Magn Reson. 2017;279:16–21. doi: 10.1016/j.jmr.2017.04.004. [DOI] [PubMed] [Google Scholar]
- 24.Wiegers EC, Philips BWJ, Heerschap A, van der Graaf M. Automatic frequency and phase alignment of in vivo J-difference-edited MR spectra by frequency domain correlation. Magn Reson Mater Physics, Biol Med. 2017 doi: 10.1007/s10334-017-0627-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Simpson R, Devenyi GA, Jezzard P, Hennessy TJ, Near J. Advanced processing and simulation of MRS data using the FID appliance (FID-A)-An open source, MATLAB-based toolkit. Magn Reson Med. 2017;77:23–33. doi: 10.1002/mrm.26091. [DOI] [PubMed] [Google Scholar]
- 26.Edden RAE, Puts NAJ, Harris AD, Barker PB, Evans CJ. Gannet: A batch-processing tool for the quantitative analysis of gamma-aminobutyric acid-edited MR spectroscopy spectra. J Magn Reson Imaging. 2014;40:1445–1452. doi: 10.1002/jmri.24478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Barkhuijsen H, de Beer R, van Ormondt D. Improved algorithm for noniterative time-domain model fitting to exponentially damped magnetic resonance signals. J Magn Reson. 1987;73:553–557. doi: 10.1016/0022-2364(87)90023-0. [DOI] [Google Scholar]
- 28.Edden RAE, Oeltzschner G, Harris AD, Puts NAJ, Chan KL, Boer VO, Schär M, Barker PB. Prospective frequency correction for macromolecule-suppressed GABA editing at 3T. J Magn Reson Imaging. 2016;44:1474–1482. doi: 10.1002/jmri.25304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Slotboom J, Nirkko A, Brekenfeld C, van Ormondt D. Reliability testing of in vivo magnetic resonance spectroscopy (MRS) signals and signal artifact reduction by order statistic filtering. Meas Sci Technol. 2009;20:104030. doi: 10.1088/0957-0233/20/10/104030. [DOI] [Google Scholar]
- 30.Mikkelsen M, Barker PB, Bhattacharyya PK, et al. Big GABA: Edited MR spectroscopy at 24 research sites. Neuroimage. 2017;159:32–45. doi: 10.1016/j.neuroimage.2017.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;327:307–310. doi: 10.1016/S0140-6736(86)90837-8. [DOI] [PubMed] [Google Scholar]
- 32.Rowland BC, Liao H, Adan F, Mariano L, Irvine J, Lin AP. Correcting for Frequency Drift in Clinical Brain MR Spectroscopy. J Neuroimaging. 2017;27:23–28. doi: 10.1111/jon.12388. [DOI] [PubMed] [Google Scholar]