Optimization and Validation of Accelerated Golden-angle Radial Sparse MRI Reconstruction with Self-Calibrating GRAPPA Operator Gridding

Abstract

Purpose

Golden-angle RAdial Sparse Parallel (GRASP) MRI reconstruction requires gridding and re-gridding to transform data between radial and Cartesian k-space. These operations are repeatedly performed in each iteration, which makes the reconstruction computationally demanding. This work aimed to accelerate GRASP reconstruction using self-calibrating GRAPPA operator gridding (GROG) and to validate its performance in clinical imaging.

Methods

GROG is an alternative gridding approach based on parallel imaging, where k-space data acquired on a non-Cartesian grid are shifted onto a Cartesian k-space grid using information from multi-coil arrays. For iterative non-Cartesian image reconstruction, GROG is performed only once as a pre-processing step. Therefore, the subsequent iterative reconstruction can be performed directly in Cartesian space, which significantly reduces computational burden. Here, a framework combining GROG with GRASP (GROG-GRASP) is first optimized and then compared with standard GRASP reconstruction in twenty-two prostate patients.

Results

GROG-GRASP achieved ~4.2-fold reduction in reconstruction time compared to GRASP (~333 minutes v.s. ~78 minutes) while maintaining image quality (SSIM≈0.97 and RMSE≈0.007). Visual image quality assessment by two experienced radiologists did not show significant differences between the two reconstruction schemes. With a GPU implementation, image reconstruction time can be further reduced to ~14 minutes.

Conclusion

GRASP reconstruction can be substantially accelerated using GROG. This framework is promising towards broader clinical application of GRASP and other iterative non-Cartesian reconstruction methods.

Introduction

Interest in the use of radial sampling for clinical MRI has been rapidly increasing during the past few years. It has been applied for many clinical studies (1) including cardiac (2–7), abdominal (8–12), breast (13–15), and neuro (16–18) imaging. Radial trajectories exhibit inherently incoherent undersampling behavior, which makes this sampling strategy an attractive acquisition scheme for the application of sparsity-based reconstruction methods (19–22). Compared to conventional Cartesian sampling, radial sampling has lower sensitivity to motion (23) and enables continuous data acquisitions when a golden-angle reordering scheme is used (24). These features are attractive for many dynamic post-contrast imaging applications.

Golden-angle RAdial Sparse Parallel (GRASP) MRI (21) is a framework that combines multi-coil compressed sensing reconstruction with golden-angle radial sampling and has been successfully applied for different clinical applications (25). However, one of the major barriers that limits broader applicability of GRASP as well as many other iterative non-Cartesian reconstruction methods in clinical routine is the long reconstruction time. This is mainly attributed to a) the iterative nature of compressed sensing and b) an additionally required step to interpolate the k-space from a non-Cartesian grid onto a Cartesian grid prior to the fast Fourier transform (FFT). Such an interpolation process is known as gridding and is usually implemented via convolution of the non-Cartesian k-space with a predefined kernel. This gridding step, together with a re-gridding step that transforms data back to non-Cartesian k-space, are repeatedly performed for each iteration in GRASP. This adds increasing burden to the reconstruction that is already computationally expensive.

Several methods can enable iterative non-Cartesian reconstruction without performing gridding/regridding during iterations, thus reducing image reconstruction burden. For example, non-Cartesian data can be simply interpolated onto a Cartesian grid in a pre-processing step prior to the iterative process (20). Alternatively, the Toeplitz-structure of the forward and backward encoding operators (i.e., E^HE) can be exploited, which allows replacing the gridding steps by a simple multiplication with the FFT of the pre-calculated point-spread function of the sampling process (26–28). GeneRalized autocalibrating partially parallel acquisitions Operator Gridding (GROG) (29) is another promising technique to speed up iterative non-Cartesian image reconstruction. GROG shifts non-Cartesian k-space data onto a Cartesian grid using parallel imaging in a one-to-one mapping process. Therefore, the synthesized k-space can be treated as a dataset of Cartesian samples, enabling reduction of reconstruction time by performing the subsequent iterative process directly in Cartesian space.

The feasibility of combining GROG with iterative non-Cartesian image reconstruction has been investigated in several studies. For example, it has been applied to non-Cartesian MR parameter mapping (30), real-time mouse imaging (31), dynamic-contrast-enhanced (DCE) MRI (32,33), and cardiac perfusion imaging (34). These results showed that GROG enables remarkable reduction of reconstruction time without sacrificing image quality or temporal fidelity. However, the approach has never been systematically evaluated in a clinical setting. In this work, we aimed to i) extend the GRASP approach by incorporating GROG, ii) further optimize this framework for improved reconstruction performance, and iii) evaluate the performance of this approach in clinical patient scans.

Methods

GROG-GRASP: Extending GRASP with Self-Calibrating GROG

Density Compensation Filter in GROG

Conventional non-Cartesian image reconstruction begins with a step for sampling density compensation, followed by convolution gridding, inverse FFT (iFFT), and deapodization to generate the final image. In radial imaging, a Ram-Lak filter, which is referred to as rDCF hereafter, is often used for density compensation. In contrast, a GROG reconstruction first shifts all radial k-space points onto a Cartesian grid, resulting in a Cartesian k-space where data are distributed in a pseudo-radial pattern (see Figure S1 in supplementary materials). The GROG process is performed as

$$S(k_x+{\delta }_x,k_y+{\delta }_y)=G_x^{\delta x}{G}_y^{\delta y}S(k_x,k_y)$$ [1]

where each radial k-space point at location [k_x,k_y] is shifted to its nearest Cartesian position at [k_x+δ_x,k_y+δ_y] by a distance of δ_x and δ_y in k_x and k_y direction, respectively. G_x and G_y represent weights used for the shifting, which can be pre-calculated using acquired radial k-space data (35). Before applying the iFFT, the sampling density is compensated by dividing the estimated Cartesian k-space by the GROG Density, which is a matrix indicating the number of samples that fall onto each Cartesian position. If no point is shifted to a given Cartesian position, the GROG Density is set to one at this position. The GROG density compensation filter (gDCF) for n spokes can then be defined as:

$$\mathit{\text{gDCF}}{\left(k_x,k_y\right)}_n=\frac{1}{\mathit{\text{GROG}}\mathit{\text{Density}}{\left(k_x,k_y\right)}_n}$$ [2]

Figure 1 compares the undersampling behavior between convolution gridding and GROG using a radial prostate dataset with 26 spokes and an in-plane matrix size of 224×224. Figure 1a shows the image reconstructed using convolution gridding with rDCF (Ram-Lak filter), which was implemented using the non-uniform FFT (NUFFT) toolbox (36). Figure 1b shows the image reconstructed using GROG with gDCF_default, where gDCF_default indicates the gDCF calculated using the same number of spokes used for image reconstruction (i.e., gDCF_n=26 in this case). While NUFFT generated a sharp image, GROG introduced noticeable blurring with gDCF_default. This can be attributed to the fact that gDCF_default prefers signal to noise ratio (SNR) over resolution as described in (26,34). Figure 1c shows images reconstructed using GROG, where gDCF was calculated with a larger number of spokes than that used for image reconstruction (n>26). With increasing n, the visual sharpness of the reconstructed images is improved, indicating that the use of gDCF with a large n can resolve blurring in GROG reconstruction.

Figure 1.

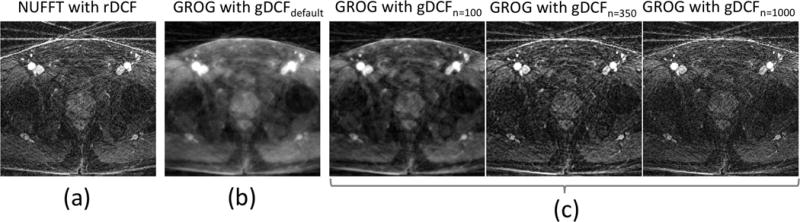
Comparison between NUFFT-based and GROG-based reconstruction of an undersampled dataset with 26 radial projections. While the reconstruction with NUFFT leads to a sharp image with dominant streaking artifacts (a), a standard GROG implementation with gDCF_default inherently prefers SNR over resolution, which introduces blurring (b). This can be overcome by modifying the GROG density compensation function (gDCF_n (c)), where n denotes the number of spokes which is used for the design of this filter. With increasing n, the blurring is resolved and results are similar compared to the image obtained with NUFFT.

From GRASP to GROG-GRASP

In the standard GRASP reconstruction (Figure 2a), the optimization starts with the dynamic multi-coil radial k-space after data sorting (21). During each iteration, the radial k-space data are first interpolated onto a Cartesian grid with a convolution, followed by an iFFT to generate an image-series. After optimization update, the image is transformed back to radial k-space to enforce data consistency. Such iteration is repeatedly performed until a certain stopping criterion is reached. The cost function is formulated as:

$$d=\underset{d}{\text{arg}min}\frac{1}{2}{\Vert Ed-\sqrt{D}S\Vert }_2^2+\lambda {\Vert Td\Vert }_1$$ [3a]

$$E=\sqrt{D}\mathit{\text{GFC}}$$ [3b]

Figure 2.

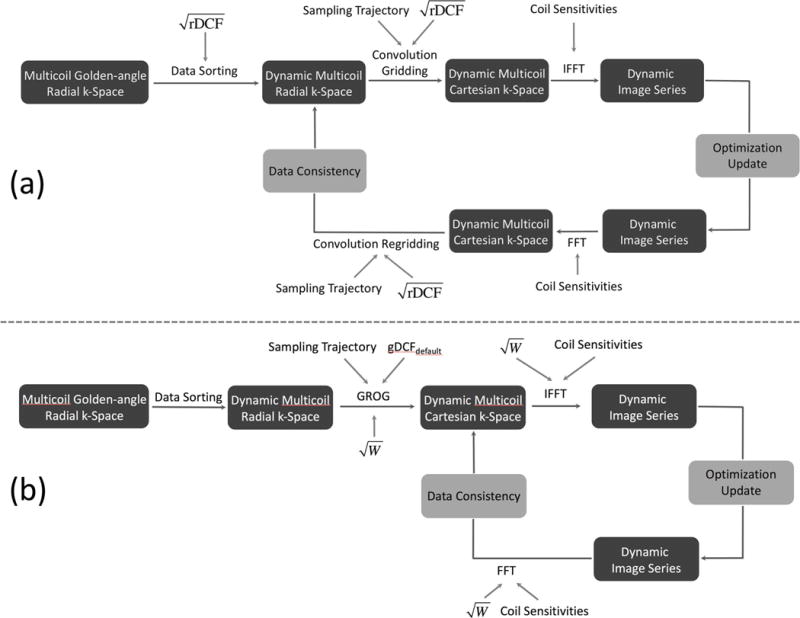
Reconstruction pipeline of conventional GRASP (a) and GROG-GRASP (b). For GRASP, computationally expensive convolution gridding and regridding steps are performed in each iteration. For GROG-GRASP, this is overcome by shifting the acquired radial k-space data with GROG on a conventional Cartesian grid as pre-processing step. Similar to the radial DCF (rDCF) which is repeatedly applied during the conventional GRASP reconstruction, a weighting filter W is employed for GROG-GRASP to improve reconstruction performance.

Here, F is the FFT operator, C represents coil sensitivity maps, d is the to-be-reconstructed dynamic image series, S is the sorted radial k-space data, G represents the convolution gridding operator, and T is a sparsifying transform. The rDCF (D in Equation 3) is included in the iterative process to speed up convergence (37). To ensure that the encoding operator E and its Hermitian transpose (denoted as E^H) are adjoint, rDCF is separated into two square root terms, one applied in a pre-compensation step before each iteration and the other one applied during each iteration as shown in Figure 2a.

In the modified GRASP framework using GROG (referred to as GROG-GRASP), GROG is performed as a pre-processing step to generate corresponding dynamic multi-coil Cartesian k-space data (Figure 2b). The iterative reconstruction is then performed by solving:

$$d=\underset{d}{\text{arg}min}\frac{1}{2}{\Vert Ed-\sqrt{W}{S}_c\Vert }_2^2+\lambda {\Vert Td\Vert }_1$$ [4a]

$$E=\sqrt{W}FC$$ [4b]

Here, S_c represents Cartesian k-space data after GROG. Therefore, mapping during the iterative process is only performed between image space and Cartesian k-space. As shown in Figure 2b, gDCF_default is applied in the GROG process to compensate for the radial sampling density. To ensure fast convergence, an additional filter, referred to as GROG weighting filter (W), is calculated using the following equation:

$$W=\frac{\mathit{\text{gDC}}{F}_n}{\mathit{\text{gDC}}{F}_{\mathit{\text{default}}}}$$ [5]

This filter is incorporated in each iteration, with a role similar to the rDCF in standard GRASP. The design of W is based on the observation from Figure 1 that gDCF for a large n resolves the blurring effect caused by the variable-density pseudo radial data distribution. When n equals the number of spokes used for reconstructing each frame, gDCF_n equals gDCF_default and therefore, no additional weighting (W=1) is applied. As in the standard GRASP reconstruction, W is separated into two square root terms to ensure that E and E^H in Equation 4 are adjoint.

The computational complexity of single-threaded 2D convolution gridding and subsequent FFT can be calculated as (38):

$$\underset{\mathit{\text{Convolution}}}{\underbrace{c_1·M·K_1,K_2}}+\underset{\mathit{\text{FFT}}}{\underbrace{c_2·N·\text{log}(N)}}$$ [6]

16/3Here, c₁ and c₂ are system and implementation dependent coefficients, M is the total number of k-space samples, K₁ and K₂ are the convolution kernel widths in two spatial dimensions, and N is the total number of pixels of the convolved grid. While the exact computation time of the convolution depends on its implementation (36), it is evident that the convolution step is computationally expensive. Therefore, eliminating this operation from the iterative reconstruction leads to faster overall reconstruction time.

Data Acquisition

In this IRB-approved and HIPAA-compliant retrospective study, MR raw data from twenty-two male patients (age=64.78±6.67 years), who were referred for clinical DCE prostate MRI exam at our institute between 02/2017 and 06/2017 and who were imaged using a radial T₁-weighted GRE sequence, were collected. Written informed consent was waived.

Each patient dataset was acquired on a clinical 3T MR scanner (MAGNETOM Prisma, Siemens Healthineers, Germany) in transverse orientation using a fat-saturated 3D stack-of-stars golden-angle radial imaging sequence (1). Golden-angle radial sampling was employed in the k_x-k_y dimension, while Cartesian sampling was used along the slice dimension. Relevant imaging parameters were: TR/TE = 4.12/1.96 ms, matrix size = 224×224×(21–26), in-plane field of view (FOV) = 240×240 mm², voxel size = 1.07×1.07×3.0 mm³, flip angle = 12°. 1755 spokes were acquired for each partition, resulting in an average total scan time of 197.45 ± 12.51 seconds. After ~15 seconds of the scan, a full-dose (0.1 mmol/kg of body weight) of contrast agent (Gadavist, Bayer Healthcare) was injected at a rate of 2 mL/sec.

Image Reconstruction

Both GRASP and GROG-GRASP reconstructions were performed in Matlab (Mathworks, MA). After coil-compression to 10 virtual channels (39), 26 consecutive spokes were grouped for one dynamic frame, resulting in a temporal resolution of ~2-3 seconds/volume. The GROG reconstruction code was obtained from https://github.com/edibella/Reconstruction. First-order finite differences along the temporal dimension were chosen as the sparsifying transform T. To ensure a reasonable balance between image quality and temporal fidelity, a fixed regularization parameter was empirically selected, which was done separately for GRASP and GROG-GRASP (21). For GRASP, convolution gridding was performed with a 6×6 Kaiser-Bessel kernel and 1.5-fold oversampling. For GROG-GRASP, the weighting filter W (Eq. 5) was calculated with n=350 (≈224∙π/2), which was empirically selected according to the Nyquist criterion. To assess the influence of the parameter n, the GROG-GRASP reconstruction was repeated with n=100 and n=1000 in one dataset.

The optimization problem for both reconstruction schemes was solved using a non-linear conjugate gradient algorithm. The stopping criterion for all reconstructions was set as 24 iterations or a change of the objective function smaller than 10⁻⁴, whichever was achieved faster. Coil sensitivity maps were estimated from the static 3D image volume reconstructed from all spokes using the adaptive combination approach (40). To further improve processing speed, GROG-GRASP was additionally performed on GPUs by using the MATLAB function “gpuArray”. Following iFFT along the slice dimension, all slices of each dataset were reconstructed sequentially. Reconstructions were performed on a server equipped with 256 GB RAM and two 6-GB NVIDIA GPU cards. The reconstruction time for each dataset was recorded for comparison.

Image Analysis

The structural similarity index (SSIM) and root-mean-square error (RMSE) between GRASP and GROG-GRASP were calculated slice-by-slice for all datasets. The results were averaged over all slices and all subjects to represent mean ± standard deviation. Additionally, two regions of interest (ROIs) from a central slice of each dataset were manually drawn in the femoral artery and the prostate. The temporal signal profiles for these two ROIs were compared between GRASP and GROG-GRASP. First, the temporal signals were converted to relative enhancement signals as follows:

$$E(t)=\frac{S(t)-S_{\mathit{\text{baseline}}}}{S_{\mathit{\text{baseline}}}}$$ [8]

where S_baseline is the signal intensity before contrast enhancement, calculated by averaging the first five time points (~15s). The initial area under the curve (IAUC), which is calculated as the area under the curve for the first 90 seconds (41), was measured for all temporal signals:

$$\mathit{\text{IAUC}}(t)={\displaystyle {\int }_0^{t}E(\tau )d\tau }$$ [9]

Additionally, the initial slope was determined:

$$\mathit{\text{Initial}}\mathit{\text{Slope}}=\frac{E(t_p)}{t_p}$$ [10]

where t_p is the time to a point where a given signal profile has the steepest gradient. IAUC and initial slope were averaged to represent mean ± standard deviation across all subjects, and Intraclass Correlation Coefficient (ICC) was calculated to assess the correlation between the signals computed from GRASP and GROG-GRASP.

Visual Image Quality Assessment

To assess image quality in a more clinically focused way, two post-contrast phases (one arterial phase and one delayed phase) were manually selected from each dataset. After pooling and randomizing the respective GRASP and GROG-GRASP images, two board-certified abdominal radiologists (H.C. and C.H., with 10 and 2 years of post-fellowship experience, respectively), who were blinded to the reconstruction schemes, scored overall image quality, sharpness of prostatic capsule and overall artifact level. A 4-point Likert-type scale was used for the scoring: overall image quality: 4=good, 3=adequate, 2=borderline, 1=non-diagnostic; sharpness of prostatic capsule: 4=good, 3=adequate, 2=partially seen, 1=not seen; overall artifact level: 4=none, 3=mild, 2=significant, 1= unreadable. The reported scores were averaged over the two readers and mean ± standard deviation was calculated for both contrast phases. A non-parametric paired two-tailed Wilcoxon signed-rank test was performed for statistical assessment, with a P-value less than 0.05 indicating statistical significance. Inter-reader variability was assessed using the Bland-Altman analysis.

Results

Figure 3 compares results from the GROG-GRASP reconstructions with different W. Reconstruction without additional weighting (W=1) generated noticeable blurring, which is consistent with the effect observed in Figure 1. Both image sharpness and convergence speed are improved when n increases. Similar results were obtained for n=350 and n=1000, confirming the selection of n=350 for GROG-GRASP.

Figure 3.

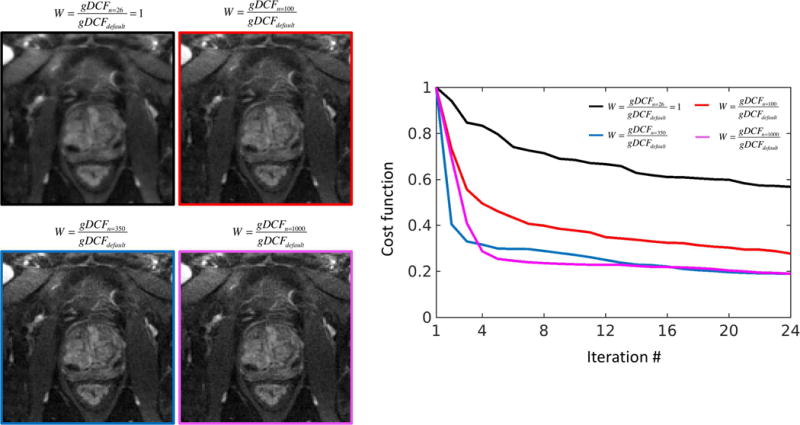
Influence of the design of the weighting filter W on GROG-GRASP image quality. Reconstruction without an additional filter (n=26, W=1) leads to slow convergence and blurring, which is improved when an additional filter (n>26) is used. While slight blurring remains for n=100, sharp images and rapid convergence are achieved when choosing n according to the Nyquist criterion (n=base resolution∙π/2≈350). Results are similar when using higher n (e.g., n=1000), suggesting that image quality is consistent within a certain range for n.

Figure 4a compares GRASP with GROG-GRASP for three different temporal frames of a representative dataset. For all phases, no visual difference was observed between the two reconstruction schemes. Figure 4b shows the corresponding temporal signal profiles from two ROIs in the femoral artery and the prostate (red and yellow circles), suggesting high temporal correlation between the two methods.

Figure 4.

(a) Three different contrast phases, reconstructed with standard GRASP (first row) and GROG-GRASP (second row). No visual differences can be seen between the two methods. This finding is confirmed by the temporal signal profiles, which show high temporal correlation (b).

The SSIM indexes and RMSE between GRASP and GROG-GRASP were 0.97 ± 0.01 and 0.007 ± 0.002, suggesting a high degree of similarity. The IAUC, initial slope, and ICC are summarized in Table 1a, indicating strong correlation between the temporal signal profiles generated from GRASP and GROG-GRASP. Table 1b summarizes the readers’ scores. No significant difference (P>0.05) was found throughout all assessment categories. The inter-reader variability is shown in Figure S2 (supplementary materials). Reconstruction times for GRASP and GROG-GRASP were 332.67 ± 32.83 minutes and 78.34 ± 8.04 minutes, respectively, averaged over all datasets. With GPU implementation, the reconstruction time of GROG-GRASP was further reduced to 14.04 ± 1.29 minutes (representative images are shown in supplementary Figure S3).

Table 1(a).

Summary of the IAUC (initial area under the curve) and the initial slope of the temporal signals, which were computed in the femoral artery and in the prostate. The ICC (intraclass correlation coefficient) indicates that the temporal signals are well-correlated between GRASP and GROG-GRASP.

		IAUC	ICC (IAUC)	Initial Slope	ICC(Initial Slope)
Femoral Artery	GRASP	72.38±17.78	0.999	0.021±0.01	0.948
	GROG-GRASP	71.49±17.93		0.022±0.01
Prostate	GRASP	51.92±18.17	0.999	0.01±0.00	0.980
	GROG-GRASP	52.42±17.92		0.01±0.00

Table 1(b).

Qualitative comparison between GRASP and GROG-GRASP for two contrast-enhancement phases. No significant differences (P>0.05) between the two reconstruction schemes were found in all assessed categories.

		Overall Image Quality	Sharpness of Prostatic Capsule	Overall Artifact Level
Arterial Phase	GRASP	3.07±0.48	3.07±0.51	3.00±0.47
	GROG-GRASP	3.05±0.47	3.10±0.52	3.02±0.51
Delayed Phase	GRASP	3.55±0.38	3.73±0.34	3.52±0.40
	GROG-GRASP	3.52±0.40	3.69±0.40	3.50±0.42

Scoring criteria:

For overall image quality, 4=good, 3=adequate, 2=borderline, 1=non-diagnostic.

For sharpness of prostatic capsule, 4=good, 3=adequate, 2=partially seen, 1=not seen.

For overall artifacts level: 4=none, 3=mild, 2=significant, 1=unreadable

Discussion

In this work, we proposed a framework that combines GRASP with self-calibrating GROG. GROG-GRASP eliminates the requirement for the convolution gridding steps within the iterative optimization, thus enabling a substantial reduction of reconstruction time compared to conventional GRASP. The performance of GROG-GRASP was validated in a patient cohort, which is an important step prior to translation of this approach into clinical practice. The SSIM, RMSE, ICC, and visual image quality assessment suggested that the combination of GRASP with GROG preserves image quality and temporal fidelity. In addition, we have also optimized the reconstruction algorithm to further improve reconstruction performance by incorporating an additional filter during the iterative process. For the implementation of this filter, the parameter n has to be chosen. However, the exact choice of n only has a minor influence on image quality, and choosing n according to the Nyquist rate (n=base resolution∙π/2) gave consistent results over all datasets used for this study.

Since GROG is used as a pre-processing step, it can benefit a broad range of iterative non-Cartesian reconstruction methods, including techniques based on k-space based or image-space based parallel imaging, compressed sensing, or their combinations. Prerequisites for successful implementation of GROG are a sufficient number of coil-array elements and adequate SNR (29). Given the wide-spread use of many-element coil arrays and the availability of a high-SNR dataset when all acquired radial spokes are combined for GROG calibration, these requirements are intrinsically fulfilled.

In this study, the performance of GROG-GRASP has been demonstrated for prostate imaging and therefore only for male subjects. However, the reconstruction performance of the proposed technique is independent of the particular application and can be extended to other applications such as cardiac or liver MRI.

Conclusion

GRASP reconstruction can be substantially accelerated using self-calibrating GROG as pre-processing step to obtain Cartesian k-space data. This permits elimination of the time-consuming gridding process from each iteration of the optimization process while maintaining image quality. The proposed combination shows promise towards implementation of GRASP and other iterative non-Cartesian reconstruction methods in clinical routine.

Supplementary Material

Supp info

Figure S1 Radial sampling patterns with different number of spokes (top row), their corresponding data distribution in Cartesian space after GROG (middle row), and zoomed GROG density (bottom row). With increasing acceleration rates, larger gaps (due to higher undersampling factor) in the outer k-space regions occur, which can lead to blurring in the reconstructed image.

Figure S2 Comparison of standard GRASP, GROG-GRASP (CPU), and GROG-GRASP (GPU) in a representative image slice. All reconstructions show comparable image quality without visible differences.

Figure S3 The inter-reader variability was assessed for both GRASP (left) and GROG-GRASP (right) with the Bland-Altman analysis. The average score for GRASP and GROG-GRASP was both 3.3, the mean score difference for GRASP and GROG-GRASP was both 0.1. This shows similar inter-reader agreement for both reconstruction schemes, suggesting that no bias for one particular reconstruction over the other occurred between the readers.