The relationships between tissue microstructure and the diffusion tensor in simulated skeletal muscle

Abstract

Purpose

To establish a series of relationships defining how muscle microstructure and diffusion tensor imaging (DTI) are related.

Methods

The relationship between key microstructural features of skeletal muscle (fiber size, fibrosis, edema, and permeability) and the diffusion tensor were systematically simulated over physiologically relevant dimensions individually, and in combination, using the numerical simulation application DifSim. Stepwise multiple regression was used to identify which microstructural features of muscle significantly predict the diffusion tensor using single-echo and multi-echo DTI pulse sequences. Simulations were also performed in models with histology informed geometry to investigate the relationship between fiber size and the diffusion tensor in models with real muscle geometry.

Results

Fiber size is the strongest predictor of λ2, λ3, MD, and FA in skeletal muscle, accounting for ~40% of the variance in the diffusion model when calculated with single-echo DTI. This increased to ~70% when diffusion measures were calculated from the short T2 component of the multi-echo DTI sequence. This non-linear relationship begins to plateau in fibers with greater than 60µm diameter.

Conclusion

As normal fiber size of a human muscle fiber is 40µm–60µm, this suggests that DTI is a sensitive tool to monitor muscle atrophy, but may be limited in measurements of muscle with larger fibers.

Introduction

Skeletal muscle is a highly organized, hierarchical tissue containing long contractile cells bundled to form fascicles, which are again bundled to form the larger whole muscle (1). These subdivisions of muscle are all packaged in layers of extracellular matrix (ECM). With injury, microstructural (cell-level) changes have been observed, which are related to impaired muscle function (2,3). Commonly observed changes in muscle microstructure with injury or pathology include fiber atrophy/hypertrophy (4,5), fibrosis (6), membrane damage (permeable fibers) (7–9), and edema (10–12). The current gold standard for studying injury- or plasticity-associated changes in muscle microstructure is histology, which is highly invasive, is semi-quantitative, and difficult to extrapolate to the entire muscle. Therefore a quantitative, non-invasive technique to study muscle microstructural changes resulting from injury would be a potentially important contribution to the clinical assessment of muscle pathologies.

Diffusion tensor imaging (DTI) is a magnetic resonance imaging (MRI) technique that has been shown to be sensitive to changes in muscle microstructure (13–15). DTI measures the anisotropic diffusion of water in muscle, which is restricted by microstructure. However, the relationship between microstructure, the actual diffusion changes, and the resultant diffusion tensor (DT) associated with muscle injury or pathology are exceedingly complex and not amenable to simple analysis. Nevertheless, certain structural and physiological quantities averaged over the voxel volume can nevertheless serve as a proxy for actual structural features and their changes. For example, several groups have shown a less restricted diffusion profile when muscles are shortened, and a more restricted diffusion profile when muscles are elongated (16–20). This effect is attributed to changes in muscle fiber diameter that occur when a whole muscle is contracted (fiber diameter increases) or elongated (fiber diameter decreases). However, such a simple explanation is complicated in injured states as less restricted diffusion is also observed when edema is present or structural integrity of the sarcolemma is compromised (fibers are more permeable to water exchange between the intra- and extra-cellular compartments), regardless of underlying changes in muscle fiber diameter (4,21,22). In addition to changes in the permeability of the sarcolemma and size of fibers, diffusion changes have been attributed to increases in T2, which results in increased signal to noise ratio, secondary to increased extra-cellular fluid volume (23–25). Non-diffusion, MR-relaxometry experiments can uncover these edema-related fluid shifts involved in maintaining metabolic and volumetric stasis between the intracellular compartments (4,12,26,27), but lacks the ability to resolve microstructural features of muscle, which directly inform physiology and performance.

Muscle exhibits a multi-exponential T2 decay signal of water, which originates from macromolecular interactions (ultrashort; <5ms), intra-cellular (short T2; 20ms–40ms) and extra-cellular (long T2; 90+ms) compartments of muscle (26–30). The ultrashort T2 compartment is often too short to be measured using spin echo imaging due to requisite echo times and is mostly ignored (10). In the presence of edema, increased fluid content is observed in the extra-cellular space around cells (11,31). Due to the changes in cellularity observed during edema, as the volume fraction of extracellular water increases, whole muscle T2 increases. However, whole muscle T2 can also be traced to intracellular origins (24,26,32). While simplification of T2 decay into a one-compartment model is adequate for normal muscle, injured or pathologic muscle exhibits multiple microstructural changes, including edema, which renders a single compartment model too simple (10,12,30). One approach to addressing this complication is multi-echo DTI, a MR technique that combines basic principles to simultaneously measure T2 and the DT, which allows quantification of diffusion originating from the short (intra-cellular) and long (extra-cellular) compartments of muscle (10,12). This technique has the potential to increase the specificity of DTI to be a better tool to measure changes in muscle microstructure.

The complexity of the relationship between muscle microstructure and the diffusion profile in both normal and injured muscle thus requires a systematic investigation if useful clinical metrics are to be derived from the measured diffusion signal. The effect of muscle microstructural changes on the measured DT can be quantified by computer simulation. Several groups have investigated the effect of imaging parameters such as noise, partial volume, and diffusion weighting strength on the DT, to inform guidelines for developing DTI protocols (23,25,33–35). Other studies have simulated the effect of fiber geometry, edema, atrophy, and permeability, on the diffusion signal in muscle (21,36,37). In this paper we utilize the DTI simulation application DifSim, which is capable of modeling an entire DTI experiment with complex tissue geometries. Therefore, the purpose of this study is to use a novel, sophisticated, in silico tool to carefully investigate the relationships between both simplified and histology informed muscle microstructure and the DT. Specifically, we will quantify the influence of muscle fiber size, fibrosis, injury induced membrane permeability, and edema, in isolation and in combination, on the DT using single- and multi-echo DTI techniques. We hypothesize intra- and extra-cellular microstructural changes in injured muscle have characteristic diffusion profiles that can be uncoupled with multi-echo DTI.

Methods

Overview of DifSim

DifSim embeds MCell, a Monte Carlo simulator for cellular microphysiology (38–40), within an MRI simulator which tracks particle location, magnetization amplitude and phase, within a user defined arbitrarily complex geometrical model (41). DifSim is capable of supporting boundary and particle interactions, and multiple molecular species with different diffusion coefficients.

The basic numerical approach of DifSim is presented here. A more complete treatment of DifSim can be found in Balls et. al 2009 (41). A more complete treatment of MCell can be found in reference #:38–40. Particles (spins) diffusing in time (t) at a position (x(t)) have a spin (j) and will accrue a phase (θ_j) generated by the spin’s displacement in the direction of the magnetic field (G(t)) gradient

$${\theta }_j(t)={\int }_{t_0}^{t}G(\tau )·x_j(\tau )d\tau$$ Equation 1

where “·” represents the dot product. If time is discretized into N_t time steps of length dt, and measure the magnetic field strength and spin location at each time t_i, equation 1 can be approximated as

$${\theta }_j(t)={\sum }_{i=0}^{N_t}G(t_i)·x_j(t_i)\mathit{\text{dt}}$$ Equation 2

The relaxation is introduced for each particle j at each time t_i by using particle magnetization vector:

$$(m_x^j,m_y^j,m_z^j)=(m_{\rho }^j\mathit{\text{cos}}({\theta }_j),m_{\rho }^j\mathit{\text{sin}}({\theta }_j),m_z^j)$$ Equation 3

as:

$$m_{\rho }^j=m_{\rho }^j(0)e^{-t/T_2}$$ Equation 4

$$m_z^j=m_z^j(0)e^{-t/T_1}+(1-e^{-t/T_1})$$ Equation 5

By simultaneously simulating the diffusion of N_p individual spins with MCell, the echo amplitude is

$$E=\frac{e^{-t/T_2}}{N_p}{\sum }_{j=1}^{N_p}{e}^{i\gamma {\theta }_j}$$ Equation 6

where γ is the gyromagnetic ratio.

Simulation DTI pulse sequence parameters

Pulse sequence parameters used in our MRI simulations were based on those used on a 7T MRI scanner at our institution (Bruker, Billerica MA) (42). A diffusion-weighted, multi-echo pulse sequence was used (12). The first echo was TE=21.76ms, with 16 equally spaced echoes at 10ms intervals, 15 gradient directions, b=500mm²/s (δ/Δ 2ms/9ms), and voxel size 200×200×200µm³.

Simulation details

Simulations were performed on one of 4 Linux clusters (Supporting Table S1). The total number of computer hours for all simulations was 27 years, 51 weeks.

The smallest barrier spacing encountered by particles was 1µm. In MCell, diffusion steps are not set to a fixed length, but are chosen to match the probability distribution of the unbounded diffusion over the length of a single time step. The average distance a molecule could move during a step was 96nm.

DT calculation

For each voxel, the DT was calculated using single-echo data (Equation 7a) and as two compartments in slow exchange (Equation 7b) from multi-echo data using custom written software in Matlab (Mathworks, Natick MA).

$$S_i(b)/S_0=e^{(-{\mathit{\text{bD}}}_i)}+\epsilon$$ Equation 7a

$$S_i(\mathit{\text{TE}},b)/S_0=f_a{e}^{\left(\frac{-\mathit{\text{TE}}}{T_{2,a}}\right)}{e}^{(-{\mathit{\text{bD}}}_{i,a})}+f_b{e}^{\left(\frac{-\mathit{\text{TE}}}{T_{2,b}}\right)}{e}^{(-{\mathit{\text{bD}}}_{i,b})}+\epsilon$$ Equation 7b

Where S_i(TE, b) is the signal along a certain gradient direction (S_i) at echo time (TE) and b-value (b), f is the volume fraction of the short (a) and long (b) transverse relaxation (T2) compartments of the apparent diffusion coefficient (D_i) along the same gradient direction, such that f_a +f_b = 1. First, a bi-exponential decay function was fit from the b=0 image from each echo using the MERA 2.03 toolbox to find f_a, f_b, T_2,a, and T_2,b (43). A nonlinear least squares fit was used to solve D_i,a and D_i,b using the fit function in Matlab (lower limit=0mm²/s; upper limit=1mm²/s). The DT was solved using a nonnegative least-squares fit using the fanDTasia toolbox (44). Diagonalization of the DT yields the eigenvalues (λ1, λ2, and λ3), which were used to calculate mean diffusivity (MD) and fractional anisotropy (FA) (Equations 8, 9). For single-echo analysis, data from the first recorded echo of the multi-echo DTI sequence was used.

$$\mathit{\text{MD}}=\frac{\lambda 1+\lambda 2+\lambda 3}{3}$$ Equation 8

$$\mathit{\text{FA}}=\sqrt{\frac{3}{2}}\sqrt{\frac{{(\lambda 1-\mathit{\text{MD}})}^2+{(\lambda 2-\mathit{\text{MD}})}^2{+(\lambda 3-\mathit{\text{MD}})}^2}{\sqrt{\lambda 1^2+\lambda 2^2+\lambda 3^2}}}$$ Equation 9

Fractional anisotropy is a normalized scalar measure of how anisotropic the diffusion profile is and varies from 0 (perfectly isotropic) to 1 (perfectly anisotropic). Mean diffusivity is a measure of the average overall diffusion. Mean diffusivity of unrestricted water is 2.5×10⁻³mm²/s. Generally, as the restricted diffusion profile increases (increased FA), there is less overall diffusion (decreased MD) and vice versa.

Simplified Model generation

As a first step, the complex geometry of skeletal muscle was reduced to simple, closely packed hexagons, which has a limited number of defining parameters that allowed us to systematically study the relationship between an idealized muscle microstructure model and the measured DT. The features of muscle microstructure studied include fiber size, fibrosis, edema, and permeability and are depicted individually in Figure 1. Ideal muscle model geometries were simplified into geometrically symmetric patterns in the x-y axis, and extruded linearly along the z-axis, which approximates but not exactly replicates real muscle microstructure. Fiber size was varied by systematically changing the diameter of the hexagon structures. Fibrosis was modeled by varying the spacing between muscle fibers. Edema was simulated by varying the volume fraction of water in the “extracellular” space. Permeability changes due to structural defects in a muscle fiber were varied by randomly defining walls of the fibers as transparent to water molecules to diffuse between the intra- and extra-cellular spaces.

Figure 1.

Schematic depicting ideally shaped hexagonal models of skeletal muscle (top row; intracellular) and the extracellular matrix (middle row; extracellular). Atrophy/hypertrophy was simulated by changing the diameter of the muscle fibers, edema was simulated by changing the extracellular water volume fraction, fibrosis was simulated by changing the spacing between muscle fibers, and permeability was simulated by allowing free transport between fiber walls into the ECM (red).

Microstructural features of skeletal muscle were varied individually and in combination over a range of physiologically relevant values (Table 1) to determine their individual contributions to the DT, individually, and in combination with one another. The basic model representative of normal healthy muscle was defined with 50µm fiber diameter, 2µm fiber spacing, 5% extracellular water volume fraction and 0% permeable walls. Individual features of muscle microstructure were investigated based on this model. Models were constructed in Google SketchUp, and triangulated using Blender (45). Intra- and extra-cellular particles were assigned different diffusion coefficients and magnetic relaxation (T1, T2) rates based on literature values. Relaxation rates and diffusion coefficients of molecular species were taken from the literature; intracellular: T1/T2: 1,740/25ms (12,46,47), D: 1.8*10⁻³mm²/s (48–50); extracellular: T1/T2: 2,500/95ms (12,47), D: 2.2*10⁻³mm²/s (51,52). Two hundred thousand particles were simulated in order to accurately converge on an analytical solution based on the diffusion coefficients and b-value chosen for this experiment (41). Each model was simulated 10 times with a different initial location of diffusing particles to measure variance in an individual model. No noise was added in order to measure the exact relationship between muscle microstructure and the DT under ideal imaging conditions. Myofilaments within a muscle fiber, or extracellular matrix proteins outside of muscle fibers, were not physically defined in this model. However, restricted diffusion from myofilaments and extracellular matrix proteins is at least partially reflected in the assignment of diffusion coefficients from previous studies of diffusion of small molecules in these tissues.

Table 1.

Microstructural features and the range over which they were varied individually and in combination of muscle with simplified geometry.

Microstructure	Units	Lower Bound	Upper Bound	Step
				Individual	Interactions
Fiber Size	µm	10	100	10	20
Permeability	% transparent fibers	0	60	20	20
Fibrosis	µm	1	10	1	2
Edema	Extra-cellular volume fraction	5	50	5	10

Histology informed geometry models

To evaluate how our results compare to real diffusion measurements of muscle, we created models with geometry derived from previous animal histology experiments. Masson’s Trichrome stained histology of muscle fibers from control, cardiotoxin injected, botulinium toxin (botox) injected, surgically denervated and surgically tenotomized rat tibialis anterior muscles at 1, 3, 7, 14 and 30 days post injury were manually segmented and triangulated in Blender (Fig. 2).

Figure 2.

Schematic depicting sample histology informed models of skeletal muscle. Fibers were manually traced from histology images.

Cardiotoxin is venom from the naja mossambica snake, and induces depolarization of the sarcolemma that results in a massive, rapid onset muscle degeneration from which muscle can heal in approximately 30 days (53). Botox is a bacterium-produced neurotoxin that prevents acetylcholine release in motor neurons and results in muscle atrophy (3). Surgical denervation creates a physical nerve injury that prevents a muscle from contracting, resulting in chronic atrophy (54). Surgical tenotomy severs the tendon attaching muscle to bone, resulting in acute fiber hypertrophy due to isometric contraction of the muscle, followed by chronic atrophy (55). Average fiber diameters were recorded for each model. Each histological image was separated into 9 individual diffusion experiments, covering a total volume of 600µm × 600µm × 200µm. Extracellular water volume fractions assigned to each model are defined in Table 2 and are approximated from histologic and MRI studies of these tissues. The same relaxation and diffusion coefficients assigned to the simplified models of muscle were applied to the histology informed models.

Table 2.

Extracellular water volume fractions applied to models with histology informed geometry.

	Day 1	Day 3	Day 7	Day 14	Day 30
Control	5	5	5	5	5
Botox	20	15	10	10	10
Denervation	10	10	10	10	10
Tenotomy	10	5	5	5	5
Cardiotoxin	X	45	35	10	5

Statistics

The relationship between individual features of muscle microstructure and the DT were quantitatively examined. To determine how the interaction between different compartments of muscle microstructure and the DT (FA and MD) are related, a stepwise multiple linear regression model was used.

To demonstrate the difference in the DT measured with single- and multi-echo DTI, a curve was fit to describe the relationship fiber size and the DT for simplified, non-edematous models using the single-echo data. Then, the same fiber size models were simulated with edema (45% extracellular water volume fraction) and the DT calculated with both single- and multi-echo DTI data. The relationship between the single, short, and long DT’s and fiber size in edematous muscle were compared to the non-edematous curve. Coefficient of determination (R²) was calculated to measure the amount of variance explained by the original model and the edematous DT’s. Then, the same equations were compared to the single, short, and long DT’s in models with histology informed geometry.

The threshold for significance (α) was set to 0.05 for all analyses. Statistics were computed using SPSS 20.0 (IBM, Armonk, NY). All data are reported as mean ± standard deviation.

Results

Individual relationships between simplified muscle geometry and the measured diffusion tensor

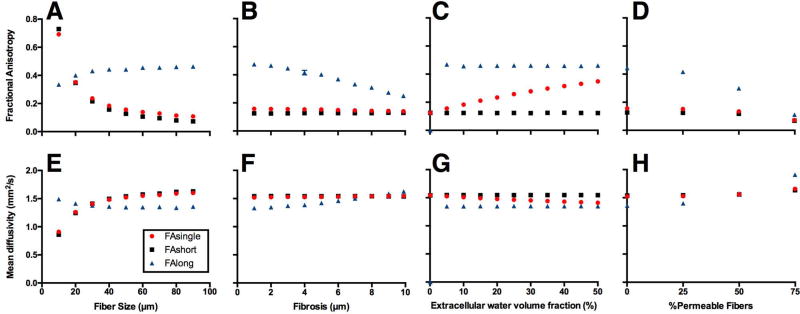
Of the independent features studied, fiber size has the largest dynamic range of the microstructural features examined in this study. Above 60µm diameter, the relationship between fiber size and the DT appears to reach a plateau (Fig. 3A, D; S Fig. 1A, E, I). The single-echo and short compartment of the multi-echo DTI pulse sequences appear to be nearly identical as fiber size, fibrosis, and permeability was varied (Fig. 3A, B, D–F, H; Supporting Fig. S1A, B, D–F, H–J, L). However, as extracellular water volume is increased (muscle becomes more edematous) the single-echo DTI measurements appear to become more similar to the long compartment of the multi-echo DTI measurements (Fig. 3C, G; Supporting Fig. S1C, G). Interestingly, there is no change in either the short or long compartment diffusion measurements as extracellular water volume fraction is increased. The relationships between microstructure and the diffusion tensor were nearly identical between λ2 and λ3 (Supporting Fig. S1E–L).

Figure 3.

Fractional anisotropy (A–D) and mean diffusivity measurements (E–H) measurements of simplified models of skeletal muscle. Diffusion measurements were made from single-echo DTI (red circles) and the short (black squares) and long (blue triangles) T2 compartments from the multi-echo DTI sequence. Fiber size (A, E), fibrosis (B, F), edema (C, G), and permeability (D, H) were varied over a physiologically relevant range of parameters defined in Table 1.

Predictive capacity of muscle microstructure on the diffusion tensor

Ten replicates of 500 models were input into the stepwise multiple linear regression model to determine which features of microstructure are the best predictors of the DT. As fiber size has a strong non-linear relationship to the DT, it was log_e transformed for all statistical analysis. Using single-echo DTI, fiber size was the best predictor of MD, λ2, λ3, and FA, explaining 40.7%–44.9% of the variance respectively (Table 3). The next best microstructural predictor of MD, λ2, λ3, and FA was permeability, explaining 29.0% to 35.7% of the variance. Edema and fibrosis together explain 3.1% to 6.4% of variance for MD, λ2, λ3, and FA. Fiber size, permeability, and fibrosis are positively correlated with MD, λ2, and λ3, and negatively correlated with FA. Edema is positively correlated with MD, and FA. Interestingly, edema was a strong predictor of λ1 (R²=0.98, β=.990), with fibrosis (R²=0.30 β=−.046) and fiber size (R²<0.10, β=.018) also significant predictors in the model.

Table 3.

Stepwise linear regression results

DTI Analysis	Diffusion Measure	Microstructure	β	Standardized β	R2
Single Echo
	λ1	Constant	1.78E-03
		Edema	4.64E-06	.990	.980
		Fibrosis	−1.08E-06	−.046	.983
		Fiber Size	1.55E-06	.018	.983
	λ2	Constant	1.59E-04
		Fiber Size	2.39E-04	.670	.449
		Permeability	5.77E-04	.581	.787
		Fibrosis	1.65E-05	.168	.815
		Edema	1.79E-06	.091	.823
	λ3	Constant	2.02E-04
		Fiber Size	2.22E-04	.638	.407
		Permeability	5.78E-04	.597	.763
		Fibrosis	1.68E-05	.176	.794
		Edema	1.23E-06	.064	.798
	MD	Constant	7.14E-04
		Fiber Size	1.54E-04	.646	.417
		Permeability	3.85E-04	.580	.754
		Edema	2.55E-06	.195	.791
		Fibrosis	1.07E-05	.164	.818
	FA	Constant	7.49E-01
		Fiber Size	−1.14E-01	−.661	.437
		Permeability	−2.59E-01	−.539	.727
		Fibrosis	−7.95E-03	−.168	.755
		Edema	5.89E-04	.062	.759
Multi-Echo (Short T2)
	λ1	Constant	1.77E-03
		Permeability	−3.16E-06	−.132	.018
		Fiber Size	−7.72E-07	−.090	.026
		Edema	2.52E-08	.054	.029
	λ2	Constant	−2.91E-04
		Fiber Size	3.99E-04	.873	.762
		Permeability	4.11E-04	.324	.866
		Fibrosis	4.20E-06	.033	.867
	λ3	Constant	−2.82E-04
		Fiber Size	3.91E-04	.870	.756
		Permeability	4.07E-04	.325	.862
		Fibrosis	4.54E-06	.037	.864
	MD	Constant	3.99E-04
		Fiber Size	2.63E-04	.871	.758
		Permeability	2.72E-04	.323	.863
		Fibrosis	2.89E-06	.035	.864
	FA	Constant	1.05
		Fiber Size	−2.10E-01	−.841	.707
		Permeability	−2.17E-01	−.313	.806
		Fibrosis	−2.15E-03	−.031	.807
Multi-Echo (Long T2)
	λ1	Constant	2.11E-03
		Permeability	2.89E-05	.362	.131
		Fibrosis	−2.26E-06	−.286	.213
		Fiber Size	4.36E-06	.152	.236
		Edema	1.82E-07	.115	.249
	λ2	Constant	1.24E-03
		Permeability	8.35E-04	.821	.673
		Fibrosis	3.86E-05	.384	.821
		Fiber Size	−7.63E-05	−.209	.865
	λ3	Constant	−2.82E-04
		Fiber Size	3.91E-04	.870	.756
		Permeability	4.07E-04	.325	.862
		Fibrosis	4.54E-06	.037	.864
	MD	Constant	1.55E-03
		Permeability	5.66E-04	.818	.669
		Fibrosis	2.52E-05	.368	.805
		Fiber Size	−6.03E-05	−.243	.863
	FA	Constant	3.07E-01
		Permeability	−3.27E-01	−.784	.615
		Fibrosis	−1.74E-02	−.421	.792
		Fiber Size	4.12E-02	.275	.867

Diffusion in the short T2 compartment calculated with multi-echo DTI was hypothesized to represent intracellular diffusion. Similar to single-echo, fiber size is a strong predictor of the short compartment of MD, λ2, λ3, and FA, explaining 70.7%–76.2% of the variance in the model (Table 3). Additionally, permeability (R²: 0.098–0.106) and fibrosis (R²: 0.001–0.002) were significant predictors of MD, λ2, λ3, and FA. Fiber size, permeability, and fibrosis are positively correlated with MD, λ2, and λ3, and negatively correlated with FA. Permeability (β= −.132), fiber size (β= −.090), and edema (β=.054) were all found to be significant predictors of λ1, however, these microstructural measurements only explain 2.9% of the variance in the model.

Diffusion in the long T2 compartment calculated with multi-echo DTI was hypothesized to represent extracellular diffusion. Permeability was the best predictor of MD, λ2, and FA (R²: 0.615–0.669), followed by fibrosis (R²: 0.135–0.177) then fiber size (R²: 0.044–0.075; Table 3). Permeability and fibrosis are positively correlated with MD and λ2 and negatively correlated with FA. Fiber size is negatively correlated with MD and λ2 and positively correlated with FA. Unexpectedly, fiber size was the strongest predictor of λ3 (R²=0.756, β=.870), followed by permeability (R²=0.106, β=.325) and fibrosis (R²=0.001, β=.037). All four microstructural features tested were significant predictors of λ1, however the total variance explained by the model was relatively low (R²=0.249) compared to other dependent variables.

Resolution of fiber size measurements using multi-echo DTI

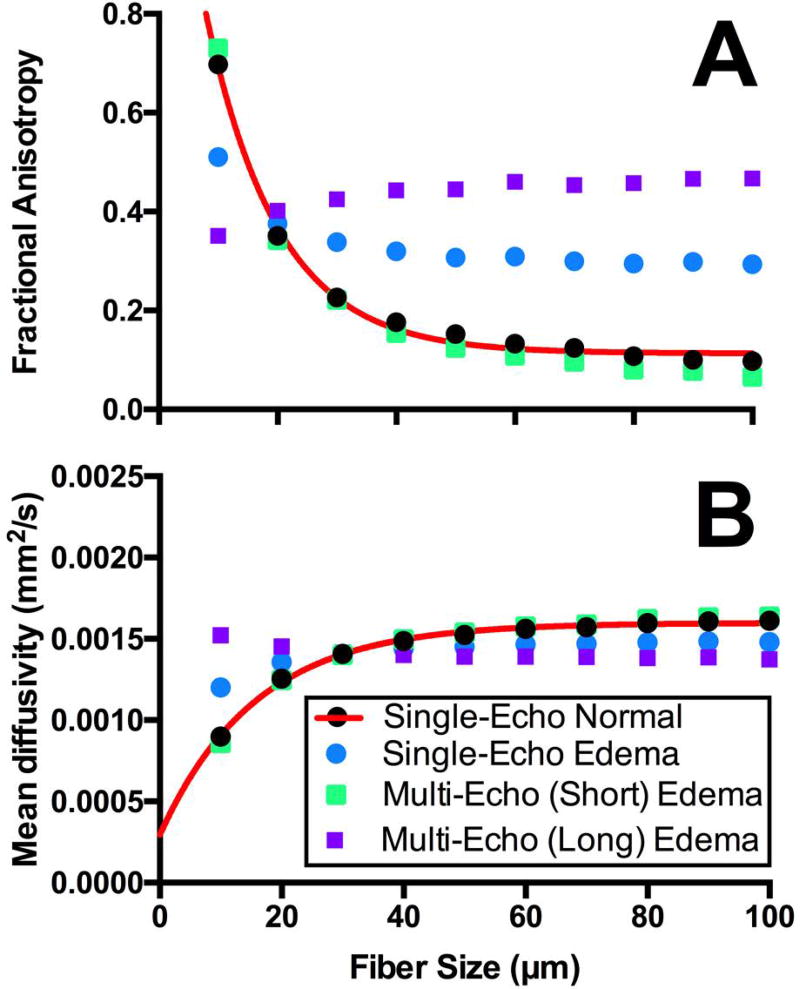
The relationship between fiber size and FA calculated from single-echo DTI for normal (5% extracellular water volume fraction) simplified muscle was fit to an exponential decay equation, which explained 99.5% of the variance in the data (Fig. 4a). When fiber size and FA were simulated under edematous conditions (45% extracellular water volume fraction), the original equation explained none of the variance when FA was calculated from single-echo DTI data (R²=−5.68) or from the long T2 compartment using multi-echo DTI analysis (R²=−76.8), and 97.9% of the variance of FA calculated from the short T2 compartment using multi-echo DTI data. Similarly, the relationship between fiber size and MD calculated from single-echo DTI for normal simplified muscle was fit to a one-phase association equation, which explained 99.6% of the variance in the data (Figure 4b). When fiber size and MD were simulated under edematous conditions, the original equation explained none of the variance when MD was calculated from single-echo DTI data (R²=−1.55) or from the long T2 compartment using multi-echo DTI analysis (R²=−35.1), and 98.7% of the variance of FA calculated from the short T2 compartment using multi-echo DTI data.

Figure 4.

Fractional anisotropy (A) and mean diffusivity (B) measurements as a function of fiber diameter measured with single-echo (circles) and multi-echo (squares) DTI for normal (black; 5% extracellular water volume fraction) and edematous (45% extracellular water volume fraction) muscle. Non-linear regression (red line) was fit to the normal muscle diffusion measurements measured with single-echo DTI. The equation for the fractional anisotropy regression is FA = (1.432 − 0.1134) * e^{−0.082*fibersize} + 0.1134. The equation for the mean diffusivity regression is $\text{MD}=2.94\ast {10}^{-4}\frac{{\text{mm}}^2}{\mathrm{s}}+(1.30\ast {10}^{-3}\frac{{\text{mm}}^2}{\mathrm{s}})\ast (1-{\mathrm{e}}^{-.064\ast \text{fibersize}})$.

Histology informed muscle geometry

Models were simulated at all time points except for the cardiotoxin day 1 injury as these muscle fibers had no discernable organized structure. Mean fiber size ranged from 35µm to 76µm in diameter (Fig. 5). In general, botox and denervation models had the smallest fibers that decreased in size with time. Average fiber size of the cardiotoxin model steadily increased over the 30-day time course.

Figure 5.

Fiber diameter measurements as a function of time for control (black circles), cardiotoxin (red squares), tenotomy (purple diamonds), botox (blue upside down triangles), and denervation (green triangles) models of skeletal muscle. Histology was obtained at day 1, 3, 7, 14, and 30 post-injury from a previous study in our lab.

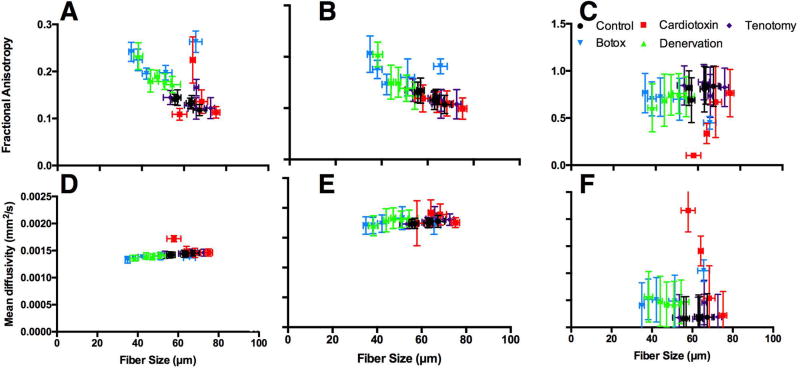
Diffusion measurements in control muscle show little change over the course of 30-days with single-echo DTI (Fig. 6A, D). Large differences in FA were observed between day 3 (FA=.12±.01), day 7 (FA=.22±.05), and day 14 (FA=.14±.03) in the cardiotoxin model when calculated using single-echo DTI, which were not reflective of the measured fiber size changes (Fig. 5, 7A). However, when FA was calculated from the short compartment of the multi-echo DTI analysis, FA appeared to steadily decrease over this time period, which better reflects fiber size changes at these time points (Fig. 6B, 7B). Botox and denervation models had the highest FA measurements with measured with both single- and multi-echo DTI, especially at later times points when fibers were smaller. In general, MD measurements made with single and the short compartment of multi-echo DTI displayed similar trends, although the short compartment measured MD had higher overall diffusivity measurements, likely due to a higher defined diffusion coefficient. FA and MD measurements calculated from the long compartment of multi-echo DTI demonstrated very high FA and low MD, likely due to the highly restricted diffusion environment of the extracellular space between fibers (Fig. 6C, F). Unlike the ideal models of muscle microstructure, no similarity was observed between λ2 and λ3 in models with histology informed geometry (Supporting Fig. S2).

Figure 6.

Fractional anisotropy (A–C) and mean diffusivity (D–F) measurements of models with histology informed geometry from control (black circles), cardiotoxin (red squares), tenotomy (purple diamonds), botox (blue upside down triangles), and denervation (green triangles) skeletal muscle as a function of average muscle fiber diameter. Diffusion measures were made with single-echo (A, D), and the short (B, E) and long (C, F) T2 compartments from the multi-echo DTI sequence.

Figure 7.

Fractional anisotropy (A–C) and mean diffusivity (D–F) measurements of models with histology informed geometry from control (black circles), cardiotoxin (red squares), tenotomy (purple diamonds), botox (blue upside down triangles), and denervation (green triangles) skeletal muscle as a function of days after injury. Diffusion measures were made with single-echo (A, D), and the short (B, E) and long (C, F) T2 compartments from the multi-echo DTI sequence.

To compare how well diffusion measurements made in the simplified hexagonal models of muscle are to diffusion measurements made in models with histology informed geometries, we compared the equations fit between fiber size and diffusion measurements (FA and MD) for normal (5% extracellular water volume content) muscle with ideal geometry to histology informed measures of diffusion (Fig. 7). The equation relating fiber size to FA in models with ideal muscle geometry explained none of the variance in FA when calculated with single-echo (R²=−0.156) or the long compartment of multi-echo DTI (R²=−10.9). However, this equation described 68.6% of the variance in FA when calculated with the short compartment of multi-echo DTI. The equation relating fiber size to MD in models with ideal muscle geometry described none of the variance in MD when calculated with single-echo (R²=−3.21), the short compartment (R²=−9.12), or the long compartment (R²=−6.50) using multi-echo DTI. Note: a negative R² is possible when a model is forced to fit data and the fit is worse than a horizontal line or the mean of the dependent variable.

Discussion and Conclusion

The use of DTI to characterize muscle structure and physiology is an active area or research with important clinical implications informing guidelines for developing DTI protocols specific to skeletal muscle (23,25,33–35). However, the complexity of the relationship between muscle health and the measured DT continues to limit DTI’s clinical utility.

The multi-echo diffusion tensor imaging is not novel to this study and has been performed previously and reported in the literature. Van Dusschoten pioneered the use of multi-echo diffusion tensor imaging in the mid 90’s. In a series of experiments, multi-echo DTI was used to separate diffusion based on T2 in simulations, vegetables, and healthy and occluded neural tissues (56,57). Stanisz et al. carried out similar experiments in optic nerve (58) and Does et al. in brain and facial nerves (59). The first studies utilizing this technique in skeletal muscle were carried out by Ababneh et al in chemically induced edematous rat paw muscles (10), and Fan et al in a chemically induced edematous tibialis anterior (12). While this technique is not new, these studies have demonstrated the ability to measure separate diffusion tensors, separated by the multi-T2 decay in biological tissues. The goal of this study was to relate diffusion tensors calculated from multi-echo DTI to microstructural features of skeletal muscle.

In this study, we report our initial developments of a program to systematically assess these complex relationships through the use of well defined, albeit simplistic, computational models within a DTI simulation environment. We have evaluated the relationship between four microstructural features of skeletal muscle (fiber size, fibrosis, edema, and permeability) individually, and in combination with one another and the DT in models with both simplified and histology informed geometry. These relationships were simulated using a standard DTI, and a multi-echo DTI pulse sequence, which was able to separate intra- and extra-cellular diffusion based on T2-relaxation of particles in the two compartments. The main finding of this study was fiber size is overall the strongest predictor of λ2, λ3, MD, and FA in skeletal muscle, accounting for ~40% of the variance in the diffusion model when calculated with single-echo DTI. This increased to ~70% when diffusion measures were calculated from the short T2 compartment from multi-echo DTI, which effectively separates intra- and extra-cellular diffusion. Additionally, the sensitivity of diffusion measurements begins to plateau at fiber sizes greater than 60µm. As the normal fiber size of a human muscle fiber is 40µm–60µm (FA: .180–.135), this suggests that DTI is a sensitive tool to monitor muscle atrophy, but may be limited in measurements of muscle hypertrophy. Comparing diffusion measurements made in models with simplified geometry versus histology informed geometry we found that fiber size was able to explain 68% of the variance in FA calculated with the short T2 compartment of the multi-echo DTI sequence. This supports that multi-echo DTI may be a useful tool to monitor fiber size changes in the presence of edema.

Healthy skeletal muscle fibers are tightly packed, polygonal structures, surrounded by hierarchical layers of thin ECM. In the simplified models in this study, muscle fibers were approximated as tessellated hexagons, since they can be tightly packed and have a uniform linear spacing. Fibrosis is commonly studied via histology, and is defined as an accumulation of ECM, in both the intrafasicular and perifasicular spaces around muscle fibers, which ultimately interferes with function (2). ECM is a dynamic structure, composed of a scaffold of connective tissue (e.g. collagen), fluid, and a variety of cells. Functionally in muscle, fibrosis results in increased whole muscle passive stiffness. However, passive mechanical properties are not correlated to the biochemical makeup, or area fraction of the ECM, albeit they normally change in the same direction (2,60). Fibrosis is a complicated process that resists a precise characterization. For the purposes of the present study, fibrosis was defined as increased spacing of fibers. The restricted diffusion coefficient of water in the ECM was chosen to remain constant as the relative volume fraction of fluid, ECM proteins, cells and cellular debris in the extracellular space is unknown in healthy or fibrotic muscle. Edema in skeletal muscle is a complex, time dependent process, which includes increased fluid transport across capillary beds, which allows for recruitment and migration of inflammatory cells into the damaged region to break down cellular debris (61). From a DTI perspective, the increased volume fraction of water has the largest effect on both the overall diffusion signal, but the overall T2-relaxation of skeletal muscle. Therefore, edema was simplified as an increase in the overall extracellular volume fraction of water particles. The concept of permeability in skeletal muscle is often not well defined and commonly used to describe two physiologic processes or states: 1. The flux of water molecules and ions across a cell membrane or, 2. damage to the cell membrane, which allows for flux of water molecules between the intra- and extra-cellular spaces. The first definition is important with respect to excitation-contraction coupling, muscle metabolism, etc, but the second definition is related to a muscle’s response to injury and may be related to impaired force production; membrane disruption tends to yield a regenerative response in muscle cells. As this second definition is more related to the microstructural changes that occur after injury in skeletal muscle, permeability was simplified in our model as fibers with walls randomly deleted.

In vivo, the presence of increased extra-cellular water due to edema in injured muscle has been shown to strongly affect the diffusion signal, and may dominate other microstructural changes (e.g. fiber atrophy), making detection of microstructure-driven diffusion signal changes difficult to resolve. This confound can be addressed with the use of multi-echo DTI, which can distinguish intra- and extra-cellular diffusion in muscle by exploiting differences in the transverse relaxation (T2) rate of intra- and extra-cellular water (10,12). However, this application of multi-echo DTI, while promising, has not been well studied in muscle in vivo. To date, single-echo DTI pulse sequences have been the predominant method in muscle DTI studies and have yielded non-specific signal changes, making microstructural changes difficult to quantify in the presence of edema. Though, multi-echo DTI has two major drawbacks. First, the duration of the scan is long (30minutes–1hour) since multiple diffusion directions must be sampled at multiple TEs. Second, multi-T2 fitting is a non-trivial technique that is prone to errors, especially when the compartments of the T2 decay are close. However, techniques such as non-negative least squares estimation and linear programming can be used to reduce the number of T2 compartments into the smallest number of discrete terms to provide an accurate estimation of the data. As this technique is susceptible to noise, care must be taken in order to maximize SNR, particularly at the shortest measured TEs.

Diffusion weighted spin-echo echo planar imaging is sensitive to the T2 relaxation of tissues due to relatively long TEs required for diffusion weighting. One technique that can be used to maximize SNR without increasing total scan time with additional signal averages, and to adequately sample the early part of the relaxation curve, is to minimize TE. Shortening the TE in a pulse sequence is complicated by many factors, including hardware limitations, the duration of the diffusion gradients and spatially encoding the diffusion signal with echo planar imaging. The use of short diffusion times with short TEs in the diffusion literature is not unique to this study, but is reported across the literature in studies utilizing a spin-echo DTI pulse sequence. While the diffusion time used in this study was short (9ms), short diffusion times have been used in studies using high-field strength (6.3T+) MRI with comparable TE (Δ/TE; 10ms/25ms Zhang et al. 2008 (62), 10ms/20ms Gineste et al. 2013 (63), 11.7ms/29ms Ababneh et al 2005 (10), 12ms/21ms Fan et al. 2008 (12), 13ms/30ms Heemskerk et al 2006 (13), 13ms/30ms Heemskerk et al 2007 (64)). In these studies, since T2 relaxation decreases with increasing magnetic field strength, time between diffusion gradients was shortened, to minimize TE in order to maximize SNR.

The main drawback of short diffusion times in spin-echo based DTI studies is the length scale of diffusion being probed (mean square displacement ~6µm) is less than the size of a muscle fiber. This results in only the fraction of the water molecules at the start of the DTI experiment that are near the sarcolemma actually undergoing restricted diffusion, which leaves molecules in the center of the fiber undergoing “unrestricted diffusion.” causing a diffusion time dependence on the diffusion tensor. Sigmund et al 2013 used a non spin-echo based DTI sequence to demonstrate that compared with short diffusion times, long diffusion times result in a decrease in diffusivity and an increase in FA (65). This may be because with longer diffusion, a larger fraction of water molecules have the opportunity to reflect off of the main barrier to diffusion, decreasing the fraction of molecules in the center of a fiber that undergo “free diffusion”. However, long diffusion times are not feasible in spin-echo based DTI, due to the short T2 of muscle. In some studies that use longer diffusion times with spin-echo based DTI sequences, issues with signal to noise ratio have been reported. For example, Hoojimans et al. (66) rejects ROIs in muscle with SNR<20, as inaccurate estimation of the diffusion tensor is common under this threshold as determined in Damon 2008 (23). In an experiment using the exact pulse sequence used in this manuscript on a 7T scanner at our institution, we have reported SNR=33.7 on a 3D printed, hydrogel diffusion phantom with muscle microstructural features (42). Similar SNR values have been measured in unreported data in skeletal muscle tissue in our lab.

One solution to balancing short transverse relaxation, TE and diffusion duration is to use stimulated echo (STE) diffusion tensor imaging, which is able to sample diffusion at longer diffusion times, while minimizing the exponential signal decay due to transverse relaxation (8,67). While the sensitivity of this technique to fiber size appears high in normal muscle, its sensitivity to fiber size in the presence of edema has not, to our knowledge, been studied. Moreover, STE sequences are non-standard in clinical application (most scanners do not have product STE sequences) and thus, from a practical standpoint they are less relevant to our goal of establishing clinical metrics. Therefore, we did not use a stimulated echo technique in this study, although its use will be a consideration in future studies.

Fiber size is a key metric in understanding the isometric force generating potential of muscle (68). In this study, we found that fiber size explains about 70% of the variance in FA when calculated with the short T2 compartment from multi-echo DTI. As FA decreased, fiber size increased and the theoretical force generating capacity of muscle fibers increase. While this finding is not in itself novel, the exponential relationship between fiber size and FA has not been previously shown. Additionally, with the diffusion sequence tested, a plateau was found for diffusion measurements in muscle fibers greater than 60µm diameter, which is on the upper boundary of normal human skeletal muscle. Clinically, this suggests that DTI is most sensitive to monitoring atrophic disease processes in skeletal muscle.

There are several limitations to this study. First, we did not investigate the effect of SNR on the DT. Future studies of these models will add Gaussian noise to each echo of the diffusion signal to generate SNR ranging from 5 to 140 to compare to previously reported studies. Second, the estimates of extracellular water volume fraction for histology informed geometry models were approximated from previous MR studies of these tissues and were not histologically measured. Third, a relatively small duration of diffusion was measured, which does not allow for all of the water molecules in a cell to be restricted by the sarcolemma. Future studies should include investigating these same models with either different diffusion parameters (i.e. longer diffusion duration) or different DTI pulse sequences (i.e. STE DTI, HARDI, or multi-shell DTI) in order to get better diffusion contrast. The models in these studies were extrapolated into 3D from 2D outlines as muscle fiber geometry is relatively uniform longitudinally in normal skeletal muscle over the diffusion distances that can be probed in a DTI experiment. Therefore, only subtle changes were observed in λ1 (along the main axis of diffusion). Techniques such as 3D high-resolution confocal laser scanning microscopy have been used to generate 3D models for diffusion simulation in an asparagus model of diffusion (69). In future iterations of these studies, similar techniques could be used to inform models with real muscle geometry in 3D. Finally, myofilaments inside, and extracellular matrix proteins outside of muscle fibers were not included in this model. However these elements of muscle microstructure do have an effect on intra- and extra-cellular diffusion (70,71). The effect of these elements on the diffusion tensor was partially accounted for by assigning diffusion coefficients measured in multiple physical studies of small macromolecules in these tissues to the intra- and extra- cellular compartments respectively. Also, DifSim partially takes into account uncertainty associated with assigning experiment-based diffusion values when determining the step length of a molecule. At the beginning of an experiment, MCell generates 2 look-up tables: 1.) a table containing 1024 values of equally probable step lengths based on the molecules assigned diffusivity, and 2.) a table with >130,000 equally probable symmetric directions (41). For each step for each molecule, a step length and radial direction are chosen at random from these tables. This provides a distribution of step lengths and directions across molecules, which differs from lattice-free walk algorithms, which combine a fixed diffusion step length with random directions.

Using in silico modeling to tightly regulate microstructure provides experimental control required to uncouple microstructure from diffusion measurements, which is impossible to perform in vivo. This was an initial study, which studied the relationship between microstructure and the DT in highly simplified, and geometrically relevant models of skeletal muscle. This study provides the framework for future studies investigating the dependence of the relationship between the diffusion and muscle microstructure on signal to noise ratio, diffusion pulse sequence parameters, and diffusion pulse sequences. However it is important to note that the findings from this study do not provide a direct platform to translate to other acquisitions with different imaging parameters. A key interpretation of these experiments is a theoretical framework that can be used to identify features of muscle microstructure DTI may be most sensitive to, and which combinations are beyond the sensitivity of the technique. This tool can be used to inform interpretation of DTI data for clinicians and researchers to non-invasively quantify muscle microstructure to aid in diagnosis, monitor disease progression, and evaluate treatment of muscle pathologies for a wide range of patients.

Supplementary Material

Supp info

Supporting Material Supporting Table S1: Computational setup for the simulation experiments. COMET is a linux cluster at the San Diego Supercomputing Center, where the majority of simulations were performed.

Supporting Figure S1: λ1 (A–D), λ2 (E–H), and λ3 (I–J) measurements of simplified models of skeletal muscle. Diffusion measurements were made from single-echo DTI (red circles) and the short (black squares) and long (blue triangles) T2 compartments from the multi-echo DTI sequence. Fiber size (A, E, I), fibrosis (B, F, J), edema (C, G, K), and permeability (D, H, L) were varied over a physiologically relevant range of parameters defined in Table 1.

Supporting Figure S2: λ1 (A–C), λ2 (D–F), and λ3 (G–I) measurements of models with histology informed geometry from control (black circles), cardiotoxin (red squares), tenotomy (purple diamonds), botox (blue upside down triangles), and denervation (green triangles) skeletal muscle as a function of average muscle fiber diameter. Diffusion measures were made with single-echo (A, D, G), and the short (B, E, H) and long (C, F, I) T2 compartments from the multi-echo DTI sequence.