Adaptive Integrated Parallel Reception, Excitation, and Shimming (iPRES-A) with Microelectromechanical Systems Switches

Abstract

Purpose

Integrated parallel reception, excitation, and shimming coil arrays with N shim loops per radio-frequency (RF) coil element (iPRES(N)) allow an RF current and N direct currents (DC) to flow in each coil element, enabling simultaneous reception/excitation and shimming of highly localized B₀ inhomogeneities. The purpose of this work was to reduce the cost and complexity of this design by reducing the number of DC power supplies required by a factor N, while maintaining a high RF and shimming performance.

Methods

In the proposed design, termed adaptive iPRES(N) (iPRES(N)-A), each coil element only requires one DC power supply, but uses microelectromechanical systems switches to adaptively distribute the DC current into the appropriate shim loops to generate the desired magnetic field for B₀ shimming. Proof-of-concept phantom experiments with an iPRES(2)-A coil and simulations in the human abdomen with an 8-channel iPRES(4)-A body coil array were performed to demonstrate the advantages of this innovative design.

Results

The iPRES(2)-A coil showed no loss in signal-to-noise ratio and provided a much more effective correction of highly localized B₀ inhomogeneities and geometric distortions than an equivalent iPRES(1) coil (88.2% vs. 32.2% lower B₀ root-mean-square error). The iPRES(4)-A coil array showed a comparable shimming performance as that of an equivalent iPRES(4) coil array (52.6% vs. 54.2% lower B₀ root-mean-square error), while only requiring 8 instead of 32 power supplies.

Conclusion

The iPRES(N)-A design retains the ability of the iPRES(N) design to shim highly localized B₀ inhomogeneities, while drastically reducing its cost and complexity.

Introduction

Magnetic susceptibility differences at air/tissue interfaces in the body induce localized inhomogeneities in the main magnetic field, B₀, which can result in signal loss, blurring, and distortions in the MRI images. Typically, B₀ inhomogeneities are corrected by using whole-body spherical harmonic (SH) shim coils located in the scanner bore (1). However, these SH shim coils are generally limited to the second order and are located far from the subject, which limits their effectiveness to shim highly localized B₀ inhomogeneities.

An alternative design, which uses a separate array of smaller shim coils located closer to the subject, was shown to provide a more effective shimming of localized B₀ inhomogeneities than SH shimming (2, 3, 4). However, this multi-coil design requires the shim coil array to be placed inside or outside the radio-frequency (RF) coil array, which in many cases either decreases the signal-to-noise ratio (SNR), because of the RF shielding between the RF coil array and the subject, or which reduces the B₀ shimming efficiency, because the shim coil array is positioned farther away from the subject.

To eliminate this trade-off, a novel coil array design, termed integrated parallel reception, excitation, and shimming (iPRES), was proposed, in which both an RF current and a direct current (DC) can flow in each coil element simultaneously, thereby enabling both RF reception/excitation and localized B₀ shimming using a single coil array (5, 6, 7). Such integrated RF/shim coil arrays can be placed close to the subject to simultaneously optimize the SNR and B₀ shimming effectiveness, while also saving space in the scanner bore. For example, the iPRES design can provide a more effective correction of localized B₀ inhomogeneities and echo planar imaging (EPI) distortions in the human brain, with no SNR loss, relative to conventional SH shimming when using slice-optimized shimming (6). In general, the B₀ shimming performance of multi-coil and iPRES coil arrays depends on the exact application and targeted anatomy in the body (see (8, 9) for a more thorough discussion on these issues).

An improved iPRES coil array design has recently been proposed, in which each RF coil element is split into multiple smaller RF-isolated shim loops to both increase the number and reduce the size of the independent magnetic fields available for B₀ shimming, which in turn enables the shimming of highly localized B₀ inhomogeneities that are spatially smaller than the RF coil elements, such as those affecting body imaging (10). This design, known as iPRES(N), where N is the number of shim loops within each RF coil element, has demonstrated superior correction of localized B₀ inhomogeneities and EPI distortions in the human abdomen when compared to the original iPRES design, hereafter referred to as iPRES(1) (10). For example, an 8-channel iPRES(3) coil array improved the B₀ homogeneity in the abdomen by 53% relative to the iPRES(1) design. However, each shim loop requires an independent DC power supply that must maintain a stable output current during gradient switching and support fast current updates for dynamic shimming, which adds cost and complexity to the system because of the N-fold increase in the number of DC power supplies and cables required for shimming.

Another shim coil design was also proposed, in which a single DC power supply and a solid-state switch matrix arranged on a cylinder around the subject are used to allow dynamic control over the DC current path to produce a magnetic field for B₀ shimming (11). Proof-of-concept phantom experiments with such a coil prototype have shown some improvement in the B₀ homogeneity. However, this coil design has a number of limitations. First, like the multi-coil design, it still requires a separate RF coil array, resulting in an inherent trade-off between SNR and shimming performance. Second, since it only uses a single DC current, the number of transistor switches needed to generate an arbitrary magnetic field for B₀ shimming, and hence to realize the full potential of this design, would likely be impractical. Finally, this shim coil cannot be placed close to the subject because the nickel-flashed transistors used in the solid-state switch matrix generate local B₀ inhomogeneities.

To address the limitations of the previous methods, we present a new coil array design, termed adaptive iPRES(N) (iPRES(N)-A), which retains the high RF and shimming performance of the iPRES(N) design, while drastically reducing the number of DC power supplies required. In this study, proof-of-concept phantom experiments with a single iPRES(2)-A coil and simulations in the human abdomen with an 8-channel iPRES(4)-A body coil array are performed to demonstrate the advantages of the proposed design. Preliminary results have been presented in abstract form (12).

Methods

iPRES(N)-A Coil Design

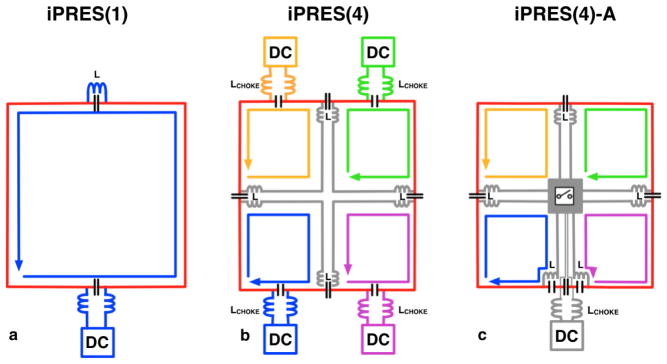
In contrast to the iPRES(N) design, which requires a separate DC power supply for each of the N shim loops within an RF coil element (Fig. 1b), the iPRES(N)-A design only requires a single DC power supply per RF coil element, but uses an RF-isolated switch matrix to adaptively distribute the DC current provided by the power supply into the appropriate shim loops to generate the desired magnetic field for B₀ shimming (Fig. 1c). By activating different combinations of switches in the switch matrix, different DC current paths, and hence different magnetic field patterns, can be generated for shimming. The number of switch states for an iPRES(N)-A coil element is equal to the sum for all k between 1 and N of the number of combinations of k activated shim loops out of N total shim loops, i.e., N!/(k!(N − k)!), multiplied by 2^k because each of the k loops can have a positive or negative current polarity, and divided by 2 because two states with opposite polarities in all k loops are the same, resulting in:

$$\sum _{k=1}^N\frac{2^{k-1}N!}{k!(N-k)!}.$$ (1)

Figure 1.

a: An iPRES(1) coil element cannot shim B₀ inhomogeneities that are spatially smaller than the RF coil element (shown by the red trace). b: An iPRES(N) coil element with N smaller RF-isolated shim loops can shim localized B₀ inhomogeneities more effectively, but requires N DC power supplies. c: An iPRES(N)-A coil element uses a switch matrix to distribute the DC current from a single power supply into the appropriate shim loops, thereby maintaining a high shimming flexibility, while reducing the cost and complexity of the system.

As in the iPRES(N) design, inductors, L, and chokes, L_choke, with a specifically designed self-resonant frequency are used to block the RF current at the Larmor frequency from flowing into the interior shim loop traces or the DC power supply, respectively, thereby maintaining the SNR of the coil.

Thus, by using a single power supply and a switch matrix rather than N power supplies to deliver DC currents into the different shim loops of an RF coil element, the ability to shim highly localized B₀ inhomogeneities is maintained, while the number of power supplies is reduced by a factor N. The iPRES(N)-A design therefore retains the advantages of the iPRES(N) design while addressing its limitation. Importantly, reducing the number of power supplies drastically reduces the system cost relative to the iPRES(N) design. For example, an 8-channel iPRES(4) coil array requires 32 DC power supplies, while an equivalent iPRES(4)-A coil array only requires 8 DC power supplies, resulting in a 4-fold reduction in the power supply cost. Further, using fewer power supplies also reduces the number of DC cables (routed between the power supplies and the coil array to supply DC currents to the shim loops) and pass-through panel filters (required to prevent RF noise from entering the scanner room through the DC cables), which reduces the system complexity as well as potential SNR losses due to suboptimal cable routing (7).

iPRES(2)-A Coil Implementation

As a proof-of-concept, a single iPRES(2)-A coil was implemented. First, a 20 × 14 cm single-turn RF coil (Fig. 2a) was constructed, tuned, and matched to resonate at 127.7 MHz using a four-port vector network analyzer (ZNB4, Rhode & Schwarz, Munich, Germany) on a 22-cm diameter cylindrical water phantom with 1.9-cm diameter tubular inserts. The coil was connected to a preamplifier via a 50 Ω transmission line and a sub-miniature, type A RF connector. A standard PIN diode was used to produce a high-impedance blocking circuit to detune the coil and protect the preamplifier during the RF transmission cycle.

Figure 2.

RF coil before (a) and after (b) iPRES(2)-A integration with the addition of four RF-isolated MEMS switches (numbered 1 to 4) within the RF coil perimeter. SNR maps before (c) and after (d) iPRES(2)-A integration showing no appreciable change in SNR.

This RF coil was then modified into an iPRES(2)-A coil by adding a 5 A, 16 V 32-channel modular DC power supply (W-IE-NE-R, Plein & Baus Corp., Springfield, OH) and interior DC traces to split the coil into two independent shim loops (Fig. 2b). Inductors, L = 800 nH, were also added to bypass any capacitor and to provide RF-isolation between the coil and the interior shim loop traces, as well as two inductors, L_choke = 800 nH, to provide RF-isolation between the coil and the DC power supply. The inductors L and L_choke were physically the same, but are delineated by two different variables for clarity. All of these inductors were measured with a bench top fixture to ensure that each part had a minimum isolation of −25 dB and had a maximum DC resistance of 0.02 Ω.

Next, four 1 cm² electrostatic microelectromechanical systems (MEMS) single-pole, single-throw switches were added to the interior of the RF coil. The MEMS switches could be activated by applying an 82 V DC bias across the gate and beam pins of the package (13) to distribute the DC current into the appropriate shim loops for B₀ shimming. The MEMS gate-beam bias activation cables were isolated from the RF coil with additional 2200 nH inductors, which prevented unwanted parasitic resonances in the coil response.

These novel MEMS switches benefit from several advantages, including a low on-resistance (≪ 1 Ω), a low power dissipation, a high DC current handling (5 A), and fast switching times suitable for dynamic shimming (< 10 μs), which are ideal for iPRES(N)-A integration (13). Further, because they were designed to be used in an MR environment, they do not induce any local B₀ inhomogeneities and can therefore be integrated onto the coil, and be placed close to the subject, without degrading the MR image quality. The RF parameters of the coil, such as the return loss (S₁₁), impedance, and loaded Q-ratio (Q_unmodified/Q_iPRES(2)−A = 1.02) were monitored during the iPRES(2)-A integration to ensure that the SNR of the coil was maintained.

SNR Measurements

SNR maps of the phantom were acquired both before and after the iPRES(2)-A integration to demonstrate that the addition of the shim loops and switch matrix within the perimeter of the RF coil did not degrade the SNR. All experiments were performed on a 3T MR750 MRI scanner (GE Healthcare, Milwaukee, WI). The SNR maps were acquired with a gradient-echo sequence (repetition time (TR) = 530 ms, echo time (TE) = 1.5 ms, flip angle = 12°, field-of-view (FOV) = 32 × 32 cm, matrix size = 64 × 64, slice thickness = 5 mm).

B₀ Shimming Experiments

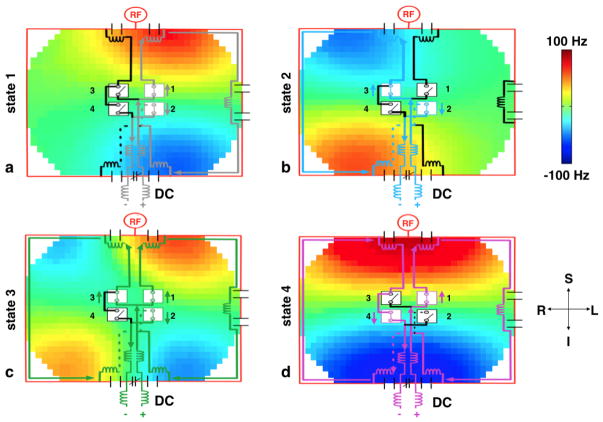
Proof-of-concept phantom experiments were performed to demonstrate that the iPRES(2)-A coil can shim different patterns of highly localized B₀ inhomogeneities with a single DC power supply. For this coil, four different combinations of MEMS switches (Table 1) could be activated to generate four unique DC current paths. Specifically, the DC current could flow in the left loop (Fig. 3a), in the right loop (Fig. 3b), in a figure-eight pattern (Fig. 3c), or along the perimeter of the coil (Fig. 3d), resulting in four unique magnetic field patterns available for B₀ shimming.

Table 1.

iPRES(2)-A coil switch states used to generate the four basis B₀ maps in Fig. 3.

State	Switch 1	Switch 2	Switch 3	Switch 4
1	on	on	off	off
2	on	off	off	on
3	on	on	off	on
4	off	on	on	off

Figure 3.

Circuit diagrams for each of the four unique iPRES(2)-A switch states shown in Table 1 (a: state 1, b: state 2, c: state 3, d: state 4, with the active DC current paths shown in gray, blue, green, and magenta, respectively), overlaid onto the corresponding basis B₀ maps. The MEMS switch control lines have been omitted for clarity.

A calibration was first performed to determine the magnetic field pattern generated by each switch state. Four B₀ maps were acquired with a DC current of 1 A applied to the iPRES(2)-A coil while each switch state was individually activated. A baseline B₀ map was also acquired with no DC current and was subtracted from each of these B₀ maps to yield four basis B₀ maps representing the magnetic field per unit current generated by each switch state. Note that the magnetic field generated by switch state 4 is equivalent to that of an iPRES(1) coil, since the magnetic field generated by the opposite DC currents flowing in the two interior shim loop traces cancel each other. Henceforth, switch state 4 will be referred to as the iPRES(1)-equivalent switch state.

Localized B₀ inhomogeneities were then introduced into the phantom by placing a perturbation loop on top of the iPRES(2)-A coil and by applying a DC current into that loop. The perturbation loop could be configured into either a single loop (Fig. 4a) or a figure-eight (Fig. 4d) configuration to generate different patterns of localized B₀ inhomogeneities that are spatially smaller than the coil. The perturbation loop was RF-isolated from the iPRES(2)-A coil by two inductors, L_choke = 800 nH, to prevent SNR loss resulting from mutual coupling between the loop and the coil.

Figure 4.

Circuit diagrams and B₀ maps with the single loop or figure-eight perturbation before shimming (a,d), showing highly localized B₀ inhomogeneities, after shimming with the optimal switch state and DC current applied to the iPRES(2)-A coil (b: state 1, e: state 3), showing a drastic reduction in B₀ inhomogeneities, and after shimming with the iPRES(1)-equivalent switch state (c,f), showing only partial or minimal reduction in B₀ inhomogeneities.

For each of the two perturbation loop configurations, B₀ maps and EPI images were acquired under four conditions:

1. Baseline: No DC current was applied in the perturbation loop or the iPRES(2)-A coil.

2. Perturbation: A DC current of 1 A was applied in the perturbation loop to generate localized B₀ inhomogeneities and to introduce geometric distortions in the EPI images.

3. iPRES(2)-A shimming: The optimal DC current to shim the perturbation with each of the four switch states was determined by minimizing the root-mean-square error (RMSE) between i) the B₀ map acquired with the perturbation applied and ii) each of the four basis B₀ maps. The optimal switch state was chosen as the one resulting in the smallest RMSE. Both the optimal switch state and its optimal DC current were then applied to the iPRES(2)-A coil to shim the perturbation.

4. iPRES(1) shimming: To demonstrate that the iPRES(2)-A coil can shim highly localized B₀ inhomogeneities much more effectively than an iPRES(1) coil, the iPRES(1)-equivalent switch state and its optimal DC current were also applied to the iPRES(2)-A coil to shim the perturbation.

The B₀ maps were acquired with an 8-echo gradient-echo sequence (same parameters as for the SNR maps, except for TE = 1.5, ..., 11.2 ms) and were computed with a linear regression of the phase images acquired at different TEs. The EPI images were acquired with a single-shot spin-echo EPI sequence (TR = 2000 ms, TE = 30 ms, FOV = 32 × 32 cm, matrix size = 128 × 128, slice thickness = 5 mm, frequency-encoding direction = right/left). The DC currents used to drive the perturbation loop and the iPRES(2)-A coil and the DC bias used to activate the MEMS switches were all provided by the 32-channel DC power supply.

B₀ Shimming Simulations

To demonstrate the advantages of the iPRES(N)-A design in a more realistic setting, simulations were also performed with 8-channel iPRES(1), iPRES(2), iPRES(3), iPRES(4), and iPRES(4)-A body coil arrays placed around the abdomen (Fig. 5a). Each RF coil element was 20 × 14 cm. In the iPRES(2) coil array, the RF coil elements were split along the superior/inferior direction. In the iPRES(3) coil array, half of them were further split along an orthogonal direction, as in our previously implemented iPRES(3) body coil array (10). In the iPRES(4) and iPRES(4)-A coil arrays, all coil elements were split into four quadrants.

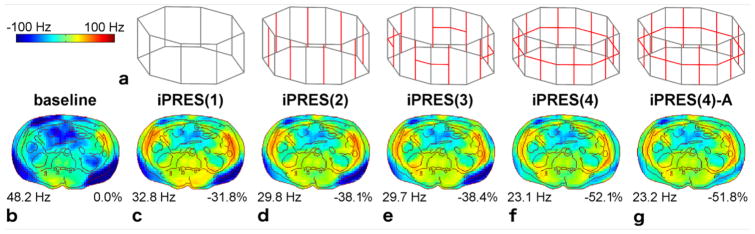
Figure 5.

a: 8-channel iPRES(1), iPRES(2), iPRES(3), iPRES(4), and iPRES(4)-A body coil arrays, with the RF coil elements shown in gray and the interior shim loop traces shown in red. b: Experimental B₀ map acquired in a representative axial slice in the abdomen of a healthy volunteer after linear shimming. c–g: Simulated B₀ maps after shimming with the coil arrays shown in (a) placed around the abdomen, showing that the shimming performance of the iPRES(4)-A coil array is comparable to that of the iPRES(4) coil array. Contour lines derived from the anatomical images are overlaid on the B₀ maps. The B₀ RMSE and reduction in RMSE relative to the baseline are shown on the bottom left and bottom right of each B₀ map, respectively.

We studied a healthy volunteer who gave written informed consent to participate in this study under a protocol approved by our Institutional Review Board. After linear shimming, B₀ maps were acquired in three representative axial slices in the abdomen with an 8-echo gradient-echo sequence (TR = 500 ms, TE = 1.1 ms,..., 8.9 ms, flip angle = 12°, FOV = 48 × 48 cm, matrix size = 64 × 64, slice thickness = 7.5 mm) and were reconstructed with a multi-point Dixon fat-water separation method (14). Given the size of the shim loops, the spatial resolution of the B₀ maps was sufficient to provide an effective shimming, while maintaining a reasonable computation time for the shim optimization (see below). In this work, only linear shimming was used in order to compare the shimming performance of the iPRES(N) and iPRES(N)-A coil arrays by themselves, with no additional contribution from second-order SH shimming. Anatomical images were also acquired with a single-shot fast-spin echo sequence, as described previously (10).

For each coil array, basis B₀ maps, representing the magnetic field generated by a DC current of 1 A separately applied in each shim loop or each switch state, were simulated by using the Biot-Savart law. The iPRES(1), iPRES(2), iPRES(3), and iPRES(4) coil arrays had 8, 16, 24, and 32 basis B₀ maps, respectively. Since each iPRES(4)-A coil element had 40 different switch states corresponding to 40 unique DC current paths (Fig. 6), the iPRES(4)-A coil array had 8 × 40 = 320 basis B₀ maps.

Figure 6.

Forty unique switch states of an iPRES(4)-A coil element, with the RF coil element shown in gray, the interior shim loop traces shown in green, and the active DC current paths shown in red.

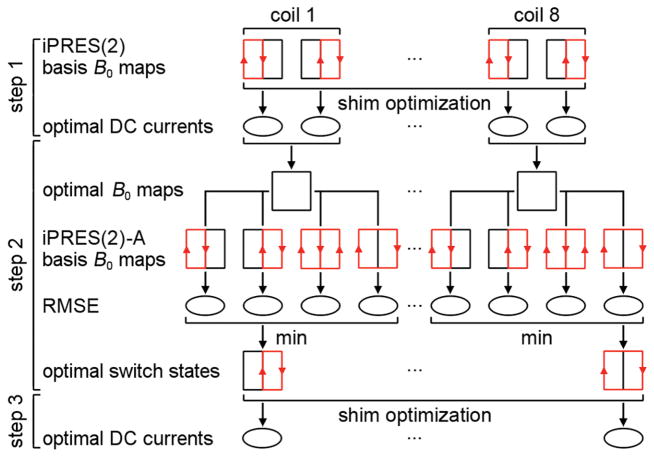
For the iPRES(1) to iPRES(4) coil arrays, the shim optimization was performed by minimizing the RMSE between i) the B₀ map to shim and ii) a linear combination of all basis B₀ maps, as described previously (10). For the single iPRES(2)-A coil used in the phantom experiments, the shim optimization was performed by minimizing the RMSE between i) the B₀ map to shim and ii) the basis B₀ map corresponding to each of the four switch states. The optimal switch state and DC current were then chosen as the ones resulting in the smallest RMSE. Applying the same method to the 8-channel iPRES(4)-A coil array would require the RMSE to be computed 40⁸ times, each time with a different set of 32 basis B₀ maps, which is not practical. Instead, the following method was used to maintain a short computation time (Fig. 7):

Figure 7.

iPRES(N)-A shim optimization method. An 8-channel iPRES(2)-A coil array is shown for simplicity, but extension to any N value is straightforward. A shim optimization is first performed for an equivalent iPRES(N) coil array (step 1), which is then used to determine the optimal switch states (step 2) and DC currents (step 3) to apply in the iPRES(N)-A coil array.

1. First, a shim optimization was performed for an equivalent iPRES(N) coil array, i.e., by minimizing the RMSE between i) the B₀ map to shim and ii) a linear combination of the iPRES(N) basis B₀ maps, resulting in a first set of optimal DC currents.

2. For each coil element, the RMSE was then computed between i) the B₀ map generated by the N optimal DC currents from step 1 and ii) each of the iPRES(N)-A basis B₀ maps. The optimal switch state for that coil element was chosen as the one resulting in the smallest RMSE, i.e., the one providing the closest magnetic field to that generated by the corresponding iPRES(N) coil element in step 1.

3. Finally, a shim optimization was performed again by minimizing the RMSE between i) the B₀ map to shim and ii) a linear combination of the iPRES(N )-A basis B₀ maps corresponding to the optimal switch states from step 2, resulting in the final set of optimal DC currents.

All computations were performed in Matlab (The MathWorks, Natick, MA) on a 768-core Linux cluster. The computation time for the shim optimization was about 30 s for the iPRES(1) to iPRES(4) coil arrays and about 1:30 min for the iPRES(4)-A coil array.

Results

SNR Measurements

SNR maps acquired before (Fig. 2c) and after (Fig. 2d) iPRES(2)-A integration into the RF coil, with corresponding average SNR values of 152.5 and 150.2, are very similar, showing that the addition of the RF-isolated MEMS switches and interior DC traces within the perimeter of the RF coil did not affect the SNR.

B₀ Shimming Experiments

Applying a DC current in the perturbation loop, either in the single loop or figure-eight configuration, produced different patterns of localized B₀ inhomogeneities (Fig. 3a,d), both of which resulted in significant geometric distortions in the EPI images (Fig. 8b,f, red arrows). Shimming the single loop or figure-eight perturbation with the optimal switch state (states 1 and 3, respectively) and optimal DC current applied to the iPRES(2)-A coil drastically reduced these B₀ inhomogeneities (Fig. 3b,e) and distortions (Fig. 8c,g, green arrows). The B₀ RMSE was reduced by 89.2% and 87.2%, respectively. In contrast, shimming the single loop or figure-eight perturbation with the iPRES(1)-equivalent switch state only partially or marginally reduced these B₀ inhomogeneities (Fig. 3c,f) and distortions (Fig. 8d,h, orange and red arrows). The B₀ RMSE was only reduced by 60.5% and 3.9%, respectively.

Figure 8.

EPI images corresponding to the B₀ maps shown in Figure 4. Perturbation loops were used to introduce B₀ inhomogeneities and the iPRES(2)-A coil was used for both imaging and B₀ shimming. EPI images with no perturbation (a,e); with the single loop or figure-eight perturbation before shimming (b,f), showing severe geometric distortions (red arrows); after shimming with the optimal switch state and DC current applied to the iPRES(2)-A coil (c,g), showing a drastic reduction in distortions (green arrows); and after shimming with the iPRES(1)-equivalent switch state (d,h), showing only partial or minimal reduction in distortions (orange and red arrows).

B₀ Shimming Simulations

Susceptibility differences at air/tissue interfaces in the body induced high-order B₀ inhomogeneities throughout the abdomen (Fig. 5b, additional results in supplementary Fig. 1). As expected, shimming with the 8-channel iPRES(1), iPRES(2), iPRES(3), and iPRES(4) body coil arrays was increasingly more effective at shimming these localized B₀ inhomogeneities (Fig. 5c–f), but at the cost of requiring an increasingly larger number of DC power supplies (8, 16, 24, and 32, respectively). The B₀ RMSE averaged across all slices was reduced by 30.9%, 34.8%, 45.2%, and 54.2%, respectively. In contrast, shimming with the 8-channel iPRES(4)-A body coil array (Fig. 5g) was nearly as effective as shimming with the iPRES(4) coil array, while only requiring 8 instead of 32 DC power supplies. The B₀ RMSE averaged across all slices was reduced by 52.6%. The average DC current amplitude per shim loop was 0.76 A, 0.75 A, 0.64 A, 0.56 A, and 0.71 A for the iPRES(1), iPRES(2), iPRES(3), iPRES(4), and iPRES(4)-A coil arrays, respectively.

Discussion and Conclusions

The proof-of-concept phantom experiments presented in this work demonstrate that the iPRES(2)-A coil can effectively shim different patterns of highly localized B₀ inhomogeneities with a single DC power supply and with no SNR loss. The simulations further demonstrate that the shimming performance of the 8-channel iPRES(4)-A body coil array is comparable to that of an equivalent iPRES(4) coil array. Taken together, these results show that the iPRES(N)-A design retains the high RF and shimming performance of the iPRES(N) design, while reducing the number of DC power supplies and cables required by a factor N, which substantially reduces the cost and complexity of the system.

A potential limitation of the proposed design is that, while an iPRES(N)-A coil array offers exactly the same DC current paths as those of an equivalent iPRES(N) coil array, it only provides one DC current rather than N independent DC currents to be distributed into the shim loops of each coil element, which may reduce the B₀ shimming performance. This issue was not found to be significant for the body coil arrays simulated in this work, since the shimming performance of the iPRES(4)-A coil array was nearly as high as that of the iPRES(4) coil array. For other coil geometries, this potential limitation can easily be addressed by increasing the number N of shim loops within each iPRES(N)-A coil element, while still using a single DC power supply. For example, the shimming performance of an iPRES(4) coil array may be higher than that of an iPRES(4)-A coil array, but similar to that of an iPRES(5)-A coil array, which would still benefit from a substantial reduction in cost and complexity relative to the iPRES(4) coil array, despite the additional shim loops.

As the number of iPRES(N)-A shim loops and MEMS switches per coil element increases, the shim loop size, or equivalently the number of shim loops within each coil element, becomes limited by the physical dimensions of the switches and of the inductors, L. Excitingly, recent advances in switch technology and fabrication are dramatically increasing the number of switches that can be integrated onto a single small package (15), resulting in a smaller switch module footprint and thus enabling smaller shim loop sizes. Further, since MEMS switches are highly integrable, a control logic bus circuit, such as a serial peripheral interface (SPI), can be added to the package to control all the MEMS switches integrated onto an iPRES(N)-A coil array with only three logic control lines and a single twisted-pair cable. For example, for an 8-channel iPRES(4)-A coil array, the number of cables required to activate all switches can be reduced by 96%, from 64 twisted-pair cables (two switches per shim loop) to 5 individual cables. In addition, the number of switches required for each shim loop can be reduced by using multi-pole, multi-throw switches instead of single-pole, single-throw switches.

In conclusion, the proposed iPRES(N)-A design can effectively shim highly localized B₀ inhomogeneities with no SNR loss, while drastically reducing the number of DC power supplies required, and hence the cost and complexity of the system, relative to the iPRES(N) design. These advantages are expected to lead to a more widespread adoption of the iPRES technology for localized B₀ shimming in both research (16, 17) and clinical applications.

Supplementary Material

Supp FigS1

Supporting Figure S1. a: 8-channel iPRES(1), iPRES(2), iPRES(3), iPRES(4), and iPRES(4)-A body coil arrays, with the RF coil elements shown in gray and the interior shim loop traces shown in red. b: Experimental B₀ maps acquired in three representative axial slices in the abdomen of a healthy volunteer after linear shimming. c–g: Simulated B₀ maps after shimming with the coil arrays shown in (a) placed around the abdomen, showing that the shimming performance of the iPRES(4)-A coil array is comparable to that of the iPRES(4) coil array. h: Anatomical images. Contour lines derived from the anatomical images are overlaid on the B₀ maps. The B₀ RMSE and reduction in RMSE relative to the baseline are shown on the bottom left and bottom right of each B₀ map, respectively.