Abstract
Purpose
To estimate multiple components within a single voxel in magnetic resonance fingerprinting (MRF) when the number and types of tissues comprising the voxel are not known a priori.
Theory
Multiple tissue components within a single voxel are potentially separable with MRF due to differences in signal evolutions of each component. The Bayesian framework for inverse problems provides a natural and flexible setting for solving this problem when the tissue composition per voxel is unknown. Assuming that only a few entries from the dictionary contribute to a mixed signal, sparsity promoting priors can be placed upon the solution.
Methods
An iterative algorithm is applied to compute the maximum a posteriori estimator of the posterior probability density to determine the MRF dictionary entries that contribute most significantly to mixed or pure voxels.
Results
Simulation results show that the algorithm is robust in finding the component tissues of mixed voxels. Preliminary in vivo data confirms this result, and also shows good agreement in voxels containing pure tissue.
Conclusions
The Bayesian framework and algorithm shown provide accurate solutions for the partial volume problem in MRF. The flexibility of the method will allow further study into different priors and hyperpriors that can be applied in the model.
Keywords: Quantitative imaging, partial volume, voxel composition
Introduction
Partial volume (PV) is a problem inherent to any imaging modality with limited spatial resolution, and MRI is no exception1. The partial volume effect occurs when the voxel size is larger than the physical structures found within a voxel, or when part of a boundary between two tissues is contained within a voxel. In these cases, the corresponding images may exhibit blurring artifacts or an appearance that averages the structures within the voxel. Different methods can be used to identify voxel composition. In the case of multiple T2 components within a voxel, multiexponential models have been used to estimate T2 relaxation times.2 A common way to handle partial volume problems is to treat the signal from a mixed voxel as a weighted sum of tissues that are thought to be present. For example, in the brain, mixed voxels are generally modeled as weighted sums of white matter, gray matter, and cerebrospinal fluid (CSF) signals.3 This type of model has been applied for segmentation of tissues in the brain3–5, to address partial volume issues in arterial spin labeling6,7 and to compute the arterial input function in cerebral perfusion MRI.8 Statistical models have also been considered,9 but again, tissue types are assumed to be known a priori. A more complicated model using a non-local means filter for denoising and Markov Random Fields for PV classification is used to calculate partial volume coefficients.10 A Bayesian classification approach has also been considered11 in which histograms are used to represent the contents of each voxel and for classification. Another approach which uses a three dimensional manifold to model partial volume effects between white matter, gray matter, and CSF12, has been applied in vivo for brain segmentation13. The common thread in these approaches is that a small, fixed subset of tissue types is assumed to be sufficient to describe each voxel signal over the image. This kind of approach can clearly fail whenever a tissue varies throughout the organ of interest, or in diseased tissues, where the individual voxel components may be completely unknown.
Magnetic resonance fingerprinting (MRF)14 is a technique that is capable of producing quantitative maps of tissue parameters such as T1 and T2 relaxation times using a pseudorandom data acquisition scheme and a pattern matching algorithm. A dictionary is created using simulations of the Bloch Equations to generate signal evolutions with different combinations of tissue properties as inputs. Acquired data are matched to the closest dictionary entry to produce accurate quantitative maps.14 MRF is not immune to the partial volume effect. For a given voxel that exhibits partial volume effects due to the presence of more than one tissue type, the match chosen from the dictionary will correspond to an entry that represents a function of several different entries corresponding to the true tissue types found within that voxel, and the effective parameter values assigned will not accurately represent the voxel composition in mixed voxels.
To remedy the problem of partial volume in MRF, a model was proposed14 and analyzed in which voxel signals could be decomposed using a least squares method as a weighted sum of two or three distinct signals, provided these signals were fixed in advance. This model has been shown to be robust to noise15 and has been evaluated, for example, in the case of white matter, gray matter, and CSF segmentation in the brain. Additionally, dictionary based methods have also been proposed16,17, which remove any erroneous weight calculation due to the complex-valued signals by allowing only real, nonnegative weight contribution. However, as with conventional non-MRF methods for partial volume, these MRF methods cannot solve the problem when the tissues present in a mixed voxel are not known a priori, as may be the case in a tumor or other pathological tissues. In these cases, fitting a mixed voxel signal with two or three incorrectly chosen dictionary entries could mask the pathological tissue as a weighted sum of healthy tissues.
This work focuses on subvoxel components in relatively distinct compartments, each of which is smaller than the voxel, but larger than the diffusion mixing distance, shown in Figure 1(a). This type of model represents situations in which there are many cells of individual tissue types present within a single voxel. In contrast, voxels which contain multiple components, that are on a smaller scale than the diffusion distance, shown in Figure 1(b), present a greater challenge to solve. A straightforward application of MRF would result in one, well-mixed component. Other methods such as MRF for chemical exchange (MRF-X)18 may be able to resolve the subvoxel composition for these cases, but this is beyond the scope of the work discussed here.
Figure 1.
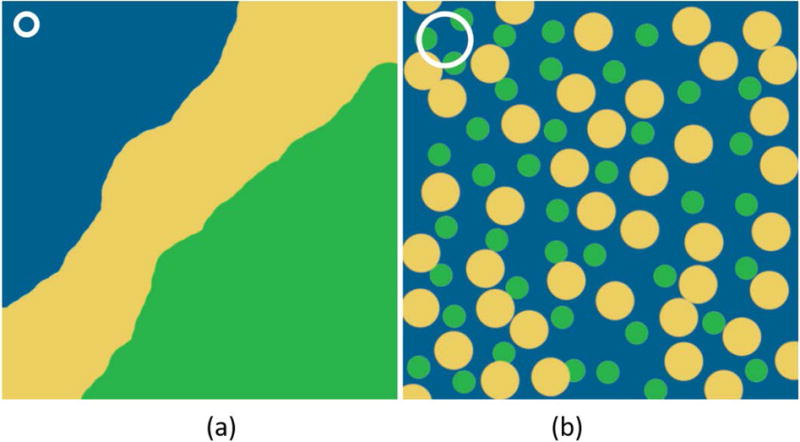
(a) A schematic of a voxel with slowly or non-exchanging components, with distinct boundaries. This is the type of voxel we propose to study in this work. (b) A diffuse, well-mixed voxel of fast-exchanging components. The white circle represents the diffusion mixing distance in both cases.
In this study, we present an alternative approach that does not require prior knowledge of the individual tissue components. In this method, given a full dictionary of potential signal evolutions, we search for a solution that represents the voxel signal using the proper number of dictionary entries as supported by the data. Under this assumption, we can take advantage of recent advances in sparse reconstruction to find a solution. In particular, we propose to use the Bayesian framework for inverse problems.19 This method provides a flexible procedure for computing a weight vector for each potential tissue using the data and prior assumptions as guides. In this framework, all unknowns are modeled as random variables with associated probability density functions, and the solution to the inverse problem is also a probability density, called the posterior distribution. Point estimates and sampling techniques can be used to compute representative solutions from the posterior density. The proposed algorithm identifies the number of entries from the MRF dictionary present within a voxel. The accuracy of the method is investigated through simulations and performance is evaluated in two healthy subjects and one of brain tumor patient.
Theory
If the dictionary used in MRF is denoted by D, and y is an observed MRF voxel signal, the partial volume problem can be formulated as the solution to the inverse problem
| [1] |
for a weight vector and noise term . As formulated in [1], the problem is ill-posed, and without adding any prior information, the solution may not be unique or may be too sensitive to small perturbations in the data. The solution should be a sparse, or near sparse, vector, with larger weights corresponding to the entries of that contribute most significantly to the mixed voxel signal. We will assume that both the signal and all dictionary entries have been normalized to have length one, that is, ||y|| = 1. Note that we use ||·|| to represent the usual Euclidean norm.
The MRF dictionary is represented as a matrix where t represents the number of time points and n is the number of parameter combinations or tissue types. An observed signal y can be represented as a weighted sum of a subset of N dictionary entries , for dictionary entries with weights . When the subset is known a priori, the weight vector × can be found as the solution to a linear least squares problem. Since the subset is generally unknown, the problem needs to be modeled using the full dictionary as in [1], where is the vector of corresponding weights and e is complex zero-mean Gaussian noise. However, solving [1] in the least squares sense, that is, minimizing will result in a dense solution, and it will be extremely difficult to pick out the few tissue types that have the most significant contributions to the voxel signal.
Using the Bayesian paradigm for inverse problems, all unknowns in the problem are modeled as random variables with associated probability density functions. The solution is the posterior density, given by Bayes' formula, , which is in terms of the likelihood and prior probability densities. The posterior density can be explored using sampling techniques, or point estimates, such as the maximum a posteriori or conditional mean estimators.
The likelihood provides the probability of obtaining the observed signal, assuming that the parameter is known. In this application, the noise is assumed to be Gaussian with zero mean and constant variance , and the likelihood density is
| [2] |
where denotes proportionality.
Construction of the Prior and Hyperprior Densities
The prior density encodes any prior knowledge or belief about the weight vector , where no assumptions are made about the observed data . The vector should be sparse, or approximately sparse, with the largest values corresponding to entries that contribute to the mixed signal. To that end, each weight is assumed to be independent and normally distributed with zero mean and variance . The prior density is then
| [3] |
for covariance matrix while a Gaussian density does not, in general, encourage sparse solutions, we note that the variance does influence the magnitude of random draws from the distribution, as it controls the spread. Hence, for a small variance , it is more likely that a random draw from ) will be close to zero, whereas a larger variance will allow a higher probability of obtaining a larger realization. An example is shown in Figure 2. Note that the weights are allowed to be complex-valued, due to the arbitrary phase observed in the MRF acquisition. Since the variance is presumed to be unknown, it will also be modeled as a random variable. To this end, each is assumed independent and identically distributed, following a Gamma distribution, with shape and scale parameters and , respectively,
| [4] |
Random draws from a Gamma distribution with properly chosen parameters and will have a higher probability of being small, while still allowing for large outliers. This in turn controls the width of the Gaussian priors placed on .20 An example of a Gamma probability density function is plotted in Figure 2. The variables are called hyperpriors.19 This type of method is also sometimes referred to as Bayesian compressive sensing21, since it provides a way to find a sparse solution in the Bayesian framework as opposed to traditional compressed sensing methods.
Figure 2.
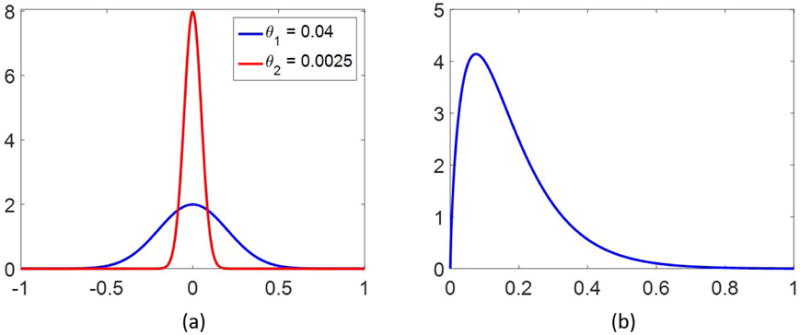
Two normal distributions are plotted in (a), both centered at 0, but with different variances, as noted. In (b) is shown a probability density function of the Gamma distribution with shape parameter α = 1.75 and scale parameter β = 0.1.
The joint probability density of the unknowns is written in terms of the conditional density as The posterior density, which is the solution to the inverse problem in the Bayesian framework, is proportional to the likelihood, prior, and hyperprior densities, and is given through Bayes’ formula as
| [5] |
Therefore, the posterior density here is
| [6] |
The function to be minimized is formulated by taking the negative logarithm of Eq. [6],
| [7] |
Methods
To obtain a point estimate for the solution to the inverse problem, the maximum a posteriori estimator is computed, minimizing the function [7], by alternating between updating and 20. After initialization of the weights and the dictionary, ( ), the variance vector is first updated via an analytical solution using simple differentiation. The kth iterate yields the updated variance
| [8] |
where . The next step is the minimization problem in , which, for fixed θ, is reduced to a linear least squares problem. This is solved using the conjugate gradient method for least squares22 with prior conditioning20 and a change of variables
| [9] |
where is a regularization parameter for the Tikhonov regularization scheme, and can be related to the noise . The CGLS iterations are stopped when the difference between the residuals at the kth and (k-1)st iteration drops below a predetermined tolerance.
Then, × is updated as
| [10] |
To further encourage sparsity and ease the computational burden, the dictionary is trimmed after each iteration by removing the columns corresponding to the smallest weight values xj, defined using a fixed percentage (5%) of the dictionary size, to form an updated dictionary D(k+1) before the next iteration proceeds. This is necessary for two reasons. First, the MRF dictionary can grow to extremely large sizes when more parameter combinations are considered or added, and pruning the dictionary will result in faster computations. Second, there are groups of dictionary entries that have similar T1 and T2 values, which, when solving an ℓ2 minimization problem, may cause the weights to spread across these similar entries. Pruning the dictionary will allow only the most significant dictionary entries to remain in the solution of this method.
Note that the number of tissue types present in a given voxel is not an input into the problem, but can be inferred based on the analysis of the final output. The algorithm is stopped based on a desired number of dictionary entries to represent the mixed voxel. This step is critical, as leaving too many dictionary entries to represent a mixed voxel will leave in incorrect and noncontributing entries in the solution. On the other hand, due to the similarity between dictionary entries with T1, T2 values that are relatively close, running the algorithm until only a small number of dictionary entries remain runs the risk of pruning a significantly contributing entry.
In practice, due to the nature of complex-valued MRF signals, the weights will be computed as complex. However, to avoid the confusion of complex or negative valued weights, after all of the iterations have been completed, the complex value will be projected to the nonnegative real line by considering the magnitude as the weight value.
Numerical simulations were performed to evaluate the accuracy of the output of the algorithm. In vivo analysis was aimed at investigating the sensitivity of the algorithm tuning parameters and demonstrating utility in identifying healthy and pathological tissues.
Simulation Data
Signals were simulated as weighted sums of entries from a dictionary computed using a FISP MRF23 sequence. The dictionary contains signal evolutions using 5970 different T1, T2 combinations and t = 3000 time points, resulting in a complex-valued matrix of size 3000 × 5970. The T1 values ranged from 10 to 2950 ms, in increments of 5 ms between 10 and 90 ms, increments of 10 ms up to 1000 ms, increments of 20 ms up to 1500, and increments of 50 ms up to 2950 ms. The T2 values ranged from 2 to 500 ms, in increments of 2 ms up to 10 ms, increments of 5 ms up to 150 ms, increments of 10 ms up to 200, and increments of 50 ms up to 500 ms.
A numerical phantom was simulated as a time series of 256 × 256 MRF frames divided into four regions, each a square of size 128 × 128 pixels, representing mixtures between the different tissue types. Mixed signals were simulated using two dictionary entries, with T1 and T2 pairs chosen to represent white matter, gray matter, brain tumor, and CSF.24 Pixels within each region were generated as the same predefined mixture of tissue types: a 50/50 mixture of white matter and gray matter, a 50/50 mixture of white matter and tumor, a 50/50 mixture of tumor and CSF, or a 90/10 mixture of white matter and tumor. The time series was then transformed into k-space using the Fourier transform, where Gaussian noise was added as a percentage of the maximum k-space value. Sampling was completed using a variable density spiral trajectory to produce both fully sampled and undersampled data, which were then reconstructed back to the image domain using gridding and the non-uniform fast Fourier transform.25 For the undersampled data set, one arm out of the full 48 spiral trajectory was used at each TR, and then rotated 7.5° for the next TR. The signal-to-noise ratio (SNR) was computed in the image domain, using the mean value of the first 256 × 256 image. The algorithm was then applied to four randomly chosen pixels within each of the regions. For each noise level, a Monte Carlo simulation was performed, repeating the entire process over ten repetitions.
An additional test was completed using the fully sampled simulated data just described, where the signals and dictionaries were truncated to represent different signal lengths in order to investigate the effect of the acquisition length on the partial volume results. For this analysis, the noise level was fixed to achieve an average SNR of 5.6, and signal lengths were 250, 500, 1000, and 2000. Note that in each case, these were the first time points out of the 3000 originally simulated.
Algorithm parameters varied slightly, and were tested more rigorously on the in vivo data.
Volunteer
To test the model on in vivo data, informed consent was obtained from three volunteers in an IRB-approved study and were scanned at 3T (Skyra, Siemens Medical, Erlangen, Germany or Verio, Siemens Medical, Erlangen, Germany). A 20-channel head receiver array was used, and the data were reconstructed using the nonuniform Fast Fourier transform25, after which adaptive coil combination was used to combine the images from each channel26.
Two volunteers were normal subjects, scanned using an MRF-FISP23 sequence. The sequence parameters are as follows: variable flip angle between 0 and 74 degrees and variable TR between 11.5-14.5 ms. For both the fully sampled and undersampled data, the FOV was 300 mm × 300 mm with matrix size 256 × 256. A variable density spiral trajectory, used in23 was used for both acquisitions, which requires 48 spiral interleaves to fully sample the outer 256 × 256 region in k-space and 24 interleaves to fully sample the innermost 25%. The acquisition window was 5.6 ms. For the undersampled data, one spiral arm was used at each TR and rotated 7.5° for the next TR. For one volunteer, fully sampled data were acquired in k-space, for the other, undersampled data were acquired using one spiral arm at each TR. The dictionary was the same as used in the simulations, containing 5970 different combinations of T1 and T2 and 3000 time points. For the fully sampled data set, voxels were analyzed from several regions of the brain to determine how the Bayesian algorithm performed in comparison to the traditional MRF matching, without the severe aliasing artifacts that are typically observed in MRF.
The undersampled data set was used to analyze the sensitivity of the algorithm to the Gamma distribution parameters α and β, as well as the regularization parameter μ, in the presence of artifacts due to undersampling. Voxels were chosen to be representative of three types: a white matter/gray matter mixture, a gray matter/CSF mixture, and pure white matter. Different algorithm parameter values were used to determine which were most successful in separating mixed voxel signals, while at the same time correctly identifying the single component in the white matter voxel.
One patient was consented and scanned27 using an MRF-bSSFP sequence prior to surgery for brain tumor resection. Based on histopathology, this patient was diagnosed with glioblastoma multiforme (GBM). Relevant sequence parameters include 300 mm × 300 mm FOV, matrix size 256 × 256, slice thickness 5 mm, flip angle varied between 0-60 degrees, and TR varied between 8.7-11.6ms. The same variable density spiral trajectory was used as described for the MRF-FISP acquisition, with one spiral used in each TR. For this bSSFP sequence, off-resonance frequency is an additional parameter that is built into the dictionary. In this case, the dictionary contains 2999 time points, 3307 combinations of T1 and T2, and 77 different off-resonance frequencies, resulting in a three-dimensional matrix of size 2999 × 3307 × 77. The T1 values range from 100 to 2950 ms, in increments of 20 ms from 100 to 1000 ms, increments of 40 ms up to 2000, and increments of 50 ms up to 2950 ms. The T2 values range from 10 to 500 ms, in increments of 5 ms from 10 to 100 ms, increments of 10 up to 300 ms, and increments of 50 ms up to 500 ms. The off-resonance values range from −300 to 290 Hz, in increments of 2 Hz for frequencies between −60 and 60 Hz, and increments of 20 Hz for frequencies outside of this range. For purposes of this work, we consider partial volume only in terms of T1 and T2 relaxation times, hence at each pixel a subdictionary of size 2999 × 3307 was chosen based on the off-resonance frequency calculated using the traditional MRF matching prior to analysis in the Bayesian MRF PV algorithm. Further details regarding the sequence parameters for the MRF acquisitions used in this work are in supporting Figure S1 and also are described in14,23.
Interpretation and Visualization
The algorithm output yields multidimensional results at each voxel of T1, T2 pairs along with corresponding weights. The dimension of each is determined by the number of iterations run in the algorithm. For in vivo data, fewer iterations were run to account for additional noise and artifacts.
For the simulation data, a k-means analysis is used to cluster the results into groups to determine the mean T1 and T2 values of each cluster.
In vivo results require a more sophisticated analysis, as we do not know the number of tissue types contained in a given voxel, in which case a k-means analysis cannot be applied. To this end, results will be visualized on a voxel-wise basis, and thus it is only feasible to visualize a sampling of the results from the slice. These results will be visualized as T1 and T2 scatter plots, corresponding to the T1 and T2 values of the dictionary entries that remain at the final iteration of the algorithm. Overlaid on top of each point will be plotted another circle, where the weight value assigned to that dictionary entry is represented by the color intensity.
Comparison to minimization
A typical approach to minimization problems when a sparse solution is desired, is to apply regularization using the ℓ1 norm,
| [11] |
Various algorithms have been developed to solve problems of this form. For comparison, we applied the fast iterative shrinkage algorithm (FISTA),28 which has been shown to be computationally efficient for problems of the form [11]. The algorithm updates the solution iteratively using soft thresholding. FISTA was applied to both the simulated and volunteer data. The value of was fixed at 0.01 for each application of FISTA. For the simulated data, the algorithm was stopped at 3000 iterations, the dimension of the data.
Results
For all results shown here, computations were completed on a standard desktop computer using MATLAB (The Mathworks, Inc.).
Simulation
The Bayesian MRF algorithm was terminated after 130 iterations, resulting in eight out of the original 5970 original dictionary entries. The algorithm took about 12 seconds to run for each pixel. Results from each region were analyzed using a k-means analysis to compute the means of each of the clusters found. Using these clusters, the weights, computed from the algorithm could be summed to give a relative fraction of each species present. The resulting mean T1 and T2 values and relative fractions of the clusters are summarized in Table 1 for several SNR values. Only one SNR level for the undersampled data is shown (with the smallest level of additive noise in k-space) due to the severe aliasing from undersampling.
Table 1.
The T1, T2, and weights corresponding to the dictionary entries used in simulation to create the mixed signals are listed in the column labeled “Ground Truth”. Next are the mean T1, T2 values which describe the results for three of the simulations (two with fully sampled data, and one with undersampled data) at different SNR values. At the end of each simulation, results were clustered into two groups using k-means, and the mean T1, T2 times for each group were calculated. These simulations were run using the full MRF time series.
| Ground Truth | Fully Sampled | Undersampled | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| SNR = 5.6 | SNR = 2.9 | SNR = 1.0 | |||||||||
|
| |||||||||||
| T1 | T2 | Weight | T1 | T2 | Weight | T1 | T2 | Weight | T1 | T2 | Weight |
| 800 | 60 | 0.5 | 958.4 | 82.8 | 0.77 | 974.0 | 82.9 | 0.83 | 957.7 | 80.6 | 0.66 |
| 1300 | 120 | 0.5 | 1305.9 | 113.1 | 0.23 | 1297.6 | 119.6 | 0.17 | 1186.7 | 102.1 | 0.34 |
|
| |||||||||||
| 800 | 60 | 0.5 | 826.2 | 67.2 | 0.48 | 903.1 | 77.1 | 0.56 | 989.1 | 90.8 | 0.63 |
| 1700 | 180 | 0.5 | 1703.3 | 174.6 | 0.52 | 1742.4 | 174.6 | 0.44 | 1674.5 | 159.1 | 0.37 |
|
| |||||||||||
| 1700 | 180 | 0.5 | 1813.28 | 195.6 | 0.64 | 1756.8 | 184.5 | 0.59 | 1723.4 | 195.7 | 0.63 |
| 2950 | 500 | 0.5 | 2823.0 | 477.1 | 0.36 | 2776.8 | 456.7 | 0.41 | 2721.6 | 399.1 | 0.37 |
|
| |||||||||||
| 800 | 60 | 0.9 | 848.7 | 69.7 | 0.93 | 850.3 | 67.7 | 0.93 | 857.6 | 66.4 | 0.91 |
| 1700 | 180 | 0.1 | 1760.5 | 153.1 | 0.07 | 1745.0 | 173.9 | 0.07 | 1744.2 | 241.2 | 0.09 |
FISTA was applied to both the fully sampled and undersampled simulated data with the number of iterations fixed at 3000. Analyzing one mixed signal using FISTA took about 110 seconds. The number of nonzero weights contributing to the mixed signal varied from 657 to 1650 for fully sampled and 492 to 1309 for undersampled. Note that this is not a parameter that can be easily fixed to yield the same number at each voxel, as is the case in the Bayesian MRF algorithm, and the number of nonzeros is far too many to make an accurate inference about the components comprising the mixed signal. Recall that for the simulations, Bayesian MRF algorithm was run until only eight dictionary entries remained, which is a stark contrast to the FISTA results. In both cases, the dictionary had 5970 total entries.
For the mixed signals in the undersampled simulation, FISTA did not always retain the correct tissue components, and, the large number of nonzeros, does not allow for a clear separation of tissue types for partial volume. Additionally, to run the 3000 iterations on one pixel took about two and a half minutes of computation for undersampled data, compared to 12 seconds for the Bayesian algorithm, in which the dictionary is reduced to the eight most significant dictionary components. A significant problem is the large number of nonzero entries in the FISTA solution after 3000 iterations, which make it too difficult to reliably differentiate the distinct components from a mixed signal. By increasing the number of iterations, we can decrease the number of nonzero dictionary entries, however, this comes at a high computational cost. For example, running 25000 iterations of FISTA will result in a solution with about 100-200 nonzero entries, however, this calculation takes almost 20 minutes at one pixel. The FISTA results for the simulated data are summarized in Table 2. Note that for comparison, the simulated data used here is the same as that used for the results in Table 1.
Table 2.
Results from FISTA computed on the simulated data. The SNR was fixed at 5.6 and 2.9, to be compared to the results from the Bayesian algorithm shown in Table 1. 3000 iterations of FISTA were completed. These simulations were run using the full MRF time series.
| Ground Truth | Fully Sampled | Undersampled | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| SNR = 5.6 | SNR = 2.9 | SNR = 1.0 | |||||||||
|
| |||||||||||
| T1 | T2 | Weight | T1 | T2 | Weight | T1 | T2 | Weight | T1 | T2 | Weight |
| 800 | 60 | 0.5 | 893.3 | 78.3 | 0.77 | 1005.4 | 87.6 | 0.96 | 1030.1 | 88.1 | 0.98 |
| 1300 | 120 | 0.5 | 1600.3 | 148.3 | 0.23 | 2036.6 | 249.9 | 0.04 | 1591.9 | 481.6 | 0.02 |
|
| |||||||||||
| 800 | 60 | 0.5 | 953.7 | 85.4 | 0.69 | 938.1 | 84.1 | 0.69 | 992.8 | 88.9 | 0.72 |
| 1700 | 180 | 0.5 | 1901.0 | 205.6 | 0.31 | 1866.5 | 192.3 | 0.31 | 1858.0 | 206.0 | 0.28 |
|
| |||||||||||
| 1700 | 180 | 0.5 | 1149.5 | 117.4 | 0.28 | 1109.7 | 113.3 | 0.28 | 1101.5 | 126.4 | 0.29 |
| 2950 | 500 | 0.5 | 233.7 | 306.2 | 0.72 | 2313.4 | 303.1 | 0.72 | 2333.9 | 293.8 | 0.71 |
|
| |||||||||||
| 800 | 60 | 0.9 | 952.7 | 78.6 | 0.97 | 921.9 | 75.9 | 0.97 | 810.0 | 67.44 | 0.82 |
| 1700 | 180 | 0.1 | 2285.4 | 263.0 | 0.03 | 2161.1 | 263.5 | 0.03 | 1450.2 | 120.0 | 0.18 |
Results for the test where acquisition length was varied are shown in Table 3. In general, the T1, T2, and corresponding weights improved as the signal length increased.
Table 3.
Simulation results when the length of the acquisition is varied. Shown are the k-means centroids for the fully sampled simulation data, at a fixed SNR of 5.6 (compare with the results in Table 1). The length of the signals and the dictionary were varied from 250 time points up to 2000, where the results in Table 1 correspond to signal length of 3000 time points.
| Length | 250 | 500 | 1000 | 2000 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | T2 | Weight | T1 | T2 | Weight | T1 | T2 | Weight | T1 | T2 | Weight | T1 | T2 | Weight |
| 800 | 60 | 0.5 | 1037.8 | 91.2 | 0.98 | 1018.76 | 86.4 | 0.83 | 991.9 | 83.9 | 0.79 | 960.1 | 82.4 | 0.73 |
| 1300 | 120 | 0.5 | 1084.3 | 442.9 | 0.02 | 1147.8 | 117.0 | 0.17 | 1221.8 | 118.9 | 0.21 | 1267.8 | 113.7 | 0.27 |
| 800 | 60 | 0.5 | 956.3 | 22.5 | 0.11 | 986.8 | 75.1 | 0.35 | 899.8 | 70.7 | 0.43 | 881.9 | 75.9 | 0.49 |
| 1700 | 180 | 0.5 | 1229.1 | 135.4 | 0.89 | 1348.0 | 150.1 | 0.65 | 1484.0 | 156.0 | 0.57 | 1609.8 | 159.0 | 0.51 |
| 1700 | 180 | 0.5 | 1968.6 | 418.7 | 0.55 | 1914.2 | 165.6 | 0.45 | 1897.1 | 194.7 | 0.70 | 1944.5 | 196.3 | 0.70 |
| 2950 | 500 | 0.5 | 2051.1 | 180.3 | 0.45 | 2109.9 | 393.9 | 0.55 | 2459.6 | 485.6 | 0.30 | 2684.7 | 486.3 | 0.30 |
| 800 | 60 | 0.9 | 878.9 | 54.9 | 0.64 | 898.0 | 72.4 | 0.94 | 888.7 | 73.4 | 0.97 | 873.6 | 72.8 | 0.96 |
| 1700 | 180 | 0.1 | 950.3 | 127.1 | 0.36 | 1072.5 | 115.8 | 0.06 | 1403.8 | 146.3 | 0.03 | 1284.3 | 107.5 | 0.04 |
Normal Volunteer
The data obtained from the fully sampled acquisition was used to compare the fit between the MRF match, which yields one T1, T2 pair per voxel, and the multidimensional set of T1, T2, and weights that result from the Bayesian algorithm. For a given voxel, denote by , the dictionary entry which yields the largest complex inner product, as computed in the traditional MRF matching. The MRF residual is computed as where both and are normalized to unit length. Similarly, if the Bayesian algorithm yields a set of dictionary entries di and associated weights xi, the residual for the Bayesian algorithm is computed Results for both methods were phase corrected to match . Residuals were computed at voxels within different regions in the brain; one each is assumed to correspond to pure white matter, pure CSF, partial volume white matter and gray matter, or partial volume gray matter and CSF. The residuals at each voxel within the regions are shown in Figure 3.
Figure 3.
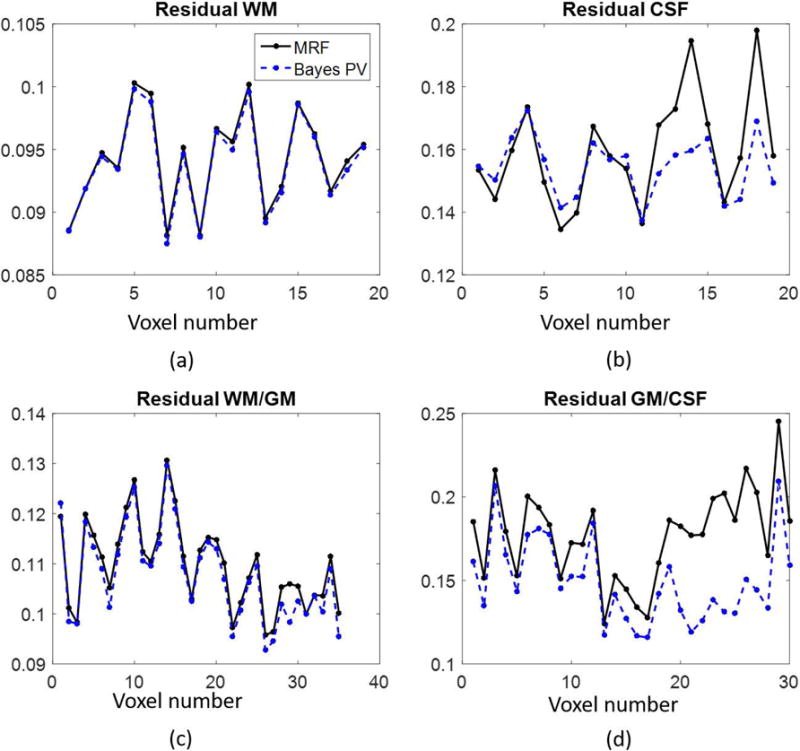
The residuals per voxel corresponding to MRF matching and the Bayesian algorithm for the fully sampled, in vivo data set. Four different ROIs were examined, two regions with presumably pure tissues (pure white matter (a) and pure CSF (b)), and two regions with assumed partial volume (white matter/gray matter (c) and gray matter/CSF (d)). Note that in regions of partial volume, the Bayesian algorithm produces smaller residuals, as shown in (c) and (d).
Three individual voxels in the undersampled data were analyzed to determine the sensitivity of the results to varying the three parameters α, β, and μ in the presence of artifacts due to aliasing. The three voxels are indicated in the MRF T1 map shown in Figure 4. The blue marker indicates a voxel with gray matter/CSF partial volume, yellow indicates white matter/gray matter partial volume, and red indicates a voxel of pure white matter. For each voxel, 110 iterations of the algorithm were run, resulting in 21 dictionary entries at the final iteration, which took approximately 12 seconds per voxel. Shown in Figure 5(a)–(c) are the scatterplot results for each of these three voxels using the fixed parameters β = 0.1, and μ = 0.01. Figures 5(a) and 5(c) use α = 1.75, whereas the white matter/gray matter voxel in Figure 5(b) uses α = 3.5.
Figure 4.
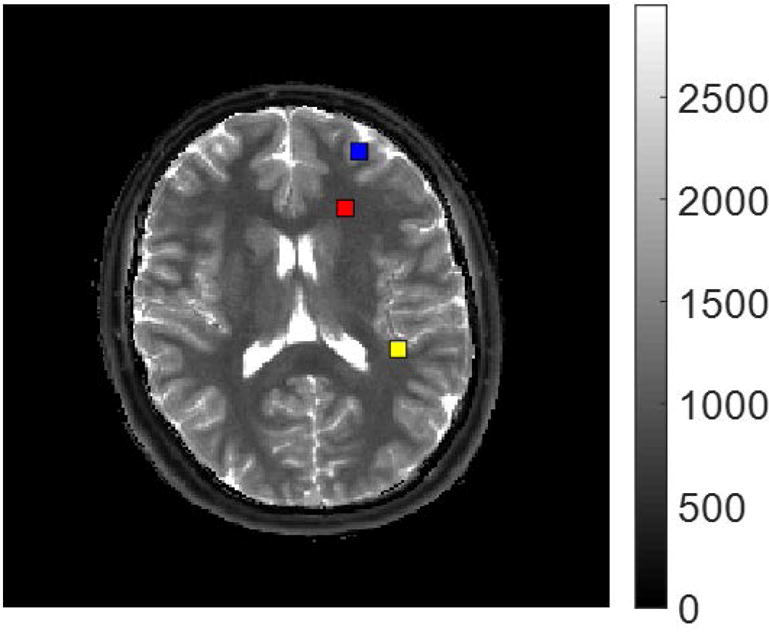
The MRF T1 map (units in ms) with the three voxels highlighted which are analyzed. The blue marker corresponds to gray matter/CSF partial volume, yellow to white matter/gray matter partial volume, and red to pure white matter.
Figure 5.
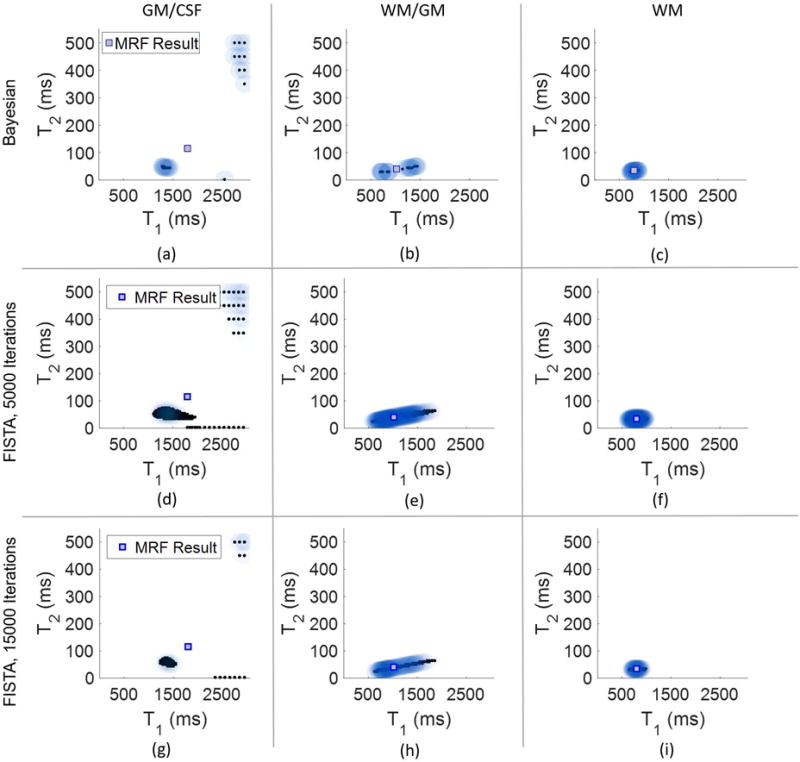
Results from analyzing the three voxels highlighted in Figure 4. The top row (plots (a)-(c)) show the results from the Bayesian algorithm using 110 iterations. The middle and bottom rows show results using FISTA, with 5,000 iterations (plots (d)-(f)) and 15,000 iterations (plots (g)-(i)). In each scatterplot is also plotted the MRF result, shown as a square.
Plots demonstrating the sensitivity of algorithm results to the Gamma distribution parameters and the regularization parameter are shown in the supporting Figures S2, S3, and S4. From these plots, appropriate ranges of the values of α, β, and μ can be deduced. In particular, the algorithm appears to be the least sensitive to the values for α and β, except, perhaps, in the case of alpha for white matter/gray matter separation. Results are most sensitive to the regularization parameter μ. When the value of μ is too small, the results tend toward a least squares solution, with little impact from the penalty term to minimize the weight variances. As the value of μ is increased, results stabilize toward a reasonable solution, but when increased further, all voxels will converge to the effective MRF result.
FISTA was also applied to the undersampled in vivo data set for the same three highlighted voxels. Here, 5000 iterations of FISTA required almost 3 minutes per voxel, and 15000 iterations required over 8 and a half minutes per voxel. The number of nonzero contributing dictionary entries again varies, with as many as 220 in the case of GM/CSF after 5000 iterations to 76 in the pure white matter voxel after 15000 iterations. Compared to the results obtained from applying FISTA in simulation, the number of nonzeros in the solution are reduced, however, to obtain results similar to the Bayesian MRF algorithm in vivo still requires far more computation time. Results from FISTA for the undersampled in vivo data are shown in Figure 5(d)–(i).
Patient
The parameters for the Gamma distribution were chosen to be , . The regularization parameter μ was fixed at 1e-3 for this experiment. The algorithm was stopped after 80 iterations when there were 46 dictionary entries remaining to explain each individual voxel signal. Stopping the algorithm early, as is done here, prevents the possible exclusion of a small, but still significant contribution from dictionary entries which may represent pathological tissue. Allowing more dictionary entries to be present in the solution will, however, require further analysis of the results than when fewer dictionary entries remain.
Five voxels chosen away from the tumor region in presumably healthy tissue were chosen for analysis, one each of pure white matter, gray matter, and CSF, along with two voxels which potentially exhibit partial volume. These results are shown in Figure 6.
Figure 6.
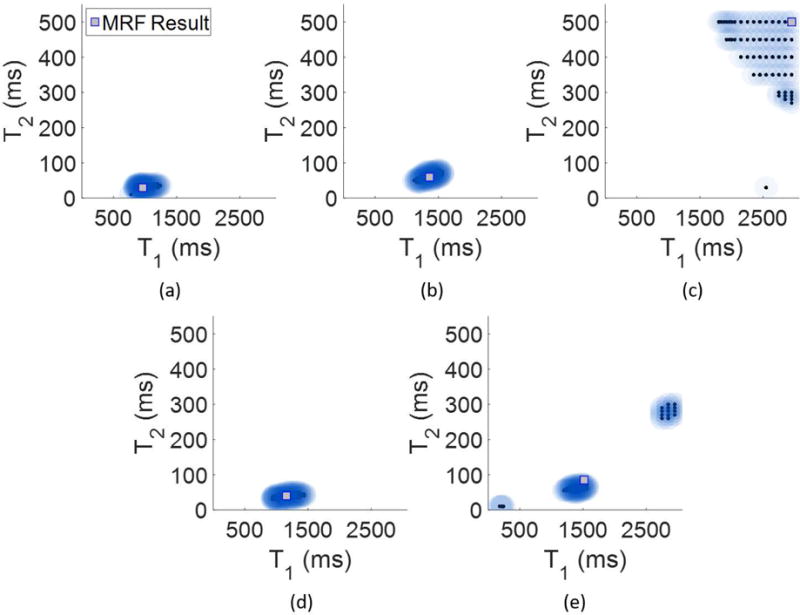
Voxel-wise algorithm results from the patient, diagnosed with a GBM. Panel (a) shows the result from a pure white matter voxel, (b) from a pure gray matter voxel and (c) from a pure CSF voxel. Panels (d) and (e) show Bayesian MRF results from two voxels which potentially exhibit partial volume. In (d) is a mix of white matter and gray matter, and in (e) is a mix of gray matter and CSF.
Regions of interest (ROIs) were drawn by a neuroradiologist to define regions of solid tumor and peritumoral white matter. Voxels were selected from these ROIs to show examples of the algorithm analysis in the pathological regions of solid tumor and peritumoral region with scatterplots shown in Figure 7. A voxel within the solid tumor indicates a dominant component with a smaller short-T2 component also present. On the other hand, the voxels from within the peritumoral region indicate a partial volume effect between a component with mid-range T1 and T2 values and a separate fluid-like component. The presence of two distinct components within these voxels suggest that the single-component MRF result may be incorrect, as it lies in between the two components found through the partial volume analysis.
Figure 7.
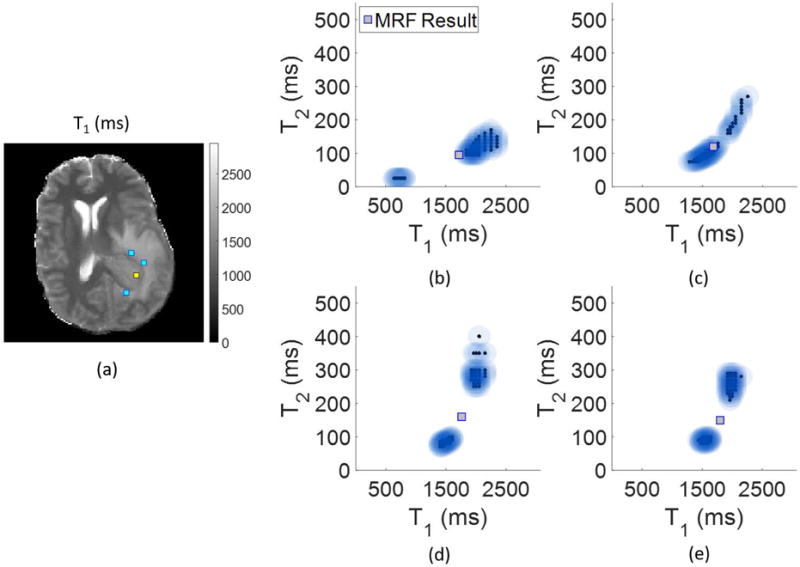
Voxel-wise Bayesian MRF results for the patient, with locations indicated on the T1 map (units in ms) in (a). In (b) is the result from within the tumor (indicated in yellow in (a)), and in (c), (d), and (e) are results from the peritumoral region (indicated in blue in (a)).
Discussion
The results from the simulated mixed signals show that the algorithm allows separation of a mixed signal into two component dictionary entries. Even when the T1 and T2 values for the component signals are relatively close together, as is the case for white matter and gray matter, the algorithm is able to clearly resolve two distinct components, though the resulting cluster centroids are less accurate due to the closeness of these T1, T2 values. This is a point for future consideration, Additionally, tests run where the signal length was varied show that the algorithm performs better when the number of time points is increased. Comparing the results from Table 3 with the first three columns of Table 1, show that the most accurate results are achieved when 3000 time points are used.
The in vivo results are also encouraging. A particular challenge of solving the partial volume problem without any prior assumptions about the tissue composition of each voxel is how to validate the model in vivo. In both the FISP and bSSFP versions of MRF, the algorithm shows agreement in areas of the brain that are highly likely to be pure tissue, as demonstrated in areas of pure white matter, gray matter, or CSF, as seen in the single voxel results. The residual comparison shown in Figure 3 suggests that even in the case of voxels containing a pure tissue, it may be more accurate to represent the subvoxel composition as a distribution of dictionary entries, rather than picking a single match. Most certainly this is the case in mixed voxels, as the MRF match is attempting to explain at least two different components with only one T1, T2 pair.
Of particular interest are the voxel results from the patient, which show the potential of the algorithm in regions of pathological tissue, where the composition within a given voxel may not be known in advance.
Comparison between our results and those from FISTA suggest that both methods may be able to identify multiple voxel components, though FISTA requires much longer computation times. The Bayesian MRF method provides results much more quickly, and will benefit from parallelization, as a fixed number of iterations can be chosen in advance, as a desired number or percentage of dictionary entries desired to represent the mixed voxel signal.
The choice of the algorithm parameters requires further optimization. In particular, these parameters may have different effects given different pathologies or mixed voxel types. Finding an optimal regularization parameter will be an important aspect of the problem, due to the impact a too large or too small regularization parameter can have on the solution.29 This is seen in Figure S4, as too small of a regularization parameter produces incorrect and results dominated by noise, however too large of a regularization parameter will cause convergence in all cases to the single-component MRF solution. In addition, since the method is iterative, with both an inner and outer loop, the stopping criteria need to be optimized as well, as this can also effect regularization. The number of iterations is fixed in advance and can be chosen based on any number of factors, by considering an L-curve29 to determine tradeoff between the residual norm and regularization, or by choosing a desired sparsity level. In the case of in vivo data, it is prudent to retain a larger number of dictionary entries to obtain the final solution, to avoid incorrectly pruning significant entries due to noise or undersampling artifacts.
In regards to the computation times shown in this work, we have not yet optimized the code through more efficient programming or parallelization. Each pixel is treated independently, so the algorithm can be parallelized resulting in a much faster implementation. Currently, the most computationally expensive step in the algorithm is the solution of the linear least squares problem [9], with the dictionary size being the main roadblock. Pruning the dictionary, as has been proposed here, significantly allows for speed up of this step; for example, in the FISP dictionary of size 3000 × 5970, solving [9] requires about 0.5 seconds in MATLAB, thus pruning the dictionary as the iterations proceed is an easy way to save time.
The noise model used in the current implementation may also require further optimization. Though complex, zero-mean Gaussian noise is used here, there are factors that may influence the behavior of the noise seen in MRF, in particular, as related to the gridding reconstruction and mulitchannel data.30 The model considered here does not take a multi-channel acquisition into account, however, relies on the pseudo-randomized spatial encoding in the original MRF implementation for the Gaussian noise assumption.
There are still avenues to explore in this methodology, and other techniques that may improve the accuracy or efficiency of this method. For example, the inverse Gamma probability distribution has similar properties to the Gamma distribution, and can also be used for the hyperprior distribution.31 Additionally, we have taken the approach here to compute a point estimator to the full posterior distribution shown in [6]. An alternative approach is to explore the posterior distribution via sampling techniques using Markov Chain Monte Carlo sampling techniques19 though the computational cost to this approach would be expensive, as there would need to be a different posterior distribution corresponding to each pixel. However, this approach may offer a valuable alternative to validate and understand the solution to this problem.
To manage and visualize the multidimensional results, there are other possibilities beyond voxel-specific scatterplots that can be explored, including k-means clustering or learning vector quantization.32 Additionally, a promising method is the mean shift algorithm,33 which has the advantage that the number of clusters do not need to be estimated from the results. In this method, the result is viewed as a probability density, and the modes are estimated using the derivative.
Conclusion
We have provided a flexible framework for approaching the partial volume problem in MRF, when tissue types are not assumed known a priori. This methodology has advantages over traditional partial volume methods, which tend to force the solution to fit two or three predefined tissue types.
Supplementary Material
Supporting Figure S1 Sequence parameters (flip angle, repetition time, and echo time) used in the MRF – FISP and MRF – bSSFP acquisitions used to acquire the data.
Supporting Figure S2 Scatterplot results from the Bayesian MRF PV algorithm over three different voxels from a normal volunteer scanned with an MRF FISP sequence. The voxels analyzed are highlighted in Figure 4(a). These results show the effect of varying the Gamma distribution parameter α, which is called the shape parameter. The other algorithm parameters are fixed for this set of results at β= 0.1 and μ = 0.01.
Supporting Figure S3 Scatterplot results from the Bayesian MRF PV algorithm over three different voxels from a normal volunteer scanned with an MRF FISP sequence. The voxels analyzed are highlighted in Figure 4(a). These results show the effect of varying the Gamma distribution parameter β, which is called the scale parameter. The other algorithm parameters are fixed for this set of results at α = 1.75 and μ = 0.01.
Supporting Figure S4 Scatterplot results from the Bayesian MRF PV algorithm over three different voxels from a normal volunteer scanned with an MRF FISP sequence. The voxels analyzed are highlighted in Figure 4(a). These results show the effect of varying the regularization parameter μ. The other algorithm parameters are fixed for this set of results at α = 1.75 and β = 0.1. Note that as the value of μ is increased, the results will converge to their respective MRF match, and will not be able to identify voxels where partial volume is present.
Acknowledgments
Support for this work was provided by NIH 1R01EB016728-01A1, NIH 5R01EB017219-02, and Siemens Healthineers.
References
- 1.Tohka J. Partial volume effect modeling for segmentation and tissue classification of brain magnetic resonance images: A review. World Journal of Radiology. 2014;6(11):855–864. doi: 10.4329/wjr.v6.i11.855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Reiter DA, Lin PC, Fishbein KW, Spencer RG. Multicomponent T 2 relaxation analysis in cartilage. Magnetic Resonance in Medicine. 2009;61(4):803–809. doi: 10.1002/mrm.21926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ruan S, Jaggi C, Xue J, Fadili J, Bloyet D. Brain tissue classification of magnetic resonance images using partial volume modeling. IEEE transactions on medical imaging. 2000;19(12):1179–87. doi: 10.1109/42.897810. [DOI] [PubMed] [Google Scholar]
- 4.Shin W, Geng X, Gu H, Zhan W, Zou Q, Yang Y. Automated brain tissue segmentation based on fractional signal mapping from inversion recovery Look-Locker acquisition. NeuroImage. 2010;52(4):1347–1354. doi: 10.1016/j.neuroimage.2010.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ahlgren A, Wirestam R, Stahlberg F, Knutsson L. Automatic brain segmentation using fractional signal modeling of a multiple flip angle, spoiled gradient-recalled echo acquisition. Magnetic Resonance Materials in Physics. 2014;27(6):551–565. doi: 10.1007/s10334-014-0439-2. [DOI] [PubMed] [Google Scholar]
- 6.Asllani I, Borogovac A, Brown TR. Regression algorithm correcting for partial volume effects in arterial spin labeling MRI. Magnetic Resonance in Medicine. 2008;60(6):1362–1371. doi: 10.1002/mrm.21670. [DOI] [PubMed] [Google Scholar]
- 7.Petr J, Schramm G, Hofheinz F, Langner J, van den Hoff J. Partial volume correction in arterial spin labeling using a Look-Locker sequence. Magnetic Resonance in Medicine. 2013;70(6):1535–1543. doi: 10.1002/mrm.24601. [DOI] [PubMed] [Google Scholar]
- 8.van Osch M, Vonken E, Bakker C, Viergever M. Correcting partial volume artifacts of the arterial input function in quantitative cerebral perfusion MRI. Magnetic Resonance in Medicine. 2001;45(3):477–485. doi: 10.1002/1522-2594(200103)45:3<477::aid-mrm1063>3.0.co;2-4. [DOI] [PubMed] [Google Scholar]
- 9.Tohka J, Zijdenbos A, Evans A. Fast and robust parameter estimation for statistical partial volume models in brain MRI. NeuroImage. 2004;23(1):84–97. doi: 10.1016/j.neuroimage.2004.05.007. [DOI] [PubMed] [Google Scholar]
- 10.Manjón JV, Tohka J, Robles M. Improved estimates of partial volume coefficients from noisy brain MRI using spatial context. NeuroImage. 2010;53(2):480–490. doi: 10.1016/j.neuroimage.2010.06.046. [DOI] [PubMed] [Google Scholar]
- 11.Laidlaw DH, Fleischer KW, Barr AH. Partial-volume Bayesian classification of material mixtures in MR volume data using voxel histograms. IEEE transactions on medical imaging. 1998;17(1):74–86. doi: 10.1109/42.668696. [DOI] [PubMed] [Google Scholar]
- 12.West J, Warntjes JBM, Lundberg P. Novel whole brain segmentation and volume estimation using quantitative MRI. European Radiology. 2012;22(5):998–1007. doi: 10.1007/s00330-011-2336-7. [DOI] [PubMed] [Google Scholar]
- 13.West J, Blystad I, Engström M, Warntjes JBM, Lundberg P. Application of Quantitative MRI for Brain Tissue Segmentation at 1.5 T and 3.0 T Field Strengths. PLoS ONE. 2013;8(9):1–12. doi: 10.1371/journal.pone.0074795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature. 2013;495:187–192. doi: 10.1038/nature11971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Deshmane A, Ma D, Jiang Y, Fisher E, Seiberlich N, Gulani V, Griswold M. Proceedings of the 22nd Annual Meeting. ISMRM; 2014. Validation of tissue characterization in mixed voxels using MR fingerprinting; p. 94. [Google Scholar]
- 16.Deshmane A, McGivney D, Jiang Y, Ma D, Griswold M. Proceedings of the 24th Annual Meeting. ISMRM; 2016. Enforcing a physical tissue model for partial volume MR fingerprinting; p. 2998. [Google Scholar]
- 17.Cao X, Liao C, Wang Z, Ye H, Chen Y, He H, Chen S, Liu H, Zhong J. Proceedings of the 24th Annual Meeting. ISMRM; 2016. An improved tissue-fraction MRF (TF-MRF) with additional fraction regularization; p. 4223. [Google Scholar]
- 18.Hamilton J, Deshmane A, Griswold M, Seiberlich N. Proceedings of the 24th Annual Meeting. ISMRM; 2016. MR fingerprinting with chemical exchange (MRF-X) for in vivo multi-component relaxation and exchange rate mapping; p. 431. [Google Scholar]
- 19.Calvetti D, Somersalo E. Introduction to Bayesian Scientific Computing: Ten Lectures on Subjective Computing. New York: Springer; 2007. [Google Scholar]
- 20.Calvetti D, Hakula H, Pursiainen S, Somersalo E. Conditionally Gaussian Hypermodels for Cerebral Source Localization. SIAM Journal on Imaging Sciences. 2009;2(3):879–909. [Google Scholar]
- 21.Ji S, Xue Y, Carin L. Bayesian compressive sensing. IEEE Transactions on Signal Processing. 2008;56(6):2346–2356. [Google Scholar]
- 22.Hestenes MR, Stiefel E. Methods of conjugate gradients for solving linear systems. Journal of Research of the National Bureau of Standards. 1952;49(6):409–436. [Google Scholar]
- 23.Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold M. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magnetic Resonance in Medicine. 2015;74(6):1621–1631. doi: 10.1002/mrm.25559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wansapura JP, Holland SK, Dunn RS, Ball WS. NMR relaxation times in the human brain at 3.0 Tesla. Journal of Magnetic Resonance Imaging. 1999;9(4):531–538. doi: 10.1002/(sici)1522-2586(199904)9:4<531::aid-jmri4>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 25.Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Transactions on Signal Processing. 2003;51(2):560–574. [Google Scholar]
- 26.Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magnetic Resonance in Medicine. 2000;43(5):682–690. doi: 10.1002/(sici)1522-2594(200005)43:5<682::aid-mrm10>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 27.Badve C, Yu A, Dastmalchian S, Rogers M, Ma D, Jiang Y, Margevicius S, Pahwa S, Lu Z, Schluchter M, et al. MR fingerprinting of adult brain tumors: Initial experience. American Journal of Neuroradiology. 2016 doi: 10.3174/ajnr.A5035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences. 2009;2(1):183–202. [Google Scholar]
- 29.Hansen PC. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Review. 1992;34(4):561–580. [Google Scholar]
- 30.Zhao B, Setsompop K, Ye H, Cauley SF, Wald LL. Maximum likelihood reconstruction for magnetic resonance fingeprinting. IEEE transactions on medical imaging. 2016;35(8):1812–1823. doi: 10.1109/TMI.2016.2531640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Calvetti D, Somersalo E. Hypermodels in the Bayesian imaging framework. Inverse Problems. 2008;24(3):34013. [Google Scholar]
- 32.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Second. New York: Springer; 2009. [Google Scholar]
- 33.Comaniciu D, Meer P. Mean Shift: A Robust Approach Toward Feature Space Analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2002;24(5):603–619. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Figure S1 Sequence parameters (flip angle, repetition time, and echo time) used in the MRF – FISP and MRF – bSSFP acquisitions used to acquire the data.
Supporting Figure S2 Scatterplot results from the Bayesian MRF PV algorithm over three different voxels from a normal volunteer scanned with an MRF FISP sequence. The voxels analyzed are highlighted in Figure 4(a). These results show the effect of varying the Gamma distribution parameter α, which is called the shape parameter. The other algorithm parameters are fixed for this set of results at β= 0.1 and μ = 0.01.
Supporting Figure S3 Scatterplot results from the Bayesian MRF PV algorithm over three different voxels from a normal volunteer scanned with an MRF FISP sequence. The voxels analyzed are highlighted in Figure 4(a). These results show the effect of varying the Gamma distribution parameter β, which is called the scale parameter. The other algorithm parameters are fixed for this set of results at α = 1.75 and μ = 0.01.
Supporting Figure S4 Scatterplot results from the Bayesian MRF PV algorithm over three different voxels from a normal volunteer scanned with an MRF FISP sequence. The voxels analyzed are highlighted in Figure 4(a). These results show the effect of varying the regularization parameter μ. The other algorithm parameters are fixed for this set of results at α = 1.75 and β = 0.1. Note that as the value of μ is increased, the results will converge to their respective MRF match, and will not be able to identify voxels where partial volume is present.


