AN ORAL PRESSURE CONVERSION RATIO AS A PREDICTOR OF VOCAL EFFICIENCY

Abstract

Voice production is an inefficient process in terms of energy expended versus acoustic energy produced. A traditional efficiency measure, glottal efficiency, relates acoustic power radiated from the mouth to aerodynamic power produced in the trachea. This efficiency ranges between 0.0001 % and 1.0 %. It involves lung pressure, and hence would appear to be a useful effort measure for a given acoustic output. Difficulty in the combined measurement of lung pressure and tracheal airflow, however, has impeded clinical application of glottal efficiency. This paper utilizes the large data base from Schutte (1980) and a few new measurements to validate a pressure conversion ratio (PCR) as a substitute for glottal efficiency. PCR has the potential for wide application due to low cost and ease of use in clinics and vocal studios.

INTRODUCTION

Phonation involves the conversion of several forms of energy into acoustic energy. Metabolic energy is used to initiate and maintain muscle contractions, aerodynamic energy is produced in the pulmonary system to drive an airstream through the vocal tract, elastic energy is stored and retrieved in stretched tissues, and kinetic energy is developed in tissue and air during oscillation of the vocal folds. The efficiency of conversion of these energies into acoustic energy in the form of sound waves is a process not often addressed in speech science. Efficiency is usually defined as a ratio of useful energy output to required energy input. A daily energy intake from food is 8.7 million Joules (J) for a human adult (www.mydailyintake.net), or about 2000 kcal. The rate of consumption, or the power input, is about 100 watts (8.7 × 10⁶ J per 86,000 s in a day). On the output side, acoustic power in speech ranges roughly between 0.01 − 1.0 mW. This power range is derived from a sound intensity level (SIL) range of 70 – 90 dB @ 30 cm from the mouth.¹ An output/input ratio yields a global efficiency of the human body for sound production on the order of 0.0001%. Such a global efficiency has little practical use because it involves too many unrelated physical processes in the body.

Efficiency calculations are more useful if localized to an organ, if not to a subcomponent of an organ. The traditional glottal efficiency measure^2,3 is calculated as the ratio of oral radiated acoustic power to aerodynamic power in the trachea. It has great theoretical appeal because it relates an acoustic output to an effort input (lung pressure, or more precisely, alveolar pressure). Effort in speaking and singing is a clinical and pedagogical issue. Unfortunately, glottal efficiency has seen limited clinical application. Two reasons are: (1) aerodynamic power is difficult to measure directly, and (2) the voice quality labeled “pressed voice” appears to have a high glottal efficiency because of its low airflow (and hence low aerodynamic power), yet clinicians warn against its use because of potential tissue damage.⁴ The difficulty with aerodynamic power measurement has led researchers toward indirect estimation of alveolar pressure and tracheal flow from oral pressure and flow.^5,6,7,8,9,10 The pressed voice issue has led researchers to search for a vocal economy measure^11,12 that maximizes acoustic output but minimizes vocal fold collision and energy dissipation in the tissues.

The economy measure proposed by Berry et al.¹¹ is an output-to-cost ratio (in dB), namely the acoustic pressure at the mouth divided by vocal fold contact stress. To make the ratio dimensionless, two reference values were selected, the usual 20 μPa for SPL at the mouth and 1.0 kPa for typical contact stress.¹³ This gave output/cost ratios in the range of 55 – 70 dB. It was shown computationally that the ratio varied with the adductory glottal width, 0.5 mm being an optimal value. While the ratio of acoustic output to contact stress is conceptually very appealing, its measurement is not yet clinically practical because contact stress between the vocal folds is difficult to measure.^14,15 Results in the Berry et al.¹¹ study were based on computer simulation only, in which contact stress is an easy calculation.

More recently, Titze¹⁶ and Titze and Laukkanen¹⁷ proposed an MFDR/MADR ratio for vocal economy, where MFDR is the maximum flow declination rate at the glottis and MADR is the maximum area declination rate of the glottis. The rationale for this ratio is that MFDR is closely related to vocal intensity,^18,19,20 whereas MADR is closely related to tissue velocity (and hence to momentum change and impact stress) prior to collision. This economy ratio is increased by raising MFDR or lowering MADR, or both. Recent advancements in high-speed kymographic imaging of vocal fold vibration have brought about the potential for obtaining this vocal economy measure on a live individual. The combined measurement techniques were demonstrated by Granqvist et al.²¹ A combination of inverse-filtering the oral flow to obtain glottal flow and its derivative, and high-speed kymographic analysis to obtain glottal area, may lead to a feasible clinical procedure. However, the cost of high-speed imaging equipment will likely remain a barrier to wide-spread clinical adoption of an MFDR/MADR ratio as a measure of vocal economy.

The purpose of the current study is to explore a third option, an aerodynamic to acoustic pressure conversion ratio, similar to a flow conversion ratio originally proposed by Isshiki.²² Isshiki called his acoustic flow to steady flow ratio at the mouth an efficiency index, but the use of the word “efficiency” could be challenged because the ratio is not energy or power based. Obtaining a flow or pressure ratio at the lips is an easy measurement that, if validated, could be applied cost-effectively in a clinic with a modest advancement in technology. Given that oral pressure is easier to measure than oral flow, we adopt an aerodynamic-to-acoustic pressure conversion ratio (PCR).The pressure measurement is made behind the lips during phonation with a controlled small lip opening. If PCR proves to be of clinical use, questions of first interest are: (1) how does the PCR measure relate to the classical vocal efficiency ratio, (2) is there a strong correlation between high PCR and “pressed voice” as described above, and (3) does PCR vary enough across individuals to have discriminatory potential?

THEORETICAL UNDERPINNINGS FOR GLOTTAL EFFICIENCY AND PRESSURE CONVERSION RATIO

As stated, glottal efficiency has traditionally been defined as the radiated acoustic power from the mouth divided by the pulmonary aerodynamic power delivered by the lungs.^2,3 In terms of sound pressure level (SPL) measured at a distance r from the mouth, glottal efficiency can be written as¹

$$E=\frac{4\pi r^2{I}_0{10}^{\mathit{\text{SPL}}/10}}{P_L{U}_g},$$ (1)

where I₀ is the standard reference intensity (10⁻¹² W/m²), P_L is the lung pressure (the term used here to represent alveolar pressure) and U_g is the mean (slow moving) airflow in the trachea. Since power is the rate of energy produced or absorbed, and since energy conservation and dissipation principles apply throughout the airway, it is guaranteed that the vocal efficiency ratio always ranges between 0.0 and 1.0. This is very satisfying from a physical standpoint, giving an exact accounting of “useful” versus “wasted” energy in the vocal system.

As mentioned briefly in the Introduction, there are several reasons why glottal efficiency has not reached wide-spread application as a vocal effort measure. First, the aerodynamic energy asymptotes to zero when the open quotient (duty ratio) in the glottis approaches zero (U_g → 0). This could prevent the vocal efficiency from having a maximum value in an intermediate range of adduction, generally thought to be healthy and efficient. Second, the radiated power from the mouth is highly dependent on mouth opening, suggesting that vocal efficiency may change with vowel. A standardized mouth configuration has not yet been adopted. Third, measurement of an airborne acoustic signal requires exact specification of the mouth-microphone distance and some guarantee of room acoustic fidelity to avoid contamination from environmental noise and sound reflections. Fourth, a direct measure of lung pressure is invasive and difficult to obtain. A shuttering technique with the syllable repetition /pa-pa-pa-…/ or /pæ- pæ- pæ…/ is generally used for indirect P_L measurement,^5,6 with the assumption that oral pressure equals lung pressure in the /p/ occlusion. Airflow is measured with a pneumotachograph flowhead or a circumferentially-vented mask placed over the mouth and nose.²³

Given the measurement challenges facing widespread adoption of the traditional measure of efficiency, we have proposed an alternative measure²⁴ using a dual cannula oral manometer. The procedure maintains a constant small lip opening to develop both a steady pressure and a time-varying (acoustic) pressure behind the lips (Fig. 1). Any measure with expected consistency benefits from standardization of at least one critical vocal tract dimension. A standard lip opening is the easiest to control. The open cannula is chosen to be short (extending the vocal tract by approximately 1–2 cm) with the tongue tip behind the lips likely being in an /o/ or an /u/ position. Subjects are asked to keep the rest of the vocal tract in a neutral position, as in /ə/. The pressure conversion ratio (PCR) is defined simply as

$$\mathit{\text{PCR}}=\frac{P_{\mathit{\text{ac}}}}{P_{\mathit{\text{dc}}}},$$ (2)

where P_ac is the oral acoustic pressure (behind the lips) and P_dc is the oral steady pressure (also behind the lips). These pressures change with mouth and tube diameter, as discussed later, but the ratio is less geometry-dependent. With this measure, three practical shortcomings are removed. First, no airborne signals are measured, removing the need to specify mouthmicrophone distance and reducing environmental interference. Second, the measurement is not dependent on the subject’s selection of lip opening because a known orifice is created at the lips. This orifice, on the order of 0.6 cm diameter, is a reasonable compromise between voiced consonants and lip-rounded vowels. Third, the controlled lip opening produces a steady (DC) pressure on the same order of magnitude as the acoustic (AC) pressure, minimizing measurement error for a ratio calculation.

Fig. 1.

Dual cannula PCR instrumentation.

The major disadvantage of the PCR ratio is that it is not energy-based. Hence, it is not bounded by a 0 – 100% range. Pressure ratios anywhere along the vocal tract can increase or decrease by cross-sectional area changes (wide or narrow diameter) without corresponding power changes. Power ratios involve a pressure-flow product. Usually acoustic flow increases when acoustic pressure decreases, and vice versa. Since flow is not measured here, validation of the pressure ratio against a true efficiency calculation is essential.

The validation begins with a simple acoustic pressure transformation in a short cannula at the lips (Figure 2). If the lip tube is acoustically short (much less than a quarter wavelength at a given frequency), then there is no significant pressure drop inside the tube, and acoustic flow continuity at the mouth-tube junction allows P_ac to be written in terms of the radiated pressure P_o at the end of the tube,

$$P_{\mathit{\text{ac}}}=(A_t/A_m)P_o,$$ (3)

where A_t/A_m is the tube-mouth area ratio. Uncertainty of the area A_m is the weakest link in this measure. Some simulation will be needed in the future to determine the sensitivity of the PCR ratio to this area and the entire vocal tract configuration. If the sensitivity is high, calibration may be needed on a per-subject basis. As an alternative, the uncertainty can be overcome by using a mouthpiece that houses the dual cannulas and maintains a fixed mouth area A_m for any subject. A preliminary design of the mouthpiece is based on a snorkeling mouthpiece, shown in Figure 3. It’s adaptability to the PCR measure will be assessed in future studies. Here, the intent was to show feasibility and the relation of PCR to efficiency.

Fig. 2.

Pressures in short tube for relating efficiency E to PCR.

Fig. 3.

Future mouthpiece design to maintain constant mouth area and house a dual cannula.

Returning to Eqn. (3), P_o can be calculated from the measured sound power and the radiation resistance. Given that the radiated output power is $P_o^2/R_r$, where R_r is the radiation resistance at the tube end, the efficiency is the ratio of the radiated power and the pulmonary power according to Eqn. (1),

$$E={\left(\frac{A_m}{A_t}\right)}^2\frac{P_{\mathit{\text{ac}}}^2/R_r}{P_L{U}_{\mathit{\text{dc}}}}.$$ (4)

Solving for P_ac and substituting into Equation 2, PCR can be related directly to efficiency,

$$\mathit{\text{PCR}}=\frac{A_t}{A_m}\sqrt{\frac{R_r{P}_L}{R_{\mathit{\text{dc}}}{P}_{\mathit{\text{dc}}}}}\sqrt{E},$$ (5)

where R_dc is the steady-flow resistance of the short tube,

$$R_{\mathit{\text{dc}}}=P_{\mathit{\text{dc}}}/U_{\mathit{\text{dc}}}.$$ (6)

Thus, PCR is proportional to the square root of E, with a proportionality factor that depends on tube and mouth dimensions. One validation issue is whether this factor is a relatively simple scale factor or whether it is subject-specific and phonation-specific. If it is subject-specific but not phonation-specific, a calibration procedure could resolve the difference. However, if the factor varies with every phonation condition (pitch, loudness, adduction, tongue position, etc.), then E and PCR become rather different measures, not necessarily highly correlated. This issue needs to be resolved in a study beyond the current one.

PCR can also be expressed in terms of sound pressure level (SPL). The radiated power (numerator in Equation (4)) is equated to the radiated power from Equation (1)

$${(A_m/A_t)}^2{P}_{\mathit{\text{ac}}}^2/R_r=4\pi r^2{I}_o{10}^{\mathit{\text{SPL}}/10}.$$ (7)

Solving for P_ac and dividing by P_dc we get

$$\mathit{\text{PCR}}=(4/3\pi )({\mathit{\text{rd}}}_t/d_m^2)(\sqrt{128\rho {\mathit{\text{c I}}}_o}/P_{\mathit{\text{dc}}}){10}^{\mathit{\text{SPL}}/20},$$ (8)

where d_t is the tube diameter, d_m is the mouth diameter ( $2\sqrt{A_m/\pi }$), I_o is the ISO standard reference intensity (10⁻¹² W/m² or 10⁻¹⁹ erg/s −cm²), and an explicit equation for radiation resistance has been used (Flanagan 1965, p. 33)

$$R_r=(128\rho c)/(9{\pi }^2{A}_t).$$ (9)

With these relations, PCR will now be estimated from Schutte’s 1980 data.

POST-HOC ANALYSIS OF SCHUTTE’S DATA

A landmark study on glottal efficiency was conducted by Schutte³ on 45 subjects with no voice pathology and 64 subjects with various voice disorders. Lung pressure, mean tracheal flow, sound pressure level, and efficiency were measured for multiple repetitions of similar vocalizations. Lung pressure was derived from esophageal pressure, and flow was measured using a flowhead (≈3cm diameter and 15 cm long tube) held between the lips during phonation. Figure 4 summarizes the results for both normal and disordered subjects’ data. Glottal efficiency is plotted against three variables: SPL in the upper left, mean flow in the upper right, and lung pressure in the lower left. The individual small data points and plus signs (+) correspond to the middle of the intensity or pressure range for each subject as given by Schutte in a table at the end of his monograph. The lines with data points give the complete range as reported by regression lines for several runs on each subject. We averaged the regression lines to compute points for efficiency versus SPL and efficiency versus lung pressure. The new points are shown with star signs (*) for disordered subjects and plus signs (+) for normal subjects. Curve fits to the new points are given in the legends of Fig. 4.

Fig. 4.

Summary of glottal efficiency data from Schutte.³ ‘+’ represent normal subjects’ data and ‘.’ represent disordered subjects’ data.

Schutte’s data did not produce much of a trend for efficiency versus mean flow rate (upper right plot). Hence, only the raw data points corresponding to mean intensity for each subject are shown. It is noteworthy that the data clustered around a mean flow rate of about 0.15 – 0.4 l/s, which is confirmed by a histogram in the lower right. Although the highest values of efficiency were for a few outliers (flow rate less than 0.1 l/s), the distribution is near Gaussian, centered on a moderate flow of 0.25 l/s. This result, not specifically emphasized by Schutte, is particularly important because it diminishes the notion that subjects lean toward pressed voice in their productions. There is only a weak correlation between increase in efficiency and decrease in mean glottal flow, which alleviates one concern with the traditional measure of efficiency. Perhaps efficiency is not the physiologic criterion for maximizing output. Transmission-line theory predicts that, for maximum power transfer from a source to a radiation load, the source impedance and the load impedance should be matched, resulting in an efficiency 50% rather than 100%.²⁵ In phonation, the efficiency is so low and raw power is so abundant that it is unclear whether speakers intend to maximize efficiency. As seen in Fig. 4, efficiency clusters around 0.01%, with values as high as 0.3% reached in Schutte’s data. Bouhuys et al.² reported a values as high as 2.0% for a singer. The generally low efficiency in voice production, and the wide range (two orders of magnitude) across speakers with different conditions, make the topic of optimization of power output and efficiency worthy of further exploration in terms of internal energy losses.

The post-hoc analysis of Schutte’s patient data to determine the discriminatory potential of efficiency between normal and disordered subjects showed three trends. First, on average, the 64 patients had slightly lower efficiency than the normal subjects. At 80 dB SPL, efficiency was 0.01 % for normals and 0.004 % for patients. At 90 dB, efficiency was 0.04 % for normal and 0.02 % for patients. Second, none of the 64 patients ever reached 100 dB SPL, whereas almost all of the normals did. Third, at low intensity, efficiency was much more variable in patients. At 70 dB, for example, midpoint values from the regression lines for patients (dots) varied between 0.0001 % efficiency and 0.002 % efficiency (more than an order of magnitude), while normal subjects showed little variation. This low intensity difference in variability is particularly interesting in light of phonation threshold pressure, a measure often used to assess “ease of phonation.” Schutte did not measure phonation threshold pressure, but data in his monograph indicate that, at 60 dB, normals had a range of 0.2 – 0.6 kPa pressure variation (not shown here), with a mean of 0.4 kPa. Patients, on the other hand, had a range of 0.25 – 4.0 kPa, with a mean of 0.6 kPa. It appears that, for clinical assessment, low SPL values should be exploited to separate the groups. At mid-SPL values, patients were able to produce sound with only a factor of 2 less efficiency than normals, using on the order of 0.8 – 1.0 kPa of lung pressure.

Statistical analysis was also used to determine if there was a significant difference between normal and disordered subjects’ data. One-way analysis of variance (ANOVA) followed by post-hoc Tukey-Kramer test with α = 0.05 was conducted on efficiency, lung pressure, glottal flow and SPL. The data were normalized to their respective maximum values so that they all range between 0 and 1 before running these tests. The results suggest that the efficiency was significantly different between the two sets of data, F = 27.3, P < 0.0001. Mean glottal flow was also significantly different between normals and patients, F=148.6, P<0.001. There was no significant difference in lung pressures between normals and patients, F = 0.21, P=0.64, and no significant difference between the sound pressure levels produced, F = 0.72, P=0.39. These results suggest that for the same lung pressure, efficiency is lower in disordered subjects and more glottal flow is needed to maintain similar sound pressure levels.

The next step in the post-hoc analysis of Schutte’s data was to convert his efficiency data to the new PCR measure. The following constants were gleaned from his publication: d_t = 3 cm, A_t/A_m = 1, R_r/R_dc = 25, P_L/P_dc = 100, giving a proportionality factor 50 between PCR and $\sqrt{E}$ in Equation (5). The P_L/P_dc value was estimated by mimicking his experiment with a tube similar to his in diameter. For simplicity, area of the mouth was assumed to be equal to tube area. As mentioned above, in future studies, the mouth/tube area ratio will be controlled more precisely with a mouthpiece. The solid line in Figure 5(a) represents curve-fitted data obtained from mean E - P_L regression lines (reported per normal and per disordered subject in Schutte’s data). The regression data were substituted directly into Equation (5). There is no distinction between normal and disordered subjects because the same P_L/P_dc ratio was used for both (no differences were reported by Schutte). The dashed lines represent curve-fitted data obtained from mean E - SPL regression lines per subject in Schutte’s data. The regression data were substituted directly into Equation (8), which does not contain the P_L/P_dc ratio. Hence, normal and patient lines are distinct. Note that PCR is on the order of 1.0 when glottal efficiency is on the order of 0.05 %. This relation can only be claimed for Schutte’s data at this point.

Fig. 5.

Predicted PCR from Schutte’s³ data. (a) PCR versus E, (b) PCR versus SPL. Solid lines are from measured P_L values and dashed lines from measured SPL values.

Figure 5(b) shows plots of PCR versus SPL. Solid lines are from predicted SPL and dashed lines are from measured E-SPL regressions for normal and disordered subjects. The predicted SPL comes from measured E-P_L regressions by considering constant flow across the vocal tract and first calculating aerodynamic power p_a

$$p_a=P_L{U}_{\mathit{\text{dc}}}.$$ (10)

The radiated power is

$$p_r={\mathit{\text{Ep}}}_a,$$ (11)

and the radiated intensity at a distance r is

$$I=\frac{p_a}{4\pi r^2}$$ (12)

from which the sound pressure level is

$$\mathit{\text{SPL}}=10{\text{ log}}_{10}(I/I_0).$$ (13)

This way E was eliminated from the equations. Note that 90 dB SPL yielded a PCR value of about 1.0, with normal subjects having values about 20 % higher than patients with disorders.

With analytic calculation of PCR from Schutte’s data, we have shown that there is a predictable relation between PCR and E. This relation was further established with direct PCR measurements on a few new human subjects.

METHODS

Six males and seven females participated in this study. All subjects reported normal, healthy speaking voices at the time of their participation, though one female subject had a history of surgical removal of a laryngeal polyp 1 year prior to participation in the study.

Subjects were first fitted with an electroglottograph (EGG) collar (Kay 6103) and a head-mounted microphone (Countryman Isomax) positioned 6 cm away from and lateral to the mouth. The microphone was calibrated to predict SPL by comparing its output to a sound level meter (C scale) reading at a 30 cm distance. SPL was used to compute PCR from Equation (8). EGG was used to calculate the open quotient Q_o, which is not a variable in the equations but serves as a comparison to Schutte’s mean airflow data. Additionally, a thin tube connected to a pressure transducer (Glottal Enterprises PT-25/MS-110) was maintained between the lips in the oral cavity by the subject. Signals from all devices were captured using an AD Instruments analog-to-digital converter and the company’s proprietary software, Labchart7.

Once comfortable with the EGG, microphone, and oral pressure tube, subjects were given a short straw to hold between the lips, 6 mm in diameter and 3 cm in length. While the assumptions made to obtain Equation (5) were based on a 1 cm long tube, it was difficult for subjects to keep a 1 cm straw in place. Consequently, a longer tube was required at this stage. (The mouthpiece to be constructed in the future for a dual-tube system will allow a shorter tube). Subjects phonated through the straw at 3 loudness levels on 3 fundamental frequencies (f_o) within normal speaking ranges. Subjects were provided with stimulus frequencies from a piano and asked to match the pitch with their phonations. Stimulus frequencies ranged from 195 Hz to 247 Hz for females and from 125 Hz to 200 Hz for males. During each 5 – 15 s phonation length, subjects used their index finger to momentarily stop airflow through the straw, mimicking the shuttering technique used to estimate lung pressure.¹⁰ The straw was shuttered regularly throughout each phonation, at a rate of approximately 1.5 interruptions per second. We analyzed 5 – 6 s per subject, or 4 successive occlusions.

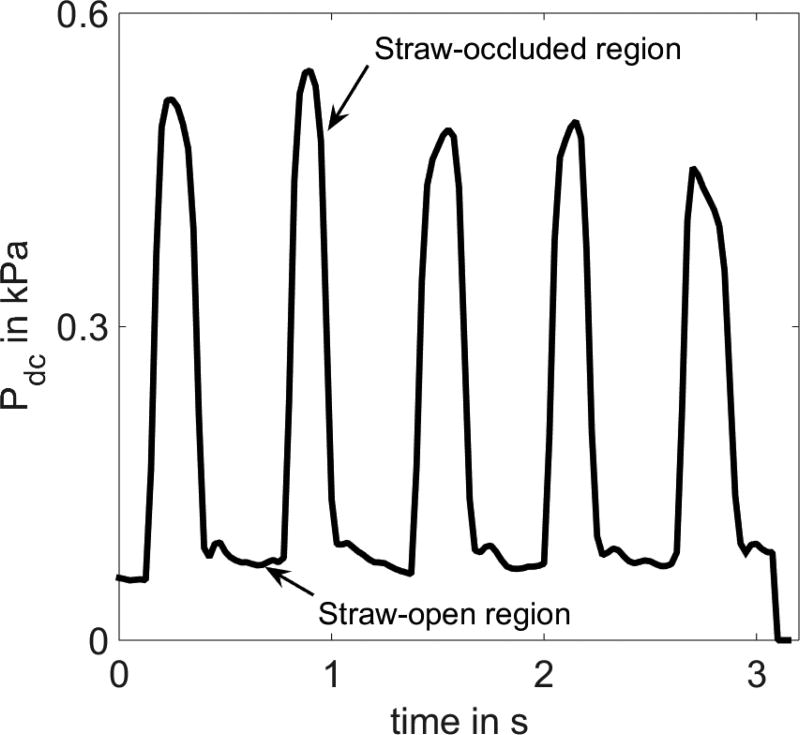
Lung pressure (P_L), sound pressure level (SPL), open quotient (Q_o) and pressure conversion ratio (PCR) were derived from the recordings for further analysis. A sliding window of 50 ms with a step size of 25 ms was used to measure these quantities. SPL, Q_o and PCR measured in each window were averaged across each straw-open segment in the shuttering regions. The pressure peak value in the straw-occluded segment was considered an estimate of the lung pressure. Figure 6 shows the DC oral pressure in the straw-open region and the straw-occluded region.

Fig. 6.

A sample DC pressure plot showing shuttering between straw-open and straw-occluded regions from human subjects.

The signal from the pressure transducer provided both steady and acoustic intraoral pressure. Open quotient (Q_o) was derived from each token of the EGG signal for voiced segments. Cepstral peak prominence (CPP)²⁶ was first applied to the EGG signal to identify voiced regions. The open quotient was then measured as a ratio of open phase duration to the glottal cycle duration, using a mean value as the threshold for open-closed decision. This mean value as a threshold overestimates Q_o somewhat, but given that the EGG waveforms did not have much asymmetry across the horizontal axis, the threshold seemed reasonable for an error free calculation. Lower thresholds tend to yield more error due to EGG irregularity. While the PCR measure did not include collecting mean airflow for comparison to Schutte’s³ data, it has been shown that open quotient is generally correlated with mean flow.¹⁸ Thus, by using an estimate of Q_o, this study provides a meaningful comparison to Schutte’s results on efficiency versus mean glottal airflow.

RESULTS

Figure 7(a) illustrates a square root fit between PCR and P_L for one female subject. A square root relation is expected from Equation (5) if all other variables are constant or offset each other, which is unlikely. It is clear, however, that PCR must go to zero when P_L goes to zero. With that constraint, the ½ power fit is more defensible than a linear regression. Figures 7(b) and (c) show similar fits for all seven female subjects and six male subjects, respectively. The curves have a goodness of fit (normalized root mean square error) of 0.52 across all subjects. PCR varied by at least 3:1 across both male and female subjects, suggesting that PCR may have discriminatory potential between subjects in terms of effort expended. In Schutte’s normal subject data, a range of 0.003 – 0.01 % efficiency was found for 1.0 kPa of lung pressure, which is the same 3:1 ratio.

Fig. 7.

(a) PCR vs. P_L data from one female subject with square root fit. (b) PCR vs. P_L curves for seven female subjects. (c) PCR vs. P_L curves for six male subjects.

Figure 8 shows range of SPL versus range of P_L, comparing our data (narrow tube) to Schutte’s data (wide tube). Range of SPL achievable by our subjects was diminished due to the narrow (0.6 cm diameter) tube compared to Schutte’s wider tube (≈3 cm diameter), a result that is predictable from sound radiation theory (Equation 9). The narrow tube produces a range of about 10 dB SPL with a 1 kPa range of pressure, while the wide tube produces a range of nearly 20 dB SPL with a 0.4 kPa range of pressure.

Fig. 8.

Relationship between P_L and SPL in narrow-tube data and wide-tube (Schutte) data.

PCR versus E as calculated from Equation (5) for our tube-mouth configuration is shown in Fig. 9. The proportionality factor between PCR and $\sqrt{E}$ was 45 for d_t = 0.6 cm, A_t/A_m = 1, R_r/R_dc = 200, P_L/P_dc = 10. This factor is very close to that obtained from Schutte’s wide tube data (recall a value of 50 in the curves of Figure 5).

Fig. 9.

PCR versus predicted efficiency E from analytical calculations.

PCR versus measured SPL is shown in Fig. 10 for all thirteen subjects, but only the minimum, maximum and mean points for individual subjects are shown on the curves for clarity. The curve obtained from analytical calculations for our tube-mouth configuration using equation (8) is also shown (thicker line and no data points). It underestimates the data for most of the subjects, suggesting a need for refinement of the constants in Eqn. (8).

Fig. 10.

PCR versus measured SPL for thirteen subjects.

Finally, Fig. 11 shows the histogram of open quotients computed during voicing regions for all thirteen subjects. It can be seen that an open quotient between 0.5 and 0.7 is prevalent, indicating that subjects were not tending towards pressed voice.

Fig. 11.

Histogram of open quotient across all the 13 subjects.

DISCUSSION AND CONCLUSIONS

The subject of vocal efficiency, almost forgotten in the literature, has been re-addressed with a simpler measure that is clinically feasible, namely a pressure conversion ratio (PCR) obtained at the mouth. The first question posed in the Introduction, how does the PCR measure relate to vocal efficiency, has been answered both theoretically and empirically. The relation is $\mathit{\text{PCR}}=k\sqrt{E}$, where k was 50 for Schutte’s data and 45 for our subject data. The value of k may be able to be maintained reasonably constant across different phonations by using a mouthpiece with fixed mouth area and otherwise neutral vocal tract. The ratios P_L/P_dc, and R_r/R_dc in Equation (5) can in the future be quantified using a bench setup and measuring P_dc, U_dc for a given P_L and the selected mouthpiece.

The second question, do efficiency and PCR have a bias toward pressed voice, has also been answered. When the objective is a specific loudness at a specific f_o, open quotients near 0.5 are produced more frequently than extreme Q_o values (near 0.0 or 1.0). It is speculated here that PCR may be governed more by maximum power transfer than by maximum efficiency. Generally, the efficiency is so low that maximization of efficiency has less pay-off than maximization of power transfer from the glottis to free space. In electrical circuit theory, it is known that maximum power transfer occurs at a 50 % efficiency, but even this value is never reached. Thus, all we can say here is that there is no bias toward pressed voice that could hinder the usefulness of the PCR measure for describing ease of phonation (or, conversely, effort) in a clinical setting.

The third question, is there sufficient variation in PCR across subjects for a discriminatory “effort” measure, has only a preliminary answer. Normal subjects showed ranges of PCR from 0.2 to 3.0, which would suggest a respectable range for variations with loudness and f_o in the speech range. However, while vocally impaired patients in Schutte’s² study produced efficiency values significantly outside of the normal range, differences were not large in the mid to high range of intensity. We expect, therefore, that PCR can best discriminate between normal subjects and patients at low intensity (near phonation threshold).

Future studies will address how PCR varies in higher f_o ranges. Preliminary data suggest that, at high f_o, there is not an increase in PCR with increased loudness. In other words, conversion from DC to AC pressures may reach a limit with increased lung pressure when the vocal folds are stiffer. Such a result would be in agreement with classic voice range profile measurements, which usually show a mid-value of f_o has the greatest SPL range, rather than the extreme values of f_o..