Morphable 3D Mesostructures and Microelectronic Devices by Multistable Buckling Mechanics

Abstract

Three-dimensional (3D) structures capable of reversible transformations in their geometrical layouts have important applications across a broad range of areas. Most morphable 3D systems rely on concepts inspired by origami/kirigami or techniques of 3D printing with responsive materials. The development of schemes that can simultaneously apply across a wide range of size scales and with classes of advanced materials found in state-of-the-art microsystem technologies remains challenging. Here, we introduce a set of concepts for morphable 3D mesostructures in diverse materials and fully formed planar devices spanning length scales from micrometers to millimeters. The approaches rely on elastomer platforms deformed in different time sequences to elastically alter the 3D geometries of supported mesostructures via non-linear mechanical buckling. Over 20 examples have been experimentally and theoretically investigated, including mesostructures that can be reshaped between different geometries as well as those that can morph into three or more distinct states. An adaptive radio frequency circuit and a concealable electromagnetic device provide examples of functionally reconfigurable microelectronic devices.

3D structures with shapes that can be qualitatively and reversibly altered between different configurations are important in a wide range of engineering applications, such as deployable space structures¹, biomedical devices^2,3, microelectromechanical systems (MEMS)^4-6, robots⁷, and metamaterials^8-12. Many such morphable 3D systems use designs inspired by the ancient arts of origami and kirigami, in part due to a myriad of shapes that can be achieved by actively folding and unfolding thin sheets with pre-defined creases and cuts^8,13-24. Recent research establishes systematic rules in lattice kirigami methods^15-17 and origami algorithms¹⁸ for achieving complex targeted 3D configurations. Furthermore, certain cellular 3D structures can be formed by stacking these folded layers²⁰, or assembling them into tubes^25-27. A different strategy exploits the foldability of prismatic geometries^9,10,28, where space-filling tessellations of polyhedra create reconfigurable 3D structures comprising a periodic assembly of rigid plates and elastic hinges. Although these design principles offer remarkable levels of freedom in reconfiguration and shape-defined mechanical responses, they most naturally apply to macroscopic structures and simple, non-functional materials. Methods that rely on residual stresses^29-32 or responsive materials (e.g, shape memory polymers or hydrogels)^33-42 provide alternatives. For example, techniques referred to as 4D printing, use heterogeneous structures formed by 3D printing of mechanically responsive materials to offer considerable flexibility in geometric designs and time evolving changes in them^34-36. Such approaches are not, however, readily applicable to high performance, planar thin film materials or to micro- or nano-scale architectures. Significant opportunities remain in the development of schemes for realizing reconfigurable 3D mesostructures in classes of materials and with component device designs found in existing forms of electronics, optoelectronics and microelectromechanical systems.

Here, we present a set of strategies and design concepts that addresses this opportunity. The ideas begin with assembly of 3D mesostructures using schemes that rely on biaxially prestrained elastomer platforms and 2D precursors. Previous publications^43-47 demonstrate that simple, biaxial release of the prestrain enables deterministic 3D assembly through continuous, smooth changes in shape. In the present work, we show that strategically selected release sequences and specially engineered precursor designs can trigger the stabilization of multiple, distinct 3D buckling modes, thereby providing capabilities for reversible reconfiguration in which the time sequence of strains applied to the elastomer platform serves as the control strategy. This type of reconfiguration corresponds to abrupt, non-linear changes in overall shape associated with distinct shifts in the trajectory from one mode to another. These options in morphable 3D mesostructures lie qualitatively beyond the scope of previously reported strategies^43-47. Fundamental studies of the bistability, and in general the multistability, behaviors inherent in the 2D-to-3D geometry transformations of the systems reported here establish general rationales for designing 3D mesostructures with distinct, reconfigurable topologies. Experimental demonstrations of over 20 examples, including complex objects with recognizable forms (e.g., octopus, spider, bird, maple leaf, house and basket) and mesostructures that can be reconfigured among 3 or 4 distinct states, illustrate the versatility of the approaches. Compatibility with modern planar technologies and affiliated thin film deposition/processing methods affords broad applicability and scalability, as demonstrated with morphable 3D mesostructures that incorporate single-crystalline silicon, metals and polymers, spanning length scales from micrometers to millimeters. An array of silicon n-channel metal-oxide-semiconductor field-effect transistors (n-MOSFET) integrated onto a shape-shifting 3D mesostructure framework serves as an example in high performance electronics. Passive radio frequency (RF) circuits and concealable RF antennas highlight applications in reconfigurable 3D systems of potential relevance in wireless communications.

Route to morphable 3D mesostructures and electronics

Figure 1a presents results of finite element analyses (FEA, see Methods section for details) that illustrate the key concepts in the context of a simple example that consist of a 3D vertical column with square cross section that can be reconfigured into a socket-type shape, segmented into four strips. The initial formation of the column (SU8, photopatternable epoxy; left top frame of Figure 1a), referred to as Shape I, relies on a mechanical assembly strategy^40,43-46 that exploits controlled compressive buckling of a patterned 2D precursor bonded to an underlying elastomer substrate at the locations of the red pads as described elsewhere (See Supplementary Fig. 1a for details). The narrow green regions that span the widths of the ribbons, oriented orthogonal to their lengths, correspond to segments with reduced thickness (2 μm vs 6 μm for the other region), to define locations of creases, or hinge points, that help to determine the overall shape and also define multistable buckling mechanics, as essential to capabilities in shape reconfiguration⁴⁶. This reconfiguration begins with application of an equal biaxial stretch (ε_x = ε_y) of the substrate, thereby enlarging the spacing between the bonding pads, such that the 3D column gradually expands and flattens until the column structure transforms into a planar geometry (i.e., two crossing ribbons), at ε_x = ε_y = 100% for this particular example. Next, release of the biaxial strain in a sequential manner, starting with ε_x and then followed by ε_y, restricts vertical motion of the central region (i.e., joint) of the structure such that it remains in contact with the substrate. The result reshapes the column into the socket shown in the right top frame of Figure 1a, namely, Shape II. Since the maximum principal strain (Supplementary Fig. 1b) in the polymer remains well below the yield strain (> 3%), the entire process is reversible, i.e., the two configurations can be reshaped into each other repetitively. Furthermore, any intermediate state during the reconfiguration process can be also maintained by holding the stretch at any level, thereby allowing control over the amplitudes of the displacements of either of the two modes. FEA predictions and experimental results on mesostructures created using this loading-path control strategy show remarkably good agreement, for all scenarios examined.

Figure 1. Morphable 3D mesostructures and integrated circuits by loading-path controlled mechanical assembly.

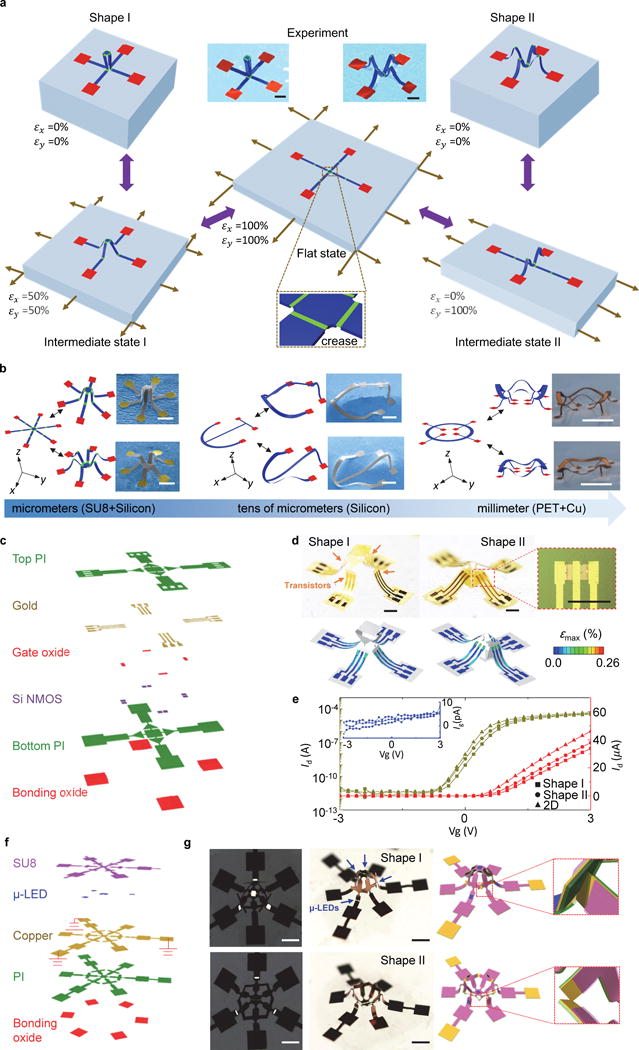
a, Conceptual illustration of the strategy through a sequence of FEA results and a pair of colorized SEM images of two 3D mesostructures. b, 2D shapes, FEA predictions and corresponding experimental images (SEM or optical) of morphable 3D mesostructures with diverse materials and length scales [left: bilayers of SU8 (1 μm at the creases and 2 μm at the other regions) and Si (50 nm); middle: Si (1.5 μm); right: bilayers of PET (50 $\mathrm{\mu }$m) and Cu (1 $\mathrm{\mu }$m)]. Shape I (upper frames) corresponds to simultaneous release and Shape II (lower frames) corresponds to sequential release (y direction first, and then x direction). Scale bars, 50 μm for the left panel; 500 μm for the middle panel; and 5 mm for the right panel. c-e, Design of a morphable 3D structure that embeds several silicon transistors, along with metal interconnects. c, The exploded view of the 2D geometry. d, Optical images of two configurations of the structure after 3D assembly. Shape I and Shape II correspond to simultaneous and sequential release, respectively. Scale bars, 200 $\text{μm}$. e, Current-voltage (I-V) characteristics of a transistor measured with the structure in Shape I, Shape II and the planar state. The color in the FEA results of d corresponds to the magnitude of maximum principal strain in the metal. f and g, Design for a morphable 3D optoelectronic device that incorporates four μ-LEDs. The left shows an exploded view of the 2D geometry, and the right shows optical images and modeling results for two device configurations (Shape I and II). Scale bars, 1 mm.

Such classes of reconfigurable 3D mesostructures can be realized in a broad set of materials, multilayer stacks and integrated devices, over various length scales. Figure 1b provides examples constructed in semiconductors, semiconductor/polymer bilayers and metal/polymer bilayers, with feature sizes spanning from ~ 1 μm to ~ 50 μm in thickness, 15 μm to 900 μm in ribbon widths, ~ 220 μm to ~ 5 mm in lateral spatial extent and ~ 50 μm to ~ 2 mm in vertical displacement. Due to the compatibility of this scheme with well-established planar technologies, this strategy is particularly useful in the integration of active or passive planar devices of various types into reconfigurable 3D frameworks, thereby allowing access to shape-changing microelectronic systems. Figure 1c-e and Supplementary Fig. 2 provide an example that consists of an array of four silicon n-MOSFET with electrodes and contact pads for electrical probing. The device is first fabricated in its planar form using conventional photolithography to define the various functional layers such as transistors, electrodes, encapsulations, and oxides for bonding to the elastomer substrate (See Figure 1c and Method section for details). The initial assembly leads to a 3D tower-shaped structure with four supporting struts, capable of changing shape into a recessed well with similar struts (Figure 1d). As in the other examples, this shape change is reversible, due to maximum principal strains in the constituent materials that remain below their thresholds for fracture or plastic deformation (Supplementary Fig. 2). Experimental results in Figure 1e show that the transistor characteristics remain unchanged by switching between these two different shapes (Figure 1d).

Figure 1f,g and Supplementary Fig. 3 provide examples that integrated multiple microscale light-emitting diodes (μ-LEDs) into a conducting framework that consists of a lithographically patterned multilayer of epoxy, copper and polyimide, as shown in Figure 1f. Here, a key aspect of the design is that the pattern of light emission can be reversibly modified not only through 3D geometric reconfiguration, but also through modification of the connectivity of the associated electrical circuits. Specifically, the circuit remains unchanged from the 2D configuration during simultaneous release (Supplementary Fig. 3), such that all of the four μ-LEDs light up in the resulting 3D geometry (Shape I). By contrast, the copper layers in the six suspended ribbons contact one another in the case of sequential release (Shape II), thereby resulting in a different circuit connectivity. In this condition, only three outer μ-LEDs light up, while the central one is off. Such a system could potentially find use in optoelectronic^48,49 and optogenetic^50,51 research, where on-demand spatial variations of light emissions in small volumes are desired.

Underlying mechanics and general design approach

Results of experiments and computational modeling suggest that only certain classes of 2D precursors lead to 3D structures that are reconfigurable by this type of loading-path strategy. Energetic analyses of two specialized cases provide context for general, rule-based procedures for designing systems with multiple stable 3D modes, as an essential requirement for reconfigurability. Specifically, two fundamental categories of geometries can be considered: one that consists of straight ribbons with creases (i.e., with reduced thickness/width in the cross sections), and the other that strategically combines straight and curved ribbons without creases.

Figure 2a presents analysis of the type of geometry examined in Fig. 1a. Two configurations, Shape I (simultaneous release) and Shape II (sequential release), are possible, as shown in Figure 2b and Supplementary Fig. 4a,b. Here, $u_z$ is the out-of-plane displacement at the central, intersection point. E_I and E_II are the strain energies associated with Shape I and Shape II, respectively. Both quantities depend on the magnitude of the strain released in the elastomer substrate ( ${\epsilon }_{\mathit{\text{release}}\_\mathit{\text{total}}}={\epsilon }_{x-\mathit{\text{release}}}+{\epsilon }_{y-\mathit{\text{release}}}$, where ε_x-release and ε_y-release are the released strain components along the x and y directions, respectively), as shown in Supplementary Fig. 4c,d. Quantitative calculations (Figure 2b and Supplementary Fig. 4a,b) show that although Shape I involves a much smaller strain energy (E_I) than Shape II (E_II), both represent local minima in the overall energy landscape. In other words, the existence of an energy barrier (E_barrier = E_peak – E_initial) and a threshold energy difference (E_diff = E_II – E_I) determine the 3D buckling modes that form during assembly, where E_peak and E_initial are the peak strain energy and the initial strain energy, respectively, during the loading process shown in Figure 2b and Supplementary Fig. 4a. Specifically, E_diff determines the configuration to emerge upon release (i.e., Shape II for E_diff < 0 and Shape I for E_diff > 0), and the mode transition can occur only when the energy barrier vanishes, i.e. E_barrier = 0. In other words, the structure maintains the initial configuration throughout the assembly for a non-zero energy barrier E_barrier. For simultaneous release, both E_diff and E_barrier are positive during the entire process, as shown in Figure 2c. In the absence of an external excitation sufficiently large to overcome the energy barrier, the 3D structure remains in Shape I. Sequential release leads to a different characteristic in the variation of E_diff. During the first stage of release ( $0\le {\epsilon }_{\mathit{\text{release}}\_\mathit{\text{total}}}\le 100\mathrm{\%}$ and ${\epsilon }_{y-\mathit{\text{release}}}=0\mathrm{\%}$), only one configuration can occur, due to the constraint imposed by the flat ribbon along the perpendicular (y) direction. During the second stage ( $100\%\le {\epsilon }_{\mathit{\text{release}}\_\mathit{\text{total}}}\le 200\mathrm{\%}$), E_diff is initially negative (Supplementary Fig. 4e), thereby causing the 3D structure to enter Shape II without the ability to switch to Shape I, due to the presence of a positive energy barrier.

Figure 2. Probabilistic energy analysis and design rationale for morphable 3D mesostructures.

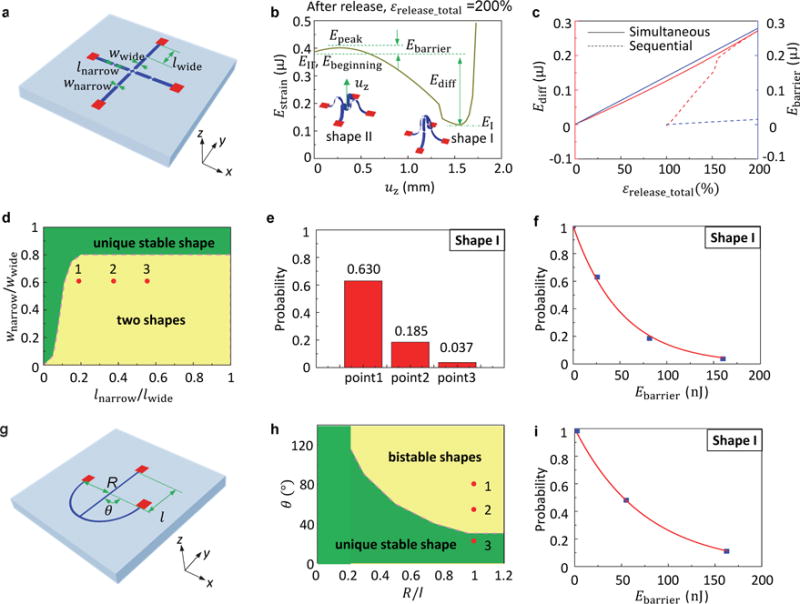
a-f, Analysis for a structure based on a straight ribbon. a, Schematic illustration of a straight ribbon structure. b, Strain energy as a function of out-of-plane displacement for ( $l_{\text{wide}},l_{\text{narrow}},w_{\text{wide}},w_{\text{narrow}},t, {\epsilon }_{\mathit{\text{pre}}}$) = (0.77 mm, 0.1 mm, 0.16 mm, 40 μm, 6 μm, 100%) and an elastic modulus of 4.02 GPa. The insets show the stable configurations at the corresponding out-of-plane displacement. Here, l, w and t are the length, width and thickness of the two constituent ribbons, respectively, and the subscripts ‘narrow’ and ‘wide’ denote the creases and other regions, respectively. c, Energy difference and energy barrier versus total release strain for 3D structures that arise from simultaneous and sequential releases. d, Design diagram in the space of length ratio and width ratio. e, Experimentally determined probability for achieving Shape I by sequential release for three different parameter combinations (w_narrow/w_wide, l_narrow/l_wide)=(0.3,0.2), (0.3,0.4) and (0.3,0.6). f, Dependence of the probability on the magnitude of the energy barrier. g-i, Analysis for the hybrid straight/curved ribbon structure. g, Schematic illustration of a hybrid straight/curved ribbon structure. h, Design diagram in the space of length ratio and arc angle. i, Dependence of the probability on the magnitude of the energy barrier.

These observations suggest that the magnitude of the energy barrier (zero or positive) governs reconfigurability by sequential release. According to the scaling law for this energy barrier (See Supplementary Note 1 and Supplementary Fig. 5 for details), a design diagram (Figure 2d) can be obtained for the 2D precursor, as in Figure 2a. Here, the regime above the pink curve gives the same configuration for simultaneous and sequential release, due to the vanishing energy barrier. Below this curve two different stable shapes arise, thereby offering the ability to achieve reconfigurable 3D structures.

Slight experimental variabilities, such as parasitic adhesion/stiction at regions adjacent to the bonding sites, can alter the energy landscape in ways that can be significant compared to the energy barrier for the unperturbed case. In such scenarios, even design parameters that suggest the existence of two modes can yield the same configuration for different release strategies. Statistical analysis of experiments on collections of three groups of 2D precursors (marked design points 1, 2 and 3) yield probabilities for realizing Shape I during sequential release (Figure 2e and Supplementary Fig. 6). This probability (P_I) increases as the design point approaches the boundary between the two regimes in Figure 2d, consistent with a decrease in the magnitude of the energy barrier. The data can be described with an exponential law (Figure 2f), i.e., $P_I=\mathit{\text{exp}}\left(\frac{-E_{\mathit{\text{barrier}}}}{E_{\mathit{\text{critical}}}}\right)$, with E_critical = 52.6 nJ. This critical energy (E_critical) scales by a factor of m³, if all of the length parameters of 3D structures scale by the same factor (m). In extremely small structures (e.g., those with micron or submicron dimensions built with 2D materials), natural thermal fluctuations could affect the reconfiguration process, since E_critical can be comparable to kT (for room temperature), where k is Boltzmann constant and T is the temperature.

Figure 2g presents an alternative class of geometry that is free of creases, where a straight ribbon intersects with an arc-shaped ribbon in the middle of the curve and bonding sites are at the other end of each ribbon. During simultaneous release, both E_diff and E_barrier are positive (Supplementary Fig. 7a-c), such that 3D structure remains in Shape I throughout. During sequential release (x direction first, and then y), E_diff is negative initially, while E_barrier is always positive (Supplementary Fig. 7b,c), leading to a different stable structure (i.e., Shape II). The design diagram for this geometry (Figure 2h) suggests that a combination of a large arc angle and a large radius/length ratio ensures the bistability. Statistical studies of experimental results similar to those described previously (Supplementary Figs 7d and 8) reveal probabilities (Figure 2i) that also follow an exponential relationship (here, with E_critical = 72.5 nJ).

This understanding of the underlying mechanics principles enables a general design rationale to complex reconfigurable 3D mesostructures (Supplementary Fig. 9). Consider, as an example, classes of geometries that consist of straight ribbons with creases at the middle and end sections, as shown in Supplementary Fig. 10. Theoretical modeling serves as the basis for layout selection, where the focus is on the distribution of creases for a prescribed 2D shape, using an algorithm of exhaustive search for bistable designs (See Supplementary Note 2 for details).

Representative morphable 3D mesostructures

With the above systematic, computationally guided design approach, diverse sets of morphable 3D mesostructures can be constructed with a variety of thin film materials over a range of length scales. Figure 3a provides three ribbon-shaped examples made of photodefinable epoxy, with creases at strategic locations (See Supplementary Note 3 for detailed discussions). Figure 3b shows a different set of ribbon-shaped mesostructures constructed with monocrystalline silicon, achieved without creases, where the designs of the curved ribbons offer the ability to select different types of deformations. Reconfigurable 3D mesostructures with membrane-shaped geometries and with hybrid ribbon/membrane geometries are also possible, as shown by Figure 3c,d. In all of these cases and the ones to follow, the assembly processes are completely elastic such that switching between modes can occur repetitively by stretching the elastomer platform back to the planar configuration, followed by strain release along different paths.

Figure 3. A broad set of 3D mesostructures morphable by loading path strategies.

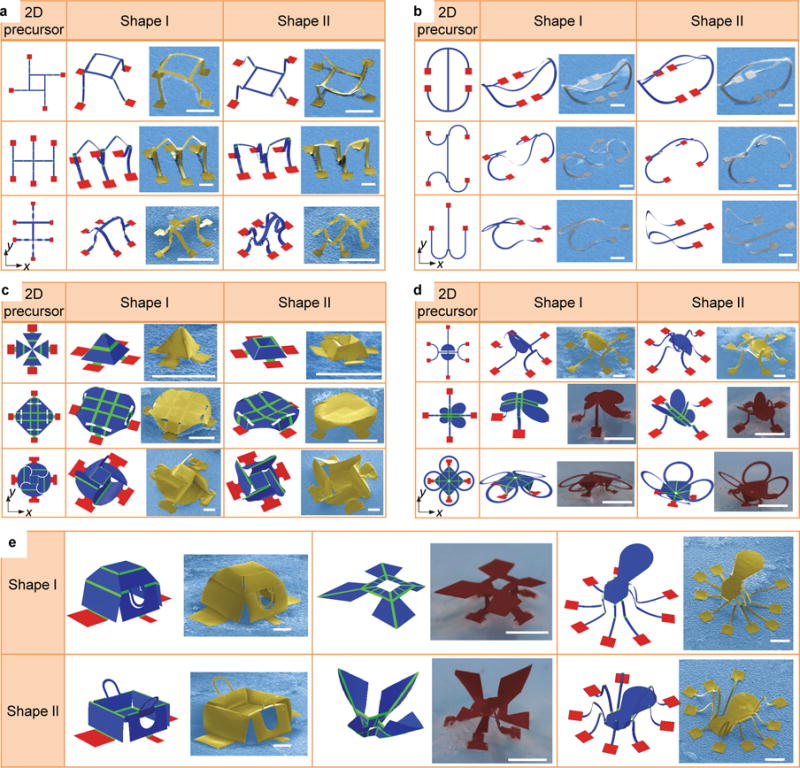
a-d, 2D geometries, FEA predictions and experimental images (SEM or optical) of morphable ribbon-shaped mesostructures with and without creases, membrane-shaped mesostructures, and hybrid ribbon/membrane mesostructures. Path I corresponds to simultaneous release, and Path II corresponds to sequential release (y direction first, and then x direction). e, FEA predictions and experimental images (SEM or optical) of morphable, recognizable objects. Certain parts of the structures are not shown in the FEA results for the second and third examples to improve the visibility of the key regions. The complete deformed configurations based on FEA can be found in Supplementary Fig. 10. In all colorized SEM and optical images, the yellow, silver and red colors correspond to SU8 (6 μm for normal region and 2 μm for crease), silicon ( $1.5\mathrm{\mu }$m) and PET (40 $\mathrm{\mu }$m), respectively. Scale bars, 400 $\mathrm{\mu }$m for samples with SU8 and silicon, and 4 mm for samples with PET.

A further extension of these design concepts allows the assembly of complex 3D mesostructures that can be switched between different recognizable geometries. Figure 3e and Supplementary Fig. 11 illustrate three examples, including the structures that can be reshaped between a ‘house’ and a ‘shopping bag’, or between a ‘maple leaf’ and a ‘bird’, or between an ‘octopus’ and a ‘spider’. The dynamic process is in Supplementary Movie 1. In all cases, FEA predictions agree well with experiments. A key aspect in the design of bistable mesostructures is to introduce elements that can either buckle upward or downward according to release sequence.

A finite proportion of samples fail to form Shape II (Figure 3) while released sequentially. The overall fabrication yields are 40%-80% for the assembly at microscale, and 80%-100% for the assembly at sub-millimeter scale (See Supplementary Figs 12-14 and Supplementary Note 4 for details and for results on cyclic switching between configurations).

In advanced versions of these design algorithms, multiple (> 2) stable modes can be realized through complex release sequences. Options include the use of additional creases in straight ribbons, the introduction of creases into hybrid straight/curved ribbons, and the introduction of extra ribbons into bi-modal reconfigurable mesostructures. Although not all of the available stable states can be accessed by the loading-path strategy, repeated trials and FEA studies enable realization of at least three distinct buckling modes with the following three release sequences: simultaneous release (Path I), and two sequential release paths, [ε_x-pre, ε_y-pre] → [ε_x-pre, 0] → [0, 0] (Path II), and [ε_x-pre, ε_y-pre] → [0, ε_y-pre] → [0, 0] (Path III). Figure 4a presents an example with three stable shapes. Here, sequential release along different directions leads to distinct 3D configurations, both of which differ significantly from the result of simultaneous release. Figure 4b, c and Supplementary Fig. 15 provide additional examples that can be reconfigured between three stable shapes. In principle, this same strategy can be extended to accommodate even more (> 3) stable shapes by careful design and complex release sequences. Figure 4d and Supplementary Movie 2 show an example that can achieve four different modes, with an ability to reshape between these 3D configurations. Supplementary Fig. 16 summarizes the number of constituent ribbon elements for all the ribbon-type reconfigurable mesostructures examined herein with 3 or 4 distinct states, as compared to their simplified designs with bistable states.

Figure 4. Morphable 3D mesostructures with multiple ( $\ge$3) stable states accessed through complex paths of sequential release.

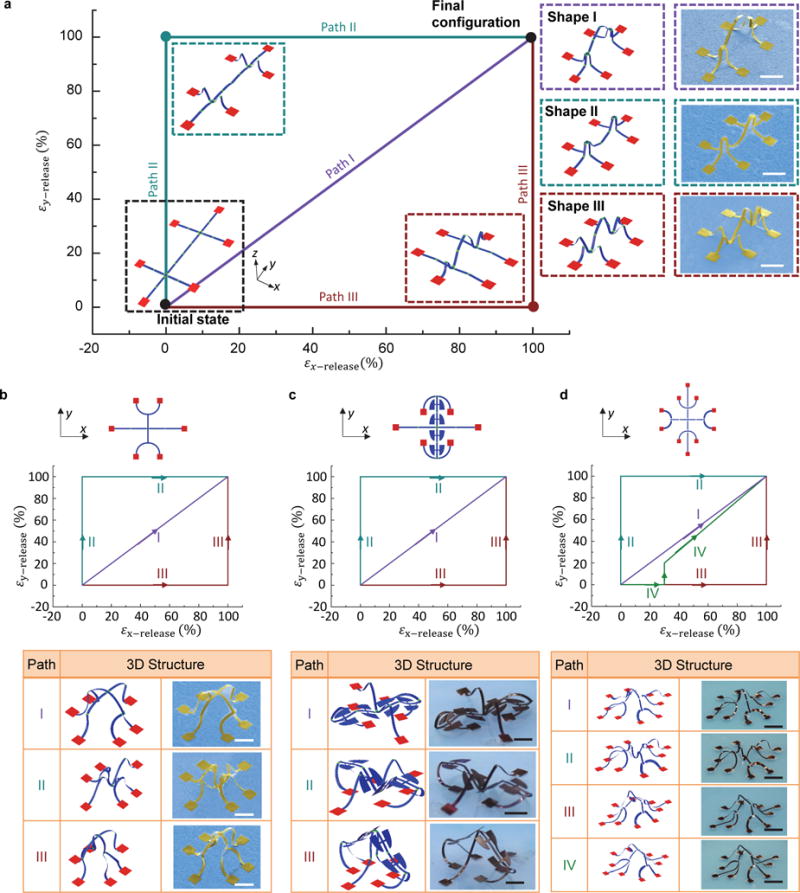
a-d, 2D geometries, release sequences, FEA predictions and experimental images (SEM or optical) of four complex ribbon networks. The yellow and dark brown colors in the colorized experimental images correspond to SU8 (6 $\mathrm{\mu }$m for normal region and 2 $\mathrm{\mu }$m for crease), and bilayer of PET (50 $\mathrm{\mu }$m) and copper (1 $\mathrm{\mu }$m), respectively. Scale bars, 400 $\mathrm{\mu }$m for SU8 mesostructures (Fig. 4a-b), and 4 mm for PET/Cu mesostructures (Fig. 4c-d).

Morphable 3D radio frequency electronic devices

Compatibility of these reconfigurable 3D structures with modern planar device technologies suggests potential for unusual classes of 3D microelectronic systems. Figure 5a-e presents a 3D radio-frequency (RF) circuit that can reconfigure reversibly between geometries that function as a low-pass filter and an inductor (Supplementary Fig. 17). The simultaneous release of biaxial prestrain (60%) forms a resonant circuit that features an inductor (helical coils in Figure 5b) and a parallel-plate capacitor (two closely spaced copper separated by PI, Shape I of Figure 5b and Supplementary Fig. 18). The sequential release yields a 3D shape that involves a large distance between the parallel plates (Shape II of Figure 5b), resulting in an open circuit at this region. Here, the LC circuit functions only as a single inductor. Electromagnetic measurements summarized in Figure 5c and Supplementary Fig. 18a show that the low pass filter has a cutoff frequency at 1.9 GHz with passband ripple as high as 2.8 dB, likely due to the mechanical instability of the soft testing fixture. In contrast, the inductor performs as a choke, providing different values of impedance to block signal at a desired frequency (Figure 5d and Supplementary Fig. 18b). This reconfigurable function might have utility as a radio switch. Specifically, Shape I turns the radio on across frequencies from 1.13 GHz to 1.36 GHz, as the return loss (S11) is less than −20 dB for this range, per Figure 5c. Meanwhile, Shape II turns the radio off by increasing the return loss beyond −1 dB, i.e., for frequencies from 1.24 GHz to 3 GHz, per Figure 5d. As such, the radio can be switched reversibly between on (for Shape I) and off (for Shape II) through mechanically-guided 3D reconfiguration, for frequencies from 1.24 GHz to 1.36 GHz. The prestrain used in the 3D assembly can be used to tune the operating frequency (Figure 5e), for example, from radiolocation service (433.05 MHz to 434.79 MHz) at ε_pre = 21~23% to the 33-centimeter band amateur radio (902 MHz to 928 MHz) at ε_pre = 39~43%. The frequency range of the radio switch also increases with the diameter of the capacitor (Supplementary Fig. 19).

Figure 5. Applications of 3D morphable mesostructures as switchable radio frequency (RF) electronic components.

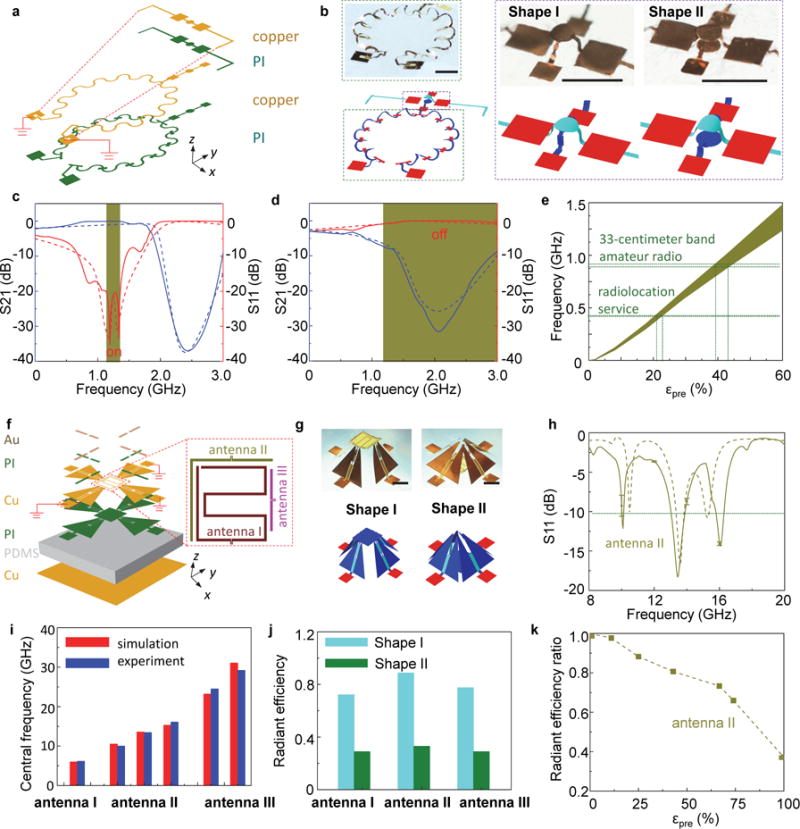
a-e, A morphable RF circuit. a, Exploded view illustration of the layer construction [Cu (3 $\mathrm{\mu }$m), PI (2 μm)]. b, FEA predictions and optical images of the overall device, and magnified view of the capacitor structure that results from different release sequences. Shape I and II result from simultaneous and sequential release (x direction first, and then y) of the elastomer substrate, respectively. Scale bars, 1 mm. c, Measured and simulated S21 and S11 versus frequency for Shape I, when the device is formed from a biaxial prestrain (ε_x-pre = ε_y-pre = 60%). d, Measured and simulated S21 and S11 versus frequency for Shape II, when the device is formed from a biaxial prestrain (ε_x-pre = ε_y-pre = 60%). e, Simulated switchable frequency band as a function of the prestrain, when the device is subject to different biaxial prestrains. f-i, A morphable electromagnetic device with shielding capability. f, Exploded view of the layer construction [thickness of each layer from top to bottom: Au (100 nm), PI (1.5 μm), Cu (9 $\mathrm{\mu }$m), PI (12 $\mathrm{\mu }$m), PDMS (5 mm), Cu (100 nm)]. g, FEA prediction (lower frames) and optical images (upper frames) of the device. Scale bars, 5 mm. h, Measured and simulated dependence of the return loss (S11) on the frequency for antenna II. i, FEA predictions and experimental measurements of the central frequency for antenna I, II and III. j, Simulated radiant efficiency for antenna I (at frequency f=6.0 GHz), II (f=13.58 GHz) and III (f=23.2 GHz) when the device is released from a biaxial prestrain (ε_x-pre = ε_y-pre = 85%). k, Simulated radiant efficiency ratio for antenna I (f=6.0 GHz) as a function of the prestrain. In c, d and h, the solid and dash lines correspond to the experiment and simulation results, respectively.

A concealable electromagnetic device represents another application in reconfigurable 3D RF electronics. The 2D precursor in this case consists of three parts, the first of which serves as an electromagnetically shielding structure; the second as three antennas for communication and a shielding structure; and the third as a support structure. The simultaneous release yields a working mode (Shape I, Figure 5g) configuration, where the antennas are elevated and exposed. The sequential release (Supplementary Fig. 20) leads to a reshaped system where the metallic support structure covers the coil, such that it is electromagnetically shielded. Figure 5h and Supplementary Fig. 21 present measurements and modeling results for the return loss (S11) associated with these three antennas. Figure 5i and Supplementary Fig. 22 show that the device can span a wide range of frequencies (from ~ 6 GHz to ~ 30 GHz). The radiant efficiencies obtained by simulation (Figure 5j) show that Shape II has a much smaller radiant efficiency than Shape I for all three antennas. Figure 5k illustrates the calculated radiant efficiency ratio of Shape II to Shape I as a function of prestrain. The ratio decreases slowly at the initial stage (e.g., ε_pre < 25%), and it drops quickly for ε_pre > 75%, as the shielding membranes in Shape II begin to close. This concept is scalable to even higher frequency ranges (> 80 GHz), as demonstrated in Supplementary Fig. 23 where the device size shrinks more than tenfold. The compatibility of these approaches with planar microfabrication techniques suggests broad scalability and diversity in choice of circuit designs.

Conclusions

In summary, the results reported here introduce a loading-path strategy and associated design approach for realizing complex classes of 3D mesostructures that are capable of qualitative shape reconfiguration through mechanically guided assembly. Fundamental studies of the underlying multistable buckling modes and associated probabilistic geometrical transformations establish the foundations for robust and reproducible engineered behaviors. Compatibility of these concepts with the most advanced classes of planar thin film materials and microsystems technologies suggest potential for broad applicability. Specific examples including dozens of 3D reconfigurable mesostructures with length scales ranging from micrometers to millimeters, across material classes from soft polymers to brittle inorganic semiconductors, illustrate the basic ideas and validate the utility of computational modeling as a design tool. Arrays of silicon n-MOSFETs or μ-LEDs integrated directly into certain of these platforms suggest opportunities in reconfigurable 3D microelectronics. Radio frequency components that can reversibly switch between different functional states through changes in shape highlight capabilities of potential relevance to advanced communication devices. Additional possibilities include transformable metamaterial structures, optical imaging platforms, microelectromechanical sensors and many others.

Methods

Finite Element Analysis

Computational models of post-buckling analyses were developed using finite element analyses (FEA) software (ABAQUS) to simulate the processes of compressive buckling. 8-node solid elements (C3D8R) and 4-node shell elements (S4R) were used for the silicone substrate and 2D precursors, respectively. Convergence of mesh sizes was tested to ensure computational accuracy. Frictionless contact was implemented to model the interface between 2D precursors and substrate. The elastic modulus (E) and Poisson’s ratio (ν) are $E_{\text{substrate}}$= 166 kPa and ${\upsilon }_{\text{substrate}}=$0.49 for substrate; $E_{\text{SU}8}$= 4.02 GPa and ${\upsilon }_{\text{SU}8}=$0.22 for SU8; $E_{\text{PI}}$= 2.5 GPa and ${\upsilon }_{\text{PI}}$=0.34 for PI; $E_{\text{Cu}}$= 119 GPa and ${\upsilon }_{\text{Cu}}=$0.34 for copper (Cu). $E_{\text{Si}}$= 130 GPa and ${\upsilon }_{\text{Si}}$=0.27 for silicon. E_PET = 2.7 GPa and ${\upsilon }_{\text{PET}}$ = 0.38 for PET.

Fabrication of 3D Mesostructures in Photodefinable Epoxy

Preparation began with formation of a sacrificial layer of thermally grown SiO₂ (600 nm, dry oxidation at 1150°C) on a silicon wafer, and uniform coating of an adhesion promoter (Omnicoat, MicroChem). The 2D precursors consisted of two layers of photodefinable epoxy (SU8 2 or SU8 5, MicroChem) sequentially patterned by spin coating and photolithography with precise alignment, in which the first and second layers of SU8 defined the matrix and the crease regions of the 2D precursors, respectively. A brief exposure to oxygen plasma removed the exposed adhesion promoter. Immersion in buffered oxide etchant (BOE, VWR International, 6:1) eliminated the exposed SiO₂ and created a thin partial undercut around the edges of the patterns of SU8. Next, photolithography defined a layer of photoresist (AZ 5214E, MicroChem, thickness ~ 1.3 μm) at all regions of the SU8 except those associated with the pads designed for bonding to the elastomer platform. The photoresist also formed an anchor around the partially undercut edges to prevent patterns from lifting from the substrate during complete elimination of the underlying SiO₂ in concentrated hydrofluoric acid (HF, 49%) for several hours. A thin layer of silicon oxide (thickness ~ 50 nm) was then deposited on the sample surface by electron beam evaporation to create the necessary surface chemistry for strong adhesion to the elastomer platform at the bonding pads. The non-bonding sites were protected from SiO₂ deposition by photoresist. Transfer printing^52,53 with a slab of polydimethylsiloxane (PDMS, Sylgard 184, 1:10) retrieved the 2D precursor from the silicon wafer and placed it on a piece of water-soluble tape (AQUASOL). A silicone elastomer substrate (Dragon Skin® 10) was stretched to a desired prestrain using a customized, biaxial stage. After exposing the elastomer and the 2D precursors (still on water-soluble tape) to ultraviolet (UV) induced ozone (Jelight UVO-Cleaner, Model 144AX) to create surfaces with hydroxyl termination on the silicone and the SiO2 on the bonding pads, the two were laminated together and then baked in a convection oven at 70 °C to yield strong adhesion via condensation reactions at the interface. Finally, dissolving the tape in warm water, removing the photoresist by rinsing with acetone, and slowly releasing the prestrain along prescribed release paths completed the assembly process.

Fabrication of 3D Mesostructures in Silicon

Preparation began with patterning the device silicon layer of a silicon-on-insulator (SOI) wafer (device Si thickness ~ 1.5 μm, SOITEC) using standard photolithography and reactive ion etching (RIE). The subsequent steps of partial undercut with BOE, photoresist patterning to cover the non-bonding regions, complete undercut with HF, transfer printing, UV ozone exposure, bonding, dissolution of the water-soluble tape, removal of the photoresist and release of the prestrain all followed procedures similar to those for the SU8 samples described above.

Fabrication of 3D Mesostructures with Sub-millimeter Scale Features

Preparation began with automated mechanical cutting of bilayers of copper (1 μm)/PET (50 μm) or single-layers of PET (40μm) into desired 2D patterns. For 2D precursors of PET (Figure 3d to f) that exploit creases, an additional non-penetrating mechanical cutting (30 μm in depth) step created the thin regions (10 μm in thickness). A thermal release tape facilitated retrieval of the films cut in this manner from their adhesive supporting mat. A stretched silicone substrate (2 mm in thickness, Dragon Skin) served as the assembly platform. Dispensing a commercial adhesive (Super Glue, Gorilla Glue Company) at the bonding sites and laminating the 2D precursors (with adhesive side down) onto the prestrained silicone substrate and curing for ~ 10 minutes at room temperature resulted in strong adhesion at the bonding sites. Slowly releasing the prestrain in the elastomer along the prescribed paths completed the assembly process.

Fabrication of 3D n-MOSFET Transistors

Preparation began with thermal growth of SiO₂ (200 nm) on a p-type SOI wafer (device Si thickness ~200 nm, SOITEC). Patterning the SiO₂ by photolithography and etching in BOE defined openings for solid-state diffusion doping with phosphorus (1000 °C for 7 min) to define the source and drain contacts. Immersion in concentrated HF for 30 min completely removed the buried oxide layer of the SOI, allowing retrieval of the device silicon layer onto the surface of a PDMS stamp for transfer printing onto a spin-cast bilayer of poly(methylmethacrylate) (PMMA, MicroChem, thickness ~200 nm) and polyimide (PI, HD MicroSystems, thickness ~2 μm) on a Si wafer. Photolithography and RIE etching isolated the device silicon into regions for individual transistors. A layer of SiO₂ (thickness ~ 400 nm) deposited by plasma-enhanced chemical vapor deposition at 200 °C served as the gate dielectric. Photolithography and BOE etching formed openings through the SiO₂ to expose the source and drain contact regions. Deposition of Cr (thickness ~ 5 nm) and Au (thickness ~ 150 nm) by electron beam evaporation followed by photolithography and wet etching defined the gate electrodes and metal interconnects. Spin coating another layer of PI (thickness ~ 2 μm) and oxygen plasma etching through a thick photoresist mask (AZ 4620, MicroChem, thickness ~ 10 μm) completed the top encapsulation. After removing the residual photoresist with acetone, the underlying PMMA layer was dissolved by immersion in acetone overnight to allow retrieval of the device onto a piece of water-soluble tape. A thin layer of SiO₂ (thickness ~ 50 nm) was deposited selectively onto the bonding sites through a shadow mask. The 3D assembly process then followed the same procedures for the SU8 and silicon samples as described above.

Fabrication of 3D Frameworks that Incorporate μ-LEDs

Preparation began by spin coating and curing PI (thickness ~ 5 μm) on a 3 μm-thick copper foil, followed by lamination of the film with the copper layer facing up onto a PDMS-coated glass slide. Photolithography and wet etching patterned the copper layer into designed geometries. Transfer printing using a mask aligner (Karl Suss MJB3) delivered the μ-LEDs (Cree® TR2227™ LEDs) onto the copper electrodes with a small amount (1-2 beads per electrode) of In/Ag solder paste (Indalloy 290, Indium Corporation). Placing the device on a hot plate at 150 °C for 1 minute electrically bonded the μ-LEDs to the electrodes. A photolithographically defined layer of SU8 (thickness ~ 4 μm) encapsulated the entire systems, leaving only the external electrodes exposed for connections to an external power supply. A thick layer of photoresist (AZ4620, MicroChem, thickness ~ 10 μm) was then patterned to mask the device during removal of the exposed PI by exposure to oxygen plasma. The remaining processes of device retrieval by a piece of water-soluble tape, selective SiO₂ deposition and 3D assembly then followed the same steps for the 3D n-MOSFET as described above.

Fabrication of 3D RF Electronic Structures

Preparation of the 3D structure in Figure 5a-e began with spin casting and curing a layer of PI (thickness ~ 2 μm) on a copper foil (thickness 3 μm, Olin Brass), followed by lamination onto a PDMS-coated glass slide, with copper side facing up. The 3D RF circuit consisted of two different 2D precursors fabricated separately and then joined together prior to 3D assembly. Patterning of each 2D precursor involved two sequential lithographic processes: 1), patterning the copper by photolithography and wet etching; 2), patterning the PI by photolithography and oxygen plasma etching through a thick photoresist mask (AZ 4620, MicroChem, thickness ~ 10 μm). A piece of water-soluble tape was used to retrieve the first layer. The second layer was then retrieved onto the same piece of tape in an aligned manner under an optical microscope. The remaining processes of selective SiO₂ deposition and 3D assembly then followed the same procedures for the 3D n-MOSFET as described above. Finally, silver paste is used to electrically connect the top and bottom copper layers to form a complete circuit.

Preparation of the large-scale 3D concealable electromagnetic device in Figure 5f-k began by laminating a commercially available PI film on copper foil (Pyralux AC091200EV, DuPont) onto a PDMS-coated glass slide, with copper facing up. Laser cutting defined the overall geometries. Standard photolithography and wet etching patterned the copper. Spin coating a thin layer of PI (thickess ~ 1.5 um) followed by deposition of Cr (thickness ~ 5 nm) and Au (thickness ~ 100 nm) defined the electromagnetic shielding layer on the four legs. The metals and PI were patterned by wet and oxygen plasma etching using layers of photoresist as masks, respectively. The remaining processes of device retrieval by a piece of water-soluble tape, selective SiO₂ deposition and 3D assembly then followed the same procedures for the 3D n-MOSFET as described above.

Preparation of the small-scale 3D concealable electromagnetic device in Supplementary Fig. 23 began with spin casting a bilayer of PMMA (thickness ~ 200 nm) and PI (thickness ~ 1.5 μm) on a Si wafer. Depositing Cr (thickness ~ 5 nm) and Au (thickness ~ 100 nm) by electron beam evaporation followed by photolithography and wet etching defined the antenna circuits. Spin casting another layer of PI (thickness ~ 1.5 um) followed by deposition and patterning of Cr (thickness ~ 5 nm) and Au (thickness ~ 100 nm) defined the electromagnetic shielding layer on the four legs. A patterned layer of SU8 (thickness ~ 3 um) defined the crease regions. After patterning the PI by oxygen plasma etching through a thick photoresist mask (AZ 4620, MicroChem, thickness ~ 10 um), the underlying PMMA layer was dissolved by immersion in acetone overnight to allow retrieval of the device onto a piece of water-soluble tape. The remaining processes of selective SiO₂ deposition and 3D assembly then followed the same procedures for the 3D n-MOSFET as described above.

Electromagnetic (EM) Measurements

Two port S-parameters were measured using the Agilent PNA8363C purpose network analyzer with Cascade Microtech air coplanar ground-signal-ground probes in the frequency range from 10 MHz to 40 GHz. Measurements of the 3D RF circuit used a test fixture shown in Supplementary Fig. 24. A thin glass slide placed underneath the contact pads allowed leveling of the probes on the soft substrate. Parasitic effects introduced by feedlines were removed using an open-through de-embedding technique to obtain the real performance of the device under test (DUT). A lumped equivalent circuit model captured the physics of the parasitic effects. Open-through de-embedding patterns are in Supplementary Fig. 24. As in Supplementary Fig. 24a, an admittance Π-network modeled the capacitive effects between the contact pads and the surrounding environment including the substrate and RF ground. An impedance network connected in series modeled the resistance and inductance of the feedlines. Supplementary Fig. 24a-c shows schematic views of patterns with the DUT, without the DUT (open case) and with connection thru directly. Corresponding lumped equivalent circuits captured the RF performance of each pattern. The narrow branches of the feedlines were bent 90° to avoid using additional lines to connect the two feedlines. The mathematical procedures to perform the open-through de-embedding are in Supplementary Fig. 25.

Electromagnetic Simulations

The finite element method was adopted in electromagnetic simulations to calculate the S parameters, central frequency and bandwidth of reconfigurable RF circuit, as well as the return loss parameter (S11) and the radiation efficiency of the antennas. The simulations used the commercial software ANSYS HFSS, in which tetrahedron elements were used in the solution with adaptive meshing convergence. The different 3D configurations of the devices enabled by the loading-path strategy were all exported from the mechanics simulation performed using the software ABAQUS, and then imported to the software ANSYS HFSS. All the metal layers in the devices, including the antennas themselves, metallic supporting structures and the metal plane underneath the substrate, are modeled by Finite Conductivity Boundary for the sake of efficiency, with use of the prescribed thicknesses. The relative permittivity ( ${\epsilon }_r$), relative permeability ( ${\mu }_r$) and conductivity ( $\sigma$) are ${\epsilon }_{r\_Cu}=1$, ${\mu }_{r\_Cu}=0.999991$ and ${\sigma }_{Cu}=5.8\times {10}^7\mathrm{S}/\mathrm{m}$; ${\epsilon }_{r\_PI}=3.5$, ${\mu }_{r\_PI}=1$ and ${\sigma }_{PI}=0\mathrm{S}/\mathrm{m}$; and ${\epsilon }_{r\_\mathit{\text{substrate}}}=2.55$, ${\mu }_{r\_\mathit{\text{substrate}}}=1$ and ${\sigma }_{\mathit{\text{substrate}}}=2.5\times {10}^{-14}\mathrm{S}/\mathrm{m}$.

Data availability

The authors declare that all relevant data supporting the finding of this study are available within the paper and its Supplementary Information files. Additional data are available from the corresponding author upon request.