Algorithms in the historical emergence of word senses

Significance

How do words develop new senses? Unlike changes in sound or grammar where there are rich formal characterizations, semantic change is poorly understood. Changes in meaning are often considered intractable, with sparse attempts at formalizing and evaluating the principles against historical data at scale. We present a data-enriched formal approach that explores the time-varying lexicon. Motivated by prominent work in cognitive science and linguistics, we develop computational algorithms that predict the historical order in which the senses of a word have emerged, and we test these predictions against records of English over the past millennium. Our findings suggest that word senses emerge in ways that minimize cognitive costs, providing an efficient mechanism for expressing new ideas via a compact lexicon.

Abstract

Human language relies on a finite lexicon to express a potentially infinite set of ideas. A key result of this tension is that words acquire novel senses over time. However, the cognitive processes that underlie the historical emergence of new word senses are poorly understood. Here, we present a computational framework that formalizes competing views of how new senses of a word might emerge by attaching to existing senses of the word. We test the ability of the models to predict the temporal order in which the senses of individual words have emerged, using an historical lexicon of English spanning the past millennium. Our findings suggest that word senses emerge in predictable ways, following an historical path that reflects cognitive efficiency, predominantly through a process of nearest-neighbor chaining. Our work contributes a formal account of the generative processes that underlie lexical evolution.

Every language must meet the challenge of expressing a potentially infinite set of emerging ideas via a finite lexicon. One way in which this challenge is met is by creating new words to express novel senses, e.g., “croggy” to refer to riding on a bicycle’s handlebars. However, a more common strategy is to reuse existing words. (See Historical Analyses of Word Form Reuse Versus Innovation for evidence that, over the history of English, new senses have been more frequently expressed via reuse of existing words than via new word forms.) Extension of existing words to new senses creates polysemy (1), the ubiquitous phenomenon (2) in which a single word form is used to express multiple, related senses, e.g., “face” refers to both “body part” and “facial expression.” Why is polysemy a dominant strategy in lexical evolution, and how do words develop new senses over time? We present a computational approach that sheds light on mechanisms that support the emergence of new word senses.

The complexity of the problem is exemplified by Wittgenstein’s observation that the many senses of the word “game” form “a complicated network of similarities overlapping and criss-crossing” (ref. 3, pp. 31–32), with nothing identifiably in common. This network includes not only “board games” and “ball games” but also “war games,” “end games,” and “hunting games,” presumably a reflection of the complex path the word game took in the historical development of its senses. Decades of research have suggested possible ways that such network structures might arise over time, but these proposals have not been formalized under a common principled framework or assessed against historical data at scale.

Our theoretical starting point is influential work from cognitive science suggesting that categories are structured in nonarbitrary ways, e.g., ref. 4. Pioneering research by Rosch (5) suggested that common semantic categories signified by words such as “bird” and “furniture” may exhibit a prototype structure, such that some members of a category are viewed as more representative than others. This proposal has been linked to process models according to which new items are incorporated into a category via comparison with the category’s prototype. This theory has also been adapted to describe how word senses might be structured (6) or extended over time (7). A prominent alternative proposal about categorization is exemplar theory, e.g., refs. 8 and 9, which suggests that all previously encountered members of a category are stored and used when categorizing novel items. Exemplar theories have also been used to describe how language might change over time, particularly with respect to phonological and semantic representations (10).

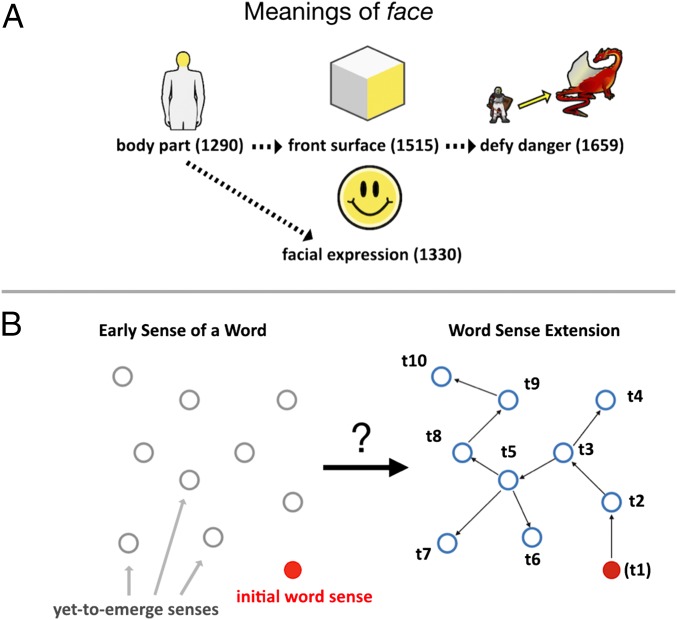
A critical addition to this theoretical terrain is the idea of chaining (6, 11) as a possible mechanism of word sense extension. Chaining links an emerging, yet to be lexicalized idea to a highly related, already lexicalized word sense. When this process repeats, a chained structure in semantic space results. Fig. 1A provides an illustration of how chaining might operate by linking different senses of the word face. Originally endowed with the sense of body part, this word was then extended to denote facial expression. The body part sense was presumably later extended metaphorically to denote the “front surface” of objects, and the more abstract idea of “defying danger,” forming a separate chain in semantic space.

Fig. 1.

Chaining and the computational problem. (A) Hypothetical sense chaining for English face. Senses and dates of appearance in parentheses are from The Historical Thesaurus of English (12). (B) Illustration of the problem. Senses of a word are represented by dots, with red indicating the earliest recorded sense. Can the order of historical sense development be predicted, and, if so, by what algorithms?

We hypothesize that chaining might be a preferred mechanism of lexical evolution because it facilitates sense extensions that are cognitively “cheap,” conforming to the general principle of cognitive economy (5). That is, words should develop new senses in ways that minimize the collective costs of generating, interpreting, and/or learning them. Chaining may provide a desirable mechanism for this purpose because it allows novel senses to develop from existing ones that are closest in meaning. For example, when seeking to express a new idea (like facial expression), speakers may most quickly and easily retrieve an existing word form with the closest-related sense (e.g., the body part sense of face), and the close proximity between these senses should facilitate comprehension in listeners (13) and language learners (14). Our proposal is consistent with existing theories (e.g., ref. 15) that suggest that language change results from demands for “a maximum of efficiency and a minimum of effort” (ref. 15, p. 324).

Although chaining seems plausible as a mechanism of sense extension, a principled specification is needed for why it might be a preferred mechanism. Further, establishing its predictive value requires testing whether it is better able to account for historical records of sense evolution—at the scale of the entire lexicon (cf. ref. 16)—than alternative mechanisms (such as the prototype and exemplar theories). The present study addresses these issues through a computational framework that explores how the senses of individual words in a lexicon have emerged over time. We show that a model of nearest-neighbor chaining—a probabilistic algorithm that approximates a minimal spanning tree over time (a concept from graph theoretical work in computer science)—predicts the order of emergence of English word senses better than alternative mechanisms.

Computational Formulation of Theory

We formulate word sense extension as a computational problem, illustrated in Fig. 1B. We ask how an individual word’s various senses could have emerged over time by “attaching to” existing senses of that word, and consider alternative extensional mechanisms that yield different “paths.” Because the space of possible extensional paths grows factorially with the number of senses a word develops (see Model Cost and Likelihood), we focus on the paths predicted by five probabilistic algorithms that have each been motivated by prior work on semantic representation. We show that the nearest-neighbor chaining algorithm tends to yield the most “cost-effective” sense extension strategy. We now present the algorithms and then define “cost.”

Algorithms of Word Sense Extension.

Given the set of senses a word has developed over history, all algorithms that we propose infer which sense is likely to emerge at time $t+1$ (i.e., the next time point in history where new senses appeared), based on existing senses of a word up to time $t$: $S(t)=\{s_0,s_1,\mathrm{\dots },s_t\}$. Beginning with the earliest sense of a word $s_0$, each algorithm predicts sequentially (from the candidate pool of yet-to-emerge senses) which will be the upcoming sense, based on a unique extensional mechanism that attaches novel senses to existing ones. As a result, each algorithm specifies a probability distribution over all of the possible historical orders in which a word’s senses could have emerged (see Model Cost and Likelihood). At each time point, an algorithm predicts the next emerging sense with a probability specified by Luce’s choice rule (17),

$$s^{\ast }\sim \frac{f(s^{\ast },S(t))}{{\sum }_{s\in S^{\ast }(t)}f(s^{\ast },S(t))}.$$ [1]

$S^{\ast }(t)$ represents the set of candidate senses given by the historical record that have not appeared up to time $t$, for a given word. Each model has a different likelihood function $f(s^{\ast },S(t))$ that specifies the mechanism that links the candidate emerging sense to the existing senses. The likelihood functions specify computations based on semantic similarity between senses, which we describe below. To make minimal assumptions, all of the models are parameter-free, and hence are on equal footing in model complexity (i.e., 0). We describe and summarize the models in Table 1, along with a null model.

Table 1.

Specification of proposed sense extension algorithms

Model	$p(s*)$
Exemplar	$\propto f(s*,S(t))=E_{s\in S(t)}[sim(s*,s)]$
Prototype	$\propto f(s*,S(t))=sim(s*,prototype(S(t)))$
Progenitor	$\propto f(s*,S(t))=sim(s*,s_0)$
Local	$\propto f(s*,S(t))=sim(s*,s_t)$
Nearest-neighbor chaining	$\propto f(s*,S(t))={\max }_{s\in S(t)}sim(s*,s)$

Random Algorithm.

This null model predicts the historical emergence of a word’s senses to be random.

Exemplar Algorithm.

This algorithm is motivated by Medin and Schaffer (8) and Nosofsky (9), whereby the emerging, to be lexicalized sense at $t+1$ is predicted with a probability based on average semantic similarity with existing, already lexicalized senses of a word up to time $t$.

Prototype Algorithm.

This algorithm is motivated by Rosch (5) and Geeraerts (7) and predicts the emerging sense at $t+1$ with a probability based on semantic similarity with the prototypical sense at time $t$. We define prototype at $t$ as the sense with the highest semantic similarity to all other existing senses of the word: $prototype(S(t))\leftarrow {\max }_{s_i\in S}{\sum }_{j\ne i}sim(s_i,s_j)$. Thus, this algorithm allows the most representative sense of a word to change as a function of time, as a word accrues more senses.

Progenitor Algorithm.

This algorithm is a “static” variant of the prototype algorithm. It assumes a fixed prototype that is always the earliest recorded or progenitor word sense. It predicts the emerging sense at $t+1$ with a probability based on semantic similarity with the progenitor sense, for each candidate sense.

Local Algorithm.

This algorithm assumes that word senses emerge in a local temporal chain, where the emerging sense at $t+1$ is sampled with a probability based on semantic similarity to the sense that appears just before it, namely at time $t$ (i.e., $s_t$). Thus, senses that appear before $t$ have no influence on the emerging sense at $t+1$. This assumption posits that an emerging sense will be minimally distant from the most recent sense of a word (i.e., local minimum), in contrast with the next algorithm, which tends to minimize distance in a global way (i.e., between all sense pairs).

Nearest-Neighbor Chaining Algorithm.

This algorithm is closely related to prior proposals about chaining. It approximates Prim’s algorithm for constructing a minimal spanning tree (18) (see Nearest-Neighbor Chaining and Minimal Spanning Tree), but with a fixed starting point; that is, it always begins with the progenitor sense of a word. The algorithm predicts the emerging sense of a word at $t+1$ with a probability based on the highest semantic similarity with any of the existing word senses up to $t$, rendering a chain that connects nearest-neighboring senses over time. In contrast with the other algorithms, this algorithm tends to construct a sense network at globally minimal cost (see Nearest-Neighbor Chaining and Minimal Spanning Tree), a metric that we describe in Cost of Word Sense Extension.

Cost of Word Sense Extension.

Sense extension can be thought of as involving costs, such that certain historical paths can be considered more cognitively efficient or cost-effective than others. For example, extending the meaning of face via body part$\to$facial expression might entail a lower cost than body part$\to$front surface of an object, since the former pair of senses appear to be more semantically related and mentally associable than the latter. If sense extension tends to minimize cost in the historical path, then, given the initial body part sense of face, we expect facial expression to emerge earlier in history than front surface of an object. Whether historical paths do minimize costs is a key empirical question that we address.

We quantify the cost of the models by considering the degree to which they minimize cognitive effort in sense extension over time. Specifically, given that a novel sense appears at a certain time point and “location” in semantic space, the cost measure determines how efficient the path toward that location is. We do not predict the location of the new sense but instead evaluate how cost-effective the aggregated spatiotemporal path toward that sense is. For a given model $m$ that prefers a certain historical path over alternatives, we define cost $c$ as

$$c(pat{h}_m)=\sum _t\sum _{s_i\in S(t),s_j\in S^{\ast }(t)}e(s_i\to s_j).$$ [2]

Namely, the cost of a model is the aggregated effort (denoted by $e$) of extending existing senses to novel ones as predicted by that model, summed over all time points where senses have emerged for a word. We operationalize effort by semantic distance, the inverse of semantic similarity. A cost-effective model should tend to minimize this quantity in the historical extensional paths that it specifies. Given that each model predicts a path probabilistically, the average cost of a model considering all possible paths is $\sum p(pat{h}_m)c(pat{h}_m)$. It can be shown that the nearest-neighbor chaining model tends to produce near–minimal-cost paths, in contrast with the other competing models (see Results, Nearest-Neighbor Chaining and Minimal Spanning Tree, and Model Cost and Likelihood). Of course, the hypothesis that historical sense extension is best predicted by a low-cost model could be wrong, because word senses may not have developed in ways that minimize costs (Model Cost and Likelihood discusses how model cost and predictive likelihood are dissociable). Whether or not they do is an empirical question that we examine next.

Results

We assess our models in three steps. First, we demonstrate, in a simulation, that the nearest-neighbor chaining model generally yields the lowest cost in posited sense extensional paths, compared with alternative models. Second, we test the models’ ability to predict the order of sense emergence against chance (i.e., against the null model), using a large digitized historical lexicon of English. Third, we evaluate the models against each other and show that nearest-neighbor chaining dominates the other models in accounting for the historical data.

Model Simulation.

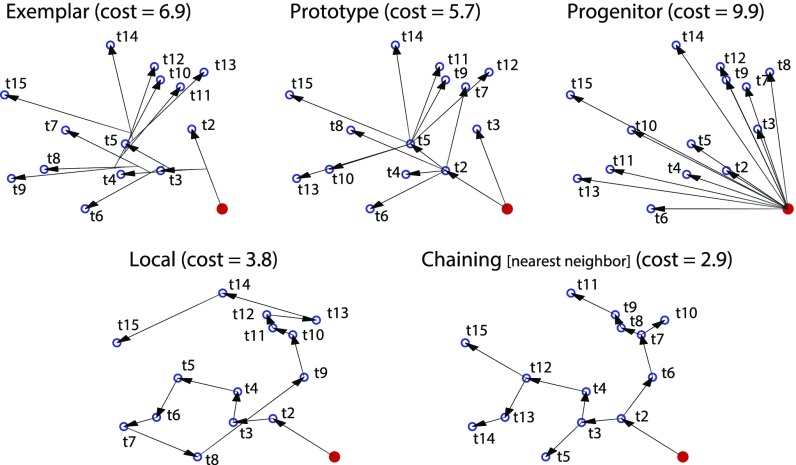
We first examined whether the nearest-neighbor model yields sense extensional paths that minimize cognitive cost. We simulated the proposed models in a hypothetically constructed semantic space, where we used Euclidean distance to represent the similarity between two senses. We used Euclidean distance only for this simulation, instead of the psychologically grounded measure of semantic similarity which we used for the empirical analyses. We placed 15 points randomly in a 2D plane that represents the semantic space of a single word, designating the bottom right point in the space as the initial sense of the word. We then applied the set of algorithms to the remaining data points and visualized the sense extensional paths specified by each algorithm. For simplicity, we display the paths based on model trajectories that maximize choice probability at each time step. The same result held when we varied the simulation parameters (see Nearest-Neighbor Chaining and Minimal Spanning Tree).

Fig. 2 shows that these algorithms yield distinct temporal paths in the simulated space. For instance, the exemplar algorithm links novel senses to all existing senses based on average distances between them (illustrated by links that develop from spaces between senses as opposed to stemming directly from senses). The prototype algorithm predicts a dynamic radial structure (6), where temporal links are established by attaching novel senses to prototype senses, while allowing the prototype to change over time. The progenitor algorithm predicts a strict radial structure where all senses stem from the earliest progenitor sense. The local algorithm predicts a temporal linkage of senses by attaching each emerging sense to the existing sense of the word that appeared one time point earlier. Finally, the nearest-neighbor chaining algorithm renders a tree structure that branches off as needed to preserve nearest-neighbor relations between emerging and existing word senses. Importantly, although both the local and nearest-neighbor chaining algorithms tend to yield lower aggregated cognitive costs in sense extension compared with the other models, the latter algorithm yields the global (as opposed to temporally local) minimal cost in semantic space.

Fig. 2.

Simulation of the proposed algorithms of word sense extension. The solid red circle symbolizes the earliest or progenitor sense of a word. The blue circles represent emerging word senses, and the arrows and time labels indicate the historical order of emergence that each algorithm predicts. The cost is taken as the aggregated Euclidean distances between word senses as traversed by the arrows.

Model Evaluation Against Historical Sense Records.

We next assessed the extent to which the proposed models predict the historical emergence of word senses better than chance. In particular, we examined each model’s ability to predict the actual orders in which English words’ senses have emerged, relative to the null model.

We used The Historical Thesaurus of English (HTE) (12)—the world’s first and largest digital historical dictionary—as a test bed. The HTE records word form–sense entries from across the past millennium, sourced from The Oxford English Dictionary and compiled by historical lexicographers and period specialists. It provides the dates of emergence, or “time stamps,” of word senses (providing ground truths for the models), and a systematic classification scheme that sorts each word sense into a conceptual taxonomic hierarchy. We defined semantic similarity between two senses based on how closely they are related in this taxonomy (see Example Calculation of Conceptual Proximity and Illustration of Verb Taxonomy for examples), and we validated this measure against human similarity judgments (see Materials and Methods).

To test the null hypothesis, we compared the proposed algorithms’ predictions regarding the historical orders of emerging word senses for about 5,000 common words of English, drawn from the British National Corpus (BNC) (19), that appear in the HTE. Because HTE does not provide word frequency information, we used the BNC to identify the most common words. We used a standard statistical measure—log likelihood ratio—to assess each algorithm against the null model (for more details and examples, see Materials and Methods and Model Cost and Likelihood). The log likelihood ratio quantifies the degree to which a model predicts the actual historical order in which a word’s senses have emerged. The null is rejected if this quantity exceeds 0, or chance level, substantially.

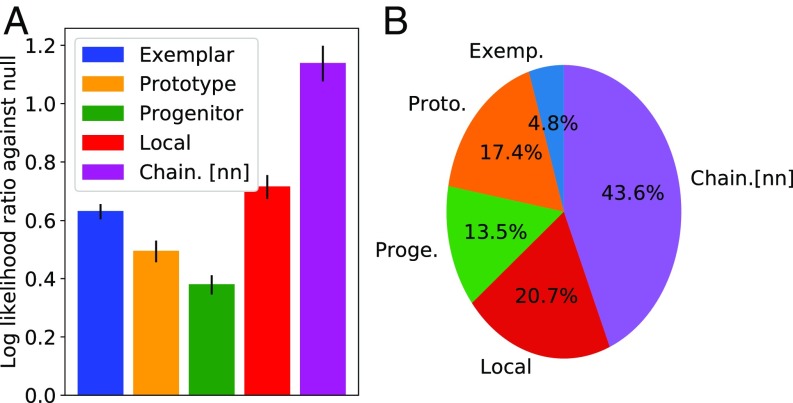
Fig. 3A summarizes the mean log likelihood ratios across the words examined. The bar plot indicates that each of the proposed algorithms yields higher predictive likelihoods on the emerging order of word senses significantly better than chance ($p<0.001$ from all one-tailed $t$ tests [$n=\mathrm{4,164}$]: exemplar, $t=47.5$; prototype, $t=26.3$; progenitor, $t=22.5$; local, $t=34.3$; and nearest-neighbor chaining, $t=36.7$). This result provides strong evidence against the null: The order in which English word senses have emerged can be predicted better than chance by taking into account the semantic similarities between senses. To control for the possibility that differences in the relative ages of words might have affected our results (e.g., some words in the BNC may have been in existence longer than others), we also ran the same test on words from the HTE that have existed continuously from Old English to the present day. We obtained similar results for each model ($p<0.001$ from all one-tailed $t$ tests [$n=\mathrm{2,648}$]: exemplar, $t=29.8$; prototype, $t=17.1$; progenitor, $t=12.1$; local, $t=23.5$; and nearest-neighbor chaining, $t=23.7$), offering additional support that a word’s senses emerge in predictable ways.

Fig. 3.

Summary of model performances. (A) Likelihood ratio test; “0.0” on the y axis indicates performance of the null model. Bar height indicates the mean log likelihood ratio averaged over the pool of most common words from the BNC corpus. Error bars indicate 95$\%$ confidence intervals across words. (B) Visualization of winner-take-all percentage breakdown among the algorithms from the same test. “Chain. [nn]” refers to the nearest-neighbor chaining model.

Predominance of Nearest-Neighbor Chaining.

To explore whether the emergence of word senses follows near–minimal-cost–chained paths, we compared the nearest-neighbor algorithm against the competitor algorithms. Fig. 3A provides support for our hypothesis: Nearest-neighbor chaining yields a substantially higher mean log likelihood compared with all competing models. Paired $t$ tests show significant differences between the chaining model and each of the competitors ($p<0.001$ from all tests [$n=\mathrm{4,164}$] with Bonferroni correction for multiple tests: against exemplar ($t=24.8$), prototype ($t=26.9$), progenitor ($t=28.2$), and local ($t=20.6$)). These results also hold for the word set that controls for age of words (see Model Comparison Controlling for Age of Words for details). Fig. 3B visualizes the model performances under a more stringent winner-take-all measure from the log likelihood ratio tests. The percentages show the relative proportions of winning cases from the five models (the null model excluded in the figure explains $10.2\%$ of the cases). As shown, nearest-neighbor chaining yields the highest percentage, best explaining the historical data.

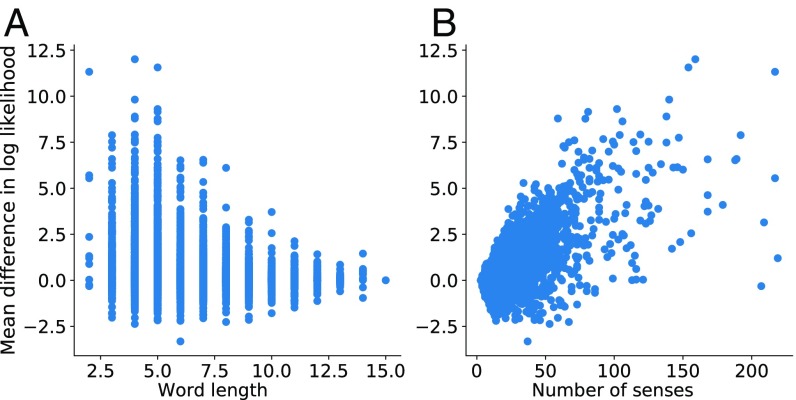
To better understand the conditions that favor chaining relative to other mechanisms of sense extension, we examined the extent to which the chaining model outperformed other models on a word-by-word basis. For each word, we calculated the pairwise difference in log likelihood between the nearest-neighbor model and the remaining models. A positive score for a word indicates that chaining outperforms competing models in predicting the historical order of emergence of that word’s senses (see Analyses of Conditions That Favor Chaining for details). We then related these chaining superiority scores to properties of the individual words, i.e., their orthographic length, and their degree of polysemy (estimated by number of recorded senses in the HTE). We expected that, because short and/or polysemous words tend to be used frequently (20), cost-effective strategies of sense extension like chaining should be most relevant for these words. Fig. 4 plots how chaining superiority scores correlate with these two variables. As can be seen, the chaining model’s success correlated strongly with number of word senses ($r=0.68$, $p<0.001$), and, to a lesser extent, with word length ($r=-0.28$; $p<0.001$). Strikingly, the correlation between number of senses and chaining superiority scores remained strong even when partialing out word length (partial correlation $\rho =0.70$, $p<0.001$), while the correlation between word length and chaining superiority was quite small after partialing out degree of polysemy ($\rho =-0.13$; $p<0.001$). These results suggest that the nearest-neighbor chaining model performed best for words that have developed many senses over time, i.e., precisely those words whose sense extensional paths could have been the most costly (see Analyses of Conditions That Favor Chaining for details and example words).

Fig. 4.

Variables that correlate with nearest-neighbor chaining superiority score. (A) Scatter plot of average difference in model log likelihoods against word length. (B) Scatter plot against number of senses.

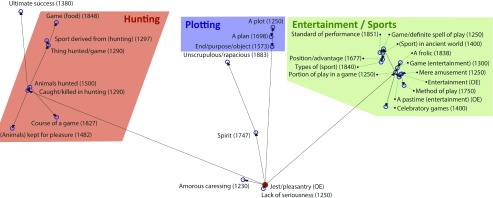
To illustrate the nearest-neighbor chaining process, we visualized its predicted path for the English word game. Fig. 5 shows a low-dimensional projection (via multidimensional scaling with a random starting point) of all emerging senses for the word game as a noun in the HTE database. As can be seen, the nearest-neighbor chaining algorithm forms a minimal-spanning-tree-like path among the senses of game, by linking nodes that are semantically close. Importantly, this process supports branching and the formation of local clusters, identified roughly in this case as “hunting” (upper left cluster), “plotting” (upper middle cluster), and “entertainment/sports” (upper right cluster) in Fig. 5. This process offers a computational basis for family resemblance (3) and polysemy, by allowing words to develop both related and distinct senses.

Fig. 5.

Historical chaining for game. Each node represents an emerging sense of game. The solid red circle marks the earliest sense recorded in the HTE. The arrows indicate the inferred path based on the nearest-neighbor chaining algorithm. The annotations include a gloss for each word sense and its recorded emergence point in the HTE.

Discussion

We provide three contributions. First, we showed why nearest-neighbor chaining might be a preferred algorithm for sense extension, making a connection to graph-theoretical work in computer science. Second, we developed an infrastructure using resources from the digital humanities, to enable large-scale computational explorations of the historical emergence of word senses. Finally, we provided a rigorous test of the ability of competing algorithms to recapitulate the evolution of English word senses over a thousand years. Our findings demonstrate that the historical order of emergence of word senses is predictable, and is best accounted for by an algorithm that tends to minimize cognitive costs over time.

The fact that the nearest-neighbor chaining model best explained the historical data—especially for words that have developed many senses over time—may reflect cognitive pressures on lexical evolution. This algorithm may minimize the costs associated with communicating new ideas and learning a lexicon. Interlocutors may find it relatively effortless to encode a new intended meaning by recycling an existing word that has a closely related sense, and addressees may find it easy to understand such new word uses (13). Further, language learners may find it easy to learn a network of senses where each sense is highly associable with other senses (14).

Much past work has described patterns of semantic change such as broadening and narrowing (21), but less progress has been made in understanding the principled mechanisms that produce such changes. Large digital databases and computational modeling techniques open new avenues for forging a deeper understanding. Our work advances previous proposals about cognitive efficiency and least effort in language change by formulating and testing algorithmic accounts of the processes that generate polysemy.

While our models focused on how the senses of individual words have emerged over time, they could be extended to address the more general question of how new senses are incorporated into the lexicon. Presumably, novel senses enter the lexicon due to communicative need, but what factors explain whether a new sense will be expressed by reusing an existing word vs. creating a new word form? What factors explain which of the existing words in a lexicon will be selected to express a new sense? Our findings suggest that new senses will often be expressed by existing words with closely related senses, but this constraint might interact with other factors that shape lexical evolution. For instance, more-frequent word forms might be preferred over rarer ones for labeling new senses, since the former word forms may be more accessible (22). Further, speakers’ knowledge of existing, generative patterns of polysemy (23–25), and their pragmatic reasoning about what senses are most likely to be understood in the current context (26), will also help explain how words accrue new senses over time, as will understanding the relative cognitive costs of generating novel words vs. reusing existing ones.

The current study focused on taxonomically based extensions of meaning: those in which extensions tend not to cross ontological domains. However, polysemy also encompasses other types of extensions, such as metonymy (27) (e.g., “dish” to refer to an object or the food it contains) and metaphorical mapping (6) (e.g., “grasping” an object vs. an idea), which often cross domains. Generating, understanding, and learning such diverse senses of words may draw on cognitive processes beyond those addressed here, and it is an open question whether the development of these forms of polysemy also minimizes cognitive costs (cf. ref. 28). Our current work provides a starting point toward unlocking the algorithms that generate new word senses in lexical evolution.

Materials and Methods

Historical Database of Word Senses.

HTE (12) is a public dictionary that includes approximately 800,000 word form–sense records, documented for a span of over 1,000 y, ranging from Old English to the present day. Each word sense in the HTE is annotated with the date of its emergence (and, where applicable, obsolescence) and part of speech, and is structured in a fine-grained taxonomic hierarchy that features about a quarter of a million concepts. Consecutive tiers of the hierarchy typically follow an “A is a B” or “A is part of B” relation. For example, one sense of the word game under the HTE code “01.07.04.04” is defined in a terms of four-tier hierarchy: The world (01)$\to$Food and drink (01.07)$\to$Hunting (01.07.04)$\to$Thing hunted/game (01.07.04.04).

Semantic Similarity.

We defined semantic similarity based on the taxonomic hierarchy in the HTE and then validated it against human judgments. We approximated psychological similarity between a pair of word senses $sim(s_i,s_j)$ by a measure bounded in the range of (0,1) (9): $sim(s_i,s_j)=e^{-d(s_i,s_j)}$. Here $d(s_i,s_j)$ represents conceptual distance between senses, which we defined by the inverse of a conceptual proximity measure [$c(\cdot ,\cdot )$] commonly used in natural language processing (29): $d(s_i,s_j)=1-c(s_i,s_j)=1-\frac{2\times |p|}{l(s_i)+l(s_j)}$; $|p|$ is the number of parent tiers shared by senses $s_i$ and $s_j$, and $l(\cdot )$ is the depth of a sense in the semantic hierarchy. This measure gives 1 if two senses are identical, and 0 if they have nothing in common. We validated this measure of semantic similarity via standard techniques in natural language processing, by evaluating its performance in predicting human judgments of word similarities (instead of judgments of sense similarities, which are not available at a broad scale). Following Resnik (30), we approximated word similarity by using the pair of senses for the two words that results in maximum sense similarity, defined as follows: $wordsim(w_i,w_j)={\max }_{s_i\in senses(w_i),s_j\in senses(w_j)}s(s_i,s_j)$. Because this word similarity measure depends solely on the relations between word senses, it serves as a proxy indicator of word sense similarity. Our measure of semantic similarity yielded a Spearman’s correlation of 0.441 ($p<0.001$) on Lex-999 (31), which is a well-known challenging dataset of human word similarity judgments. The performance of our measure of semantic similarity is better than that of the corpus-based skip-gram (Word2Vec) model, which has been trained on 1 billion words of Wikipedia text (32) and is roughly on par with the same model trained on 300 billion words (33). In addition, our measure of semantic similarity obtained a Spearman’s correlation of 0.467 ($p<.001$) on Sim-353 (34), another common dataset of human word relatedness judgments, which is comparable to the state-of-the-art Global Vectors for Word Representation word vector model, which has been trained on 6 billion words (33, 35). We also considered the linear version of similarity without the exponential transformation (i.e., $c(s_i,s_j)$), but the fit to human data was substantially worse (Spearman’s correlations 0.361 on Lex-999 and 0.139 on Sim-353), so we chose not to use it for our analyses.

Model Evaluation.

We used log likelihood ratio $LLR=\log ({\mathcal{L}}_m/{\mathcal{L}}_{null})$ to assess the performance of each proposed algorithm against the null. For any given word, the predictive density of the null can be determined theoretically, and it is the inverse of factorial of $N-1$ for a word with $N$ senses: ${\mathcal{L}}_{null}=1\times 1/N-1\times 1/N-2\times \mathrm{\dots }\times 1/1=1/(N-1)!$. Because each model is parameter-free, metrics that take into account model complexity such as the Akaike/Bayesian Information Criterion would yield equivalent results to those from this likelihood measure. For a stream of senses, the likelihood $\mathcal{L}$ is the joint probability of observing such a sequence under a certain model ${\mathcal{L}}_m=p(pat{h}_{true})=p(s_0)p(s_1|s_0)p(s_2|s_1,s_0)\mathrm{\dots }p(s_t|s_{t-1},\mathrm{\dots },s_0)$. We assumed that the initial sense is always given, so $p(s_0)=1$. At each year where emerging senses appeared, we removed senses that had become obsolete by that year according to the time stamps in the HTE, so those senses had no influence on model prediction.