Significance
If contained in a single population a complex metabolic pathway can impose a burden on the host, decreasing the system’s overall productivity. This limitation can be overcome by division of labor (DOL), where distinct populations perform different steps of the pathway, thus reducing the burden on each population. By compartmentalizing reactions, however, DOL reduces their efficiency by introducing a transport barrier for metabolites and enzymes. It remains unclear how the trade-off between reducing burden and decreasing reaction efficiency dictates the potential benefit of DOL. Through the analysis of different metabolic pathways we derive a general criterion establishing when DOL outperforms a single population. Our results can guide rational engineering of metabolic pathways and provide insights into operation of natural pathways.
Keywords: division of labor, metabolic engineering, systems biology, microbial communities, mathematical modeling
Abstract
Metabolic pathways are often engineered in single microbial populations. However, the introduction of heterologous circuits into the host can create a substantial metabolic burden that limits the overall productivity of the system. This limitation could be overcome by metabolic division of labor (DOL), whereby distinct populations perform different steps in a metabolic pathway, reducing the burden each population will experience. While conceptually appealing, the conditions when DOL is advantageous have not been rigorously established. Here, we have analyzed 24 common architectures of metabolic pathways in which DOL can be implemented. Our analysis reveals general criteria defining the conditions that favor DOL, accounting for the burden or benefit of the pathway activity on the host populations as well as the transport and turnover of enzymes and intermediate metabolites. These criteria can help guide engineering of metabolic pathways and have implications for understanding evolution of natural microbial communities.
In conjunction with synthetic and systems biology, metabolic pathway engineering, or the reprogramming of a cell’s metabolism for increased production of a desired metabolite, has enabled the biosynthesis of diverse chemicals for the food, biofuels, pharmaceuticals, textiles, and cosmetic industries (1–5). Although metabolic engineering is typically done in clonal populations, the single-population approach presents several limitations, especially for complex metabolic pathways. First, it is challenging to optimize multiple pathways while avoiding cross-talk in a single population (6–9). Second, negative pathway effects on the host cell, such as toxicity, could drive mutations that result in loss of function over time (10–13). Third, the burden of having all engineered components in a single population could reduce the total biomass and, in turn, the overall synthesis rate of the final product (14–17).
These limitations may be overcome by metabolic division of labor (DOL), in which different populations execute different but complementary metabolic tasks. DOL can reduce overall complexity by dividing up one or multiple processes such that each population contains only a subset of the overall pathway, thereby reducing the complexity within individual cells. This, in turn, can diminish the metabolic burden experienced by each population. Unlike previous studies of DOL that consider evolutionary benefit or cost (18, 19), we focus on the physical separation of different steps in a pathway without considering the adaptive value of such a separation.
DOL has been observed in several metabolic pathways in nature, and several synthetic systems demonstrate the feasibility of its implementation. For example, the nitrification pathway often operates through DOL: ammonia-oxidizing bacteria convert ammonia to nitrite and nitrite-oxidizing bacteria convert nitrite to nitrate (20). Similarly, Acetobacterium woodii and Pelobacter acidigallici are each responsible for a part of converting syringate to acetate (21). Cross-feeding in a mixed population is another example of DOL, since each population is responsible for producing different metabolites that are shared among the community (22–24). Finally, DOL has been adopted in the engineering of synthetic consortia for various applications. These include biosynthesis of useful compounds (25–28), bioprocessing (29, 30), bioremediation (31, 32), and biological computation (33, 34).
While conceptually appealing, DOL has constraints. In certain cases, one or more intermediates may be shared between two or more populations. However, limitations in molecular transport across the cell membrane and dilution of the intermediate(s) in the extracellular space can reduce the efficiency of metabolic reactions by reducing the effective concentrations of enzymes or substrates. To address this issue, metabolic pathways can often be engineered to minimize intermediate losses both in single-cell and DOL contexts (35). Depending on the pathway, DOL could also require constituent populations to compete for nutrients or space, and this too can reduce product yield and system stability. Given that DOL can either help or hurt system performance, the conditions that favor DOL remain to be rigorously established. To this end, we have analyzed several metabolic pathway architectures to determine the conditions that would favor or disfavor DOL.
Model Formulation
For each system we formulated a minimal model using ordinary differential equations for intracellular and extracellular metabolite concentrations depending on the system architecture. In all cases we assume a well-mixed system (or sufficiently fast metabolite transport), negligible intracellular degradation of metabolite, excess of initial substrate, and transport via passive diffusion. Moreover, in our models a population represents a phenotype such that they are differentiated by the tasks that they accomplish. Here we present the dimensionless forms of the model; see SI Appendix, section 2.1 for detailed justifications of our assumptions and derivations of all models.
Modeling Kinetics of an Intracellular Pathway.
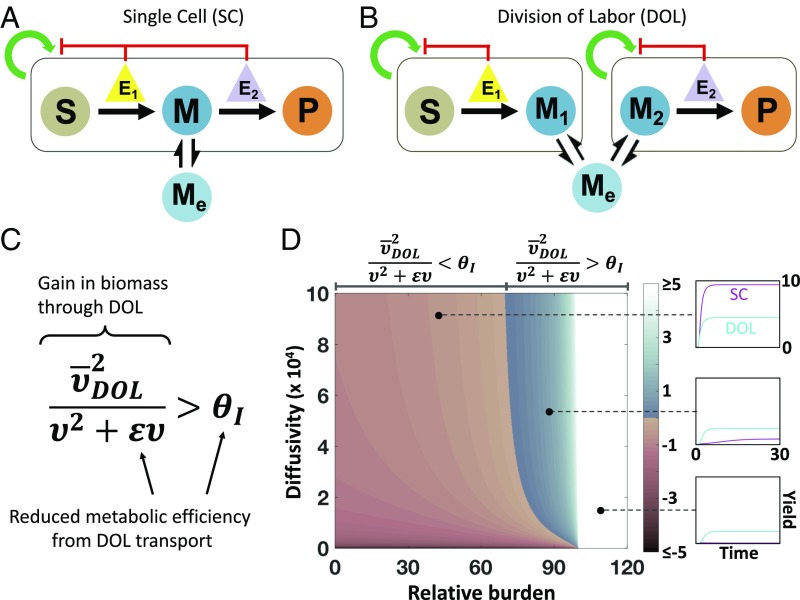
Consider conversion of a substrate (S) into an intermediate metabolite (M) by one enzyme (E1), then to a final product (P) by a second enzyme (E2). This pathway can be implemented in a single-cell population (SC) (Fig. 1A). The rates of change in intracellular and extracellular products are given by
| [1] |
| [2] |
| [3] |
Here, is the turnover rate constant of M in the extracellular space; η is the transport rate constant of M across the cell membrane; ei (i = 1, 2) is the steady-state concentration of Ei per cell; αi (i = 1, 2) is the production rate of M and P, respectively; and υ is the steady-state cell volume of the SC population. We assume the enzymes are always present at steady state in each cell.
Fig. 1.
Design criterion of DOL. (A) Model framework for an intracellular pathway within a single population (SC). Substrate (S) is converted to intracellular intermediate (M), which diffuses into the extracellular environment (Me) and is directly converted to final product (P). Enzyme expression (E1 and E2) suppress the growth of the population. (B) Model framework for an intracellular pathway within two populations (DOL). S is converted to intracellular intermediate (M1), which diffuses into extracellular environment (Me) and then into population 2 (M2), where it is converted to P. Enzyme expression (E1 and E2) suppresses the growth of the population they are contained in. (C) The design criterion defines when DOL is favored over SC. The left-hand side of the inequality represents the gain in biomass by DOL; the right-hand side represents the inefficiency of DOL. (D) The criterion determines the parametric spaces where each design strategy is favored. The color of the heat map indicates the magnitude of . Expressions for each term in the inequality are detailed in the main text and SI Appendix. To the left of the border , SC produces more P than DOL (Top). To the right of the border, DOL produces more P than SC (Middle). Above a certain level of burden, DOL always outperforms SC because the SC population goes extinct (white region, Bottom). Past a maximum level of burden, both DOL populations go extinct (black region).
If M can diffuse across the cell membrane, the above-described pathway can also be implemented in two populations, realizing DOL (Fig. 1B). In DOL, the first population only expresses E1, while the second only expresses E2. P is synthesized in the second population by using M produced and released from the first population. For this scenario, the corresponding rates of changes of intracellular and extracellular products are given by
| [4] |
| [5] |
| [6] |
| [7] |
where υi (i = 1, 2) is the steady-state cell volume of each DOL population.
Modeling Cell Growth.
We assume all populations follow logistic growth and cell size is constant such that cell volume is proportional to total biomass (Eqs. 8–10). Thus, we model SC cell volume using a dimensionless logistic equation:
| [8] |
where is the turnover rate constant of the population, μ is the growth rate constant of the population, and is the carrying capacity. We also assume that μ is affected by the potential burden of enzyme expression and metabolite growth effects.
In DOL, we further assume that the populations consume different resources and do not compete. If so, each population will have its own carrying capacity. Therefore, the DOL growth equations can be simplified to
| [9] |
| [10] |
where , , and (i = 1, 2) are the turnover rate constant, the specific growth rate, and the carrying capacity of the ith population. This assumption allows us to establish a simple model to ensure coexistence of the two populations. It is directly applicable when different members of a community have nonoverlapping metabolism (36–39). In general, the coexistence can be achieved by other mechanisms such as mutualism (22–24). Regardless of the mechanism, our results (discussed below) remain the same.
Growth Rates Due to Metabolic Burden and Additional Growth Effects.
Expression of heterologous enzymes can negatively affect maximum growth rates in microbial hosts (40–43). This can result from funneling resources away from cell growth toward expression and maintenance of the enzymes or the energetic constraints of the pathway itself (i.e., the pathway is endergonic) (16, 44, 45). We model this metabolic burden of enzyme expression using decreasing Hill functions similar to previous studies (40, 46) (Eqs. 11–13). Again, this assumption does not change our results (discussed below). In the dimensionless SC model, the cell growth rate, influenced by E1 and E2, is given by
| [11] |
where G represents additional intermediate growth effects such as toxic byproducts or crucial metabolites on the SC population; represents the total metabolic burden of expressing both enzymes, where β is the metabolic burden per unit of E1 (henceforth called relative burden of E1), γ is the metabolic burden per unit of E2 (henceforth called relative burden of E2), and n is the Hill coefficient. G and are multipliers of and take values between 0 and 1. In DOL, the total metabolic burden experienced by the SC population is split between the two DOL populations:
| [12] |
| [13] |
where G1 and G2 represent growth effects from M and/or P on each DOL population; and represent the burden of expressing each enzyme. Similar to the SC model, and are multipliers of , and and are multipliers of , all of which take values between 0 and 1.
Results
Deriving a Criterion of DOL.
The dynamics of each configuration can be described using simple kinetic models, each consisting of coupled ordinary differential equations (Eqs. 1–3 for SC; Eqs. 4–7 for DOL). We solve these equations to obtain the steady-state concentrations of the total P for SC and DOL respectively:
| [14] |
| [15] |
We consider DOL to be favored if it leads to higher total product yield, or . Given Eqs. 14 and 15, this inequality can be alternatively represented by (Fig. 1C)
| [16] |
where and reflect the inefficiency of DOL due to transport of M and is the geometric mean of the steady-state cell density in DOL (see SI Appendix, section 2.3 for derivation). The left-hand side of Eq. 16 is approximately the ratio of the mean DOL density to the SC cell density, which represents the net gain in biomass by utilizing DOL. Meanwhile, the right-hand side represents the reduced per-cell productivity of DOL. Thus, Eq. 16 represents a criterion of DOL: For DOL to outperform a single population its gain in total biomass must overcome its pathway inefficiency. This general form of the criterion is independent of downstream assumptions associated with modeling growth such as separate carrying capacities and burden formulation. If and , DOL does not reduce efficiency, and maximizing product yield is the same as maximizing biomass.
If the transport of M is much faster than its turnover (, we have . If we also assume that the populations and enzymes are approximately identical (, , , , and ), Eq. 16 simplifies to
| [17] |
Eq. 17 suggests that the metabolic burden caused by each enzyme and host growth parameters determine if DOL is favored. In comparison, kinetic parameters do not significantly affect which strategy performs better (SI Appendix, Fig. S1). Higher burden, due to increasing enzyme expression level (e) or increasing burden per unit amount of enzyme , favors DOL. In contrast, increasing maximum growth rate or decreasing population turnover allows the population to support higher burden, favoring SC. That is, DOL is favored when the pathway burden overcomes both the host’s resilience to burden and the inefficiency of DOL. Moreover, the extent by which one strategy outperforms the other varies with these parameters: For example, SC performs increasingly better as the burden decreases (Fig. 1D). By contrast, at high burden DOL yields higher biomass that ultimately outweighs its pathway inefficiency because not all cells perform all traits, thus reducing the burden per population.
Generalizing the Criterion for Alternative Pathway Mechanisms and Architectures.
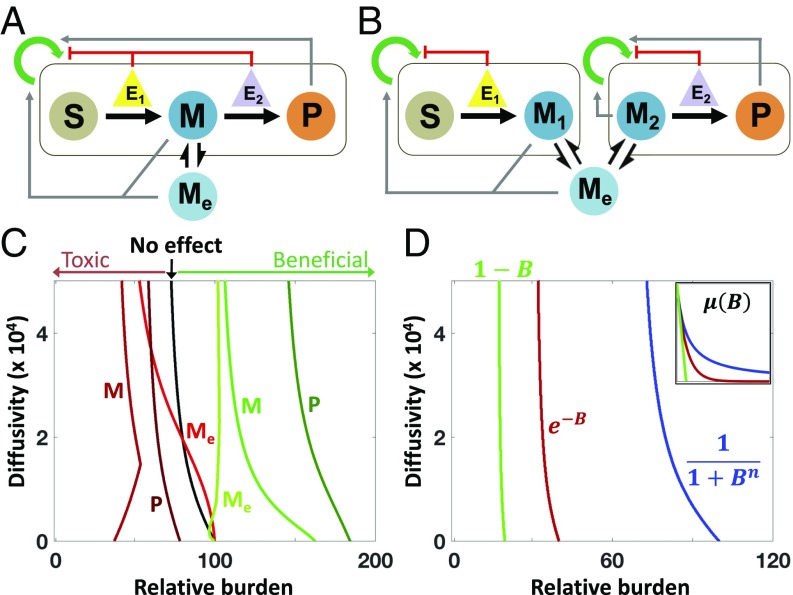
Our criterion implicitly accounts for diverse effects on growth by intermediates, products, and enzymes. For example, one or several metabolites could promote or suppress population growth (Fig. 2 A and B), which has been shown experimentally (47–49). Alternatively, burden of enzyme expression could follow a different mathematical form, or the pathway could generate beneficial side-products (50–52) (SI Appendix, section 3.4.1).
Fig. 2.
The impact of growth effects of metabolites and enzymes. (A) SC architecture with growth effects: Metabolites can promote or inhibit growth of the population. (B) DOL architecture with growth effects: Metabolites can promote or inhibit growth of one or both populations. (C) The analytical border separating SC- and DOL-favored parametric spaces shifts with different product growth effects. Beneficial metabolites reduce the effective burden experienced by the populations, increasing the parameter space where SC outperforms DOL (border shifts right). Toxic metabolites increase the effective burden experienced by the populations, increasing the parameter space where DOL outperforms SC (border shifts left). The mathematical expressions of each metabolite growth effect are given by SI Appendix, Eqs. S3.7–S3.12. At low diffusivity, the shapes of the borders for Toxic M and Beneficial Me change such that at low burden increasing diffusivity favors SC. In this range of parameters, increasing diffusivity improves SC cell growth (reducing M in the former and increasing Me in the latter), outweighing the loss in efficiency that would otherwise favor DOL. Additionally, at low diffusivity, a portion of the border for toxic Me is on the right side of the base because in this region toxic Me is more impactful on DOL than SC; however, DOL is still more favored overall in this scenario. (D) The border separating SC- and DOL-favored parametric spaces shifts with different mathematical representations of metabolic burden. B represents the total metabolic burden of enzyme expression, and each mathematical form determines the impact of the burden on growth. Changing the mathematical representation of burden does not change the form of the criterion. Rather, the magnitude of the burden determines the parametric spaces where each design strategy is favored. Higher burden shifts the border to the left, favoring DOL. (D, Inset) Growth rate as a function of relative burden for each mathematical representation of burden. In this example, parameters are chosen such that Hill-type burden reduces growth the least and linear burden reduces growth the most.
Growth effects act through modulation of , , and in Eq. 3 and therefore do not change the form of the criterion. Instead, they affect how the boundary shifts in a specific parametric space (Fig. 2 C and D and SI Appendix, Fig. S3). If the intermediate or product promotes the growth of the host(s), SC becomes favored for a broader range of parameter values; otherwise, DOL is favored for a broader range of parameters (Fig. 2C; see SI Appendix, Eqs. S3.7–S3.12 for corresponding metabolite growth effect expressions). Similarly, DOL is favored if the pathway imposes a greater burden on the host(s) (Fig. 2D): Here, the linear dependence and exponential dependence are assumed to cause more growth reduction than the Hill dependence, but ultimately the expression for burden does not change the form of the criterion (see SI Appendix, section 3.1.1 for burden expressions). Additional kinetic interactions also do not change the general form of the criterion (SI Appendix, section 3.4). For example, introducing intracellular metabolite turnover into the model only increases the complexity of θI (SI Appendix, section 3.4.5).
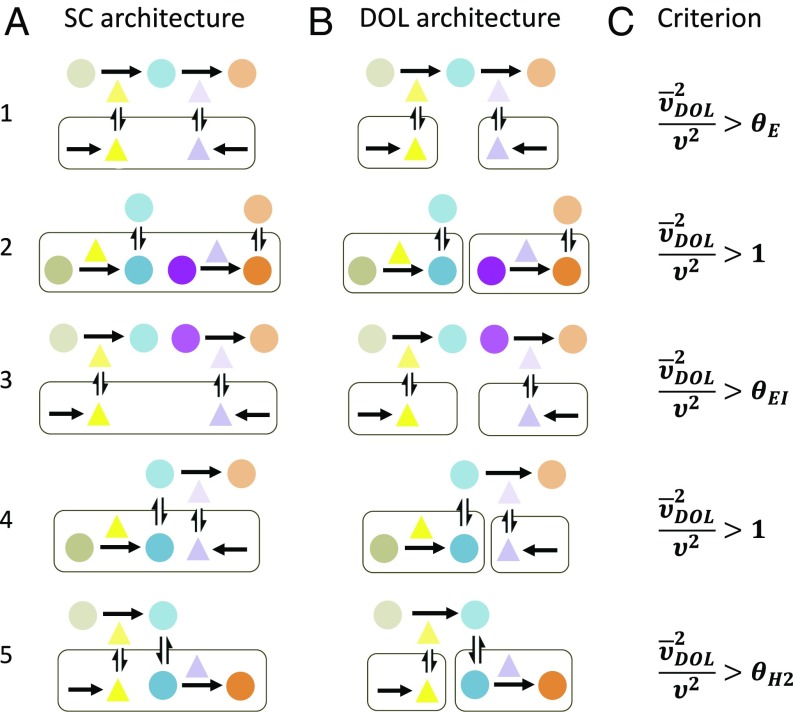
The basic form of the criterion is maintained for common pathway architectures (Fig. 3; see SI Appendix, section 4.1 for details on model formulations and derivations). The first architecture, an extracellular pathway, reflects processes such as synthesis of exoenzymes that break down complex compounds for metabolism (53, 54). The next two architectures represent two cases of independent pathways—one inside the cell and one outside the cell—and are analogous to metabolic specialization (55). Cross-feeding is also an example of intracellular independent pathways (22–24) since, according to our results, incorporating additional metabolite transport and growth effects would not change the form of the criterion. The last two architectures represent hybrid intracellular–extracellular pathways, where one step happens inside the cell and the other step happens in the extracellular space. The first hybrid architecture can be found in biosynthesis of exopolysaccharides for biofilm formation, where the polysaccharide is produced inside the cell before undergoing extracellular enzymatic modifications (56). The final architecture accounts for metabolic pathways involved in biofuel biosynthesis, which comprises two core steps: first, the digestion of biomass by extracellular enzymes and, second, the conversion of the resulting simplified sugars into biofuels (29, 30). The same criterion is also applicable for pathways longer than two steps (SI Appendix, section 5).
Fig. 3.
The criterion is applicable to different configurations of DOL. (A) Different SC architectures. (1) An extracellular pathway: Extracellular intermediate is converted to final product by two extracellular enzymes, both of which are synthesized by one population. (2) Two independent intracellular pathways: One population contains two pathways, each producing a different product. (3) Two independent extracellular pathways: One population synthesizes both extracellular enzymes catalyzing two separate pathways. (4) Hybrid pathway 1: Intermediate is produced within the cell and is converted to final product extracellularly by enzyme secreted out of the same cell. (5) Hybrid pathway 2: Intermediate is produced extracellularly by enzyme secreted from the cell and is converted to final product within the cell. (B) The corresponding DOL architectures. (1) Each population synthesizes one enzyme. (2) Each population contains one pathway. (3) Each population synthesizes one enzyme. (4) Hybrid pathway 1: The first population produces the intermediate, and the second population secretes the enzyme. (5) Hybrid pathway 2: The first population secretes the enzyme, and the second population converts M into P. (C) The design inequalities dictating when DOL is favored over SC are similar or identical in form for various pathway architectures that can utilize DOL. Expressions of the correction terms can be found in SI Appendix. Each inequality is derived using the same assumptions as the base models.
Despite the different pathway architectures, the corresponding criteria are almost identical, only varying in their expressions for . Specifically, the different mathematical forms of the criteria reflect the pros and cons of DOL in each pathway architecture. Regardless, fundamental prediction of these criteria is qualitatively the same: DOL is favored if it improves overall cell density sufficiently to overcome the inefficiency DOL causes in transport and resource sharing. Notably, , which reflects DOL’s inefficiency in the base model, is not present in these criteria because both SC and DOL require metabolite and/or enzyme transport. As a result, we also generalize from the criteria that it is easier for DOL to outperform SC if all or part of the entire pathway occurs in the extracellular space.
Discussion
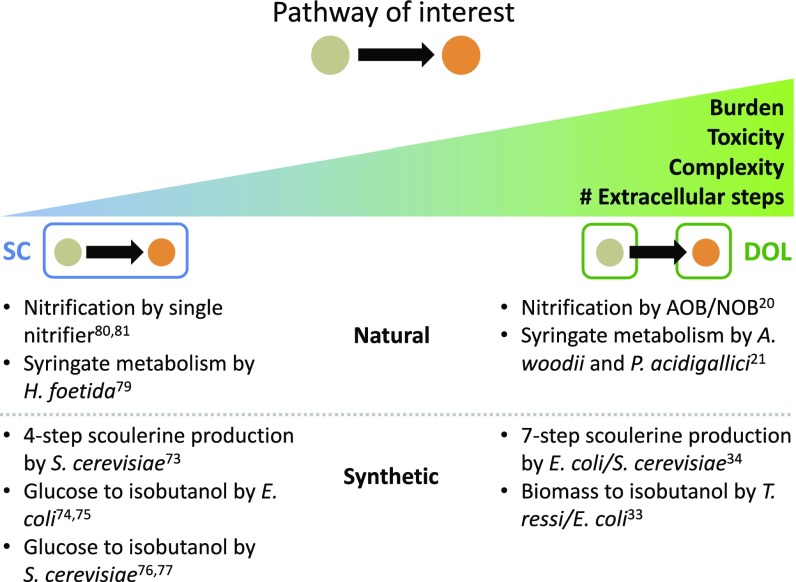
DOL has been hypothesized as an effective design strategy for engineering sophisticated functionality (57–60). Indeed, there are several synthetic systems featuring DOL between members of each community. However, despite numerous examples the conditions favoring DOL have not yet been rigorously established. This is in part because DOL is seemingly implemented ad hoc, and most DOL examples lack SC versions of the same pathway with which to compare. From our analysis we derive a general criterion that dictates the conditions when DOL outperforms SC and establishes design principles for engineering metabolic pathways via DOL. Unlike previous studies (46, 55, 61), our results are applicable to many different pathway architectures and configurations (as the case-specific criteria are derivatives of the general criterion) and can determine which design strategy to use given pathway parameters. It also provides a concrete basis, namely maximization of the overall productivity, to interpret and guide applications of DOL (Fig. 4). Our results indicate that DOL is favored when the pathway reduces overall cell fitness such as in cases of high metabolic burden or toxicity. This can result from an increasing complexity of the overall pathway, highly burdensome enzymes (requiring lots of resources to express or function), or generation of toxic intermediates or products. Additionally, DOL will likely outperform SC if all or part of the pathway occurs outside the cells because such pathways are transport-limited in both configurations (thus DOL is no longer as inefficient relative to SC).
Fig. 4.
General design guidelines derived from the criteria. Given a pathway of interest, high enzyme burden, toxicity of intermediates/products, pathway complexity, or number of extracellular steps will promote DOL over SC. Indeed, many natural and synthetic examples in literature follow this trend.
Indeed, these conclusions are reflected in the implementation of several engineered pathways. Pathways implemented in DOL often involve high complexity, comprising several steps, each catalyzed by a different enzyme (25, 26, 28). If a pathway has been engineered both in SC and in DOL, the DOL implementation typically contains more steps that require additional enzymes to express (this could be in part due to less effort in optimizing DOL implementations). For example, an engineered Escherichia coli–Saccharomyces cerevisiae coculture produces scoulerine from dopamine in a seven-enzyme pathway (27), whereas an S. cerevisiae monoculture only uses four enzymes starting from the intermediate norlaudanosoline (62). Similarly, a Trichoderma ressi–E. coli coculture converts biomass pretreated with ammonia fiber expansion into isobutanol (26). In contrast, the same product can be produced with fewer steps from glucose in E. coli and S. cerevisiae monocultures (63, 64). In these cases, a longer pathway is likely to generate a substantial burden on a single population, thus favoring a DOL implementation. Additionally, many examples of DOL involve intermediates, products, or byproducts that are toxic to at least one of the populations (25, 26, 29, 31), consistent with our criterion (Fig. 2C). Finally, several pathways implemented using DOL are partially or completely catalyzed in the extracellular environment where DOL’s pathway inefficiency in comparison with SC is less pronounced (26, 29).
For pathways in nature, natural selection does not directly constrain the pathway yield. In cases where the yield promotes host growth, however, maximizing the productivity of such pathways would have an adaptive value (49–52). Therefore, we can apply our criteria to interpret these particular pathways under the basis of optimizing metabolic productivity. For example, both syringate metabolism and nitrification generate energy for the cells and can exist in either SC or DOL configurations (20, 50, 65–68). Given the analogous overall architectures of the pathways in either configuration, what constrained these different implementations remains an open question. In both cases, the SC populations were predicted to have a lower growth rate but higher yield based on kinetic theory of optimal pathway length (51). Similarly, our criteria predict the SC population would have a lower growth rate due to the higher metabolic burden of expressing more enzymes. This is consistent with experimental results—the SC cases were found to grow in biofilms, where a slower-growing organism would have a higher fitness than the fast-growing one due to a biofilm’s low substrate and biomass mixing (51, 65, 67–69). Others propose that diffusion barriers and substrate concentration gradients in biofilms could create niches where SC outcompetes DOL (68, 70). Incorporating biofilm transport limitations into our criterion would also favor SC by increasing in Eq. 16. Moreover, in nitrification the SC nitrifiers lack enzymes for assimilatory nitrite reduction, whereas nitrite-oxidizing bacteria in DOL nitrification express assimilatory nitrite reductases (67, 68, 71, 72). Expressing fewer enzymes could reduce the metabolic load on SC, increasing its relative fitness in ammonia-containing environments where those enzymes are not necessary.
Supplementary Material
Acknowledgments
We thank J. Bethke, T. Lawson, M. Lynch, D. Needs, and W. Shou for insightful comments and suggestions. This study was partially supported by US Army Research Office Grant W911NF-14-1-0490 (to D.K., S.B., and L.Y.), National Science Foundation Grant CBET-0953202 (to L.Y.), National Institutes of Health Grant 1R01-GM098642 (to L.Y.), and a David and Lucile Packard Fellowship (to L.Y.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1716888115/-/DCSupplemental.
References
- 1.Ajikumar PK, et al. Isoprenoid pathway optimization for Taxol precursor overproduction in Escherichia coli. Science. 2010;330:70–74. doi: 10.1126/science.1191652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Berry A, Dodge TC, Pepsin M, Weyler W. Application of metabolic engineering to improve both the production and use of biotech indigo. J Ind Microbiol Biotechnol. 2002;28:127–133. doi: 10.1038/sj.jim.7000228. [DOI] [PubMed] [Google Scholar]
- 3.Paddon CJ, et al. High-level semi-synthetic production of the potent antimalarial artemisinin. Nature. 2013;496:528–532. doi: 10.1038/nature12051. [DOI] [PubMed] [Google Scholar]
- 4.Xia XX, et al. Native-sized recombinant spider silk protein produced in metabolically engineered Escherichia coli results in a strong fiber. Proc Natl Acad Sci USA. 2010;107:14059–14063. doi: 10.1073/pnas.1003366107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ye X, et al. Engineering the provitamin A (beta-carotene) biosynthetic pathway into (carotenoid-free) rice endosperm. Science. 2000;287:303–305. doi: 10.1126/science.287.5451.303. [DOI] [PubMed] [Google Scholar]
- 6.Mather WH, Hasty J, Tsimring LS, Williams RJ. Translational cross talk in gene networks. Biophys J. 2013;104:2564–2572. doi: 10.1016/j.bpj.2013.04.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mutalik VK, Qi L, Guimaraes JC, Lucks JB, Arkin AP. Rationally designed families of orthogonal RNA regulators of translation. Nat Chem Biol. 2012;8:447–454. doi: 10.1038/nchembio.919. [DOI] [PubMed] [Google Scholar]
- 8.Rhodius VA, et al. Design of orthogonal genetic switches based on a crosstalk map of σs, anti-σs, and promoters. Mol Syst Biol. 2013;9:702. doi: 10.1038/msb.2013.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhang C, Tsoi R, You L. Addressing biological uncertainties in engineering gene circuits. Integr Biol. 2016;8:456–464. doi: 10.1039/c5ib00275c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hottes AK, et al. Bacterial adaptation through loss of function. PLoS Genet. 2013;9:e1003617. doi: 10.1371/journal.pgen.1003617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Koskiniemi S, Sun S, Berg OG, Andersson DI. Selection-driven gene loss in bacteria. PLoS Genet. 2012;8:e1002787. doi: 10.1371/journal.pgen.1002787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Arkin AP, Fletcher DA. Fast, cheap and somewhat in control. Genome Biol. 2006;7:114. doi: 10.1186/gb-2006-7-8-114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.You L, Cox RS, 3rd, Weiss R, Arnold FH. Programmed population control by cell-cell communication and regulated killing. Nature. 2004;428:868–871. doi: 10.1038/nature02491. [DOI] [PubMed] [Google Scholar]
- 14.Karim AS, Curran KA, Alper HS. Characterization of plasmid burden and copy number in Saccharomyces cerevisiae for optimization of metabolic engineering applications. FEMS Yeast Res. 2013;13:107–116. doi: 10.1111/1567-1364.12016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Heyland J, Blank LM, Schmid A. Quantification of metabolic limitations during recombinant protein production in Escherichia coli. J Biotechnol. 2011;155:178–184. doi: 10.1016/j.jbiotec.2011.06.016. [DOI] [PubMed] [Google Scholar]
- 16.Wu G, et al. Metabolic burden: Cornerstones in synthetic biology and metabolic engineering applications. Trends Biotechnol. 2016;34:652–664. doi: 10.1016/j.tibtech.2016.02.010. [DOI] [PubMed] [Google Scholar]
- 17.Hoffmann F, Rinas U. On-line estimation of the metabolic burden resulting from the synthesis of plasmid-encoded and heat-shock proteins by monitoring respiratory energy generation. Biotechnol Bioeng. 2001;76:333–340. doi: 10.1002/bit.10098. [DOI] [PubMed] [Google Scholar]
- 18.West SA, Cooper GA. Division of labour in microorganisms: An evolutionary perspective. Nat Rev Microbiol. 2016;14:716–723. doi: 10.1038/nrmicro.2016.111. [DOI] [PubMed] [Google Scholar]
- 19.van Gestel J, Vlamakis H, Kolter R. Division of labor in biofilms: The ecology of cell differentiation. Microbiol Spectr. 2015;3:MB-0002-2014. doi: 10.1128/microbiolspec.MB-0002-2014. [DOI] [PubMed] [Google Scholar]
- 20.Bock E, Wagner M. Oxidation of inorganic nitrogen compounds as an energy source. In: Dworkin M, Falkow S, Rosenberg E, Schleifer K-H, Stackebrandt E, editors. The Prokaryotes: Volume 2: Ecophysiology and Biochemistry. Springer; New York: 2006. pp. 457–495. [Google Scholar]
- 21.Schink B, Pfennig N. Fermentation of trihydroxybenzenes by Pelobacter-acidigallici gen-nov sp-nov a new strictly anaerobic, non-sporeforming bacterium. Arch Microbiol. 1982;133:195–201. [Google Scholar]
- 22.Morris BE, Henneberger R, Huber H, Moissl-Eichinger C. Microbial syntrophy: Interaction for the common good. FEMS Microbiol Rev. 2013;37:384–406. doi: 10.1111/1574-6976.12019. [DOI] [PubMed] [Google Scholar]
- 23.Shou W, Ram S, Vilar JM. Synthetic cooperation in engineered yeast populations. Proc Natl Acad Sci USA. 2007;104:1877–1882. doi: 10.1073/pnas.0610575104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wintermute EH, Silver PA. Emergent cooperation in microbial metabolism. Mol Syst Biol. 2010;6:407. doi: 10.1038/msb.2010.66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhou K, Qiao K, Edgar S, Stephanopoulos G. Distributing a metabolic pathway among a microbial consortium enhances production of natural products. Nat Biotechnol. 2015;33:377–383. doi: 10.1038/nbt.3095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Minty JJ, et al. Design and characterization of synthetic fungal-bacterial consortia for direct production of isobutanol from cellulosic biomass. Proc Natl Acad Sci USA. 2013;110:14592–14597. doi: 10.1073/pnas.1218447110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Minami H, et al. Microbial production of plant benzylisoquinoline alkaloids. Proc Natl Acad Sci USA. 2008;105:7393–7398. doi: 10.1073/pnas.0802981105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Koizumi S, Endo T, Tabata K, Ozaki A. Large-scale production of UDP-galactose and globotriose by coupling metabolically engineered bacteria. Nat Biotechnol. 1998;16:847–850. doi: 10.1038/nbt0998-847. [DOI] [PubMed] [Google Scholar]
- 29.Zuroff TR, Xiques SB, Curtis WR. Consortia-mediated bioprocessing of cellulose to ethanol with a symbiotic Clostridium phytofermentans/yeast co-culture. Biotechnol Biofuels. 2013;6:59. doi: 10.1186/1754-6834-6-59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lynd LR, Weimer PJ, van Zyl WH, Pretorius IS. Microbial cellulose utilization: Fundamentals and biotechnology. Microbiol Mol Biol Rev. 2002;66:506–577. doi: 10.1128/MMBR.66.3.506-577.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chen C, Ren N, Wang A, Liu L, Lee DJ. Functional consortium for denitrifying sulfide removal process. Appl Microbiol Biotechnol. 2010;86:353–358. doi: 10.1007/s00253-009-2367-z. [DOI] [PubMed] [Google Scholar]
- 32.Chen Y, Lin CJ, Jones G, Fu S, Zhan H. Enhancing biodegradation of wastewater by microbial consortia with fractional factorial design. J Hazard Mater. 2009;171:948–953. doi: 10.1016/j.jhazmat.2009.06.100. [DOI] [PubMed] [Google Scholar]
- 33.Tamsir A, Tabor JJ, Voigt CA. Robust multicellular computing using genetically encoded NOR gates and chemical ‘wires’. Nature. 2011;469:212–215. doi: 10.1038/nature09565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Regot S, et al. Distributed biological computation with multicellular engineered networks. Nature. 2011;469:207–211. doi: 10.1038/nature09679. [DOI] [PubMed] [Google Scholar]
- 35.Dueber JE, et al. Synthetic protein scaffolds provide modular control over metabolic flux. Nat Biotechnol. 2009;27:753–759. doi: 10.1038/nbt.1557. [DOI] [PubMed] [Google Scholar]
- 36.Rainey PB, Travisano M. Adaptive radiation in a heterogeneous environment. Nature. 1998;394:69–72. doi: 10.1038/27900. [DOI] [PubMed] [Google Scholar]
- 37.Baran R, et al. Exometabolite niche partitioning among sympatric soil bacteria. Nat Commun. 2015;6:8289. doi: 10.1038/ncomms9289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Eiteman MA, Lee SA, Altman E. A co-fermentation strategy to consume sugar mixtures effectively. J Biol Eng. 2008;2:3. doi: 10.1186/1754-1611-2-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Unrean P, Srienc F. Continuous production of ethanol from hexoses and pentoses using immobilized mixed cultures of Escherichia coli strains. J Biotechnol. 2010;150:215–223. doi: 10.1016/j.jbiotec.2010.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tan C, Marguet P, You L. Emergent bistability by a growth-modulating positive feedback circuit. Nat Chem Biol. 2009;5:842–848. doi: 10.1038/nchembio.218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lee ME, Aswani A, Han AS, Tomlin CJ, Dueber JE. Expression-level optimization of a multi-enzyme pathway in the absence of a high-throughput assay. Nucleic Acids Res. 2013;41:10668–10678. doi: 10.1093/nar/gkt809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Glick BR. Metabolic load and heterologous gene expression. Biotechnol Adv. 1995;13:247–261. doi: 10.1016/0734-9750(95)00004-a. [DOI] [PubMed] [Google Scholar]
- 43.Klumpp S, Zhang Z, Hwa T. Growth rate-dependent global effects on gene expression in bacteria. Cell. 2009;139:1366–1375. doi: 10.1016/j.cell.2009.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Dekel E, Alon U. Optimality and evolutionary tuning of the expression level of a protein. Nature. 2005;436:588–592. doi: 10.1038/nature03842. [DOI] [PubMed] [Google Scholar]
- 45.Rosano GL, Ceccarelli EA. Recombinant protein expression in Escherichia coli: Advances and challenges. Front Microbiol. 2014;5:172. doi: 10.3389/fmicb.2014.00172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Harvey E, Heys J, Gedeon T. Quantifying the effects of the division of labor in metabolic pathways. J Theor Biol. 2014;360:222–242. doi: 10.1016/j.jtbi.2014.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Martin VJ, Pitera DJ, Withers ST, Newman JD, Keasling JD. Engineering a mevalonate pathway in Escherichia coli for production of terpenoids. Nat Biotechnol. 2003;21:796–802. doi: 10.1038/nbt833. [DOI] [PubMed] [Google Scholar]
- 48.Roe AJ, O’Byrne C, McLaggan D, Booth IR. Inhibition of Escherichia coli growth by acetic acid: A problem with methionine biosynthesis and homocysteine toxicity. Microbiology. 2002;148:2215–2222. doi: 10.1099/00221287-148-7-2215. [DOI] [PubMed] [Google Scholar]
- 49.Lewis NE, Nagarajan H, Palsson BO. Constraining the metabolic genotype-phenotype relationship using a phylogeny of in silico methods. Nat Rev Microbiol. 2012;10:291–305. doi: 10.1038/nrmicro2737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kreft JU, Schink B. Demethylation and degradation of phenylmethylethers by the sulfide-methylating homoacetogenic bacterium strain Tmbs-4. Arch Microbiol. 1993;159:308–315. [Google Scholar]
- 51.Costa E, Pérez J, Kreft JU. Why is metabolic labour divided in nitrification? Trends Microbiol. 2006;14:213–219. doi: 10.1016/j.tim.2006.03.006. [DOI] [PubMed] [Google Scholar]
- 52.Akram M. Citric acid cycle and role of its intermediates in metabolism. Cell Biochem Biophys. 2014;68:475–478. doi: 10.1007/s12013-013-9750-1. [DOI] [PubMed] [Google Scholar]
- 53.Guevara C, Zambrano MM. Sugarcane cellulose utilization by a defined microbial consortium. FEMS Microbiol Lett. 2006;255:52–58. doi: 10.1111/j.1574-6968.2005.00050.x. [DOI] [PubMed] [Google Scholar]
- 54.Wu M, Chen L, Tian Y, Ding Y, Dick WA. Degradation of polycyclic aromatic hydrocarbons by microbial consortia enriched from three soils using two different culture media. Environ Pollut. 2013;178:152–158. doi: 10.1016/j.envpol.2013.03.004. [DOI] [PubMed] [Google Scholar]
- 55.Rueffler C, Hermisson J, Wagner GP. Evolution of functional specialization and division of labor. Proc Natl Acad Sci USA. 2012;109:E326–E335. doi: 10.1073/pnas.1110521109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Whitfield GB, Marmont LS, Howell PL. Enzymatic modifications of exopolysaccharides enhance bacterial persistence. Front Microbiol. 2015;6:471. doi: 10.3389/fmicb.2015.00471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Brenner K, You L, Arnold FH. Engineering microbial consortia: A new frontier in synthetic biology. Trends Biotechnol. 2008;26:483–489. doi: 10.1016/j.tibtech.2008.05.004. [DOI] [PubMed] [Google Scholar]
- 58.Li B, You L. Synthetic biology: Division of logic labour. Nature. 2011;469:171–172. doi: 10.1038/469171a. [DOI] [PubMed] [Google Scholar]
- 59.Bacchus W, Fussenegger M. Engineering of synthetic intercellular communication systems. Metab Eng. 2013;16:33–41. doi: 10.1016/j.ymben.2012.12.001. [DOI] [PubMed] [Google Scholar]
- 60.Shong J, Jimenez Diaz MR, Collins CH. Towards synthetic microbial consortia for bioprocessing. Curr Opin Biotechnol. 2012;23:798–802. doi: 10.1016/j.copbio.2012.02.001. [DOI] [PubMed] [Google Scholar]
- 61.Stump SM, Klausmeier CA. Competition and coexistence between a syntrophic consortium and a metabolic generalist, and its effect on productivity. J Theor Biol. 2016;404:348–360. doi: 10.1016/j.jtbi.2016.06.019. [DOI] [PubMed] [Google Scholar]
- 62.Hawkins KM, Smolke CD. Production of benzylisoquinoline alkaloids in Saccharomyces cerevisiae. Nat Chem Biol. 2008;4:564–573. doi: 10.1038/nchembio.105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Atsumi S, Hanai T, Liao JC. Non-fermentative pathways for synthesis of branched-chain higher alcohols as biofuels. Nature. 2008;451:86–89. doi: 10.1038/nature06450. [DOI] [PubMed] [Google Scholar]
- 64.Avalos JL, Fink GR, Stephanopoulos G. Compartmentalization of metabolic pathways in yeast mitochondria improves the production of branched-chain alcohols. Nat Biotechnol. 2013;31:335–341. doi: 10.1038/nbt.2509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bak F, Finster K, Rothfuss F. Formation of dimethylsulfide and methanethiol from methoxylated aromatic-compounds and inorganic sulfide by newly isolated anaerobic-bacteria. Arch Microbiol. 1992;157:529–534. [Google Scholar]
- 66.Liesack W, Bak F, Kreft JU, Stackebrandt E. Holophaga foetida gen. nov., sp. nov., a new, homoacetogenic bacterium degrading methoxylated aromatic compounds. Arch Microbiol. 1994;162:85–90. doi: 10.1007/BF00264378. [DOI] [PubMed] [Google Scholar]
- 67.van Kessel MA, et al. Complete nitrification by a single microorganism. Nature. 2015;528:555–559. doi: 10.1038/nature16459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Daims H, et al. Complete nitrification by Nitrospira bacteria. Nature. 2015;528:504–509. doi: 10.1038/nature16461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kreft JU. Biofilms promote altruism. Microbiology. 2004;150:2751–2760. doi: 10.1099/mic.0.26829-0. [DOI] [PubMed] [Google Scholar]
- 70.Maixner F, et al. Nitrite concentration influences the population structure of Nitrospira-like bacteria. Environ Microbiol. 2006;8:1487–1495. doi: 10.1111/j.1462-2920.2006.01033.x. [DOI] [PubMed] [Google Scholar]
- 71.Koch H, et al. Expanded metabolic versatility of ubiquitous nitrite-oxidizing bacteria from the genus Nitrospira. Proc Natl Acad Sci USA. 2015;112:11371–11376. doi: 10.1073/pnas.1506533112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Lücker S, et al. A Nitrospira metagenome illuminates the physiology and evolution of globally important nitrite-oxidizing bacteria. Proc Natl Acad Sci USA. 2010;107:13479–13484. doi: 10.1073/pnas.1003860107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.