Significance
Dengue hemorrhagic fever poses a major problem for public health officials in Thailand. The number and location of cases vary dramatically from year to year, which makes planning prevention and treatment activities before the dengue season difficult. We develop statistical models with biologically motivated covariates to make forecasts for each Thai province every year. The forecasts from our models have less error than those of a baseline model on out-of-sample data. Furthermore, the forecasts from a model based on incidence occurring before the start of the rainy season successfully order provinces by outbreak risk. These early, accurate forecasts of dengue hemorrhagic fever incidence could help public health officials determine where to allocate their resources in the future.
Keywords: dengue, forecasting, infectious disease, statistics
Abstract
Dengue hemorrhagic fever (DHF), a severe manifestation of dengue viral infection that can cause severe bleeding, organ impairment, and even death, affects between 15,000 and 105,000 people each year in Thailand. While all Thai provinces experience at least one DHF case most years, the distribution of cases shifts regionally from year to year. Accurately forecasting where DHF outbreaks occur before the dengue season could help public health officials prioritize public health activities. We develop statistical models that use biologically plausible covariates, observed by April each year, to forecast the cumulative DHF incidence for the remainder of the year. We perform cross-validation during the training phase (2000–2009) to select the covariates for these models. A parsimonious model based on preseason incidence outperforms the 10-y median for 65% of province-level annual forecasts, reduces the mean absolute error by 19%, and successfully forecasts outbreaks (area under the receiver operating characteristic curve = 0.84) over the testing period (2010–2014). We find that functions of past incidence contribute most strongly to model performance, whereas the importance of environmental covariates varies regionally. This work illustrates that accurate forecasts of dengue risk are possible in a policy-relevant timeframe.
Dengue, a mosquito-borne virus prevalent throughout the tropics and subtropics, infects an estimated 390 million people every year (1). While the majority of infections are mild or asymptomatic, the more severe forms of dengue infection—dengue shock syndrome (DSS) and dengue hemorrhagic fever (DHF)—can result in organ failure or death (2). The number of symptomatic dengue infections has doubled every 10 y since 1990, in contrast to the declining incidence of most other communicable diseases (3).
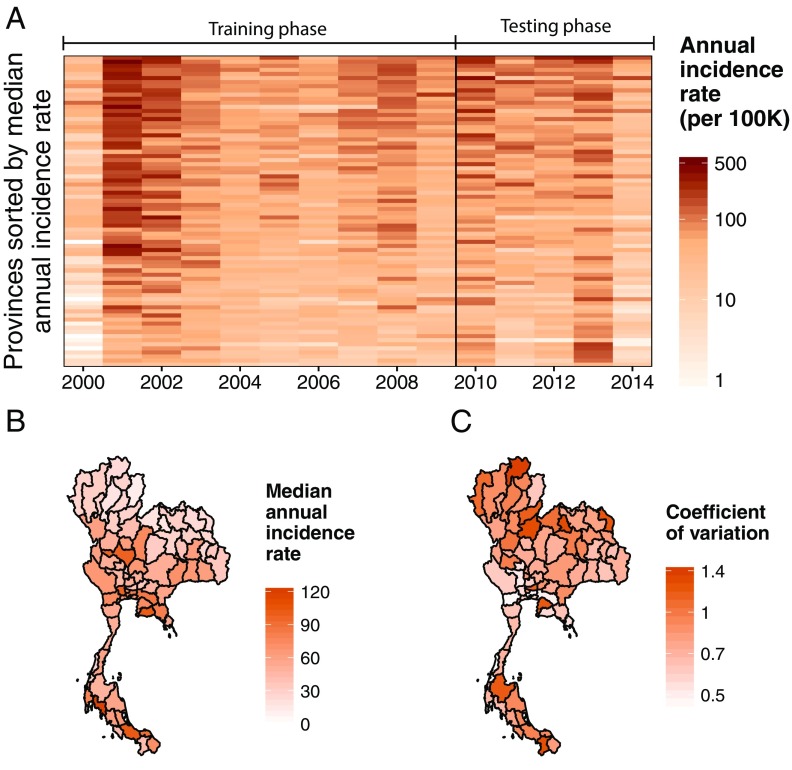
In Thailand, dengue infection is endemic, with substantial annual and geographic variation in incidence across its 76 provinces and 13 health regions (Fig. 1). Over the past 15 y, an average of 43,137 (range 14,952–106,320) DHF cases have been reported to the Thailand Ministry of Public Health (MOPH) each year. Within a typical year, incidence rates in different provinces can vary by an order of magnitude, with some provinces experiencing less than 10 DHF cases per 100,000 population and others over 100 per 100,000 population.
Fig. 1.
The temporal and spatial distribution of annual DHF incidence rates in Thailand. (A) The annual DHF incidence rate per 100,000 population for each Thai province and year used in this study. (B) The median annual DHF incidence rate per 100,000 population for each province from 2000 to 2014. (C) The coefficient of variation (SD divided by the mean) of the annual DHF incidence rate for each province.
Public health officials must determine where to allocate resources to manage the problems caused by dengue viral infection. A newly approved vaccine may be able to reduce the number of dengue infections if properly regimented (4). For those already infected, effective case management can reduce the case fatality rate of severe dengue (5). With sufficient advance notice, public health officials could implement prevention programs and conduct interventions in regions that have the highest epidemic risk. Effective long-term forecasts would provide more timely information to aid in prioritizing these public health activities.
Prior dengue forecasting efforts by members of our group and others have focused on short timescales (weeks or months) (6–10). These studies showed the importance of recent case counts and seasonality on the immediate trajectory of dengue incidence. In 2015, the National Oceanic and Atmospheric Administration (NOAA) and the Centers for Disease Control hosted a competition to make within-season forecasts for annual dengue incidence, epidemic peak, and peak height for San Juan, Puerto Rico, and Iquitos, Peru (dengueforecasting.noaa.gov). Groups that used methods relying solely on functions of incidence performed well relative to baseline forecasts (11, 12) and were among the top performers in the competition (13).
Whether an infectious disease spreads within a population depends on the transmission rate of the disease and the number of susceptible individuals (14, 15); thus, long-term forecasting models for DHF incidence may need to account for climatic factors that could affect transmission as well as population susceptibility. Climatic factors, such as temperature, rainfall, and humidity, may impact both the prevalence and the distribution of the dengue vector, the Aedes mosquito (16–18), as well as the transmission efficiency of dengue virus (1, 19, 20). During the low-dengue season, these climatic factors may be indicative of incidence in the next high-dengue season, perhaps due to their role in vector survival and larval development (21). Even in ideal conditions for disease transmission, there needs to be a sufficiently large susceptible population for a disease to spread. Dengue has complex immunological dynamics that make tracking the number of susceptible individuals within a population difficult. The vast majority of first dengue infections are asymptomatic, while second infections are more likely to result in severe outcomes, such as DHF and DSS (22, 23). Infection by any of its four serotypes may offer temporary immunity to the other serotypes and lifelong immunity to the contracted serotype (2, 24–26), although there is some evidence that repeat infections of the same serotype may occur (27, 28).
A useful forecasting model needs to make better predictions than a baseline model on out-of-sample observations (29). For decades, researchers have split their data into “training” and “testing” samples to separate the fitting and evaluation processes (30, 31). Cross-validation is a popular technique for estimating the expected prediction error; thus, minimizing the cross-validation error on the training sample might be expected to improve predictions over the testing sample. However, this can lead forecasters to select models that “overfit” on the training sample and therefore, do not perform well on the testing sample (32). Hence, it is prudent for researchers to also select a parsimonious model with more cross-validation error that might perform better on out-of-sample data (31, 32). In the testing phase, using a sensible baseline model as a comparison allows researchers to measure how much a forecasting model improves over a benchmark in an interpretable manner (33).
Using demographic, weather, and dengue data from 2000 to 2009, we selected two models using a cross-validated variable selection procedure to make probabilistic forecasts of the annual DHF incidence for 2010–2014. We chose to predict DHF cases, because reporting for this severe form of dengue is thought to be more consistent across time and space, while still being a primary indicator of the burden of disease (9). We compare the forecasts from these models with baseline forecasts derived from a province’s median DHF incidence rate over the past 10 y. We use the probabilistic distributions to estimate the outbreak risk for each province. We investigate features of our forecasting models, including regional variations in performance and the most informative covariates. In doing so, we show that producing accurate forecasts that add value for public health decision-makers is a viable endeavor.
Results
Models Selected for Forecasting.
We obtained data on DHF cases (from the MOPH), population (National Statistical Office of Thailand), and weather (NOAA) (9, 34–38). These data were summarized across timeframes ranging from 1 mo to 1 y to create 34 covariates for consideration by our model selection algorithm (Table 1 and Table S1). We calculated an additional covariate, “estimated relative susceptibility,” based on the assumption that an infected person will be protected against all dengue serotypes for a period of roughly 2 y (26). We made forecasts using the data available in April of each year, the month when the MOPH has historically finalized the incidence reports obtained from all provinces for the prior calendar year. Hence, all “annual” forecasts are for DHF incidence between April and December of the year that they are made. Across the 15 y used in this study, 87% of the DHF cases occurred between April and December of each year.
Table 1.
Justifications for types of covariates considered for inclusion before model selection
| Covariate type | Reason for inclusion |
| Incidence | Large dengue outbreaks may temporarily deplete the susceptible population (24–26); larger dengue seasons often start earlier (21) |
| Demographics | Higher population density may facilitate dengue transmission (39) |
| Humidity | Humidity may improve the survival rate of Aedes mosquito eggs (16, 21) |
| Rainfall | Rainfall is essential for Aedes mosquito breeding and may have a positive effect on dengue transmission (1, 17) |
| Temperature | Temperatures must be warm enough for Aedes mosquitoes to imbibe blood (18) but cool enough for optimal survival of eggs (16) |
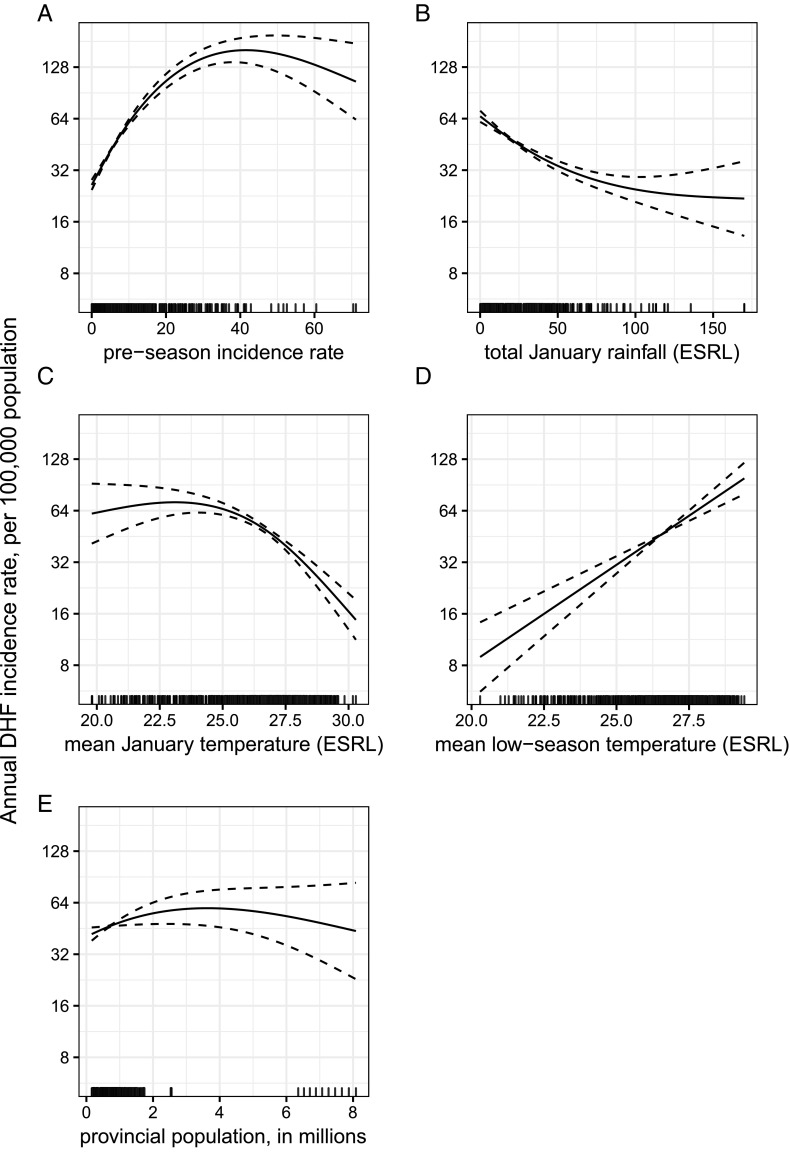
We used leave 1 y out cross-validation to predict the DHF incidence across the 760 province-years in the training phase (76 provinces for each year from 2000 to 2009). Of the 202 candidate models considered, the model with the smallest leave 1 y out cross-validated mean absolute error (CV MAE) included five covariates: preseason (January to March) incidence rate, total January rainfall, mean January temperature, mean temperature during the low-dengue season (November to March; henceforth “low season”), and population size (Fig. 2). To avoid overfitting on the training phase, we also chose the model with the fewest covariates within one SD of the minimum CV MAE (31). Using this procedure, we selected a model that included only preseason incidence. We refer to these models as the “weather, incidence, and population (WIP) model” and the “incidence-only model.”
Fig. 2.
The WIP model covariate fit curves. The solid lines represent the average association between each covariate in the WIP model and annual DHF incidence per 100,000 population during the training phase, fixing all other covariates at their mean. The dashed lines are the CIs of each association defined as two SEs above and below the mean association. (A–E) The covariates are arranged by performance in the Wald test from largest reduction in deviance (A) to smallest reduction in deviance (E).
Forecasting Performance in the Testing Phase.
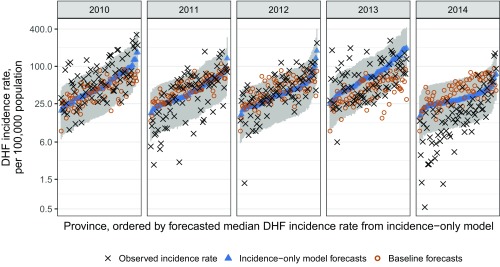
Across the 380 province-years in the testing phase (2010–2014), forecasts from the incidence-only model were more accurate than forecasts from the WIP model [relative mean absolute error (rMAE) = 93% (33)] and baseline forecasts derived from the 10-y median incidence rate (rMAE = 81%). The incidence-only model forecasts were closer to the observed DHF incidence than those of the WIP model in 217 of 380 (57%) province-years and better than baseline forecasts in 246 of 380 (65%) province-years (Table S2). In each year, the incidence-only model outperformed both the WIP model and the baseline forecasts in aggregate [i.e., the all-province mean absolute error (MAE) was lower and more forecasts were closer to the observed incidences] (Fig. 3 and Table S3). Across all testing-phase province-years, the 80% prediction interval from the incidence-only model covered 80% of the observed DHF incidences compared with 70% covered by the WIP 80% prediction interval.
Fig. 3.
Incidence-only model forecasts for each year of the testing phase compared with the baseline forecasts and the observed values. Forecasts for the annual DHF incidence rate per 100,000 population from the incidence-only model (blue triangles with gray 80% prediction intervals), baseline forecasts (red circles), and observed values (black x) for each province and year in the testing phase are shown.
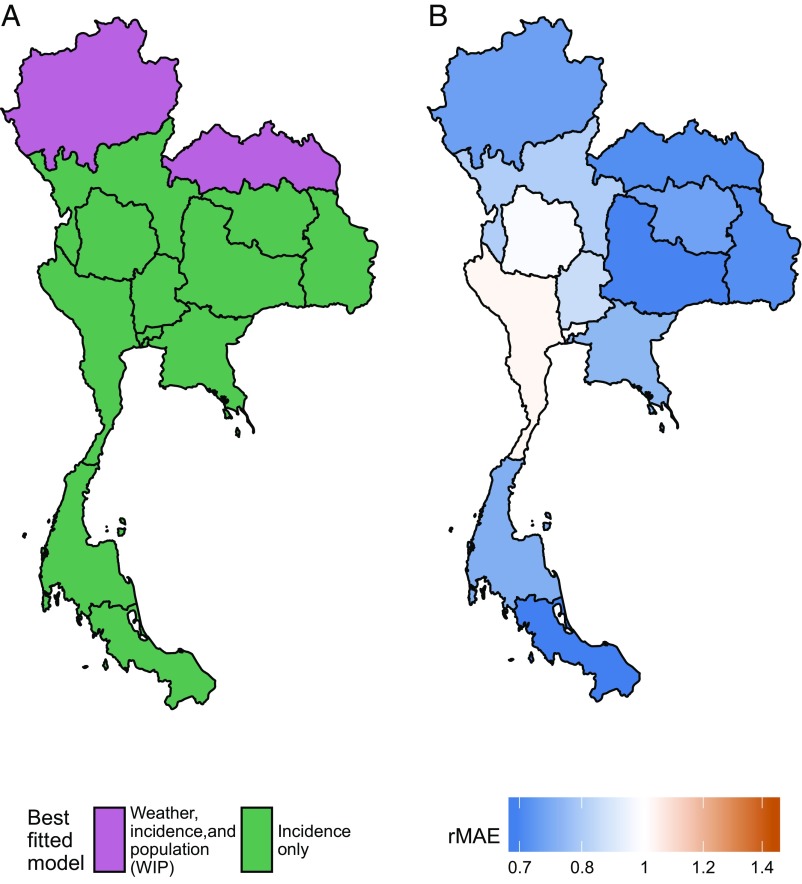
The testing-phase performance of each model varied across Thailand’s 13 MOPH health regions (Fig. S2). The incidence-only model performed best in 10 of 13 (77%) regions, the WIP model performed best in 2 of 13 (15%) regions, and the baseline forecasts performed best in 1 of 13 (8%) regions (Fig. 4 and Table S4). The WIP model made better forecasts relative to the baseline forecasts for regions that experience colder (MOPH regions 1, 7, and 8) or rainier (MOPH regions 11 and 12) low seasons than for the rest of Thailand. In these regions, climatic suitability for mosquito breeding varies between years; hence, a model with climate covariates can provide a strong early indication of annual incidence. Conversely, the WIP model performed especially poorly in Bangkok, which has consistently warm weather and moderate rainfall from year to year.
Fig. 4.
Geographic variation in model and performance. (A) The best fitted model in the testing phase for each MOPH region, which shows spatial patterns of performance. (B) The rMAEs of the forecasts for each MOPH region from the models in A over the baseline forecasts (i.e., the two northernmost MOPH regions show the rMAE of the WIP model forecasts, while the rest show the rMAE of the incidence-only model forecasts). Areas with less error than the baseline are blue, areas with more error than the baseline are red, and areas equal to the baseline are white.
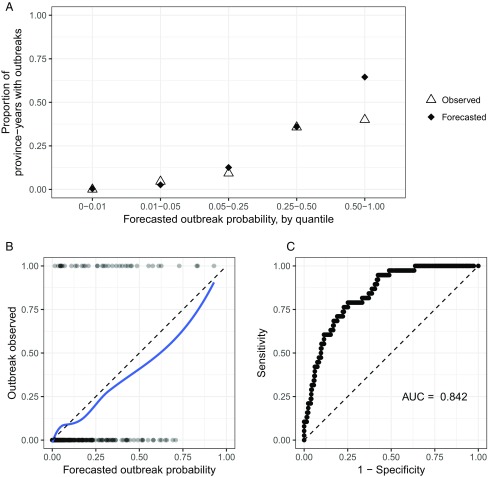
We quantified the risk of an outbreak for each province-year using samples from the predictive distributions of the incidence-only model. We define an “outbreak” to be when a province experiences a DHF incidence rate that is greater than two SDs above its 10-y median rate. In the testing phase, there were outbreaks in 38 of 380 (10%) province-years. Across all testing-phase province-years, the forecasted outbreak probability had a strong correspondence with the likelihood of a province experiencing an outbreak (Fig. 5B). Correspondence was particularly good in the 360 province-years when forecasted outbreak probabilities were less than 0.5 (Fig. 5A). Due to the unlikely nature of outbreaks, the incidence-only model only forecasted outbreak probabilities above 0.5 for 20 province-years (5% of all forecasts); however, 8 of 38 (21%) outbreaks occurred during these province-years. The incidence-only model correctly ordered the outbreak probabilities of any two randomly chosen province-years 84% of the time (Fig. 5C) (40).
Fig. 5.
The performance of outbreak forecasts by the incidence-only model. (A) The proportion of province-years that observed an outbreak by their forecasted outbreak probability, which is binned into quantiles. An outbreak is defined as an annual DHF incidence rate greater than two SDs above the median annual DHF incidence rate for the past 10 y. For each forecasted outbreak quantile, the black diamonds indicate the expected proportion of province-years with an outbreak based on incidence-only model forecasts, and the hollow triangles indicate the observed proportion of province-years with an outbreak. (B) The forecasted probability of an outbreak for each province-year in the testing phase and whether an outbreak was observed. The blue loess smoothed line shows the probability of observing an outbreak for a given forecasted outbreak probability from the incidence-only model. (C) The receiver operating characteristic curve based on the incidence-only model’s sensitivity and specificity on outbreak forecasts. The area under the receiver operating characteristic curve (AUC) is indicated below the line of no discrimination (dashed).
Discussion
We have shown that it is possible to make accurate forecasts of annual DHF incidence for Thailand at the province level using data available to policymakers before each year’s dengue season. Testing forecasts from a parsimonious model performed better than forecasts based on 10-y median incidence rates. Furthermore, this model successfully ordered provinces by their risk of experiencing an outbreak. These forecasts can provide timely and valuable information to policymakers as they prepare for the coming dengue season. By integrating biological and statistical approaches, these models push the envelope on how early it may be possible to accurately forecast annual dengue incidence. However, further improvements are needed for these forecasts to have their maximum impact.
The inclusion of climatic covariates did not consistently add value to forecasts relative to the incidence-only model. While there is biological evidence that Aedes mosquitoes are affected by climatic factors (1, 16, 18), the use of such factors in dengue forecasting efforts has shown mixed results (6–8, 10, 17, 19, 41, 42). These findings suggest that the associations between climate covariates and dengue either differ across time and space or are spurious correlations. Alternatively, climate may be one of several necessary but insufficient factors along with susceptibility and recent incidence, the combination of which results in ideal conditions for dengue transmission. Building a forecasting model that incorporates interactions between covariates is an area for future work.
The relative estimated susceptibility covariate was not selected for inclusion in either of the final models. This crude approximation of a complex mechanistic feature of disease was a component of the best six-covariate model; however, that model had a larger CV MAE during the training phase than the WIP model. A susceptibility term built on our mechanistic understanding of the disease process that more accurately captures the transient cross-protection between dengue serotypes could add value to a forecasting model.
Although we have shown ability to successfully forecast DHF incidence before the dengue season, many of the planning activities of the Thailand MOPH occur even further in advance; thus, the ability to make forecasts earlier in the year may be useful for public health policy. Historically, the MOPH has finalized each year’s dengue reports in the next April. This effectively sets the earliest possible date that annual forecasts can be made if they are to be based on complete data. An accurate model of reporting delays or timelier reporting could shift this date earlier. Likewise, forecasters could build a series of models optimized for data available at different times of the year.
To aid in the translation of this research into practice, we created sortable spreadsheet reports with results for each year that were then disseminated within the MOPH (Tables S5–S9). These reports are used for ranking provinces based on the forecasted probability of an outbreak and prioritizing locations for targeted interventions. This operational interpretation of the results emphasizes the importance of the relative rankings being accurate. The finding that 84% of the time our model would correctly rank two randomly selected province-years by outbreak probability directly supports the use of these forecasts in practice.
Making timely forecasts of infectious disease incidence is a challenging but important task. Accurate forecasts could play an important role in implementing targeted interventions designed to reduce transmission, such as helping to determine the location and timing of vector control activities and the mobilization of additional resources as well as reporting risk of infection to the public. Additionally, they could play a critical role in a systematic study of how well different interventions prevent or reduce the size of disease outbreaks. Collaborative efforts between public health agencies and academic- or industry-based teams with predictive modeling expertise are critical to helping propel this field forward. With the rapid growth and maturation of disease surveillance systems worldwide, developing our understanding of the best methods for creating and evaluating forecasts of infectious disease should continue to be a global health priority.
Materials and Methods
Weather Covariate Screening.
To investigate the utility of weather for forecasting annual DHF incidence, we included a variety of temperature, humidity, and rainfall covariates across several seasonal periods (Table S1). We downloaded weather station data from NOAA, which provided daily rain and temperature estimates for weather stations in 35 provinces (34, 35). Using the stationaRy (43) package in R (44), we obtained integrated surface data from the National Climatic Data Center (NCDC) (36). These data consist of temperature and humidity measurements from weather stations in 65 provinces (including all 35 provinces from the NOAA dataset) at 6-h intervals. For all provinces, we downloaded monthly temperature and rainfall data on 0.5 × 0.5-latitude–longitude resolution from the Earth System Research Laboratory (ESRL) at NOAA (37, 38).
For the NOAA and NCDC weather station data, we found the most consistently reported weather station for each province and extracted the daily maximum and minimum temperature, maximum humidity, and rainfall. We aggregated these measures into monthly covariates for maximum, minimum, and mean temperature, maximum and mean humidity, and maximum and total rainfall across January, February, and March. We also aggregated weather covariates across the low season from November to March, when fewer DHF cases have occurred historically on average. This time of season aligns with the dry season in Thailand, which has reduced temperatures and precipitation compared with the high-dengue season (from April to October) that corresponds with the rainy season.
We removed any covariates for which more than one-half of the aggregated observations from one source were missing. For example, with NOAA data, if 263 province-years (one-half of 35 provinces for 15 y) of observations were missing for a covariate, it was removed, such as was the case for low-season minimum and maximum temperatures. The ESRL data, from which the three covariates in the WIP model were derived, had one observation per month and were completely reported across all provinces.
Relative Estimated Susceptibility.
The estimated relative susceptibility covariate is a standardized rolling sum of cases from the previous 2 y. This is based on the approximate duration of time after infection with one dengue serotype that an individual may experience cross-protection from a subsequent heterologous infection (26). We calculate this quantity with the following equations:
where is the estimated relative susceptibility; is the observed incidence; and is the population in province in year . Each year, the susceptibility for the prior year () is updated by removing the people who were infected in the past year (), as we assume that they are immune to one serotype of dengue and cross-protected against the other serotypes. Furthermore, the cross-protection for people who were infected 3 y prior () will have worn off, and they are reintroduced to the pool of susceptible individuals. We assume that each province starts with an estimated relative susceptibility equal to the average incidence rate over the training phase (). This accounts for the fact that provinces with larger susceptible populations are more likely to have greater incidence than provinces with smaller susceptible populations (14). When there are no data for the year 3 y prior, is used in place of . Using rates instead of raw counts yields a covariate that can be compared across provinces with different population sizes. Although there are more cases of nonhemorrhagic dengue fever and asymptomatic cases than observed DHF cases, DHF cases may serve as a proxy for the underlying disease dynamics (1).
Model Structure and Estimation.
The model that we used to forecast annual DHF incidence for this study is a generalized additive model (31). Specifically, we use a generalized additive model with a negative binomial family, separate penalized smoothing splines for each covariate, and province-level random effects:
| [1] |
| [2] |
| [3] |
We model the incidence () for province in year as following a negative binomial distribution with the mean equal to the province population () times the incidence rate () and a dispersion parameter . After a log transformation, we model the mean of this distribution using an intercept (), a random effect for each province (), and a cubic spline for each of covariates [].
To obtain predictive distribution samples, we use a two-stage procedure to incorporate the uncertainty from our model parameter estimates and from the negative binomial distribution. We first draw 100 sample parameter sets from a multivariate normal distribution with mean equal to the point estimates of the parameters () from Eqs. 2 and 3 and covariance equal to the matrix of SEs. Each of these sampled parameter sets yields a corresponding . We then draw 100 samples from the negative binomial distribution given in Eq. 1 for each with the fixed estimate of to obtain a sample of size 10,000 from the predictive distribution for . We calculate the point estimate for each province-year, , as the median of these samples from the predictive distribution. The lower and upper limits of the 80% prediction intervals were defined by taking the 10th and 90th percentiles of these samples from the predictive distribution.
Model Selection Algorithm.
To choose the covariates to include in the forecasting models, we used a forward–backward stepwise algorithm to minimize the leave 1 y out CV MAE during the training phase (45). Starting with a null model, we iteratively added or removed the covariate that reduced the CV MAE the most at each step. The model with the smallest CV MAE at the end of the iterative process was the WIP model. To guard against the possibility of overfitting, we also selected the nested model with the fewest covariates within one SD of the WIP model CV MAE (31), which was the incidence-only model.
To choose the number of knots for each covariate spline, we cross-validated every single-covariate model by varying the number of knots from three to eight, which we conducted before the forward–backward stepwise algorithm above. We chose the model with the fewest knots within one SD of the smallest CV MAE for each covariate. We fixed this number of knots for each covariate spline for all multivariate models.
MAE.
We used MAE as our metric to select models during the training phase and rMAE to evaluate the models during the testing phase. Forecasts were made on the log scale; thus, our MAE took the form
where is the total number of province-years in block , which could be the entire training or testing phase or a subset to 1 y, province, or region. This form of the MAE has the interpretation that precision is relative to magnitude [e.g., predicting an incidence of 12 when an incidence of 7 is observed would have the same absolute error as predicting an incidence of 120 when an incidence of 70 is observed: ].
The testing-phase point predictions were compared with baseline forecasts using rMAE, an intuitive, scalable, and stable metric for evaluating forecasts (29):
This metric can be interpreted as the percentage of error observed in the forecasting model relative to that in the baseline forecasts (e.g., if and , then the forecasting model’s predictions were 25% closer to the observed value than the baseline forecasts).
Data and Code Availability.
All data processing and analysis were performed in R version 3.3.1 (2017-03-16) (44). The code and data for this analysis are publicly available at https://doi.org/10.5281/zenodo.1158752.
Supplementary Material
Acknowledgments
This project was funded by NIH National Institute of Allergy and Infectious Diseases Grant 1R01AI102939 and National Institute of General Medical Sciences (NIGMS) Grant R35GM119582. The findings and conclusions in this manuscript are those of the authors and do not necessarily represent the views of the NIH or the NIGMS. The funders had no role in study design, data collection and analysis, decision to present, or preparation of the presentation.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The data and code reported in this paper are publicly available in a Zenodo repository, https://doi.org/10.5281/zenodo.1158752.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1714457115/-/DCSupplemental.
References
- 1.Bhatt S, et al. The global distribution and burden of dengue. Nature. 2013;496:504–507. doi: 10.1038/nature12060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rigau-Pérez JG, et al. Dengue and dengue haemorrhagic fever. Lancet. 1998;352:971–977. doi: 10.1016/s0140-6736(97)12483-7. [DOI] [PubMed] [Google Scholar]
- 3.Stanaway JD, et al. The global burden of dengue: An analysis from the global burden of disease study 2013. Lancet Infect Dis. 2016;16:712–723. doi: 10.1016/S1473-3099(16)00026-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ferguson NM, et al. Benefits and risks of the Sanofi-Pasteur dengue vaccine: Modeling optimal deployment. Science. 2016;353:1033–1036. doi: 10.1126/science.aaf9590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kalayanarooj S. Standardized clinical management: Evidence of reduction of dengue haemorrhagic fever case-fatality rate in Thailand. Dengue Bull. 1999;23:10–17. [Google Scholar]
- 6.Wu PC, Guo HR, Lung SC, Lin CY, Su HJ. Weather as an effective predictor for occurrence of dengue fever in Taiwan. Acta Tropica. 2007;103:50–57. doi: 10.1016/j.actatropica.2007.05.014. [DOI] [PubMed] [Google Scholar]
- 7.Lowe R, et al. Spatio-temporal modelling of climate-sensitive disease risk: Towards an early warning system for dengue in Brazil. Comput Geosci. 2011;37:371–381. [Google Scholar]
- 8.Hii YL, Zhu H, Ng N, Ng LC, Rocklöv J. Forecast of dengue incidence using temperature and rainfall. PLoS Negl Trop Dis. 2012;6:e1908. doi: 10.1371/journal.pntd.0001908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Reich NG, et al. Challenges in real-time prediction of infectious disease: A case study of dengue in Thailand. PLoS Negl Trop Dis. 2016;10:e0004761. doi: 10.1371/journal.pntd.0004761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Johansson MA, Reich NG, Hota A, Brownstein JS, Santillana M. Evaluating the performance of infectious disease forecasts: A comparison of climate-driven and seasonal dengue forecasts for Mexico. Sci Rep. 2016;6:33707. doi: 10.1038/srep33707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yamana TK, Kandula S, Shaman J. Superensemble forecasts of dengue outbreaks. J R Soc Interface. 2016;13:20160410. doi: 10.1098/rsif.2016.0410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ray EL, Sakrejda K, Lauer SA, Johansson MA, Reich NG. Infectious disease prediction with kernel conditional density estimation. Stat Med. 2017;36:4908–4929. doi: 10.1002/sim.7488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Johnson LR, et al. 2017. Phenomenological forecasting of disease incidence using heteroskedastic Gaussian processes: A dengue case study. arXiv:1702.00261.
- 14.Keeling MJ, Rohani P. Modeling Infectious Diseases in Humans and Animals. Vol 47. Princeton Univ Press; Princeton: 2007. p. 385. [Google Scholar]
- 15.Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc Lond A Math Phys Eng Sci. 1927;115:700–721. [Google Scholar]
- 16.Juliano SA, O’Meara GF, Morrill JR, Cutwa MM. Desiccation and thermal tolerance of eggs and the coexistence of competing mosquitoes. Oecologia. 2002;130:458–469. doi: 10.1007/s004420100811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Scott TW, et al. Longitudinal studies of Aedes aegypti (Diptera: Culicidae) in Thailand and Puerto Rico: Population dynamics. J Med Entomol. 2000;37:77–88. doi: 10.1603/0022-2585-37.1.77. [DOI] [PubMed] [Google Scholar]
- 18.Brady OJ, et al. Modelling adult Aedes aegypti and Aedes albopictus survival at different temperatures in laboratory and field settings. Parasit Vectors. 2013;6:351. doi: 10.1186/1756-3305-6-351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Johansson MA, Dominici F, Glass GE. Local and global effects of climate on dengue transmission in Puerto Rico. PLoS Negl Trop Dis. 2009;3:e382. doi: 10.1371/journal.pntd.0000382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Huber JH, Childs ML, Caldwell JM, Mordecai EA. 2017. Seasonal temperature variation influences climate suitability for dengue, chikungunya, and Zika transmission. bioRxiv:230383.
- 21.Campbell KM, Lin CD, Iamsirithaworn S, Scott TW. The complex relationship between weather and dengue virus transmission in Thailand. Am J Trop Med Hyg. 2013;89:1066–1080. doi: 10.4269/ajtmh.13-0321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Burke DS, Nisalak A, Johnson DE, Scott RM. A prospective study of dengue infections in Bangkok. Am J Trop Med Hyg. 1988;38:172–180. doi: 10.4269/ajtmh.1988.38.172. [DOI] [PubMed] [Google Scholar]
- 23.Endy TP, et al. Epidemiology of inapparent and symptomatic acute dengue virus infection: A prospective study of primary school children in Kamphaeng Phet, Thailand. Am J Epidemiol. 2002;156:40–51. doi: 10.1093/aje/kwf005. [DOI] [PubMed] [Google Scholar]
- 24.Adams B, et al. Cross-protective immunity can account for the alternating epidemic pattern of dengue virus serotypes circulating in Bangkok. Proc Natl Acad Sci USA. 2006;103:14234–14239. doi: 10.1073/pnas.0602768103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wearing HJ, Rohani P. Ecological and immunological determinants of dengue epidemics. Proc Natl Acad Sci USA. 2006;103:11802–11807. doi: 10.1073/pnas.0602960103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Reich NG, et al. Interactions between serotypes of dengue highlight epidemiological impact of cross-immunity. J R Soc Interface. 2013;10:20130414. doi: 10.1098/rsif.2013.0414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Forshey BM, et al. Incomplete protection against dengue virus type 2 Re-infection in Peru. PLoS Negl Trop Dis. 2016;10:1–17. doi: 10.1371/journal.pntd.0004398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Waggoner JJ, et al. Homotypic dengue virus Reinfections in Nicaraguan children. J Infect Dis. 2016;214:986–993. doi: 10.1093/infdis/jiw099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Reich NG, et al. Case study in evaluating time series prediction models using the relative mean absolute error. Am Stat. 2016;70:285–292. doi: 10.1080/00031305.2016.1148631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Stone M. Cross-validatory choice and assessment of statistical predictions. J R Stat Soc Ser B. 1974;36:111–147. [Google Scholar]
- 31.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Vol 2. Springer; Berlin: 2009. pp. 1–758. [Google Scholar]
- 32.Ng AY. Preventing “overfitting” of cross-validation data. In: Fisher DH, editor. Proceedings of the Fourteenth International Conference on Machine Learning. Morgan Kaufmann; San Francisco: 1997. pp. 245–253. [Google Scholar]
- 33.Hyndman RJ, Koehler AB. Another look at measures of forecast accuracy. Int J Forecast. 2006;22:679–688. [Google Scholar]
- 34.Menne MJ, et al. 2012. Data from ‘‘Global Historical Climatology Network-Daily, Version 3. Thailand weather stations." NOAA National Climatic Data Center. https://data.nodc.noaa.gov/cgi-bin/iso?id=gov.noaa.ncdc:C00861.
- 35.Menne MJ, Durre I, Vose RS, Gleason BE, Houston TG. An overview of the global historical climatology network-daily Database. J Atmos Oceanic Technol. 2012;29:897–910. [Google Scholar]
- 36. National Climatic Data Center (2015) Federal climate complex data documentation for integrated surface data (National Climatic Data Center, Asheville, NC). Available at https://www1.ncdc.noaa.gov/pub/data/ish/ish-format-document.pdf. Accessed August 20, 2015.
- 37.Fan Y, van den Dool H. A global monthly land surface air temperature analysis for 1948–present. J Geophys Res Atmos. 2008;113 [Google Scholar]
- 38.Adler RF, et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979–present) J Hydrometeorol. 2003;4:1147–1167. doi: 10.3390/atmos9040138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.MdG T, et al. Dynamics of dengue virus circulation: A silent epidemic in a complex urban area. Trop Med Int Health. 2002;7:757–762. doi: 10.1046/j.1365-3156.2002.00930.x. [DOI] [PubMed] [Google Scholar]
- 40.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- 41.Lowe R, Cazelles B, Paul R, Rodó X. Quantifying the added value of climate information in a spatio-temporal dengue model. Stochastic Environ Res Risk Assess. 2016;30:2067–2078. [Google Scholar]
- 42.Lowe R, et al. Evaluating probabilistic dengue risk forecasts from a prototype early warning system for Brazil. eLife. 2016;5:e11285. doi: 10.7554/eLife.11285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Iannone R. 2015. stationaRy: Get Hourly Meteorological Data from Global Stations (R package), Version 0.4.1. Available at https://github.com/rich-iannone/stationaRy. Accessed August 20, 2015.
- 44.R Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna: 2017. [Google Scholar]
- 45.Draper NR, Smith H. Applied Regression Analysis. Wiley; New York: 1998. p. 736. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data processing and analysis were performed in R version 3.3.1 (2017-03-16) (44). The code and data for this analysis are publicly available at https://doi.org/10.5281/zenodo.1158752.