Trophic redundancy reduces vulnerability to extinction cascades

Significance

Initial species loss can lead to follow-on extinctions because of the interconnectedness of species in ecosystems. The loss of biodiversity through human impact can change the structure of ecological communities, which, models predict, can affect the likelihood of secondary extinctions. Uniquely, we provide an empirical demonstration of this with a plant-insect food web experiment by focusing on a particular secondary extinction mechanism. This mechanistic approach leads to specific, empirically testable hypotheses that can inform the development of predictive models on the consequences of changes in ecological community structure.

Abstract

Current species extinction rates are at unprecedentedly high levels. While human activities can be the direct cause of some extinctions, it is becoming increasingly clear that species extinctions themselves can be the cause of further extinctions, since species affect each other through the network of ecological interactions among them. There is concern that the simplification of ecosystems, due to the loss of species and ecological interactions, increases their vulnerability to such secondary extinctions. It is predicted that more complex food webs will be less vulnerable to secondary extinctions due to greater trophic redundancy that can buffer against the effects of species loss. Here, we demonstrate in a field experiment with replicated plant-insect communities, that the probability of secondary extinctions is indeed smaller in food webs that include trophic redundancy. Harvesting one species of parasitoid wasp led to secondary extinctions of other, indirectly linked, species at the same trophic level. This effect was markedly stronger in simple communities than for the same species within a more complex food web. We show that this is due to functional redundancy in the more complex food webs and confirm this mechanism with a food web simulation model by highlighting the importance of the presence and strength of trophic links providing redundancy to those links that were lost. Our results demonstrate that biodiversity loss, leading to a reduction in redundant interactions, can increase the vulnerability of ecosystems to secondary extinctions, which, when they occur, can then lead to further simplification and run-away extinction cascades.

Human activities, such as overexploitation and habitat destruction and alteration, are causing a high rate of species extinctions (1–3). Primary extinctions as the direct result of these activities can lead to secondary extinctions, for example, due to loss of essential prey species or changes in community dynamics (4–6), as linkages in the food web are lost (7). A major question that remains is how the network structure of food webs affects their vulnerability to secondary extinctions (8, 9). This is particularly important because species extinctions will lead to alterations in food web structure that could lead to increased vulnerability; this would mean that food webs can initially lose species without resulting in secondary extinctions, but as complexity is eroded, vulnerability increases to the point where the loss of one more species leads to an extinction cascade and community collapse (10).

Understanding the relationship between food web complexity and stability is therefore important, and this topic has long interested ecologists (8, 9). However, theoretical predictions from different models vary widely, partly due to the multifaceted nature of “complexity” and many different definitions of “stability” (9, 11–14), and also because of the varying degree of biological realism, such as diversity of ecological interaction types included in a model, which can affect the sign of the relationship (15). Further studies have provided a number of sometimes conflicting and interacting theoretical predictions on the relationship between food web complexity and extinction cascades (16–18). To date, it has not been possible to test any of these predictions empirically. However, by considering the mechanisms by which secondary extinctions happen, and how these might be affected by specific elements of food web complexity, we can formulate specific and empirically testable hypotheses.

Higher order consumer species (carnivores) have, for example, long been thought to have positive indirect effects on each other by regulating the populations of their respective prey, and thereby preventing competitive exclusion of each other’s prey (19–21). Loss of a carnivore species from a community could therefore lead to dominance of its prey at the lower trophic level and subsequent secondary extinctions of other carnivores (22, 23). An important element of food web complexity is its connectance (the proportion of possible trophic links that is realized). Higher connectance may affect vulnerability to secondary extinctions among higher order consumers because it is likely to be associated with greater diet overlap, and therefore greater trophic redundancy (17); there is a greater chance that the effects of an extinct species on the population dynamics of other species will be compensated for by the effects of other species with links to the same prey. Here, we therefore test the hypothesis that redundant trophic links reduce the likelihood of secondary extinctions at the same trophic level following the primary extinction of a second-order consumer.

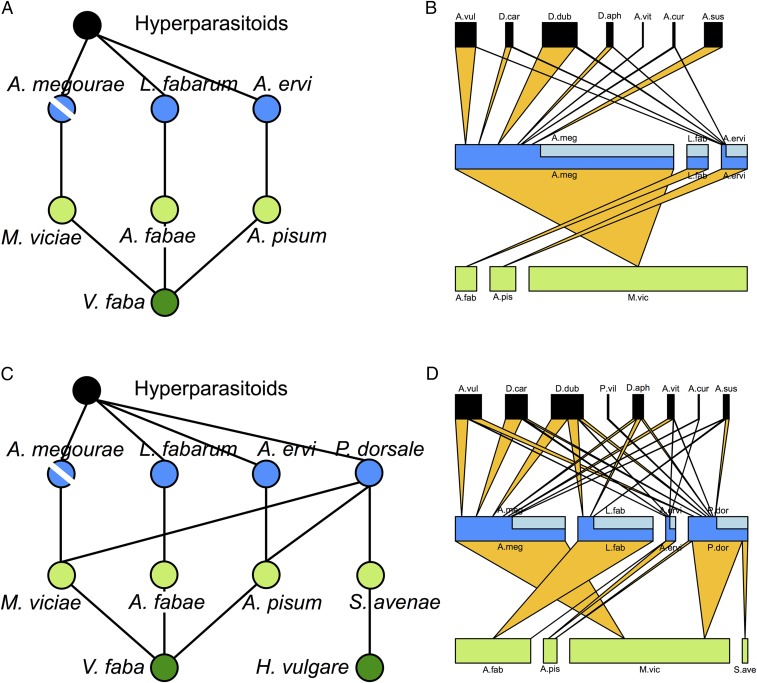
We assembled replicate communities of four trophic levels, consisting of plants, herbivorous insects (aphids), primary parasitoid wasps, and hyperparasitoid wasps in outdoor mesocosms. We focused on a food web module of three aphid species feeding on the same host plant and their respective specialist parasitoids plus associated hyperparasitoids that feed on the latter. We have previously demonstrated that primary extinction of any of the parasitoids in this system leads to secondary extinctions at the same trophic level and that the mechanism for this is transmission through competitive interactions at the herbivore level following release from top-down regulation (22, 23). We assembled replicated simple communities that contained only the focal module and no trophic redundancy (Fig. 1A) and more complex communities that contained the module with the same species composition, alongside an additional plant species, aphid species, and generalist parasitoid species that explicitly provided redundancy for the trophic link of the species targeted for primary extinction (Fig. 1C). The communities were exposed to the natural background community of hyperparasitoids and then left to develop for approximately three generations (resulting food webs are shown in Fig. 1 B and D), after which we started harvesting the parasitoid Aphidius megourae, simulating local extinction, in half of the replicates and monitored the persistence of populations of the other parasitoid species in the focal module.

Fig. 1.

Experimental insect food webs. The food web structure for assembled insect communities with lower (A) and higher (C) food web complexity is shown. We tested for secondary extinctions at the parasitoid trophic level in the species L. fabarum and A. ervi following the functional extinction of A. megourae (indicated by a diagonal line through its node). The resulting food web structures (excluding plants) as observed in the field experiment for communities with lower (B) and higher (D) food web complexity are presented as quantitative host-parasitoid-hyperparasitoid networks. For the primary parasitoids, the light blue areas of the bars indicate the proportion of parasitoids that have not been hyperparasitized. The networks show interactions for primary parasitoids feeding on aphids and hyperparasitoids as a fourth trophic level attacking the primary parasitoids. A. cur, A. cursor; A. ervi, A. ervi; A. fab, A. fabae; A. meg, A. megourae; A. pis, A. pisum; A. sus, A. suspensus; A. vit, A. victrix; A. vul, A. vulgaris; D. aph, D. aphidum; D. car, D. carpenteri; D. dub, D. dubiosus; L. fab, L. fabarum; M. vic, M. viciae; P. dor, P. dorsale; P. vil, P. villosa; S. ave, S. avenae.

Because it was not possible in an experiment with real organisms to manipulate trophic redundancy without also affecting species richness or species identity, we used a simulation model to test whether differences in secondary extinctions could be due to differences in diversity rather than the hypothesized mechanism. With this model, we recreated the experiment in silico with two additional community structures in which redundancy was increased without changing diversity and diversity was increased without changing redundancy, respectively. Furthermore, we tested whether the strength of the redundant link, relative to the “lost” link, affected secondary extinctions in the complex community, as would be predicted if trophic redundancy is indeed the important factor.

Results and Discussion

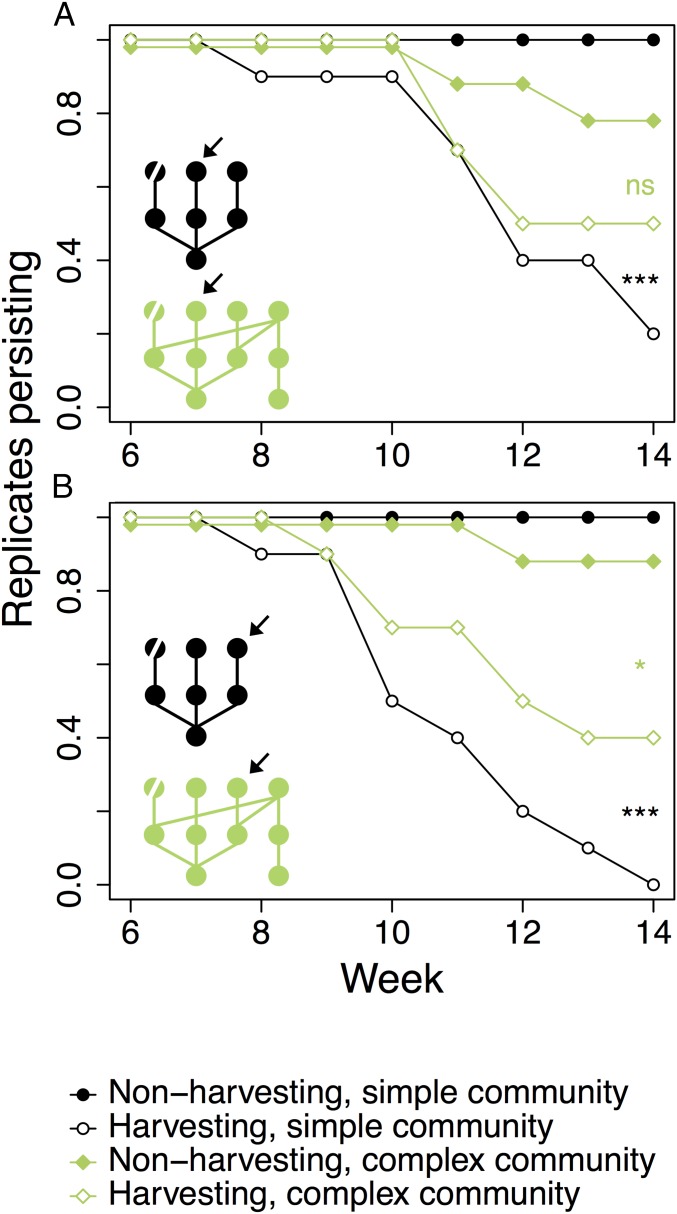
Repeated harvesting of the parasitoid A. megourae reduced its average abundance by 52%, with 104.6 per mesocosm (SE = 12.0) in control communities and 54.9 (SE = 9.94) in harvested communities (Fig. S1; harvesting: F_1;28 = 10.29, P = 0.0033), with no difference between simple and complex communities. Harvesting the parasitoid A. megourae indirectly led to increased extinction rates of the parasitoid species Lysiphlebus fabarum and Aphidius ervi (Fig. 2 and Table S1; Cox proportional hazards model harvesting effect: z = 3.54, P < 0.001). These secondary extinctions were more likely in the simple insect communities than in the more complex insect communities, as indicated by the significant statistical interaction between the harvesting and food web structure treatments (z = −2.01, P < 0.05). This result is consistent with the prediction that trophic redundancy reduces vulnerability to secondary extinctions. It is striking that these effects on extinction probability can be observed even against the background of seasonal environmental variation and associated fluctuations in population densities of the species (Fig. S1).

Fig. 2.

Secondary extinctions. The persistence of L. fabarum (A) and A. ervi (B) parasitoid populations in simple (black line, circle) or complex (green line, diamond) communities with either the parasitoid A. megourae harvested (open symbols) or nonharvesting controls (closed symbols) is shown. Each treatment was replicated 10 times. *P < 0.05 and ***P < 0.001, significance levels for Kaplan–Meier survival curves between harvesting treatments and controls with the same community structure. ns, nonsignificant. Note the greater indirect effect of harvesting in simple communities (black lines/symbols) in both species. The arrow indicates the position of the species represented in the panel in the food webs, with the harvested parasitoid A. megourae indicated by a diagonal line through its node.

To explain this effect further, we need to look at the mechanism behind the secondary extinctions. We have previously shown that a release from top-down control of the host or prey of harvested second-order consumer species leads to an increase in competition among herbivore species, with associated reductions in density. This reduces host/prey-searching efficiency of the other carnivore species in the system due to increased interference by nonhost/prey (a nontrophic effect) triggering their extinctions even if their host/prey is still present at low numbers (22, 23). In both the complex and simple communities, the aphid Megoura viciae was released from top-down control by the parasitoid A. megourae in harvested communities. M. viciae aphid densities were twice as high in harvested communities compared with control communities at the end of the experiment (Fig. S1; harvesting × week: F_1;317 = 5.19, P = 0.0234). Moreover M. viciae density was generally much higher in the simple communities with, on average, 8,800 (SE = 733) individuals per mesocosm compared with 6,320 (SE = 656) individuals per mesocosm in complex communities (community: F_1;28 = 7.02, P = 0.0131), and therefore also resource competition between M. viciae and the other aphids. The complex communities included the generalist parasitoid Praon dorsale, which, alongside the specialist A. megourae, attacked the aphid M. viciae. This additional trophic link kept the aphid M. viciae at lower densities, especially in the harvesting treatments, and reduced competitive pressure on the other aphids. The parasitism rate of M. viciae (combining parasitism by the specialist parasitoid A. megourae and the generalist parasitoid P. dorsale) was indeed lower in harvested communities, an effect that increased through time (harvesting × week: z = −3.81, P < 0.001). The parasitism rate of M. viciae was higher in more complex communities (0.015%) than in simple communities (0.008%) (community: z = 1.85, P = 0.063), indicating more efficient top-down control in the more complex communities (Fig. S2).

Our experimental communities also contained third-order consumers in the form of hyperparasitoids, and the possibility that the effects of harvesting were transmitted through links with this trophic level has to be considered. The hyperparasitoid community composition was very similar for the different treatments (Fig. S3), while the parasitoid-hyperparasitoid quantitative networks show more interactions and a higher connectance in more complex communities (Fig. S4). The harvesting of A. megourae caused significantly higher hyperparasitism rates for primary parasitoid species; however, this increase was not affected by community complexity (Fig. S5 and Table S2), so it cannot explain the difference in vulnerability to secondary extinctions between the communities. Irrespective of harvesting, hyperparasitism rates were higher in the more complex communities (Table S2), which one might expect would make the primary parasitoids in these communities more vulnerable to extinction. However, because the extinction rate was, in fact, higher in the simple communities, this is either too simplistic a view of their population dynamics or this effect was weak compared with the herbivore-mediated effect that caused the secondary extinctions.

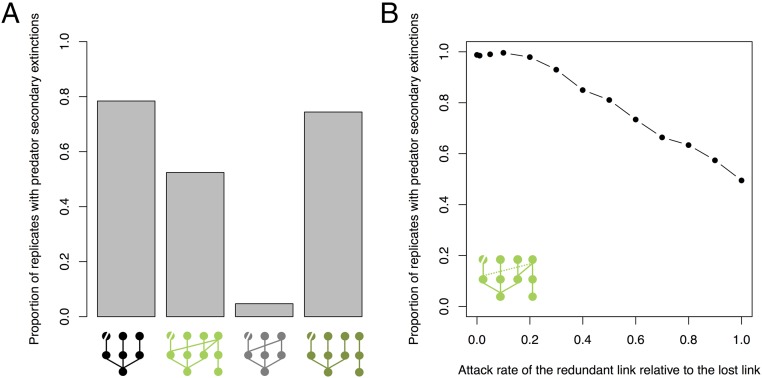
The model simulations further demonstrate that trophic redundancy, rather than species richness, is responsible for the observed difference in secondary extinctions between the simple and complex communities. Using a generalized Lotka–Volterra model, we simulated four different food web scenarios based on our experimental food web structure (Fig. 3A). Each scenario was replicated 1,000 times with the species’ parameters randomly drawn from a uniform distribution for each replicate (more details are provided in Materials and Methods). For each food web scenario, the proportion of carnivore secondary extinctions after the removal of the target species was recorded. The first two scenarios replicate the experimental food web structures and provide the same result in that secondary extinctions are less common in the complex community (Fig. 3A). In the third scenario, redundancy is added to the simple community without altering diversity, and secondary extinctions are much reduced in this case. In the final scenario, diversity is the same as in the complex community, but redundancy is eliminated (which leads to two unconnected food web modules). In that case, secondary extinctions are not different from those in the “simple” food web. Thus, these simulations provide clear evidence for a redundancy effect but no evidence for a diversity effect (Fig. 3A and Fig. S6A). We then tested the redundancy effect by varying the strength of the redundant trophic link provided by the generalist relative to the lost feeding link by the specialist in the scenario that replicated the food web structure of the complex communities in the experiment. We varied the strength of the generalist link between 0 (no link) and 1 (equal to the lost link). There is a clear negative relationship between the relative strength of the redundant link and the probability of secondary extinctions among carnivores (Fig. 3B and Fig. S6B). Extensive sensitivity analysis demonstrates the robustness of these results (Fig. S7).

Fig. 3.

Predator secondary extinctions in the modeled food web scenarios. The proportions of replicates with predator secondary extinctions in four different food web structures (A) and as a function of the predator attack rate in the redundant link relative to other predator attack rates (B) are shown. Each food web scenario was replicated 1,000 times with varying model parameter values. The food web structure modeled in each scenario is represented below the panels, with the removed species indicated by a diagonal line through its node. The dotted line in B indicates the position of the redundant link in the food web.

We have demonstrated experimentally that trophic link redundancy can provide robustness against secondary extinction cascades following the harvesting of one species under this particular (and arguably common) secondary extinction mechanism. Different elements of food web complexity have been found in dynamic models to affect the vulnerability of ecological communities to extinction cascades. Species richness can either decrease (17) or increase (16, 24) the risk of secondary extinctions; higher connectance generally reduces the risk of a secondary extinction following the primary extinction of a random species but increases the risk following the loss of a top predator (18), which appears to be the species most at risk for extinction (25). Greater modularity decreases the extent of extinction cascades because secondary extinctions are largely confined to the module in which the primary extinction occurred (26), an effect that increases with increasing connectance. This wide variety of predictions and interacting effects indicates that it is difficult to draw general conclusions about the relationship between broad descriptors of food web structure and vulnerability to secondary extinctions. Our results demonstrate that focusing on specific, empirically tested mechanisms of secondary extinction can lead to empirically testable hypotheses. The insights gained from these empirical tests can then further inform theory. With regard to trophic redundancy, we suggest that generalism degree may be a more relevant measure of complexity than connectance. Interestingly, it has been shown that generalism degree in food webs decreases more strongly in response to habitat modification than connectance (27), suggesting that increasingly human-modified landscapes are more vulnerable to extinction cascades.

This study highlights that biodiversity loss leading to simplified ecosystems can increase their vulnerability to cascading extinctions that can gather pace with each subsequent extinction, which may help to explain the substantial reduction in biodiversity typically observed in disturbed ecosystems (28). Previously, all knowledge on the relationship between food web structure and extinction cascades was based on theory alone. Our experimental evidence demonstrates that these effects are real, and should therefore be taken into consideration in the debate on the relative conservation value of pristine and disturbed habitats (29), especially as the latter often display a simplified food web structure (27).

Materials and Methods

Study System.

The plant-aphid-parasitoid communities consisted of bean plants (Vicia faba, L., var. the Sutton) as a resource for three aphid species: (i) the black bean aphid Aphis fabae (Scopoli), (ii) the pea aphid Acyrthosiphon pisum (Harris), and (iii) the vetch aphid Megoura viciae (Buckton), each attacked by a specialist parasitoid, with these being L. fabarum (Marshall), A. ervi (Haliday), and A. megourae (Stary), respectively. In complex communities, barley plants (Hordeum vulgare L.) were added as a resource for the grain aphid Sitobion avenae (Fabricius). In these more complex communities, we also included the generalist parasitoid P. dorsale (Haliday), which attacked the aphid species S. avenae, A. pisum, and M. viciae. Connectance for the aphid-primary parasitoid interaction network was 0.08 in the simple communities and 0.11 in the more complex communities. All communities were exposed to the natural hyperparasitoid community, which, in contrast to aphids and primary parasitoids, could naturally colonize the mesocosms by laying eggs in aphid mummies that were attached to the mesh (parasitized aphids have the tendency to leave the host plants and to mummify in other places). We recorded eight hyperparasitoid species: Alloxysta victrix (Westwood, 1833), Alloxysta cursor (Hartig, 1840), Phaenoglyphis villosa (Hartig, 1841), Asaphes vulgaris (Walker, 1834), Asaphes suspensus (Nees, 1834), Dendrocerus carpenteri (Curtis, 1829), Dendrocerus aphidum (Rondani, 1877), and Dendrocerus dubiosus (Kieffer, 1907).

Field Experiment.

The experiment was conducted within 40 mesocosms (Rovero Agro Quick Field Cages), each measuring 2 × 2 × 2 m (with a mesh size of 0.22 × 0.31 mm and a light transmission ability of 77%), in a field site on the Penryn Campus of the University of Exeter. The mesocosms were secured in the ground using structural poles buried 20 cm into the ground, with ground sheeting used at the base to restrict the introduction of invertebrates. Within each mesocosm, there were two 80-cm-high tables, with each supporting three trays upon which two pots of four 2-wk-old bean plants (var. the Sutton) were placed. For all treatments in week 1, five aphids each of M. viciae, A. pisum, and A. fabae were placed on pots with bean plants. In addition, in the complex communities, five S. avenae aphids were placed on pots with 2-wk-old barley, with one pot placed on each tray. The aphids were allowed to grow in the mesocosms for 2 wk, at which point two more bean pots and one barley pot without aphids were also placed on each tray to provide a food source for growing populations. This was also repeated after a further 2 wk, resulting in six pots with beans and two pots with barley (the latter in complex communities only) per tray (six trays per mesocosm). On week 2, two adult, mated female parasitoids of A. megourae, A. ervi, and L. fabarum were released into the cages, along with two adult, mated female P. dorsale released into the complex communities. Plants were grown in (Melcourt) Peat Free All Purpose Compost.

Four treatments were used in this study: (i) simple community, nonharvested; (ii) simple community, harvested; (iii) complex community, nonharvested; and (iv) complex community, harvested. Complex communities, as described above, included generalist species (P. dorsale) as well as another aphid species (S. avenae) and plant species (H. vulgare). In harvested treatments, we experimentally simulated the functional loss of the parasitoid species A. megourae by harvesting its mummies twice weekly. After a parasitoid has attacked an aphid, the parasitoid wasp develops inside the living aphid and, after a couple of days, forms the so-called aphid mummy when pupating. All mummies visible in a 20-min time frame per mesocosm were harvested by being pinched between a pair of tweezers. Harvesting treatment was started after all species were established in the communities (three parasitoid generations). To monitor the 40 replicate communities, all species on and around half of all pots per tray were counted once a week (three pots with beans and one pot with barley). In the case of a species not being detected with this method, the entire cage was searched to confirm extinctions. The oldest two bean plants (and oldest barley plant in the complex cages) per tray were replaced weekly with 2-wk-old plants. The old plants were cut, with the foliage and all aphids and mummies left in the cages so as to not alter the community structure (22). During dry spells, the plants of all cages were watered. Every week, all aphids and mummies were counted, and 10% of mummies were sampled every second week to estimate the hyperparasitism rate and hyperparasitoid species. If fewer than 10 mummies of any species were seen, that species was exempt from that week’s hyperparasitism sample. Each treatment was replicated 10 times, with mesocosms located 1.5 m apart from each other in a block design. A block was formed of four mesocosms in a row, and each mesocosm was randomly assigned to one of the four treatments, allowing us to separate the variation based on any potential environmental gradients, such as wind exposure and exposure to hyperparasitoids, from the treatment variation in the data. Temperatures did not differ between inside and outside the mesocosms (22). The experiment ran for 14 wk from June 5, 2015 to December 8, 2015.

Statistical Analysis.

To compare extinction probability between the different treatments, we recorded the number of weeks that each parasitoid species persisted in each of the 40 mesocosms. Species that persisted in mesocosms until the end of the experiment were treated as censored data. We used the Cox proportional hazard model from the survival package (30) in the open-source software R 3.1.0 (31) to test for the impact of the complexity and harvesting factors and their interaction on parasitoid species persistence in the communities. We further included parasitoid species identity of the nonharvested specialist parasitoids (L. fabarum and A. ervi) and interaction with the treatments harvesting and aphid distribution in the model to test for species-specific differences in response to the treatments. Proportional hazard assumptions were tested by inspecting Kaplan–Meier survival curves and with a cox.zph test (32). Single treatments were compared with Kaplan–Meier survival curves and a log-rank test as implemented in the R-function survdiff (33).

Aphid and parasitoid population densities were analyzed with linear mixed effect models with log- or square root-transformed density data as the dependent variable with a normal error distribution. Harvesting treatment, community complexity treatment, and the interaction between the two treatments were included as fixed factors. To account for systematic trends over time, we included week and week squared as covariates. Mesocosm identity nested in a block was used as a random intercept in the model. Because the residuals of these models showed a significant partial temporal autocorrelation, we included a first-order autoregression for the residuals. This was done using the function lme from the package nlme (34). The parasitism rate of M. viciae was tested with general linear mixed effects models, including harvesting, complexity, and week as fixed factors and block and mesocosm as random factors assuming binomial error structure. The response variable was a binary variable containing the number of mummified aphids and the number of live aphids per mesocosm. For the latter analyses, we used glmer from the r-package lme4 (35). The hyperparasitism rate of primary parasitoids (A. megourae, A. ervi, and L. fabarum) was similarly analyzed using a combined variable with hyperparasitized and nonhyperparasitized mummies. We also tested for treatment effects of the species richness and diversity of hyperparasitoid communities. Hyperparasitoid community composition between treatments was compared with nonmetric multidimensional scaling plots using the r-package vegan (36). The reported data used in the above analyses are presented in the Datasets S1–S3.

Food Web Modeling.

As in previous food web simulations on extinction cascades (17), community dynamics were modeled using the generalized Lotka–Volterra equation:

$$\frac{d{N}_i}{dt}=N_i\left(b_i+{\displaystyle \sum _{j=1}^n}{a}_{ij}{N}_j\right),$$

where N_i is the density of species i, n is the number of species in the community, b_i is the intrinsic growth rate of species i, and a_ij is the per capita effect of species j on the per capita growth rate of species i. Basal species (i.e., plants) have a positive intrinsic growth rate (b_i > 0) and are self-limited (a_ii = −b_i/K_i < 0, where K_i is plant species i carrying capacity). For consumer species (i.e., aphids, aphid parasitoids), b_i < 0 and a_ii = 0. When species j consumes or attacks species i, a_ij < 0 and a_ji = −a_ij (a_ij = 0 otherwise). For each simulation of community dynamics, model parameters were drawn from the following uniform distributions: b_i from [1;2], [−0.6;−0.4], and [−0.7;−0.5] for plants, herbivores, and carnivores, respectively; a_ii from [0.3;0.6] and [0.2;0.6] for the per capita effects of herbivores and carnivores, respectively; and K_i from [5;15]. These parameter ranges were chosen such that coexistence between species was possible in all tested food web configurations. Values of per capita effects of carnivores are within the range of parasitoid attack rates measured in the study system (37).

We compared four food web scenarios. The first two scenarios corresponded to the simple and complex communities considered in the experiment. The third scenario was based on the simple community, but with a functional redundant trophic link added. The fourth scenario was based on the complex community, but with the functional redundant trophic links removed. For each food web scenario, we simulated the dynamics of 1,000 communities, varying in their parameter values, following the removal of the target carnivore species. In each simulation, we ensured that all species could coexist at equilibrium (i.e., equilibrium feasibility) before target species removal. If parameter values did not allow coexistence, a new set of parameter values was randomly selected. Initial densities were set equal to expected equilibrium densities when all species are present, except for the removed target species, for which density was set equal to 0. In each simulation, community dynamics were then run for 100 time units and the number of secondary extinctions, as well as time to first secondary extinction, were recorded for carnivore species. We considered a species was extinct when its density was below 10⁻¹⁰.

In addition to the comparison between the four food web scenarios, we investigated how the strength of the redundant link to the lost feeding link, noted as a_redund, determined the occurrence of secondary extinctions of carnivore species in the complex community (i.e., in food web scenario 2). To do so, a_redund was uniformly drawn from the random distribution [0.2s; 0.6s], with s varying between 0 and 1. When s = 0, the redundant link to the lost feeding link is absent, while when s = 1, it has the same strength as other feeding links. For each value of s, 1,000 community dynamics were simulated, varying in their parameter values. To assess the sensitivity of our results to the chosen parameter values, we performed an extensive sensitivity analysis of the model to changes in the mean and variance of all six random distributions from which species parameters were drawn. We used Latin hypercube sampling to select 100 combinations of parameter distributions, corresponding to 100 sets of simulations, with the function randomLHS in the R package lhs (Table S3). For each set of simulations, we performed 500 replicated simulations of community dynamics in each food web scenario and 100 replicated simulations for each value of s in the complex community scenario (Fig. S7).

All model simulations were performed using the function lsoda from the R package deSolve (38).