Demographic compensation does not rescue populations at a trailing range edge

Significance

While climate change is causing poleward shifts in many species’ geographic distributions, some species’ ranges have remained stable, particularly at low-latitude limits. One explanation for why some species’ ranges have not shifted is demographic compensation across a species’ range, whereby declines in demographic processes like survival or reproduction are offset by increases in others, potentially buffering populations from extinction. However, we have limited understanding of whether demographic compensation can prevent collapse of populations facing climate change. We examined the demography of natural populations of a perennial herb spanning a broad latitudinal gradient. Despite increases in reproduction, low-latitude populations declined due to diminished survival, growth, and recruitment. Thus, demographic compensation may not be sufficient to rescue low-latitude, trailing-edge populations from extinction.

Abstract

Species’ geographic ranges and climatic niches are likely to be increasingly mismatched due to rapid climate change. If a species’ range and niche are out of equilibrium, then population performance should decrease from high-latitude “leading” range edges, where populations are expanding into recently ameliorated habitats, to low-latitude “trailing” range edges, where populations are contracting from newly unsuitable areas. Demographic compensation is a phenomenon whereby declines in some vital rates are offset by increases in others across time or space. In theory, demographic compensation could increase the range of environments over which populations can succeed and forestall range contraction at trailing edges. An outstanding question is whether range limits and range contractions reflect inadequate demographic compensation across environmental gradients, causing population declines at range edges. We collected demographic data from 32 populations of the scarlet monkeyflower (Erythranthe cardinalis) spanning 11° of latitude in western North America and used integral projection models to evaluate population dynamics and assess demographic compensation across the species’ range. During the 5-y study period, which included multiple years of severe drought and warming, population growth rates decreased from north to south, consistent with leading-trailing dynamics. Southern populations at the trailing range edge declined due to reduced survival, growth, and recruitment, despite compensatory increases in reproduction and faster life-history characteristics. These results suggest that demographic compensation may only delay population collapse without the return of more favorable conditions or the contribution of other buffering mechanisms such as evolutionary rescue.

The geographic range, encompassing the set of populations where a species occurs across the landscape, is a fundamental unit of ecology and biogeography. Understanding how and why populations vary across the range and disappear beyond range edges is critical for a variety of problems, from explaining rarity to forecasting range shifts. Because population dynamics are the net result of vital rates such as recruitment, survival, and reproduction, spatial variation in populations must result from variation in at least some of these vital rates and their combined effects on population growth.

Many hypotheses to explain species’ ranges assume that geographic ranges are spatial expressions of species’ ecological niches (1). For example, the “abundant center hypothesis” posits that vital rates, population growth, and abundance peak in optimal habitat at the geographic center of the range and decline toward range edges (Fig. 1A) (2). However, empirical support for this hypothesis is mixed (3–5), likely because spatial and environmental gradients can be decoupled (6, 7); environmental optima need not be at the geographical center, and range-edge populations might occupy patches of optimal habitat. Further, vital rates can respond differently to the same environmental gradient and need not all decline toward range edges. For example, survival might decrease with temperature while fecundity increases, a phenomenon called “demographic compensation” (8).

Fig. 1.

Predictions of how population growth rate (λ) and vital rates (survival probability and reproduction) should vary with latitude in the absence (A and B) and presence (C and D) of demographic compensation under hypotheses of equilibrium (A and C) and disequilibrium (B and D) between the species’ range and niche. Life-history theory predicts negative correlations between vital rates such that fast life-history strategies (e.g., high reproduction but low survival or growth from one year to the next) are favored at low latitudes, whereas slow life-history strategies (e.g., low reproduction but high survival or growth from one year to the next) are favored at high latitudes. Adapted from ref. 8.

If demographic compensation among vital rates were complete, then population growth would be invariant over time (temporal compensation; ref. 8) or across the geographic range (spatial compensation, the focus of this study). Even incomplete compensation could increase the range of environments over which populations can succeed and decrease spatial or temporal variation in population growth compared to populations without compensatory changes in vital rates (Fig. 1 A and B vs. Fig. 1 C and D). The presence of temporal demographic compensation may forestall extinctions due to climate change, at least until populations reach a tipping point beyond which all vital rates decrease and populations crash (9). When spatial and temporal gradients share similar environmental drivers, then the presence of spatial compensation can suggest a capacity for future buffering (8, 9).

Spatial variation in vital rates creates life-history differences that can often be summarized by a fast–slow continuum. “Fast” life histories have rapid development, high fecundity, reduced longevity, and short generation times, while “slow” life histories have the opposite (10). Theory predicts that selection should favor increased allocation to fast life-history traits when survival is low or unpredictable (e.g., in temporally variable environments), particularly of adults relative to juveniles (11–14). In contrast, for delayed reproduction to be favorable, potential increases in fecundity by older, larger individuals must outweigh the risk of mortality before the next opportunity for reproduction. In some temperate plant species, populations from lower latitudes are more frequently annual (15) and reproduce at an earlier age than those from higher latitudes (16), creating a fast–slow continuum from low to high latitudes. If demographic compensation is driven by life-history shifts, then negative correlations in vital rates should follow the tradeoffs predicted by the fast–slow continuum (Fig. 1). In particular, we expect that low-latitude populations will exhibit faster life-history characteristics than high-latitude populations across a species’ range (Fig. 1). Aside from the potential role of demographic compensation in buffering populations from climate change, an outstanding question is whether range limits reflect inadequate compensatory life-history shifts across space, causing population growth to fall below replacement levels at range edges.

Although niche-based hypotheses about the causes of range limits assume equilibrium between species’ distributions and the environment, it is well documented that ranges expand, contract, and shift over time. Lags in responses to temporal environmental variation create “leading” range edges where populations are expanding into newly suitable habitat and “trailing” range edges where populations are contracting from newly unsuitable habitat (17, 18). Such disequilibrium between the environment and ranges arises because adaptation, demography, and dispersal are usually slower than rates of environmental change over a range of time scales, from glacial–interglacial periods (19) to recent anthropogenic climate change (20). This dynamic view predicts a linear relationship between vital rates or population growth rate (λ) and range position, from low vital rates and declining populations at the trailing edge to high vital rates and stable or growing populations at the leading edge (Fig. 1B). It also predicts that demographic compensation is insufficient to rescue populations at the trailing edge.

In this study, we examine spatial variation in vital rates and deterministic λ of 32 populations over five growing seasons (2010–2014) across nearly the entire latitudinal range (11 of 12 degrees) (Fig. 2A) of the scarlet monkeyflower, Erythranthe (formerly Mimulus) cardinalis. E. cardinalis is a perennial herb with a well-described and extensively protected distribution in western North America that spans a broad climatic gradient (Fig. 2 B and C). Our specific objectives were (i) to examine how vital rates and λ vary among populations across the range; (ii) to determine which vital rates drive spatial variation in λ; and (iii) to test whether demographic compensation among vital rates buffers spatial variation in λ.

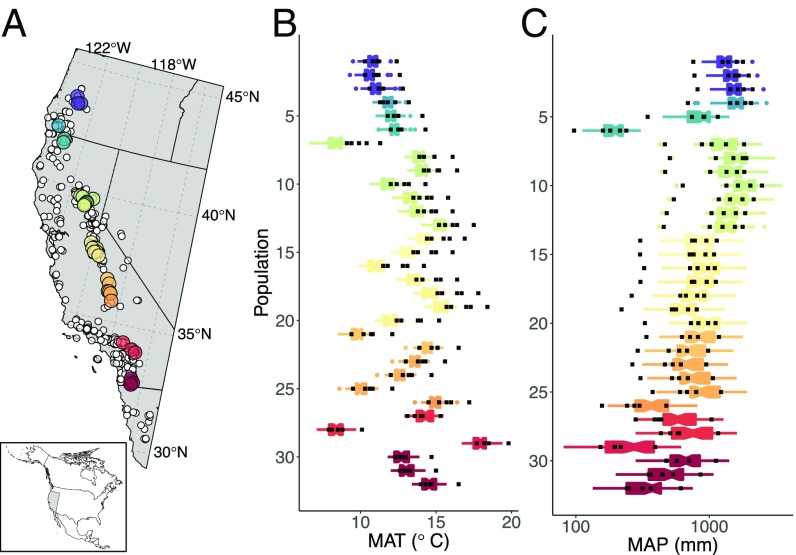
Fig. 2.

(A) Map of 32 study populations across the geographic distribution of the scarlet monkeyflower. Populations are colored to scale with latitude, with warm colors corresponding to low latitudes and cool colors corresponding to high latitudes; white points correspond to all known occurrences of E. cardinalis (49). (B and C) For each study population, distribution of mean annual temperature (MAT) (B) and mean annual precipitation (MAP, log₁₀ scale) (C) across the period of 1951–2000 (boxplots) and census years 2010–2014 (square symbols) derived from ClimateWNA version 5.41 (50). Narrowest portions of bars represent medians, notches approximate a 95% confidence interval around the median, boxes show the interquartile range, and whiskers correspond to the most extreme values within 1.5× the interquartile range.

Results

Spatial Variation in λ and Vital Rates.

Asymptotic projections of λ increased linearly from the southern edge of the range, where λ was uniformly <1, toward the northern edge, where most populations were stable or increasing (P = 0.001, R² = 0.28) (Fig. 3A and SI Appendix, Table S1). Because individual plant size and its relationship to vital rates varied with latitude (Fig. 3 B–F and SI Appendix, Fig. S1), we examined latitudinal variation in vital rates at population-specific size quantiles. Similarly to λ, the probability of recruitment and the growth of medium-sized plants increased linearly from south to north (Fig. 3D and SI Appendix, Fig. S2 and Table S2). Although not statistically significant, the probability of flowering tended to decrease from south to north (Fig. 3E), particularly for small and medium-sized plants (SI Appendix, Fig. S2 and Table S2). Two other vital rates had nonlinear relationships with latitude. The probability of survival peaked at midlatitudes and declined toward northern and southern latitudes (Fig. 3C), while mean offspring size increased northward and southward from midlatitudes (SI Appendix, Fig. S2 and Table S2). Fruit number did not vary with latitude (Fig. 3F and SI Appendix, Fig. S2 and Table S2).

Fig. 3.

(A) λ as a function of latitude. Points correspond to each population’s λ value as projected from the IPM, with vertical bars showing bias-corrected 95% confidence intervals derived from a bootstrapping procedure (SI Appendix, SI Methods and Table S1). The solid line is the fitted line from a linear model, and gray shading shows the 95% confidence interval around the fitted line. The dashed line at λ = 1 indicates the threshold for stable population growth. (B) Distribution of individual plant size (ln-transformed stem length in centimeters) for each population at year = t. Boxplot elements are as in Fig. 2. (C–F) Vital rates as a function of size (SI Appendix, Table S5). Gray points represent observed values across all populations, and colored lines represent model predictions based on population-specific coefficients (SI Appendix, Table S1). The Inset in F shows the same data and fitted lines but omitting individuals with >800 fruits.

Assessment of Which Vital Rates Explain Spatial Variation in λ.

Using a generalized additive model of the natural logarithm of λ [ln (λ)] as a function of vital rate parameters (SI Appendix, SI Methods), we found that nearly all (91.9%) of the variation in population growth across the range was explained by spatial variation in vital rates. Variance in growth and survival probability explained most of the variation in ln (λ) (44.31 and 34.56%, respectively). Much of the remaining variation in ln (λ) was explained by variance in recruitment probability (13.65%). Probability of flowering (0.66%), number of fruits (2.88%), number of seeds per fruit (0.52%), and the mean and SD of the size distribution of offspring (3.42%) explained the small remaining variation.

Demographic Compensation.

If spatial demographic compensation were operating across the range of E. cardinalis, there would be more negative correlations than expected by chance among sensitivity-weighted vital rates (i.e., the contributions of vital rates to population growth). We found four statistically significant negative correlations out of 21 possible pairwise correlations: between contributions of survival and flowering probabilities, survival probability and number of fruits, number of fruits and recruitment probability, and number of fruits and the size distribution of offspring (P < 0.05) (Table 1 and SI Appendix, Fig. S3). The observed proportion of negative correlations was significantly greater than expected by chance (P = 0.0196), consistent with significant spatial demographic compensation based on a recently described permutation test (8).

Table 1.

Pairwise Spearman rank correlations among vital rate contributions

Vital rate	Growth	Probability of flowering	Fruit number	Seeds per fruit	Probability of recruitment	Distribution of offspring size
Probability of survival	0.17 (0.829)	−0.40 (0.012)	−0.47 (0.004)	0.08 (0.671)	0.37 (0.981)	−0.16 (0.184)
Growth		−0.22 (0.112)	0.17 (0.832)	−0.07 (0.343)	0.20 (0.868)	−0.24 (0.092)
Probability of flowering			0.62 (1.000)	0.36 (0.978)	−0.21 (0.128)	−0.13 (0.233)
Fruit number				0.11 (0.726)	−0.38 (0.017)	−0.30 (0.047)
Seeds per fruit					−0.26 (0.075)	−0.23 (0.098)
Probability of recruitment						−0.12 (0.254)

P values are shown in parentheses. Statistically significant (P < 0.05) correlation coefficients are shown in bold.

Population-specific vital rate contributions to λ varied with latitude (Fig. 4 and SI Appendix, Table S3). Contributions of survival probability and fruit number were unimodal with respect to latitude but in opposing patterns, as in the equilibrium scenario of Fig. 1C. Survival contributions peaked at midlatitudes, where survival rates increased the local λ above the range-wide average, and decreased toward the north and south, where survival rates decreased the local λ below the range-wide average (Fig. 4 and SI Appendix, Table S3). Fruit number showed a weaker but opposing pattern, with the largest negative contributions at midlatitudes and positive contributions in the north and south (Fig. 4 and SI Appendix, Table S3). Other vital rates showed patterns consistent with the disequilibrium scenario of Fig. 1D. Namely, the contributions of growth and recruitment increased from negative values in the south to positive values in the north, while those for flowering probability did the opposite (Fig. 4 and SI Appendix, Table S3). Contributions of offspring size did not vary with latitude (Fig. 4 and SI Appendix, Table S3). Consistent with the analysis determining which vital rates explain spatial variation in λ, the magnitudes of population-specific vital rate contributions to λ were highest for survival probability and growth (Fig. 4 A and B) and lowest for flowering probability (Fig. 4C). Thus, the positive effects of flowering probability were too small to rescue λ in southern populations.

Fig. 4.

(A–F) Population-specific contributions of each vital rate as functions of latitude. Points correspond to observed vital rate contributions to latitudinal variation in λ, with error bars representing bias-corrected 95% confidence intervals derived from a bootstrapping procedure (SI Appendix, SI Methods). Solid lines represent linear and quadratic terms (based on best linear models) with P < 0.05 (SI Appendix, Table S3).

Discussion

Demographic compensation has been proposed as a mechanism for buffering populations from environmental variation, but few studies have examined the role of demographic compensation and life-history shifts in preventing population collapse. Consistent with disequilibrium between the range and niche, we found that λ increased with latitude during the 5-y study period, which included multiple years of severe drought and warming. This suggests that high-latitude, leading-edge populations have increased in recently ameliorated areas while low-latitude, trailing-edge populations have decreased in newly unfavorable environments, although this pattern could be altered by temporal variation (see below). Differences in growth, survival, and recruitment drove spatial variation in λ, with growth and recruitment probabilities increasing with latitude and survival probabilities decreasing from midlatitudes toward the northern and southern edges. Demographic compensation among vital rates means that single vital rates may be poor proxies for overall population performance because they respond differently to the same environmental gradient. However, although we found measurable spatial demographic compensation, small positive contributions from a greater probability of flowering and greater fruit number did not buffer southern populations from the large, negative effects of low survival, growth, and recruitment. Below, we place our key findings in the context of life-history strategies and recent climate change.

Disequilibrium Between Range and Niche Limits.

In contrast with many experimental and observational studies showing that performance is generally reduced at range edges and that range limits often coincide with niche limits (21–24), we found that populations at the northern and southern edges behaved differently. Most northern populations were either stable or growing. This is probably due to recent amelioration of growth constraints, although in theory it could be due to the immigration of preadapted genotypes from further south. Alternatively, species with a sharp boundary between suitable and unsuitable habitat could exhibit high population growth even at a range edge (sensu Fig. 1B). We consider this unlikely along a gradual latitudinal gradient. The pattern to date suggests a “lean” range shift (25, 26), where range limits have remained stable but the central tendency of the distribution is moving northward within the existing range. A lean range shift suggests disequilibrium with climate at both the leading and trailing edges, with disequilibrium at leading edges involving lags in colonization and disequilibrium at trailing edges involving delays in extinction (27).

Inadequate Demographic Compensation.

Demographic compensation may expand the range of environments across which population growth is positive (9). In this study, greater flowering probability and fruit number in low-latitude populations (resulting in small, positive contributions to variation in λ) (Fig. 4 C and D) suggest that λ could have been even lower at the southern edge in the absence of demographic compensation. However, even with statistically significant spatial demographic compensation across the geographic range of E. cardinalis, population growth was substantially lower in low-latitude populations relative to mid- and high-latitude populations. Compensatory increases in reproductive vital rates in low-latitude populations were simply too small to offset the large, negative contributions of survival, growth, and recruitment (Fig. 4 and SI Appendix, Figs. S2 and S3). In contrast, low probabilities of survival and flowering in high-latitude populations were offset by high growth and recruitment (Fig. 4 and SI Appendix, Figs. S2 and S3), thus promoting population growth. By providing one of few formal tests of demographic compensation, this study adds to a growing body of work on demographic compensation at various spatial scales (e.g., refs. 8, 9, 28, and 29).

Latitudinal Gradient in Life-History Strategy.

The spatial variation in vital rates and their contributions to λ that we observed is consistent with life-history theory predicting tradeoffs along the fast–slow continuum (12, 15, 30–33) and with genetically based differences among populations (34). Low-latitude populations of E. cardinalis experience greater interannual variation in precipitation (Fig. 2C and SI Appendix, Fig. S4) and germinate, photosynthesize, and grow faster in a common garden (34). Further, low-latitude populations exhibit a faster, more annualized life history in nature (evidenced by low growth and survival but high flowering probabilities). Conversely, high-latitude populations from more temporally stable environments grow more slowly (34) and are uniformly perennial (evidenced by high growth and low flowering probabilities) (Fig. 4 and SI Appendix, Fig. S2). The lower rates of survival in northern populations are most evident in intercepts rather than in the slopes of the models describing survival as a function of size, suggesting that survival increases quickly with size (Fig. 2 and SI Appendix, Table S1). Countergradient variation in growth patterns, where southern populations have high growth capacity in a common garden (34) but low actual growth in the field, suggests that southern plants grow rapidly to the reproductive stage and then switch allocation away from vegetative growth. Interestingly, one northern population with extremely high estimated population growth (population 4; SI Appendix, Table S1) is in unusually unstable substrate and has annual life-history characteristics that are more typical of southern populations (e.g., large negative contribution of survival and high positive contributions for reproduction) (Fig. 4). Because high-latitude populations have already begun to experience climates historically found further south (Fig. 2B), the behavior of population 4 during this study might provide a window into the potential population dynamics of southern populations under more favorable conditions.

Population Dynamics During a Period of Severe Drought and Heat.

Our findings are based on a snapshot of population dynamics during a period of extreme climatic events. In particular, California experienced a severe drought from 2012 through 2014 (35, 36), compounded by record high temperatures (37) in three of the five study years (Fig. 2 B and C and SI Appendix, Figs. S4–S6). Nonetheless, the study encompassed a broad range of the historical variation in climate, particularly at high and low latitudes. For northern and southern populations, the study years encompass approximately the 25th percentile of historical temperature to extremely high temperatures (Fig. 2B). Southern populations showed a similar span for precipitation, from approximately the 25th percentile of historical precipitation to much wetter than the historical mean, whereas northern populations encountered severe drought to extremely wet conditions during the study (Fig. 2C and SI Appendix, Figs. S4 and S6B). The study years for midlatitude populations overlapped the least with their historical distributions, from roughly median historical temperatures to extremely warm temperatures (Fig. 2B) and from severe drought to the 75th percentile of historical precipitation (Fig. 2C and SI Appendix, Fig. S4). Had we captured a cool and wet year during the study at midlatitudes, some of the central populations might have increased rather than being stable.

The interaction of temperature and precipitation, as well as the sequencing of events, also influences population responses. For example, 2014 was extremely warm across the entire latitudinal transect, but it was much drier than average only in south-central populations (SI Appendix, Fig. S6). Also, although the study years spanned a large range of variation in the south, from cool and wet to hot and dry, they also included more consecutive years of anomalously hot and dry conditions compared with the north (SI Appendix, Fig. S6). Given the greater historical variability in precipitation in the south, more time may be needed to accurately capture long-term population dynamics. We expect southern populations, with their fast life-history characteristics, have a high potential to recover if more favorable conditions return in the future, even if infrequently.

While our demographic data were drawn from years representing extreme conditions, these are exactly the conditions likely to become more frequent as climate change accelerates and drought increasingly coincides with record warming (37). Indeed, the patterns observed spatially were mirrored by patterns observed temporally within the southern trailing edge region (SI Appendix, SI Methods, SI Results and Discussion, Fig. S7, and Table S7). Specifically, survival and flowering had opposing trends across years, but increased flowering was not sufficient to compensate for low survival. Thus, despite some evidence for spatial and temporal demographic compensation, such compensation was not sufficient to rescue trailing-edge populations from population declines during a period of severe drought and warming. Although demographic compensation alone did not stabilize trailing-edge populations during the study, in theory it could buy time for evolutionary rescue by delaying extinction (38). Continued monitoring to link yearly variation in weather to yearly variation in vital rates and population growth will permit more robust projections of long-term responses to changing climate. As additional demographic data accumulate for multiple generations, populations, and species across broad spatial scales and environmental gradients, we will gain a more comprehensive understanding of how the environment and geography shape vital rates and, in turn, population dynamics, allowing better forecasts of range shifts.

Materials and Methods

Study System.

E. cardinalis (Phrymaceae) is a perennial forb that grows along seeps, streamsides, and riverbanks in western North America. Individuals can spread via rhizomes, but recruitment occurs primarily from seeds. The species’ latitudinal range extends from central Oregon to northern Baja California, Mexico (Fig. 2A). Within this extent, populations occur across a broad range of elevations and climates (Fig. 2 B and C and SI Appendix, Table S4), from sea level up to ca. 2,400 m (39). However, latitude and elevation of occurrences covary (Pearson r = −0.57, P < 0.05), such that northern populations are primarily at low elevations, while southern populations can reach higher elevations.

Demographic Surveys.

We established census transects in 32 populations spanning almost the full latitudinal extent of the species’ range (Fig. 2A and SI Appendix, SI Methods and Table S4). Censuses were conducted each autumn, after most annual reproduction was complete, from 2010 to 2014 to record annual survival (0 or 1), growth (see below), probability of flowering (0 or 1), number of fruits, and recruitment (the proportion of seeds from previous year that germinated). In total, the fates of 11,246 plants were recorded (range: 32–1,439 individuals per population; $\overline{N}$ = 351 individuals) (SI Appendix, Table S4). To estimate size and annual growth for each plant, up to five nonflowering and five flowering stems were measured from the ground to the base of the last pair of leaves; all remaining stems were tallied, and total stem length was estimated by extrapolating from the average stem length of the 10 measured stems, which accurately captures total stem length (40). Plant reproduction was estimated as the product of the number of mature fruits on up to five stems of a given individual × the total number of flowering stems on that individual × the population mean seed number per fruit in a given year (SI Appendix, SI Methods). Based on experimental seed additions (SI Appendix, SI Methods), seed dormancy was set to zero, and seedling recruitment was estimated by dividing the number of recruits by total seed production in the prior year.

IPMs.

To estimate λ for each population, we used integral projection models (IPMs), where vital rates are modeled as continuous functions of individual plant size (41, 42). IPMs are similar to stage-structured matrix projection models but are better-suited for species such as E. cardinalis that have no natural size breaks for defining discrete stages (SI Appendix, SI Methods) (41). To construct IPMs for each population, we first pooled data across all populations (n = 32) and years (n = 4 annual transitions) to construct a global model of each of four vital rates (survival probability, growth, flowering probability, and fruit number) (SI Appendix, Table S5) as a function of size (ln-transformed total stem length in year t, fixed effect), year (random effect), and population (random effect) (SI Appendix, SI Methods). We extracted population-specific coefficients (slope and intercept) for each vital rate function to parameterize the IPM for each population (SI Appendix, Table S1). Due to small sample sizes in some populations in some years, we constructed the IPM for a given population using data from all years, accounting for year via inclusion as a random effect in all vital rate models (SI Appendix, SI Methods). Final vital rate models, including random effects structure, are provided in SI Appendix, Table S5, and population-specific coefficients (averaged across years) used to parameterize each model are in SI Appendix, Table S1.

We used the fitted vital rate models to build a discretized matrix with 100 size bins, ranging from 0.9 times the minimum to 1.1 times the maximum size observed in each population. To correct for the “eviction” of individuals falling beyond this size range (43), we assigned individuals to the smallest size bin in the case of offspring and to the largest size bin in the case of large adults (44). We then calculated λ as the dominant eigenvalue of the discretized matrix. We performed all analyses in R 3.4.2 using code modified from appendices in Merow et al. (44) and Rees et al. (45). To obtain 95% confidence intervals around λ estimates for each population, we bootstrapped the data 2,000 times, allowing for assessment of whether λ was statistically different from 1 (SI Appendix, SI Methods).

Analysis of Latitude vs. λ and Vital Rates.

To assess how λ varies across latitude, we used linear regressions with λ as the response variable and latitude as the predictor variable. We compared models with and without quadratic terms and used bias-corrected Akaike information criterion (AIC_c) to select the best models. For vital rates that varied with size (survival, growth, flowering probability, and fruit number), we first divided individuals into population-specific small (0–20% quantile), medium (40–60% quantile), and large (80–100% quantile) size classes. We then calculated population- and size-specific survival probability (the observed proportion of individuals that survived from year t to year t + 1), growth (mean size in year t + 1), flowering probability (the observed proportion of individuals that flowered in year t), and fruit number (mean fruit number in year t, omitting small and medium size classes because plants in these classes flowered in only a small subset of populations). We regressed mean vital rates for each size class against latitude, with and without a quadratic term, and used AIC_c for model selection (SI Appendix, Table S2). Because the study populations spanned ∼1,700 m in elevation, we performed similar analyses with elevation as a predictor variable but found no statistically significant relationships between elevation and vital rates or λ, and models including latitude alone performed better than any models including latitude and elevation. Thus, here we present only results including latitude as a predictor variable.

Assessment of Which Vital Rates Explain Spatial Variation in λ.

To identify which vital rates contributed most to observed differences in λ among populations, we initially performed a standard life table response experiment (46), but the range of variation in parameter values among populations resulted in a poor linear approximation of λ as a nonlinear function of the parameters that vary among populations. Instead, we fit a generalized additive model (GAM) with ln (λ) as the response variable (λ was transformed to meet model assumptions) and smoothed functions of vital rate parameters as explanatory variables (SI Appendix, SI Methods and refs. 47 and 48). To obtain contributions for each vital rate as a whole (rather than for each parameter in each vital rate function), we summed across all coefficients of a given vital rate (e.g., the survival contribution equals the survival slope contribution plus the survival intercept contribution) (SI Appendix, SI Methods). Vital rate contributions to variability in ln (λ) were normalized to sum to 100%. These contributions are shaped by both the spatial variation in each vital rate and the sensitivity of λ to each vital rate.

Demographic Compensation.

Following Villellas et al. (8), we inferred demographic compensation across the species’ range by determining whether the observed data harbor a greater proportion of negative correlations among sensitivity-weighted vital rates (i.e., contributions) than expected by chance (SI Appendix, SI Methods). To test whether there are more negative correlations among vital rate contributions than expected by chance, we obtained Spearman rank correlations between all pairs of vital rate contributions. We then determined the observed percentage of correlations that were significantly negative (P < 0.05) based on a one-tailed test because compensation involves only negative correlations among vital rate contributions. Next, in each of 10,000 iterations, we randomly permuted contributions for each vital rate among populations, calculated Spearman rank correlations, and determined the percentage of significantly negative correlations. Thus, we obtained a null distribution of percentages of negative correlations against which we could compare our observed percentage. We inferred statistically significant demographic compensation based on the proportion of values in the null distribution that were greater than or equal to the observed percentage of negative correlations (8). To assist in our interpretation of the test of demographic compensation, we also examined how vital rate contributions varied with latitude. We used linear regression to model each vital rate contribution as a function of latitude with and without quadratic terms and then used AIC_c for model selection (SI Appendix, Table S3).