Predicting anisotropic thermal displacements for hydrogens from solid-state NMR: A study on hydrogen bonding in polymorphs of palmitic acid

Abstract

The hydrogen-bonding environments at the COOH moiety in eight polycrystalline polymorphs of palmitic acid are explored using solid-state NMR. Although most phases have no previously reported crystal structure, measured ¹³C chemical shift tensors for COOH moieties, combined with DFT modeling establish that all phases crystallize with a cyclic dimer $(R_2^2(8))$ hydrogen bonding arrangement. Phases A₂, B_m and E_m have localized OH hydrogens while phase C has a dynamically disordered OH hydrogen. The phase designated A_s is a mix of five forms, including 27.4% of B_m and four novel phases not fully characterized here due to insufficient sample mass. For phases A₂, B_m, E_m, and C the anisotropic uncertainties in the COOH hydrogen atom positions are established using a Monte Carlo sampling scheme. Sampled points are retained or rejected at the ± 1σ level based upon agreement of DFT computed ¹³COOH tensors with experimental values. The collection of retained hydrogen positions bear a remarkable resemblance to the anisotropic displacement parameters (i.e. thermal ellipsoids) from diffraction studies. We posit that this similarity is no mere coincidence and that the two are fundamentally related. The volumes of NMR-derived anisotropic displacement ellipsoids for phases with localized OH hydrogens are 4.1 times smaller than those derived from single crystal x-ray diffraction and 1.8 times smaller than the volume of benchmark single crystal neutron diffraction values.

Table of contents

Solid-state NMR and DFT methods establish anisotropic thermal displacements for COOH hydrogens in several polymorphs of palmitic acid.

Introduction

Polymorphism in solids is relatively common with a recent survey reporting that roughly one-third of the structures in the Cambridge Structural Database exhibit more than one phase.¹ Pharmaceutical studies designed specifically to discover new phases found that between 50% and 75% of compounds considered crystallize in more than one phase.¹ Knowledge of the specific phase of a material is important because different phases can vary in their physical properties. For example, a material must crystallize in a non-centrosymmetric space group in order to exhibit second order harmonic generation. Other properties such as color, solubility and density can also vary with polymorphic form.

The n-alkyl monocarboxylic acids are a group of compounds that have been extensively studied and found to exhibit a rich variety of polymorphism.^2,3 Acids containing an even number of carbons crystallize in at least seven different phases designated A₂, A_super, B_m, B_o, E_m, E_o, and C.⁴ The n-alkyl acids having an odd number of carbons crystallize in at least five distinct phases denoted A’, B’, C’, C” and D’.⁵ While the phases of many n-alkyl monocarboxylic acids have been characterized crystallographically, others remain relatively unstudied. For example, palmitic acid (C₁₆H₃₂O₂) has only one reported crystalline phase.^2,6 Recently, our laboratory has characterized 8 forms of palmitic acid. Characterizing the hydrogen bonding environment in these forms is important because the COOH groups in different phases of a given n-alkyl acid can vary due to the presence or absence of disordered hydrogens.⁷ This difference in hydrogen bonding is purported to correlate with hydrogen bond strength, with disordered acids forming stronger bonds.^8,9 In these cases, the hydrogen bond is strong enough to lower the barrier and allow increased motion (exchange) between the hydrogen bond donor and acceptor, so that the hydrogen transits more freely and can even, in very strong/low-barrier hydrogen bonding situations, sit symmetrically between the two.^10,11,12,13 The use of the term “disorder” in this context can be somewhat misleading as the structure of the heavy atoms across the crystal is in fact homogeneous, but the acidic hydrogen atom is moving freely within a broader potential well. Conventional x-ray crystallography cannot always distinguish between localized and disordered hydrogen bonding because the difference involves primarily the COOH hydrogens and these sites are seldom well characterized.

Solid-state NMR (SSNMR) offers an alternative approach for positioning hydrogens within hydrogen bonds. Several SSNMR techniques have now been used to locate both disordered^14,15 and localized protons in N–H⋯N,^{16,17,18,19,20,21,22} N–H⋯O,^{18,19,23,24,25} O–H⋯O^{9,18,26,27,28,29} and other bonds.^30,31 The ability to locate hydrogens also allows nitrogen sites to be classified as NH₃⁺, NH₂, NH or non-protonated.^20,32 Techniques are also now available for rapidly evaluating ¹⁴N containing hydrogen bonds.^20,32 The aim of the present study is to use differences in ¹³C shift tensors to characterize the hydrogen bonding environment at the COOH moiety in the different polymorphs of palmitic acid. In the following we demonstrate that phase C includes a disordered COOH hydrogen, while all other phases contain localized hydrogens. A method for estimating anisotropic uncertainties for COOH hydrogen positions based upon NMR comparisons is also presented. This approach is similar to the characterization of anisotropic positional accuracy in NMR crystallography recently introduced by Hofstetter and Emsley,³³ but importantly allows for the case of bond breakage and formation present in systems undergoing proton exchange. The prior study of anisotropic displacements is based upon molecular dynamics,³³ an approach that usually precludes the possibility of bond cleavage unless specialized potentials are utilized. It is notable that other experimental SSNMR techniques can also monitor COOH hydrogen bond breaking and forming events.³⁴ The methodology introduced herein also allows phases with no known crystal structure to be accurately characterized.

Experimental

Samples of palmitic acid prepared as phases A₂, A_s, E_m, and B_m were obtained from Dr. Evelyn Moreno-Calvo (Institut de Ciencia de Materials de Barcelona) and evaluated as received. A description of sample preparation of each phase and more complete crystallographic characterizations will be given elsewhere. A sample of palmitic acid phase C was obtained by dissolving palmitic acid in toluene then allowing the solvent to slowly evaporate.⁶

Solid-state NMR ¹³C tensor principal values for phase A₂ were acquired on a Varian Infinity operating at 599.78920 and 150.83191 MHz for ¹H and ¹³C, respectively. The ¹³C tensor data for phase E_m was collected using a Chemagnetics CMX operating at 400.11880 and 100.61916 MHz for ¹H and ¹³C, respectively. A Chemagnetics CMX operating at 200.04338 and 50.30559 MHz for ¹H and ¹³C, respectively, was used to obtain ¹³C tensor data for phases B_m and C. The FIREMAT method³⁵ was employed to acquire tensor data for phases B_m, C and E_m. As only a few milligrams of phase A₂ were available, tensor data for this phase were acquired by analyzing the intensity of sidebands obtained from a 1D CP/MAS experiment. No tensor data was obtained for phase A_s since it was a mixed phase solid and the mass of each phase was too low for effective analysis. For phase A_s, only 1D isotropic ¹³C shifts were obtained using CP/MAS. For all analyses, TPPM ¹H decoupling³⁶ was employed and all ¹³C shifts were referenced on the TMS scale using the methyl resonance of hexamethyl benzene at 17.35 ppm as a secondary chemical shift reference. A summary of other relevant analysis parameters is given in Table 1.

Table 1.

Analysis parameters for acquisition of ¹³C tensor data for phases of palmitic acid.

	A2	As	Bm	C	Em
Spinning speed (Hz)	4000	4000	527	527	527
Recycle time (s)	25.0	30.0	20.0	25.0	23.0
1H 90° pulse (µs)	3.1	4.5	3.9	3.9	4.2
13C 180° pulse (µs)	—	—	8.7	8.7	9.2
Evolution spectral width (kHz)	—	—	26.9	26.9	26.9
Acquisition spectral width (kHz)	40.0	40.0	65.4	65.4	65.4
Evolution digital resolution (Hz/point)	—	—	15.9	15.9	58.6
Acquisition digital resolution (Hz/point)	78.1	19.5	15.9	15.9	26.2
# evolution points	—	—	51	51	51
# scans/evol. Point	20488	8132	576	576	576
Contact time (ms)	3.0	1.0	3.0	3.0	3.0
Analysis method	CP/MAS	CP/MAS	FIREMAT	FIREMAT	FIREMAT
Total analysis time	17 h	2.8 d	6.8 d	8.5 d	15.6 d

Computed tensors were calculated using Gaussian 03 at the B3PW91/D95** level of theory. All computed tensor values were corrected for basis set superposition error using the counterpoise method.^37,38 Alternative functionals and basis sets could also be considered. However, because all structural comparisons are ultimately made using an F-test, the results are somewhat independent of the particular functional chosen. This is because the F-test is relatively tolerant to systematic errors since such errors are present in both structures being compared and therefore cancel in the ratio used to compute the F value. Computed tensor data for only the central molecule of the trimer were used for all statistical comparison with experimental data. A plot of computed shielding versus shifts for phases A₂, B_m and E_m was made and fit using a least-squares procedure. All data were converted to the icosahedral representation before plotting as recommended by Alderman et al.³⁹ These data were linear and strongly correlated (R² = 0.9981) and the optimal conversion of shield to shift was found to be shift = (shielding −198.825)/(−1.061).

An elemental analysis of palmitic acid phase C was performed (Atlantic Microlab) to determine if this phase is a free carboxylic acid or a salt. This analysis found C=75.03%, O=12.68% and H=12.58% with a reported error of ± 0.3%. Predicted values for the free acid (C₁₆H₃₂O₂) are C=74.94%, O=12.48% and H=12.58%. This close match supports the conclusion that phase C contains a COOH moiety.

The Monte Carlo sampling process employed the butyric acid dimer model described previously for lauric acid.⁹ This fragment-based approach has been demonstrated to account for most lattice effects by directly comparing computed shift tensors with those calculated using periodic boundary methods.⁹ For structures having a localized OH hydrogen, an initial structure with an O–H bond length of 1.16 Å was used. For the dynamically disordered phase C, two initial structures with O–H bond lengths of 1.16 Å and 1.46 Å were employed. In each case, a total of 2500 new OH hydrogen positions were randomly generated using a process that samples points in a cube shape with new points constrained to lie within ± 0.5 Å of the initial position in each direction (i.e. X, Y or Z). The sampling process allows both of the OH hydrogens to potentially move in each iteration. For each structure generated, ¹³C shift tensors were computed as described above and the calculated ¹³COOH tensors then compared to experimental values using an F-test as described elsewhere.⁴⁰ Calculated tensors within one standard deviation (i.e. ± 1σ) of experimental data were retained. A poor fit in either of the two tensors was considered grounds for rejection of a given structure. All retained positions were averaged to identify new hydrogen positions. In all cases, the initial OH hydrogen position differed from the average position (r̄). To correct for this difference, the OH hydrogen was translated to the average position. Since each of the retained structures have known bond lengths (r_i), the error in OH bond lengths were computed from σ = [Σ(r_i−r̄)²/(N−1)]^1/2, where N denotes the number of retained structures. Anisotropic displacement parameters were computed based on variations of the retained points from the average positions as more fully described in the text.

Results and discussion

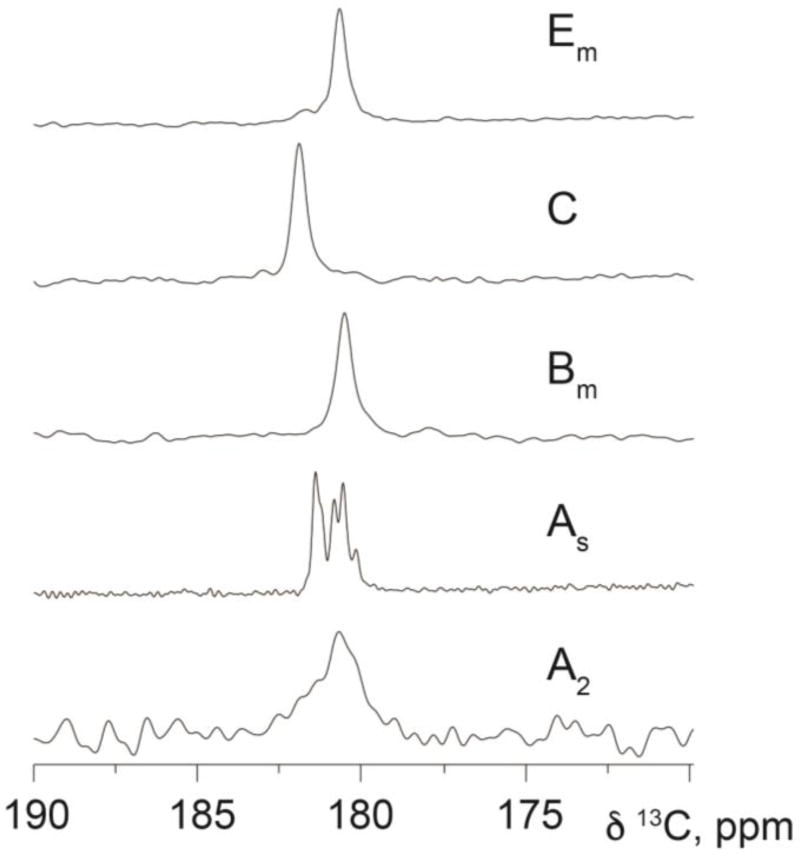
In this study, five samples of palmitic acid were obtained and evaluated including forms tentatively identified as A₂, A_s, B_m, C and E_m. Chemical shift tensor data were measured for ¹³COOH sites in all phases except A_s using methods described in Experimental. Phase A_s exhibits five resonances, but only 1D ¹³C isotropic shifts were recorded due to the small amount of material available. While four of the ¹³COOH resonances do not match chemical shifts of the other forms (i.e. A₂, E_m or C), the final resonance corresponds to the frequency of B_m and was thus provisionally designated B_m. Admittedly, two or more of the resonances in A_s may originate from a single phase containing multiple molecules per asymmetric unit. However, significant differences in peak intensities in A_s suggest that it is more likely that the spectrum consists of 5 distinct phases. A plot of all ¹³COOH isotropic resonances is shown in Figure 1 and supports the conclusion that at least 8 unique phases of palmitic acid are identified by this work. At present, only phase C has an established crystal structure.^2,6 Table 2 lists the measured ¹³COOH tensors and isotropic shifts.

Figure 1.

A plot of the ¹³COOH isotropic resonances measured for the phases of palmitic acid studied here. All measured peaks are unique except for one of the signals of phase A_s that potentially corresponds to form B_m, thus a total of at least 8 unique phases are identified from this study. The wider lines observed in phases E_m, C and B_m are a result of acquiring these data on a lower field (4.9 T) spectrometer. Phases A_s and A₂ were acquired, respectively, at field strengths of 14.1 T and 9.4 T. Phase A₂ is crystalline and the unusually wide line observed in this phase is presumed to arise from a small average particle size.

Table 2.

Measured ¹³C tensor principal and isotropic shift values for the COOH groups in the polymorphs of palmitic acid evaluated here.

Phase	δ11 (ppm)	δ22 (ppm)	δ33 (ppm)	δiso. (ppm)
A2	256.1	177.8	106.3	180.71
As	—	—	—	180.18
	—	—	—	180.58a
	—	—	—	180.85
	—	—	—	181.27
	—	—	—	181.44
Bm	257.9	174.5	109.3	180.56
C	233.5	203.3	109.1	181.98
Em	251.9	176.6	113.7	180.73

^aThis resonance represents approximately 27% of a form matching the isotropic shift of B_m.

The hydrogen bonding environment of a COOH is strongly reflected in the ¹³C tensor data. In prior work,⁴¹ Gu et al. established that a ¹³COOH can be distinguished from a ¹³COO⁻ by the magnitude of the δ₁₁ tensor shift. A δ₁₁ shift greater than 250 ppm indicates that a COOH is present, while shifts less than 250 ppm are observed for COO⁻ sites. Hydrogen bonding strength is indicated by the magnitude of the δ₂₂-shift, with stronger hydrogen bonds producing higher frequency δ₂₂ values. Hydrogen bonded COOH’s were found to have an average δ₂₂ shift of 158 ppm with the most strongly hydrogen bonded COOH sites having a δ₂₂ shift of 174 ppm. The δ₃₃ shift exhibited only small variations and was not used in structural analysis. Subsequent work by Kalakewich et al.⁹ expanded upon these conclusions by demonstrating that proton disordered COOH sites have ¹³C principal values that are indistinguishable from COO⁻ moieties. Taken together, these prior studies indicate that palmitic acid phases A₂, B_m, and E_m contain COOH groups that are strongly hydrogen bonded. A similar comparison suggests that phase C contains a COO⁻ or an H disordered COOH due to the δ₁₁ shift of 233.5 ppm. Elemental analysis unambiguously shows that no counter ion is present in phase C and gives a near-perfect match for a protonated COOH (see Experimental). Hence, phase C appears to include a disordered COOH hydrogen.

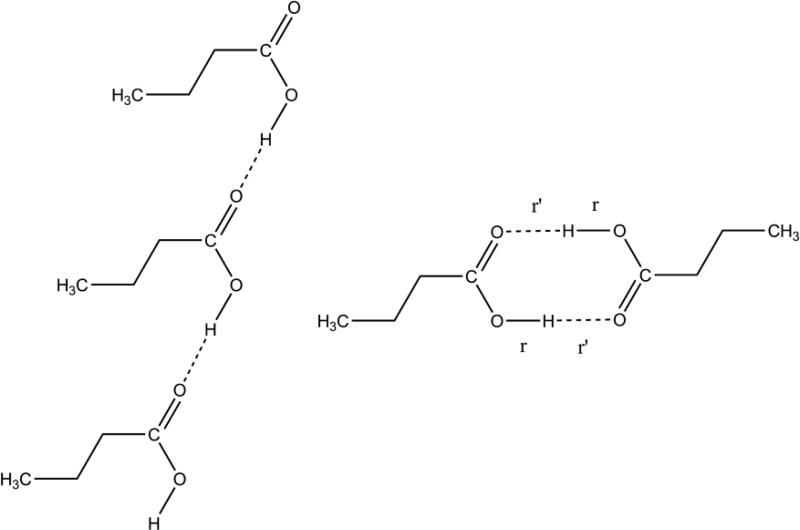
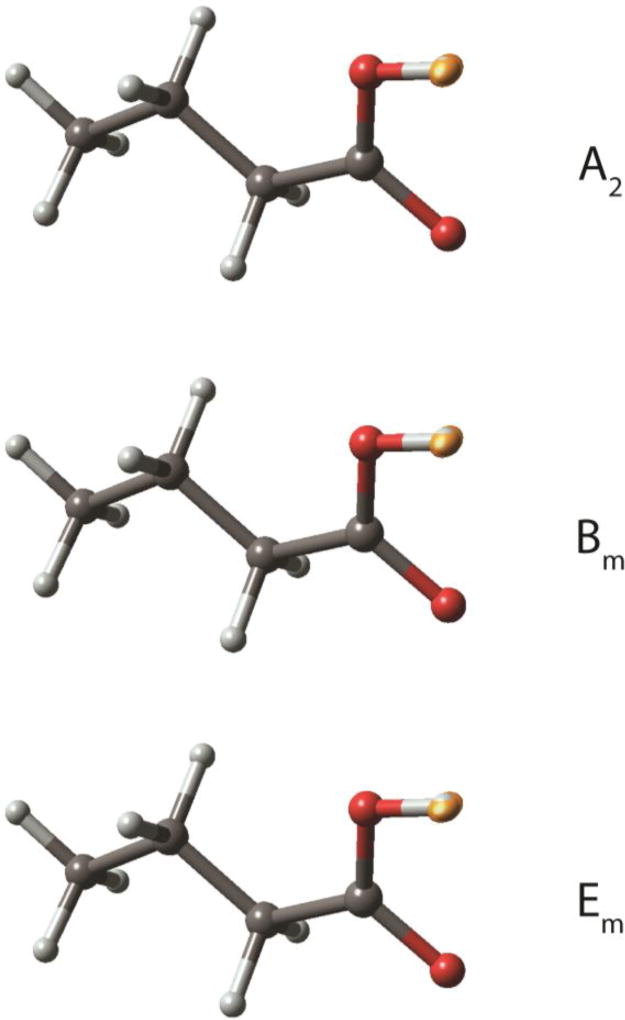
The comparison of palmitic acids tensor data with prior studies is invaluable in predicting carboxyl protonation or hydrogen disorder and in estimating hydrogen-bond strength. Nevertheless, this approach is limited in the sense that it does not predict longer-range order, such as hydrogen bonding geometry. This deficiency makes it desirable to include an independent technique to extend structural conclusions. A second analysis was therefore performed involving a comparison of experimental ¹³C tensor data for the COOH with DFT computed tensor data for model structures with the two most common hydrogen bonding geometries. This approach has been used in numerous studies and demonstrated to provide accurate structures.^{40,42,43,44,45,46,47,48} This technique has the advantage that a wide variety of structural models can be evaluated. In the case of palmitic acid, butyric acid was used as a model since it contains all the features of palmitic acid out to the γ–position. It is known that sites beyond the γ–position have very little influence on measured shifts in most structures,⁴⁹ and butyric acid has been demonstrated to be a suitable model for the closely related molecule, lauric acid.⁸ For all phases, two model structures were evaluated based upon motifs observed in prior studies:⁵⁰ a cyclic dimer and a trimeric catemer containing an antiplanar COOH hydrogen (Figure 2). The cyclic dimer with r ≈ 1.0 Å and r’ ≈ 1.6 Å, often referred to as an $R_2^2(8)$ hydrogen bond,⁵¹ is the most commonly observed arrangement for carboxylic acids containing only one COOH group, while the catemer is rarely encountered.⁵⁰ In preparing model structures, a series of compounds were generated in which r was systematically lengthened and r’ decreased by the same amount. This process maintains a constant O⋯O distance between pairs in the cyclic dimer and allows the position of the hydrogens (including disordered hydrogens) to be located very accurately to within ± 0.02–0.07 Å.^8,52 The cyclic dimer structure with $R_2^2(8)$ hydrogen bonding and r ≈ 1.0 Å and r’ ≈ 1.6 Å was found to be the best fit for phases A₂, B_m and E_m. In all cases, the trans orientation (i.e. a C_β–C_α–C=O dihedral angle of 180°) was statistically preferred over the cis structure (Figure 3a).

Figure 2.

Model structures evaluated to determine hydrogen bonding distances and longer-range order in various polymorphs of palmitic acid. Structures considered were a catemer (left) and a cyclic dimer (right). In each case, an energy-minimized structure was obtained (B3LYP/D95*) and ¹³C tensors computed (B3PW91/D95**). Only tensor data from the central molecule of the trimer were considered. Comparison of computed tensor values with experimental data allowed a best fit to be determined. The cyclic dimer with r ≈ 1.00 Å and r’ ≈ 1.63 Å best represents phases A₂, B_m and E_m. Phase C also matches the dimer with a disordered O–H proton having two probable positions at 1.23 ± 0.06 Å and 1.46 ± 0.03 Å. No structural determination was made for phase A_s since tensor data were not obtained due to the limited amount of material available. The trimeric catemer model was rejected as a feasible structure for any of the observed phases with a statistical confidence of > 99%.

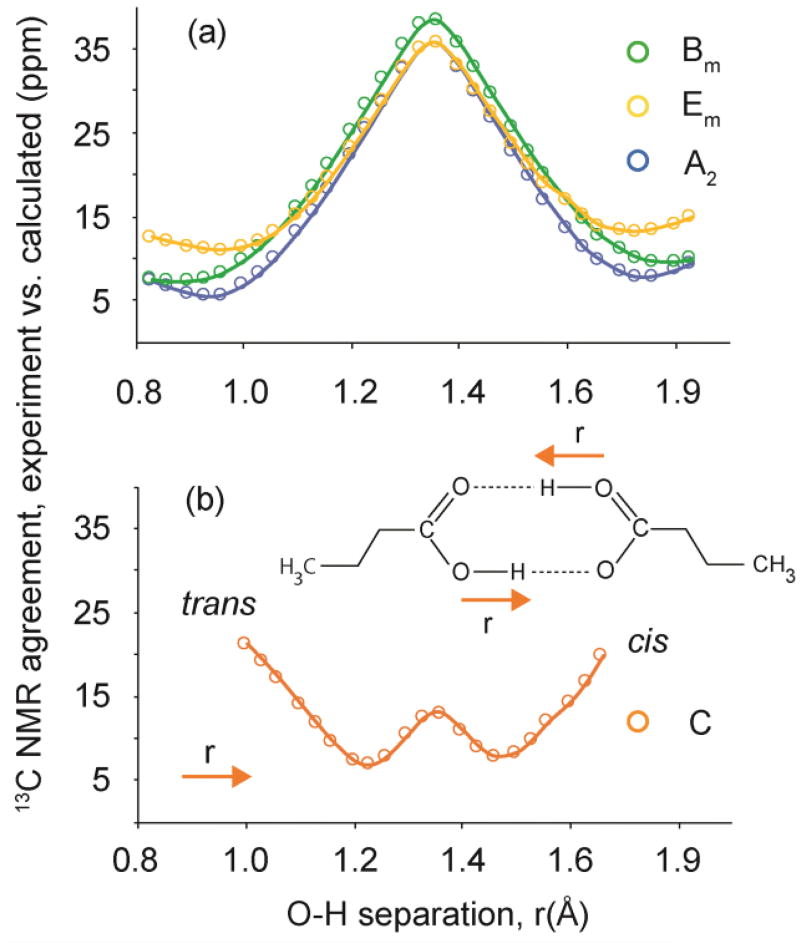
Figure 3.

Plots illustrating the agreement between experimental ¹³COOH tensor values for all phases (A₂, B_m, E_m, and C) and DFT computed values for model structures with various O–H bond distances (r). Plot (a) shows that the best agreement for phases A₂, B_m, and E_m is a trans structure having O–H bond lengths of 0.93 ± 0.08 Å, 0.86 ± 0.11 Å and 0.96 ± 0.10 Å, respectively. Plot (b) illustrates that phase C agrees with DFT predictions at O–H bond lengths of 1.23 ± 0.06 Å and 1.46 ± 0.03 Å. The δ₁₁ tensor component of phase C corresponds closely to those measured previously in COO⁻ moieties,⁴¹ however, elemental analysis indicates that a COOH is present. These conflicting observations are consistent with the presence of COOH hydrogen disorder in which the proton that is dynamically disordered symmetrically about the midpoint between two oxygens separated by 2.63 Å.

Phase C also matches uniquely to the cyclic dimer, but a plot of r versus the rms agreement between computed and experimental tensor data shows good agreement at two O–H bond lengths, r = 1.23 ± 0.06 Å and r = 1.46 ± 0.03 Å (Figure 3b). Thus, it appears that the COOH proton is disordered, either in the static sense with local variations in the hydrogen placement, or dynamically, with the proton rapidly sampling two local structural minima. Static disorder is considered unfeasible here because only one ¹³COOH resonances is observed experimentally. Two lines would be expected in a ¹³C isotropic spectrum of a sample with static disorder. To evaluate the influence of such dynamic averaging on the NMR parameters for phase C, the shift tensors for all structures with O–H bond lengths within ± 1σ (as judged using F-values)⁴⁰ of the global minimum in Figure 3b were averaged (i.e. 1.16–1.26 Å and 1.43–1.50 Å). The average rms error for these structures was 8.0 ppm, an agreement with experimental data that is statistically indistinguishable from the pair of best-fitting static structures having uncertainties of 6.8 and 7.8 ppm. This analysis predicts an average O–H bond length of 1.32 Å corresponding to the midpoint between oxygen atoms in the hydrogen bond, but suggests that the proton has two locally most probable locations at r = 1.23 and r = 1.46 Å. Again, we note the correlation between the lengthening of the donor-proton distance and a stronger hydrogen bond with a concomitant decrease in the barrier to exchange.

In a more constrained approach to a time averaged representation, dynamically exchanging COOH protons can be assumed to sample both minima on the NMR timescale and modeled by averaging two contributing structures lying on either side of a symmetric double well. In this analysis, each structure is constrained to have an identical OH hydrogen distance from the center (1.32 Å in this case) with matched displacements in either direction. This model requiring symmetrical hydrogen transfers was previously shown to accurately describe hydrogen exchange in benzoic acid.^53,54 Tensor computed for the two structures are averaged with the assumption of equal populations. Employing this approach, an average O–H bond length of 1.34 Å is guaranteed by construction. Deviation about this point of ± 0.11 Å give the best fit with experimental data

The trimeric catamer model featuring an antiplanar COOH hydrogen and an O–H bond length of 1.0 Å (Figure 2) had an error of 42.1 ppm and thus was rejected as a feasible structure at a statistical confidence of 99.3%. Adding disorder to the catameric model is not feasible because the OH bond formed in the new structure would include a C–O–H valence angle of 180° and is therefore unrealistic. The rejection of the catameric structure is consistent with the experimental observation that the antiplanar hydrogen orientation is observed only when the OH can participate in an intramolecular O–H⋯O hydrogen bond.⁵⁰ In addition, the antiplanar OH hydrogen orientation is energetically less favorable than the synplanar orientation by 2–4 kcal/mol.^55,56

The comparison of palmitic acids tensor data with modeling results described herein and in prior work⁴¹ accounts for most structural features of the phases studied here. Yet, one feature of the spectra in Figure 1 is worthy of further comment. Specifically, wide isotropic lines, as observed in the ¹³C spectrum of phase A₂, are often interpreted as arising from an amorphous solid. Amorphous phases lack long-range order and sometimes exhibit a high degree of molecular motion. Crystalline solids can be distinguished from amorphous materials by observing their ¹H/¹³C cross-polarization behavior.⁵⁷ Crystalline materials experience effective cross-polarization over significantly longer contact times, while the motion present in amorphous materials leads to faster relaxation during the cross-polarization process (i.e. shorter T_1ρ values). In the case of phase A₂, the cross-polarization behavior was found to be consistent with that observed for crystalline solids (see Experimental). Observation of long cross-polarization times in A₂ also indicates that local motion at the COOH is negligible. This observation is significant because motion can significantly broaden linewidths. Motion also averages shift tensor values and can thus be detected by the observation of a diminished span (i.e. δ₁₁–δ₃₃). Phase A₂ exhibits the largest span of any of the phases of palmitic acid evaluated here and thus ¹³COOH tensors do not support the hypothesis of local COOH motion in A₂. Finally, it is known that wide isotropic lines can occur in solids due to small average particle size.⁵⁸ Thus phase A₂ appears to be a crystalline phase composed of very small particles.

Modeling anisotropic displacements in hydrogen positions with NMR

The analyses described above serve to establish OH bond lengths and hydrogen bonding geometries in most phases of palmitic acid. Other NMR studies have also demonstrated an ability to provide accurate bond lengths involving hydrogen and other atoms.^59,60 But to be truly meaningful, measurement of bond lengths must include uncertainties in the three-dimensional atomic positions. Such uncertainties are commonly reported in x-ray crystal structures as anisotropic displacement parameters (ADPs) and illustrated as ellipsoids. These displacement parameters reflect the fact that small amplitude vibrational and librational motions occur at individual atomic sites, even at 0 K.⁶¹ Displacements can also be caused by larger scale motions such as conformational changes. Here, anisotropic uncertainties in COOH hydrogen positions are established using the Monte Carlo sampling approach together with DFT calculations. The methodology developed is applicable to both materials with known crystal structures and to microcrystalline solids not suitable for traditional crystallography.

A variety of procedures is now available for generating candidate structures that reflect thermal agitation by sampling atomic positions around an initial atomic site.^{62,63,64,65,66} Here, a Monte Carlo scheme was employed to sample COOH hydrogen positions. While this approach is computationally expensive and classical, atomic displacements in solids are known to arise from a number of causes other than normal mode vibrations, such as deviations from ideal periodicity, density variations and hydrogen tunnelling.⁶⁷ Subtle improvements to crystal structures comparable to thermal displacements have recently been demonstrated from structural relaxation methods that include a dispersion correction.⁶⁸ The Monte Carlo approach is expected to obtain similar results by explicitly sampling positions that might otherwise be omitted. Overall, an approach such a Monte Carlo that samples displacements other than those accessible through normal vibrational modes is desirable. Here a total of 2500 COOH hydrogen positions in the butyric acid dimer were sampled around the initial OH positions and shift tensors computed for each structure. This approach assumes that non-hydrogen positions remain stationary because these sites have significantly smaller motions than hydrogens due to their higher masses. Additionally, it is assumed that motion of the carbon and oxygen atoms of the carboxyl moiety are only weakly coupled to hydrogen motion. Such assumptions were necessary to make feasible the large number of calculations. The ¹³COOH tensors calculated for each sampled point were then compared with experimental NMR data and points agreeing with experimental data within ± 1σ (i.e. 8.0 ppm for ¹³COOH sites)⁹ were retained. The retained structures define the confidence interval for anisotropic displacements in atomic coordinates of the hydrogen atoms.

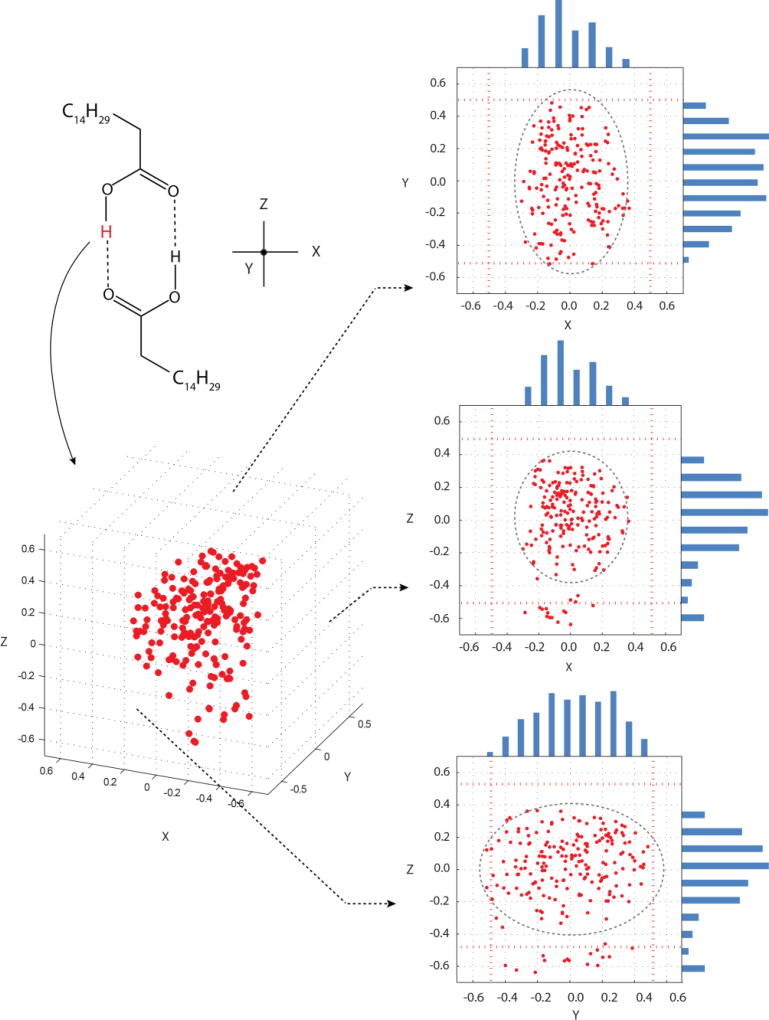
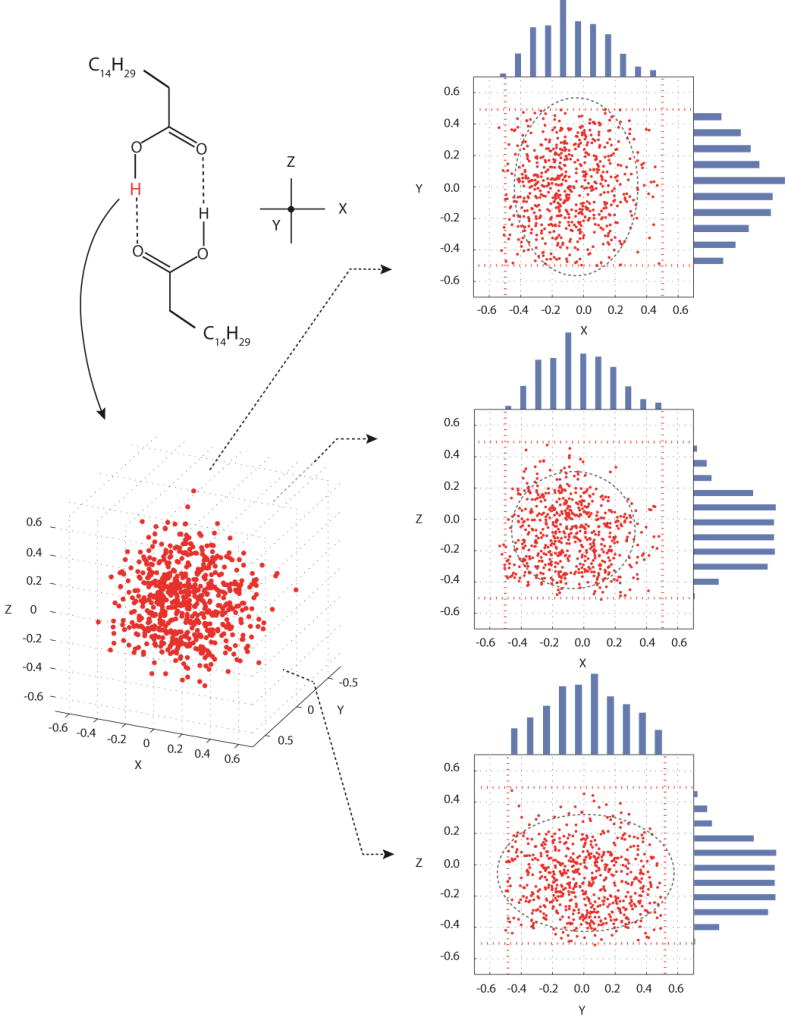
A plot of the points retained for phase A₂ is illustrated in Figure 4 and similar plots were obtained for phases B_m and E_m (not shown). In all cases, an ellipsoidal distribution of hydrogen positions was retained with the smallest uncertainty in hydrogen position found to be in the direction perpendicular to the O–H bond but within the plane of the dimer (i.e. X-axis of Fig. 4) with root-mean-squared uncertainties ranging from 0.14–0.15 Å. The uncertainty along the O–H bond (Z-axis in Fig. 4) was roughly 1.2 times larger than that observed along the X-axis. The largest uncertainty was out of the plane of the dimer and along the Y-axis of Figure 4. This uncertainty is predicted to be approximately 1.6 times larger than the error along the X-axis. The observation of large out-of-plane hydrogen displacement mirrors that found for thermal ellipsoids⁶⁹ and is consistent with IR data where the O–H⋯O out-of-plane vibration requires the least energy of any vibration involving the OH hydrogen. A complete list of uncertainties along the X, Y, and Z-axes for each phase is given in Table 3. At present, crystal structures for phases A₂, B_m and E_m are not known and therefore a direct comparison of NMR and diffraction displacement errors is not possible. Thus, to place these uncertainties in context, data from the neutron diffraction structure of acetic acid⁶⁹ obtained at room temperature are included in Table 3. The acetic acid neutron structure includes a localized OH hydrogen in a similar hydrogen bonding arrangement and thus provides a suitable model structure for evaluating phases A₂, B_m and E_m. In phases with localized hydrogens the NMR derived ellipsoids having volumes 1.8 times smaller than the corresponding neutron value,⁶⁹ on average.

Figure 4.

A plot of COOH hydrogen positions retained for palmitic acid phase A₂, based on agreement of computed ¹³COOH tensors for each point with experimental ¹³COOH values at the ±1σ level. Projections onto the XY, XZ and YZ-planes are included together with histograms along each axis. Outlier points along the Z-axis represent a small probability that the cis orientation can occur. Red dashed lines denote sampling boundaries of ±0.5 Å from the initial hydrogen position. Estimates of uncertainties in atom positions are shown by ellipsoids drawn at the ±2σ level. These ellipsoids illustrate that slight truncation of the Y-dimension has only a minor influence on the predicted positional uncertainties. Nearly identical plots were obtained for phases B_m and E_m, thus these plots are not shown.

Table 3.

The NMR predicted root-mean-square deviations for COOH hydrogen positons along the X, Y and Z-axes for each phase of palmitic acid.

Phasea	X (Å)	Y (Å)	Z (Å)	Ellipsoid volume (Å3)
A2	0.156	0.247	0.174	0.028
Bm	0.148	0.242	0.170	0.026
Em	0.139	0.241	0.186	0.026
C	0.219	0.246	0.207	0.046
Neutronb	0.193	0.228	0.266	0.049

^aPhases A₂, B_m and E_m are predicted to have localized OH hydrogens while phase C includes delocalized OH hydrogens.

^bNeutron data were obtained for acetic acid in a 1:1 complex with phosphoric acid at 295 K and is representative of a structure containing a localized hydrogen similar to phases A₂, B_m and E_m of palmitic acid.

In selecting hydrogen positions, it was necessary to verify that a sufficient range of positions was sampled to accurately predict the entire range of possible motion for each of the directions. Figure 4 includes histograms for each axis showing that adequate sampling was performed. It is notable that in the Z-direction, a few points are retained well outside of the main distribution. In these cases, our sampling occasionally extended to the point that the O–H hydrogen was transferred onto the C=O of the neighboring molecule. In other words, our sampling range allowed the initial trans structure to be converted into the cis orientation. Prior work has demonstrated that the cis and trans structures can have very similar ¹³COOH tensors,⁸ thus it is not surprising that there is some agreement for the cis structure. However, in all cases the trans structure represents the majority of statistically preferred data points. This is consistent with the 1D models above (Figure 3a) in which the cis structures have chemical shifts close to the best fit.

The retained points in Figure 4 allow an average hydrogen position to be determined. Because NMR data reflect a structure averaged by fast (i.e. THz)⁶² small-amplitude vibrations and librations, an effective way to include these motions is to average modeled atom positions derived from molecular dynamics or other methods.^62,63,64,65 In the case of palmitic acid, averaging the hydrogen positions creates slightly different bond lengths and valence angles than those reported above for the static model. This is to be expected as the Monte Carlo sampling is considerably less constrained that the earlier model. Averaged bond lengths and valance angles for phases with localized OH hydrogens are shown in Table 4. In all cases, the averaged O–H bond lengths in Table 4 are in good agreement with neutron benchmark data.^69,70,71 However, it is notable that the averaged C–O–H valence angles are larger than the corresponding neutron values by approximately 10°. The origin of this difference requires further study.

Table 4.

Bond lengths for palmitic acid phases containing an ordered OH hydrogen after averaging the Monte Carlo sampled data points.

Phase	O–H bond length (Å)	C–O–H valence angle (°)
A2	0.96 ± 0.07	118.8 ± 1.2
As	–	–
Bm	0.94 ± 0.07	119.5 ± 1.1
Em	1.01 ± 0.07	121.6 ± 1.0
Neutrona	1.00 ± 0.01	110.2 ± 0.25

^aThese reference data (N=3) include only data from monocarboxylic acids^69,70,71

The sample averaging process described above for the OH hydrogen, results in different hydrogen positions than those observed in the initial model. This is because the center of mass of the retained data points typically does not coincide with the hydrogen positon obtained from a one-dimensional analysis of bond length (e.g. Figure 3). One way to correct for this difference is to translate the hydrogen to the center of mass of the retained coordinates and such adjustments were made for all phases characterized herein. This process thus represents an NMR refinement to the original coordinates. Recently, there has been significant interest in refining crystal structures based on NMR agreement and several methods have been reported.^68,72,73 The averaging process utilized here offers another option for NMR–based refinement.

The Monte Carlo sampling of COOH hydrogen positions was also employed to characterize disorder in phase C. The initial hydrogen position was obtained from a recent study of OH disorder in lauric acid and involves a dimeric structure with $R_2^2(8)$ hydrogen bonding and two minima at r = 1.16 Å and 1.46 Å.⁹ These initial structures were selected due to the close structural similarities to palmitic acid and also because it is important to assess the ability of the methodology described herein to select a global minimum from various starting points. For each initial structure, 2500 additional points were sampled in the X, Y and Z-directions over a range of ± 0.5 Å. Shift tensors were computed for each structure and a subset of these structures was retained based on agreement with experimental data using the procedure described above for phases A₂, B_m and E_m. Regardless of the initial structure selected, the average hydrogen position was found to be at r = 1.26 ± 0.09 Å. Notably, the prediction of a hydrogen located at the midpoint between oxygens is consistent with prior NMR^16,17 and neutron diffraction⁷⁴ studies of low barrier hydrogen bonds and also predictions made herein (vida supra) for an averaged structure. Retained points are illustrated in Figure 5 and a comparison of structural parameters with benchmark neutron values is shown in Table 5. Presumably the selection of a single most probable point rather than a pair of points, as in the 1D fitting above (Figure 3b), is a result of sampling in three dimensions. When adjustments are possible in all directions significantly more energetic options are available and the most probable position changes slightly. The smallest uncertainty in phase C was found to occur along the Z-axis (approximately along the O–H bond). Uncertainties perpendicular to this bond were 1.1 to 1.2 times larger than those along the Z-axis, thus the retained ellipsoids are approximately spherical. The uncertainties in the X, Y, and Z-directions are given in Table 3. Significantly, the volume of the hydrogen ellipsoids in phase C is, on average, 42.7% larger than the ellipsoids for localized hydrogens, consistent with greater freedom for hydrogen atom motion and a corresponding disordered structure.

Figure 5.

A plot of COOH hydrogen positions found to be feasible for palmitic acid phase C, based on agreement of the ¹³COOH computed tensor for each point with the experimental ¹³COOH values at the ± 1σ level. Projections onto the XY, XZ and YZ-planes are included together with histograms along each axis. Red dashed lines denote sampling boundaries of ± 0.5 Å from the initial hydrogen position. Estimates of uncertainties in atom positions are shown by ellipsoids drawn at the ±2σ level. These ellipsoids illustrate that the slight truncation of the Y-dimension has only a minor influence on the predicted positional uncertainties.

Table 5.

Bond lengths for palmitic acid phase C after averaging the Monte Carlo sampled data points.

Phase	O–H bond length (Å)	C–O–H valence angle (°)
C	1.26 ± 0.09	114.3 ± 1.8
Neutrona	1.32 ± 0.03	-

^aRoom temperature neutron diffraction structure of benzoic acid.⁷⁴

An unusual feature of Figure 5 can be observed in the projection onto the XZ-plane. Retained points are correlated in these two dimensions with the greatest number of points grouped into the lower left quadrant (i.e. −X and −Z directions). The result occurs because the vibrational and librational motions aren’t directly aligned with the X and Z-axes. In this case, axes have been defined to correspond to bonds in the model structure with the Z–axis aligned with O–H bond direction and the C–O–H moiety lying in the XZ–plane. Thus, the OH hydrogen in phase C experiences displacements within the XZ-plane that deviate from the O–H bond direction toward the −X direction. In other words, these displacements are directed toward the outside of the eight-atom ring defining the dimer. In contrast, the corresponding displacements in phases with localized hydrogens occur largely along the OH bond or perpendicular to this direction, an observation consistent with neutron diffraction prediction in acetic acid.⁶⁹

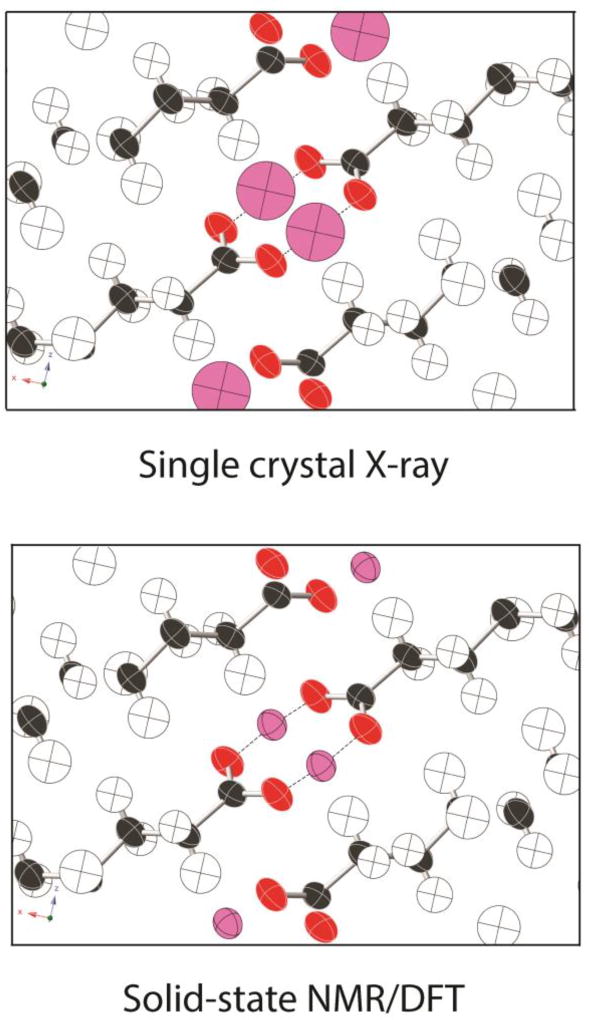
The uncertainties in hydrogen positions reported in Table 3 for all phases are listed as root-mean-square deviations with units of length (Å). The internationally accepted standard for reporting such anisotropic displacements in crystallographic studies is the “mean-square displacement” with units of length squared.⁶⁷ This parameter is computed as $\frac{1}{N}\sum {(x_i-\overline{x})}^2$ where x_i and x̄ denote, respectively, the displacement of individual data points from a mean atomic position and the mean position in the x-direction. Analogous equations are used for displacements in the y and z-directions. Mean-square displacements are usually denoted simply as U_ii. To ensure consistency with more conventional crystallographic studies, uncertainties for all phases of palmitic acid studies herein are also reported here as mean-square displacements. These displacement values, when reported in the principal axis system (where U is diagonal), are simply the square of the root-mean-square uncertainties reported in Table 3. All U_ii data are listed in Table 6 together with benchmark data from neutron diffraction.⁶⁹ Displacements refer to a structure oriented so that the OH hydrogen is located at the origin, the O–H bond lies along the +Z axis and the C–O–H moiety is in the XZ–plane. The full anisotropic displacement tensor can be obtained for phase C because its crystal structure is known, allowing NMR-derived values to be oriented relative to the unit cell. For all other phases, crystal structures are not presently known, thus only the principal components are reported here. Displacement ellipsoids are illustrated in Figure 6 for phases with localized hydrogens. Figure 7 illustrates NMR-derived ellipsoids for the hydrogen-disordered phase C and includes a comparison of the hydrogen position predicted from single crystal x-ray diffraction. Significantly, the NMR-derived ellipsoids in phase C are 7.6 times smaller than the corresponding values from x-ray diffraction.⁶ Moreover, the NMR-predicted values are anisotropic (i.e. ellipsoidal) showing differences in displacement magnitudes in the X, Y and X-directions while the x-ray data are isotropic with a spherical distribution. NMR-derived ellipsoids were also obtained for phase C from TensorView for direct comparison to the ellipsoids in Figure 6 and this illustration is included as Electronic Supplementary Information. Anisotropic displacement data are seldom provided for hydrogen atoms from x-ray diffraction studies. The ability to also obtain such displacement information from NMR emphasizes the complimentary nature of x-ray diffraction and NMR methods. We note, however, that techniques are now available for refining routine x-ray data to an accuracy similar to that obtained from neutron diffraction.^75,76,77 At present, these refinement methods are underutilized.

Table 6.

The mean-square displacement values for the 4 phases of palmitic acid.

Phase	Uxx	UYY	UZZ	UXY	UXZ	UYZ
A2	0.0242	0.0610	0.0303	–	–	–
Bm	0.0219	0.0588	0.0290	–	–	–
Em	0.0192	0.0582	0.0346	–	–	–
C	0.0487	0.0507	0.0516	0.0023	0.0068	0.0054
Neutrona	0.0418	0.0669	0.0518	−0.0029	0.0062	−0.0089

^aObtained from acetic acid at −140°C

Figure 6.

An illustration of the NMR-derived anisotropic displacement ellipsoids for the COOH hydrogen in phases A₂, B_m and E_m. More quantitative measures of the in-plane and out-of-plane deviations for each dimension are given in Table 6. Small differences in the size of the ellipsoids along the X-direction (i.e. perpendicular to the O–H bond and within the COOH plane) in these phases can be observed from the OH hydrogen extending beyond the ellipsoids in that dimension. All plots were prepared using the program TensorView (see Electronic Supplementary Information). A comparable TensorView plot of phase C is included as Electronic Supplementary Information to provide a direct comparison.

Figure 7.

A comparison of the X-ray derived isotropic COOH hydrogen positions (top, pink atoms) and the NMR-derived anisotropic displacement parameters for these hydrogens (bottom). The NMR analysis predicts a COOH hydrogen volume 7.6 times smaller than the corresponding volume from single crystal x-ray diffraction. Only COOH hydrogen positions differ between the two structures with all other atomic positions obtained from single crystal x-ray diffraction coordinates of phase C.

We note that the NMR-derived ellipsoids show a remarkable similarity to the thermal ellipsoids from x-ray crystallography. We posit that this is no mere coincidence, that the two are intrinsically related. Both depend fundamentally on the electronic wavefunction for a given set of nuclear coordinates under the Born-Oppenheimer approximation; as the nuclear coordinates are varied, the new electronic wavefunction determines both the chemical shift for that arrangement and the overall energy, which defines the vibrational potential well. Wavefunctions that vary slowly with position are associated both with slowly varying NMR parameters (with correspondingly large ranges in the errors) and large amplitude nuclear motions (with correspondingly large thermal ellipsoids). While the precise relationship between these parameters is the subject of ongoing work, we conjecture that the two are fundamentally tied and proportional.

All decisions regarding structural selection (described above) were made based exclusively on agreement between experimental and theoretical ¹³C shift tensor data. Computed energies could also have been included as an additional constraint on acceptable structures. Here energy comparisons were not included because the aim was to see what structural conclusions one can make solely from SSNMR information. This choice also ensures that experimental information is considered in all selections. It is notable that differences in the structures retained here involve only small changes at two hydrogens. Thus, the energy differences between retained structures are anticipated to be relatively small. In the more general case where all atoms included variations (e.g. ref. 33), combining energy comparisons with SSNMR data may prove beneficial.

A potential concern regarding the structural selection process is the decision to assume static carbon and oxygen positions. Since the structures ultimately selected by this NMR approach are found to have smaller anisotropic displacement ellipsoids than both single crystal x-ray and neutron diffraction structures, it is important to assess how this assumption of static non-hydrogen sites influences predicted ellipsoid volume. A comprehensive study of carbon and oxygen thermal motions involving Monte Carlo sampled positions would require a considerable number of candidate structures and is beyond the scope of the current study. Instead, a preliminary assessment was performed here involving six structures having deviations in COOH hydrogen positon of ± 1σ in the X, Y and Z-directions. The magnitudes of the X, Y and Y-deviations were, respectively, ±0.148 Å, ±0.243 Å and ±0.176 Å (i.e. the average of the values in Table 3). All modeling was performed using the butyric acid dimer described above and included identical hydrogen distortions in each monomer in order to mimic the symmetrical hydrogen bond motion previously observed in benzoic acid.^53,54. Each structure was allowed to relax (B3LYP/D95**) at all positon except the COOH hydrogen which was retained in the ± 1σ distorted position in both partners of the dimer. Shift tensors were then computed (B3PW91/D95**) for both the relaxed structure and the distorted structure before relaxation. Computed ¹³COOH shift tensors were compared before and after refinement for a given structure. In five of the six structures, the ¹³COOH tensors in the relaxed structure were statistically indistinguishable (i.e rmsd < 8.0 ppm) from the structure having fixed carbons and oxygen positions. In a single case, having the OH hydrogen moved in the +Z-direction, the relaxed structure differed from the fixed heavy atom structure by +1.5σ. This outcome indicates a need for minor correction to the ellipsoid in the +Z-direction (along the OH bond). In general, however, these results indicate that our neglect of heavy atom thermal motion does not significantly influence the predicted ellipsoid volume. The single case in which our analysis does require adjustment (i.e. +Z-direction), the difference from the ±1σ was small and we anticipate that only a minor correction to ellipsoid volume is needed. Admittedly, this analysis only includes relaxed heavy atom position from a DFT refinement and fails to map the entire space near non-hydrogen atoms. Future work will seek to more systematically evaluate the region near all atom and provide ADPs for both hydrogens and non-hydrogen sites.

Phase changes in palmitic acid from SSNMR sample spinning

The ¹³C shift tensor analyses described herein were all performed at spinning speeds less than 4.0 kHz. Higher spinning speeds are often used to acquire hydrogen shifts. These analyses are desirable since differences in ¹H shifts at COOH sites have been shown to correlate with differences in hydrogen bonding.^18,26 Specifically, stronger hydrogen bonding corresponds to high frequency ¹H shifts. Thus, more rapid spinning (17 kHz) of all phases of palmitic acid was performed to measure the COO¹H shifts. Surprisingly, such spinning caused the A₂, A_s, B_m and E_m phases to undergo a phase transition to form C. Thus, only the ¹H spectrum for phase C was obtained. This result indicates that, for the 8 phases studied here, phase C is the minimum energy form of palmitic acid.

Conclusions

Prior studies of hydrogen bonding in n-alkyl acids have concluded that OH hydrogen disorder is observed only in phase C of acids having an even number of carbons.² The present study provides the first experimental evidence for polymorphs of palmitic acid other than phase C and supports the prediction of localized OH hydrogens in these new phases. The three phases present as contaminants in phase A_s, although uncharacterized herein due to insufficient material, are expected to also include localized OH hydrogens based on prior precedent² and the results obtained here.

The disordered OH hydrogen in phase C is positioned, on average, midway between oxygen atoms. Such an arrangement has been shown⁷⁸ to create unusually strong hydrogen bonds having partial covalent character. Theoretical methods also predict that disordered hydrogen bonds are stronger than localized O–H⋯O bonds.⁹ Based on these results the strongest hydrogen bonding in polymorphs of palmitic acid is presumed to occur in phase C. We note the possibility that phase C actually includes a hydrogen located midway between oxygen atoms with no barrier between heteroatoms. Such arrangements are known to occur in formally charged species,^10,11,12,13 and the similarities of these species to phase C and invites additional theoretical and experimental work.

The results presented here provide anisotropic displacement parameters for the OH hydrogens in four polymorphs of palmitic acid solely from solid-state NMR data and theoretical calculations. Both dynamically disordered and well-ordered sites are equally well described by this approach. Significantly, the average NMR predicted volumes for displacement ellipsoids in phases with localized OH hydrogens (i.e. A₂, B_m and E_m) are smaller than comparable benchmark neutron diffraction volumes by a factor of 1.8.⁶⁹ Although the approach described herein has been applied to hydrogens, it can also be employed to obtain anisotropic displacement ellipsoids for non-hydrogens atoms with no modification. The methodology developed herein also provides a new path for refining hydrogen coordinates based on NMR information. A more general refinement of non-hydrogen atoms should also be feasible using this approach. Since solid-state NMR is most commonly performed on powders, this structural refinement is applicable to materials that fail to form crystals suitable for crystallography.

The work described here rely on ¹³C shift tensor data to monitor changes at the OH hydrogen. It is reasonable to assume that OH ¹H shift tensor data may provide an even better way to evaluate hydrogen bonding differences and such studies may prove beneficial.