Mechanical parameters of the molecular motor myosin II determined in permeabilised fibres from slow and fast skeletal muscles of the rabbit

Abstract

Key points

• The different performance of slow and fast muscles is mainly attributed to diversity of the myosin heavy chain (MHC) isoform expressed within them.

• In this study fast sarcomere‐level mechanics has been applied to Ca²⁺‐activated single permeabilised fibres isolated from soleus (containing the slow myosin isoform) and psoas (containing the fast myosin isoform) muscles of rabbit for a comparative definition of the mechano‐kinetics of force generation by slow and fast myosin isoforms in situ.

• The stiffness and the force of the slow myosin isoform are three times smaller than those of the fast isoform, suggesting that the stiffness of the myosin motor is a determinant of the isoform‐dependent functional diversity between skeletal muscles.

• These results open the question of the mechanism that can reconcile the reduced performance of the slow MHC with the higher efficiency of the slow muscle.

Abstract

The skeletal muscle exhibits large functional differences depending on the myosin heavy chain (MHC) isoform expressed in its molecular motor, myosin II. The differences in the mechanical features of force generation by myosin isoforms were investigated in situ by using fast sarcomere‐level mechanical methods in permeabilised fibres (sarcomere length 2.4 μm, temperature 12°C, 4% dextran T‐500) from slow (soleus, containing the MHC‐1 isoform) and fast (psoas, containing the MHC‐2X isoform) skeletal muscle of the rabbit. The stiffness of the half‐sarcomere was determined at the plateau of Ca²⁺‐activated isometric contractions and in rigor and analysed with a model that accounted for the filament compliance to estimate the stiffness of the myosin motor (ε). ε was 0.56 ± 0.04 and 1.70 ± 0.37 pN nm⁻¹ for the slow and fast isoform, respectively, while the average strain per attached motor (s ₀) was similar (∼3.3 nm) in both isoforms. Consequently the force per motor (F ₀ = εs ₀) was three times smaller in the slow isoform than in the fast isoform (1.89 ± 0.43 versus 5.35 ± 1.51 pN). The fraction of actin‐attached motors responsible for maximum isometric force at saturating Ca²⁺ (T _0,4.5) was 0.47 ± 0.09 in soleus fibres, 70% larger than that in psoas fibres (0.29 ± 0.08), so that F ₀ in slow fibres was decreased by only 53%. The lower stiffness and force of the slow myosin isoform open the question of the molecular basis of the higher efficiency of slow muscle with respect to fast muscle.

Key points

• The different performance of slow and fast muscles is mainly attributed to diversity of the myosin heavy chain (MHC) isoform expressed within them.

• In this study fast sarcomere‐level mechanics has been applied to Ca²⁺‐activated single permeabilised fibres isolated from soleus (containing the slow myosin isoform) and psoas (containing the fast myosin isoform) muscles of rabbit for a comparative definition of the mechano‐kinetics of force generation by slow and fast myosin isoforms in situ.

• The stiffness and the force of the slow myosin isoform are three times smaller than those of the fast isoform, suggesting that the stiffness of the myosin motor is a determinant of the isoform‐dependent functional diversity between skeletal muscles.

• These results open the question of the mechanism that can reconcile the reduced performance of the slow MHC with the higher efficiency of the slow muscle.

Introduction

Skeletal muscles allow walking, running and breathing by converting chemical energy into force and movement. At the level of the half‐sarcomere, the functional units of the striated muscle, force and shortening, are generated by cyclic interactions between the array of the molecular motor myosin II, extending from the thick filaments, and the interdigitating thin (actin‐containing) filaments. In each interaction the hydrolysis of one ATP molecule on the myosin catalytic site provides about 90 zJ of free energy (Pate & Cooke, 1989b; Smith et al. 2008), allowing the motor to exert force (up to 6 pN in isometric contraction) and reciprocal sliding (6–10 nm depending on the external load in isotonic contraction; Rayment et al. 1993b; Piazzesi et al. 2007). Cyclic asynchronous ATP‐driven interactions of the motors and thousands of half‐sarcomeres in series amplify the small movement, allowing steady macroscopic shortening of muscle.

Skeletal muscles exhibit a large variability in their mechanical performance: parameters such as the speed of isometric force development, the unloaded shortening velocity, the maximum power output and the rate of ATP hydrolysis vary from one muscle to another according to their functional tasks. Muscles involved in maintenance of posture exhibit lower shortening speed at any given load, develop lower power and consume ATP at a lower rate than muscles involved in movement. At the same time the efficiency of energy conversion in slow muscle has been reported to be at least similar or higher than that in fast muscle (Woledge, 1968; Barclay et al. 1993, 2010; He et al. 2000; Reggiani, 2007). These differences are attributed to the myosin heavy chain (MHC) isoform expressed in different skeletal muscles (Schiaffino & Reggiani, 2011). Muscles responsible for maintenance of posture contain fibres expressing mostly the slow MHC isoform (MHC‐1) while those involved in movement contain fibres expressing mostly the fast MHC isoform (MHC‐2X). At the molecular level, the functional differences could be due to the properties of the myosin motor per se (i.e. stiffness and force) and/or the properties emerging from the motor organisation in array (i.e. the number of motors attached to actin or their degree of coordination).

In the face of the importance of the definition of these parameters, there is only one relevant study in the literature concerning the comparison of the mechanical properties of slow and fast myosin isoforms in situ (Brenner et al. 2012). In that work the mechanical and kinetic properties of skinned fibres from the slow human muscle (soleus) were determined and compared to those from the fast muscle of the rabbit (psoas). In spite of the limits of resolution of the method, which do not allow nanometre–microsecond measurements at the level of the sarcomere and thus the direct determination of the absolute values of the elastic constants of the half‐sarcomere components, it was found that the stiffness of the slow myosin isoform is 2–3 times smaller than that of the fast isoform. In that study, moreover, the compliance of the various elements contributing to the half‐sarcomere compliance was likely to have been overestimated by the absence of the osmotic recovery of the interfilamentary lattice spacing after the increase following the skinning procedure (Linari et al. 2007).

In this study, fast sarcomere‐level mechanics has been used to investigate the differences in the mechanical and kinetic properties of slow and fast myosin isoforms in situ during isometric contraction. The study has been performed on single permeabilised (skinned) fibres isolated from soleus (containing the slow myosin isoform) and psoas (containing the fast myosin isoform) muscles of the same animal, the rabbit, to avoid any source of variability generated by different animal species. Half‐sarcomere force and stiffness measurements were made in the Ca²⁺‐activated fibres during isometric contraction and in the same fibres in rigor to determine the stiffness and the force of the actin‐attached myosin motor and the fraction of motors attached. The results show that the slow myosin isoform exhibits a stiffness and a force three times smaller than the fast isoform. This finding suggests that the stiffness of the myosin motor is a determinant of the isoform‐dependent functional diversity between skeletal muscles and, considering that the efficiency of slow muscles is similar to or higher than that of the fast muscles, opens the question of the mechanism that underlies the high efficiency of the slow muscle.

Methods

Animals and Ethical Approval

All animals were treated in accordance with both the Italian regulation on animal experimentation (authorization n. 956/2015 PR) in compliance with Decreto Legislativo 26/2014 and the EU regulation (directive 2010/63). Adult male New Zealand white rabbit (4–5 kg) were sacrificed by injection of an overdose of sodium pentobarbitone (150 mg/kg) in the marginal ear vein. Three rabbits were used for this work. Small bundles (50–100 fibres) of soleus and psoas muscles were stored in skinning solution containing 50% glycerol at −20 °C for 3–4 weeks as already described (Goldman et al. 1984; Linari et al. 2007). All animals have been kept with free access to food and water prior to use.

Fibre preparation and mechanical apparatus

Experiments were performed on glycerol‐pearmeabilised fibre segments from soleus and psoas muscles of the adult male New Zealand White rabbit (4–5 kg). Single fibres were prepared just before the experiment as already described (Goldman et al. 1984; Linari et al. 2007). The increase of interfilamentary distance following cell membrane permeabilisation was reversed by the addition of the osmotic agent Dextran T‐500 (4 g/100 ml, 4% w/v). This concentration is known to reverse the permeabilisation‐induced increase of interfilamentary spacing and CSA to a value close to that before skinning (Matsubara & Elliott, 1972; Maughan & Godt, 1979; Brenner & Yu, 1991; Kawai et al. 1993; Linari et al. 1998, 2007). Based on the finding that resting intact slow and fast muscle fibres from mice have the same interfilamentary distance (Zappe & Maeda, 1985), the same amount of dextran was used for both fibre types.

A fibre segment 4–6 mm long was mounted between the lever arms of a loudspeaker motor and a capacitance force transducer as previously described (Linari et al. 2007 and references therein). Sarcomere length, width (w) and height (h) of the fibre were measured at 0.5 mm intervals in the 3–4 mm central segment of the relaxed fibre with a ×40 dry objective (Zeiss, NA 0.60) and a ×25 eyepiece. The fibre length (L ₀) was adjusted to have a sarcomere length of about 2.4 μm. The fibre cross‐sectional area (CSA) was determined assuming the fibre cross‐section is elliptical (CSA = π/4wh) and its value, in the presence of 4% dextran, ranged between 5000 and 7400 μm² in single fibres from soleus muscle and 3600 and 5700 μm² in single fibres from psoas muscle. The CSA was 43 ± 4% (slow fibres) and 39 ± 1% (fast fibres) larger in the absence of dextran. Fibres were activated by temperature jump using a solution exchange system as previously described (Linari et al. 2007). The fibre was kept in activating solution at the test temperature (12°C) for 3–5 s for the mechanical measurements. A striation follower (Huxley et al. 1981) allowed nanometre–microsecond resolution recording of length changes in a selected population of sarcomeres (range 500–1200 sarcomeres) starting at the time the optic path was permitted through the glass window in the floor of the test temperature drop (see Linari et al. 2007 for details).

Fraction of cross‐sectional area occupied by myofibrils

To evaluate the force per myosin motor from the isometric force, the fraction of the CSA of the fibre occupied by the myofibrils had to be determined in both soleus and psoas muscles. For this, bundles from soleus and psoas muscles such as those used for the mechanical experiments were used for evaluation with electron microscopy (EM) of the effects of skinning and osmotic compression on both the myofibrillar and extramyofibrillar space. For EM measurements in freshly dissected bundles, immediately after the dissection from the muscle the bundles (held at constant length by clamping their extremities before the cut) were transferred to fixative solution (3.5% glutaraldehyde in 0.1 m sodium cacodylate (NaCaCo) buffer, pH 7.2. For EM measurements on skinned bundles, bundles kept for 1 week in the storage solution (see Table 1B) at −20°C were washed in relaxing solution (see Table 1A) (±dextran) and transferred into fixative solution (±dextran). All the three kinds of fixed bundles were stored at 4°C to be shipped to the Chieti laboratory, where they were post‐fixed, embedded, stained en bloc and sectioned for electron microscopy, as described previously (Boncompagni et al. 2009). Ultrathin sections (thickness ∼50 nm), were examined after staining in 4% uranyl acetate and lead citrate, with a Morgagni Series 268D electron microscope (FEI Company, Brno, Czech Republic), equipped with Megaview III digital camera (Munster, Germany) at 60 kV. Estimates of the relative fibre volume occupied by myofibrils were calculated in transverse sections with the stereology point counting technique (Loud, 1962; Mobley & Eisenberg, 1975). Briefly, two micrographs from each fibre (sample size: 26 fibres for each group) were taken at magnification of 22,000 excluding nuclei and subsarcolemmal regions. A grid of an orthogonal array of dots at a spacing of 0.35 μm was superimposed on each micrograph. The relative fibre CSA occupied by the myofibrils versus intermyofibrillar space was then calculated by dividing the total number of dots by the number of dots falling on either compartment. The measurements were performed in bundles freshly dissected and after skinning (kept 1 week in storage solution, see Table 1B) without and with the addition of 4% dextran (see Fig. 1).

Table 1.

Composition of solutions

A. Solutions used during the experiments
	Na2ATP	MgCl2	EGTA	HDTA	CaEGTA	TES	Na2CP	GSH
Relaxing	5.44	7.7	25	—	—	100	19.11	10
Pre‐activating	5.45	6.93	0.1	24.9	—	100	19.49	10
Activating	5.49	6.76	—	—	25	100	19.49	10
Rigor	—	3.22	53	—	—	100	—	10

B. Solutions used to prepare and store skinned fibres
	Na2ATP	MgCl2	EGTA	Imidazole	KP	NaN3	PMSF	Glycerol
Skinning solution	2.5	2.5	5	10	170	—	0.1	—
Storage solution	2.5	2.5	5	10	170	5	—	50%

All concentrations are in mm except glycerol (v/v). ATP, adenosine 5′‐triphosphate; EGTA ethylene glycol‐bis (β‐aminoethyl ether)‐N,N,N′,N′‐tetraacetic acid; HDTA, 1,6 diaminohexane‐N,N,N′,N′‐tetraacetic acid; TES, N‐tris[hydroxymethyl]methyl‐2‐aminoethanesulphonic acid; CP, phosphocreatine disodium salt hydrate; GSH, glutathione; KP, potassium propionate; PMSF, phenylmethylsulphonyl fluoride. 1 mg ml⁻¹ creatine phosphokinase, 10 μm trans‐epoxysuccinyl‐l‐leucylamido‐(4‐guanidino) butane (E‐64) and 20 μg ml⁻¹ leupeptin, were added to all solutions. pH (adjusted with KOH) was 7.1 at the different temperatures used (A), and 7.0 at 20°C (B). Ionic strength ranged between 188 and 195 mm; free Mg²⁺ was 1.3 mm and MgATP was 5 mm. HDTA was obtained from Fluka (Buchs, Switzerland); all other chemicals were from Sigma‐Aldrich.

Figure 1. Intermyofibrillar space quantification.

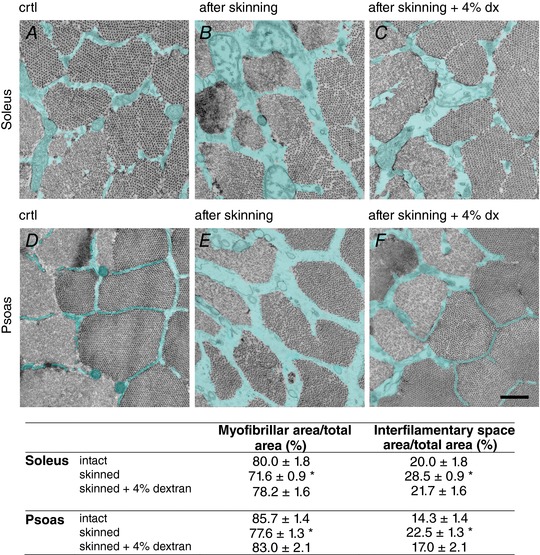
A–F, representative electron micrographs of cross sections of fibres from soleus (upper row) and psoas (lower row) muscles fixed before (A and D) after the skinning procedure (B and E) and after the skinning procedure in the presence of 4% dextran (C and F). The intermyofibrillar space is labelled in cyan. Scale bar: 0.5 μm. The percentage of myofibrillar area and intermyofibrillar space area over the total area are reported in the table for the slow and fast fibres as means ± SEM. Student's t test: ^* P < 0.05 with respect to the intact value within each fibre type.

Half‐sarcomere stiffness measurements

Step length changes (ranging from −4 to +4 nm per half‐sarcomere (hs), stretch positive), completed in 110 μs, were imposed on the isometrically contracting fibre. Half‐sarcomere stiffness was estimated by the slope of the relation between the tension attained at the end of the step and the change in sarcomere length (T ₁ relation). To enhance the precision of stiffness measurements, a train of different‐sized steps at 200 ms intervals was applied during each activation and, to maintain the isometric tension before the test step constant, each test step was followed, after a 50 ms pause, by a step of the same size but opposite direction (see Fig. 3 A).

Figure 3. Protocol for measuring the half‐sarcomere stiffness of a slow fibre during isometric contraction at saturating [Ca²⁺] (A) and at a similar force in rigor (B).

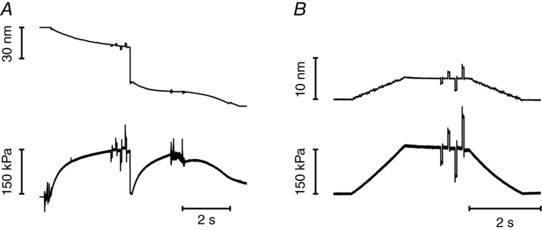
Upper trace, length change per half‐sarcomere; lower trace, force. The same step sequence was imposed on both activated and rigor fibre. Step amplitudes in the sequence were −1.5, +1.5, −3.0, +3.0 nm per hs. A step of opposite direction was imposed 50 ms after each test step to return the length and the force close to their values before the step. The interval between the test steps was 200 ms. Force is expressed relative to the CSA in relaxing solution (5150 μm²). Fibre length, 5.3 mm; segment length under the striation follower, 0.93 mm; average segment sarcomere length, 2.45 μm; test temperature, 12.2°C. For rigor (same fibre), average segment sarcomere length, 2.42 μm; temperature, 12.1°C; CSA, 4030 μm².

Analysis of the half‐sarcomere compliance

It has been shown that the half‐sarcomere stiffness is not directly proportional to the number of attached force generating motors because actin and myosin filaments are not infinitely rigid and their strain is a significant part of the half‐sarcomere strain (Y) (Huxley et al. 1994; Wakabayashi et al. 1994; Linari et al. 1998, 2007; Piazzesi et al. 2007).

The contribution of myofilament compliance (C _f) to the half‐sarcomere compliance (C _hs) was estimated by determining the relation between Y and isometric force (T), obtained from stiffness measurements during isometric contractions, at different pCa (range 6.8–4.5). Under these conditions, T changes in proportion to the fraction of attached motors (Linari et al. 2007), so that the strain in the motors (s ₀) is constant and Y changes with T in relation to C _f (Martyn et al. 2002; Linari et al. 2007; Seebohm et al. 2009; Fusi et al. 2014). A mechanical model of the half‐sarcomere (Fusi et al. 2014) was used to extract from the C _hs–T relation the estimates of s ₀ and C _f.

Stiffness measurements in rigor

Rigor was induced by MgATP depletion at low temperature (1°C). Stiffness was measured at different steady forces (similar to those developed by activated fibres at different pCa) obtained by slowly stretching the rigor fibre starting from the low level of force (about 0.1 of the isometric force attained at saturating pCa) developed at the end of the rigorisation procedure. The same length step protocol as that used for activated fibres was applied to the rigor fibres (see Fig. 3 B).

Myosin isoform identification

The fibre type was defined on the basis of MHC isoforms used as molecular markers. The MHC isoform composition of each fibre used for the mechanical experiments was determined by means of 8% polyacrylamide gel electrophoresis after denaturation in sodium dodecyl sulphate (SDS‐PAGE), following the procedure described by Talmadge & Roy (1993). In agreement with previous work (Aigner et al. 1993; Janmot & d’ Albis, 1994; Tikunov et al. 2001; Pellegrino et al. 2003), for each fibre, the gel shows only one band in the region of molecular mass (MW) corresponding to the molecular mass of the slow MHC‐1 for fibres from soleus and of the fast MHC‐2X for fibres from psoas (see Fig. 2 C).

Figure 2. Force development following a T‐jump in slow (A) and fast (B) fibres and identification of fibre types (C).

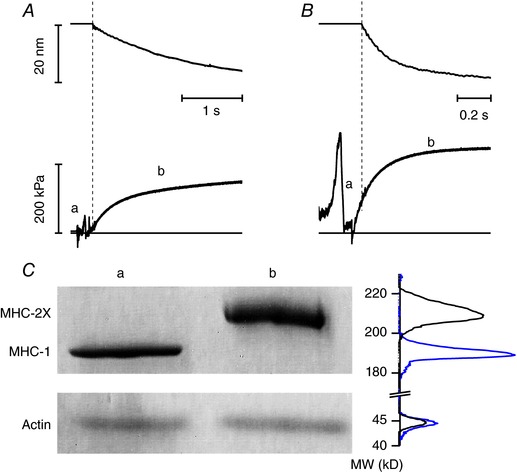
A and B, upper panels, hs length change; lower panels, force response. The horizontal line in the lower panels indicates zero force. During the period (a) the fibre travels in air and within the shadow zone of the chamber. The dashed vertical lines mark the start of the period (b) when the striation follower signal is recorded. Slow fibre (A): fibre length, 5 mm; segment length under the striation follower, 1.1 mm; average segment sarcomere length, 2.48 μm; test temperature, 12.5°C; CSA 5000 μm². Fast fibre (B): fibre length, 5.2 mm; segment length under the striation follower, 0.9 mm; average segment sarcomere length, 2.46 μm; test temperature, 12.4°C; CSA, 5700 μm². C, MHC isoform identification in the fibre by SDS‐PAGE in the area of migration of myosin heavy chain (upper panel) and actin (lower panel). Lane a: single fibre from soleus muscle, which shows pure MHC‐1content; lane b: single fibre from psoas muscle, which shows pure MHC‐2X content. On the right of the lanes are shown the projections of the mass density along the vertical axis after horizontal integration: grey, slow fibre; black, fast fibre. [Color figure can be viewed at http://wileyonlinelibrary.com]

Solutions

The composition of the solutions for mechanical experiments (Table 1) was calculated with a computer program similar to that described by Brandt et al. (1972) and Goldman et al. (1984). Cysteine and cysteine/serine protease inhibitors (trans‐epoxysuccinil‐l‐leucylamido‐(4‐guanidine) butane, E‐64, 10 μm; leupeptin, 20 μg ml⁻¹) were added to all solutions, in order to preserve lattice proteins and thus sarcomere homogeneity. The control solution contains ∼1 mm P_i from two sources: P_i contamination in the experimental buffer and accumulation of P_i inside the fibre during contraction (Pate & Cooke, 1989a). The activating solution at a given pCa (range 6.8–4.5) was obtained by mixing relaxing and activating solutions.

Data collection and analysis

Force, motor position and sarcomere length signals were recorded with a multifunction I/O board (PXIe‐6358, National Instruments, Austin, TX, USA), and a dedicated program written in LabVIEW (National Instruments) was used for signal recording and analysis. The errors reported in this work are SEM.

Results

Fractional volume occupied by myofibrils

The percentage of cross‐sectional area of the fibre occupied by myofibrils versus the intermyofibrillar space (containing cytosol and other cellular components such as sarcoplasmic reticulum and mitochondria) was estimated from electron micrographs of ultrathin slices of both psoas and soleus fibres (Fig. 1; uncoloured sections, myofibrils; cyan sections, intermyofibrillar space). Before skinning, the proportion of fibre area occupied by the myofibrils was 80.0 ± 1.8% in soleus fibres (Fig. 1A) and 85.7 ± 1.4% in psoas fibres (Fig. 1D) and the intermyofibrillar space was 20.0 ± 0.7% in soleus fibres and 14.3 ± 0.7% in psoas fibres. Membrane permeabilisation of both fast and slow fibres significantly increased the intermyofibrillar space (42–51%) more than the area occupied by the myofibrils (9–10%), showing that the ∼40% increase in the cross‐sectional area following fibre swelling (see Methods) was contributed more by the interfilamentary space swelling than by the myofibrillar space swelling. The increase of area by skinning was statistically significant for both myofibrillar and intermyofibrillar spaces (P < 0.01, Student's t test). Addition of 4% dextran reversed the effect of skinning on both spaces (Fig. 1), which nearly recovered their values before skinning (relative areas occupied by the myofibrils, 78.2 ± 1.6% in soleus fibres and 83.0 ± 2.1% in psoas fibres, and intermyofibrillar spaces 21.7 ± 1.6% in soleus fibres and 17.0 ± 2.1% in psoas fibres). Thus in the presence of 4% dextran for either fibre type the area occupied by the myofilaments was not significantly different from that before skinning (P > 0.2).

Isometric force development

Following a temperature jump from 1 to 12°C imposed under isometric conditions in the activating solution at saturating [Ca²⁺] (pCa 4.5), the force rose to a steady value (T _0,4.5), which, relative to the force developed at low temperature, was larger by a factor of 10 in the slow fibres and a factor of 3 in the fast fibres (lower traces in Fig. 2 A and B). The signal recording the sarcomere length change (upper traces) started with a delay with respect to the force developed at the test temperature, due to the time taken by the fibre travelling in the test temperature drop to get into the field of view of the striation follower. The time course of force rise following the temperature jump was one order of magnitude slower in slow fibres. A similar difference was observed for the time course of the force redevelopment after a period of unloaded shortening (30–50 nm per half‐sarcomere) at the test temperature. The time course of force development following the temperature jump and the force redevelopment following unloaded shortening is not a single exponential (Caremani et al. 2008). Since the latter part of force recovery is influenced by a slow component due to the rise of sarcomere inhomogeneity and this component appears more marked in slow fibres, we considered the most convenient way to extract information on the kinetics of force development to apply the empirical method of measuring the half‐time of force development, t _1/2. t _1/2 of force redevelopment was 413 ± 4 ms in slow fibres (n = 7) and 48 ± 1 ms in fast fibres (n = 8). The reciprocal of t _1/2 (k _TR) was 2.42 ± 0.02 s⁻¹ and 20.9 ± 0.6 s⁻¹ in slow and fast fibres, respectively. T _0,4.5 was 141 ± 13 kPa in slow fibres and 264 ± 8 kPa (about twice) in fast fibres. At the end of the experiment the MHC isoform composition was determined by SDS‐gel electrophoresis (Fig. 2 C): within the limit of precision of the method used here, slow and fast fibres contained pure isoforms, MHC‐1 and MHC‐2X, respectively.

Half‐sarcomere stiffness and motor strain in isometric contraction at different pCa

Slow and fast fibres were activated under isometric conditions to measure the maximum steady force T ₀ at different [Ca²⁺] (pCa range, 6.8–4.5). For each T ₀ the half‐sarcomere stiffness (k ₀) was determined by superimposing on T ₀ length steps in the range +4 to −4 nm per hs (Fig. 3 A and left column in Fig. 4 A for a slow fibre). k ₀ was estimated as the slope of the relation between the force attained at the end of the steps and the size of the steps (T ₁ relation, open symbols in Fig. 4 B, slow fibre, and Fig. 4 C, fast fibre). k ₀ decreased with the reduction of T ₀ in both slow and fast fibres (compare circles, saturating calcium, and squares, subsaturating calcium). However, the rightward shift of the abscissa intercept of the linear fits (dashed lines) indicates that in both fibre types the reduction of k ₀ was smaller than the reduction of the force. This was reflected in the k ₀–T ₀ relations shown in Fig. 5 A, where the points for both fast fibres (open circles) and slow fibres (filled circles) show an upward deviation with respect to the straight lines drawn from their respective T _0,4.5 to the origin (continuous line, slow fibres; and dashed line, fast fibres). It is interesting to note that k ₀ was the same in the two fibre types at the same absolute values of forces. The reciprocal of k ₀, C _hs, showed about the same hyperbolic‐like dependence on force (Fig. 5 B) for both slow (filled circles) and fast (open circles) fibres. At T _0,4.5, C _hs was 39.5 ± 4.7 nm MPa⁻¹ and 27.4 ± 2.0 nm MPa⁻¹ in slow and fast fibres, respectively (Table 2). The hs strain, Y ₀, calculated as the product C _hs T ₀, increased linearly with T ₀ in slow (filled circles) as well as in fast (open circles) fibres for forces >40 kPa while it showed a downward concavity for forces <40 kPa (Fig. 5 C).

Figure 4. Measurements of the half‐sarcomere stiffness during isometric contraction and in rigor.

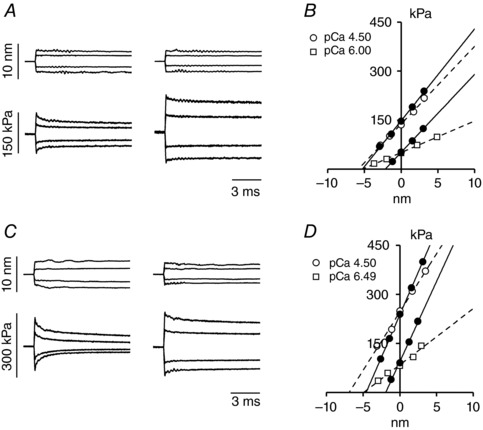
A and C, superimposed hs length changes (upper traces) and force response (lower traces) for steps of different sizes in activating solution at saturating [Ca²⁺] (left column) and in rigor (right column) at a force about T _0,4.5 in a slow fibre (A) and in a fast fibre (C). B and D, T ₁ relations at different pCa (open symbols) and in rigor at forces about T _0,4.5 and 1/3 × T _0,4.5 (filled symbols) determined in a slow fibre (B) and in a fast fibre (D). Lines are linear regression equations fit to the active (dashed) or rigor (continuous) data. The abscissa intercept of each line is the average strain of the half‐sarcomere before the length step (Y ₀). Slow fibre: same fibre as in Fig. 3. Fast fibre: fibre length, 5.3 mm; segment length under the striation follower, 0.93 mm; average segment sarcomere length, 2.46 μm; test temperature, 12.2°C; CSA, 5700 μm².

Figure 5. Half‐sarcomere stiffness in isometric contraction and in rigor and derived parameters.

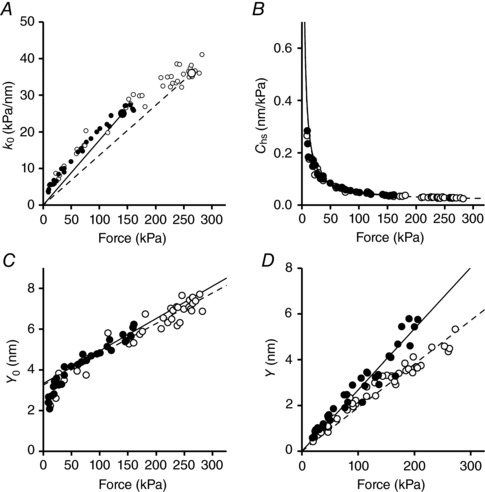
In all panels filled circles and continuous lines refer to slow fibres and open circles and dashed lines to fast fibres. Dependence on force of hs‐stiffness (A), hs‐compliance (B) and hs‐strain (C). The lines in A connect the average T _0,4.5 (larger symbols) with the origin. In C the lines are the linear regression fit to data for forces >40 kPa. In B the lines are calculated with the parameters estimated from the fits in C. D, hs–strain relation in rigor; the lines are the linear regressions fit to data forced to pass through zero. Data from 9 and 10 fibres for soleus and psoas, respectively.

Table 2.

Estimate of the mechanical parameters of the half‐sarcomere and of the myosin motor in slow and fast fibres

Parameter	Units	MHC‐1	MHC‐2X
A, measured parameters
Isometric force (T 0)	kPa	141 ± 13	264 ± 8
Filament compliance (C f)	nm MPa−1	15.9 ± 1.0	15.1 ± 1.0
hs compliance in activated fibres	nm MPa−1	39.5 ± 4.7	27.4 ± 2.0
hs compliance in rigor	nm MPa−1	26.8 ± 0.5	19.0 ± 0.3
Myosin head strain (s 0)	nm	3.33 ± 0.16	3.26 ± 0.20
B, lattice geometry and force per myosin head site
Myosin to myosin spacing*	nm	41
Myofibrillar volume density**	%	78.2 ± 1.6	83.0 ± 2.1
Myosin head sites (×1017)	m−2	1.58 ± 0.03	1.68 ± 0.04
Force per myosin head site	pN	0.89 ± 0.08	1.57 ± 0.06
C, fraction of attached myosin motors and derived parameters
Proportion of attached motors		0.47 ± 0.09	0.29 ± 0.08
Force per attached motor head	pN	1.89 ± 0.44	5.35 ± 1.51
Stiffness of the myosin motor	pN nm−1	0.56 ± 0.04	1.70 ± 0.37

Parameters were measured in the presence of the osmotic agent dextran T‐500 (4 g/100 ml). For the calculation in C the average value of filament compliance and myosin head strain determined for the slow and fast fibres in A were used (C _f = 15.5 ± 0.7 nm MPa⁻¹, s ₀ = 3.30 ± 0.12 nm). Data from 9 and 10 fibres for soleus and psoas, respectively. ^*Values for mammalian skeletal muscle reported by Zappe & Maeda (1985), whole muscle from soleus and EDL, and for skinned fibres from psoas muscle after addition of 4% dextran to relaxing solution (Brenner & Yu, 1991; Kawai et al. 1993). ^**Values in the presence of 4% dextran (see Fig. 1).

In agreement with the finding in intact frog fibres during isometric force development (Fusi et al. 2014), at forces >40 kPa, the activated half‐sarcomere can be reduced to a mechanical model where an elastic element representing the motor array, with stiffness proportional to the number of attached motors, is in series with an elastic element representing the equivalent myofilament compliance (C _f) (Model 1, Fig. 6 A). In fact, in skinned fibres, the Ca²⁺‐dependent modulation of T ₀ occurs through a corresponding change in the number of attached motors (Linari et al. 2007). Thus the motor strain s ₀ is constant independent of T ₀ and Y ₀ increases with force with a slope that is explained by the increase in the strain of the myofilaments with constant compliance C _f according to:

$$Y_0(T_0)=C_{\mathrm{f}}·T_0+s_0$$ (1)

Figure 6. Models representing the elements contributing to the half‐sarcomere compliance (A and B), and dependence of the hs compliance on force in slow (C) and fast (D) fibres.

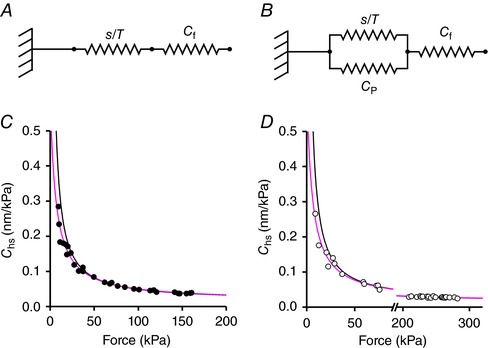
In Model 1 (A), the myofilament compliance (C _f) is in series with an array of myosin motor with a compliance s/T. In Model 2 (B) an elastic element with compliance C _P is in parallel with the array of motors. In C and D experimental data are the same as those reported in Fig. 5 B; lines represent the C _hs–force relations calculated in the absence (black line, eqn (1) from Model 1) or in the presence (grey line, eqn (3) from Model 2) of C _P, the elastic element in parallel with the myosin motors. [Color figure can be viewed at http://wileyonlinelibrary.com]

C _f and s ₀, estimated by fitting eqn (1) to Y ₀–T ₀ values at forces >40 kPa (Table 2), did not differ significantly between slow (15.9 ± 1.0 nm MPa⁻¹ and 3.33 ± 0.16 nm) and fast (15.1 ± 1.0 nm MPa⁻¹ and 3.26 ± 0.20 nm) fibres. P was >0.5 in all cases (Student's t test). According to eqn (1) C _hs depends on T according to the equation:

$$C_{\mathrm{hs}}(T_0)=C_{\mathrm{f}}+s_0/T_0$$ (2)

where s ₀/T ₀ (=1/e ₀) is the compliance of the array of attached motors at T ₀. Considering the whole range of the Y ₀–T ₀ data in Fig. 5 C, the relation for both slow and fast fibres exhibits a downward concavity at forces <40 kPa. A more detailed mechanical model of the half‐sarcomere is necessary, in which an elastic element in parallel with the motor array explains the deviation from the linear relation (Model 2, Fig. 6 B). In this case C _hs depends on T ₀ according to the equation:

$$C_{\mathrm{hs}}(T_0)=C_{\mathrm{f}}+s_0\times C_{\mathrm{P}}/(s_0+C_{\mathrm{P}}·T_0)$$ (3)

In Fig. 6, the fit of the C _hs–T ₀ relation with Model 2 (grey line) is compared to the fit with Model 1 (black line) either for slow (Fig. 6 C) or fast (Fig. 6 D) fibres. The relevant parameters are given in Table 3. The value of the compliance of the element in parallel with the myosin motors (C _P) was 589 ± 130 nm MPa⁻¹ in the slow fibres and 627 ± 102 nm MPa⁻¹ in the fast fibres and thus was constant independent of the fibre type. The above analysis shows that in both slow and fast fibres the non‐linear behaviour of the half‐sarcomere elasticity at different [Ca²⁺]‐modulated isometric force values can be explained by an elastic element in parallel with the array of myosin motors with a constant stiffness that is similar in slow and fast fibres and is more than one order of magnitude larger than the compliance of the array of myosin motors working in parallel in the half‐sarcomere at saturating [Ca²⁺] in both slow and fast fibres. More precisely the ratio C _P/C _cb was 590 nm MPa⁻¹/24 nm MPa⁻¹ = 25 in the slow fibres and 627 nm MPa⁻¹/11.9 nm MPa⁻¹ = 53 in the fast fibres. Consequently, the estimates of C _f and s ₀ with Model 2 do not differ significantly (P > 0.6) from those calculated with Model 1.

Table 3.

Estimate of the mechanical parameters of the half‐sarcomere with Model 1 and 2 in slow and fast fibres

	Slow fibres			Fast fibres
Model	s 0 (nm)	C f (nm MPa−1)	C P (nm MPa−1)	s 0 (nm)	C f (nm MPa−1)	C P (nm MPa−1)
Model 1	3.33 ± 0.16	15.9 ± 1.4		3.26 ± 0.20	15.1 ± 1.0
Model 2	3.67 ± 0.53	15.3 ± 6.0	589 ± 130	3.41 ± 0.27	15.1 ± 2.0	627 ± 102

Half‐sarcomere strain in rigor

The difference in T _0,4.5 between slow and fast fibres could be related to a different force of the myosin isoform and/or to a different number of motors attached to actin. Since the average strain of the motors at T _0,4.5 (s ₀) is the same in both fibre types, a difference in the force per motor would imply a corresponding difference in motor stiffness. To clarify this point the half‐sarcomere stiffness was measured in rigor, a condition where all the myosin motors are attached to actin (Cooke & Franks, 1980; Thomas & Cooke, 1980), so that any difference in the half‐sarcomere stiffness between slow and fast fibres reflects a difference in stiffness between the myosin isoforms. The same length step protocol as that used in activated fibres was applied to both slow and fast fibres in rigor (Fig. 3 B and right column in Fig. 4 A for a slow fibre). Different levels of steady force T (range 0.1–1.2T _0,4.5) were attained by slowly stretching the rigorised fibres by different amounts (L, 2–10 nm per hs). The T ₁ relations are shown by filled symbols in Fig. 4 B (slow fibres) and Fig. 4 C (fast fibres). The force has been normalised to the CSA of the relaxed fibre, considering that the number of myofilaments per fibre remains the same independent of the reduced CSA in rigor. The half‐sarcomere stiffness in rigor (k _r, measured by the slope of the linear fit, continuous lines) was larger than in the activated fibre (open symbols and dashed lines in Fig. 4 B and Fig. 4 C), as expected considering that in the activated fibres only a fraction of the myosin motors are attached to the actin filament. Furthermore, k _r was larger in the fast fibres than in the slow fibres and, within the same fibre type, k _r was independent of T, as shown by the parallel rightward shift of the T ₁ relations as force is reduced. Consequently, in the whole range of rigor forces considered, Y increased in proportion to T (Fig. 5 D, filled circles, slow fibres; open circles, fast fibres). This is expected in rigor where all the elastic components of the half‐sarcomere, the myofilaments and the array of myosin motors, are strained in proportion to force. The relation between the half‐sarcomere strain, Y, and the steady rigor force, T, showed a larger slope in slow than in fast fibres. The linear fit to the pooled Y–T points (lines in Fig. 5 D) gave a slope of 26.8 ± 0.5 nm MPa⁻¹ in slow fibres and 19.0 ± 0.3 nm MPa⁻¹ in fast fibres. The slope of the relation is the half‐sarcomere compliance in rigor (C _hsr), and thus C _hsr in slow fibres was 41% larger than in fast fibres and, given that C _f is the same in both fibre types, this indicates that the compliance of the motor array (1/e _r) was larger in the slow myosin isoform than in the fast myosin isoform.

1/e _r can be determined by subtracting C _f from C _hsr and was 11.3 ± 1.2 nm MPa⁻¹ in slow fibres and 3.5 ± 0.8 nm MPa⁻¹ in fast fibres. Correspondingly the stiffness of the motor array in rigor (e _r) was 88.5 ± 6.7 and 285.7 ± 62.0 kPa nm⁻¹, respectively. The stiffness of the myosin motor (ε) can be determined by dividing e _r by the density of motors per square metre in the half‐sarcomere (n), calculated using the myofibrillar density determined with the electron microscopy: n was 1.58 × 10¹⁷ and 1.68 × 10¹⁷ m⁻² for slow and fast fibres, respectively (Table 2B). ε for the slow isoform was 0.56 ± 0.04 pN nm⁻¹, and 1.70 ± 0.37 pN nm⁻¹ for the fast isoform; this last value is in agreement with that reported in a previous work (Linari et al. 2007) and with in vitro mechanical measurements (Lewalle et al. 2008). Thus ε for the slow isoform was about 1/3 of that of the fast isoform. A factor of 3 difference between stiffness of the slow and fast myosin isoform has been found also by Brenner et al. (2012) comparing slow human fibres with fast rabbit fibres. In that study both stiffness values were smaller, likely because of the expanded interfilamentary lattice (Linari et al. 2007). The stiffness of slow and fast myosin isoforms was found to be different by a factor of 3 also using single molecule mechanics by laser trapping on myosins purified from the rat muscle (Capitanio et al. 2006), even if the absolute values were slightly smaller than those reported with in situ measurements here.

Force per motor and fraction of myosin motors responsible for active force

Since the average strain of the motors during isometric contraction (s ₀) was ∼3.3 nm independent of the myosin isoform, the finding that the stiffness of the slow myosin isoform was 3 times smaller than that of the fast isoform implies that F ₀, the average force developed by the motor in isometric contraction was 3 times smaller in the slow isoform. In fact F ₀ (= εs ₀) was 1.89 ± 0.43 pN in the slow isoform and 5.35 ± 1.51 pN in the fast isoform. T _0,4.5 was only 2 times smaller in the slow fibres than in the fast fibres, suggesting that the fraction of motors attached in the slow fibres (β) is larger than in the fast fibres, partly counteracting the three times smaller force per motor. β can be determined by the ratio between the stiffness of the motor array during isometric contraction (1/(C _hs − C _f)) and the stiffness of the motor array in rigor (1/(C _hsr − C _f)). β was 0.47 ± 0.09 in slow fibres and 0.29 ± 0.08 in fast fibres. Thus β in slow fibres was about 60% larger than in fast fibres, even if the large error reduces the statistical significance of this conclusion (P > 0.05).

Discussion

Fast sarcomere‐level mechanics in Ca²⁺‐activated skinned fibres from rabbit slow (soleus, expressing the MHC‐1 isoform) and fast (psoas, expressing the MHC‐2X isoform) muscles is used to define the mechano‐kinetic properties of the slow and fast myosin isoforms during isometric contraction: the stiffness and the average force of the actin‐attached motor, the fraction of motors attached, the kinetics underlying isometric force development. In slow fibres the stiffness per myosin motor is 0.56 pN nm⁻¹, about three times smaller than in fast fibres (1.70 pN nm⁻¹). According to the crystallographic model of force generation based on the tilting of the light chain domain (the lever arm) about its fulcrum on the catalytic domain firmly attached to actin (Rayment et al. 1993a), the stiffness between the catalytic domain and the extremity of the lever arm (the head‐rod junction) that transfers force and movement to the thick filament is responsible for the gain in the coupling between the conformational change and the produced force. A lower motor stiffness provides a lower force for the same conformational change. For the same average strain of the motor in isometric contraction in slow and fast isoforms (3.3 nm), the force developed by the slow isoform (∼1.9 pN) is about one‐third of that developed by the fast isoform (∼5.4 pN). The effect of the reduced motor stiffness of slow fibres on the force of the half‐sarcomere is attenuated by the larger fraction of myosin motors attached in the half‐thick filament, so that the force per CSA developed by the slow fibres is about one‐half of that developed by the fast fibres.

Contributions of different structures to half‐sarcomere elasticity

The structural components contributing to the half‐sarcomere elasticity are the thick and thin filaments, the array of myosin motors attached to actin and an elastic element in parallel with motors (Ford et al. 1981; Linari et al. 1998, 2007; Bagni et al. 2002; Piazzesi et al. 2007; Colombini et al. 2010; Brunello et al. 2014; Fusi et al. 2014). In both slow and fast fibres, the compliance of this element (C _P) is so large (∼600 nm MPa⁻¹) that at forces >40 kPa its effect on the estimate of the compliances of the other elements is negligible. C _f, measured by the slope of the half‐sarcomere strain–force relation, is 15.5 nm MPa⁻¹ and s ₀, the ordinate intercept of the relation, which measures the average strain in the attached myosin motor in isometric contraction, is 3.3 nm. At forces <40 kPa, the presence of the parallel element with constant compliance C _P emerges because the progressive reduction in number of attached motors with the reduction of T makes its contribution significant with respect to that of the motor array. Within the limits of our resolution, C _P has the same value in slow and fast fibres, as expected from a parallel elasticity generated by a protein different from the myosin motor (titin or myosin‐binding protein C). The value of C _P in demembranated fibres is ∼2 times that found in intact fibres of the frog. This higher value could be related to the mechanical properties of the parallel elasticity per se (mammals versus amphibians) or to a difference in the properties of the milieu surrounding the contractile material (skinned versus intact), which reduces the stiffness of the parallel elasticity. Further experiments are necessary to clarify this point and identify the origin of C _P.

Kinetics underlying the isometric contraction

The relevant kinetic parameters estimated in the isometric contractions of slow and fast fibres are the fraction of attached myosin motors (β) and the rate of force development (k _TR). Based on a simple two‐state mechano‐kinetic model (Huxley, 1957), β and k _TR are related to the apparent rate constants of attachment (f) and detachment (g) of motors according to the following equations: β = f/(f + g) and k _TR = f + g. Knowing β and k _TR, f (= βk _TR) and g (= k _TR(1 − β)) can be calculated (Table 4): in slow fibres f and g are 5 and 12 times smaller than in fast fibres, respectively. A ∼10 times reduction in g is in agreement with previous work, while a 5 times reduction in f is one order of magnitude smaller than what previously reported (Millar & Homsher, 1992; Brenner et al. 2012). In this respect it must be noted that these estimates are likley to be influenced by the method for determining k _TR. Our sarcomere‐level mechanics allows complete force redevelopment following a period of unloaded shortening (30–40 nm per hs, Fig. 3 A), avoiding the stretching manoeuvre that may alter the kinetics of force redevelopment. Moreover, as the time course of force rise is not described by a single exponential and its later part may be influenced by the development of sarcomere inhomogeneity (which is likely different in slow and fast fibres), a convenient empirical estimate of k _TR is obtained by taking the reciprocal of t _1/2. Our analysis appears quite solid, also in relation to the independent estimate of β. From the finding that β is larger in the slow than in the fast fibres, it necessarily follows that the reduction of f between slow and fast fibres must be smaller than the reduction of g. The finding in the literature (Millar & Homsher, 1992; Brenner et al. 2012) that in the slow isoform g is reduced by a factor of 10 (like in this work), while f is reduced by a factor of 50 (10 times more than in this work), would imply a large reduction in β, which is inconsistent with the evidence, reported here, that β increases.

Table 4.

Estimate of the relevant kinetic parameters

	Slow fibres	Fast fibres
f (s−1)	1.14	6.06
g (s−1)	1.28	14.84
k CAT (s−1)	0.60	4.30

Based on our f and g estimates, the predicted ATP hydrolysis rate under isometric conditions (k _CAT = fg/(f + g)) in slow fibres is 14% of that in fast fibres (Table 4). A 10 times smaller k _CAT for the slow isoform is in quite good agreement with the experimental observations showing that the isometric ATPase rate is 0.05 and 0.41 mm s⁻¹ in slow and fast fibres, respectively (Potma et al. 1995). With a concentration of the myosin heads of 0.15 mm, k _CAT become 0.33 and 2.73 s⁻¹ respectively. The comparison with the absolute values reported in Table 4 shows that our estimates based on mechanical parameters (k _TR and β) give k _CAT values twice those obtained from direct ATPase rate measurements. Assuming that the ATPase measuremnets are correct, a possible reason for the discrepancy is that k _TR calculated by the reciprocal of t _1/2 is overestimated because it is reporting a step of the ATPase cycle.

The rate of ATP hydrolysis measured in solution is the same for slow and fast myosin isoforms (Marston & Taylor, 1980). Thus, assuming that the rate of the ATP hydrolysis is the same in skinned fibres as in solution because the ATP hydrolysis occurs in detached motors (Millar & Homsher, 1992), this step does not explain the lower ATPase rate in slow fibres. In fast fibres the release of P_i is a relatively fast process (Dantzig et al. 1992) and k _CAT would be limited by the rate of ADP release (Linari et al. 2010; Caremani et al. 2015). On the contrary in slow fibres the rate of P_i release is a slow process (Millar & Homsher, 1992), suggesting that not only the release of ADP but also the release of P_i would limit k _CAT. Under these conditions the finding that the fraction of motors attached in isometric contraction is 60% larger in slow fibres supports the idea that P_i can be released from the catalytic site after the formation of a strong binding of myosin on actin (Caremani et al. 2013).

Stiffness of the myosin motor and amino acid sequence of the converter domain

The domain of the actomyosin complex giving the main contribution to the compliance of the attached motor is unknown. One possible source is the 9 nm‐long α‐helix which may undergo bending (Uyeda et al. 1996; Dobbie et al. 1998; Irving et al. 2000); alternatively, the regions of major distortion could be the junction between the catalytic and light chain domains (Dobbie et al. 1998), the converter domain, as suggested by single amino acid mutations in this region (Kohler et al. 2002; Seebohm et al. 2009; Brenner et al. 2014). In slow fibres from soleus muscle of human, it has been found that a single natural mutation occurring in the converter domain (708–780 region) of the slow β‐MHC isoform is responsible for a large change in motor stiffness. In fact, when proline at position 713 or valine at position 719 is replaced with tryptophan the stiffness of the myosin motor increases 2–3 times. Comparison of the available amino acid sequence in of six species of mammals of different size (mouse, cattle, rabbit, pig, dog and human, Fig. 7) shows a sequence difference in the converter of 16–20% between the slow and fast myosin isoforms, while there is almost no difference within slow or fast isoforms. If the converter domain plays a major role in determining the motor stiffness, the difference in stiffness between slow and fast myosin isoforms found here for rabbit should be present also in all the other species.

Figure 7. Amino acid sequences of the converter domain of MHC‐1 and MHC‐2X isoforms in six species of mammals.

Numbers at the beginning and at the end of each sequence are the residues of start and end of the domain. Differences between slow and fast isoforms within a species are in bold. Myosin heavy chain sequences were found at the NCBI (National Centre for Biotechnological Information; Bethesda, MD, USA). The sequences of the converter region were aligned using the BLAST program available at NCBI.

Energetics of slow and fast muscle

The efficiency of energy conversion in slow muscle is similar to (Barclay et al. 1993; He et al. 2000) or higher than (Woledge, 1968; Barclay et al. 2010) that in fast muscles. At the molecular level the work is the product between the force exerted by the actin‐attached motor and the amount of filament sliding undergone while it is attached. In the fast muscle (tibialis anterior) of frog (Rana temporaria) the maximum efficiency (0.45) is related to individual myosin motors converting the energy from the hydrolysis of one ATP molecule (83 zJ) by maintaining a force of about 6 pN while pulling an actin filament through a 6 nm stroke (Piazzesi et al. 2007). The finding that the slow myosin isoform bears a force about one‐third of the fast myosin isoform implies that the same maximum efficiency can be attained only if, for the same free energy available from the ATP hydrolysis, the amount of sliding accounted for by the molecular motor is three times larger. Assuming that the force and the sliding distance of the fast isoform are 5.4 pN and 6 nm, respectively (Piazzesi et al. 2007), for the slow myosin isoform to get the same efficiency with a force of 1.8 pN (this work), a sliding distance of 18 nm, well beyond the limits imposed by the structural working stroke (Rayment et al. 1993b), is necessary. To solve the problem that, in spite of a three times difference in force, the efficiency of the free energy conversion of the two isoforms is similar, further investigation is necessary to measure the size of the working stroke in slow muscles by eliciting its synchronous execution with a stepwise drop in force superimposed on isometric contraction (Piazzesi et al. 2002; Caremani et al. 2013).

Additional information

Competing interests

None declared.

Author contributions

Mechanical experiments were performed at PhysioLab, Department of Biology of the University of Florence and the electron microscopy experiments at of the University of Chieti. The experiments were performed by V.P., S.B., F.P., I.P., F.P. and M.C. All the authors contributed to the conception and design of the experiments, the collection, analysis and interpretation of data, and drafting the article or revising it critically for important intellectual content. All authors approved the final version of the manuscript and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship and all those who qualify for authorship are listed.

Funding

This study was supported by (a) Ente Cassa di Risparmio di Firenze Project 2015.0902 (Italy); (b) Telethon Project GGP12282 (Italy); (c) Italian Telethon ONLUS Foundation (Rome, Italy): GGP13213 to FP; and (d) Italian Ministry of Health, (Rome, Italy): GR‐2011‐02352681 to S.B.