Neural mediators of changes of mind about perceptual decisions

Abstract

Changing one’s mind on the basis of new evidence is a hallmark of cognitive flexibility. To revise our confidence in a previous decision, new evidence should be used to update beliefs about choice accuracy, but how this process unfolds in the human brain remains unknown. Here we manipulated whether additional sensory evidence supports or negates a previous motion direction discrimination judgment while recording markers of neural activity in the human brain using fMRI. A signature of post-decision evidence (change in log-odds correct) was selectively observed in the activity of posterior medial frontal cortex (pMFC). In contrast, distinct activity profiles in anterior prefrontal cortex (aPFC) mediated the impact of post-decision evidence on subjective confidence, independently of changes in decision value. Together our findings reveal candidate neural mediators of post-decisional changes of mind in the human brain, and indicate possible targets for ameliorating deficits in cognitive flexibility.

John-Maynard Keynes allegedly said, “When the facts change, I change my mind”. Updating beliefs on the receipt of new evidence is a hallmark of cognitive flexibility. Previous work has focused on how newly arriving evidence for each choice option is evaluated to guide ongoing motor actions in the coordinate frame of a perceptual discrimination decision (e.g. left vs. right)^1–4. However, revising one’s confidence about an already-made choice imposes a different coordinate frame on the evidence, and requires weighting the evidence comparatively with respect to the choice^5–7. Here, we leveraged a novel extension of a classic motion discrimination task to investigate the computational signatures of such assessment and to investigate how new evidence leads to changes in decision confidence (Figure 1), while recording markers of neural activity in the human brain using functional magnetic resonance imaging (fMRI). We confirmed behaviorally that post-decision motion led to systematic changes in confidence about the accuracy of a previous decision. This design allowed us to study the underpinnings of changes of mind by analyzing how new evidence impacts confidence bidirectionally, in a graded fashion, rather than only on a subset of trials on which discrete choice reversals are observed.

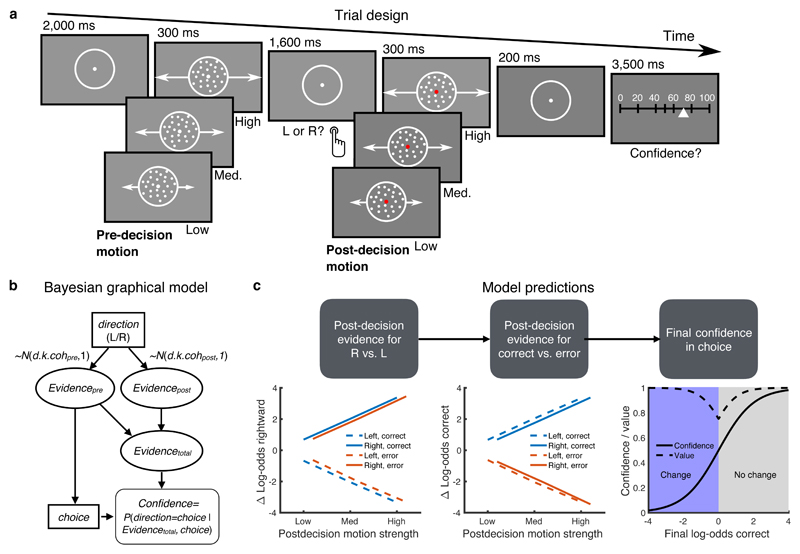
Figure 1. Post-decision evidence task and computational framework.

A) Task design. Participants made an initial left/right motion discrimination judgment, after which they saw additional post-decision motion of variable coherence moving in the same direction as pre-decision motion. They were asked to rate their confidence in their initial choice on a scale from 0% (certainly wrong) – 100% (certainly correct). Confidence scale steps were additionally labeled with the words “certainly wrong”, “probably wrong”, “maybe wrong”, “maybe correct”, “probably correct”, “certainly correct” (not shown). B) Bayesian graphical model indicating how pre- and post-decision motion samples are combined with the chosen action to update an estimate of decision confidence. C) Simulated decision variables from the model in (B) showing a distinction between updating evidence in the coordinate frame of motion direction (left panel) and choice accuracy (middle panel) as a function of post-decision motion strength and choice. A change in log-odds correct (“post-decision evidence”; PDE) is revealed by a qualitative interaction between post-decision motion strength and choice accuracy (middle panel). The right panel indicates the expected mapping between log-odds correct and both final confidence/decision value. Confidence and value are dissociated on change-of-mind trials (confidence < 0.5) through use of a quadratic scoring rule, which rewards subjects for both being confident and right, and unconfident and wrong.

We hypothesized that brain regions in the human frontal lobe implicated in performance monitoring (posterior medial frontal cortex (pMFC), encompassing dorsal anterior cingulate cortex^8,9 and pre-supplementary motor area¹⁰) and metacognition (anterior prefrontal cortex; aPFC^11–14) would play a central role in updating beliefs about previous choice accuracy. Tracking evidence in the coordinate frame of choice accuracy rests on computing a probability that a previous choice was (in)correct given the new evidence available, or a change in log-odds correct⁵. When this quantity (which we refer to as “post-decision evidence” or PDE) is sufficiently low the alternative option becomes more favourable³. A Bayesian observer predicts a qualitative signature of PDE in both behaviour and neural activity. Specifically, we expect a positive relationship between PDE and motion strength on correct trials (because new evidence serves to a confirm a previous choice) and a negative relationship on error trials (because new evidence disconfirms a previous choice; Figure 1C, middle panel).

A further step in the computational chain is to use PDE to update one’s final (subjective) confidence in a choice (Figure 1C, righthand panel). For an ideal observer, there is a systematic and direct relationship between PDE and subsequent changes in confidence. However it is known that subjective confidence estimates do not always track objective changes in performance^15,16, and previous studies suggest the prefrontal cortex as a key determinant of such metacognitive fidelity^11,13. Moreover, a key challenge when interpreting confidence-related neural activity is dissociating distinct variables that may be correlated due to a particular task manipulation¹⁷. For instance, changes in confidence are often correlated with both evidence strength and the expected value of a choice (although see 18,19). Here we carefully separated these quantities through use of an incentive scheme in which subjects were rewarded for being highly confident and right, and unconfident and wrong, ensuring changes in final confidence were decoupled from subjective value (Figure 1C, righthand panel). We additionally used mediation analyses to formally identify brain activity capturing the impact of model PDE on subjective confidence reports, which were obtained at the end of every trial²⁰. This approach has proven fruitful in studying the neural basis of other subjective states such as pain while controlling for lower-level effects of sensory stimulation²¹, but has not previously been applied in studies of decision-making. Together our findings reveal a division of labour in which pMFC activity tracks post-decision evidence, whereas lateral aPFC additionally mediates the impact of post-decision evidence on confidence, independently of decision value.

Results

Participants carried out the perceptual decision task outlined in Figure 1A, first in a behavioural session (N=25 subjects), and subsequently while undergoing fMRI (N=22 subjects). The subject’s goal was to make accurate decisions about the direction of random dot motion, and then to estimate confidence in their initial choice. A new sample of dot motion in the same (correct) direction was displayed after the subject’s choice but before their confidence rating. Subjects were rewarded for the accuracy of their confidence judgments, and thus the value of a trial increased both when they became more accurate about being right and more accurate about being wrong (see Figure 1C and Methods). A fully factorial design crossed 3 pre-decision coherence levels with 3 post-decision coherence levels yielding 9 experimental conditions. Together these features of the task design allowed us to dissociate motion strength and decision value from changes of mind, as shown in Figure 1C. To equate evidence strength across individuals, before the main task each participant performed a calibration procedure to identify a set of motion coherences that led to approximately 60%, 75% and 90% accuracy (Supplementary Figure 1). Examination of the empirical cross-correlation between task features and behaviour (motion strength, confidence, value and response times) confirmed a limited correlation between predictors (maximum absolute mean r = 0.38 for fMRI session; Supplementary Figure 2).

Choice, confidence and changes of mind

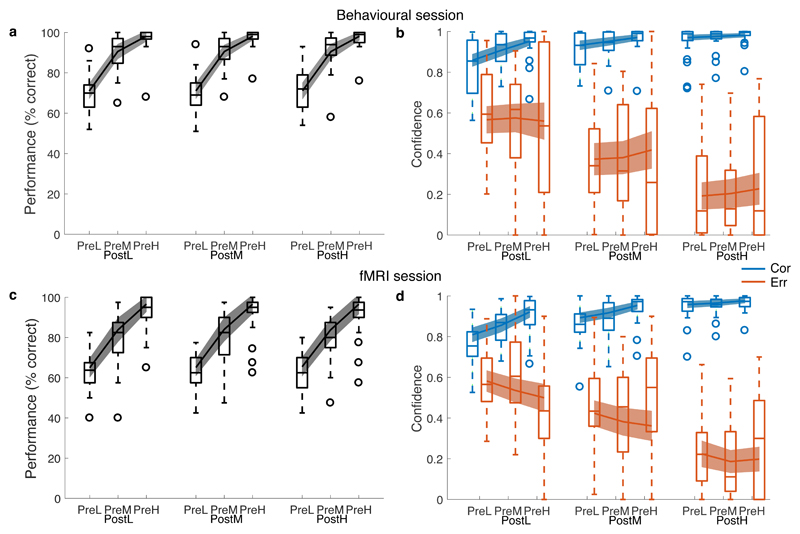
As expected, stronger pre-decision motion led to increases in response accuracy (behavioural session: hierarchical logistic regression, β = 9.21 (0.78), z = 11.8, P < 2 × 10^-16; fMRI session: β = 7.00 (0.70), z = 10.0, P < 2.0 × 10^-16; Figure 2A, C and Supplementary Table 1). We observed robust changes of confidence in response to post-decision motion (Figure 2B, D). Specifically, we found that after an erroneous decision, stronger post-decision motion led to progressively lower confidence (behavioural session: hierarchical linear regression, β = -1.15 (0.14), χ²(1) = 71.8, P < 2.2 × 10^-16; fMRI session: β = -1.05 (0.11), χ²(1) = 88.0, P < 2.2 × 10^-16; Supplementary Table 2) whereas after a correct decision, confidence was increased due to the confirmatory influence of new evidence (behavioural session: β = 0.41 (0.08), χ²(1) = 26.3, P = 3.0 × 10^-7; fMRI session: β = 0.54 (0.08), χ²(1) = 44.7, P = 2.3 × 10^-11). Binary changes of mind are revealed by confidence levels lower than 0.5 (i.e., greater confidence in the alternative response) with strong post-decision motion accordingly leading to more frequent binary changes of mind (behavioural session, mean = 11.7 % of trials; fMRI session, mean = 18.4 % of trials) than weak post-decision motion (behavioural session, mean = 10.4 % of trials; fMRI session, mean = 14.8 % of trials). Subjects were well calibrated, with final confidence approximately tracking aggregate performance (Supplementary Figure 3).

Figure 2. Behavioural results.

Upper panels show data collected in an initial behavioural session (900 trials per subject, N=25 subjects); lower panels show behavioural data collected during the fMRI session (360 trials per subject, N=22 subjects). In each panel data are separated by pre- and post-decision motion coherence (L=low; M=medium; H=high). A, C) Performance (% correct). B, D) Aggregate confidence ratings separated according to whether the decision was correct (blue) or incorrect (orange). Lines show data simulated from the best-fitting Bayesian+RT model parameters. Data are plotted as boxplots for each condition in which horizontal lines indicate median values, boxes indicate 25-75% interquartile range and whiskers indicate minimum and maximum values; data points outside of 1.5 × the interquartile range are shown separately as circles. For model simulations, error bars reflect 95% confidence intervals for the mean. See also Supplementary Figure 5.

Computational model of post-decisional change in confidence

We compared between a set of alternative computational models of how confidence is affected by post-decision motion strength (see Methods for details). All models generalize signal detection theory, with a single free parameter k mapping pre- and post-decision motion strength (coherence) onto an internal decision variable (Figure 1B). Extensions to an ideal observer model explored the impact of asymmetric weighting parameters on pre- and post-decision motion^6,7, asymmetric weighting of confirmatory and disconfirmatory evidence⁶, flexible mappings between probability correct and reported confidence²², and the influence of initial response time²³ (see Methods and Supplementary Figure 4). We assessed model fit by examining generalization across testing sessions to avoid overfitting; the best-fitting Bayesian+RT model was able to capture both the relationship between pre-decision motion strength and choice accuracy, and the impact of post-decision motion on changes in confidence (Figure 2 and Supplementary Figure 5) (difference in median log-likelihood relative to next best model: behavioural->fMRI, 1932; fMRI->behavioural, 1298; Supplementary Figure 4). The β_RT parameter of this model was negative in both cases (behavioural session: β_RT = -0.73 (0.26); fMRI session: β_RT = -0.37 (0.22); Supplementary Table 3) indicating that faster initial decisions boosted final confidence. We note that a qualitative signature of PDE in Figure 1C is common to all model variants, and makes clear predictions for interrogation of brain imaging data, which we turn to next.

Neural representations of post-decision evidence

We sought to identify fMRI activity patterns consistent with tracking PDE in the coordinate frame of choice accuracy (changes in log-odds correct due to post-decision motion). Such patterns are characterized by a change in the sign of the relationship between post-decision motion strength and brain activity on correct vs. error trials (Figure 1C, middle panel). This change in sign is qualitative and we remain agnostic about its direction at the level of the fMRI signal – it is plausible that a particular neural population encodes increasing rather than decreasing likelihood of change of mind, in which case we would observe a positive relationship on error trials and a negative relationship on correct trials.

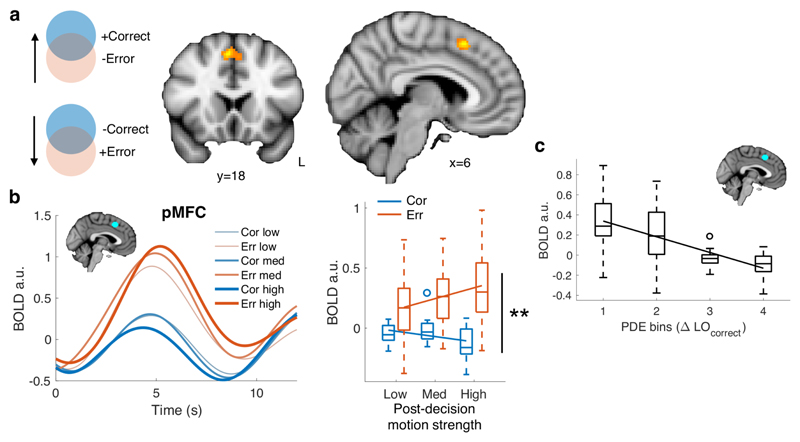
We first computed interaction contrasts (positive or negative) between post-decision motion strength and choice accuracy, to identify patterns of activity that mirror a signature of PDE. Interaction effects were observed whole-brain corrected at both the voxel- and cluster-level in pMFC (Figure 3A; peak: [6 18 50], P_voxelFWE = 0.002; P_clusterFWE < 0.001) and at the cluster-level in right insula (peak: [44 14 -6], P_clusterFWE = 0.009; Supplementary Table 4). Accordingly, in an independently defined pMFC ROI, we obtained a significant interaction between post-decision motion strength and initial decision accuracy in single-trial activity estimates aligned to the onset of post-decision motion (Figure 3B and Supplementary Table 5; β = -0.11 (0.037), χ²(1) = 9.35, P = 0.0022). This interaction effect was driven by an increase on error trials, and decrease on correct trials (Figure 3B).

Figure 3. Neural signatures of post-decision evidence.

A) Whole-brain statistical parametric map for the interaction contrast error/correct × post-decision motion strength, thresholded at P < 0.05 FWE corrected, cluster-defining threshold P < 0.001 (coronal section, y=18; saggital section, x=6). Activation in pMFC was significant corrected for multiple comparisons at both the voxel- and cluster-level (peak MNI coordinate: [6 18 50]). N=22 subjects. B) fMRI signal extracted from an independent pMFC ROI and sorted according to the subject’s choice accuracy (orange = error, blue = correct) and post-decision motion strength. The left panel shows activity timecourses aligned to the onset of pre-decision motion (trial start); the right panel shows condition-specific activity estimated from regressors aligned to the onset of post-decision motion. A significant interaction between choice accuracy and post-decision motion strength was obtained in pMFC; **, hierarchical regression, two-tailed Type III Wald χ²test, P = 0.0022. N=22 subjects. C) Average BOLD signal in the pMFC ROI as a function of post-decision evidence extracted from the Bayesian+RT model fit (change in log-odds correct). For visualization, post-decision evidence is collapsed into 4 equally spaced bins per subject. N=22 subjects. In panels B and C, BOLD data are plotted as boxplots for each condition in which horizontal lines indicate median values, boxes indicate 25-75% interquartile range and whiskers indicate minimum and maximum values; data points outside of 1.5 × the interquartile range are shown separately as circles. Solid lines show the mean of subject-level linear fits.

Finally, to corroborate our model-free analysis, we extracted the predicted PDE $(L{O}_{correct}^{post})$ on each trial from the Bayesian+RT model fitted to each subject’s in-scanner behavioural data. As expected from the model-free pattern, a negative linear relationship was observed between model PDE and pMFC activity (Figure 3C; β = -0.052 (0.0085), χ²(1) = 37.3, P = 1.03 × 10^-9). No relationship was observed between pre-decision evidence $(L{O}_{correct}^{pre})$ and pMFC activity (β = -0.013 (0.013), χ²(1) = 1.10, P = 0.30), indicating specific engagement during post-decisional changes of confidence. To establish the anatomical specificity of the effect of PDE on brain activity we interrogated prefrontal and striatal ROIs also implicated in decision confidence and metacognition (ventral striatum, vmPFC and bilateral aPFC areas 46, FPl and FPm from the atlas of Neubert et al.²⁴; Supplementary Figures 6, 7 and Supplementary Table 5). None of these ROIs showed an interaction between post-decision motion strength and choice (P > 0.05) and contrasts of regression coefficients revealed greater interaction effects in pMFC compared to aPFC subregions (area 46: χ²(1) = 3.7, P = 0.054; FPl: χ²(1) = 5.0, P = 0.026; FPm: χ²(1) = 10.9, P = 0.00095).

Neural mediators of final confidence

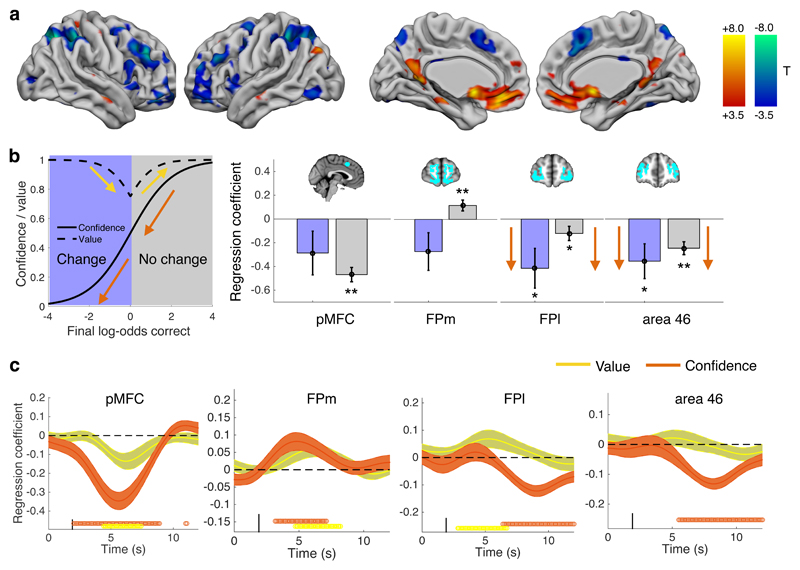
Having identified a putative neural signature of PDE in pMFC, we next searched for brain areas tracking subjects’ final confidence in a decision. One computationally plausible hypothesis is that such updates of final confidence are mediated by anatomically distinct networks involved in metacognition^25,26. Anterior prefrontal cortex (aPFC) is a leading candidate as this region is implicated in metacognitive assessment of both perceptual and economic decisions^12,14,18. In a whole-brain analysis we found widespread activity showing both positive and negative relationships with final confidence (Figure 4A; Supplementary Table 6) in regions including pMFC (negative relationship), medial aPFC (positive relationship) and lateral aPFC (negative relationship), consistent with previous studies^12,14,18,27.

Figure 4. Neural signatures of final confidence in choice.

A) Whole-brain analysis of activity related to final confidence reports on each trial. Cool colours indicate negative relationships; hot colours indicate positive relationships. Thresholded at P < 0.05, FWE corrected for multiple comparisons, cluster-defining threshold P < 0.001. N=22 subjects. B) Hierarchical regression coefficients relating confidence to single-trial activity estimates on both change and no-change of mind trials. Orange arrows indicate that the pattern of coefficients is consistent in sign, as predicted for regions tracking the full range of final confidence in an initial choice. Yellow arrows indicate a flip in sign, as predicted for regions tracking changes in decision value. Error bars indicate standard errors of the coefficient means. ** P < 0.01, * P < 0.05, two-tailed Type III Wald χ²test; see Supplementary Table 7. N=22 subjects. C) Multiple regressions of confidence and value on activity timecourse in ROIs. Points below timecourse indicate significant excursions of T-statistics assessed using two-tailed permutation tests. Error bars indicate standard errors of the coefficient mean. N=22 subjects.

We further sought to establish whether aPFC activation continues to track confidence shifts on trials in which discrete changes of mind were recorded (confidence levels < 0.5). Activity that tracks such changes of mind should show a consistent positive/negative slope across both change and no-change trials; in contrast, activity tracking decision value should reverse its relationship with confidence on change trials (due to the increasing reward available for betting against one’s choice; Figure 4B). In a split regression analysis, we found that regression coefficients in lateral aPFC ROIs were significantly negative on both change and no-change trials (Figure 4B and Supplementary Table 7; area 46: change trials β = -0.36 (0.15), χ²(1) = 5.9, P = 0.015; no-change trials β = -0.25 (0.-54), χ²(1) = 20.6, P = 5.6 × 10^-6; FPl: change trials β = -0.41 (0.17), χ²(1) = 6.1, P = 0.013; no-change trials β = -0.12 (0.15), χ²(1) = 4.1, P = 0.044). In contrast, regression coefficients in FPm flipped in sign on change vs. no-change trials (Figure 4B). Accordingly, when regressing regional timeseries against both confidence and value in the same GLM, we found that confidence but not value covaried with a late signal in area 46 and FPl (Figure 4C). Conversely, and consistent with previous reports^18,19, FPm (and also pMFC, vmPFC and ventral striatal ROIs; see Supplementary Figure 7) showed simultaneous correlates of both confidence and value. These results support a conclusion that lateral aPFC subregions are specifically engaged when subjects change their minds about a previous decision on the basis of new evidence.

A key question is how PDE (encoded in pMFC) leads to subsequent shifts in final confidence in a previous decision. To test this hypothesis, we used multi-level mediation analysis^21,28 to jointly test for effects of PDE (from subject-specific fits of the Bayesian+RT computational model) on brain activity (path a), brain activity on final confidence (path b) and mediation (a × b) effects (Figure 5), while controlling for both response times and pre-decision evidence. A mediator can be interpreted as an indirect pathway through a brain area that links PDE with changes in subjective confidence, implying that if such a region were disrupted, this relationship would also be disrupted or abolished. We examined mediation both in anatomically defined aPFC subregions and at the voxel level across the whole brain.

Figure 5. Neural mediation of PDE on final confidence.

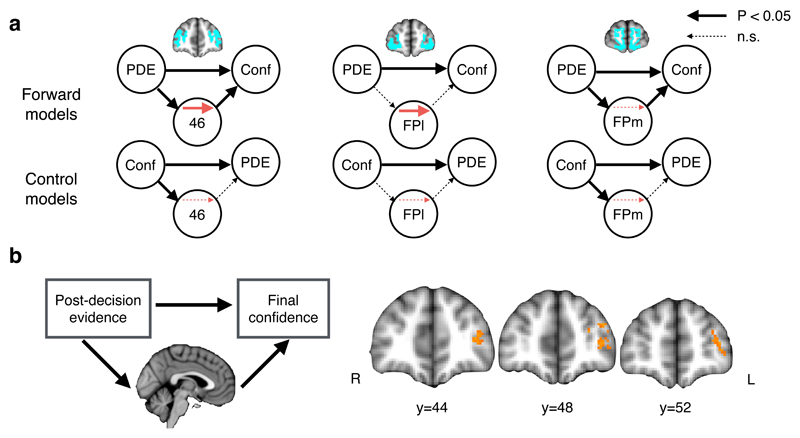
A) Multi-level mediation analysis assessing whether the effect of PDE on final confidence is mediated by activity in anatomically defined aPFC ROIs. For each ROI, the upper row of models indicates forward mediation; the lower row indicates reverse mediation (of confidence onto PDE). Mediation was observed only for forward models in areas 46 and FPl (red arrows). Arrow thickness reflects two-tailed bootstrapped P-values; see Supplementary Table 8 for statistics. N=22 subjects. B) The model used in (A) was fit to each voxel independently to create a map of P-values for the mediation (a × b) effect in aPFC. Thresholded at P < 0.05 FWE corrected at the cluster level using Monte Carlo simulation, cluster-defining threshold P < 0.001. N=22 subjects. See also Supplementary Figure 8.

In line with our hypothesis, activity in area 46 and FPl was found to mediate the impact of PDE on final confidence (Figure 5A and Supplementary Table 8; a × b effect: area 46, P = 0.0027; FPl, P = 0.0056). While mediation modeling is correlational, precluding a direct inference on directionality, we note that control models in which PDE and confidence were reversed did not result in a significant mediation effect in either area 46 (P = 0.54) or FPl (P = 0.46). Mediation may be driven either by consistent effects of paths a and b across the group, or by covariance between stimulus- and report-related responses²¹. In area 46 there was evidence for consistent main effects of path a and b in the group as a whole. In contrast, in FPl, mediation was driven by the covariance of a and b paths across subjects. Finally, in a voxel-based mediation analysis we observed a significant cluster in left lateral aPFC (Figure 5B), corroborating our ROI analysis.

In an exploratory whole-brain analysis we also observed clusters in pMFC and bilateral parietal cortex that, together with aPFC, met whole-brain corrected statistical criteria for mediation (Supplementary Figure 8). This result is consistent with pMFC activity both tracking PDE (Figure 3C) and covarying with final confidence (Figure 4A). Taken together, our findings indicate complementary roles for frontal subregions in changes of mind: pMFC (but not aPFC) activity tracks PDE, whereas lateral aPFC additionally mediates changes in final confidence estimates, independently of decision value.

Discussion

Changing one’s mind on the basis of new evidence is a hallmark of cognitive flexibility. Such reversals are supported computationally by sensitivity to post-decision evidence – if I have made an error, and the new evidence is compelling, I should change my mind. Here we leveraged a novel manipulation of post-decisional information in perceptual decision-making to study this process. Participants appropriately increased their confidence when new evidence was supportive of an initial decision, and decreased their confidence when it was contradictory. A signature of post-decision evidence encoding – a change in log-odds correct – was identified in the activity of posterior medial frontal cortex (pMFC). We further observed that distinct activity profiles in lateral aPFC mediated the impact of post-decision evidence on subjective confidence.

Previous work has focused on how stimulus evidence may reverse the accumulation of evidence in circuits coding for one or other choice option (e.g. left or right). To update one’s confidence in a previous choice, new evidence in the coordinate frame of stimulus/response may be further transformed into the coordinate frame of choice accuracy⁵. These schemes are not mutually exclusive – to update an ongoing action plan, it may be sufficient to continue accumulating evidence in a “pipeline” directly guiding the movement towards one or other target^2,3, while in parallel revising one’s belief in the accuracy of a previous choice^25,26. In an elegant behavioural study, van den Berg and colleagues demonstrated that a single stream of evidence may continue to accumulate during action initiation, and via a comparison to thresholds specified in stimulus/response space (i.e. log-odds rightward), be used to guide changes of both decision and (response-specific) confidence³. Here, by introducing a novel manipulation of post-decisional information, we reveal a circumscribed activity pattern in pMFC consistent with tracking PDE in the frame of choice accuracy. Examining mutual interactions between evidence coded in the frame of stimulus/response identity or choice accuracy is beyond the design of the current study, but may be profitably investigated by tracking each of these coordinate frames using techniques with high temporal resolution such as magnetoencephalography.

Even in the absence of a direct manipulation of post-decision evidence, signal detection models of decision confidence predict an interaction between stimulus strength and choice accuracy^16,29. We also observed such a pattern in our behavioural data – confidence decreased on error trials, and increased on correct trials, when pre-decision motion was stronger (Supplementary Table 2; this effect was tempered by the influence of response times on error-trial confidence, as shown by the fits of the Bayesian+RT model in Figure 2). However we note that the interaction effect in pMFC was primarily driven by post- not pre-decision evidence (Supplementary Table 5) indicating a distinct role in post-decisional changes of mind. An interaction between stimulus strength and choice accuracy has also been observed in the activity of rodent orbitofrontal cortex in the absence of a post-decision evidence manipulation²⁹, and inactivation of this region impairs confidence-guided behaviours³⁰. Searching for signatures of PDE in other species may therefore shed light on mechanisms supporting changes of mind that are conserved (e.g. in homologies of pMFC³¹), and those that may be unique to humans (e.g. those supported by granular aPFC).

The function of pMFC in human cognition has been the subject of extended scrutiny and debate. A well-established finding is that a paracingulate region activates to self-errors, consistent with its role as a cortical generator of the error-related negativity^8–10. More recently, studies have linked dorsal anterior cingulate activity to a broader role in behavioural switching away from a default option³². Our findings complement these lines of work by characterizing a computation related to changes of mind. Specifically, our analysis indicates that pMFC activity tracks whether an initial choice should be revised in light of newly acquired information. The peak activation in this contrast was obtained in pre-SMA, dorsal to the rostral cingulate zone³³. While previous studies of error detection have focused on all-or-nothing, endogenous error responses in pMFC, our findings suggest a more computationally sophisticated picture: pMFC activity tracked graded changes in log-odds correct^34,35 (Figure 3C). Together our results indicate that error monitoring, confidence and changes of mind may represent different behavioural manifestations of a common computation supported by inputs to pMFC^25,36,37.

Beyond pMFC, we found a widespread network of regions where activity tracks final confidence including negative correlations in lateral PFC, parietal cortex and pMFC, and positive correlations in vmPFC and precuneus, consistent with previous findings^{12,14,18,19,27}. Building on an analogous body of work on the neural substrates of subjective pain^21,38, we leveraged mediation analysis to formally unpack an inter-relationship between post-decision evidence, brain activity and the final confidence subjects held in their decision. Lateral aPFC (areas 46 and FPl) activity mediated the impact of post-decision evidence on subjective confidence. Lateral aPFC has previously been implicated in self-evaluation of decision performance^12,14,18, and receives a significant anatomical projection from pMFC³⁹. It is notable that in the current study, the activity profile of lateral aPFC covaried with final confidence in both mediation and regression analyses, but did not track post-decision evidence or decision value per se. It is therefore plausible that lateral aPFC supports a representation of choice quality that contributes to metacognitive control of future behavior^40–42. Together with aPFC, exploratory whole-brain analyses also indicated posterior parietal cortex as a mediator of the impact of PDE on confidence, consistent with a role for a broader frontoparietal network in metacognition and confidence formation^43,44.

In previous research it has proven difficult to isolate changes in decision confidence from other confounding variables. The probability of a previous decision remaining correct is often correlated with expected value. In other words, if subjects are motivated to be accurate, decision confidence usually scales with decision value. Here we separated expected value from confidence by allowing subjects to gain reward by betting against their original decision using the quadratic scoring rule. This rule returns maximum reward both when a correct trial is rated with high confidence and an incorrect trial is rated with low confidence (Figure 1C). In medial PFC we found a U-shaped pattern of activity in relation to reported confidence, consistent with previous findings that both confidence and value are multiplexed on the medial surface^18,19. In contrast, lateral aPFC activity covaried with confidence but not value, indicating a specific role in changes of mind.

In conclusion, by integrating computational modeling with human fMRI, we reveal a neural signature of how new evidence is integrated to support graded changes of mind. Multiple coordinate frames are in play when new evidence leads to shifts in beliefs – from coding evidence in support of one or other decision option, to updating the accuracy of a choice, to communicating changes in confidence. Neuroimaging revealed complementary roles for frontal subregions in changes of mind: post-decision evidence was tracked by pMFC, while aPFC additionally mediated final confidence in choice. Failure of such updating mechanisms may lead to impairments to cognitive flexibility and/or an inability to discard previously held beliefs^45,46. Together our findings shed light on the building blocks of changes of mind in the human brain, and indicate possible targets for amelioration of such deficits.

Online Methods

Participants

Twenty-five participants gave written informed consent to take part in a study conducted across two separate days. No statistical tests were used to pre-determine the sample size which is similar to those reported in previous publications^14,32,40. A behavioural experiment was administered on the first day and an fMRI experiment on the second day. Twenty-five participants were included in the analysis of behavioural data (14 females, mean age 24.0, SD = 3.6). In the fMRI experiment, one participant was excluded due to excess head motion and one participant was excluded due to lack of variability in confidence ratings (308/360 trials were rated as 100% confident). A further participant attended only the first behavioural session. Twenty-two participants were included in the analysis of fMRI data (12 females, mean age 24.1, SD = 3.4). The study was approved by NYU’s University Committee on Activities Involving Human Subjects, all relevant ethical regulations were followed, and participants provided written consent before the experiment.

Stimuli

The experiment was programmed in Matlab 2014b (MathWorks) using Psychtoolbox (version 3.0.12; ^47,48). In the behavioural session stimuli were presented on an iMac desktop monitor viewed at a distance of approximately 45cm. In the scanner, stimuli were presented via a projector at an approximate viewing distance of 58cm. Stimuli consisted of random-dot kinematograms (RDKs). Each RDK consisted of a field of random dots (0.12° diameter) contained in a 7° circular white aperture. Each set of dots lasted for 1 video frame and was replotted 3 frames later⁴⁹. Each time the same set of dots was replotted, a subset determined by the percent coherence was offset from their original location in the direction of motion and the remaining dots were replotted randomly. Motion direction was either to the left or right along the horizontal meridian. Coherently moving dots moved at a speed of 5°/s and the number of dots in each frame was specified to create a density of 30 dots/deg²/s. Each RDK lasted for 300ms.

Task and procedure

Participants attended the laboratory on two different days. On the first day they completed a calibration session to obtain their psychometric function for motion discrimination, followed by 900 trials of the main experiment shown in Figure 1A. On the second day participants completed the fMRI scan. Data collection and analysis were not performed blind to the conditions of the experiments.

Behavioural session

Calibration phase: Before performing the main task each participant performed 240 trials of motion direction estimation without confidence ratings or additional post-decision motion. These trials were equally distributed across 6 coherence levels: 3%, 8%, 12%, 24%, 48% and 100%. Motion direction (left or right) was randomized and independent of coherence. Judgments were made using the left or right arrow keys on a standard computer keyboard after the offset of each stimulus, and the response was unspeeded. During the calibration phase (but not the experiment phase), auditory feedback was delivered to indicate whether the judgment was correct (high pitched tone) or incorrect (low pitched tone). The intertrial interval was 1s. The three coherence levels that resulted in 60%, 75% and 90% correct choices were individually determined for each subject using probit regression. These coherence levels were then stored for use in the experiment phase.

Experiment phase: In the main experiment subjects completed 900 trials of the task shown in Figure 1A. Each trial consisted of the following events in sequence. A central fixation point (0.2° diameter) and empty aperture were presented, followed by an RDK of low, medium or high coherence. Following the offset of the RDK participants were asked to make a judgment as to whether the movement of the dots was to the left or the right. Their response triggered a second post-decision RDK that was shown after a delay of 100ms. The second post-decision RDK was always in the same (correct) direction as the first pre-decision RDK, but of a variable coherence. Subjects were instructed that this was “bonus” motion that they could use to inform their confidence in their initial response. They were told that the bonus motion was always in the same direction as the regular motion, but were not informed that it may vary in strength. A fully factorial design crossed 3 pre-decision coherence levels with 3 post-decision coherence levels yielding 9 experimental conditions each with 100 trials. Trial order was fully randomized for each subject.

After the bonus motion was displayed, an empty aperture was presented for 200ms and then participants were asked to indicate their confidence in their initial judgment on a horizontal scale (length = 14°) ranging from 0-100%. Confidence responses were made with a mouse click controlled by the right hand and could be made anywhere along the scale. Half of subjects saw the scale labeled with 0% on the left and 100% on the right and half saw the reverse orientation, with scale orientation fixed across both the behavioural and fMRI sessions. A vertical red cursor provided feedback as to the selected rating. In the behavioural session there was no time limit for either the response or the confidence rating, and no feedback was given as to whether the response was correct or incorrect.

fMRI session

During the structural scan at the start of the fMRI experiment, participants carried out a “top-up” calibration session consisting of 120 trials of left/right motion judgments without confidence ratings. Three randomly interleaved QUEST adaptive staircases were used to estimate coherence levels associated with 60%, 75% and 90% correct performance. The prior for each staircase was centered on the corresponding coherence estimate derived from the behavioural calibration session.

Prior to entering the scanner, participants were re-familiarized with the task and confidence rating scale. The task was identical to that described above except for the following changes. Response deadlines of 1.5s and 3s were imposed for the initial decision and confidence rating, respectively. Both motion judgments and confidence ratings were made via an fMRI button box held in the right hand. To rate confidence, participants used their index and middle fingers to move a cursor in steps of 10% to the left or right of the scale. The initial cursor location on each trial was randomized. The rating was confirmed by pressing a third button with the ring finger, after which the cursor changed from white to red for 500ms. During each of the 4 scanner runs participants completed 90 trials.

After the main experiment we carried out a localizer scan for motion-related activity. During this scan participants passively viewed 20 alternating displays of moving and stationary dots, each lasting 12s. Equal numbers of leftward and rightward moving dot displays were included at a constant coherence of 50%.

Scoring rule for confidence ratings

Confidence ratings were incentivized using the quadratic scoring rule (QSR)⁵⁰:

$$\text{points}=100*\left[1-{\left(correc{t}_i-con{f}_i\right)}^2\right]$$

where correct_i is equal to 1 on trial i if the choice was correct and 0 otherwise, and conf_i is the subject’s confidence rating on trial i entered as a probability between 0 and 1. The QSR is a proper scoring rule in that maximum earnings are obtained by jointly maximizing the accuracy of choices and confidence ratings⁵¹. For every 5,000 points subjects received an extra $1. This scoring rule ensures that confidence is orthogonal to the reward the subject expects to receive for each trial. Maximal reward is obtained both when one is maximally confident and right, and minimally confident and wrong (Figure 1C).

The confidence scale was labeled both with scale steps of 0%, 20%, 40%, 60%, 80% and 100% (positioned above the line) and, following Boldt and Yeung³⁴, verbal confidence labels of “certainly wrong”, “probably wrong”, “maybe wrong”, “maybe correct”, “probably correct” and “certainly correct” (positioned below the line). The scale midpoint was marked with a vertical tick halfway between the 40% and 60% labels. Prior to taking part in the main experiment participants underwent a training session to instruct them in the use of the confidence scale. Following Moore and Healy⁵², participants were first instructed:

“You can win points by matching your confidence to your performance. Specifically, the number of points you earn is based on a rule that calculates how closely your confidence tracks your performance: points = 100 ∗ [1 − (accuracy − confidence)²]. This formula may appear complicated, but what it means for you is very simple: You will get paid the most if you honestly report your best guess about the likelihood of being correct. You can earn between 0 and 100 points for each trial.”

Participants were then asked where they should click on the scale if they were sure they responded either correctly or incorrectly. They were then informed:

“The correct answers were: If you are sure you responded correctly, you should respond 100% confidence/certainly correct. If you are sure you picked the wrong direction, you should respond 0% confidence/certainly wrong. If you are not 100% sure about being correct or incorrect you should select a location in between according to the following descriptions on the confidence scale: probably incorrect = 20% confidence; maybe incorrect = 40% confidence; maybe correct = 60% confidence; probably correct = 80% confidence. You can also click anywhere in between these percentages.”

Statistics

Effects of condition on confidence ratings and accuracy were assessed using hierarchical mixed-effects regression using the lme4 package in R (Version 3.3.3; ⁵³). For confidence ratings we constructed linear models separately for correct and incorrect trials. Pre- and post-decision coherence values and their interaction were entered as separate predictors of confidence. Log response times were also included in the model. We obtained P-values for regression coefficients using the car package for R⁵⁴. Mixed-effects logistic regression was used to quantify the effect of condition on response accuracy. In all regressions we modeled subject-level slopes and intercepts, and report coefficients and statistics at the population level. The distribution of residuals in regression models was assumed to be normal but this was not formally tested.

Computational models

Bayesian model

We developed a Bayesian model of choice and confidence that is grounded in signal detection theory. Subjects receive two internal samples, X_pre generated from pre-decision motion and X_post from post-decision motion. Motion direction d ∈ [−1 1] determines the sample means with Gaussian signal-to-noise depending linearly on coherence θ_pre or θ_post via sensitivity parameter k:

$$\begin{array}{c}{X}_{pre}\sim N\left(dk{\theta }_{pre},1\right)\\ X_{post}\sim N\left(dk{\theta }_{post},1\right)\end{array}$$

We assume that subjects do not know the coherence levels on a particular trial (θ_pre and θ_post) which are nuisance parameters that do not carry any information about the correct choice. We therefore approximate the likelihood of X_pre and X_post as a Gaussian with mean μ and variance σ² determined by a mixture of Gaussians across each of the three possible coherence levels. Starting with X_pre:

$$P\left(X_{pre}|d=1\right)={\displaystyle \sum _{{\theta }_{pre}}p\left({\theta }_{pre}\right)N\left(k{\theta }_{pre},1\right)}$$

As each of the three coherence levels are equally likely by design $(p({\theta }_{pre})=0.33)$ we can define the mean as:

$$\mu =\frac{\sum k{\theta }_{pre}}{3}$$

The aggregate variance σ² can be decomposed into both between- and within-condition variance. From the law of total variance:

$$\begin{array}{c}{\sigma }^2={{\displaystyle \sum _{{\theta }_{pre}}p\left({\theta }_{pre}\right)\left[E\left[X_{pre}|k{\theta }_{pre}\right]-\mu \right]}}^2+{\displaystyle \sum _{{\theta }_{pre}}p\left({\theta }_{pre}\right)}\text{Var}\left(X_{pre}|k{\theta }_{pre}\right)\\ {\sigma }^2={\displaystyle \sum _{{\theta }_{pre}}p\left({\theta }_{pre}\right)}{\left[k{\theta }_{pre}-\mu \right]}^2+1\end{array}$$

Because the possible values of θ are the same pre- and post-decision, μ and σ² are the same for both X_pre and X_post. Actions a are made by comparing X_pre to a criterion parameter m that accommodates any stimulus-independent biases towards the leftward or rightward response, a = sign(X_pre − m).

Each sample, X_pre and X_post, updates the log posterior odds of motion direction (rightward or leftward), LO_dir, which under flat priors is equal to the log-likelihood:

$$\begin{array}{c}L{O}_{dir}^{pre}=\text{log}\frac{P\left(d=1|X_{pre}\right)}{P\left(d=-1|X_{pre}\right)}=\text{log}\frac{P\left(X_{pre}|d=1\right)}{P\left(X_{pre}|d=-1\right)}\\ L{O}_{dir}^{post}=\text{log}\frac{P\left(d=1|X_{post}\right)}{P\left(d=-1|X_{post}\right)}=\text{log}\frac{P\left(X_{post}|d=1\right)}{P\left(X_{post}|d=-1\right)}\end{array}$$

where, due to the Gaussian generative model for X, LO_dir is equal to:

$$\begin{array}{c}L{O}_{dir}=\text{log}\frac{e^{{\left(\mu +X\right)}^2/2{\sigma }^2}}{e^{{\left(\mu -X\right)}^2/2{\sigma }^2}}\\ L{O}_{dir}=\frac{2\mu X}{{\sigma }^2}\end{array}$$

The total accumulated evidence for rightward vs. leftward motion at the end of the trial is:

$$L{O}_{dir}^{total}=L{O}_{dir}^{pre}+L{O}_{dir}^{post}$$

Positive values indicate greater belief in rightward motion; negative values greater belief in leftward motion.

To update confidence in one’s choice, the belief in motion direction (LO_dir) is transformed into a belief about decision accuracy (LO_correct) conditional on the chosen action:

If a = 1:

$$L{O}_{correct}=L{O}_{dir}$$

Otherwise:

$$L{O}_{correct}=-L{O}_{dir}$$

As for LO_dir, LO_correct can be decomposed into pre- and post-decisional components:

$$L{O}_{correct}^{total}=L{O}_{correct}^{pre}+L{O}_{correct}^{post}$$

The final log odds correct is then transformed to a probability to generate a confidence rating on a 0-1 scale:

$$\text{Confidence}=\frac{1}{1+\text{exp}\left(-L{O}_{correct}^{total}\right)}$$

Extensions of Bayesian model

Temporal weighting 

We considered that subjects may apply differential weights to pre- and post-decision motion when computing confidence^6,7. To capture this possibility, we introduced free parameters w_pre and w_post that controlled the relative weights applied to pre- and post-decision evidence:

$$L{O}_{correct}^{total}=w_{pre}L{O}_{correct}^{pre}+w_{post}L{O}_{correct}^{post}$$

Choice weighting 

We considered that subjects might pay selective attention to post-decision evidence dependent on whether it is consistent/inconsistent with their initial choice (a form of commitment bias; this is similar to the “selective reduced-gain” model of Bronfman et al.⁶). To capture such effects, we introduced two weighting parameters w_con and w_incon that differentially weight confirmatory and disconfirmatory post-decision evidence:

If sign$(L{O}_{dir}^{post})$ = sign(a):

$$L{O}_{correct}^{total}=L{O}_{correct}^{pre}+w_{con}L{O}_{correct}^{post}$$

Otherwise:

$$L{O}_{correct}^{total}=L{O}_{correct}^{pre}+w_{incon}L{O}_{correct}^{post}$$

Choice bias 

A second variant of commitment bias operates to boost confidence in the chosen response without altering sensitivity to post-decision evidence (the choice acts as a prior on subsequent confidence formation²⁵; this is similar to Bronfman et al.’s “value-shift” model⁶). To capture such effects, we introduced a parameter b that modulated final confidence dependent on the choice:

$$\begin{array}{c}L{O}_{dir}^{bias}=\text{sign}(a)*\text{log}\left(\frac{b}{1-b}\right)\\ L{O}_{dir}^{total}=L{O}_{dir}^{pre}+L{O}_{dir}^{post}+L{O}_{dir}^{bias}\end{array}$$

If a = 1:

$$L{O}_{correct}^{total}=L{O}_{dir}^{total}$$

Otherwise:

$$L{O}_{correct}^{total}=-L{O}_{dir}^{total}$$

Nonlinear confidence mapping 

The ideal observer model assumes that subjects faithfully report probability correct, which maximizes the quadratic scoring rule (QSR). We also considered that subjects misperceive the scoring rule (or, equivalently, apply a nonlinear mapping between probability correct and reported confidence), with consequences for how particular confidence ratings were selected. For instance, subjects may overweight the extremes of the scale due to perceiving these extremes as returning greater reward.

Such misperceptions can be captured by allowing a flexible mapping between the model’s confidence and reported confidence. We implemented a one-parameter scaling of log-odds²² which is able to capture both under- and overweighting of extreme confidence ratings:

$$\begin{array}{c}LO(\pi (c))=\gamma .\text{log}\left(\frac{c}{1-c}\right)\\ \text{Confidence}=\frac{1}{1+\text{exp}(-LO(\pi \left(c\right)\left)\right)}\end{array}$$

where c denotes the interim output of the model’s estimate of probability correct.

When γ = 1, π(c) = c, and there is no distortion. When γ > 1, the curve relating model confidence to reported confidence is S-shaped, whereas when 0 < γ < 1, an inverted-S-shaped curve is obtained.

Informing confidence with decision time 

Finally we considered that in all models subjects may use decision time from the initial decision as a cue to confidence²³. To capture this possibility we modulated the final $L{O}_{correct}^{total}$ of both the Bayesian and extended models by response time via a free parameter β_RT:

$$L{O}_{correct}^{total}\leftarrow L{O}_{correct}^{total}+{\beta }_{RT}\text{log}(RT)$$

In the case of the mapping model the modulation by decision time was applied prior to passing $L{O}_{correct}^{total}$ through the nonlinear mapping function.

This set of model extensions led to a factorial combination of 5 model variants (ideal Bayesian, temporal weighting, choice weighting, choice bias, mapping) × 2 (non-response time dependent, response time dependent) = 10 models which were fitted to each subject/dataset as described below.

Model fitting

We used Markov chain Monte Carlo methods implemented in STAN⁵⁵ to sample from posterior distributions of parameters given motion directions d, motion coherences θ_pre and θ_post, subjects’ choices a and confidence ratings r.

Pseudo-code for the Bayesian model is given below (following STAN convention, scale parameters are written as standard deviations):

Priors:

$$\begin{array}{r}\hfill m\sim N(0,10)\\ \hfill k\sim N(0,10)\end{array}$$

Model:

$$\begin{array}{c}{X}_{pre}\sim N(dk{\theta }_{pre},1)\\ X_{post}\sim N(dk{\theta }_{post},1)\\ a\sim \text{Bernoulli}\_\text{logit}(100\ast (X_{pre}-m))\\ r\sim N(\text{conf},0.025)\end{array}$$

“conf” is the output of the confidence computation detailed above. The logit function implements a steep softmax relating X_pre to a and is applied for computational stability. The mapping between model confidence and observed confidence allowed a small degree of imprecision (σ = 0.025) in subjects’ ratings, roughly equivalent to grouping continuous ratings made on a 0-1 scale into ten bins.

We placed weakly informative priors over coefficients in the extended models for computational stability. In the weighted models, w parameters were drawn from N(1, 1) distributions bounded below by 0 and above by 5. In the bias model, b was drawn from a uniform [0 1] distribution. In the nonlinear mapping model, γ was drawn from a positively constrained N(1, 1) distribution. In the RT models, β_RT was drawn from a N(0, 10) distribution.

We fitted each model with 12,000 samples divided across 3 chains separately for each subject’s fMRI and behavioural datasets. 1000 samples per chain were discarded for burn-in, resulting in 9,000 stored samples. Chains were visually checked for convergence and Gelman and Rubin’s potential scale reduction factor R̂ was calculated for all parameters. For the majority (469 out of 470) of models/subjects, R̂ values were all < 1.1, indicating good convergence. The fit of the choice weighted+RT model to the behavioural session data failed to converge for one subject; this log-likelihood value was omitted from the model comparison calculations detailed below.

Model comparison

To compare models we assessed the ability of a model fit to behavioural data to capture the data of the same subject in the fMRI session, and vice-versa. For each subject and model we drew 1000 samples from posterior distributions of fitted parameters and generated synthetic choice and confidence data. The trialwise log-likelihood (itself a sum of choice and confidence rating log-likelihoods) was summed across trials and stored for each parameter draw, and then averaged across draws to return a subject- and model-specific cross-validated log-likelihood. Fitted parameter values from the best-fitting Bayesian+RT model for behavioural and fMRI sessions are listed in Supplementary Table 3.

Model simulations

To visualize qualitative features of the Bayesian model (Figure 1B) we simulated 10,000 trials from each condition of the factorial design with k=4 and m=0. Pre- and post-decision motion coherences were crossed in a fully factorial design and drawn from the set 0%, 25% or 50%. True motion direction d was selected randomly on each trial.

To determine the ability of the best-fitting Bayesian+RT model to account for subjects’ choices and confidence ratings (a posterior predictive check), we drew 1000 samples from posterior distributions of fitted parameters and for each draw simulated one trial sequence with these parameter settings and averaged over simulations. To obtain regressors for fMRI and mediation analyses we also stored values of pre-decision evidence $(L{O}_{correct}^{pre})$ and post-decision evidence $(L{O}_{correct}^{post})$ averaged over 5000 trials per condition (3 pre-decision coherence levels × 3 post-decision coherence levels × 2 choice accuracies).

fMRI acquisition and preprocessing

Whole-brain fMRI images were acquired using a 3T Allegra scanner (Siemens) with an NM011 Head transmit coil (Nova Medical, Wakefield, MA) at New York University’s Center for Brain Imaging. BOLD-sensitive echo-planar images (EPI) were acquired using a Siemens epi2d BOLD sequence (42 transverse slices, TR = 2.34s; echo time = 30ms; 3 x 3 x 3 mm resolution voxels; flip angle = 90 degrees; 64 x 64 matrix; slice tilt -30deg T > C; interleaved acquisition). The main experiment consisted of 4 runs of 315 volumes, and the localizer scan consisted of a single run of 211 volumes. A high-resolution T1-weighted anatomical scan (MPRAGE, 1x1x1 mm voxels, 176 slices) and local field maps were also acquired.

All preprocessing was carried out using SPM12 v6225 (Statistical Parametric Mapping; www.fil.ion.ucl.ac.uk/spm). The first 5 volumes of each run were discarded to allow for T1 equilibration. Functional images were slice-time corrected, realigned and unwarped using the collected field maps⁵⁶. Structural T1-weighted images were coregistered to the mean functional image of each subject using the iterative mutual information-based algorithm. Each participant’s structural image was segmented into gray matter, white matter and cerebral spinal fluid images using a nonlinear deformation field to map it onto a template tissue probability map⁵⁷. These deformations were applied to both structural and functional images to create new images spatially normalized to Montreal Neurological Institute space and interpolated to 2x2x2 mm voxels. Normalized images were spatially smoothed using a Gaussian kernel with full-width half-maximum of 6mm.

fMRI analysis

We employed a combination of region-of-interest (ROI) analyses on trial-by-trial activity estimates, multilevel mediation models and standard whole-brain general linear model (GLM) approaches.

Whole-brain univariate analysis

We used SPM12 for first-level analyses. In all GLMs, regressors were convolved with a canonical hemodynamic response function. Motion correction parameters estimated from the realignment procedure and their first temporal derivatives were entered as nuisance covariates, and low-frequency drifts were removed using a high-pass filter (128 s cutoff).

GLM1 

GLM1 was constructed to examine activity associated with changes in post-decision motion strength. Correct and incorrect trials were modeled as separate stick functions timelocked to the onset of the post-decision motion plus parametric modulations by post-decision motion strength (low= -1, medium = 0, high = 1). Additional regressors were also included at the onset of pre-decision motion (parametrically modulated by pre-decision motion strength and log response times) and confidence rating period.

GLM2 

GLM2 was constructed to examine activity associated with changes in reported confidence. A stick function timelocked to confidence rating onset was parametrically modulated by reported confidence. Regressors were also included at the onset of pre-decision motion (parametrically modulated by log response times) and post-decision motion.

ROI analysis

A priori regions of interest were specified as follows. The pMFC ROI was an 8mm sphere around peak coordinates (MNI coordinates [x, y, z] = [0 17 46]) obtained from our previous study of decision confidence¹². Anterior prefrontal ROIs were obtained from the right-hemisphere atlas developed by Neubert et al.²⁴ (area 46, FPl and FPm) and mirrored to the left hemisphere to create bilateral masks. The vmPFC ROI was an 8mm sphere around peak coordinates [-1 46 -7] obtained from a meta-analysis of value-related activity⁵⁸. The ventral striatum ROI was specified anatomically from the Oxford-Imanova Striatal Structural atlas included with FSL (http://fsl.fmrib.ox.ac.uk). Within each ROI we averaged single-trial beta estimates over voxels, scaled the timeseries to have zero mean and unit SD, and computed the mean activity per condition.

Quantification of single-trial response magnitudes 

To facilitate both ROI and mediation analyses we estimated single-trial BOLD responses as a beta timeseries. This was achieved by specifying a GLM design matrix with separate regressors (stick functions) for each trial, each aligned to either the onset of the post-decision motion stimulus (for PDE analyses in Figure 3) or the confidence rating period (for mediation models and regressions on confidence; Figures 4 and 5). Each regressor was convolved with a canonical hemodynamic response function (HRF). Motion correction parameters estimated from the realignment procedure and their first temporal derivatives were entered as nuisance covariates, and low-frequency drifts were removed using a high-pass filter (128 s cutoff). One important consideration in using single-trial estimates is that the beta for a given trial can be strongly affected by acquisition artifacts that co-occur with that trial (e.g. motion or scanner pulse artifacts). For each subject we therefore computed the grand mean beta estimate across both voxels and trials, and excluded any trial whose mean beta estimate across voxels exceeded 3 SDs from this grand mean³⁸. An average of 3.6 trials per subject (1.0%; maximum = 9 trials) were excluded.

To visualize the relationship between activity and task variables over time we also extracted the pre-processed BOLD data per TR. Low-frequency drifts (estimated using a cosine basis set, 128 s cutoff) and motion parameters plus their first temporal derivatives were regressed out of the signal, and the residual activity was oversampled at 10 Hz. Timecourses were extracted from 12 second windows timelocked to the onset of pre-decision motion. To construct Figure 4C we applied a GLM (see below) to each timepoint resulting in a timecourse of beta weights for each regressor. Nonparametric permutation tests were used to assess significant group-level significance of beta weights. For each permutation, we randomised the assignment between BOLD timeseries and trial labels and recalculated the group-level T-statistic comparing beta weights against zero (10,000 permutations). Individual timepoints were labeled as significant if the true T-statistic fell outside the 2.5 or 97.5 percentiles of the null distribution.

ROI GLMs 

As in our regression analyses of behavior, we modeled subject-level slopes and intercepts, and report coefficients and statistics at the population level. To test for an interaction between response accuracy and post-decision evidence, we fitted the following model to each ROI beta series:

$$\begin{gathered} \text{BOLD}\sim \text{accuracy}+\text{pre\_decision\_coherence}+\text{post\_decision\_coherence} \\ +\text{accuracy}*\text{pre\_decision\_coherence}+\text{accuracy}*\text{post\_decision\_coherence}+\text{log(RT)} \end{gathered}$$

Accuracy was specified as error=-1, correct=1; pre- and post-decision coherence were specified as low=-1, medium=0, high=1.

To estimate relationships between ROI activity and pre- and post-decision evidence from the fitted computational model (i.e. log-odds correct) we fitted the following model:

$\begin{array}{l}\text{BOLD}\sim L{O}_{correct}^{pre}+L{O}_{correct}^{post}+\text{log}(RT)\end{array}$

To assess relationships between confidence and activity on both change and no-change of mind trials, we conducted a segmented regression analysis. This method partitions the independent variable into discrete intervals, and a separate slope is fit to each interval. Here, we separated the effect of confidence on change (confidence <= 0.5) and no-change (confidence > 0.5) trials, and fit the following model:

$\text{BOLD}\sim \text{change\_confidence}+\text{no\_change\_confidence}+\text{log(RT)}$

Multilevel mediation analysis 

We performed multilevel mediation analysis of a standard three-variable model²⁰ using the Mediation Toolbox (http://wagerlab.colorado.edu/tools). Mediation analysis assesses whether covariance between two variables (X and Y) is explained by a third variable (the mediator, M). Significant mediation is obtained when inclusion of M in a path model of the effects of X on Y significantly alters the slope of the X-Y relationship. When applied to fMRI data, mediation analysis thus extends the standard univariate model by incorporating an additional outcome variable (in this case, confidence reports) and jointly testing three effects of interest: the impact of X (post-decision evidence, $L{O}_{correct}^{post}$) on brain activity (path a); the impact of brain activity on Y (confidence reports), controlling for X (path b); and formal mediation of X on Y by brain activity M. In all models we included log reaction times and pre-decision evidence $(L{O}_{correct}^{pre})$ as covariates of no interest.

The Mediation Toolbox permits a multi-level implementation of the standard mediation model, treating participant as a random effect⁵⁹. Significance estimates for paths a, b and a × b are computed through bootstrapping. We estimated distributions of subject-level path coefficients by drawing 10,000 random samples with replacement. Two-tailed p-values were calculated at each voxel/ROI from the bootstrap confidence interval⁶⁰.

Whole-brain statistical inference 

Single-subject contrast images were entered into a second-level random effects analysis using one-sample t-tests against zero to assess group-level significance. To correct for multiple comparisons we used Gaussian random field theory as implemented in SPM12 to obtain clusters satisfying P<0.05, family-wise error (FWE) corrected at a cluster-defining threshold of P<0.001. Numerical simulations and tests of empirical data collected under the null hypothesis show that this combination of cluster-defining threshold and RFT produces appropriate control of false positives^61,62.

To apply multiple comparisons correction to the multilevel mediation model output we took a non-parametric approach due to second-level images already comprising bootstrapped P-values. The cluster extent threshold for FWE correction was estimated based on Monte Carlo simulation (100,000 iterations) using the 3dClustSim routine in AFNI (version compiled September 2015; http://afni.nimh.nih.gov) and SPM 12’s estimate of the intrinsic smoothness of the residuals. Again this method in conjunction with a cluster-defining threshold of P < 0.001 provides appropriate control over false positives^61,62. Statistical maps were visualized using FSLview (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki) and Surf Ice (https://www.nitrc.org/projects/surfice/).

Life Sciences Reporting Summary

Further information on experimental design is available in the Life Sciences Reporting Summary.