Abstract
Protein–spherical nucleic acid conjugates (Pro-SNAs) are an emerging class of bioconjugates that have properties defined by their protein cores and dense shell of oligonucleotides. They have been used as building blocks in DNA-driven crystal engineering strategies and show promise as agents that can cross cell membranes and affect both protein and DNA-mediated processes inside cells. However, ionic environments surrounding proteins can influence their activity and conformational stability, and functionalizing proteins with DNA substantively changes the surrounding ionic environment in a nonuniform manner. Techniques typically used to determine protein structure fail to capture such irregular ionic distributions. Here, we determine the counterion radial distribution profile surrounding Pro-SNAs dispersed in RbCl with 1 nm resolution through in situ anomalous small-angle X-ray scattering (ASAXS) and classical density functional theory (DFT). SAXS analysis also reveals the radial extension of the DNA and the linker used to covalently attach the DNA to the protein surface. At the experimental salt concentration of 50 mM RbCl, Rb+ cations compensate ∼90% of the negative charge due to the DNA and linker. Above 75 mM, DFT calculations predict overcompensation of the DNA charge by Rb+. This study suggests a method for exploring Pro-SNA structure and function in different environments through predictions of ionic cloud densities as a function of salt concentration, DNA grafting density, and length. Overall, our study demonstrates that solution X-ray scattering combined with DFT can discern counterionic distribution and submolecular features of highly charged, complex nanoparticle constructs such as Pro-SNAs and related nucleic acid conjugate materials.
Short abstract
The nanoscale structure of protein−DNA conjugates and the distribution of counterions surrounding these macroions are determined via in situ X-ray scattering and DFT.
Introduction
The structure and function of biological macromolecules are intimately coupled to their ionic environment. For example, protein turnover and enzymatic catalysis both depend on electrostatic interactions.1 The local electrostatic environment can affect the pKa values of critical amino acids involved in acid/base catalysis1 while substrates are guided to the active site via electric potentials.2 Electrostatic interactions dictate both local and long-range structure. For instance, the association of oligonucleotides with charge-compensating multivalent counterions induces the condensation and packaging of viral genomes,3,4 the asymmetric charge distribution of cations around DNA stabilizes specific DNA conformations,5 and crystallization via the “salting out” effect enables the determination of many protein structures via X-ray crystallography.6 Also, salt concentration and pH influence the folding and denaturation of proteins, which dictate their biological function.7,8 These examples suggest that the structure and functionality of bionanoconstructs formed by functionalizing proteins with nucleic acids [e.g., protein–spherical nucleic acid conjugates (Pro-SNAs)]9 should be highly sensitive to their ionic environment. Certain Pro-SNA conjugates (e.g., Figure 1) retain the native enzymatic functionality of the protein core9 and exhibit advantageous characteristics that arise from their dense DNA coating. For example, they are internalized by cells without the need for transfection agents,10 and have been used as building blocks for protein crystal engineering via deliberately designed Watson–Crick hybridization interactions between DNA on neighboring proteins.9,11 Pro-SNAs and related structures that differ in core shape but with comparable DNA densities also exhibit characteristics common to conventional Au-SNAs,12 such as the enhanced resistance of the tethered DNA to enzymatic degradation13 and cooperative melting behavior of their DNA-linked assemblies.14 These properties are hypothesized to arise, in part, due to high local concentrations of cationic counterions associated with these negatively charged nanoparticles. Indirect evidence that the structure of the ion cloud surrounding Pro-SNAs influences inter-Pro-SNA interactions as well the interaction of Pro-SNA with other types of SNA conjugates is obtained in studies on crystallization via Watson–Crick hybridization. This method has been used to induce the assembly of Pro-SNAs, or combinations of Pro-SNAs and AuNP-SNAs, into crystalline superlattices.9 In the latter case, varying the salt concentration, which directly affects the ion distribution and the range and strength of the interaction between SNAs,15 induced transitions between distinct crystalline phases.16 Thus, a thorough elucidation of the ionic environment surrounding Pro-SNA conjugates would enable a deeper understanding of their properties, and support future efforts to exploit the structure–function relationships of Pro-SNAs, as well as the related class of high density DNA-functionalized nanomaterials for diagnostic,17,18 therapeutic,19,20 and crystal engineering applications.21−23
Figure 1.
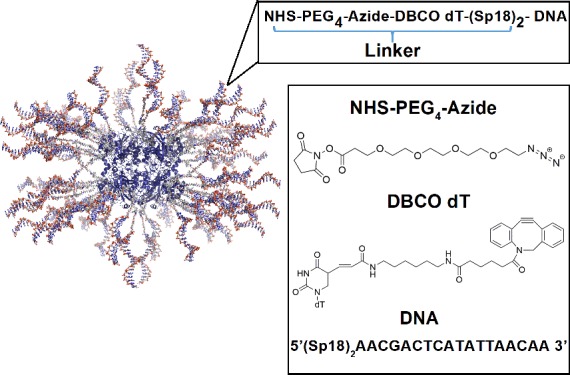
Schematic illustration of Cg catalase functionalized with 18 base long ss-DNA strands. Each strand is composed of a linker region (L) composed of an NHS-PEG4-azide moiety and a DBCO dT group covalently anchoring the DNA to the protein surface (inset).
As illustrated in Figure 1, the Pro-SNA conjugate employed in this study is composed of a Corynebacterium glutamicum (Cg) catalase core that is densely grafted with ∼40 DNA strands that are 18 bases long via a two-step synthetic scheme where (1) surface amines are converted to azides and (2) azides are reacted with oligonucleotides containing a terminal strained cyclooctyne (DBCO). (For details, see Materials and Methods.) The oligonucleotide (D) is anchored to the protein core via a linker region (L) consisting of a tetraethylene glycol spacer from the NHS polyethylene glycol (PEG)4 cross-linker, a spacer between the DBCO and thymidine moieties of the DBCO dT synthetic phosphoramidite, and two hexaethylene glycol spacers introduced at the 5′-terminus of the oligonucleotide during synthesis. These Pro-SNAs were dispersed in 50 mM RbCl to a final concentration of 1 μM or 4 μM.
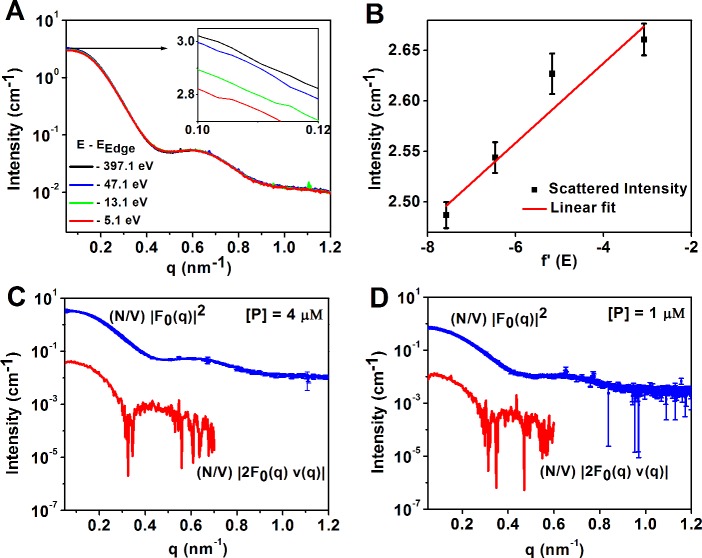
Small angle X-ray scattering (SAXS) is an ideal in situ probe for characterizing the structure of nanoscale particles due to the penetrating power and small wavelength (∼1 Å) of high energy X-rays. However, while SAXS can resolve the size of the Pro-SNA conjugate, the electron density contrast between the Pro-SNA conjugate, counterions, and surrounding solvent is not sufficient to distinguish the distribution of ions surrounding the particle. For this we turn to anomalous SAXS (ASAXS), which can be used to provide elemental specificity to sense the scattering contribution from ions surrounding the particle. ASAXS has been successfully employed to extract the ion density24−26 surrounding double stranded DNA27,28 and polymer brushes.24 Although ASAXS could not be used to determine the counterion distribution surrounding Au-SNAs due to the strong scattering from the electron dense Au cores,29 the relatively low electron density of the protein core in a Pro-SNA enables the use of ASAXS in this case. As described below, Rb+ is chosen as the monovalent counterion for Pro-SNAs because its core electron binding energy (EK = 15.200 keV) is sufficiently high for solution ASAXS, which necessitates the use of high energy X-rays (E > ∼10 keV) to overcome the X-ray absorption in the aqueous medium.
ASAXS deduction of the counterionic distribution profile relies on the measurement of subtle changes in the X-ray energy (E) dependent scattering from the overall particle–counterion system. These changes arise due to a sharp reduction in the scattering strength of the selected counterion species at X-ray energies close to one of its core electron binding energies (absorption edge). At X-ray energies below an absorption edge, the background subtracted intensity from noninteracting, isolated particles in solution is approximately (Supporting Information section S1)
| 1 |
where q = 4π sinθ/λ is the modulus of the scattering vector, 2θ is the scattering angle, and λ is the wavelength of the incident X-rays. Equation 1 used for the decomposition described above is an approximation. The full form of the ASAXS equation is quadratic in f′(E) due to a third purely resonant term: [f′(E) v(q)]2 (see eq S2).24,30,31 However, in our case the approximation in eq 1 is valid due to the relatively low magnitude of the purely resonant term as demonstrated by model ASAXS calculations and analysis of experimental data (section S1). Here N/V represents the concentration of particles (Pro-SNAs in this case). F0(q) is the form factor from a single Pro-SNA, which includes contributions from the associated excess counterions (here, Rb+), at an X-ray energy far below a Rb+ absorption edge (here, K edge: EK = 15.200 keV). Therefore, |F0(q)|2 is the nonresonant contribution to the scattered intensity from a single Pro-SNA with its associated, excess Rb+ ions. The resonant second cross term contains the dispersion correction f′(E). This is a negative number (Figure 2A, section S2), which accounts for the reduction in the effective number of electrons [f0 + f′(E) = 36 + f′(E)] that contribute to the scattering from a single Rb+ ion near EK.32 Most importantly, the cross term also contains v(q), the Fourier transform of the excess Rb+ density [nRb+(r) – nb], where nb represents the bulk Rb+ number density.
Figure 2.

(A) Experimentally determined anomalous dispersion correction f′(E) for Rb as a function of incident X-ray energy near the Rb K-edge (see also Figure S2A,B). (B) Model SAXS intensity calculations of the nonresonant term (black) and the magnitude of the resonant (at E = EK – 5 eV) term (red) in eq 1. The positions of the sharp minima that are exclusive to the resonant term magnitude correspond to the q values where v(q) changes sign (inset, blue).
It is important to note that the native catalase protein has an isoelectric point (pI) of 5.4.33 Thus, at neutral pH, the contribution of the protein core to the overall charge of the Pro-SNA is minimal34 [−17 for the protein core (Figure S3A) vs −840 for the linker and DNA shell]. ASAXS measurements on unmodified proteins (Figure S3B and text in section S3) support the assumption that the protein core does not exhibit an appreciable effect on the counterion distribution.
Results
ASAXS possesses the sensitivity needed to resolve the counterionic structure for our Pro-SNA case, as demonstrated by the following model calculations. The two terms in eq 1 are calculated for f′Rb= −7.58, corresponding to an incident photon energy 5 eV below the Rb+ K-edge. For these calculations, we assign uniform electron densities to the protein core and DNA shell, and further assume that the distribution of Rb+ ions within the shell falls off as the inverse square of the radial distance from the surface of the core (Figure S1 and text in section S1). The scattered intensity (Figure 2B) is dominated by the nonresonant term |F0(q)|2 while the modulus of the resonant term |2F0(q) f′(E) v(q)| is an order of magnitude lower in intensity. This demonstrates the inherent challenge of ASAXS in this case. Nevertheless, we show that the Fourier transform v(q) can be extracted over a sufficiently large range of q to determine the counterion distribution profile with nanometer resolution.
The radial distribution profile of
Rb+ was obtained
from a comparison of the cross-term 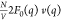 profile
with classical-DFT calculations,
while characteristics of the Pro-SNA conjugate, such as the size of
the protein core and DNA shell, were determined by fitting the nonresonant
intensity profile
profile
with classical-DFT calculations,
while characteristics of the Pro-SNA conjugate, such as the size of
the protein core and DNA shell, were determined by fitting the nonresonant
intensity profile 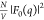 with parametrized geometric models. These
two terms are separated out by a simultaneous analysis of the background
subtracted SAXS intensity profiles ΔI(q, E) at four different X-ray energies
below the Rb+ K-edge, which are shown for the case of 4
μM Pro-SNA in 50 mM RbCl in Figure 3A. The four intensity profiles are easily
distinguishable at low q when plotted on a linear
scale (Figure 3A inset).
At low q, ΔI(q, E) and, therefore, 2f′(E)[F0(q) v(q)], monotonically increase with increasing EK– E. This is the expected
trend based on the E dependence of f′ (Figure 2A) and because F0(q)
and v(q) are positive at low q. These observations imply that the nonresonant term
with parametrized geometric models. These
two terms are separated out by a simultaneous analysis of the background
subtracted SAXS intensity profiles ΔI(q, E) at four different X-ray energies
below the Rb+ K-edge, which are shown for the case of 4
μM Pro-SNA in 50 mM RbCl in Figure 3A. The four intensity profiles are easily
distinguishable at low q when plotted on a linear
scale (Figure 3A inset).
At low q, ΔI(q, E) and, therefore, 2f′(E)[F0(q) v(q)], monotonically increase with increasing EK– E. This is the expected
trend based on the E dependence of f′ (Figure 2A) and because F0(q)
and v(q) are positive at low q. These observations imply that the nonresonant term 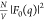 and the cross
term
and the cross
term 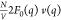 can be separated out as the intercepts
and the slopes of the linear fits to the four [f′(E), ΔI(q, E)] data points at each q, over an extended q range (see also section S4).
An example of such a linear fit of ΔI(q, E) vs f′(E) at q = 0.13 nm–1 is
shown in Figure 3B.
The nonresonant term |F0(q)|2 and cross term |2F0(q) v(q)| are shown in Figures 3C and 3D for the cases of 4 μM Pro-SNA and 1 μM Pro-SNA
in 50 mM RbCl, respectively. In both cases, the profile
can be separated out as the intercepts
and the slopes of the linear fits to the four [f′(E), ΔI(q, E)] data points at each q, over an extended q range (see also section S4).
An example of such a linear fit of ΔI(q, E) vs f′(E) at q = 0.13 nm–1 is
shown in Figure 3B.
The nonresonant term |F0(q)|2 and cross term |2F0(q) v(q)| are shown in Figures 3C and 3D for the cases of 4 μM Pro-SNA and 1 μM Pro-SNA
in 50 mM RbCl, respectively. In both cases, the profile 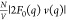 is reported only up to q = 0.7 nm–1 due to uncertainties greater than 70%
beyond this q (Figure S4F). As shown below, the extracted profiles (nonresonant and cross
terms) for the two concentration cases differ by a multiplicative
constant (
is reported only up to q = 0.7 nm–1 due to uncertainties greater than 70%
beyond this q (Figure S4F). As shown below, the extracted profiles (nonresonant and cross
terms) for the two concentration cases differ by a multiplicative
constant (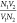 ) but are otherwise
identical. These observations
demonstrate reproducibility and prove that, for the concentrations
used in this study, the Pro-SNA behave as isolated particles. That
is, the results discussed here are devoid of any interparticle interaction
effects.
) but are otherwise
identical. These observations
demonstrate reproducibility and prove that, for the concentrations
used in this study, the Pro-SNA behave as isolated particles. That
is, the results discussed here are devoid of any interparticle interaction
effects.
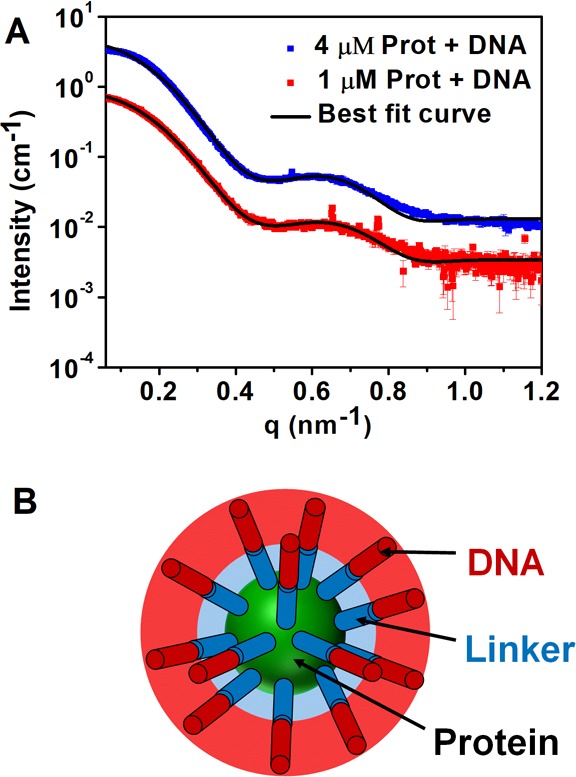
Figure 3.
(A) Background subtracted SAXS intensity profiles at four incident energies below the Rb K-edge, with a magnified view at low q (inset). (B) Linear fit to the SAXS intensities ΔI(q, E) vs f′(E) at q = 0.13 nm–1. (C, D) Extracted nonresonant (blue) and cross-term (red) profiles (eq 1) for 1 μM and 4 μM Pro-SNA in 50 mM RbCl.
A visual examination shows drastic qualitative
differences between
the extracted 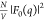 and
and 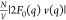 profiles (Figures 3C and 3D). Specifically,
in qualitative agreement with model calculations in Figure 2B, for both the 1 and 4 μM
Pro-SNA cases the first minimum of the
profiles (Figures 3C and 3D). Specifically,
in qualitative agreement with model calculations in Figure 2B, for both the 1 and 4 μM
Pro-SNA cases the first minimum of the 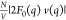 profile occurs at q ∼
0.30 nm–1 in comparison to the first minimum at q ∼ 0.47 nm–1 for the nonresonant
(
profile occurs at q ∼
0.30 nm–1 in comparison to the first minimum at q ∼ 0.47 nm–1 for the nonresonant
(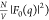 intensity profile. This difference is clearly
due to the effect of v(q): the Fourier
transform of the excess Rb+ density. As shown through detailed
quantitative analysis below, the difference arises because of the
absence of Rb+ in the core (protein) region and because
the Rb+ distribution extends beyond the DNA shell. The
above qualitative comparison between the two extracted profiles demonstrates
that ASAXS is sensitive to v(q)
and hence the Rb+ distribution surrounding Pro-SNA.
intensity profile. This difference is clearly
due to the effect of v(q): the Fourier
transform of the excess Rb+ density. As shown through detailed
quantitative analysis below, the difference arises because of the
absence of Rb+ in the core (protein) region and because
the Rb+ distribution extends beyond the DNA shell. The
above qualitative comparison between the two extracted profiles demonstrates
that ASAXS is sensitive to v(q)
and hence the Rb+ distribution surrounding Pro-SNA.
We first describe the structural attributes of the Pro-SNA conjugate,
deduced from fitting the nonresonant 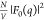 intensity profiles
in Figures 3C and 3D with a spherical core–shell model (eq S12). By fitting the SAXS intensity profile of a bare protein
without DNA (Figure S5) to the form factor
for a homogeneous sphere, the parameters for the protein core were
fixed. This fit yielded a radius Rprot = 4.5 nm (section S5), which corresponds
to a radius of gyration of Rg = √(3/5)
× R = 3.5 nm. Our simplified approach agrees
well with the value obtained using CRYSOL35 software (Rg = 3.7 nm), which employs
a fully atomistic model derived from diffraction experiments on Cg catalase single crystals.36
intensity profiles
in Figures 3C and 3D with a spherical core–shell model (eq S12). By fitting the SAXS intensity profile of a bare protein
without DNA (Figure S5) to the form factor
for a homogeneous sphere, the parameters for the protein core were
fixed. This fit yielded a radius Rprot = 4.5 nm (section S5), which corresponds
to a radius of gyration of Rg = √(3/5)
× R = 3.5 nm. Our simplified approach agrees
well with the value obtained using CRYSOL35 software (Rg = 3.7 nm), which employs
a fully atomistic model derived from diffraction experiments on Cg catalase single crystals.36
The nonresonant contribution to the total scattered intensity from the Pro-SNA, |F0(q)|2, was thereafter fit (Figure 4A) by a spherical core–shell model (Figure 4B).
Figure 4.
(A) Fit of the extracted nonresonant term to a core–shell model of the Pro-SNA conjugate. The multiplicative offset between the two SAXS profiles (4) is consistent with the ratio (4) of the nominal protein concentrations. (B) Cartoon representation of the core–shell model used to approximate variations in the electron density of the Pro-SNA conjugate.
The DNA and linker segments were modeled as cylinders each with a fixed radius of 0.5 nm and fixed number of electrons based on chemical composition (eq S12 and section S6). The protein concentration and the lengths of the linker and DNA were used as fitting parameters. As expected, the best-fit values of the linker and DNA lengths (summarized in Table 1) are in close agreement for the two protein concentrations, with deviations being within the uncertainties of the fit parameters. A detailed analysis of the cross-term profiles allows extraction of the Rb+ radial distribution.
Table 1. Structural Characteristics of the Pro-SNA Conjugate Obtained by Fitting the Extracted Nonresonant Intensity Profile to a Spherical Core–Shell Model.
| protein
concn (μM) |
length
(nm) |
||
|---|---|---|---|
| nominal | fitted | linker | DNA |
| 1 | 1.3 ± 0.2 | 3.9 ± 0.5 | 5.0 ± 0.6 |
| 4 | 5.2 ± 0.5 | 4.0 ± 0.4 | 5.1 ± 0.5 |
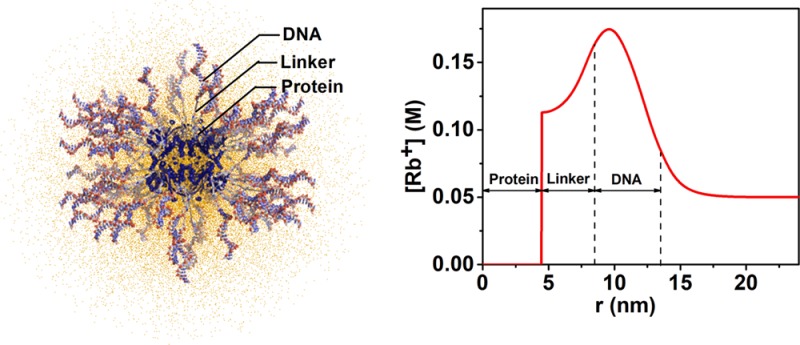
To determine the structure of the counterion cloud surrounding the Pro-SNA conjugate, we employed classical DFT to compute Rb+ density profiles. Excess Rb+ density profiles (nRb+(r, θ, ϕ) – nb) were calculated by independently varying the linker (L) and DNA (D) lengths in increments of 0.5 nm. These profiles were angular averaged for comparison with the ASAXS data. For details, see section S7. The DFT-derived and the ASAXS-extracted cross-term profiles show very good agreement for L = 4 nm and D = 5 nm as illustrated in Figures 5B and 5C for the cases of 1 and 4 μM Pro-SNA concentrations (see section S7 for goodness of fit). It should be noted that no multiplicative scaling factors were utilized to match the DFT-calculated and the ASAXS-derived profiles. Figure 5A shows the corresponding Rb+ radial distribution profile. For comparison, Figure 5A also shows a simplified geometric model for the excess Rb+ density profile that results when each unit of negative charge on the DNA backbone is compensated by exactly one Rb+ counterion and when a uniform distribution of Rb+ neutralizes the charges in the linker region. In comparison to the geometric model, the DFT-derived distribution profile presents smoother variations. This is intuitively expected because sharp gradients would lead to unphysical osmotic pressure buildup.
Figure 5.
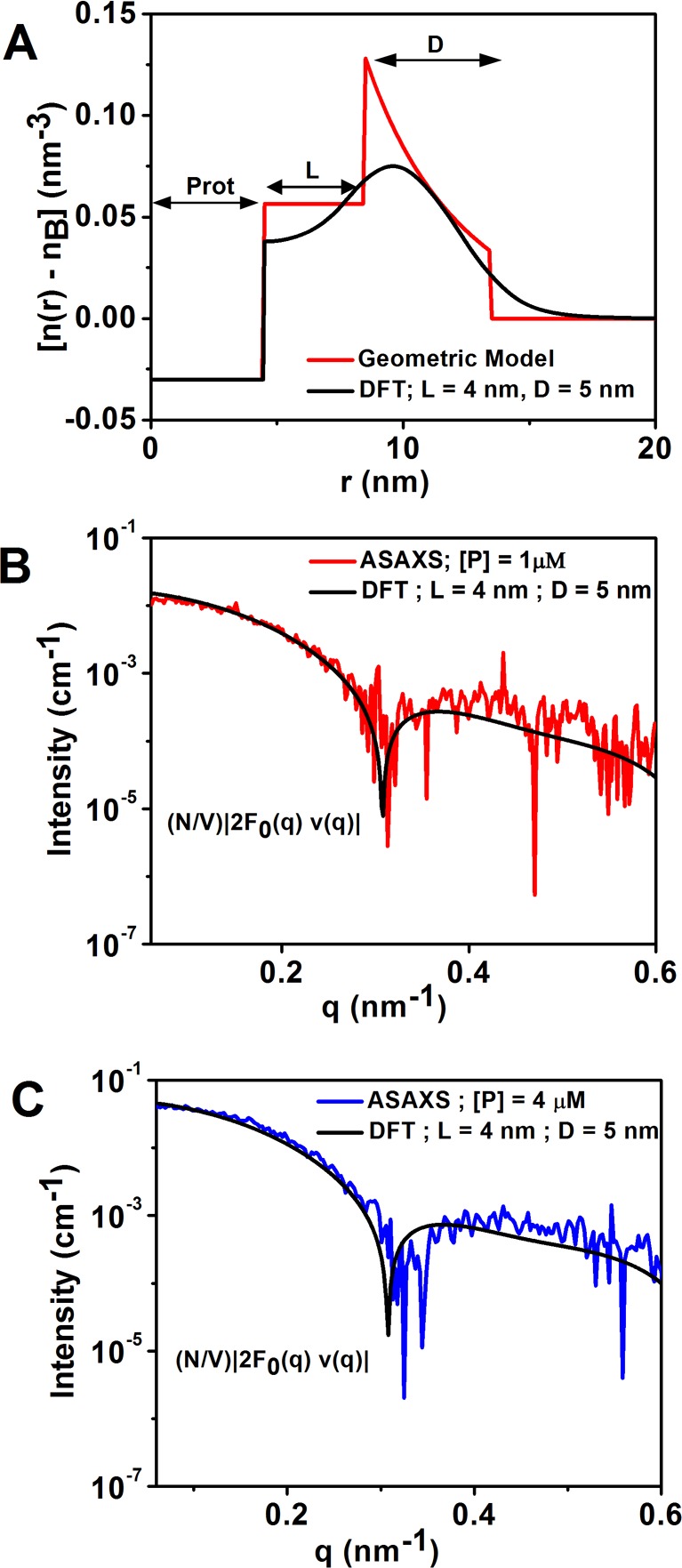
(A) DFT-derived model of the excess Rb+ density [n(r) – nb] as a function of radial distance from the center of the protein core for L = 4 nm and D = 5 nm (black). Also depicted is a simplified geometric model (red) for the excess Rb+ distribution profile. (B, C) Direct comparison of the DFT-derived to ASAXS-extracted 2|F0(q) v(q)| profile for 1 μM (B) and 4 μM Pro-SNA (C).
It must be mentioned here that throughout the analysis we have (i) modeled the Pro-SNA as a sphere and (ii) assumed only radial distance (r) dependence for the Rb+ density. The radius of gyration of Cg catalase calculated about orthogonal x, y, and z axes defined with respect to its Protein Data Bank structure is 2.8 nm, 3.2 nm, and 2.7 nm, respectively. In addition, its asphericity is only 0.056, indicating that although Cg catalase is slightly prolate, it is nearly spherical. Finally, the linker chains are large and flexible. We hypothesize that these chains will move to minimize their surface energy with the solvent, further reducing the asphericity of the excluded volume around the protein. Finally, the inherent 3D orientational averaging in solution-SAXS coupled with the low resolution of our SAXS data further smears out any small anisotropies. This validates the approximations that the protein core is spherical and that the Rb+ distribution only depends on the radial distance from the protein core.
Overall, the combined solution X-ray scattering–DFT analysis reveals certain key features regarding the Rb+ ion distribution profile and the structural features of Pro-SNA:
-
(i)
Within the shell, Rb+counterions compensate ∼90% of the total negative charge on the DNA and linker segments: Integration of the DFT-derived Rb+ charge density profile (Figure 5A) up to r = Rprot + L + D gives the total number of Rb+ ions located within the DNA corona. The ratio of this number to the total charge on the linkers and DNA is the compensated charge fraction fc = 90% (±3%) for the two data sets. This is equivalent to our earlier study for monovalent cations surrounding an Au-SNA29 where the denser core gold nanoparticle required the use of heavy-ion replacement SAXS, rather than ASAXS.
-
(ii)
The highest Rb+ion concentration within the DNA shell is ∼0.175 M, and the effective “Debye length” for the conjugate is ∼1.3 nm: For both 1 μM and 4 μM protein concentrations, the best fit DFT model predicts a maximum Rb+ concentration of ∼0.175 M. This represents a 3.5-fold enhancement over the bulk solution concentration of 0.05 M. Further, the excess Rb+ density falls to 1/e of its value at the edge of the DNA shell at a distance of 1.3 nm beyond the shell. This ASAXS–DFT estimate for the Debye length (κ–1) is comparable to the expected κ–1 = 1.34 nm for a monovalent electrolyte (here RbCl) at 50 mM concentration.
-
(iii)
The lengths of the linker and ssDNA segments are L = 4 ± 0.5 nm and D = 5 ± 0.6 nm, respectively. This D value implies an average rise/base of ∼0.27 nm for the ssDNA at 50 mM RbCl.
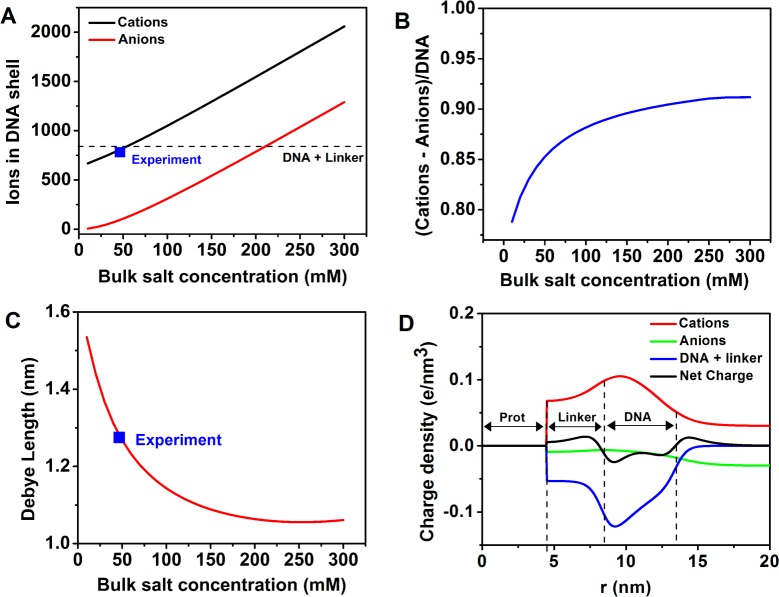
These results demonstrate the ability of the combined DFT–ASAXS approach to determine the local ion densities surrounding Pro-SNA conjugates. Specifically, once the Pro-SNA structural parameters are known (from SAXS), the ASAXS–DFT approach can predict the ionic distribution profile surrounding these bioconjugates. We use this to provide estimations of the ion distribution surrounding Pro-SNA over an extended salt concentration regime (10–300 mM) that encompasses the physiologically relevant (∼150 mM) monovalent salt concentrations. The results of these calculations are summarized in Figure 6.
Figure 6.
(A) DFT-derived predictions of the total number of Rb+ cations (black) and Cl– anions (red) within the DNA shell. The experimentally probed salt concentration (50 mM RbCl) is indicated by the blue marker and the total charge of the DNA and linker by the dashed line. (B) DFT calculated ratio of the effective number of cations within the shell (cations – anions) to the DNA + linker charge. (C) Effective Debye length as a function of bulk salt concentration. (D) Charge density profiles due to the cations (red), anions (green), DNA + linker (blue), and the net charge (black) as a function of radial distance (r) from the center of the protein for [RbCl] = 50 mM.
The total number of cations (Rb+) and anions (Cl–) within the DNA shell increases with increasing bulk salt concentration as shown in Figure 6A. At the experimentally probed salt concentration (50 mM RbCl), the Rb+ cations are found to compensate ∼90% of the negative charge from the DNA and linker (Figure 6A, dashed line). This is expected because even in salt free conditions the concentration of the condensed ions (f) strongly reduces the huge electrostatic energy of the ion penetrable Pro-SNA conjugate of size R provided the concentration of Pro-SNA (cp) is not zero,37 to an effective absolute charge that scales as −R ln(cp), which is much less than the bare absolute charge. The addition of salt further lowers the entropic barrier for the counterions in solution, causing the fraction of condensed counterions to increase even more. The high charge on the Pro-SNA (−840) coupled with the 50 mM RbCl salt concentration in our system contributes to the high extent (90%) of charge neutralization observed. Molecular dynamics simulations using the primitive model and Coulomb interactions give 90% cancelation at about 80 mM of NaCl when using spherical nanoparticles with 40 chains of 18 ssDNA bases grafted and a linker of 10 beads, which is consistent with our DFT and experimental results. Above ∼75 mM, the number of cations within the DNA shell is predicted to exceed the negative charge from the DNA and linkers. The ratio of the effective number of cations within the shell (cations – anions) to the DNA charge asymptotically approaches ∼0.9 as the bulk salt concentration is increased to 300 mM as depicted in Figure 6B. These results can be qualitatively justified by considering the competition between the concentration gradient dependent osmotic pressure and the charge mediated electrostatic forces. As the salt concentration increases, the number of anions brought into the shell increases due to the enhanced osmotic pressure. To maintain the near electroneutrality conditions in the DNA shell, the negatively charged DNA and linkers scavenge an increasing number of Rb+ from the bulk solution. In particular, we emphasize that the DFT approach does not include ionic correlations, which decrease the free energy of the system, and can induce DNA charge overcompensation in some special cases (in the presence of multivalent cations, for example).38 The variation in the effective Debye length with bulk salt concentration agrees qualitatively with Debye–Huckel theory, as depicted in Figure 6C. For the experimentally probed 50 mM bulk RbCl case, Figure 6D depicts the DFT-derived charge density profiles for the cations, anions, and DNA + linker, as well as the net charge. DFT calculations at all values of bulk salt concentration predict qualitatively similar variations in the net charge density profile of the Pro-SNA. In particular, the mobile Rb+ ions occupy the regions between the protein surface and the start of the DNA and at the end of the DNA resulting in a net positive charge at the ends of the DNA segment (Figure 6D, black line). The minimum in the net charge density profile between ∼7.5 nm and ∼13.5 nm is due to the large negative charge of the DNA. Finally, the DFT calculations predict that not all the charge compensating Rb+ ions are confined within the DNA shell, but instead utilize the space beyond the shell (as parametrized by the effective Debye length) to neutralize the DNA’s negative charge. These calculations provide an estimate of the local potential energy variations that may be experienced by small molecules in their interaction with Pro-SNA conjugates.
Conclusions
We have performed the first study of the structure and counterionic cloud environment of a protein–spherical nucleic acid conjugate. The combined use of ASAXS–DFT yields the radial distribution profile for the counterions, including a maximum in the enhancement of the counterionic density in the DNA shell that was 3.5× greater than the bulk solution concentration of 50 mM RbCl. Furthermore, the SAXS analysis with parametrized geometric models deciphered the structural attributes of the DNA corona (linker and DNA lengths) with 1 nm resolution. Our ASAXS results also serve to validate DFT derived predictions of the ion distribution at the experimentally probed salt concentration. This enables the extension of DFT calculations to regimes encompassing physiologically relevant salt concentrations with greater fidelity. At physiological conditions (above 75 mM), the number of cations within the DNA shell is predicted to exceed the negative charge due to the DNA and linkers. The overcompensation by cations here is not due to ionic correlations but originates from the osmotic pressure differences between the bulk and the DNA shell, which induces a nonzero concentration of anions in the DNA shell that is compensated by cations.
This work demonstrates the sensitivity of ASAXS–DFT in deciphering the structure of the counterionic cloud surrounding Pro-SNAs and facilitates future investigations into the origins of their novel properties. For example, the influence of competing monovalent and divalent ion distributions on the enzymatic degradation of the DNA shell can be studied. High local concentrations of monovalent cations surrounding spherical nucleic acids contribute to the inhibition of the activity of certain nucleases, such as DNase I, and thus promote the intracellular stability of spherical nucleic acid conjugates.13 The opposite is true for divalent cations. Further, the knowledge of the local charge environment around SNAs made possible using our approach should provide valuable insights into the interactions of these conjugates with small molecules and other solution bound species. Such studies will be directly relevant to the biodiagnostic and therapeutic efficacies of Pro-SNAs and other high DNA density nanoparticle conjugates. Furthermore, ASAXS measurements may be performed on Pro-SNA crystalline assemblies formed by Watson–Crick hybridization. The enhanced structural order, which manifests in diffraction peaks, should extend the q range and, thereby, the spatial resolution for the Pro-SNA structure and the counterion distribution profile.
Materials and Methods
Sample Preparation
All the oligonucleotides used in this study were synthesized on controlled pore glass (CPG) solid supports on a MM48 BioAutomation DNA synthesizer or an ABI 392/394 synthesizer using reagents from Glen Research. The synthesized DNA strands were subsequently purified using RP-HPLC on a Varian ProStar HPLC system. The base sequence of the single stranded DNA used is as follows: 5′-DBCO dT-(Sp18)2-AACGACTCATATTAACAA-3′. DBCO dT refers to a dibenzocyclooctyne phosphoramidite (Figure 1), and Sp18 refers to a hexaethylene glycol spacer. The oligonucleotides were conjugated to proteins using previously established methods.9
Briefly, catalase from Corynebacterium glutamicum was obtained from Sigma-Aldrich (Product number: 02071) and suspended in a buffer containing 100 mM sodium bicarbonate (pH 9.0, 0.5 M NaCl) by ultrafiltration. The concentration of the protein was determined by UV–vis absorption spectroscopy using a molar extinction coefficient (ε405) of 324,000 M–1 cm–1.33 The surface-accessible amine functional groups on the protein were converted into azides by adding 6 mg of tetraethylene glycol linkers containing an N-hydroxysuccinimide (NHS) ester and an azide group on opposing termini (Figure 1) to a 100 μL solution containing 50 μM protein. This reaction was then allowed to proceed for 2 h at 25 °C while shaking at 1000 rpm on a Benchmark Multitherm shaker. The unreacted linkers were then removed by five rounds of ultracentrifugation, after which the number of azide labels on the protein was determined by MALDI mass spectrometry. The difference in the observed mass of the native and azide-labeled enzyme was used to quantify the number of azide linkers per protein by making use of the fact that each attached linker adds a mass of 274 Da to the mass of the native protein.9 These azide-modified proteins were then functionalized with DBCO modified DNA through the use of a strain promoted cycloaddition reaction (Cu-free “click chemistry”) between the surface bound azides on the protein and the DBCO moieties on the 5′ end of the synthetic oligonucleotides. Each protein–DNA functionalization reaction typically contained 1 μM protein and 300 μM DNA (300× excess) suspended in phosphate buffered saline (PBS). This reaction was incubated for 3 days at 25 °C while shaking at 1000 rpm on a Benchmark Multitherm shaker, after which the unreacted DNA was removed by 10 rounds of ultrafiltration using Millipore Amicon Ultra 100 kDa centrifugal filter units. The DNA loading density was determined by using UV–vis absorption spectroscopy with the appropriate molar extinction coefficients for the protein (ε405 = 324,000 M–1 cm–1) and DNA (ε260 = 188,300 M–1 cm–1). The Pro-SNA conjugates were then exchanged into 50 mM RbCl prior to the SAXS measurements.
X-ray Measurements
All the SAXS measurements were performed at beamline 5 ID-D of the Advanced Photon Source at the Argonne National Lab. In order to avoid strong fluorescence at and above the Rb K-edge (15.2 keV), SAXS measurements were performed at four incident X-ray energies below the absorption edge (summarized in Figure 2A (inset)). The spot size of the incident beam at the sample was 0.25 × 0.25 mm2, and the average incident flux was ∼1011 photons/s. In order to minimize air scattering, a capillary tube housed in an in-vacuum flow cell was utilized. Additionally, the entire beam path was also placed under vacuum. An ion chamber positioned before the flow cell was used to monitor the flux of incident beam, while a cadmium tungstate scintillating crystal followed by a pin diode embedded in the beam stop was used to monitor the transmitted beam. The intensities of the incident and transmitted beams were used to normalize the scattered intensities collected on a Rayonix area detector placed at 7.5 m from the sample (accessible range of q ∼ 0.022–1.35 nm–1 at 15 keV). To prevent radiation damage, the entire sample volume was continuously flowing at 3 mm/s through the 1.5 mm diameter quartz capillary during data collection. The measurements were carried out at room temperature. At each energy, 5 frames were collected with an exposure time of 3 s per frame. For a given protein concentration, all the measurements were performed using the same capillary tube. The capillary was thoroughly washed with ∼10 mL of pure water and sodium hydroxide between measurements. To ensure that the background signal was unchanged due to particle aggregation or sticking, SAXS profiles of the empty capillary, water, and 50 mM RbCl buffer were collected before and after each sample measurement. Five frames were collected with an exposure time of 10 s/frame for the empty capillary, water, and buffer. The 1D scattered intensity profiles for the sample, empty capillary, water, and buffer were obtained through azimuthal integration of the collected 2D SAXS patterns, while taking into account the solid angle, flat-field, transmission, and polarization corrections. The data were converted to an absolute scale following standard procedures.39 Briefly, the data from pure water, obtained as the difference between the scattered intensities from the capillary filled with water and the empty capillary, were fitted with straight lines. The intercept of these best-fit lines through the near constant water scattering was set at 0.0165 cm–1, which is the absolute intensity (scattering cross section/volume) for water at T = 25 °C.39 Thereafter, all the data were scaled accordingly.
Density Functional Theory
The Boltzmann distribution
of Rb+ and Cl– was calculated using classical
density functional theory.29,40 A conical unit cell
was used, where the two axes represent the distance from the protein
center and the polar angle with a DNA strand. This cone was symmetric
about rotation along the radial axis. Therefore, a 2D grid was used,
with the spacing in the radial direction given by 0.05 D lengths and
0.005 radians in the θ direction. The maximum angle was calculated
by dividing the solid angle of a sphere evenly among the 40 DNA chains.
The maximum radius extends 8 D lengths from the end of the DNA. An
impervious and uncharged spherical core with the SAXS-derived Rprot = 4.5 nm and a DNA loading density of 40
strands/particle was used. The region surrounding the protein where
the linkers connect it and the DNA was modeled with a −3 charge
distributed uniformly across the volume. The ssDNA was modeled as
a −18 charge with the distribution given as the product of
three hyperbolic tangent functions with slopes of 1.2. These functions
represent the boundaries of the beginning of the DNA, the diameter
of the DNA at 1.2 nm, and the end of the DNA. The diameters of the
cation and anion used were 0.298 and 0.362 nm, in order to represent
hydrated Rb+ and Cl– respectively. The
concentration of the salt reservoir was 50 mM. The average concentration
of ions was calculated as a function of distance from the nanoparticle
center. Rb+(r, θ) densities were
angle-averaged to obtain r-dependent Rb+ density profiles (nRb+(r) – nb). v(q), the Fourier transform of the average cation density
difference with the bulk, was then calculated using trapezoidal integration.
The form factor F0(q)
obtained from fitting of the nonresonant intensities and the Pro-SNA
concentrations (Figure 4 and Table 1) was
finally multiplied with v(q) to
produce a series of calculated cross-term profiles 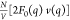 . The sizes of linker and ssDNA regions
are unknown. These were allowed to vary in 0.5 nm increments in order
to minimize the difference between the Huber error of the expected
resonant intensity and the predicted resonant intensity.
. The sizes of linker and ssDNA regions
are unknown. These were allowed to vary in 0.5 nm increments in order
to minimize the difference between the Huber error of the expected
resonant intensity and the predicted resonant intensity.
Acknowledgments
Research was supported primarily by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, DOE-BES, under Award No. DE-SC0018093 (experimental work), by the Center for Bio-Inspired Energy Science, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award No. DE-SC0000989 (sample synthesis and computational support), by the Sherman Fairchild Foundation, Inc. (computational support), and by the Vannevar Bush Faculty Fellowship program sponsored by the Basic Research Office of the Assistant Secretary of Defense for Research and Engineering and funded by the Office of Naval Research through Grant N00014-15-1-0043 (substrate functionalization). L.M.M. gratefully acknowledges support from a National Defense Science and Engineering Graduate fellowship. The SAXS experiments were performed at the APS 5ID-D beamline, which is supported through E. I. duPont de Nemours & Co., Northwestern University (NU), The Dow Chemical Co., and the NSF funded MRSEC at NU (DMR-1720139). Use of the APS was supported by DOE-BES (DE-AC02-06CH11357). We thank Steven Weigand of DND-CAT for assistance with the SAXS setup and data reduction. SAXS experiments were also performed at APS Sector 12ID-C. We thank Soenke Seifert at Sector 12 for his assistance with the SAXS setup at Sector 12ID-C. Mass spectroscopy (MALDI) measurements were made at IMSERC at Northwestern University, which has received support from the Soft and Hybrid Nanotechnology Experimental Resource (NSF ECCS-1542205); the State of Illinois and International Institute for Nanotechnology.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.7b00577.
SAXS model functions and calculations, ASAXS and charge on native proteins, edge energy calibration, and DFT error estimation (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Bowers E. M.; Ragland L. O.; Byers L. D. Salt effects on β-glucosidase: pH-profile narrowing. Biochim. Biophys. Acta, Proteins Proteomics 2007, 1774 (12), 1500–1507. 10.1016/j.bbapap.2007.10.007. [DOI] [PubMed] [Google Scholar]
- Sharp K.; Fine R.; Schulten K.; Honig B. Brownian dynamics simulation of diffusion to irregular bodies. J. Phys. Chem. 1987, 91 (13), 3624–3631. 10.1021/j100297a032. [DOI] [Google Scholar]
- Solis F. J.; Olvera de la Cruz M. Collapse of flexible polyelectrolytes in multivalent salt solutions. J. Chem. Phys. 2000, 112 (4), 2030–2035. 10.1063/1.480763. [DOI] [Google Scholar]
- Gelbart W. M.; Bruinsma R. F.; Pincus P. A.; Parsegian V. A. DNA-Inspired Electrostatics. Phys. Today 2000, 53 (9), 38–44. 10.1063/1.1325230. [DOI] [Google Scholar]
- McFail-Isom L.; Sines C. C.; Williams L. D. DNA structure: cations in charge?. Curr. Opin. Struct. Biol. 1999, 9 (3), 298–304. 10.1016/S0959-440X(99)80040-2. [DOI] [PubMed] [Google Scholar]
- Duong-Ly K. C.; Gabelli S. B. Chapter Seven - Salting out of Proteins Using Ammonium Sulfate Precipitation. Methods Enzymol. 2014, 541, 85–94. 10.1016/B978-0-12-420119-4.00007-0. [DOI] [PubMed] [Google Scholar]
- Dill K. A. Dominant forces in protein folding. Biochemistry 1990, 29 (31), 7133–7155. 10.1021/bi00483a001. [DOI] [PubMed] [Google Scholar]
- Lindman S.; Xue W.-F.; Szczepankiewicz O.; Bauer M. C.; Nilsson H.; Linse S. Salting the charged surface: pH and salt dependence of protein G B1 stability. Biophys. J. 2006, 90 (8), 2911–2921. 10.1529/biophysj.105.071050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodin J. D.; Auyeung E.; Mirkin C. A. DNA-mediated engineering of multicomponent enzyme crystals. Proc. Natl. Acad. Sci. U. S. A. 2015, 112 (15), 4564–4569. 10.1073/pnas.1503533112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodin J. D.; Sprangers A. J.; McMillan J. R.; Mirkin C. A. DNA-Mediated Cellular Delivery of Functional Enzymes. J. Am. Chem. Soc. 2015, 137 (47), 14838–14841. 10.1021/jacs.5b09711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMillan J. R.; Brodin J. D.; Millan J. A.; Lee B.; Olvera de la Cruz M.; Mirkin C. A. Modulating Nanoparticle Superlattice Structure Using Proteins with Tunable Bond Distributions. J. Am. Chem. Soc. 2017, 139 (5), 1754–1757. 10.1021/jacs.6b11893. [DOI] [PubMed] [Google Scholar]
- Mirkin C. A.; Letsinger R. L.; Mucic R. C.; Storhoff J. J. A DNA-based method for rationally assembling nanoparticles into macroscopic materials. Nature 1996, 382, 607–609. 10.1038/382607a0. [DOI] [PubMed] [Google Scholar]
- Seferos D. S.; Prigodich A. E.; Giljohann D. A.; Patel P. C.; Mirkin C. A. Polyvalent DNA nanoparticle conjugates stabilize nucleic acids. Nano Lett. 2009, 9 (1), 308–311. 10.1021/nl802958f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin R.; Wu G.; Li Z.; Mirkin C. A.; Schatz G. C. What Controls the Melting Properties of DNA-Linked Gold Nanoparticle Assemblies?. J. Am. Chem. Soc. 2003, 125 (6), 1643–1654. 10.1021/ja021096v. [DOI] [PubMed] [Google Scholar]
- Li Y.; Girard M.; Shen M.; Millan J. A.; Olvera de la Cruz M. Strong attractions and repulsions mediated by monovalent salts. Proc. Natl. Acad. Sci. U. S. A. 2017, 114 (45), 11838–11843. 10.1073/pnas.1713168114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang M. X.; Brodin J. D.; Millan J. A.; Seo S. E.; Girard M.; Olvera de la Cruz M.; Lee B.; Mirkin C. A. Altering DNA-Programmable Colloidal Crystallization Paths by Modulating Particle Repulsion. Nano Lett. 2017, 17 (8), 5126–5132. 10.1021/acs.nanolett.7b02502. [DOI] [PubMed] [Google Scholar]
- Storhoff J. J.; Elghanian R.; Mucic R. C.; Mirkin C. A.; Letsinger R. L. One-Pot Colorimetric Differentiation of Polynucleotides with Single Base Imperfections Using Gold Nanoparticle Probes. J. Am. Chem. Soc. 1998, 120 (9), 1959–1964. 10.1021/ja972332i. [DOI] [Google Scholar]
- Taton T. A.; Mirkin C. A.; Letsinger R. L. Scanometric DNA Array Detection with Nanoparticle Probes. Science 2000, 289 (5485), 1757–1760. 10.1126/science.289.5485.1757. [DOI] [PubMed] [Google Scholar]
- Giljohann D. A.; Seferos D. S.; Prigodich A. E.; Patel P. C.; Mirkin C. A. Gene Regulation with Polyvalent siRNA-Nanoparticle Conjugates. J. Am. Chem. Soc. 2009, 131 (6), 2072–2073. 10.1021/ja808719p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen S. A.; Day E. S.; Ko C. H.; Hurley L. A.; Luciano J. P.; Kouri F. M.; Merkel T. J.; Luthi A. J.; Patel P. C.; Cutler J. I.; Daniel W. L.; Scott A. W.; Rotz M. W.; Meade T. J.; Giljohann D. A.; Mirkin C. A.; Stegh A. H. Spherical Nucleic Acid Nanoparticle Conjugates as an RNAi-Based Therapy for Glioblastoma. Sci. Transl. Med. 2013, 5 (209), 209ra152. 10.1126/scitranslmed.3006839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S. Y.; Lytton-Jean A. K. R.; Lee B.; Weigand S.; Schatz G. C.; Mirkin C. A. DNA-programmable nanoparticle crystallization. Nature 2008, 451 (7178), 553–556. 10.1038/nature06508. [DOI] [PubMed] [Google Scholar]
- Macfarlane R. J.; Lee B.; Jones M. R.; Harris N.; Schatz G. C.; Mirkin C. A. Nanoparticle Superlattice Engineering with DNA. Science 2011, 334 (6053), 204–208. 10.1126/science.1210493. [DOI] [PubMed] [Google Scholar]
- Auyeung E.; Li T. I. N. G.; Senesi A. J.; Schmucker A. L.; Pals B. C.; de la Cruz M. O.; Mirkin C. A. DNA-mediated nanoparticle crystallization into Wulff polyhedra. Nature 2014, 505, 73–77. 10.1038/nature12739. [DOI] [PubMed] [Google Scholar]
- Dingenouts N.; Patel M.; Rosenfeldt S.; Pontoni D.; Narayanan T.; Ballauff M. Counterion distribution around a spherical polyelectrolyte brush probed by anomalous small-angle X-ray scattering. Macromolecules 2004, 37 (21), 8152–8159. 10.1021/ma048828j. [DOI] [Google Scholar]
- Patel M.; Rosenfeldt S.; Ballauff M.; Dingenouts N.; Pontoni D.; Narayanan T. Analysis of the correlation of counterions to rod-like macroions by anomalous small-angle X-ray scattering. Phys. Chem. Chem. Phys. 2004, 6 (11), 2962–2967. 10.1039/b402155j. [DOI] [Google Scholar]
- Das R.; Mills T.; Kwok L.; Maskel G.; Millett I.; Doniach S.; Finkelstein K.; Herschlag D.; Pollack L. Counterion Distribution around DNA Probed by Solution X-Ray Scattering. Phys. Rev. Lett. 2003, 90 (18), 188103–188103. 10.1103/PhysRevLett.90.188103. [DOI] [PubMed] [Google Scholar]
- Pabit S. a.; Meisburger S. P.; Li L.; Blose J. M.; Jones C. D.; Pollack L. Counting ions around DNA with anomalous small-angle X-ray scattering. J. Am. Chem. Soc. 2010, 132 (46), 16334–6. 10.1021/ja107259y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andresen K.; Das R.; Park H. Y.; Smith H.; Kwok L. W.; Lamb J. S.; Kirkland E. J.; Herschlag D.; Finkelstein K. D.; Pollack L. Spatial distribution of competing ions around DNA in solution. Phys. Rev. Lett. 2004, 93 (24), 248103. 10.1103/PhysRevLett.93.248103. [DOI] [PubMed] [Google Scholar]
- Kewalramani S.; Zwanikken J. W.; Macfarlane R. J.; Leung C.-Y.; Olvera de la Cruz M.; Mirkin C. A.; Bedzyk M. J. Counterion Distribution Surrounding Spherical Nucleic Acid–Au Nanoparticle Conjugates Probed by Small-Angle X-ray Scattering. ACS Nano 2013, 7 (12), 11301–11309. 10.1021/nn405109z. [DOI] [PubMed] [Google Scholar]
- Goerigk G.; Huber K.; Schweins R. Probing the extent of the Sr2+ ion condensation to anionic polyacrylate coils: A quantitative anomalous small-angle x-ray scattering study. J. Chem. Phys. 2007, 127 (15), 154908. 10.1063/1.2787008. [DOI] [PubMed] [Google Scholar]
- Goerigk G.; Lages S.; Huber K. Systematic Limitations in Concentration Analysis via Anomalous Small-Angle X-ray Scattering in the Small Structure Limit. Polymers 2016, 8 (3), 85. 10.3390/polym8030085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans G.; Pettifer R. F. CHOOCH: a program for deriving anomalous-scattering factors from X-ray fluorescence spectra. J. Appl. Crystallogr. 2001, 34 (1), 82–86. 10.1107/S0021889800014655. [DOI] [Google Scholar]
- Samejima T.; Yang J. T. Reconstitution of acid-denatured catalase. J. Biol. Chem. 1963, 238 (10), 3256–3261. [PubMed] [Google Scholar]
- Kozlowski L. P. IPC–Isoelectric Point Calculator. Biol. Direct 2016, 11 (1), 55. 10.1186/s13062-016-0159-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svergun D.; Barberato C.; Koch M. H. J. CRYSOL – a Program to Evaluate X-ray Solution Scattering of Biological Macromolecules from Atomic Coordinates. J. Appl. Crystallogr. 1995, 28, 768–773. 10.1107/S0021889895007047. [DOI] [Google Scholar]
- Candelaresi M.; Gumiero A.; Adamczyk K.; Robb K.; Bellota-Anton C.; Sangal V.; Munnoch J.; Greetham G. M.; Towrie M.; Hoskisson P. A.; Parker A. W.; Tucker N. P.; Walsh M. A.; Hunt N. T. A Structural and Dynamic Investigation of the Inhibition of Catalase by Nitric Oxide. Org. Biomol. Chem. 2013, 11, 7778–7778. 10.1039/c3ob41977k. [DOI] [PubMed] [Google Scholar]
- González-Mozuelos P.; de la Cruz M. O. Ion condensation in salt-free dilute polyelectrolyte solutions. J. Chem. Phys. 1995, 103 (8), 3145–3157. 10.1063/1.470248. [DOI] [Google Scholar]
- Raspaud E.; Chaperon I.; Leforestier A.; Livolant F. Spermine-induced aggregation of DNA, nucleosome, and chromatin. Biophys. J. 1999, 77 (3), 1547–1555. 10.1016/S0006-3495(99)77002-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan L.; Degen M.; Bendle S.; Grupido N.; Ilavsky J. The absolute calibration of a small-angle scattering instrument with a laboratory X-ray source. J. Phys. Conf. Ser., IOP Publishing 2010, 247, 012005. 10.1088/1742-6596/247/1/012005. [DOI] [Google Scholar]
- Zwanikken J. W.; Guo P.; Mirkin C. A.; Olvera de la Cruz M. Local Ionic Environment around Polyvalent Nucleic Acid-Functionalized Nanoparticles. J. Phys. Chem. C 2011, 115 (33), 16368–16373. 10.1021/jp205583j. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.