Abstract
Tortuous aneurysmal arteries are often associated with a higher risk of rupture but the mechanism remains unclear. The goal of this study was to analyze the buckling and post-buckling behaviors of aneurysmal arteries under pulsatile flow. To accomplish this goal, we analyzed the buckling behavior of model carotid and abdominal aorta with aneurysms by utilizing fluid-structure interaction (FSI) method with realistic waveforms boundary conditions. FSI simulations were done under steady-state and pulsatile flow for normal (1.5) and reduced (1.3) axial stretch ratios to investigate the influence of aneurysm, pulsatile lumen pressure and axial tension on stability. Our results indicated that aneurysmal artery buckled at the critical buckling pressure and its deflection nonlinearly increased with increasing lumen pressure. Buckling elevates the peak stress (up to 118%). The maximum aneurysm wall stress at pulsatile FSI flow was (29%) higher than under static pressure at the peak lumen pressure of 130 mmHg. Buckling results show an increase in lumen shear stress at the inner side of the maximum deflection. Vortex flow was dramatically enlarged with increasing lumen pressure and artery diameter. Aneurysmal arteries are more susceptible than normal arteries to mechanical instability which causes high stresses in the aneurysm wall that could lead to aneurysm rupture.
Keywords: Aneurysm, fluid-structure interaction, critical buckling pressure, finite element analysis, computational fluid dynamics
1. Introduction
Arterial aneurysms, permanent focal dilations, often occur in cerebral arteries, carotid arteries and aorta and aneurysm rupture leads to very high death rates (Upchurch and Schaub 2006; Vorp 2007). Abdominal aortic aneurysm (AAA) is the most common type of aneurysm and is the 13th leading cause of death. Aneurysm is often detected by medical imaging and is often asymptomatic until rupture (Chervu et al. 1995). Aneurysm size is commonly used as an indicator of aneurysm rupture risk, but many small aneurysms do rupture (Vorp 2007). It is believed that the wall stress is a better predictor of aneurysm rupture than maximum diameter in surgical selection (Fillinger et al. 2003; Li and Kleinstreuer 2006; Elefteriades 2008; Georgakarakos et al. 2010). Mechanically, aneurysm rupture occurs when the stress in the aneurysm wall exceeds its failure strength. Therefore, it is necessary to better understand the wall stress in aneurysms under physiological and pathological conditions.
Aneurysms are usually affiliated with tortuous arteries (Mukherjee et al. 1989; Hatakeyama et al. 2001; Fillinger et al. 2004; Arends et al. 2008) and aneurysmal tortuosity has been suggested as a risk factor for AAA rupture (Hatakeyama et al. 2001; Fillinger et al. 2004; Rodríguez et al. 2008; Georgakarakos et al. 2010). Artery buckling could lead to tortuous vessels associated with aging and cardiovascular diseases (Han 2009b, 2012). It has been demonstrated that aneurysmal and normal arteries buckle when the lumen pressure exceeds the critical buckling pressure which is a function of material properties, dimensions, and axial stretch ratio (Han 2009b, 2012; Han et al. 2013; Lee et al. 2014; Khalafvand and Han 2015). The critical buckling pressure is the critical pressure value at which the artery become unstable with quick increase in deflection due to buckling can significantly affect the wall stress in normal and aneurysmal arteries (Han 2007; Liu and Han 2012).
On the other hand, aneurysm formation could reduce the axial tension and hence decrease the critical buckling pressure and thus making the vessel more vulnerable to buckling (Michineau et al. 2010; Lee et al. 2014).
Flow and wall stress analyses of normal and aneurysmal arteries have been studied extensively using computational solid stress (CSS) and fluid-structure interaction (FSI) methods in order to understand the mechanisms of aneurysm rupture and predict rupture locations (Marra et al. 2006; Scotti and Finol 2007; Scotti et al. 2008; Datir et al. 2011; Chandra et al. 2013; Lee et al. 2014; Khalafvand and Han 2015). FSI studies have investigated the morphological factors that affect the wall stress distribution in aneurysmal arteries with influence of intraluminal thrombus (Bluestein et al. 2009; Chandra et al. 2013) arterial wall material (Rissland et al. 2008; Xenos et al. 2010), vessel geometry (Finol et al. 2003; Scotti et al. 2005; Li and Kleinstreuer 2006). Recently, Lee et al. (2014) studied the stability of aneurysmal arteries under static pressure. Their analysis showed that the deflection increases nonlinearly with increasing lumen pressure and aneurysmal arteries had a smaller critical buckling pressure than normal vessels. However, the effects of blood flow on stability of aneurysmal arteries were not considered. Very recently, Khalafvand and Han (2015) investigated the effects of axial tension and flow rate on a normal carotid artery stability under steady-state and pulsatile flow using 3D FSI modeling. Their results demonstrated that pulsatile pressure affects the critical pressure while the flow rate magnitude had a negligible influence (<5%) on the critical buckling pressure for both steady-state flow and pulsatile flow. Artery buckling has significant effects on the lumen blood flow and wall stress in normal arteries (Khalafvand and Han 2015). It is evident that aneurysms and geometric variations would affect flow and arterial wall stress (Chesnutt and Han 2011; Datir et al. 2011). Thus, the FSI modeling is needed to better understand the buckling of aneurysmal arteries under pulsatile flow conditions.
The aim of this study is to assess the stability of fusiform aneurysmal arteries under steady and pulsatile flow using 3D FSI simulation. By doing so, we hope to capture the morphological factors that result in aneurysmal arteries instability.
2. Methods
The mechanical instability of aneurysmal arteries, both the critical buckling pressure and post-buckling deflection behavior were investigated using FSI modeling of aneurysmal arteries. In addition, the effects of pulsatile pressure were illustrated by comparing the FSI results with the results from a static internal pressure and steady flow simulations.
2.1. Geometry
It has been proven that spherically shaped aneurysm (length-to-diameter ration, L/D = 1) demonstrated a higher critical buckling pressure than elliptically shaped aneurysm (L/D ≠ 1) (Lee et al. 2014). Therefore, a cylindrical artery model with a spherically shaped aneurysm (fusiform) was created based on the dimensions and material properties of aneurysmal arteries from our previous study (Lee et al. 2014) (see Figure 1).
Figure 1.

Schematic of finite element discretization of three-dimensional aneurysmal artery model including fluid, solid medium interfaces in a longitudinal cross section.
2.1.1. Aneurysmal carotid artery
Based on our previous measurements (Lee et al. 2012; Khalafvand and Han 2015), a porcine carotid artery model was created with an internal radius of 2 mm, external radius of 3 mm, thickness of 1 mm and neck length of 46 mm with an aneurysm length and diameter of 10 mm, and aneurysm wall thickness of 1 mm. Based on our previous study (Khalafvand and Han 2015), an entry section of length Le = 20 mm and a tail section of Lo = 20 mm were attached to the model to reduce the inlet and outlet boundaries effects and to obtain fully developed flow.
2.1.2. Abdominal aorta with an aneurysm
To better understand the buckling behavior of large arteries, an abdominal aorta with a lumen diameter of 17 mm, wall thickness of 1.5 mm, neck length of 80 mm, aneurysm length and diameter of 30 mm, aneurysm wall thickness of 1.5 mm, and entry and tail length of 40 mm was created (Lee et al. 2014).
Aneurysmal carotid and aorta arteries models were created for the load-free configuration. Our previous studies demonstrated that the effect of residual stress on artery buckling is negligible for given material properties and for large opening angles (Lee et al. 2012; Liu et al. 2014; Fatemifar and Han 2016). Thus, the residual stress was ignored in the models.
2.2. Fluidmodel
To describe the deformable fluid and solid domains, an arbitrary Lagrangian-Eulerian (ALE) approach was employed to update the fluid mesh to follow the structure motion. The momentum and continuity equations in ALE form are given by Equations (1) and (2).
| (1) |
| (2) |
Where ρ is the fluid density, V is the fluid velocity vector, Vg is the moving reference velocity, p is the pressure, and τf is the fluid stress tensor. The term (V – Vg) is used to reflect the relative velocity of the fluid with respect to the moving reference velocity. Blood was modeled to be Homogeneous, incompressible, and Newtonian fluid. This is an acceptable assumption for large vessels with inner diameter greater than approximately 0.5 mm as a result of relatively constant apparent viscosity of blood at high shear rates (> 100/s) (Milnor 1989; Perktold et al. 1991) with a density of 1050 Kgm−3 and dynamic viscosity of 0.00316 Pa.s, representing human blood properties at 37 °C. The laminar flow was supposed since the peak Reynolds number of 1781 was smaller than the critical Reynolds number of 2300 for smooth pipes.
2.3. Structure model
A Lagrangian coordinate system is adapted to the solid domain in order to capture the arterial wall displacement due to the hemodynamic forces. The governing equation for the arterial wall is the momentum conservation given by Equations (3) and (4) (Bathe 2013)
| (3) |
| (4) |
Where σij is the solid stress tensor, Dijkl is the Lagrangian elasticity tensor, εkl is the solid strain tensor, ρs is the arterial wall density, and d̈s is the local acceleration of the solid.
These two domains are coupled through dynamic (traction equilibrium) and kinematic (displacement compatibility) conditions, shown in Equations (5) and (6)
| (5) |
| (6) |
Where df and ds denote the fluid and solid displacement vectors at the interface, vg, ds are the fluid and solid velocity vectors, and n is the outward unit normal vector of the interface.
Based on our prior experimental study of porcine carotid arteries, the arterial wall was assumed to behave as an incompressible, homogeneous, and anisotropic non-linear material as described by the Ogden–Holzapfel two-fiber strain-energy function (Lee et al. 2012; Liu and Han 2012; Liu et al. 2014). The aneurysmal wall was considered to have the same material parameters as the arterial. The arterial material model is defined by Equation (7)
| (7) |
The first and second terms indicate the isotropic and anisotropic part, respectively. Where μn, αn, k1 and k2 are the material constants, λ1, λ2 and λ3 are principal stretches, I4 and I6 are Cauchy-Green deformation tensor constants. As obtained by Khalafvand and Han (2015), Ogden material constants for the artery wall are α1 = 1.3, α2 = 5, α3 = 0.5, μ1 = μ2 = μ3 = 5662, k1 = 3449.5 Pa, k2 = 0.496 Pa with a axial fiber angle of 48.09°, density of 1060 Kgm−3 and bulk modulus of 2.4e07.
2.4. Boundary conditions
Experimental measurements have shown that the mean flow rate of carotid and abdominal aorta arteries are 370 and 1360 ml/min, respectively (Demolis et al. 1991; Holdsworth et al. 1999; Li and Kleinstreuer 2006). Vascular diseases and surgery may reduce the normal axial stretch ratio of blood vessels (1.5) (Han et al. 2003). In addition, to investigate the effect of blood flow on the critical buckling pressure and post-buckling deflection, an aneurysmal carotid artery and an aneurysmal abdominal aorta respectively with a mean flow rate of 370 ml/min and 1360 ml/min under normal (1.5) and reduced (1.3) stretch ratio have been simulated. At the arterial ends, there is only one degree of freedom per node in radial direction to prevent stress concentration. The external pressure on the outer surface was prescribed to be zero.
Arteries are subjected to a large axial tension in vivo (Han et al. 2003). So, the axial strain should be applied to achieve the physiological level of living tissues. The FSI simulations consisting of two phases. First, a designated axial stretch (i.e. 1.3 or 1.5) was implemented on all nodes at the arterial ends in 10 time steps (0.1 s). In this interval, the steady-state flow with a uniform inlet steady velocity and outlet pressure was applied to achieve diastolic velocity and pressure (i.e. 0.23 m/s and 80 mmHg for normal conditions). Then, the results of steady-state flow initialized the pulsatile flow simulation. During the second phase, the time-dependent inlet velocity and outlet pressure were used as a boundary conditions for aneurysmal artery. As discussed by our previous study (Khalafvand and Han 2015), in the absence of porcine carotid arterial flow data, the patient-specific inlet velocity and outlet pressure from a healthy 23-year-old subject which measured by Hirata et al. (2006) were considered for pulsatile flow simulation. The human inlet velocity and outlet pressure waves are shown in Figure 2. In the CSS analysis, a static pressures in the range of 10–130 mmHg were employedtothe internal lumenofartery which was axially stretched to a desired stretch ratios. The entry and tail sections were considered as fixed with no buckling or rotation, yet radial expansion was possible. The lateral deflection was determinedas the displacement of the artery central line from its initial baseline at zero pressure. The critical buckling pressure was defined as the lateral deflection became about 1 mm from the initial position.
Figure 2.
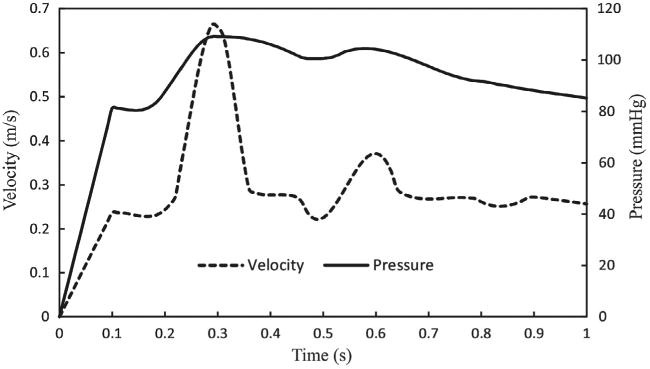
Inlet velocity and outlet pressure boundary conditions.
The simulation of the aneurysmal artery under static pressure and steady-state flow were done to compare the deflection behavior with pulsatile flow results. We used the same boundary conditions for steady-state flow as pulsatile flow simulation except that the time-dependent inlet and outlet boundary conditions were substituted by uniform inlet steady velocity and constant outlet pressure.
2.5. Model implementation
We used the finite element solver ADINA (v9.0, ADINA R&D, Inc., Watertown, MA) to solve the fully coupled FSI and CSS models. The fluid was modeled with 3D four-node flow-condition-based interpolation (FCBI) elements. The 3D 27-node solid elements were utilized for the solid domain. The solid domain was employed the large displacement and large strain in conjunction with mixed pressure-displacement interpolation for the arterial wall. The governing equations were solved by sparse matrix solver based on Gaussian elimination. The full Newton method with direct FSI solution coupling which has a maximum of 100 iterations per time step was employed. Force and displacement relaxation factors in the range of 0.45–0.65 were used to maintain the solution stability. To achieve the optimum grid size, the number of elements increased in the solid and fluid domains by a factor of 1.2 until the global flow and solid characteristics between the grids became less than 3%. The maximum lateral deflection and the maximum wall shear stress at the maximum deflection area were selected as an indicator of convergence for the solid and fluid domains, respectively. The aneurysmal carotid and abdominal aorta final grids are, respectively, composed of 16,896 and 33,024 hexahedral (brick) elements for the solid, 28,910 and 108,142 tetrahedral elements for the fluid domains.
3. Results
The simulation repeated for three cardiac cycles to achieve the periodic solutions. We have considered the third cycle results to analyze since the solution has been periodic. The third cycle solution time has been mapped from t = 0 to t = 1s.
3.1. Post-buckling deflection and critical buckling pressure
Our simulation captured the buckling behavior of the aneurysmal artery. The initially straight vessel become curved due to buckling under increased pressure (Figure 3). The lateral deflection starts when the lumen pressure reached the critical buckling pressure and continued to increase nonlinearly with increasing lumen pressure post-buckling.
Figure 3.
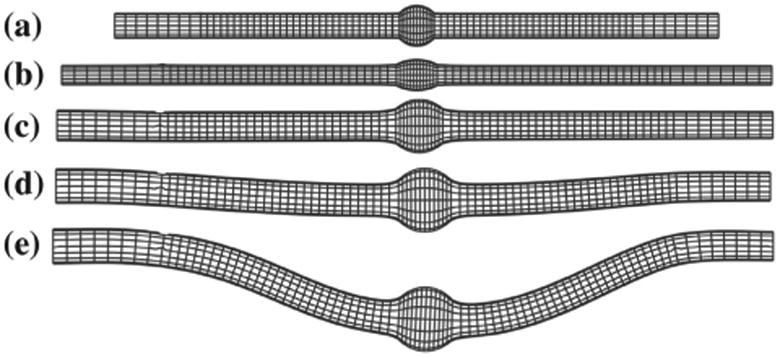
Deflection of an aneurysmal artery under increasing lumen pressure: (a) initial condition with no load (b) axially stretched (c) inflated under lumen pressure without buckling (d) initial buckling (e) post-buckling.
The maximum deflection at the middle of the buckled artery as a function of mean lumen pressure for the aneurysmal artery under steady-state, pulsatile flow, and static pressure with normal and reduced stretch ratios are plotted in Figure 4. The results showed that artery buckled at a critical pressure. The aneurysmal artery at a given stretch ratio had a similar post-buckling behavior under steady-state and pulsatile flow. The deflection of aneurysmal artery under static pressure was smaller than under steady steady-state and pulsatile flow, yet the trends were similar.
Figure 4.
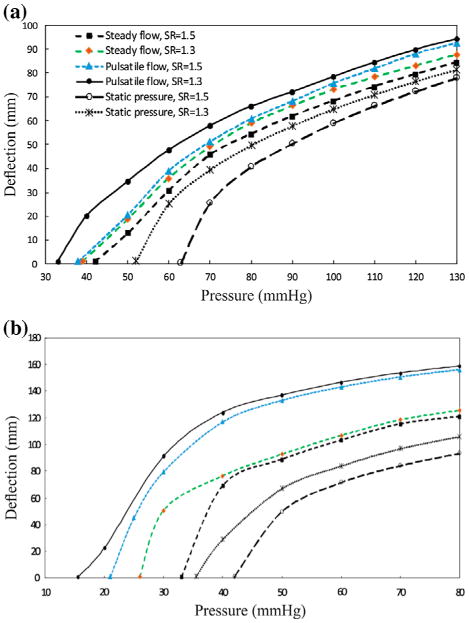
Comparison of the buckling behavior of the aneurysmal artery as a function of the mean lumen pressure under steady-state, pulsatile flow, and static pressure with a stretch ratios of 1.3 and 1.5 (a) aneurysmal carotid artery (b) aneurysmal abdominal aorta.
The comparison of the critical buckling pressure for aneurysmal artery under different types of pressures is presented in Table 1. The results demonstrated that diameter and axial stretch ratio of artery could change the critical buckling pressure. For an artery at a given axial stretch ratio, the critical buckling pressure is the heisted under static pressure and the lowest under pulsatile pressure. For the steady-state flow, the critical buckling pressure had 15–40% higher value than the pulsatile flow.
Table 1.
Critical buckling pressure (mmHg) under steady-state, pulsatile flow, and static pressure (SR = stretch ratio; Qm = mean flow rate).
| Aneurysmal artery | SR | Steady-state flow | Pulsatile flow | Static pressure |
|---|---|---|---|---|
| Carotid | 1.3 | 39 | 33 | 52 |
| 1.5 | 42 | 38 | 63 | |
| Abdominal aorta | 1.3 | 26 | 15.5 | 35.5 |
| 1.5 | 33 | 21 | 42 |
3.2. Flow field pattern and effective stress under pulsatile flow
The deflection of aneurysmal artery changes the flow velocity profile that leads to vortex formation at the center of the aneurysm (Figure 5). In the first half of the artery, the fully developed velocity profile changes its direction toward the outer side and then the recirculation zone is formed at the middle of the aneurysm. Then, the direction turns toward the inner side in the second half of the artery. The maximum effective stress located at inner side of the wall at the maximum deflection area. The effective stress alters at the region where the artery curvature changes.
Figure 5.
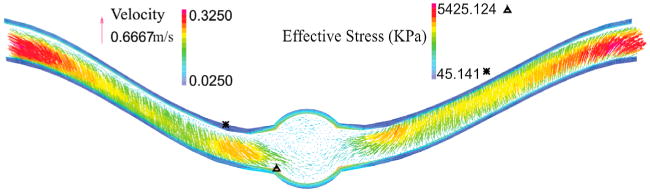
Velocity vector and effective stress for the aneurysmal carotid artery under pulsatile flow with a lumen pressure of 130 mmHg and a stretch ratio of 1.3 at the time of maximum deflection.
The maximum lumen shear stress, which is located at the outer side of the bend at the maximum deflection area, increased with increasing pressure (Figure 6). High shear stresses are located at the middle of the neck length and near the aneurysm due to the curvature alternation. Similar patterns are observed for the temporal variations of the lumen shear stress at the inner and outer sides of the bend at the maximum deflection area. The time averages of wall shear stress for normal and reduced stretch ratios with a mean pressures of 60 and 130 mmHg are reported in Table 2. The results demonstrated that the lumen shear stress depended on the mean lumen pressure and the axial stretch ratio. The time average of wall shear stress increases with mean lumen pressure and while it shows a decreasing trend with axial tension. The negative shear stress is due to flow separation and recirculation zone at the inner side.
Figure 6.
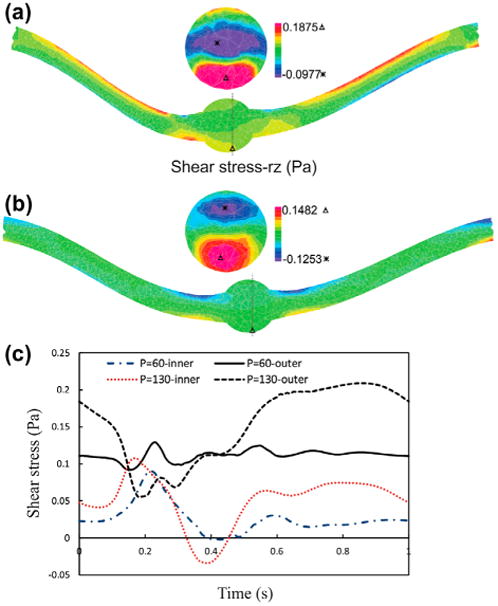
The lumen shear stress- rz contours of aneurysmal carotid artery under pulsatile flow with a stretch ratio of 1.3 and lumen pressure of: (a) Pm = 130 mmHg. (b) Pm = 60 mmHg.
Table 2.
The time average of wall shear stress (Pa) for the aneurysmal carotid artery under pulsatile flow with a stretch ratio of 1.3 and 1.5 and mean pressure of Pm = 60 and 130 mmHg at the inner and outer sides of the bend at the maximum deflection area.
| SR = 1.3 | SR= 1.5 | ||||||
|---|---|---|---|---|---|---|---|
|
|
|
||||||
| Pm = 60mmHg | Pm = 130mmHg | Pm = 60mmHg | Pm = 130 mmHg | ||||
| Inner | Outer | Inner | Outer | Inner | Outer | Inner | Outer |
| 0.026 | 0.111 | 0.051 | 0.153 | 0.014 | 0.094 | 0.051 | 0.122 |
Buckling changes the particle trace pathlines and pressure contours under pulsatile flow (Figure 7). Particles pursue the deflection of the neck length since the flow velocity profile is fully developed at the entrance. But the velocity decreases as the flow enters the aneurysm and some vortices form. Mean lumen pressure and axial stretch ratio control the recirculation zone size. Mean lumen pressure and axial stretch ratio are directly and inversely proportional to the size of the recirculation zone, respectively. The pressure contours represent that the maximum and minimum of the lumen pressure are located respectively at the outer and inner sides of the bend as a result of centrifugal effect. Due to the large diameter in abdominal aorta, the deflection magnitude and recirculation zone size increase.
Figure 7.
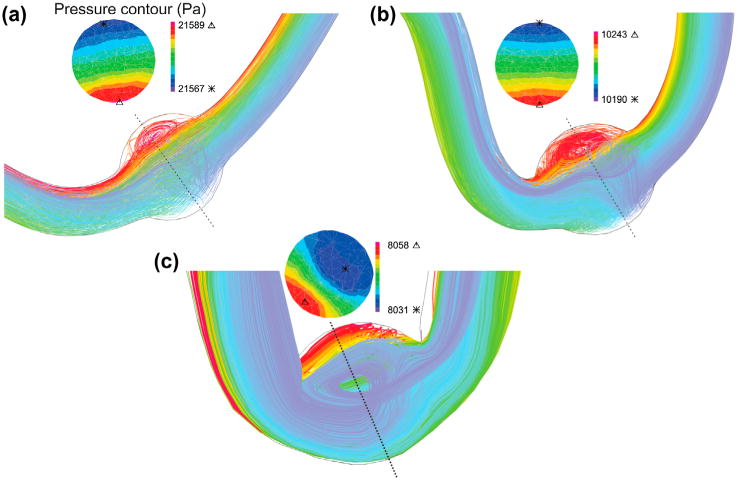
Particle trace plots of the pathlines and pressure contours at the maximum deflection area for the aneurysmal artery under pulsatile flow with a stretch ratio of 1.5 for a mean pressure of: (a) aneurysmal carotid artery with Pm = 60 mmHg (b) aneurysmal carotid artery with Pm = 130 mmHg (c) aneurysmal abdominal aorta with Pm = 40 mmHg.
Artery buckling alters the flow velocity profile at the maximum deflection area (Figure 8). First, the flow is accelerated to reach its peak and so the velocity vectors are attached to the aneurysm wall due to its high velocity. At the peak systolic flow, the flow pattern is symmetric. At the end of systole, which is the time of maximum deflection, a symmetric vortex appears near the aneurysm wall since the flow is decelerated, yet the flow moves forward at the center of the aneurysm. During diastole, the flow velocity slightly rises and dissolves the vortices. Then a small vortex emerges in the middle of the aneurysm at the end of diastole.
Figure 8.
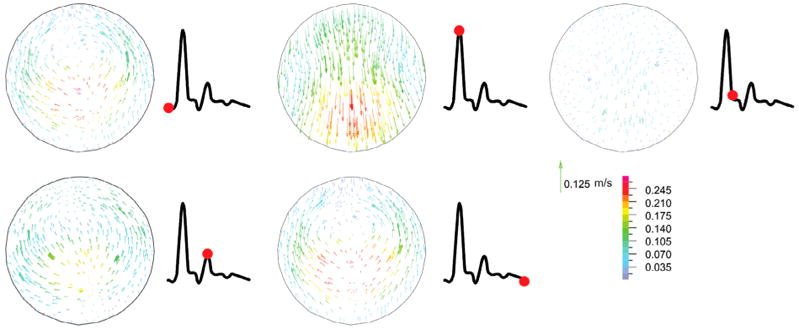
Velocity vectors for the aneurysmal carotid artery under pulsatile flow with a stretch ratio of 1.5 and lumen pressure of 130 mmHg at the maximum deflection area sections through the different phases of the cardiac cycle (at time t = 0.07, 0.18, 0.33, 0.49, and 1 s, respectively). The red point on the black line graph shows the respective time instant on the velocity curve.
Figure 9 indicates the velocity profile of aneurysmal abdominal aorta under pulsatile flow with a stretch ratio of 1.5 at the maximum deflection time. As the artery buckles, the fully developed velocity profile changes and reaches its minimum at the maximum deflection area. Same as aneurysmal carotid artery, the velocity increases in the second half of the artery.
Figure 9.
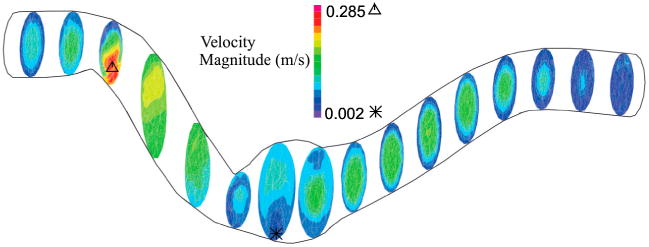
Velocity profile for aneurysmal abdominal aorta under pulsatile flow with a stretch ratio of 1.5 and lumen pressure of 40 mmHg at the maximum deflection time.
3.3. Arterial wall stress under pulsatile flow
The perimeter of the aneurysm lumen surface was divided equally by four points (inner, outer, M1, M2) at the maximum deflection area to investigate the wall stress changes. To probe the wall stresses, four lines passing through the above mentioned points were chosen (Figure 10). Figure 10 shows the temporal variation of normal stresses (radial, circumferential, axial) and shear stresses (rθ, rz, θz) at the inner, outer, M1, M2 at the maximum deflection area. A comparison with an unbuckled aneurysmal artery, which has one-third of the vessel length at the same pressure and stretch ratio is presented (Khalafvand and Han 2015). In both cases, the normal stresses are the dominant since shear stresses are one order of magnitude smaller. Due to symmetry, a considerable overlap is observed between the normal stresses at M1 and M2 points. It is seen that all stress components have two peaks which are related to the two peaks in the pressure wave. The unbuckled aneurysmal artery reaches its maximum normal stress 100 ms sooner than the buckled aneurysmal artery. Buckling leads to a 32% increase in peak radial stress, 118% in peak circumferential stress, and 116% in peak axial stress compared to the unbuckled aneurysmal artery. The circumferential and axial stresses reach their maximum value of 550 and 546 KPa at outer and M1 points, respectively.
Figure 10.
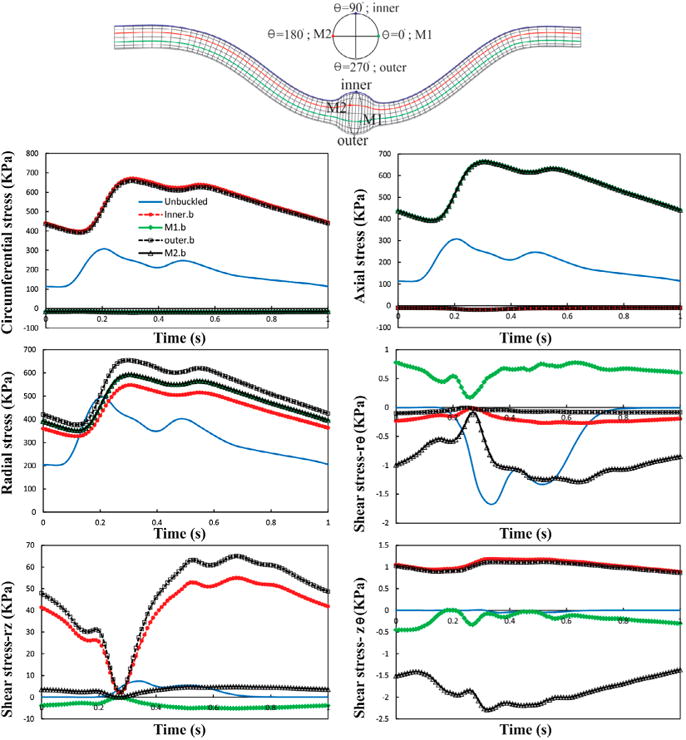
Temporal variation of normal and shear stresses for the aneurysmal carotid artery under pulsatile lumen pressure of 80 mmHg with a stretch ratio of 1.5 at the inner, outer, M1, and M2 points. The results are compared with an unbuckled aneurysmal carotid artery under the same conditions.
3.4. Spatial changes of wall stress under pulsatile flow
Buckling leads to dramatic spatial changes of normal stresses at the maximum deflection time (Figures 11 and 12). The results indicate that increasing lumen pressure causes higher wall stresses. Symmetric variation patterns are observed along the circumferential and axial locations in the buckled aneurysmal artery. Circumferential variation of radial stress is almost constant except for high mean lumen pressures. The peak of axial and circumferential stresses occurs near the region where the curvature of lumen surface changes. Outer and inner points have maximum circumferential stress while the maximum axial stress occurs at M1 and M2 points.
Figure 11.
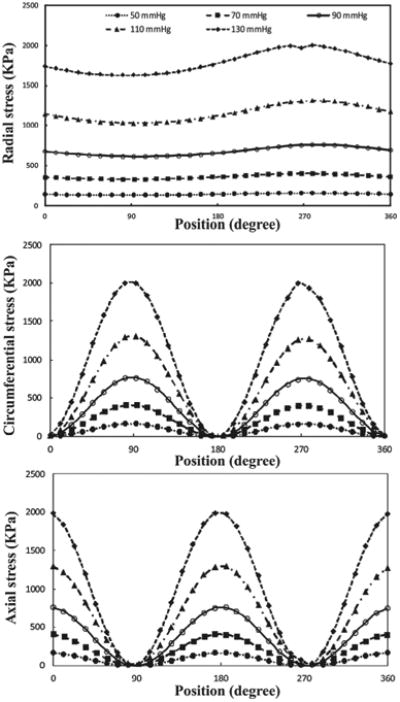
Circumferential variation of wall stress of aneurysmal carotid artery for the outlet pulsatile pressures in the range of 50–130 mmHg with a stretch ratio of 1.3 at the time of maximum deflection.
Figure 12.
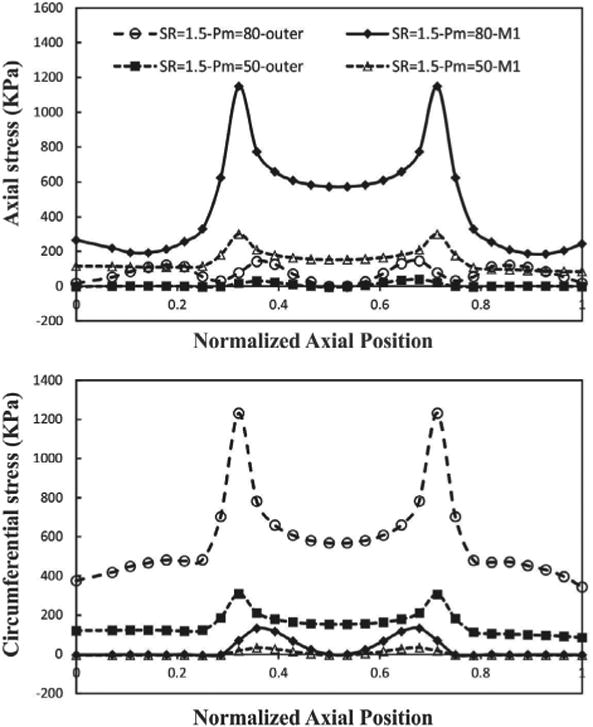
Axial variation of wall stress of aneurysmal carotid artery along the outer and M1 curves for the outlet pulsatile pressure of 50 and 80 mmHg with a stretch ratio of 1.5 at the time of maximum deflection.
4. Discussion
This study investigated the buckling behavior of the aneurysmal arteries (fusiform aneurysm) under static pressure, steady-state flow, and pulsatile flow. Fusiform Aneurysm often occurs in arteries and aneurysmal arteries are often tortuous along its central line. In this study, aneurysmal arterial models were created by adding a spherically shaped dilation (Lee et al. 2014). The results demonstrated that the aneurysmal artery buckled and became tortuous under a lumen pressure higher than the critical pressure. The deflection of aneurysmal artery increases nonlinearly with mean lumen pressure. For all loading conditions, the critical buckling pressure is 7–26% smaller at an axial stretch ratio of 1.3 than at 1.5. Mechanical instability alters the stress distribution patterns and also increases the peak wall stress. It is seen that the trend of buckling under steady-state and pulsatile flow are similar at low frequency (<5 Hz).
In general, aneurysm walls differ from normal arteries. As the aneurysms commonly seen in humans are thinner and weaker than normal walls. Our previous study had examined the aneurysmal wall stiffness on aneurysmal artery buckling and demonstrated that wall stiffness does not affect the trend of artery buckling (Lee et al. 2014). Thus, we used the same material constants for simplicity. Our results indicate that aneurysms would reduce the stability of arteries. In addition, the presence of an aneurysm resulted in a higher lumen stress compared to the normal artery under the same lumen pressure. These are consistent with our previous results and suggest that it is reasonable to use the same material parameters.
4.1. Model validation
In our previous study (Lee et al. 2014), buckling tests were done in porcine carotid arteries with small aneurysms created using elastase treatment to determine the effect of aneurysms on arterial buckling instability and the effect of buckling on aneurysm wall stress. Comparison of our results with previous experimental results by Lee et al. (2014) validates our model results. While in the arteries were tied at the ends to diameter matched cannulate restraining the ends from any movement, arteries in vivo are supported by surrounding tissues and the overall lengths are fixed between the anatomical positions due to branch and surrounding tissue tethering. In this study, we constrained all of DOF except in radial direction at the end of artery to approximate the in vivo conditions. In addition, although we assumed fixed boundary condition at the both ends, this boundary condition is applicable to arteries under various boundary conditions using equivalent length (Han 2009a, 2009b).
The results from the transient FSI analysis demonstrated a higher the maximum aneurysm wall stress up to 29% compared with a static pressure-deformation study at the peak lumen pressure of 130 mmHg which is in line with the results reported by Scotti et al. (2008). The maximum wall stress is located at the inner wall of the aneurysm which is consistent with the results of FSI studies on thoracic aortic aneurysm by Tan et al. (2009) and AAA by Leung et al. (2006). We also found that changing the axial stretch ratio and flow conditions alter the critical buckling pressure. The critical buckling pressure under pulsatile flow is 15–40% (<12 mmHg) smaller than steady-state flow which is in agreement with the results of a recent study by Khalafvand and Han (2015) for normal arteries.
4.2. Limitations
There are a few limitations in the present study. First, an idealized aneurysm shape with uniform wall thickness was used based on the dimensions measured from our previous experiment, instead of the actual patient-specific irregular aneurysm shape was chosen for simplicity to illustrate the effect of pulsatile blood flow on stability of aneurysmal arteries. Further studies are needed to fully investigate the effect of patient-specific non-uniform wall thickness model in the presence and absence of intra-luminal thrombosis on critical buckling pressure. While including these detailed information improves accuracy of FSI analysis, the current idealized model illustrated how aneurysm affect artery stability.
Second, we have ignored the effects of surrounding tissue, and non-Newtonian blood flow on the buckling behavior. The effects of surrounding tissue on artery stability have been illustrated by our previous theoretical and experimental studies (Han 2009a; Lee et al. 2012) and we think the effect on aneurysmal arteries will be similar. Due to the high shear rates in large arteries, non-Newtonian behavior of blood flow could be negligible (Milnor 1989; Perktold et al. 1991).
Finally, we have used human carotid flow and pressure waveform with a frequency of 1 Hz instead of porcine carotid artery data, while porcine carotid artery data are not available (Huo et al. 2007). In addition, though two fixed ends were used for the aneurysmal artery, different boundary conditions could be applied to the model using an equivalent length (Han et al. 2013).
4.3. Clinical relevance
Tortuosity often occurs in aneurysmal arteries associated with high risk of rupture (Hatakeyama et al. 2001; Fillinger et al. 2004; Johnson et al. 2007). Tortuous arteries associated with aneurysm could alter the blood flow and may lead to intraluminal thrombus (ILT) formation that related to wall stress alternation in the aneurysm (Tan et al. 2009; Biasetti et al. 2011; Wang et al. 2002). Our results showed that increasing lumen pressure beyond the critical buckling pressure may lead to tortuosity in aneurysmal artery and hence heighten their rupture risk. In addition, buckled aneurysmal arteries in comparison with unbuckled ones, have higher peak wall stresses. Our results indicate that the recirculation zone appears during peak-systole, at the time of maximum deflection, results in local flow stagnation. As the lumen pressure increases, the stagnation zone size increases as does the particle (platelet) residence within the aneurysm, which in turn may initiate the intraluminal thrombus development (Suh et al. 2011). This is consistent with the results revealed from clinical examinations that the growth of ILT might indicate the risk of aneurysm rupture (Stenbaek et al. 2000). Consequently, this new finding would help to predict aneurysm growth in the long term and helpful for clinical diagnosis and treatment.
4.4. Significance
This study is novel in studying the instability of fusiform aneurysmal arteries under various loading conditions (static pressure, steady-state flow, and pulsatile flow). This is different from previous studies that only looked at buckling of normal arteries under static pressure, or pulsatile pressure (Han 2007; Liu and Han 2012; Khalafvand and Han 2015). The previous study on aneurysmal artery stability only examined the buckling under static pressure (Lee et al. 2014). Our current FSI simulations demonstrated that the formation of an aneurysm reduces the critical buckling pressure under pulsatile flow condition, consistent with previous experimental results (Lee et al. 2014). Furthermore, the presence of an aneurysm in tortuous arteries results in vortex flow in the aneurysm. This vortex flow undermines artery stability and reduces the critical buckling pressure, thus aneurysmal arteries are more vulnerable to buckle. Comparison of CSS and FSI simulations showed that the fluid flow has a significant effect on critical buckling pressure. For example, the deflection of the arterial wall is a largely function of the lumen flow under pulsatile flow. The lumen flow due to the generated shear forces causes mechanical instability which can alter the critical buckling pressure and buckling deformation in aneurysmal arteries. However, in steady-state flow, since inlet velocity and outlet pressure are constant, the critical buckling pressure is lower than pulsatile flow. In addition, the magnitude of critical buckling pressure in static pressure simulation is higher than the steady-state and pulsatile flow since there is not any lumen flow in static pressure simulation. The current results broaden our knowledge of the aneurysmal arteries stability under steady state and pulsatile flow to predict the result of surgical intervention.
5. Conclusions
Our fully coupled FSI analysis illustrated that aneurysmal artery deflects under lumen pressure that exceeds a critical buckling pressure and increases nonlinearly with lumen pressure. The critical mean buckling pressure is 15–40% smaller at pulsatile flow than steady-state flow, while their deflection versus lumen pressure curves nearly overlap each other at both stretch ratios. Increasing axial tension will increases the critical buckling pressure under static pressure, steady-state flow, and pulsatile flow. Buckling increases the peak wall stress by 118% in the aneurysm. Buckling results in an increment in lumen shear stress at the inner side of the wall, due to an enlargement in the aneurysm recirculation zone. It also increases the normal stresses at the outer side of the wall.
Acknowledgments
The authors gratefully acknowledge the AUT High performance Computing Research Center for providing access to their computational facilities and Dr. Madjid Soltani (K.N. Toosi University of Technology) for his help. We also thank the partial support of HL095852 from NIH (Han).
Funding: This work was partially supported by the Foundation for the National Institutes of Health [grant number HL095852].
Footnotes
Disclosure statement: No potential conflict of interest was reported by the authors.
References
- Arends J, Perkins KD, Zhang J, Polyakov I, Lee E. A new technique for the surgical creation of aneurysms in an in vivo tortuous vessel model to test neurovascular devices. J Invest Surg. 2008;21(1):39–45. doi: 10.1080/08941930701834189. [DOI] [PubMed] [Google Scholar]
- Bathe K. Adina theory and modeling guide. III. ADINA CFD & FSI. ADINA R&D; Watertown (MA): 2013. [Google Scholar]
- Biasetti J, Hussain F, Gasser TC. Blood flow and coherent vortices in the normal and aneurysmatic aortas: a fluid dynamical approach to intra-luminal thrombus formation. J Roy Soc Interface. 2011;8:1449–1461. doi: 10.1098/rsif.2011.0041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bluestein D, Dumont K, De Beule M, Ricotta J, Impellizzeri P, Verhegghe B, Verdonck P. Intraluminal thrombus and risk of rupture in patient specific abdominal aortic aneurysm – fsi modelling. Comput Methods Biomech Biomed Engin. 2009;12(1):73–81. doi: 10.1080/10255840903077170. [DOI] [PubMed] [Google Scholar]
- Chandra S, Raut SS, Jana A, Biederman RW, Doyle M, Muluk SC, Finol EA. Fluid-structure interaction modeling of abdominal aortic aneurysms: the impact of patient-specific inflow conditions and fluid/solid coupling. J Biomech Eng. 2013;135(8):0810011–08100114. doi: 10.1115/1.4024275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chervu A, Clagett GP, Valentine RJ, Myers SI, Rossi PJ. Role of physical examination in detection of abdominal aortic aneurysms. Surgery. 1995;117(4):454–457. doi: 10.1016/s0039-6060(05)80067-4. http://www.sciencedirect.com/science/article/pii/S0039606005800674. [DOI] [PubMed] [Google Scholar]
- Chesnutt JKW, Han HC. Tortuosity triggers platelet activation and thrombus formation in microvessels. J Biomech Eng. 2011;133(12):121004–121004-11. doi: 10.1115/1.4005478. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3489919/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datir P, Lee AY, Lamm SD, Han HC. Effects of geometric variations on the buckling of arteries. Int J Appl Mech. 2011;3(2):385–406. doi: 10.1142/S1758825111001044. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3266375/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demolis PD, Asmar RG, Levy BI, Safar ME. Non-invasive evaluation of the conduit function and the buffering function of large arteries in man. Clin Physiol. 1991;11(6):553–564. doi: 10.1111/j.1475-097x.1991.tb00675.x. http://dx.doi.org/10.1111/j.1475-097X.1991.tb00675.x. [DOI] [PubMed] [Google Scholar]
- Elefteriades JA. Thoracic aortic aneurysm: Reading the enemy's playbook. Yale J Biol Med. 2008;81(4):175–186. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2605304/ [PMC free article] [PubMed] [Google Scholar]
- Fatemifar F, Han HC. Effect of axial stretch on lumen collapse of arteries. J Biomech Eng. 2016;138:12124503–124503-6. doi: 10.1115/1.4034785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fillinger MF, Marra SP, Raghavan ML, Kennedy FE. Prediction of rupture risk in abdominal aortic aneurysm during observation: wall stress versus diameter. J Vasc Surg. 2003;37(4):724–32. doi: 10.1067/mva.2003.213. [DOI] [PubMed] [Google Scholar]
- Fillinger MF, Racusin J, Baker RK, Cronenwett JL, Teutelink A, Schermerhorn ML, Zwolak RM, Powell RJ, Walsh DB, Rzucidlo EM. Anatomic characteristics of ruptured abdominal aortic aneurysm on conventional ct scans: implications for rupture risk. J Vasc Surg. 2004;39(6):1243–1252. doi: 10.1016/j.jvs.2004.02.025. [DOI] [PubMed] [Google Scholar]
- Finol EA, Keyhani K, Amon CH. The effect of asymmetry in abdominal aortic aneurysms under physiologically realistic pulsatile flow conditions. J Biomech Eng. 2003;125(2):207–217. doi: 10.1115/1.1543991. [DOI] [PubMed] [Google Scholar]
- Georgakarakos E, Ioannou CV, Kamarianakis Y, Papaharilaou Y, Kostas T, Manousaki E, Katsamouris AN. The role of geometric parameters in the prediction of abdominal aortic aneurysm wall stress. Eur J Vasc Endovasc Surg. 2010;39(1):42–48. doi: 10.1016/j.ejvs.2009.09.026. [DOI] [PubMed] [Google Scholar]
- Han HC. A biomechanical model of artery buckling. J Biomech. 2007;40(16):3672–3678. doi: 10.1016/j.jbiomech.2007.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han HC. Blood vessel buckling within soft surrounding tissue generates tortuosity. J Biomech. 2009a;42(16):2797–2801. doi: 10.1016/j.jbiomech.2009.07.033. [DOI] [PubMed] [Google Scholar]
- Han HC. The theoretical foundation for artery buckling under internal pressure. J Biomech Eng. 2009b;131(12):124501. doi: 10.1115/1.4000080. [DOI] [PubMed] [Google Scholar]
- Han HC. Twisted blood vessels: Symptoms, etiology and biomechanical mechanisms. J Vascular Res. 2012;49(3):185–197. doi: 10.1159/000335123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han HC, Chesnutt JKW, Garcia JR, Liu Q, Wen Q. Artery buckling: new phenotypes, models, and applications. Ann Biomed Eng. 2013;41(7):1399–1410. doi: 10.1007/s10439-012-0707-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han HC, Ku DN, Vito RP. Arterial wall adaptation under elevated longitudinal stretch in organ culture. Ann Biomed Eng. 2003;31(4):403–411. doi: 10.1114/1.1561291. [DOI] [PubMed] [Google Scholar]
- Hatakeyama T, Shigematsu H, Muto T. Risk factors for rupture of abdominal aortic aneurysm based on three-dimensional study. J Vascular Surg. 2001;33(3):453–461. doi: 10.1067/mva.2001.111731. [DOI] [PubMed] [Google Scholar]
- Hirata K, Yaginuma T, O'Rourke MF, Kawakami M. Age-related changes in carotid artery flow and pressure pulses: possible implications for cerebral microvascular disease. Stroke J Cerebral Circulation. 2006;37(10):2552–2556. doi: 10.1161/01.STR.0000242289.20381.f4. [DOI] [PubMed] [Google Scholar]
- Holdsworth D, Norley C, Frayne R, Steinman D, Rutt B. Characterization of common carotid artery blood-flow waveforms in normal human subjects. Physiol Meas. 1999;20:219–240. doi: 10.1088/0967-3334/20/3/301. [DOI] [PubMed] [Google Scholar]
- Huo Y, Wischgoll T, Kassab GS. Flow patterns in three-dimensional porcine epicardial coronary arterial tree. Amer J Physiol Heart Circ Physiol. 2007;293:H2959–H2970. doi: 10.1152/ajpheart.00586.2007. [DOI] [PubMed] [Google Scholar]
- Johnson PT, Chen JK, Loeys BL, Dietz HC, Fishman EK. Loeys-dietz syndrome: Mdct angiography findings. Amer J Roentgenology. 2007;189(1):W29–W35. doi: 10.2214/AJR.06.1316. [DOI] [PubMed] [Google Scholar]
- Khalafvand SS, Han HC. Stability of carotid artery under steady-state and pulsatile blood flow: A fluid-structure interaction study. J Biomech Eng. 2015;137(6):061007–061007. doi: 10.1115/1.4030011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee AY, Han B, Lamm SD, Fierro CA, Han HC. Effects of elastin degradation and surrounding matrix support on artery stability. Am J Physiol Heart Circ Physiol. 2012;302(4):H873–H884. doi: 10.1152/ajpheart.00463.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee AY, Sanyal A, Xiao Y, Shadfan R, Han HC. Mechanical instability of normal and aneurysmal arteries. J Biomech. 2014;47(16):3868–3875. doi: 10.1016/j.jbiomech.2014.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung JH, Wright AR, Cheshire N, Crane J, Thom SA, Hughes AD, Xu Y. Fluid structure interaction of patient specific abdominal aortic aneurysms: a comparison with solid stress models. Biomed Eng Online. 2006;5:33. doi: 10.1186/1475-925X-5-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinstreuer LiZ C. Effects of blood flow and vessel geometry on wall stress and rupture risk of abdominal aortic aneurysms. J Med Eng Technol. 2006;30(5):283–297. doi: 10.1080/03091900500217406. [DOI] [PubMed] [Google Scholar]
- Liu Q, Han HC. Mechanical buckling of artery under pulsatile pressure. J Biomech. 2012;45(7):1192–1198. doi: 10.1016/j.jbiomech.2012.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Q, Wen Q, Mottahedi M, Han HC. Artery buckling analysis using a four-fiber wall model. J Biomech. 2014;47(11):2790–2796. doi: 10.1016/j.jbiomech.2014.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marra SP, Kennedy FE, Kinkaid JN, Fillinger MF. Elastic and rupture properties of porcine aortic tissue measured using inflation testing. Cardiovasc Eng. 2006;6(4):123–131. doi: 10.1007/s10558-006-9021-5. [DOI] [PubMed] [Google Scholar]
- Michineau S, Dai J, Gervais M, Zidi M, Clowes AW, Becquemin JP, Michel JB, Allaire E. Aortic length changes during abdominal aortic aneurysm formation, expansion and stabilisation in a rat model. Eur J Vasc Endovasc Surg. 2010;40(4):468–474. doi: 10.1016/j.ejvs.2010.05.001. [DOI] [PubMed] [Google Scholar]
- Milnor WR. Hemodynamics. Baltimore (MD): Williams and Wilkins; 1989. [Google Scholar]
- Mukherjee D, Mayberry JC, Inahara T, Greig JD. The relationship of the abdominal aortic aneurysm to the tortuous internal carotid artery: is there one? Arch Surg. 1989;124(8):955–956. doi: 10.1001/archsurg.1989.01410080091014. [DOI] [PubMed] [Google Scholar]
- Perktold K, Resch M, Peter RO. Three-dimensional numerical analysis of pulsatile flow and wall shear stress in the carotid artery bifurcation. J Biomech. 1991;24(6):409–420. doi: 10.1016/0021-9290(91)90029-m. [DOI] [PubMed] [Google Scholar]
- Rissland P, Alemu Y, Einav S, Ricotta J, Bluestein D. Abdominal aortic aneurysm risk of rupture: patient-specific fsi simulations using anisotropic model. J Biomech Eng. 2008;131(3):031001–031001. doi: 10.1115/1.3005200. [DOI] [PubMed] [Google Scholar]
- Rodríguez JF, Ruiz C, Doblaré M, Holzapfel GA. Mechanical stresses in abdominal aortic aneurysms: influence of diameter, asymmetry, and material anisotropy. J Biomech Eng. 2008;130(2):021023–021023. doi: 10.1115/1.2898830. [DOI] [PubMed] [Google Scholar]
- Scotti CM, Finol EA. Compliant biomechanics of abdominal aortic aneurysms: A fluid-structure interaction study. Comput Struct. 2007;85:11–14. 1097–1113. [Google Scholar]
- Scotti CM, Jimenez J, Muluk SC, Finol EA. Wall stress and flow dynamics in abdominal aortic aneurysms: finite element analysis vs. fluid-structure interaction. Comput Methods Biomech Biomed Engin. 2008;11(3):301–322. doi: 10.1080/10255840701827412. [DOI] [PubMed] [Google Scholar]
- Scotti CM, Shkolnik AD, Muluk SC, Finol EA. Fluid-structure interaction in abdominal aortic aneurysms: effects of asymmetry and wall thickness. Biomed Eng OnLine. 2005;4:64. doi: 10.1186/1475-925X-4-64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stenbaek J, Kalin B, Swedenborg J. Growth of thrombus may be a better predictor of rupture than diameter in patients with abdominal aortic aneurysms. Eur J Vasc Endovasc Surg. 2000;20(5):466–469. doi: 10.1053/ejvs.2000.1217. [DOI] [PubMed] [Google Scholar]
- Suh GY, Les AS, Tenforde AS, Shadden SC, Spilker RL, Yeung JJ, Cheng CP, Herfkens RJ, Dalman RL, Taylor CA. Quantification of particle residence time in abdominal aortic aneurysms using magnetic resonance imaging and computational fluid dynamics. Ann Biomed Eng. 2011;39(2):864–883. doi: 10.1007/s10439-010-0202-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan FPP, Torii R, Borghi A, Mohiaddin RH, Wood NB, Xu XY. Fluid-structure interaction analysis of wall stress and flow patterns in a thoracic aortic aneurysm. Int J Appl Mech. 2009;01(01):179–199. [Google Scholar]
- Upchurch JGR, Schaub TA. Abdominal aortic aneurysm. Am Fam Physician. 2006;73(7):1198–1204. [PubMed] [Google Scholar]
- Vorp DA. Biomechanics of abdominal aortic aneurysm. J Biomech. 2007;40(9):1887–1902. doi: 10.1016/j.jbiomech.2006.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang DHJ, Makaroun MS, Webster MW, Vorp DA. Effect of intraluminal thrombus on wall stress in patient-specific models of abdominal aortic aneurysm. J Vasc Surg. 2002;36(3):598–604. doi: 10.1067/mva.2002.126087. [DOI] [PubMed] [Google Scholar]
- Xenos M, Rambhia SH, Alemu Y, Einav S, Labropoulos N, Tassiopoulos A, Ricotta JJ, Bluestein D. Patient-based abdominal aortic aneurysm rupture risk prediction with fluid structure interaction modeling. Ann Biomed Eng. 2010;38(11):3323–3337. doi: 10.1007/s10439-010-0094-3. [DOI] [PubMed] [Google Scholar]


