Antennal scales improve signal detection efficiency in moths

Qike Wang; Yidan Shang; Douglas S Hilton; Kiao Inthavong; Dong Zhang; Mark A Elgar

doi:10.1098/rspb.2017.2832

. 2018 Mar 14;285(1874):20172832. doi: 10.1098/rspb.2017.2832

Antennal scales improve signal detection efficiency in moths

Qike Wang ^1,^✉, Yidan Shang ², Douglas S Hilton ³, Kiao Inthavong ², Dong Zhang ⁴, Mark A Elgar ¹

PMCID: PMC5879631 PMID: 29540519

Abstract

The elaborate bipectinate antennae of male moths are thought to increase their sensitivity to female sex pheromones, and so should be favoured by selection. Yet simple filamentous antennae are the most common structure among moths. The stereotypic arrangements of scales on the surface of antennae may resolve this paradox. We use computational fluid dynamics techniques to model how scales on the filamentous antennae of moths affect the passage of different particles in the airflow across the flagellum in both small and large moths. We found that the scales provide an effective solution to improve the efficacy of filamentous antennae, by increasing the concentration of nanoparticles, which resemble pheromones, around the antennae. The smaller moths have a greater increase in antennal efficiency than larger moths. The scales also divert microparticles, which resemble dust, away from the antennal surface, thereby reducing contamination. The positive correlations between antennal scale angles and sensilla number across Heliozelidae moths are consistent with the predictions of our model.

Keywords: antennal scales, computational fluid dynamics, chemical communication, pheromone, signal receiver

1. Introduction

Insects live in a sensory world full of odours, which are cues revealing the location of resources or signals that communicate specific information to particular receivers [1,2]. Effective communication requires the intended receivers to perceive signals precisely. Unlike visual or acoustic modalities, olfactory sensory systems additionally require physical contact between the odorant and specific sensory receptors [3]. It is widely understood that the shape and size of the antennae play an important role in perception efficiency [1,4,5]: indeed, Darwin predicted that sexual selection will favour elaborate, bipectinate antennae in male moths, as they ensure more rapid detection of female sex pheromones [6,7]. The strength of selection will depend on several factors, including female mating frequency, population density, the nature of the sex pheromone and dispersal distances [8,9]. Bipectinate antennae, with their numerous branches, provide a larger surface area to support more sensilla, thereby increasing the probability of interactions between sensilla and female sex-pheromone molecules [10]. Given the importance of rapidly detecting pheromones, it is surprising that the majority of moth species have simple, filamentous antennae [11,12], which raises the question why are bipectinate antennae not more prevalent among moths?

The paradox may be explained by the costs of elaborate antennae, in terms of neural tissue [13,14] and of aerodynamic drag during flight [15,16]. Phylogenetic comparative analyses support this view: species with elaborate antennae are typically larger than those with simple antennae, but there was no significant association between population density and the type of antenna, after controlling for body size and phylogeny [8]. Filamentous antennae support fewer sensilla than elaborate antennae of the same length [17], but there is no evidence that the strength of sexual selection in moth species with simple antennae is weaker than for those with elaborate antennae. The solution to improving the perception of sex pheromones may lie in an ubiquitous morphological feature of moth antennae.

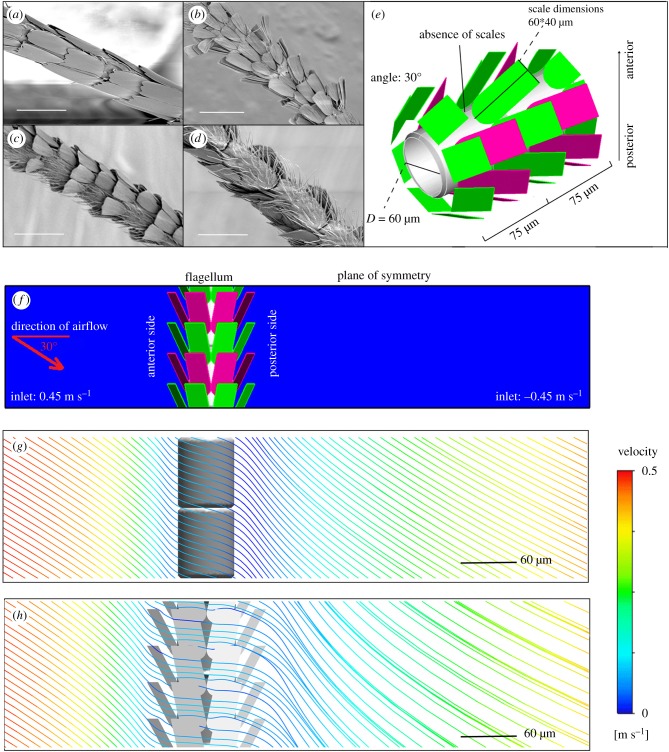
Across a wide range of moth families, filamentous antennae are commonly covered in numerous scales, which are typically arranged in one of four categories (figure 1a–d): (i) parallel to or covering the flagellum (Par); (ii) forming an angle to the flagellum with two complete rings per segment (Com); (iii) intermittently present in every two rings (Int) or (iv) missing a row on both rings (Mis). The function of scales on the body and wings of moths have been documented [18,19], but their function on the antennae has received little attention. They may provide some limited protection to the sensilla because many of them are exposed in areas with missing scales (figure 1a–d; electronic supplementary material, figure S1c,f,g). Nevertheless, the scales increase the diameter of the antennae and must, therefore, increase aerodynamic drag, so there is likely to be a benefit that offsets this cost. One possibility is that the scales disturb the airflow around the antennae, thereby increasing the likelihood of exposing the receptors to odour molecules.

Figure 1. — Construction of antennal models and boundary conditions. (*a–d*) The different scale arrangements of Heliozelidae moth antennae: (a) parallel to flagellum (Par), (b) complete rings (*Com*), (c) missing scales intermittently in every two rings (*Int*) or (d) missing a row of scales (*Mis*), scale bar 50 µm. (e) Dimensions of the antennal model of *Int* antenna with the diameter of 60 µm, green and red indicates different rings of scales. (f) Computer model boundary conditions. (g) Airflow speed and flow-field pattern of antenna with *Par* scale arrangement. (h) Airflow speed and flow-field pattern of antenna with *Com* scale arrangement: the flow field is disturbed and slowed down by the scales.

Here we use computational fluid dynamics (CFD) to simulate the airflow field around antennae of different sizes and with different scale arrangements. CFD can provide insights into the flow pattern around the antennae of insects that are impossible to study using traditional experimental methods. We investigate the efficacy of antennae with different scale arrangements, by calculating nano- and microparticle concentrations, based on particle trajectories using Lagrangian particle trajectories, to reveal the distribution of pheromone molecules and dust in the space around the antennae. It is widely understood that pheromone perception is determined by the frequency of interactions between the odorant molecules and receptors, which are housed in the antennal sensilla [20]. Thus, species that typically detect low concentrations of pheromone are expected to have larger numbers of sensilla than species typically detecting higher concentrations [1,21,22]. Accordingly, a greater investment in the number of receptors and sensilla, perhaps in response to lower pheromone plumes, will be accompanied by other aerodynamic mechanisms that improve pheromone detection. We use data from a family of day flying moths, Heliozelidae, to ask whether the arrangement of scales on the antennae is associated with sensilla number, predicting that species with a greater investment in sensilla number will have scale arrangements that maximize antennal efficiency, as reflected in the CFD simulations.

2. Methods

(a). Model construction and parameter derivation

(i). Antenna computational model

The species-specific arrangement of scales on moth antennae typically falls into one of four categories (figure 1a–d): parallel to the flagellum (Par); complete rings (Com); missing scales intermittently (Int) and missing a row of scales (Mis). In some species, the arrangement can change from the proximal to distal end of the antennae, but the scale arrangement of each species is determined from approximately mid-point of the total length of the antennae. The Par arrangement is defined as the scales forming an angle less than 3° to the antennae. The dimensions of simple antennae were taken from Heliozelidae moths and previously published species for three-dimensional model construction and comparative analysis. The data from published species are listed in electronic supplementary material, table S1, and the list of Heliozelidae species and their scale arrangements are given in electronic supplementary material, table S2. Where these metrics were not provided, we measured the flagellum diameter in Nano Measurer 1.2 using the given scale bars, and the results were rounded up.

The models of moth antenna were reconstructed using ICEM 17.0 (Ansys, Inc.) based on SEM images (electronic supplementary material), where the four-scale arrangements and dimensions were obtained from specimens of Heliozelidae moths and published works (electronic supplementary material, table S1 and S2). SEM images show the various arrangements of scales on the surface of the flagellum (figure 1a–d). The flagellum, or surface of the antennae, was represented by a smooth cylinder, with a diameter of 60 µm for smaller moths and 120 µm for larger moths, which covers the range of sizes of most moths (electronic supplementary material, table S1). The diameter of the flagellum is extremely small in comparison with its length and so by focusing on the region around the scales, the flagellum curvature can be ignored and treated as straight and considered as infinite in length.

We investigated the effects of four-scale arrangements (figure 1a–d): parallel (Par), complete (Com), intermittent (Int) and missing a row (Mis). Smooth cylinders were used to represent Par antennae because the scales that closely attach to the flagella have very low Reynolds number, and so Par antennae also represent antennae without scales. We simplified the surface ridges and the distal serrated edges of the scales because they have insignificant effects on the laminar airflow. For the 60 µm antennae, each scale comprised a semicircle with a 30 µm chord attached to the flagellum, and a rectangle with a length of 45 µm and width of 30 µm, resulting in scales with a total length of 60 µm. The angle between the flagellum and the scale was 30°. A complete ring of scales (arrangement Com) comprised eight scales evenly distributed around the circumference of the flagellum (green scales in figure 1e), while the rings with missing scales are comprised of six scales (red scales in figure 1e). Each segment of arrangement Int includes a complete ring and a ring with missing scales, and both rings on the segments of arrangement Mis have missing scales. The gap between consecutive circumferences containing the scales was 37.5 µm, thus every 75 µm represented one period along the axial direction. The parameters were increased proportionally for the larger antenna of 120 µm. The wind speed was set at 0.45 m s⁻¹, and the air temperature at 25°C. The antenna was aligned to an oncoming flow at an angle of 30° based on our observations (figure 1f).

The micrometre-sized structure and the low wind speed resulted in the low Reynolds number (≈5) based on the antenna cylindrical diameter of 60 µm. The Navier–Stokes equations describe fluid motion under a continuum mechanics approach. Since the antennae exist in the order of micrometres, the Knudsen number (K_n) is used to determine whether a continuum approach or a molecular approach should be applied, based on the ratio of the mean free path of the gas (λ) to a characteristic length scale of the flow (L),

In this case, L is the antennae diameter. Previous studies [23,24] showed that the no-slip boundary condition fails for 10⁻³ ≤ K_n ≤ 10⁻¹, however, others [25] state the transition regime can be given between 10⁻¹ ≤ K_n ≤ 10¹ and flows are classified as free molecular flows when the Knudsen numbers are higher than 10. The K_n number in our cases is in the range of 5.7 × 10⁻⁴ to 2.3 × 10⁻³, which suggests that a continuum approach can be applied for both small and large moth antennae. We should, however, expect some uncertainty related to some slip flow occurring at the wall boundaries.

(ii). Computational model and mesh generation

We modelled two periods of the flagellum scales on the antenna and applied periodic boundary conditions at the flagellum to achieve an infinitely long assumption along the axial direction. Owing to the symmetric geometry, a ‘symmetry plane’ was generated to split the antenna into two parts. The computational domain was 750 µm length × 150 µm width × 300 µm height with one symmetry plane boundary condition. To represent a far-field condition, the top boundary of the ambient environment that enclosed the upper part of the antenna was set to be zero-shear stress wall. The wind speed was set at 0.45 m s⁻¹ towards the opposite direction at the front and back sides of the box according to the previous documentations [26]. Moths are capable of adjusting the angle of their antennae to suit different circumstances [27]. Thus, antennae may constantly encounter airflow from all directions during flight and resting position. In this simulation, the antenna was aligned to an oncoming flow at an angle of 30° to represent one of the most common scenarios during the flight of moths. A tetrahedral mesh was created with refinements around the antenna, and especially near the scales. We conducted a mesh independence test by measuring the length of recirculation region at the downstream side of large moth antennae (Mis) and chose a sufficient mesh with 2.6 million cells for simulation.

The airflow was treated as a steady laminar flow. Pheromone agglomerates were modelled as dispersed (individual) particles moving through the pre-calculated steady-state flow field. The particle trajectories were determined from Newton's second law, using a force balance equation of the particle.

(iii). Particle selection and simulation

We investigated the behaviour of two types of particles that moths may encounter in the air: sex pheromones (nanoparticles) and common dust (microparticles). We used cis-9-octadecen-1-ol (D = 3.85 × 10⁻⁶ m² s⁻¹) [28,29] to represent the moth sex pheromones, because it belongs to one of the most commonly identified groups (higher enols) of sex pheromones in moths [8], and the diffusion coefficient of this pheromone is available [28]. The diffusion coefficient of ‘higher enols’ groups of pheromones is dominated by the hydroxyl group rather than the length of the carbon backbone or the position of the double bond, and so enols identified in other moths should have a similar diffusion coefficient. We also used particles with a diameter of 1 µm to represent atmospheric dust encountered by the antennae. Particles with a larger diameter were not studied because their Brownian motion was sufficiently low, and unlikely to enter the space between or under scales.

The airflow was treated as a steady laminar flow angled at 30° to the antennae, based on our own observation of antennal positioning in moth flight. Pheromone agglomerates were modelled as dispersed particles moving along the steady-state flow field. The particle trajectories were determined from Newton's Second Law of a force balance equation on the particle. The particle size was estimated by the pheromone diffusivity,

D is the pheromone diffusivity in the air, k is the Boltzman constant and T is the environmental temperature of 25°C. We take cis-9-octadecen-1-ol (D = 3.85 × 10⁻⁶ m² s⁻¹) to represent the pheromones. Thus, the particle size d was 1.13 nm.

Airflow obeyed continuity and momentum equations:

and

where ρ is the air density, i and j denote spatial components, u is air velocity and ν is kinematic viscosity of the air. The equations for airflow and the pressure–velocity coupling were solved with the QUICK scheme and SIMPLE method, respectively, using CFD software Ansys Fluent 17.0 (Ansys Inc.).

The nanoparticles were modelled as a dispersed phase using the one-way coupled Lagrangian approach, which independently simulates the particle motion in the pre-calculated airflow field. The movement of each individual particle was governed by the drag force and Brownian motion:

where the superscript ‘p’ refers to the particle phase. The drag force f_D followed Stokes drag law

where μ is the air viscosity and C_c the Cunningham correlation factor,

λ is the mean free path of air molecules assumed to be 65 nm at room temperature.

(iv). Relative antennal detection efficiency

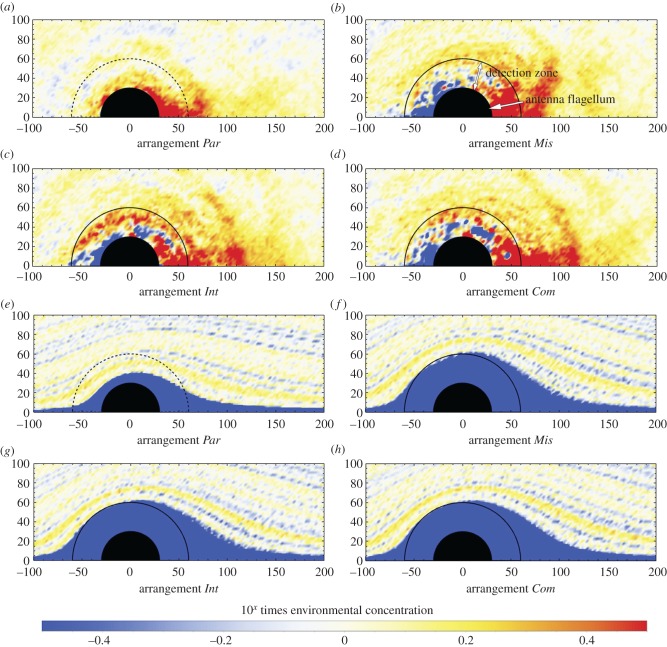
We compared the detection efficiency of different antennae sizes and scale arrangements, by converting particle trajectories to pheromone concentrations using the particle source in cell (PSI-C) method [30,31]. The model assumed that particles interact with receptors located on the sensilla (and hence are perceived by the moth) if they occur in the ‘detection’ zone, defined as the space between the flagellum and the tips of the scales. Inspection of SEM micrographs indicates that most of the antennal sensilla, excluding mechanoreceptor sensilla, are located within this space and are largely covered by the scales (figure 1a–d; electronic supplementary material, figure S1a–d). We plot the spatial distribution of the relative concentration of different particles in small (figure 2a–h) and large (electronic supplementary material, figure S2a–h) antennae, and then integrate the relative concentration of particles against angles in the detection zone to calculate the relative number of particles that can be perceived by the moth. These results were further compared with the antennal detection efficiency of Par arrangements (which also represents antennae without scales) to calculate the relative detection efficiency of each arrangement on different sized antennae (table 1).

Figure 2. — The distribution of nano- and microparticle concentrations around the 60 µm diameter antennae with different scale arrangements. The antennal scales increase the concentration of nanoparticles (*a–d*) and reduce the concentration of microparticles in the perception zone (marked by black semicircle) (*e–h*).

Table 1.

Relative antennal detection efficiency of nano- and microparticles of the different antennae. Relative pheromone detection efficiency is consistently greater for smaller than larger antennae with the same scale arrangement. Similarly, relative detection efficiency to dust is consistently lower for smaller than larger antennae with the same scale arrangement. Relative detection efficiency is standardized against the Par scale arrangement (equivalent to no scales) of the same antennal size.

		relative efficiency to Par (%)
	antennae size	Mis	Int	Com
nanoparticles (pheromone)	small	124.7	138.7	147.5
nanoparticles (pheromone)	large	115.0	132.5	118.3
microparticles (dust)	small	3.6	1.3	1.2
microparticles (dust)	large	7.8	6.6	7.2

Open in a new tab

The pheromone concentration in each cell can be estimated by calculating the sum of residence time:

where C_j and V_j is the local pheromone concentration and volume in the jth cell, M is the particle mass and Inline graphic is the residence time of the ith particle trajectory in the jth cell. To balance the accuracy and concentration stability, the computational domain was divided into 300 parts along the x-axis and 120 parts along the z-axis. In this study, as we focused on the pheromone concentration on the plane perpendicular with the axial direction of the antennae, the space along the y-axis remained the same. A relative concentration RC_j was introduced to emphasize the inhomogeneity of pheromone in the space, based on the ratio of local and far-field concentrations.

To select particles that can be perceived by sensilla in this model, we defined the detection zone as the space between the surface of the flagellum and the tips of the scales. Our observation shows that except for the mechanical sensilla, most of the antennal sensilla are located within this space and protected by the scales (figure 1a–d). We defined the size of the detection zone of antennae with parallel scales (Pa) as that of the other scale arrangements of the same antennal size, thereby allowing standardized comparisons between all-scale arrangements.

We assume that the pores on the surface of sensilla that lead to the receptors are linearly distributed along the sensilla, from the root to the tip. Then, the density of pores can be estimated by

where A is a constant; r is the distance between a point in the detection zone and the centre axis of the flagellum and r₀ is the radius of the flagellum. When integrated through the whole detection zone, the total detection efficiency is

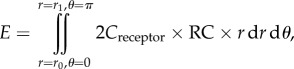where r₁ is the upper limit of the detection zone. The relative signal concentration is defined by the ratio of particle concentration at any point and the environmental particle concentration at airflow speed of 0 m s⁻¹. When normalized by the detection efficiency in a static environment, the relative total detection efficiency can be defined as:

In addition, to estimate the detection efficiency around the sensilla, the angular relative detection efficiency at angle of θ (θ = 0 at the front and θ = π at the rear of the sensilla) was defined as:

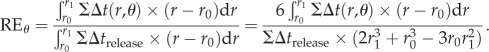We integrated the relative signal intensity in the detection zone in large and small antennae with all four-scale arrangements to calculate the relative total detection efficiency.

(b). Comparative study of antennal morphology

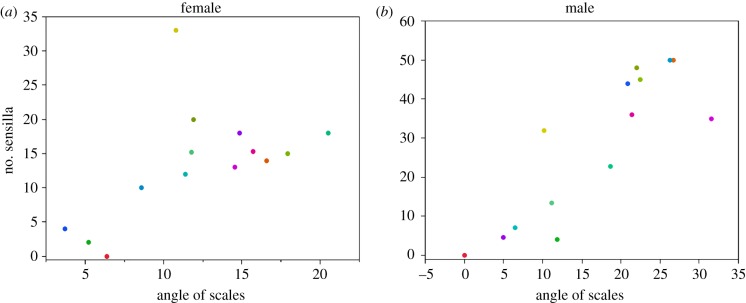
We evaluated some predictions of the model against patterns of antennal morphology across species of Heliozelidae moths (electronic supplementary material, table S2), by obtaining data from moths collected from various locations in Australia. The samples were air-dried, gold-coated and observed using a Philips XL30 electron microscope. The angle between the scales and the flagellum were measured in Photoshop CS5 from SEM images taken from the middle sections of the antennae, from where the number of trichoid and basiconic sensilla on each segment were also recorded. We used a stepwise multiple regression model to test the impact of the angle of scales, the area of each segment and the number of segments on the sensilla number, using JMP 10 (SAS). To reduce the leverage of genera comprising multiple species, we used the average value for each genera for this test. We report correlations between sensilla number and the angle of the scales only: the other variables had non-significant (p > 0.05) effects. A phylogeny of this clade of moths is not currently available, so phylogenetic regression analysis is not possible. However, it is not our intention to explore evolutionary relationships, and the distribution of species (figure 4) indicates that any patterns are unlikely to be leveraged by clusters of closely related genera.

Figure 4. — The correlation between the number of sensilla and the angle of scales in male and female moths. The number of sensilla is positively correlated with the angle of scales in female (a), and male (b) moths among different genera of Heliozelidae. Each point represents one single genus. Female: F_1,12 = 5.04, r² = 0.30, p = 0.044, male: F_1,12 = 32.64, r² = 0.73, p < 0.0001.

3. Results

(a). Flow-field pattern

The airflow streamlines demonstrate the airflow conditions around the antennae. The scales have a profound impact on the airflow speed and direction around the antennae (figure 1g,h). For antennae with scales, the flow velocity declines rapidly upstream from the antennae and then gradually increases downstream (figure 1h). By contrast, the flow velocity for antennae without scales (equivalent to the Par arrangement) declines upstream and increases downstream rapidly (figure 1g).

The airflow streamlines are distorted by the scales in the direction perpendicular to the surface of the antenna, and then resumes its direction downstream. The flow streamlines between the scales show that airflow can enter the space between each of the rings of scales (figure 1h), indicating that odour molecules can enter the space between the scales and antenna. The disturbance caused by the scales creates bundles of airflow downstream of the antenna, which is absent in antennae with the Par arrangement (figure 1g).

(b). Particle spatial distribution

Our simulations reveal two functions of antennal scales: increasing pheromone concentration around the sensilla and minimizing the concentration and thus contamination by larger particles of dust. The particle concentration in these analyses is normalized by the environmental concentration. For both large and small antennae, there is a large area of high nanoparticle (pheromones) concentration at the downstream side of the flagellum, where flow separation occurs, and around the upper half of the detection zone (figure 2a–d; electronic supplementary material, figure S2a–d, marked by black semicircles). A low concentration of nanoparticles is found only around the stagnation point (figure 2b–d; electronic supplementary material, figure S2b–d, left-hand side) near the flagellum of antennae with scales. This pattern corresponds to measures of pheromone concentration in the boundary layer near the antennae of sphinx moths Manduca sexta at the stagnation point [32].

The concentration distribution of microparticles (dust) shows a completely different pattern (figure 2e–h; electronic supplementary material, figure S2e–h). The microparticles strictly follow the airflow in all of the scaled antennae, resulting in a microparticle-free zone, which broadly overlaps the detection zone (figure 2f–h; electronic supplementary material, figure S2f–h). In the absence of scales, these particles flow close to the antennal flagellum, where they may contaminate the sensilla (figure 2e).

(c). Relative antennal detection efficiency and function of scales

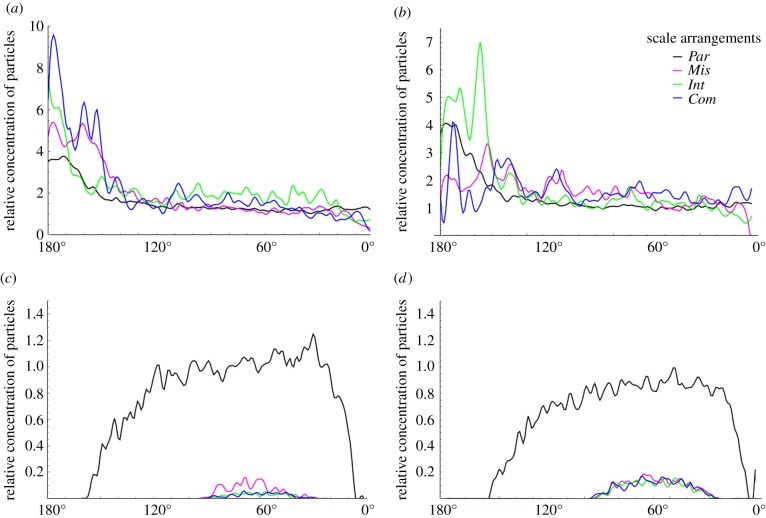
We examined the influence of antennal scale arrangements on the likelihood that receptors on the sensilla detect pheromone molecules, by plotting the relative concentration of nano- and microparticles within the detection zone (antennal detection efficiency) against different angles of the antennae on both small (figure 3a,c) and large (figure 3b,d) antennae from 180° (downstream side) to 0°(upstream side). The Par arrangement (equivalent to antennae without scales) shows the lowest antennal detection efficiency of sex pheromones, irrespective of antennal size. Scales increase the antennal detection efficiency of sex pheromones by 15–48% (table 1), depending on the scale arrangement and antennal size. The antennal detection efficiency of sex pheromones is consistently greater for smaller than larger antennae with the same scale arrangement. This suggests that scales are comparatively more effective for smaller than larger antennae. Remarkably, the presence of scales dramatically reduces the concentration of dust in the detection zone to less than 8% of that for antennae without scales (table 1).

Figure 3. — Relative antennal efficiencies of particles against different directions of antennae with different scale arrangements. In comparison with the antennae with the *Par* scale arrangement, all other antennae increase the concentration of nanoparticles while significantly reducing that of microparticles in most of the directions from 180°(downstream side) to 0°(upstream side). (a) Nanoparticles, 60 µm diameter antenna, (b) nanoparticles, 120 µm diameter antenna, (c) microparticles, 60 µm diameter antenna and (d) microparticles, 120 µm diameter antenna.

(d). Correlation between angle of scales and the number of sensilla

Our model predicts that within a certain range, increasing the angle of the scales increases odorant–receptor interactions. Accordingly, we expect a positive correlation between scale angle and sensilla numbers across different species of moths. This prediction is supported by comparative data of 15 genera (30 species) of Heliozelidae moths: there is a positive correlation between the number of sensilla and the angle of scales in female (figure 4a; F_1,12 = 5.04, r² = 0.30, p = 0.044) and male moths (figure 4b; F_1,12 = 32.64, r² = 0.73, p < 0.0001).

4. Discussion

Antennal scales provide a remarkably simple solution to improving the efficacy of signal reception of moths with filamentous antennae: an improvement that is more substantial in smaller than larger moths. The scales concentrate the signal molecules to the downwind side of the antennae and towards the distal end of the sensilla where there are typically more pores that allow chemicals to enter the sensilla and interact with the receptors [21,33] (electronic supplementary material, figure S1f–h). By creating an area with slow airflow around the antennae, the scales ensure pheromones linger within the detection zone, thereby increasing the efficiency with which they interact with receptors. Furthermore, the scales are also effective at diverting larger particles, such as dust. Particles of this size have less Brownian movement intensity and are thus kept away from the antennae by the airflow. This means that these particles are less likely to encounter the sensilla, thereby reducing any interference with signal reception through contamination of the sensilla. The latter is particularly important for species, like moths, that cannot groom the full length of their antennae.

The patterns of pheromone concentration described by our model reveals how the spatial organization of particular types of sensilla reflects their specialized function [34]. The tallest (not necessarily the longest) sensilla on moth antennae usually support mechanoreceptors (electronic supplementary material, figure S1a,b,d) that sit well above the scales and are largely unaffected by any airflow disturbance. The scales cannot protect these sensilla, which may explain why they are sometimes covered in dust (electronic supplementary material, figure S1e). Moth sex pheromones contact the receptors through the pores on trichoid sensilla [34,35], and the higher concentrations of pheromone molecules at the upper region of the detection zone nicely overlaps with the distribution of these pores (electronic supplementary material, figure S2f–h). By contrast, the shorter basiconic sensilla and coeloconic sensilla detect other airborne signals, such as plant-associated odours, which usually have a higher diffusion coefficient [35]. Interestingly, the higher diffusivity of these molecules allows them to penetrate closer to the antenna, where they may interact with the shorter basiconic and coeloconic sensilla. The latter can also react to amines or water [36], which have the highest diffusivity and whose movement is largely unaffected by the scales. Consistent with our model, coeloconic sensilla are significantly shorter than basiconic and trichoid sensilla and, in some species, are located inside deep depressions on the antennal surface.

Our relatively simple simulation revealed patterns of pheromone capture that are consistent with several general features of antennal morphology among moths, and which affirm the view that these scales form an integral part of pheromone perception. First, the adaptive function of antennal scales is supported by the positive interspecific correlation between sensilla number and scale angle across heliozelid moths: the arrangement of scales is linked with the number of sensilla, presumably enhancing the ability of the moth to detect pheromones. Second, in several species, the angle of scales increases towards the distal end of the antennae where there are typically greater numbers of sensilla (see, e.g. electronic supplementary material, figure S3). Third, the scales are usually only parallel to the surface at the antennal scape and pedicel, where trichoid and basiconic sensilla, typically associated with chemoreception, are absent (electronic supplementary material, figure S3). It is, perhaps, curious that scales are not present on the filamentous antennae of other insects, such as cockroaches and mantises. There may be many explanations, but perhaps other kinds of microstructures of the antennae are involved—for example, the numerous dents on the antennae of bees may modify the flow of pheromone molecules across the antennae.

Our model provides some insights into why elaborate antennae are more commonly associated with larger species of moths [8]. For smaller moths with filamentous antennae, antennal scales improve signal detection by 25–48%. This contrasts with the smaller improvement of between 15 and 32% for larger moths with similar, filamentous antennae. More complex, bipectinate antennae may be favoured in large moths because they offer an additional surface area that can support more sensilla and thus greater capacity to perceive chemical signals [8]. However, increasing antennal surface area by adding branches may not necessarily translate into greater signal perception because the more complex antennae may obstruct the airflow. This suggests an alternative perspective: that the structure of antennae and their diverse appendages may be critical for increasing the efficacy of detecting targeted molecules, rather than simply increasing the number of sensilla.

Supplementary Material

Additonal methods and results

rspb20172832supp1.docx^{(6.4MB, docx)}

Acknowledgements

We thank Liz Milla for her help with collecting specimens.

Data accessibility

This article has no additional data.

Authors' contributions

Q.W. and M.A.E. designed this study and wrote the manuscript, Y.S. and K.I. performed the simulations, D.S.H. provided the specimens for species comparison and manuscript preparation, and D.Z. helped in manuscript preparation.

Competing interests

The authors declare no conflict of interest.

Funding

The research was supported by the Fundamental Research Funds for the Central Universities (JC2015-04 to D.Z.), National Science Foundation of China (31572305 to D.Z.) and the Australian Research Council (DP120100162 to M.A.E.).

References

1.Chapman RF. 1982. Chemoreception: the significance of receptor numbers. Adv. Insect Physiol. 16, 247–356. ( 10.1016/s0065-2806(08)60155-1) [DOI] [Google Scholar]
2.Wyatt TD. 2014. Pheromones and animal behavior: chemical signals and signatures. Cambridge, UK: Cambridge University Press. [Google Scholar]
3.Kohl J, Huoviala P, Jefferis GS. 2015. Pheromone processing in Drosophila. Curr. Opin. Neurobiol. 34, 149–157. ( 10.1016/j.conb.2015.06.009) [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Spaethe J, Brockmann A, Halbig C, Tautz J. 2007. Size determines antennal sensitivity and behavioral threshold to odors in bumblebee workers. Naturwissenschaften 94, 733–739. ( 10.1007/s00114-007-0251-1) [DOI] [PubMed] [Google Scholar]
5.Wcislo WT. 1995. Sensilla numbers and antennal morphology of parasitic and non-parasitic bees (Hymenoptera: Apoidea). Int. J. Insect Morphol. Embryol. 24, 63–81. ( 10.1016/0020-7322(94)E0006-B) [DOI] [Google Scholar]
6.Darwin C. 1871. The descent of man and selection in relation to sex. London, UK: Murray. [Google Scholar]
7.Allen CE, Zwaan BJ, Brakefield PM. 2011. Evolution of sexual dimorphism in the Lepidoptera. Annu. Rev. Entomol. 56, 445–464. ( 10.1146/annurev-ento-120709-144828) [DOI] [PubMed] [Google Scholar]
8.Symonds MRE, Johnson TL, Elgar MA. 2012. Pheromone production, male abundance, body size, and the evolution of elaborate antennae in moths. Ecol. Evol. 2, 227–246. ( 10.1002/ece3.81) [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Johnson TL, Symonds MR, Elgar MA. 2017. Sexual selection on receptor organ traits: younger females attract males with longer antennae. Sci. Nat. 104, 44 ( 10.1007/s00114-017-1466-4) [DOI] [PubMed] [Google Scholar]
10.Greenfield MD. 2002. Signalers and receivers: mechanisms and evolution of arthropod communication. Oxford, UK: Oxford University Press. [Google Scholar]
11.Symonds MR, Elgar MA. 2008. The evolution of pheromone diversity. Trends Ecol. Evol. 23, 220–228. ( 10.1016/j.tree.2007.11.009) [DOI] [PubMed] [Google Scholar]
12.Mankin RW, Mayer MS. 1984. The insect antenna is not a molecular sieve. Experientia 40, 1251–1252. ( 10.1007/bf01946658) [DOI] [Google Scholar]
13.Stockl A, Heinze S, Charalabidis A, el Jundi B, Warrant E, Kelber A. 2016. Differential investment in visual and olfactory brain areas reflects behavioural choices in hawk moths. Sci. Rep. 6, 26041 ( 10.1038/srep26041) [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Niven JE, Laughlin SB. 2008. Energy limitation as a selective pressure on the evolution of sensory systems. J. Exp. Biol. 211, 1792–1804. ( 10.1242/jeb.017574) [DOI] [PubMed] [Google Scholar]
15.Sane SP. 2006. Induced airflow in flying insects I. A theoretical model of the induced flow. J. Exp. Biol. 209, 32–42. ( 10.1242/jeb.01957) [DOI] [PubMed] [Google Scholar]
16.Vogel S. 1983. How much air passes through a silkmoth's antenna? J. Insect. Physiol. 29, 597 601–599 602. ( 10.1016/0022-1910(83)90027-6) [DOI] [Google Scholar]
17.Davis DR, Stonis J. 2007. A revision of the New World plant-mining moths of the family Opostegidae (Lepidoptera: Nepticuloidea). Smithson Contr. Zool. 0, 1–212. ( 10.5479/si.00810282.625) [DOI] [Google Scholar]
18.Müller FA, Kunz C, Gräf S. 2016. Bio-inspired functional surfaces based on laser-induced periodic surface structures. Materials 9, 476 ( 10.3390/ma9060476) [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Barber JR, Kawahara AY. 2013. Hawkmoths produce anti-bat ultrasound. Biol. Lett. 9, 20130161 ( 10.1098/rsbl.2013.0161) [DOI] [PMC free article] [PubMed] [Google Scholar]
20.van Naters WVDG, Carlson JR. 2007. Receptors and neurons for fly odors in Drosophila. Curr. Biol. 17, 606–612. ( 10.1016/j.cub.2007.02.043) [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Greenfield MD. 1981. Moth sex pheromones: an evolutionary perspective. Fla. Entomol 64, 4–17. ( 10.2307/3494597) [DOI] [Google Scholar]
22.Bau J, Justus KA, Loudon C, Carde RT. 2005. Electroantennographic resolution of pulsed pheromone plumes in two species of moths with bipectinate antennae. Chem. Senses 30, 771–780. ( 10.1093/chemse/bji069) [DOI] [PubMed] [Google Scholar]
23.Karniadakis G, Beskok A, Aluru N. 2005. Microflows and nanoflows: fundamentals and simulation New York, NY: Springer-Verlag. [Google Scholar]
24.Gad-el-Hak M. 2001. Flow physics in MEMS. Mécanique Indust. 2, 313–341. ( 10.1016/S1296-2139(01)01112-5) [DOI] [Google Scholar]
25.Teschner T-R, Könözsy L, Jenkins KW. 2016. Progress in particle-based multiscale and hybrid methods for flow applications. Microfluid. Nanofluid. 20, 1–38. ( 10.1007/s10404-016-1729-y) [DOI] [Google Scholar]
26.Marsh D, Kennedy J, Ludlow A. 1978. An analysis of anemotactic zigzagging flight in male moths stimulated by pheromone. Physiol. Entomol. 3, 221–240. ( 10.1111/j.1365-3032.1978.tb00152.x) [DOI] [Google Scholar]
27.Kloppenburg P, Camazine SM, Sun XJ, Randolph P, Hildebrand JG. 1997. Organization of the antennal motor system in the sphinx moth Manduca sexta. Cell Tissue Res. 287, 425–433. ( 10.1007/s004410050767) [DOI] [PubMed] [Google Scholar]
28.Yaws CL, Gabbula C. 2003. Yaws' handbook of thermodynamic and physical properties of chemical compounds. New York, NY: Knovel. [Google Scholar]
29.Pires EV, Mendonca AD, Vanickova L, Serra NSJ, da Silva RDC, dos Santos DC, Campos RD, Sant'Ana AEG, do Nascimento RR. 2016. Identification and field and laboratory tests of the sex pheromone of Cerconota anonella Sepp. (Lepidoptera: Oecophoridae). J. Appl. Entomol. 140, 72–80. ( 10.1111/jen.12228) [DOI] [Google Scholar]
30.Zhang Z, Chen Q. 2007. Comparison of the Eulerian and Lagrangian methods for predicting particle transport in enclosed spaces. ASTM Spec. Tech. Publ. 41, 5236–5248. ( 10.1016/j.atmosenv.2006.05.086) [DOI] [Google Scholar]
31.Li X, Yan Y, Shang Y, Tu J. 2015. An Eulerian–Eulerian model for particulate matter transport in indoor spaces. Build. Environ. 86, 191–202. ( 10.1016/j.buildenv.2015.01.010) [DOI] [Google Scholar]
32.Schneider R, Lanzen J, Moore P. 1998. Boundary-layer effect on chemical signal movement near the antennae of the sphinx moth, Manduca sexta: temporal filters for olfaction. J. Comp. Physiol. A 182, 287–298. ( 10.1007/s003590050179) [DOI] [Google Scholar]
33.Sun X, Wang MQ, Zhang G. 2011. Ultrastructural observations on antennal sensilla of Cnaphalocrocis medinalis (Lepidoptera: Pyralidae). Microsc. Res. Tech. 74, 113–121. ( 10.1002/jemt.20880) [DOI] [PubMed] [Google Scholar]
34.Binyameen M, Anderson P, Ignell R, Seada MA, Hansson BS, Schlyter F. 2012. Spatial organization of antennal olfactory sensory neurons in the fe male: Spodoptera littoralis moth: differences in sensitivity and temporal characteristics. Chem. Senses 37, 613–629. ( 10.1093/chemse/bjs043) [DOI] [PubMed] [Google Scholar]
35.Ghaninia M, Olsson SB, Hansson BS. 2014. Physiological organization and topographic mapping of the antennal olfactory sensory neurons in female hawkmoths, Manduca sexta. Chem. Senses 39, 655–671. ( 10.1093/chemse/bju037) [DOI] [PubMed] [Google Scholar]
36.Yao CA, Ignell R, Carlson JR. 2005. Chemosensory coding by neurons in the coeloconic sensilla of the Drosophila antenna. J. Neurosci. 25, 8359–8367. ( 10.1523/jneurosci.2432-05.2005) [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Additonal methods and results

rspb20172832supp1.docx^{(6.4MB, docx)}

Data Availability Statement

This article has no additional data.

[RSPB20172832C1] 1.Chapman RF. 1982. Chemoreception: the significance of receptor numbers. Adv. Insect Physiol. 16, 247–356. ( 10.1016/s0065-2806(08)60155-1) [DOI] [Google Scholar]

[RSPB20172832C2] 2.Wyatt TD. 2014. Pheromones and animal behavior: chemical signals and signatures. Cambridge, UK: Cambridge University Press. [Google Scholar]

[RSPB20172832C3] 3.Kohl J, Huoviala P, Jefferis GS. 2015. Pheromone processing in Drosophila. Curr. Opin. Neurobiol. 34, 149–157. ( 10.1016/j.conb.2015.06.009) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20172832C4] 4.Spaethe J, Brockmann A, Halbig C, Tautz J. 2007. Size determines antennal sensitivity and behavioral threshold to odors in bumblebee workers. Naturwissenschaften 94, 733–739. ( 10.1007/s00114-007-0251-1) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C5] 5.Wcislo WT. 1995. Sensilla numbers and antennal morphology of parasitic and non-parasitic bees (Hymenoptera: Apoidea). Int. J. Insect Morphol. Embryol. 24, 63–81. ( 10.1016/0020-7322(94)E0006-B) [DOI] [Google Scholar]

[RSPB20172832C6] 6.Darwin C. 1871. The descent of man and selection in relation to sex. London, UK: Murray. [Google Scholar]

[RSPB20172832C7] 7.Allen CE, Zwaan BJ, Brakefield PM. 2011. Evolution of sexual dimorphism in the Lepidoptera. Annu. Rev. Entomol. 56, 445–464. ( 10.1146/annurev-ento-120709-144828) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C8] 8.Symonds MRE, Johnson TL, Elgar MA. 2012. Pheromone production, male abundance, body size, and the evolution of elaborate antennae in moths. Ecol. Evol. 2, 227–246. ( 10.1002/ece3.81) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20172832C9] 9.Johnson TL, Symonds MR, Elgar MA. 2017. Sexual selection on receptor organ traits: younger females attract males with longer antennae. Sci. Nat. 104, 44 ( 10.1007/s00114-017-1466-4) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C10] 10.Greenfield MD. 2002. Signalers and receivers: mechanisms and evolution of arthropod communication. Oxford, UK: Oxford University Press. [Google Scholar]

[RSPB20172832C11] 11.Symonds MR, Elgar MA. 2008. The evolution of pheromone diversity. Trends Ecol. Evol. 23, 220–228. ( 10.1016/j.tree.2007.11.009) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C12] 12.Mankin RW, Mayer MS. 1984. The insect antenna is not a molecular sieve. Experientia 40, 1251–1252. ( 10.1007/bf01946658) [DOI] [Google Scholar]

[RSPB20172832C13] 13.Stockl A, Heinze S, Charalabidis A, el Jundi B, Warrant E, Kelber A. 2016. Differential investment in visual and olfactory brain areas reflects behavioural choices in hawk moths. Sci. Rep. 6, 26041 ( 10.1038/srep26041) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20172832C14] 14.Niven JE, Laughlin SB. 2008. Energy limitation as a selective pressure on the evolution of sensory systems. J. Exp. Biol. 211, 1792–1804. ( 10.1242/jeb.017574) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C15] 15.Sane SP. 2006. Induced airflow in flying insects I. A theoretical model of the induced flow. J. Exp. Biol. 209, 32–42. ( 10.1242/jeb.01957) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C16] 16.Vogel S. 1983. How much air passes through a silkmoth's antenna? J. Insect. Physiol. 29, 597 601–599 602. ( 10.1016/0022-1910(83)90027-6) [DOI] [Google Scholar]

[RSPB20172832C17] 17.Davis DR, Stonis J. 2007. A revision of the New World plant-mining moths of the family Opostegidae (Lepidoptera: Nepticuloidea). Smithson Contr. Zool. 0, 1–212. ( 10.5479/si.00810282.625) [DOI] [Google Scholar]

[RSPB20172832C18] 18.Müller FA, Kunz C, Gräf S. 2016. Bio-inspired functional surfaces based on laser-induced periodic surface structures. Materials 9, 476 ( 10.3390/ma9060476) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20172832C19] 19.Barber JR, Kawahara AY. 2013. Hawkmoths produce anti-bat ultrasound. Biol. Lett. 9, 20130161 ( 10.1098/rsbl.2013.0161) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20172832C20] 20.van Naters WVDG, Carlson JR. 2007. Receptors and neurons for fly odors in Drosophila. Curr. Biol. 17, 606–612. ( 10.1016/j.cub.2007.02.043) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSPB20172832C21] 21.Greenfield MD. 1981. Moth sex pheromones: an evolutionary perspective. Fla. Entomol 64, 4–17. ( 10.2307/3494597) [DOI] [Google Scholar]

[RSPB20172832C22] 22.Bau J, Justus KA, Loudon C, Carde RT. 2005. Electroantennographic resolution of pulsed pheromone plumes in two species of moths with bipectinate antennae. Chem. Senses 30, 771–780. ( 10.1093/chemse/bji069) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C23] 23.Karniadakis G, Beskok A, Aluru N. 2005. Microflows and nanoflows: fundamentals and simulation New York, NY: Springer-Verlag. [Google Scholar]

[RSPB20172832C24] 24.Gad-el-Hak M. 2001. Flow physics in MEMS. Mécanique Indust. 2, 313–341. ( 10.1016/S1296-2139(01)01112-5) [DOI] [Google Scholar]

[RSPB20172832C25] 25.Teschner T-R, Könözsy L, Jenkins KW. 2016. Progress in particle-based multiscale and hybrid methods for flow applications. Microfluid. Nanofluid. 20, 1–38. ( 10.1007/s10404-016-1729-y) [DOI] [Google Scholar]

[RSPB20172832C26] 26.Marsh D, Kennedy J, Ludlow A. 1978. An analysis of anemotactic zigzagging flight in male moths stimulated by pheromone. Physiol. Entomol. 3, 221–240. ( 10.1111/j.1365-3032.1978.tb00152.x) [DOI] [Google Scholar]

[RSPB20172832C27] 27.Kloppenburg P, Camazine SM, Sun XJ, Randolph P, Hildebrand JG. 1997. Organization of the antennal motor system in the sphinx moth Manduca sexta. Cell Tissue Res. 287, 425–433. ( 10.1007/s004410050767) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C28] 28.Yaws CL, Gabbula C. 2003. Yaws' handbook of thermodynamic and physical properties of chemical compounds. New York, NY: Knovel. [Google Scholar]

[RSPB20172832C29] 29.Pires EV, Mendonca AD, Vanickova L, Serra NSJ, da Silva RDC, dos Santos DC, Campos RD, Sant'Ana AEG, do Nascimento RR. 2016. Identification and field and laboratory tests of the sex pheromone of Cerconota anonella Sepp. (Lepidoptera: Oecophoridae). J. Appl. Entomol. 140, 72–80. ( 10.1111/jen.12228) [DOI] [Google Scholar]

[RSPB20172832C30] 30.Zhang Z, Chen Q. 2007. Comparison of the Eulerian and Lagrangian methods for predicting particle transport in enclosed spaces. ASTM Spec. Tech. Publ. 41, 5236–5248. ( 10.1016/j.atmosenv.2006.05.086) [DOI] [Google Scholar]

[RSPB20172832C31] 31.Li X, Yan Y, Shang Y, Tu J. 2015. An Eulerian–Eulerian model for particulate matter transport in indoor spaces. Build. Environ. 86, 191–202. ( 10.1016/j.buildenv.2015.01.010) [DOI] [Google Scholar]

[RSPB20172832C32] 32.Schneider R, Lanzen J, Moore P. 1998. Boundary-layer effect on chemical signal movement near the antennae of the sphinx moth, Manduca sexta: temporal filters for olfaction. J. Comp. Physiol. A 182, 287–298. ( 10.1007/s003590050179) [DOI] [Google Scholar]

[RSPB20172832C33] 33.Sun X, Wang MQ, Zhang G. 2011. Ultrastructural observations on antennal sensilla of Cnaphalocrocis medinalis (Lepidoptera: Pyralidae). Microsc. Res. Tech. 74, 113–121. ( 10.1002/jemt.20880) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C34] 34.Binyameen M, Anderson P, Ignell R, Seada MA, Hansson BS, Schlyter F. 2012. Spatial organization of antennal olfactory sensory neurons in the fe male: Spodoptera littoralis moth: differences in sensitivity and temporal characteristics. Chem. Senses 37, 613–629. ( 10.1093/chemse/bjs043) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C35] 35.Ghaninia M, Olsson SB, Hansson BS. 2014. Physiological organization and topographic mapping of the antennal olfactory sensory neurons in female hawkmoths, Manduca sexta. Chem. Senses 39, 655–671. ( 10.1093/chemse/bju037) [DOI] [PubMed] [Google Scholar]

[RSPB20172832C36] 36.Yao CA, Ignell R, Carlson JR. 2005. Chemosensory coding by neurons in the coeloconic sensilla of the Drosophila antenna. J. Neurosci. 25, 8359–8367. ( 10.1523/jneurosci.2432-05.2005) [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Antennal scales improve signal detection efficiency in moths

Qike Wang

Yidan Shang

Douglas S Hilton

Kiao Inthavong

Dong Zhang

Mark A Elgar

Abstract

1. Introduction

Figure 1.

2. Methods

(a). Model construction and parameter derivation

(i). Antenna computational model

(ii). Computational model and mesh generation

(iii). Particle selection and simulation

(iv). Relative antennal detection efficiency

Figure 2.

Table 1.

(b). Comparative study of antennal morphology

Figure 4.

3. Results

(a). Flow-field pattern

(b). Particle spatial distribution

(c). Relative antennal detection efficiency and function of scales

Figure 3.

(d). Correlation between angle of scales and the number of sensilla

4. Discussion

Supplementary Material

Acknowledgements

Data accessibility

Authors' contributions

Competing interests

Funding

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases