Direct observation of ultrafast large-scale dynamics of an enzyme under turnover conditions

Significance

The potential effect of conformational dynamics of enzymes on their chemical steps has been intensely debated recently. We use single-molecule FRET experiments on adenylate kinase (AK) to shed new light on this question. AK closes its domains to bring its two substrate close together for reaction. We show that domain closure takes only microseconds to complete, which is two orders of magnitude faster than the chemical reaction. Nevertheless, active-site mutants that reduce the rate of domain closure also reduce the reaction rate, suggesting a connection between the two phenomena. We propose that ultrafast domain closure is used by enzymes as a mechanism to optimize mutual orientation of substrates, a novel mode of coupling between conformational dynamics and catalysis.

Abstract

The functional cycle of many proteins involves large-scale motions of domains and subunits. The relation between conformational dynamics and the chemical steps of enzymes remains under debate. Here we show that in the presence of substrates, domain motions of an enzyme can take place on the microsecond time scale, yet exert influence on the much-slower chemical step. We study the domain closure reaction of the enzyme adenylate kinase from Escherichia coli while in action (i.e., under turnover conditions), using single-molecule FRET spectroscopy. We find that substrate binding increases dramatically domain closing and opening times, making them as short as ∼15 and ∼45 µs, respectively. These large-scale conformational dynamics are likely the fastest measured to date, and are ∼100–200 times faster than the enzymatic turnover rate. Some active-site mutants are shown to fully or partially prevent the substrate-induced increase in domain closure times, while at the same time they also reduce enzymatic activity, establishing a clear connection between the two phenomena, despite their disparate time scales. Based on these surprising observations, we propose a paradigm for the mode of action of enzymes, in which numerous cycles of conformational rearrangement are required to find a mutual orientation of substrates that is optimal for the chemical reaction.

Proteins have evolved to harness large-scale motions of domains and subunits to promote their activity (1–3). Such conformational dynamics are often initiated by the binding of ligands, forming the basis for allostery. The relation between ligand-induced dynamics and the chemical steps of enzymes has been under intense scrutiny (4–7)—in particular, whether protein motions can enhance catalysis has been extensively debated. Large-scale conformational changes involve the motions of whole domains or subunits. For example, a relative bending around a hinge in the interdomain region brings the two domains of the enzyme phosphoglycerate kinase closer together to form the active site (8), and the transition of hemoglobin between the T and R states involves a relative rotation of the subunits with respect to each other (9).

Adenylate kinase (AK) has served as a valuable model for studies of catalysis-related conformational dynamics, particularly in relation to multiple substrates. This abundant enzyme plays a key role in the maintenance of ATP levels in cells by catalyzing the reaction ATP + AMP $\rightleftarrows$ ADP + ADP (10). It consists of three domains: the large CORE domain, the LID domain that binds ATP, and the nucleotide binding (NMPbind) domain that binds AMP (Fig. 1A). Schulz and coworkers studied multiple forms of the enzyme and used X-ray crystallography to show that the LID and NMPbind domains undergo a major conformational change upon substrate binding, termed domain closure (11, 12). NMR studies (13, 14) and single-molecule FRET (smFRET) experiments (14, 15), all performed with substrate analogs or inhibitors, suggested that domain opening following the chemical reaction is rate limiting for the catalytic cycle of AK. Here we revisit the domain closure reaction of AK from Escherichia coli using much-improved smFRET methodology, including a recently developed analysis method (16) that can retrieve conformational dynamics down to the microsecond time scale. We show that, surprisingly, domain closure in AK in the presence of bona fide substrates is in fact two order of magnitude faster than the enzyme’s chemical reaction.

Fig. 1.

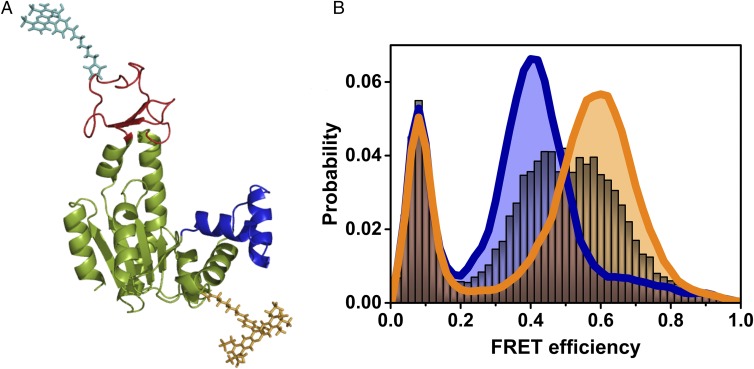
Single-molecule studies of the conformational dynamics of AK. (A) Structure of the open conformation of AK, with the LID domain in red and the NMPbind domain in blue (based on PDB ID code 4AKE). Donor (cyan) and acceptor (dark yellow) dyes attached to the CORE and LID domains, respectively, are depicted. (B) FRET efficiency histograms of AK in the absence of substrate (royal blue) and in the presence of saturating substrate concentrations (1 mM ATP, 1 mM AMP, and 160 µM ADP, orange), suggesting mostly open and closed conformations, respectively. In the presence of 2.5 μM ATP (with 1 mM AMP and 8.4 μM of ADP), a single broad peak is observed (gray), indicating fast exchange between open and closed conformations. The population with FRET efficiency < 0.2 is due to molecules without an active acceptor.

Results

Large-Scale Conformational Dynamics of AK Measured with smFRET.

Molecules of E. coli AK were labeled with FRET dyes at positions 73 and 142, which correspond to the CORE and the LID domains, respectively (Fig. 1A and SI Methods). We selected these two sites to maximize the difference in FRET efficiency between the open and closed conformations of the protein. Freely diffusing AK molecules emitted bursts of photons as they passed through a focused laser beam, and the arrival times of individual photons were registered on two detectors, one for the donor and one for the acceptor. Initially, all photons belonging to one molecule passing through the focus were used to calculate a FRET efficiency value. Histograms were created from thousands of such values (each histogram involved ∼15,000 photon bursts), and showed a peak FRET efficiency value of 0.4 in the absence of substrates, which shifted to a peak value of 0.6 upon addition of saturating concentrations of ATP (1 mM in the presence of 1 mM AMP and 160 µM ADP; Fig. 1B). This large shift suggested that the protein indeed populates one of two states: mostly open in the absence of ATP and mostly closed in the presence of substrate.

At intermediate ATP concentrations, a broad peak appeared in the histogram, with a FRET efficiency value in between the above two (Fig. 1B, gray histogram). The appearance of a broad peak rather than two separate and narrower peaks suggested fast exchange between two conformations, open and closed, presenting low and high FRET efficiency values, respectively (17). A series of data sets was obtained at increasing concentrations of ATP and ADP and a fixed AMP concentration of 1 mM. For each ATP concentration, an ADP concentration was selected to maintain the system under equilibrium, as verified experimentally (Fig. S1 and Table S1). Fluorescence bursts with a high photon flux, emanating from molecules that diffused through the center of the laser focus, were selected for further analysis. Observation of individual fluorescence bursts of AK molecules revealed the occurrence of fast transitions between low and high FRET efficiency values (Fig. 2 A–C), with anticorrelated jumps in the donor and acceptor channels between two levels. The frequency of jumps increased significantly as the concentration of ATP was increased from 0.5 μM (with 3.7 μM ADP; Fig. 2A) to 1 mM (with 160 μM ADP; Fig. 2C). Simulations suggested a jump rate of ∼${10}^4$ s⁻¹ (Fig. S2).

Fig. 2.

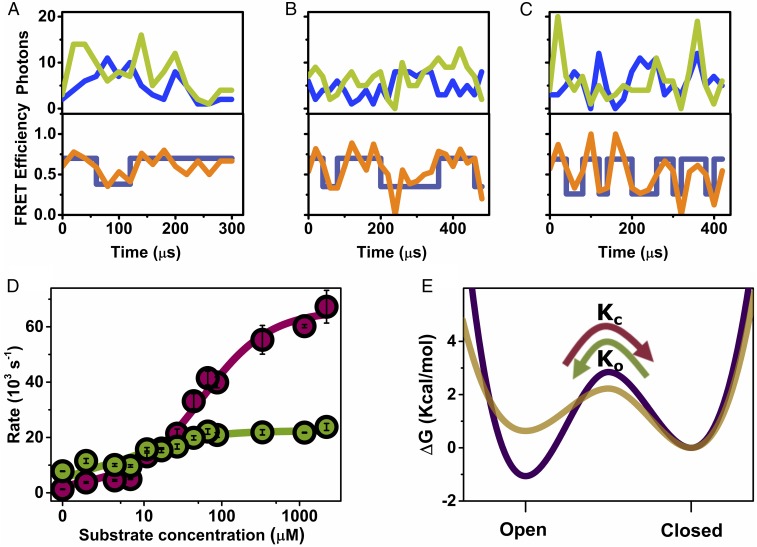
Domain closure dynamics under turnover conditions. (A–C) smFRET trajectories measured at increasing substrate concentration (ATP + ADP; Table S1): 4.2 μM (A), 16.8 μM (B), and 1.16 mM (C), with AMP at a fixed concentration of 1 mM. Top in each part shows donor (blue) and acceptor (light green) signals binned in 20 µs bins, and the Bottom shows the calculated FRET efficiency (orange), and the state of the system at each time bin, as calculated by the Viterbi algorithm based on the H²MM analysis (dark blue). (D) Closing and opening rates (cherry and green circles, respectively) as a function of substrate concentration, obtained from H²MM analysis of a series of smFRET experiments. Error bars represent standard errors of the mean. Continuous lines are fits to the model described in the text, from which closing and opening rate constants for the unbound and bound states of the enzyme were extracted. (E) Free energy profiles for the unbound (purple) and bound (gold) enzyme, calculated from the fitted rates (with an assumed preexponential factor of 1 μs in the Kramers rate expression) (38), indicate that the open conformation is more stable than the closed conformation in the unbound state, with the situation inverted in the bound state. The transition state free energy is reduced in the bound state, leading to faster domain closure dynamics. The curvatures and shapes of the free energy profiles were selected for visualization purposes only.

Analysis of smFRET Trajectories Yields a Dynamic Model for Domain Closure.

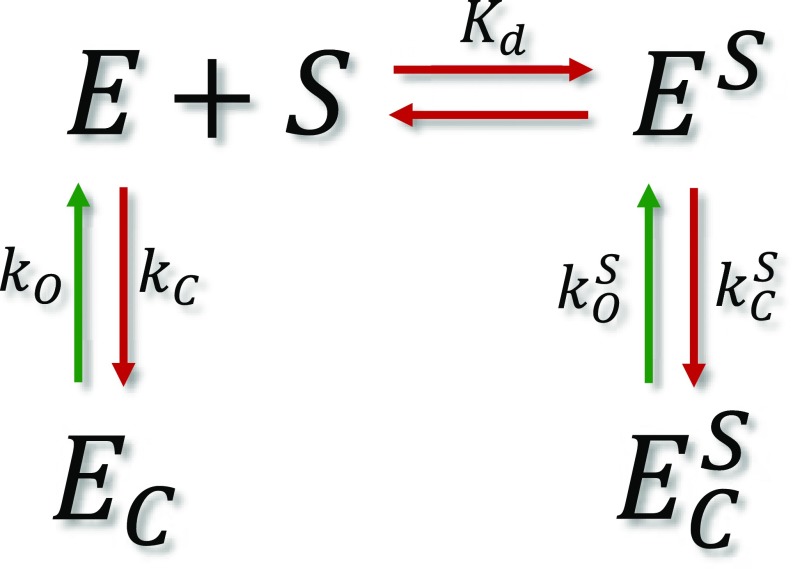
To accurately obtain the rates of domain closure in AK as a function of substrate concentration, we turned to H²MM, an analysis algorithm developed recently in our laboratory (16). This analysis uses photon arrival times as input for an optimization process that obtains populations and kinetic rates. The model we used involved only two states, open and closed, and analysis results were validated using three different independent methods, described in detail in SI Text, Figs. S3–S6, and Table S2. Analysis with three states did not yield better results. The domain closing and opening rates obtained by H²MM are shown in Fig. 2D as a function of substrate concentration (ATP + ADP; Table S1), and the populations of the open state are shown in Fig. S7. The analysis showed that, in the absence of substrate, 85% of the population is in the open state, while in the presence of saturating concentrations of substrates only 20% is in the open state. Surprisingly, it was found that both closing and opening rates increased dramatically upon substrate binding. The trend of the rise of the closing rate was different from that of the opening rate. To account for this behavior, we developed a model, which involves two sets of rates, one for the substrate-bound protein and one for the unbound protein. The model can be represented by Scheme 1.

Scheme 1.

Kinetic model for domain closure of bound and unbound enzyme molecules. The terms in the scheme are defined in the text.

In this scheme, E and E_C are the unbound enzyme in its open and closed conformations, and E^S and $E_C^S$ are the bound enzyme in its open and closed conformations, respectively. K_d is the substrate dissociation constant, $k_C$ and $k_O$ are the domain closing and opening rates of the unbound enzyme, whereas $k_C^S$ and $k_O^S$ are the domain closing and opening rates for the bound enzyme. The closing process occurs from E and E^S that interchange by substrate binding, but the opening process occurs from states that do not interchange, because the closed enzyme cannot release the substrate. Expressions for the apparent rate constants for the closing and opening reactions were derived (Methods), and used to fit the experimental results (continuous lines in Fig. 2D).

From the fit we find that $K_{\text{d}}=55\pm 6$ μM, which matches nicely literature values (15, 18). We also find that $k_C=\left(2.2\pm 1\right)\times {10}^3$ s⁻¹ and $k_O=\left(5.2\pm 1.5\right)\times {10}^3$ s⁻¹, while $k_C^S=(66.0\pm 0.2)\times {10}^3$ s⁻¹ and $k_O^S=\left(22.4\pm 0.1\right)\times {10}^3$ s⁻¹. Thus, in the bound state of the protein the closing and opening rates are ∼10 times higher than in the unbound states, and are likely the fastest rates measured for a large-scale conformational change. Further, these rates are two orders of magnitude higher than the turnover rate of the enzyme, which is just 399 ± 14 s⁻¹. This finding is in stark contrast to previous literature (14, 15), which suggested that the opening reaction is rate limiting for the enzymatic reaction of AK. It is possible that previous work failed to observe the fast closing and opening rates due to the small changes in FRET efficiency values between the two states (which depended on the labeling positions selected in each experiment), as well as the more limited amount of single-molecule data.

It is illuminating to convert the four rates into two free energy profiles (FEPs), one for the unbound protein and one for the bound protein (Fig. 2E) (19). The protein switches between these two FEPs when it binds its substrates. On the unbound FEP the open state is more stable than the closed state, but on the bound FEP the open state is destabilized, making it less stable than the closed state. In addition, the transition state free energy is lower on the bound FEP, making both closing and opening reactions significantly faster than for the unbound protein.

Manipulating Conformational Dynamics with Substrate Analogs and Point Mutations.

It has been debated whether the domain closure of AK involves independent or cooperative motions of the LID and NMPbind domains (20, 21). Lee et al. (20) used all-atom structure-based simulation to study AK conformational transitions using Lorentzian attractive interactions based on native structures. They identified a dominant transition state that involves the LID-closed−NMPbind-open state. However, Pelz et al. (21) used single-molecule optical tweezers to measure the substrate-dependent forces that drive AK into a closed conformation. By using a substrate analog that binds both sites simultaneously, they directly showed that closing and opening of both lids is cooperative.

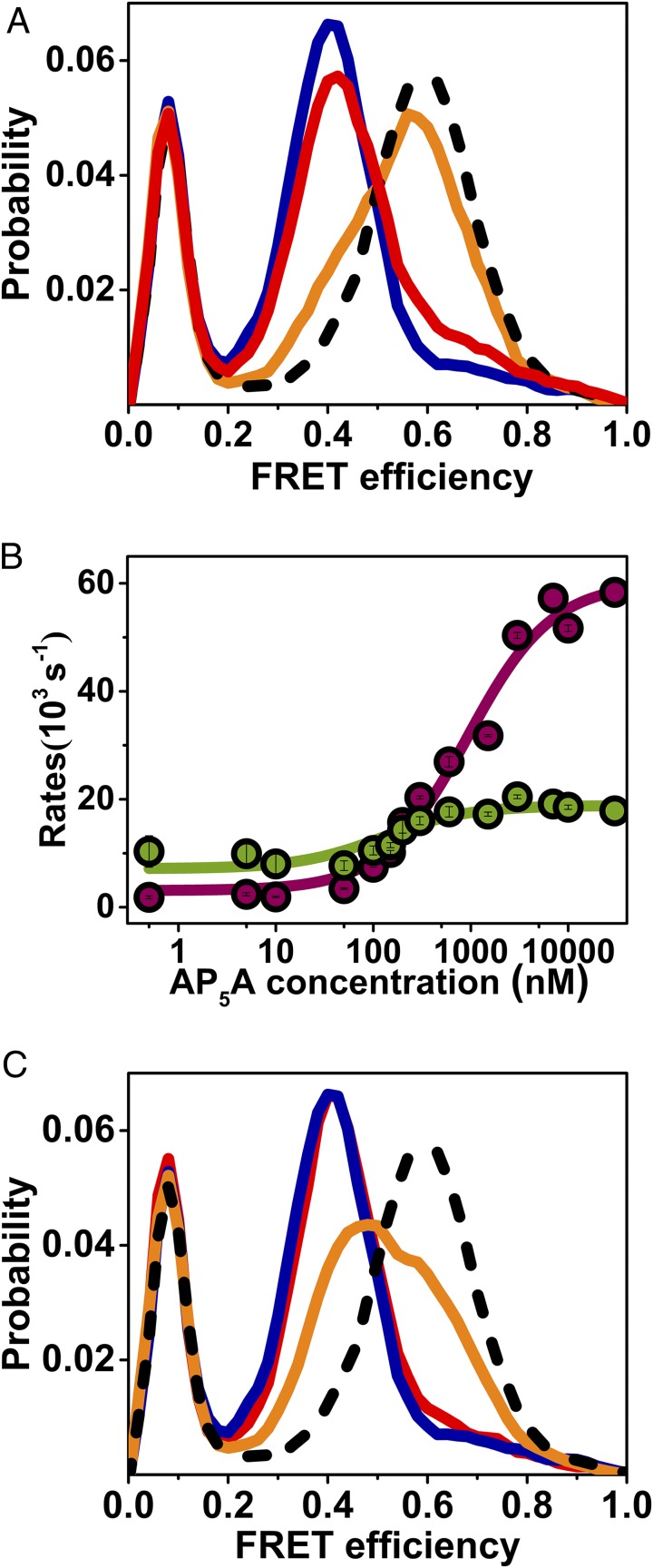
To shed additional light on this issue, we studied the effect of ATP in the absence of AMP or ADP. It was found that even a high concentration of ATP (50 μM) led to only a minimal change of the FRET efficiency histogram (Fig. 3A), proving that substrate binding to both LID and NMPbind domains is required for domain closure, and ruling out independent conformational changes. We further tracked the dynamics of the LID domain in the absence of the chemical step, using the two-substrate mimicking inhibitor P¹,P⁵-Di(adenosine-5′)pentaphosphate (AP₅A; Fig. S8) (22). AP₅A induced concentration-dependent changes in the closing and opening rates (Fig. 3B) that were similar to those observed with ATP, though shifted to lower concentrations, suggesting that it is the binding of the substrates that switches the enzyme from one FEP to the other, irrespective of the chemical step. We also studied domain closure dynamics with AMP-PNP, a nonhydrolysable analog of ATP with a similar K_d (23), and found that even at a high concentration and in the presence of AMP, the equilibrium did not fully shift to the closed conformation as in the presence of ATP and AMP (Fig. 3C). This finding is intriguing, because the only difference between ATP and AMP-PNP is the replacement of the oxygen between the β and γ phosphates by an amine. It suggests that the conformation of the substrate is crucial for the induction of the transition between the bound and unbound FEPs.

Fig. 3.

smFRET experiments shed light on mechanistic aspects of domain closure. (A) Substrate binding to both domains is required for domain closure. FRET efficiency histograms of AK in the absence of substrate (royal blue), with 50 μM ATP (red), with 50 μM ATP and 1 mM AMP (orange), and with 50 μM ATP, 1 mM AMP, and a suitable concentration of ADP to maintain equilibrium (dashed black line). (B) The two-substrate mimicking inhibitor, AP₅A, leads to a concentration dependence of the closing and opening rates (cherry and green, respectively) similar to ATP. (C) The nonhydrolyzable ATP analog, AMP-PNP, does not fully shift the equilibrium to the closed conformation even at a high concentration. At 50 μM AMP-PNP and 1 mM AMP (red), the FRET efficiency histogram is similar to the one without any substrate (royal blue), while at 1 mM AMP-PNP and 1 mM AMP (orange), the histogram has shifted only halfway to the position obtained with 1 mM ATP and 1 mM AMP and a suitable amount of ADP (dashed black line).

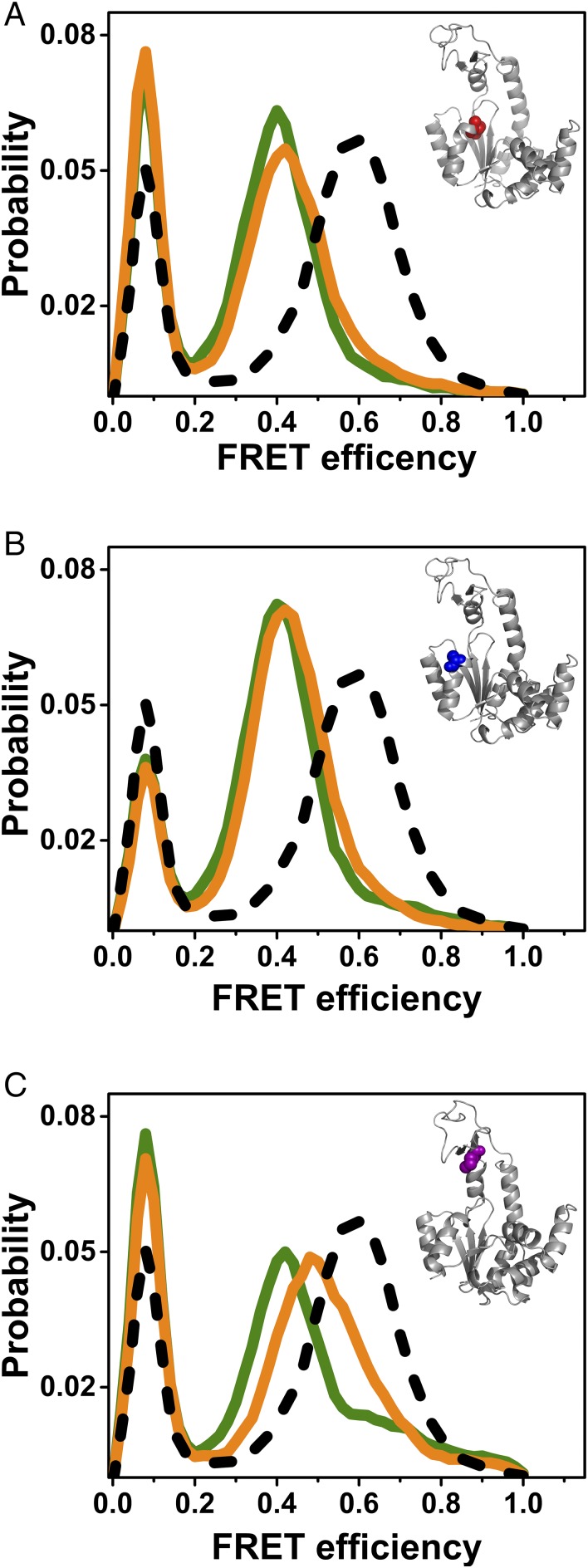
To shed further light on the relation between substrate binding and FEP switching, we turned to study AK variants in which protein residues involved in substrate binding (11) were mutated. We found that mutations that fully or partially prevented switching between the two FEPs [K13M (24), Fig. 4A; T15A (25), Fig. 4B; and R123M (26), Fig. 4C] also reduced the enzyme’s turnover rate significantly (Table 1). These findings suggest that FEP switching has an effect on enzymatic turnover, and that specific substrate interactions with residues involved in catalysis are responsible also for the change in dynamics. It should be noted, however, that mutation could also reduce the turnover rate without affecting FEP switching, as found with the mutant R88M (26) (Fig. S9 and Table 1).

Fig. 4.

Point mutations affect the conformational dynamics of AK. The mutations K13M (A), T15A (B), and R123M (C) reduced the turnover rate to different degrees (Table 1), but fully or partially prevented switching from the unbound FEP to the bound FEP. Indeed, at saturating concentrations of the substrates (1 mM ATP and AMP together with 164 µM ADP for K13M and R123M; 10 mM ATP and 15 mM AMP together with 0.1 mM ADP for T15A), only a small population of the closed conformation was noted in FRET efficiency histograms (orange), compared with the wild-type enzyme (dashed black line). In green are FRET efficiency histograms of the apo mutant enzymes. Insets show the structure of AK with the mutated residues marked in color.

Table 1.

Michaelis–Menten parameters of AK variants

Variant	kcat, s−1	KmATP, μM	KmAMP, μM
WT AK	400 ± 10	58 ± 5	120 ± 20
Labeled AK	390 ± 10	69 ± 5	130 ± 30
K13M	0.23 ± 0.01	66 ± 9	39 ± 3
T15A	110 ± 6	1,300 ± 200	4,200 ± 700
R88M	4 ± 0.3	180 ± 30	1,160 ± 700
R123M	3.5 ± 0.1	51 ± 8	32 ± 5

The parameters were obtained from fits of the Michaelis–Menten equation to results of steady-state kinetic experiments, carried out as described in SI Methods.

Discussion

The smFRET experiments presented in this work provide a detailed view of the domain closure reaction of AK and its relation to the enzymatic reaction. Although the enzyme opens and closes its domains even in the absence of substrates, it remains in the open conformation most of the time. Substrate binding to the protein changes the conformational dynamics, making domain closure much faster and also making the closed conformation more likely. The switching between the unbound and bound FEPs is mediated by the same protein residues that bind ATP and are involved in the catalytic mechanism of the enzyme. The remarkably high rate of domain closure on the bound FEP implies that the enzyme opens and closes multiple times before a single chemical step occurs. This finding defies the common intuition regarding catalysis-related conformational changes, which would suggest that a closing event is accompanied by a catalytic event (13–15). It leads us to suggest a new picture of how enzymes whose reaction involves more than one substrate organize their active sites for the chemical step.

There is some consensus that substrate binding to enzymes primes them for their reaction (27). This requires binding of substrates at relatively unique conformations. However, it has been shown that ligand binding to proteins might involve some level of heterogeneity (28). Enzymes with several substrates, like AK, bind them while in an open conformation and form the proper configuration of the active site only after binding (29). However, ligand-binding disorder could prevent these proteins from arriving at the right configuration once they bring their substrates together. This conundrum can be solved by reorganization of the active site in the closed conformation, which might be difficult to achieve due to friction between protein segments. A second and better solution can involve multiple opening and closing cycles that eventually bring the protein to the conformation most conducive for reaction. We propose that the incompatibility between the domain closure rates and the turnover rate in AK is nothing but a manifestation of such a stochastic active-site reformation process. Thus, the fast closing and opening rates in the bound state lead eventually to an active site conformation in which the two substrates are exactly positioned for an in-line phosphoryl transfer reaction (11). This picture of the connection between dynamics and chemistry in AK is further discussed in Scheme S1.

Our proposal thus constitutes a unique paradigm for the operation of multiple-substrate enzymes. There has been some discussion in the literature on the possibility of a “dynamic” contribution to the reactivity of enzymes. For example, Bhabha et al. (30) found that a mutant of dihydorfolate reductase that abrogates its structural fluctuations also impairs the chemical step, and suggested that this provides a link between dynamics and chemistry in enzymes, a proposal that was later refuted (31, 32). Similarly, a direct coupling of dynamics and the chemical step in AK was also disputed on theoretical grounds (33). Here we build on the separation of time scales between the conformational dynamics and the chemical step to propose that the domain closure reaction acts like a “bath” of fluctuations to bring the active site of the enzyme to the right conformation for reaction. The coupling of a reaction to a bath is a well-known concept in chemical physics (34). The current work shows experimentally that a large-scale conformational change of a protein can play the role of a bath. It will be interesting to find how general this proposed mechanism is as the conformational dynamics of additional enzymes are revealed in similar detail to this one.

Methods

Photon-by-Photon Hidden Markov Model Analysis.

Hidden Markov Model (HMM) analysis has been used as a statistical tool for analyzing single-molecule data to extract kinetic and thermodynamic properties (35–37). HMM analysis is based on the concept that the states of a system are hidden, and only a series of observables is available to the experimentalist. The purpose of the analysis is to reveal the hidden states and obtain model parameters. We have recently developed an algorithm that allows using the standard HMM methods to analyze data on the level of individual photons, therefore pushing the time resolution to the microsecond time scale (16).

In photon-by-photon HMM analysis, we first bin the data to the point that the probability to find more than one photon within a bin is negligible (typically, 10-ns bins are used). In the time interval between any two photons there are in principle multiple time bins. A transition between two states of the system may occur in any of these time bins. The algorithm needs to take into account this additional level of “hidden” information, and was therefore termed H²MM. We have shown in our previous work (16) that H²MM can be used to treat data obtained from diffusing molecules, because it handles photon arrival times as input. H²MM was found capable of resolving transitions on the microsecond time scale. The algorithm is commensurate with all the HMM machinery, including the Viterbi algorithm, which can be used to delineate the single best state sequence in the data.

In the case of the AK data, H²MM was implemented in the following way. First, fluorescence bursts with FRET efficiency values less than 0.2 were removed from the analysis since they came from molecules that lacked an active acceptor dye. Our model assumed two states of the system (open or closed) and the analysis was performed on the data. To confirm that the analysis fully converged and reached the highest global log-likelihood (i.e., did not get confined to a local minimum in parameter space), at least 50 calculations were conducted, starting with different initial conditions. The interconversion rates together with the FRET efficiencies and the initial values of the state probabilities were extracted from the run with the highest log-likelihood.

Kinetic Model for AK Domain Closure.

The apparent rate constants for the closing and opening reactions were derived based on the following schemes:

$$\text{Closing}\hspace{0.17em}\text{reaction}:E_C+S\stackrel{k_C}{\leftarrow }E+S\underset{K_d}{\leftrightarrow }{E}^S\stackrel{k_C^S}{\to }{E}_C^S$$

$$\text{Opening}\hspace{0.17em}\text{reaction}:E_C+S\stackrel{k_O}{\to }E+S;E_C^S\stackrel{k_O^S}{\to }{E}^S$$

In these schemes, E and E_C are the unbound enzyme in its open and closed conformations, and $E^S$ and $E_C^S$ are the bound enzyme in its open and closed conformations, respectively. K_d is the substrate dissociation constant. $k_C$ and $k_O$ are the domain closing and opening rates of the unbound enzyme, and $k_C^S$ and $k_O^S$ are the domain closing and opening rates for the bound enzyme. Note the differences in the schemes for the closing and opening reactions: the closing reaction involves the binding reaction directly, whereas the opening reaction involves it only indirectly, through its effect on the populations of E_C and $E_C^S$.

Solving the kinetic equations based on the above schemes, we get the following expressions for the rates:

$$k_{\text{Close}}^{app}=E\cdot k_C+E^S\cdot k_C^S=\frac{\left[S\right]\cdot k_C^S+K_{\text{d}}\cdot k_C}{K_{\text{d}}+\left[S\right]}$$

$$k_{\text{Open}}^{app}=E_C\cdot k_O+E_C^S\cdot k_O^S=\frac{\left[S\right]\cdot k_O^S+G\cdot k_O}{G+\left[S\right]};G=\frac{K_{\text{d}}\cdot K_c}{K_C^S}$$

In these equations $K_C=k_C/k_O$ is the equilibrium constant for domain closure of the unbound enzyme and $K_C^S=k_C^S/k_O^S$ is the equilibrium constant for domain closure of the bound enzyme.