Significance
The mechanism of activation of GTPases is a problem of general interest, but despite major effort this issue has not been fully resolved in the case of EF-Tu and EF-G. The open questions include the discrimination between two-water (2W) and one-water (1W) mechanisms and the importance of the allosteric contribution in the activation process. Here, we revisit the above questions by comparing simulations of both EF-Tu and EF-G, as well as by analyzing mutational effects. It is found that both the 2W and 1W mechanisms are possible, but in either case, the activation is an allosteric effect. We also conclude that the allosteric activation is common to other GTPases.
Keywords: allosteric activation, GTPase, EF-Tu, EF-G
Abstract
Many cellular processes are controlled by GTPases, and gaining quantitative understanding of the activation of such processes has been a major challenge. In particular, it is crucial to obtain reliable free-energy surfaces for the relevant reaction paths both in solution and in GTPases active sites. Here, we revisit the energetics of the activation of EF-G and EF-Tu by the ribosome and explore the nature of the catalysis of the GTPase reaction. The comparison of EF-Tu to EF-G allows us to explore the impact of possible problems with the available structure of EF-Tu. Additionally, mutational effects are used for a careful validation of the emerging conclusions. It is found that the reaction may proceed by both a two-water mechanism and a one-water (GTP as a base) mechanism. However, in both cases, the activation involves a structural allosteric effect, which is likely to be a general-activation mechanism for all GTPases.
Understanding the action of GTPases is a crucial requirement for elucidating the control of many important cellular processes. In fact, detailed understanding of key problems in biology may boil down to the understanding of the correct reaction mechanism in the protein and to the elucidation of the origin of the corresponding activation of the catalytic process.
An excellent example is the mechanism of the elongation cycle in protein synthesis, that uses the elongation factor Tu (EF-Tu) to deliver aminoacyl-tRNA (aa-tRNA) to the mRNA-programmed ribosome, and the elongation factor G (EF-G) to help the translocation of the tRNA–mRNA complex on the ribosome. More specifically, the GTP-bound state of EF-Tu forms a high-affinity ternary complex with the aa-tRNA. Upon binding of the ternary complex to the ribosome, the aa-tRNA occupies the A-site of the ribosome, and when the codon–anticodon interaction is cognate, the GTPase activity of the EF-Tu is increased significantly. The conformational change following the GTP hydrolysis to GDP and a leaving phosphate group (Pi), leads to a dissociation of the EF-Tu from the ribosome and accommodation of the aa-tRNA on the A-site for a peptidyl transfer. A similar type of activation occurs with EF-G when it binds with the pretranslocation state. The ribosome-bound EF-G complex then catalyzes the movement of the tRNA–mRNA complex in the 30S subunit to produce the posttranslocation state, which leads to the release of the EF-G–GDP complex and restores the ribosome for the next translation cycle (1–3).
Major advances in structural studies led to the elucidation of the structure of EF-Tu and EF-G in the active complex with the ribosome (EF-Tu′, EF-G′) and in the inactive form (EF-Tu, EF-G) (4–10). However, despite those studies and major biochemical advances, there are still open questions on the detailed activation of EF-Tu and EF-G (1–3, 11). One fundamental question is whether the activation involves a major allosteric contribution. At this point, we would like to clarify that the issue of allosteric activation has been presented differently by different workers, including problematic focus on dynamical effects and population shifts, rather than on the change of the free-energy landscape (for analysis, see ref. 11 and references therein). Here, we are focused on structural allosteric activation, where an additional factor (in our case, the ribosome) changes the structure of the enzyme (e.g., going from EF-Tu to EF-Tu′), and changes the free-energy surface for the enzymatic reaction in a way that leads to a lowering of the activation barrier. In this way, a mutational effect that changes the barrier by moving the groups in the active site to another configuration, rather than by a direct interaction between the mutated residue and the substrate, is also classified here as an allosteric effect.
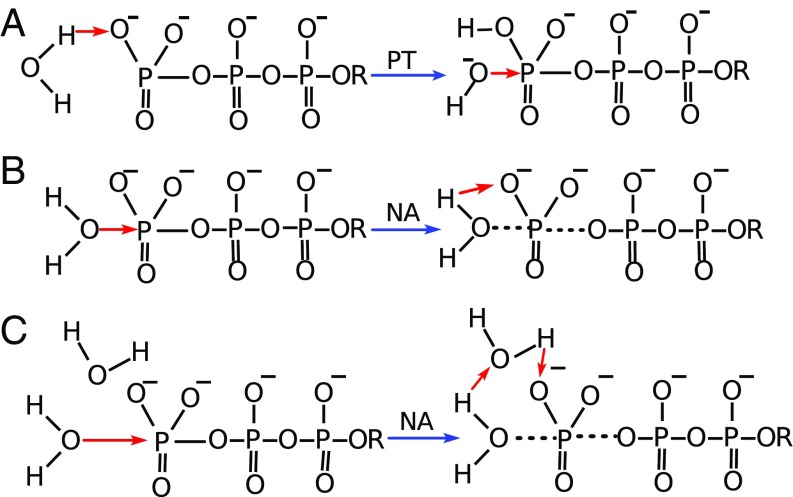
Another key question is the nature of the catalytic reaction in the protein. The corresponding reaction in water can occur through the optional paths drawn in Fig. 1. These options include our original phosphate as a base (12) one-water (1W) mechanism (Fig. 1A), where the attacking water approaches the phosphate with the protons directed towards the phosphate oxygens and transfers a proton to the oxygen, leading to an associative hydrolysis. This mechanism has evolved to the 1W′ version (Fig. 1B), after realizing that most ab initio calculations (11) give a least energy path where the attacking water approaches the phosphate head on, with the oxygen first. A key issue that was unsolved at the stage of ref. 13 was the nature of the proton transfer (PT) from the attacking water. This issue that has only been resolved in the comparative studies of ref. 14, where it is shown that the PT involves a second water molecule (the 2W of Fig. 1C).
Fig. 1.
The first steps of various mechanistic options for the hydrolysis of generic triphosphate monoester in solution. The red arrows correspond to the reaction coordinate, and the black dashed lines correspond to the partial bond formation/breaking. NA and PT are abbreviations for the nucleophilic attack and the proton transfer, respectively. [A represents the mechanistic option where the PT from the nucleophilic water to the phosphate oxygen occurs before the NA (1W)]. B represents the mechanism where the proton is transferred directly from the attacking water to the substrate, but NA precedes the PT step (1W′), while C denotes a two-water mechanism (2W), where the NA is the first step and a PT through a second water follows the NA. The red arrows in the products of the first steps represent the changes in the second step.
While the 2W mechanism has been established for the solution reaction, the situation with respect to the mechanism in the protein has not been fully resolved. In this respect, it is important to acknowledge that the real controversy does not require to consider all proposals, since some of them have been shown to be unrealistic (see discussion in refs. 11 and 15). For example, the work of ref. 16 involves major problems, including the presumption that our 1W mechanism would give about a 50 kcal/mol barrier. These workers did not realize that the method used by them cannot give the 1W barrier even in bulk water, and that with proper sampling the barrier in the enzyme should be about 20 kcal/mol. The mechanistic proposals of ref. 16 were rejected both by our systematic study (15) and the work of ref. 17. Other works (e.g., ref. 18) have promoted correctly a 2W-type mechanism but have other problems that are discussed in ref. 15.
Basically, despite several mechanistic suggestions (11), two major proposals emerged as the results of careful simulations (15, 17). Our simulations (15) showed the 2W mechanism (where the role of the second water can also be fulfilled by a protein residue) as the most likely mechanism in the protein. The view of ref. 15 also emphasized the allosteric activation. The other view has been advanced by the simulations of Åqvist and coworkers (17, 19), who have supported the 1W (phosphate as a base mechanism) (Fig. 1A) for EF-Tu′ and agreed with ref. 15 on the mechanism for Ras/Gap. These researchers have not supported the allosteric idea in EF-Tu (except implicitly by focusing on H84). Below, we will expand on these two views.
The point that is agreed upon is that His84 in EF-Tu′ (Escherichia coli) is not a general base [a related view was first pointed out by us, while excluding the Gln61 as a base mechanism in Ras/GAP (20)]. This computational finding was also supported by experimental pH profiles (1, 21) and by structural arguments (22) as well as by subsequent pKa calculations (17), but some early disagreement existed (23). The agreement in computational studies has been somewhat skewed by Åqvist and coworkers (17, 19), who questioned our treatment of the charged state of His84 (13, 15). Since this problematic assertion has continued even after the clarification of the corresponding misunderstanding (15), we will reclarify this issue in Concluding Remarks.
Accepting the idea of protonated His84 (13), we should still consider the key open question about the mechanism of the GTP hydrolysis in the EF-Tu–ribosome and EF-G–ribosome complexes. As stated above, one of the two options is the 2W mechanism supported by ref. 15. In further supporting the 2W mechanism, we should address the argument of refs. 17 and 19 that the structure available for EF-Tu′ (7) (that was used in ref. 15) is suboptimal, since the PGH backbone should be similar to those in EF-G′, to produce optimal catalysis. It is also important to address the argument (17, 19) that the second water molecule, which is needed for the 2W mechanism, is presumably not observed and thus cannot be used in the protein reaction. The misunderstanding reflected in such an assertion will be clarified in Exploring the 2W Mechanism.
A crucial point that has been emphasized since our early works on RasGAP (24) is the role of allosteric effects in the activation of GTPases. Our point has been that, upon activation, the preorganization of the P-loop and other critical polar elements changes significantly, thus helping the transition state (TS) stabilization. This issue is still somewhat controversial and needs further exploration.
The second mechanistic option considered is the 1W mechanism [our original phosphate as a base mechanism (12)]. This mechanism has been promoted recently by Åqvist and coworkers (17, 19), who have focused mainly on the interaction between the protonated His84 and the nucleophilic OH−, as well as on the effect of other residues on this ion.
Here, we revisit the important issue of the catalytic activation of EF-Tu and the related EF-G system, using rigorous computational studies, and new experimental information including mutational (21) and structural studies of EF-G (8–10). We will discuss misunderstandings in the critiques of our findings and focus on using the similarity between EF-Tu′ and EF-G′, to draw conclusions about the catalytic mechanism in each case.
Our study indicates that both the 1W and 2W mechanisms can be operated in EF-Tu′ and EF-G′, but regardless of the mechanism the activation is an allosteric process.
Exploring the 2W Mechanism
Using the calibrated empirical valence bond (EVB) surface for the 2W mechanism in water [all EVB parameters (with a few modifications) were taken from ref. 15], we simulated the 2W reaction both in EF-Tu′ and EF-G′. These studies were focused on the nucleophilic attack step, since the activation barrier of the PT through the second water had been found to be around 1 kcal/mol (we used same barrier in all of the studied systems).
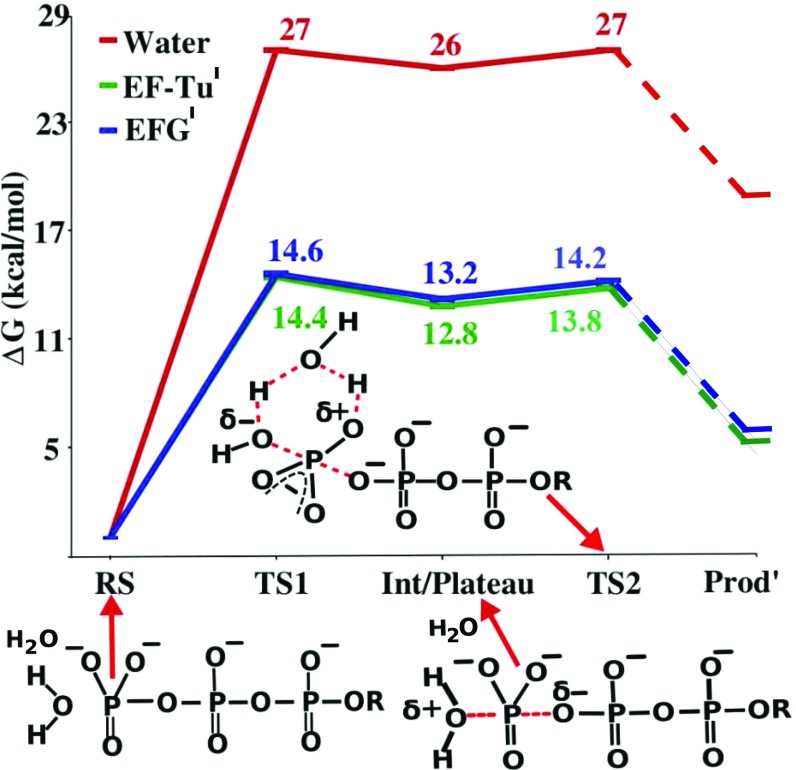
The calculated and experimental free energies for the wild type, as well as different mutant of EF-Tu′ and EF-G′ are given in Table 1. Some calculated profiles are shown in Fig. 2. As seen from the table, the activation free energies for both EF-Tu′ and EF-G′ are in good agreement with the corresponding experimental values. This agreement suggests that the 2W mechanism can be the working mechanism for both EF-Tu′ (as has already been shown in our previous works) and EF-G′. Note that the calculated reaction barrier of EF-Tu′ is lower than EF-G′, which is consistent with the experimental findings.
Table 1.
The calculated results for the 2W mechanism and the corresponding observed values
| System | ∆g‡1 | ∆Gо1 | ∆g‡cal | ∆g‡exp |
| Water | 27.0 | 26.0 | 27.0 | 27.0* |
| EF-Tu′(wild)2W | 14.4 | 12.8 | 13.8 | <14.0† |
| EF-Tu′(H84NP)2W | 17.0 | 16.1 | 17.1 | — |
| EF-Tu′(H84A)2W | 21.8 | 20.4 | 21.4 | 21.2† |
| EF-Tu′(H84Q)2W | 18.7 | 17.5 | 18.5 | ∼18.4§ |
| EF-Tu′(D21A)2W | 18.6 | 17.3 | 18.3 | 18.4§ |
| EF-G′(wild)2W | 14.6 | 13.2 | 14.2 | 14.1¶ |
| EF-G′(H87A)2W | 25.0 | 23.7 | 24.7 | >22# |
∆g‡1 and ∆g‡cal are the calculated activation free energy for the nucleophilic attack step and the total reaction, respectively. ∆Gо1 is the reaction free energy of the first step. ∆g‡exp is the activation free energy obtained from the experimentally determined rate of the hydrolysis. 2W denotes the two-water mechanism for GTP hydrolysis.
From ref. 33.
From ref. 1.
From ref. 21.
From ref. 34.
From ref. 35.
Fig. 2.
The free-energy profile for the hydrolysis of GTP using the 2W mechanism in water, in EF-Tu′ and in EF-G′. RS, TS1, Int, and TS2 represent the reactant state, the transition state of the NA step, the intermediate, and the transition state of the PT, respectively. Note that the Prod′ denotes a state where the proton has just been transferred to the phosphate oxygen. The actual product is lower in energy than Prod′.
It might also be useful to repeat a point that has already been made in ref. 15 but overlooked in refs. 17 and 19, where it has been argued that it is unlikely to have a 2W mechanism, since a second water is not observed in the crystal structure of EF-Tu′. However, as has been explained and quantified in ref. 15, it costs very little energy to pull an additional water molecule to the active site in either the reactant state (RS) or in the TS. It was also pointed out that an additional water was resolved in a close distance to the γ-phosphate of EF-G′ (see figure 6B of ref. 8).
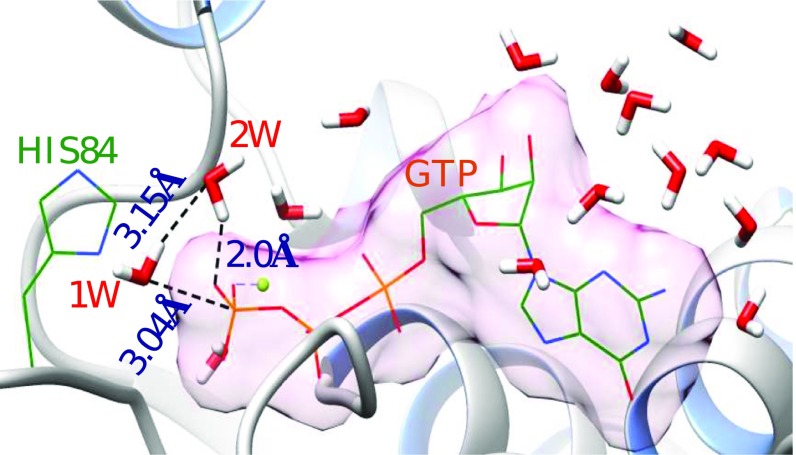
To further resolve the issue of the additional water, we used our water flooding (WF) approach (25) to generate the water molecules that were likely to be in the active site. As shown in Fig. 3, in addition to the two observed water molecules, several other water molecules are present, that can easily participate in the catalytic reaction.
Fig. 3.
A structure of the EF-Tu′–GTP complex obtained after a water flooding calculation. GTP and H84 are shown in wireframe model. The water molecules are shown in stick model. 1W and 2W represent the nucleophilic and the second water of the 2W mechanism, respectively. Except the Hs of the water molecules, all other H atoms are removed for clarity. Different elements such as P (orange), O (red), N (blue), C (dark green), H (white), and Mg (light green) are represented in different colors. The vdw surface (light pink) of GTP was calculated using Chimera (32).
Note that using an optimal or suboptimal structure appears to have little effect on the small energy requires for the penetration of additional water to the correct position on the reaction path.
Exploring the Phosphate as a Base (1W) Mechanism
To reexamine the energetics of the stepwise one-water mechanism of ref. 19 (our original phosphate as a base mechanism), we studied this mechanism in EF-Tu′. In this mechanism, the PT is assumed to be the first step, followed by the nucleophilic attack. Furthermore, we have followed the assumption of ref. 19 that the nucleophilic attack step is a concerted process. That is, we forced the bond breaking between the γ-phosphate and the bridging oxygen and the bond making between nucleophilic oxygen and γ-phosphate to occur simultaneously. The ∆Gо1 and ∆g‡2 for the water reaction were taken from ref. 19, and they are similar to that of ref. 15. However, the corresponding concerted potential energy surface is different from the surface obtained in ref. 15 and leads to somewhat lower barrier.
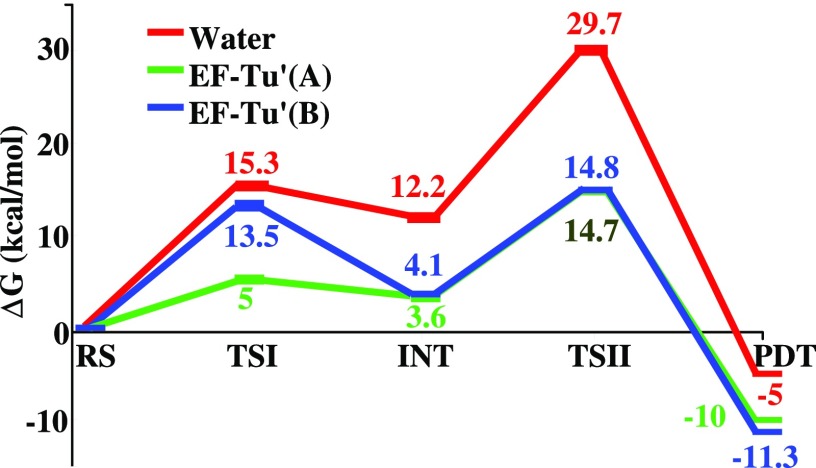
The results of the simulations are shown in Fig. 4. As can be seen from the figure, the calculated activation free energy is in a good agreement with the relevant experimental results. However, although our calculated total activation energy is close to the value reported in ref. 19, the calculated ∆g‡1 is higher than that reported in ref. 19. We would also like to mention that the ∼4 kcal/mol higher barrier in ref. 15 than in the present work can be attributed to the use of a different pathway.
Fig. 4.
The free-energy profile for the GTP hydrolysis via the 1W mechanism, in water and in EF-Tu′. EF-Tu′(A) denotes the free-energy profile obtained by ref. 19. EF-Tu′(B) denotes our calculated free-energy profile. RS, TSI, INT, TSII, and PDT represent, respectively, the reactant state, transition state of the PT process, intermediate, transition state of the NA, and the product state.
We also considered the report (19) that almost 6 kcal/mol destabilization of the hydroxide ion state was obtained when the conformation of PGH loop was changed from an optimal to suboptimal conformation. This issue has been explored by constraining the conformation of the PGH loop of EF-Tu′ like the corresponding conformation in EF-G′, and performing two different EVB calculations. In the first case, we turned off the residual charges of the main chain atoms of the PGH loop, and in the second case the normal residual charges were used. These calculations were restricted to the PT step, where the suboptimality should play a major role. The corresponding results (in Table 2) show that the constrained PGH loop does not stabilize the hydroxide state as explained in ref. 19. Interestingly, it can be also seen that the nonpolar PGH loop (constrained) has stabilized the hydroxide formation slightly more than the polar PGH loop (constrained). The activation free energies in the polar and nonpolar cases are similar. This indicates that, in our simulation, the PGH loop is not affecting significantly the OH− state electrostatically in the 1W (phosphate as a base) mechanism. It would be important to note that we used constraints to restrain the EF-Tu′ to a EF-G′–like conformation, whereas in ref. 19, it had been restrained to make a suboptimal EF-Tu′ conformation. It is also possible that the constraint in ref. 19 prevented a full relaxation in the relevant space. Moreover, ref. 15 found that different constraints give different results.
Table 2.
The effect of constraint and polarity on the PT step of the 1W mechanism
∆g‡1 and ∆G°1 are the calculated activation free energy and reaction free energy for the PT step, respectively. [1W denotes the one-water (phosphate as base) mechanism.]
Unconstrained PGH loop.
Constrained PGH loop [force constant of 10 kcal/mol (on each main chain atom of the PGH loop) was used to constrain a conformation like that of the PGH loop of EF-G′].
The PGH loop was constrained and zero charges were assigned on the main-chain atoms.
Finally, in view of the different conclusions about the effect of the PGH loop, we find the results from EF-G′ to be very useful, since in this case we do not have a suboptimal structure.
Mutational Studies
One way to distinguish between different catalytic proposals is to consider the relevant effects of mutations. Thus, we have studied mutational effects and the corresponding calculations are summarized in Table 1. Most of the mutational calculations, which are presented in Table 1, focused on the effects of the histidine (H84/87 in EF-Tu′/EF-G′). In this respect, it is useful to address the presumption (17, 19) that we have not used protonated His84, since figure S2 of ref. 13 does not show a proton on His84. However, the figure was never supposed to represent what was used in the calculations. Most importantly, the fact that ref. 13 describes the effect of the protonation of His84 in several key calculations (e.g., pKa calculations and the effect of a mutation that neutralizes the positive charge on His84), clarifies that a protonated His84 has been used. Of course, it is also useful to consider the fact that ref. 15 shows the effect of deprotonating His84 in a series of detailed calculations. Obviously, the use of a protonated His84 is also consistent with our conclusion that His84 cannot serve as a base and our finding that the protonated His84 is pulled near the substrate in the cognate configuration due to its electrostatic interaction with the sarcin–ricin loop.
In analyzing the results of Table 1, we start by noting that the 2W model is fully consistent with the observed mutational results. In particular, we note that the observed effect of both the H84A and H84Q mutants in EF-Tu′ has been reproduced. We also reproduced the result of the H84A mutant in our earlier works, but in ref. 13 the effect of H84Q could not be reproduced, possibly because the mutant had not moved sufficiently from the EF-Tu′ conformation in that study (where also the 1W′ rather than the 2W mechanism was used). However, establishing the allosteric effect of the H84A mutant has been the key point of ref. 13. At any rate, the present calculations (Table 1) confirm our point that the actual 2W mechanism reproduces the observed mutational effects in EF-Tu′. Moreover, it is concluded in ref. 15 that the H84NP mutation in the 2W mechanism gives a significant anticatalytic effect, rather than no effect as implied by ref. 19. In considering the effect of the mutations, it is useful to note that the current study of the H84NP mutant leads to an increase in the activation energy (and very similar barrier to that of the 1W′ path). This is in variant with the results obtained in ref. 19, where the simulation of the 1W′ mechanism has been reported to give a higher barrier with the protonated His84, than that with the neutral His84. However, it is unclear whether ref. 19 implemented the rather complex, ab initio-based parameters (or the actual attack mode) that had been used in our 1W′ and 2W mechanisms.
At any rate, we note here that our calculations of the activation free energy for the 2W mechanism in the H84A and H84Q mutants of EF-Tu′, and the H87A mutant of EF-G′ have reproduced the observed trend. These findings support the viability of the 2W mechanism and help us to determine the allosteric contribution of His84 in the EF-Tu′ catalyzed hydrolysis.
Finally, we have also reproduced the effect of the D21A mutation on the activation barrier in the 2W mechanism, and the corresponding consequences are discussed in the next section.
It is useful to note that the calculations of mutational effects may drastically underestimate the observed effect, if for example a calculation would keep the mutated 84th residue in the active position of His84, while the actual mutation might result in a movement of this residue to the inactive orientation. Thus, it would be extremely important to obtain structural information on the mutated EF-Tu′ (or EF-G′).
Comparing the contribution of His87 in EF-G′ to the corresponding contributions of His84 in EF-Tu′ (Fig. 5), indicates that His87 in EF-G′ stabilizes the TS more than His84 in EF-Tu′. This observation helps us to realize why the H87A mutation can lead to a total inactivation of the GTP hydrolysis by EF-G′ (26), compared with a partial inactivation by the H84A mutation in EF-Tu′.
Fig. 5.
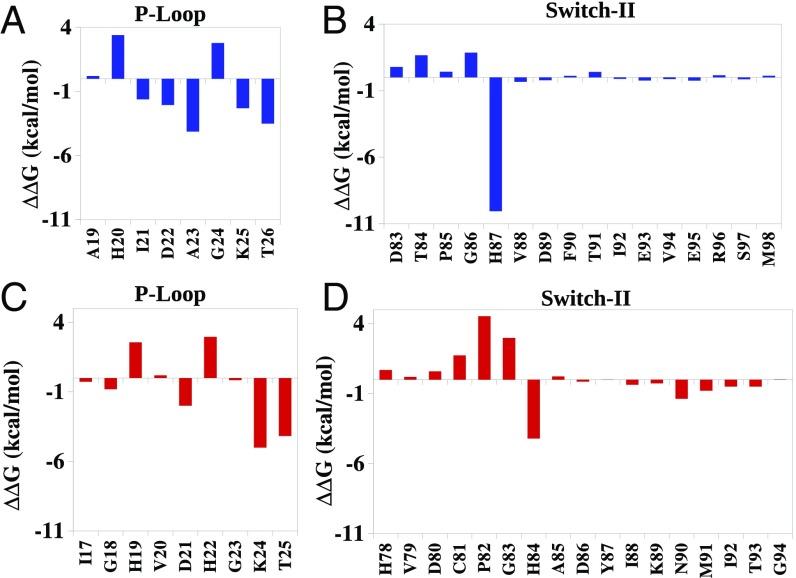
Allosteric contributions (the change in the calculated group contributions upon moving from EF-Tu to EF-Tu′ or EF-G to EF-G′ for the transition from the RS to the TS) of different residues of the P-loop and switch II of EF-Tu (red) and EF-G (blue), in the 2W mechanism. A and B, and C and D represent the allosteric contributions for changing the charges of the phosphate groups of GTP in EF-G and EF-Tu, respectively [effective dielectric constant εeff for ionizable residues (except Lys) =10; Lys = 20].
Allosteric Activation
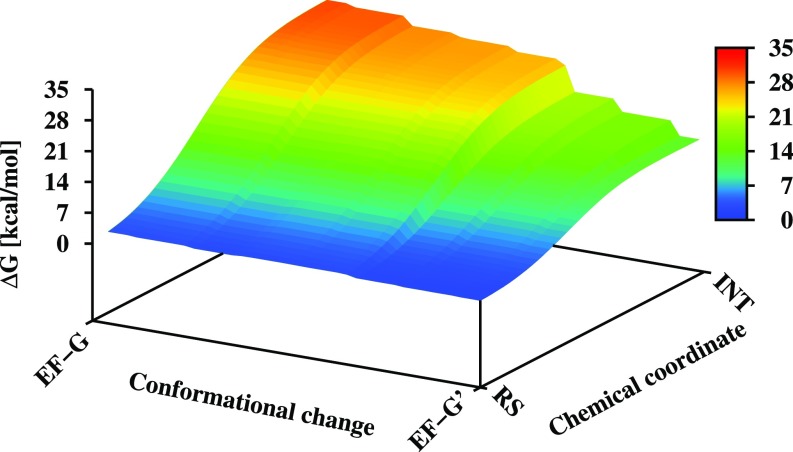
The relationship between the conformational change upon binding to the ribosome and the catalytic effect is described in Fig. 6. As can be seen from the figure, the structural change leads to a major reduction in the activation barrier and thus presents an allosteric effect (structural change induced by an effector lead to change in function). To establish the nature of the allosteric activation, we evaluated separately the contributions from different protein residues in the inactive and active structures of EF-Tu and EF-G, on the triphosphate group of the GTP and on the attacking water molecule.
Fig. 6.
A qualitative free-energy landscape for the coupling between chemical coordinate and conformational coordinate. The y axis represents the reaction coordinate for the nucleophilic step in the 2W mechanism. The x axis represents the conformational change going from inactive EF-G to active EF-G (EF-G′). The figure was generated as described in Supporting Information, section S4. For simplicity, we did not attempt to determine the conformational free energy and set the corresponding change to zero.
The results of the allosteric calculations for the 2W mechanism are summarized in Figs. 5 and 7, which depict the contributions of the protein residues to the change in activation barrier upon structural change. It should be noted that the exact magnitude of the contributions depends on the sampling, but the overall contributions from different regions are reliable. Now, in variant with the implication of ref. 17, it appears that the TS stabilization is different in EF-Tu and EF-Tu′ not only because of His84 and the stabilization of the OH− but also due to the change in the interaction between the phosphate and the active site residues (Fig. 5 and Fig. S2).
Fig. 7.
Allosteric contributions of different residues of the P-loop and switch II of EF-Tu (red) and EF-G (blue) in the 2W mechanism. A and B, and C and D represent the allosteric contribution for changing the charge of the nucleophilic water in EF-G and EF-Tu, respectively [effective dielectric constant εeff for ionizable residues (except Lys) = 10; Lys = 20].
The structural allosteric activation is also supported by the effect of the D21A mutation in EF-Tu′. This residue is located on the P-loop and the fact that its mutation slows down the reaction indicated that part of the effect is due to reducing the TS stabilization by the P-loop. More importantly, as seen from Fig. 5, the effect of the ionized D21 changes significantly between the EF-Tu and EF-Tu′. Thus, it is an allosteric effect. This change in effect between EF-Tu and EF-Tu′ is also observed experimentally (21).
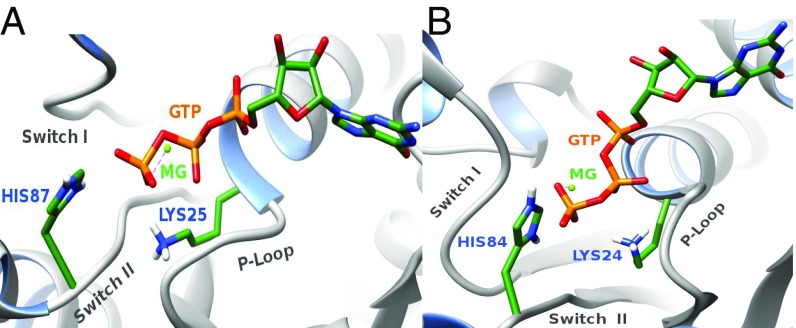
Another conserved P-loop residue Lys25 (EF-G′) or Lys24 (EF-Tu′) contributes significantly to the stabilization of the TS. Interestingly, our allosteric activation calculations show that Lys24 in EF-Tu′ stabilizes the TS more than Lys25 in EF-G′ (Fig. 5). The orientation of the lysine –NH+3 group (Fig. 8) might be the reason for this difference in stabilization (also see ref. 27). In EF-Tu′ when the bridged oxygen (Oβγ) of the GTP gets partial negative charge in the TS, the ionized lysine can effectively stabilize this partial negative charge. On the other hand, in EF-G the Lys25 is pointing toward switch II; thus, it interacts with the GTP through Oβγ and the γ-phosphate. As a result, when the γ-phosphate moves further away from the Oβγ in the TS, the interaction between lysine and GTP decreases. This could lead to smaller allosteric contribution by Lys25 in EF-G′. Nevertheless, it is important to note that Lys residue is in general flexible and tends to move its positive charge to solution. This usually makes the effect of such residues smaller than that which would be estimated with a fixed lysine.
Fig. 8.
Orientation of the lysin of the P-loop in (A) EF-G′ and (B) EF-Tu′. In EF-G′, Lys25 (blue) is orientated toward the switch II (gray), whereas in EF-Tu′, Lys24 (blue) is orientated toward the GTP (orange) but not toward switch II (gray).
It can also be seen from Fig. 5 that the overall PGH loop contribution in EF-G is quite different from that in EF-Tu. To clarify this issue, we also calculated the allosteric contribution for the 2W mechanism, when the conformation of the PGH loop of EF-Tu′ was constrained to be like that of EF-G′ (Fig. S3). The PGH loop has shown to be more effective in the stabilization of the TS when it is constrained to a EF-G′–like conformation. Interestingly, the constraint on the PGH loop has also influenced the P-loop and increased the stabilizing contribution of different residues in the P-loop. Thus, the PGH loop orientation does affect the GTPase hydrolysis rate, not just by interacting with the nucleophilic water molecule (compare Figs. 5 and 7 and Fig. S3) but also by allosterically stabilizing the phosphate at the TS.
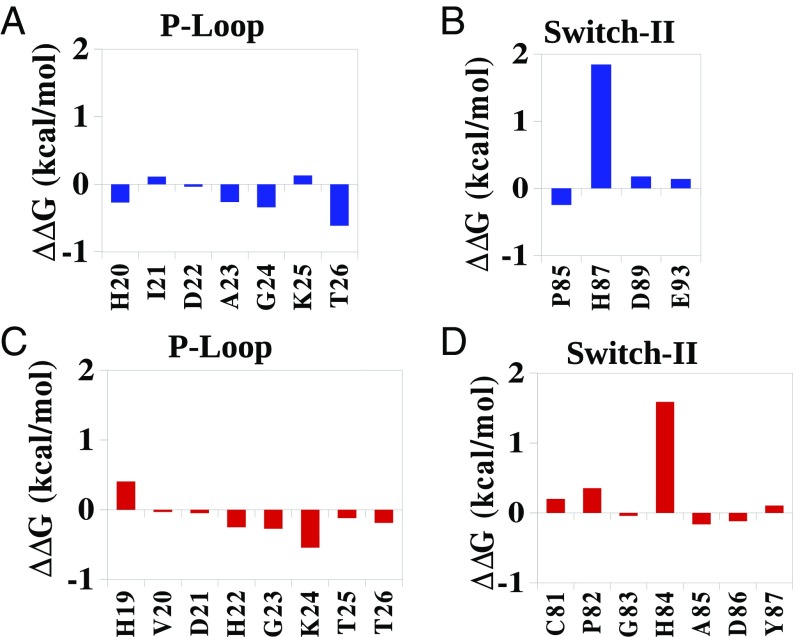
It might be interesting to see whether the 1W mechanism also involves allosteric activation or not. The electrostatic group contributions were calculated for the rate-limiting step of the reaction (Fig. S2). It is clear that, even for the 1W mechanism, the activation for GTP hydrolysis involves an allosteric effect.
Overall, by comparing EF-Tu to EF-Tu′ and EF-G to EF-G′, we demonstrate that the catalysis is not just due to the direct interaction between the reacting system and the histidine charges. It is also important to recognize that all reasonable mechanistic options seem to involve an electrostatic allosteric effect. Thus, the actual question is whether it is due to just the generation of the electrostatic interaction between His84/His87 and the substrate on moving to EF-Tu′/EF-G′, or to other additional changes in group contributions. Note that our calculations are consistent with the experimental study of Maracci et al. (21), who explored mutational effects in different states.
Concluding Remarks
Our systematic study explored the energetics of the GTP hydrolysis by EF-Tu and EF-G, considering both the 2W and 1W mechanisms. It is found that both mechanisms can account for the observed catalytic rates of the activated EF-Tu′, EF-G′, and their mutants. Moreover, both systems are found to be activated by allosteric effects.
We note here that our calculations are reproducible and that the difference between the TSs in EF-Tu and EF-Tu′ cannot be determined just by comparing the corresponding X-ray structures (an implication that has been shown to be problematic in the supporting information of ref. 15), but requires free-energy calculations that consider the substrate position both in the TS and in the RS. Here, it is important to demonstrate (as we did) that the effect is not just due to the direct interaction between the reacting system and the His84 charges. Thus, while recognizing that the motion of His84 from EF-Tu to EF-Tu′ is an allosteric effect, the additional question is whether it is due to just the generation of the electrostatic interaction between His84 and the substrate on moving to EF-Tu′ or due to other additional changes in group contributions.
Although the results of the restraint on the PGH loop may depend on the restraint coordinates and implementation, the finding that we obtained the same results with the EF-G′ structure and with the unconstrained EF-Tu′ gives justification to the use of the available structure of EF-Tu (even if the effect of the PGH loop conformation is not fully agreed upon). Moreover, if the change in conformation of the PGH loop contributes to catalysis, its contribution is still allosteric.
One of the interesting arguments in favor of the 1W mechanism in EF-Tu′ has been advanced in refs. 28 and 29, by impressive entropy calculations. However, it has been eloquently demonstrated in ref. 29 that the overall trend reflects the charge separation between the positively charged His and the attacking nucleophile (which does not occur in RasGAP). An overall similar charge separation occurs in the 2W mechanism in EF-Tu′. Thus, it would be useful to explore the entropic effects in the 2W mechanism.
In retrospect, perhaps the strongest point that establishes the allosteric effect is an analysis of the mutational studies of Rodnina and coworkers (21). That is, the direct contribution from His84 is around 4.5 kcal/mol, if we take the H84Q mutant as a reference, while the overall observed contribution to catalysis upon going from EF-Tu to EF-Tu′ is around 9 kcal/mol. This means that a major part of the activation does not come directly from the electrostatic effect of His84 but from the structural changes in other parts of the protein. Furthermore, as stated above, the effect of His84 by itself is also allosteric effect, since it is induced by the structural changes associated with the interaction with the ribosome.
In conclusion, this work shows that regardless of the possible (but not essential) variation in the mechanism of the GTP hydrolysis, in all mechanistic options, GTPases are associated with a movement of a negative charge from the γ-phosphate to the β-phosphate (as was first found in ref. 24) (see also in ref. 30). The allosteric structural changes are designed to activate the catalysis by interacting with the motion of the reacting charge. In view of the finding of allosteric activation in RasGAP, EF-Tu–ribosome, and EF-G–ribosome, we believe that such mechanism is common to all GTPases.
Materials and Methods
The EVB method was used to investigate the mechanisms that were discussed above. The method and the detailed implementation of the calculations are described in Supporting Information, section S1.
To generate water molecules that are likely to be at the catalytic active site, we used the WF method (25). The details of the method and the implementation of the calculations are given in Supporting Information, section S2.
The electrostatic group contribution calculation was performed using the PDLD/S-LRA method (for details, see Supporting Information, section S3 and ref. 31).
Supplementary Material
Acknowledgments
We acknowledge the University of Southern California’s High Performance Computing and Communications Center for computer time. We also thank the Extreme Science and Engineering Discovery Environment for computer time. D.M. also thanks Dr. R. P. Bora for his guidance. This work was supported by National Science Foundation Grant MCB-1707167, National Cancer Institute Grant 1U19CA105010, and NIH Grant R35 GM122472.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1800054115/-/DCSupplemental.
References
- 1.Daviter T, Wieden HJ, Rodnina MV. Essential role of histidine 84 in elongation factor Tu for the chemical step of GTP hydrolysis on the ribosome. J Mol Biol. 2003;332:689–699. doi: 10.1016/s0022-2836(03)00947-1. [DOI] [PubMed] [Google Scholar]
- 2.Liljas A, Ehrenberg M. Structural Aspects of Protein Synthesis. World Scientific; Singapore: 2004. [Google Scholar]
- 3.Agirrezabala X, Frank J. Elongation in translation as a dynamic interaction among the ribosome, tRNA, and elongation factors EF-G and EF-Tu. Q Rev Biophys. 2009;42:159–200. doi: 10.1017/S0033583509990060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nissen P, et al. Crystal structure of the ternary complex of Phe-tRNAPhe, EF-Tu, and a GTP analog. Science. 1995;270:1464–1472. doi: 10.1126/science.270.5241.1464. [DOI] [PubMed] [Google Scholar]
- 5.Parmeggiani A, et al. Structural basis of the action of pulvomycin and GE2270 A on elongation factor Tu. Biochemistry. 2006;45:6846–6857. doi: 10.1021/bi0525122. [DOI] [PubMed] [Google Scholar]
- 6.Hansson S, Singh R, Gudkov AT, Liljas A, Logan DT. Crystal structure of a mutant elongation factor G trapped with a GTP analogue. FEBS Lett. 2005;579:4492–4497. doi: 10.1016/j.febslet.2005.07.016. [DOI] [PubMed] [Google Scholar]
- 7.Voorhees RM, Schmeing TM, Kelley AC, Ramakrishnan V. The mechanism for activation of GTP hydrolysis on the ribosome. Science. 2010;330:835–838. doi: 10.1126/science.1194460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tourigny DS, Fernández IS, Kelley AC, Ramakrishnan V. Elongation factor G bound to the ribosome in an intermediate state of translocation. Science. 2013;340:1235490. doi: 10.1126/science.1235490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen Y, Feng S, Kumar V, Ero R, Gao YG. Structure of EF-G-ribosome complex in a pretranslocation state. Nat Struct Mol Biol. 2015;22:272. doi: 10.1038/nsmb0315-272a. [DOI] [PubMed] [Google Scholar]
- 10.Pulk A, Cate JHD. Control of ribosomal subunit rotation by elongation factor G. Science. 2013;340:1235970. doi: 10.1126/science.1235970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kamerlin SCL, Sharma PK, Prasad RB, Warshel A. Why nature really chose phosphate. Q Rev Biophys. 2013;46:1–132. doi: 10.1017/S0033583512000157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schweins T, Langen R, Warshel A. Why have mutagenesis studies not located the general base in ras p21. Nat Struct Biol. 1994;1:476–484. doi: 10.1038/nsb0794-476. [DOI] [PubMed] [Google Scholar]
- 13.Adamczyk AJ, Warshel A. Converting structural information into an allosteric-energy-based picture for elongation factor Tu activation by the ribosome. Proc Natl Acad Sci USA. 2011;108:9827–9832. doi: 10.1073/pnas.1105714108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Plotnikov NV, Prasad BR, Chakrabarty S, Chu ZT, Warshel A. Quantifying the mechanism of phosphate monoester hydrolysis in aqueous solution by evaluating the relevant ab initio QM/MM free-energy surfaces. J Phys Chem B. 2013;117:12807–12819. doi: 10.1021/jp4020146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Prasad BR, Plotnikov NV, Lameira J, Warshel A. Quantitative exploration of the molecular origin of the activation of GTPase. Proc Natl Acad Sci USA. 2013;110:20509–20514. doi: 10.1073/pnas.1319854110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aleksandrov A, Field M. Mechanism of activation of elongation factor Tu by ribosome: Catalytic histidine activates GTP by protonation. RNA. 2013;19:1218–1225. doi: 10.1261/rna.040097.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wallin G, Kamerlin SCL, Åqvist J. Energetics of activation of GTP hydrolysis on the ribosome. Nat Commun. 2013;4:1733. doi: 10.1038/ncomms2741. [DOI] [PubMed] [Google Scholar]
- 18.Grigorenko BL, Nemukhin AV, Shadrina MS, Topol IA, Burt SK. Mechanisms of guanosine triphosphate hydrolysis by Ras and Ras-GAP proteins as rationalized by ab initio QM/MM simulations. Proteins. 2007;66:456–466. doi: 10.1002/prot.21228. [DOI] [PubMed] [Google Scholar]
- 19.Åqvist J, Kamerlin SCL. The conformation of a catalytic loop is central to GTPase activity on the ribosome. Biochemistry. 2015;54:546–556. doi: 10.1021/bi501373g. [DOI] [PubMed] [Google Scholar]
- 20.Langen R, Schweins T, Warshel A. On the mechanism of guanosine triphosphate hydrolysis in ras p21 proteins. Biochemistry. 1992;31:8691–8696. doi: 10.1021/bi00152a002. [DOI] [PubMed] [Google Scholar]
- 21.Maracci C, Peske F, Dannies E, Pohl C, Rodnina MV. Ribosome-induced tuning of GTP hydrolysis by a translational GTPase. Proc Natl Acad Sci USA. 2014;111:14418–14423. doi: 10.1073/pnas.1412676111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liljas A, Ehrenberg M, Åqvist J. Comment on “The mechanism for activation of GTP hydrolysis on the ribosome.”. Science. 2011;333:37, author reply 37. doi: 10.1126/science.1202532. [DOI] [PubMed] [Google Scholar]
- 23.Liljas A, Ehrenberg M, Åqvist J, Ramakrishnan V. Response to comment on “The mechanism for activation of GTP hydrolysis on the ribosome.”. Science. 2011;333:37, author reply 37. doi: 10.1126/science.1202532. [DOI] [PubMed] [Google Scholar]
- 24.Glennon TM, Villà J, Warshel A. How does GAP catalyze the GTPase reaction of Ras? A computer simulation study. Biochemistry. 2000;39:9641–9651. doi: 10.1021/bi000640e. [DOI] [PubMed] [Google Scholar]
- 25.Yoon H, Kolev V, Warshel A. Validating the water flooding approach by comparing it to grand canonical Monte Carlo simulations. J Phys Chem B. 2017;121:9358–9365. doi: 10.1021/acs.jpcb.7b07726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Holtkamp W, et al. GTP hydrolysis by EF-G synchronizes tRNA movement on small and large ribosomal subunits. EMBO J. 2014;33:1073–1085. doi: 10.1002/embj.201387465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hansson S, Singh R, Gudkov AT, Liljas A, Logan DT. Structural insights into fusidic acid resistance and sensitivity in EF-G. J Mol Biol. 2005;348:939–949. doi: 10.1016/j.jmb.2005.02.066. [DOI] [PubMed] [Google Scholar]
- 28.Åqvist J, Kamerlin SC. Exceptionally large entropy contributions enable the high rates of GTP hydrolysis on the ribosome. Sci Rep. 2015;5:15817. doi: 10.1038/srep15817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Åqvist J, Kamerlin SC. Conserved motifs in different classes of GTPases dictate their specific modes of catalysis. ACS Catal. 2016;6:1737–1743. [Google Scholar]
- 30.Muegge I, Schweins T, Langen R, Warshel A. Electrostatic control of GTP and GDP binding in the oncoprotein p21ras. Structure. 1996;4:475–489. doi: 10.1016/s0969-2126(96)00052-4. [DOI] [PubMed] [Google Scholar]
- 31.Warshel A, Sharma PK, Kato M, Parson WW. Modeling electrostatic effects in proteins. Biochim Biophys Acta. 2006;1764:1647–1676. doi: 10.1016/j.bbapap.2006.08.007. [DOI] [PubMed] [Google Scholar]
- 32.Pettersen EF, et al. UCSF Chimera—a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 33.Kirby A, Varvoglis A. The reactivity of phosphate esters. Monoester hydrolysis. J Am Chem Soc. 1967;89:415–423. [Google Scholar]
- 34.Savelsbergh A, et al. An elongation factor G-induced ribosome rearrangement precedes tRNA-mRNA translocation. Mol Cell. 2003;11:1517–1523. doi: 10.1016/s1097-2765(03)00230-2. [DOI] [PubMed] [Google Scholar]
- 35.Cunha CE, et al. Dual use of GTP hydrolysis by elongation factor G on the ribosome. Translation (Austin) 2013;1:e24315. doi: 10.4161/trla.24315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kamerlin SCL, Warshel A. The EVB as a quantitative tool for formulating simulations and analyzing biological and chemical reactions. Faraday Discuss. 2010;145:71–106. doi: 10.1039/B907354J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lee FS, Chu ZT, Warshel A. Microscopic and semimicroscopic calculations of electrostatic energies in proteins by the POLARIS and ENZYMIX programs. J Comput Chem. 1993;14:161–185. [Google Scholar]
- 38.Warshel A, et al. 2012. Molaris-Xg (University of Southern California, Los Angeles), Version 9.15.
- 39.Dunbrack RL., Jr Rotamer libraries in the 21st century. Curr Opin Struct Biol. 2002;12:431–440. doi: 10.1016/s0959-440x(02)00344-5. [DOI] [PubMed] [Google Scholar]
- 40.King G, Warshel A. A surface constrained all‐atom solvent model for effective simulations of polar solutions. J Chem Phys. 1989;91:3647–3661. [Google Scholar]
- 41.Lee FS, Warshel A. A local reaction field method for fast evaluation of long‐range electrostatic interactions in molecular simulations. J Chem Phys. 1992;97:3100–3107. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.