Fitting unanchored puzzle pieces in the skeleton: appropriate 3D scapular positions for the quadrupedal support in tetrapods

Abstract

Deducing the scapular positions of extinct tetrapod skeletons remains difficult, because the scapulae and rib cage are connected with each other not directly by skeletal joint, but by thoracic muscles. In extant non‐testudine quadrupedal tetrapods, the top positions of the scapulae/suprascapulae occur at the anterior portion of the rib cage, above the vertebral column and near the median plane. The adequacy of this position was tested using three‐dimensional mechanical models of Felis, Rattus and Chamaeleo that assumed stances on a forelimb on a single side and the hindlimbs. The net moment about the acetabulum generated by the gravity force and the contractive forces of the anti‐gravity thoracic muscles, and the resistance of the rib to vertical compression between the downward gravity and upward lifting force from the anti‐gravity thoracic muscle depend on the scapular position. The scapular position common among quadrupeds corresponds to the place at which the roll and yaw moments of the uplifted portion of the body are negligible, where the pitch moment is large enough to lift the body, and above the ribs having high strength against vertical compression. These relationships between scapular position and rib cage morphology should allow reliable reconstruction of limb postures of extinct taxa.

Introduction

The scapula and rib cage in tetrapods are connected by thoracic muscles, but have no direct skeletal linkages (Fig. 1; Fujiwara et al. 2009). Therefore, deducing the scapular position in relation to the trunk is one of the most challenging issues in reconstructing the postures of extinct tetrapod taxa, including prehistoric mammals and dinosaurs, whose soft tissues decompose post mortem (Fujiwara et al. 2009). The difficulty of reconstructing the forelimb positions is not the case for the more ancestral state, whose pectoral girdle is directly connected to the skull (e.g. Panderichthys, the basal elpistostegalian sarcopterygians; McGonnell, 2001; Daeschler et al. 2006). However, the accuracy of the scapular position in the skeletal reconstruction of extinct taxa has rarely been considered (Thompson & Holmes, 2007; Witton & Naish, 2008; Sellers et al. 2009), and the scapulae have been randomly positioned in their skeletal mounts (Figs S1 and S2).

Figure 1.

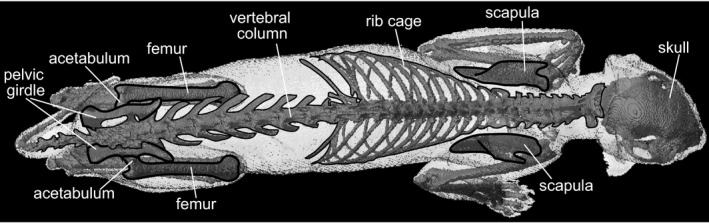
Positional relationships among body skeletons in vivo of Felis shown in the dorsal view. Note that the hindlimb skeletons are directly connected to the vertebral column via the pelvic girdle, whereas the forelimb skeletons have no direct skeletal connection to the rib cage.

Some studies have estimated the scapular positions in extinct tetrapods using fossils in which the skeletal connections were largely preserved (Senter, 2006; Schwarz et al. 2007; Senter & Robins, 2015), although the approach is based on an unsolid assumption that the scapulae are retained in the life positions relative to the trunks in fossil remains. For more mechanical approaches, the bending moments of the vertebral column (Christian & Preuschoft, 1996) and the bending strengths of the rib against vertical compression (Fujiwara et al. 2009) have been used as the indices of the cranio‐caudal scapular position in quadrupedal amniote tetrapods, although the dorso‐ventral and medio‐lateral scapular positions remain unresolved. In another study, stress analysis of simple structural models synthesized from polyhedral finite elements assuming the trunk is supported on a forelimb was conducted for crocodile and sauropod dinosaur models to estimate the appropriate scapular angle to the rib cage (Hohn, 2011), although the approach was not developed for deducing the scapular position to the trunk.

As mentioned above, the scapular position to the trunk remains uncertain. However, irrespective of whether the scapulae are flexible in terms of the orientation to the trunk (English, 1978), the top positions of the scapulae/suprascapulae in extant non‐testudine quadrupedal tetrapods seem to be retained in a limited range of position to the trunk – near the median plane and above the anterior‐most portion of the rib cage during the stance phases (Table 1; Figs 2a and S3).

Table 1.

Cineradiographies that indicate the positional relationship between the scapulae and rib cage taken for quadrupedal locomotion on the ground in tetrapods

Taxa	Order	Genera	References
Anura	Ranidae	Rana	Jenkins & Shubin (1998)
Lepidosauromorpha	Varanidae	Varanus	Jenkins & Goslow (1983)
	Chamaeleonidae	Chamaeleo	Fischer et al. (2010)
Crocodylia	Alligatoridae	Alligator	Baier & Gatesy (2013)
Monotremata	Tachyglossidae	Tachyglossus	Jenkins (1970), Pridmore (1985)
	Ornithorhynchidae	Ornithorhynchus	Pridmore (1985)
Didelphiomorphia	Didelphidae	Didelphis	Jenkins (1971), Jenkins & Weijs (1979)
		Monodelphis	Pridmore (1992)
Soricomorpha	Soricidae	Blarina	Riskin et al. (2016)
Hyracoidea	Procaviidae	Procavia	Fischer (1994)
Carnivora	Canidae	Canis	Fischer & Lilje (2012)
	Felidae	Felis	Macpherson & Ye (1998)
Artiodactyla	Bovidae	Capra	Carroll & Biewener (2009)
Scandentia	Tupaiidae	Tupaia	Schilling & Fischer (1999), Schilling (2005a)
Primates	Lemuridae	Eulemur	Schmidt & Fischer (2000)
	Cebidae	Saimiri	Schmidt (2005)
Lagomorpha	Ochotonidae	Ochotona	Fischer & Lehmann (1998), Schilling (2005b)
Rodentia	Caviidae	Cavia	Rocha‐Barbosa et al. (2005)
	Cricetidae	Microtus	Riskin et al. (2016)
	Spalacidae	Spalax	Gambaryan et al. (2005)
	Muridae	Rattus	Jenkins (1974), Schmidt & Fischer (2011), Vidal et al. (2004), Schilling (2005a,b), Alaverdashvili et al. (2008), Bonnan et al. (2016)

Figure 2.

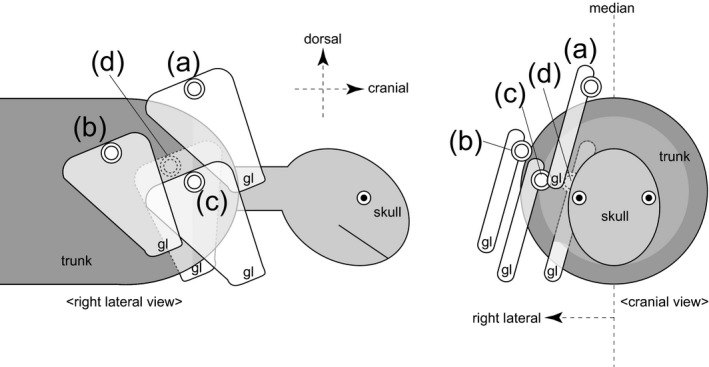
Diagrams showing the difference of the scapular positions to the trunk in right lateral and cranial views. The scapulae are on (a) cranio‐dorso‐medial, (b) cranio‐ventro‐lateral and (c) caudo‐lateral positions, and (d) inside the ribcage. The dorsal portion of the scapular blade (double‐lined circle) and the glenoid (gl) were marked for each scapular position.

The scapular position described above, which is shared by the non‐testudine quadrupedal tetrapods (Fig. 2a), is also shared by taxa that use their forelimbs for body support to a greater or lesser extent, such as birds (Aves) with flying ability (e.g. Columba; Fig. S4a; Baier et al. 2013), and semi‐aquatic quadrupedal tetrapods, such as otariid pinnipeds (e.g. Callorhinus; Fig. S5a; Dennison et al. 2009). On the other hand, these positions are not applicable to turtles (Testudines) whose scapulae are positioned inside the rib cage (Figs 2d and S6; Walker, 1971; Nagashima et al. 2013), and other tetrapods that do not use their forelimbs for terrestrial support, including obligate bipedal tetrapods such as the casuariiform birds, whose forelimbs are extremely reduced (e.g. Casuarius; Fig. S4b; Beale, 1985; Wagner & Kirberger, 2001), and obligate aquatic tetrapods, such as cetaceans (e.g. Tursiops; Fig. S5b; Moran et al. 2015). The scapulae of these non‐forelimb‐users are located on the lateral aspect of the rib cage, away from the median plane (Fig. 2b,c).

Given these observations, the positions of the dorsal margin of the scapula shared among non‐testudine quadrupedal tetrapods are expected to be appropriate for stable body support during quadrupedal gait. If the adequacy of the scapular position shared among the extant quadrupedal taxa is clarified from the biomechanical point of view, it would provide strong evidence for the appropriate reconstruction of these positions in extinct quadrupedal taxa.

Mechanical models and hypotheses

In this study, mechanical models of a phase during slow quadrupedal walk with a symmetric gait were considered, because this gait is employed by many terrestrial quadrupedal tetrapods (Gray, 1968; Gambaryan, 1974; Jenkins, 1974; Cohen & Gans, 1975; Hildebrand, 1989; Schutt et al. 1997; Fischer, 1999; Vidal et al. 2004; Wada et al. 2006; Biknevicius & Reilly, 2007; Fischer et al. 2010; Schmidt & Fischer, 2011). The limbs make contact with the ground in a specific order during this gait, and the quadrupedal animal requires support on either side of the forelimbs and hindlimbs at a certain phase of the slow walk sequence (Gray, 1968; Cartmill et al. 2002; Farrell et al. 2014). In the phase during which the animal stands on its hindlimbs and one forelimb, the rest of the body (the head, axial skeleton and contralateral forelimb) is uplifted by these limbs (Fig. 3). An asymmetric gait employed by many quadrupedal animals, such as some crocodilians, kangaroos, lagomorphs, vampire bats, horses and many other mammals (Gray, 1968; Gambaryan, 1974; Schutt et al. 1997; Renous et al. 2002), was not considered, because both sides of the forelimb share much of the timing of their stance phase.

Figure 3.

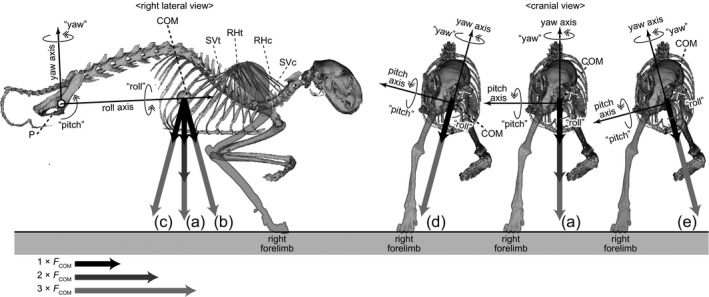
3D rotation model of Felis constructed in this study shown in right lateral and cranial views. The model assumes a stance on the right forelimb, and the body is supported via thoracic muscles (RHc, m. rhomboideus cervicis; RHt, m. rhomboideus thoracis; SVc, m. serratus ventralis cervicis; SVt, m. serratus ventralis thoracis). The roll, yaw and pitch axes through the acetabulum (point P) are perpendicular with each other. A plane parallel to the roll and yaw axes is defined as the ‘reference plane’. The uplifted body elements are allowed to rotate about the point P. The uplifted body elements are subjected to the downward force (F_COM) at the centre of mass (COM) generated by acceleration, and to the contractile forces of the thoracic muscles (RHc, RHt, SVc and SVt). Moment analyses were conducted under different orientations of the COM acceleration: (a) vertical; (b) 15° anterior; (c) 15° posterior; (d) 15° rightward; and (e) 15° leftward accelerations (see Table S3).

The posterior portion of the axial skeleton is directly connected to the hindlimb skeletons by acetabular joints, and the lifting force from the hindlimbs during the stance is transmitted directly to the axial skeleton (Fig. 3; Christian & Preuschoft, 1996). In contrast, the scapulae and trunk are connected not by skeletal joints directly (Fig. 3), but by thoracic muscles, including the musculus serratus ventralis and m. rhomboideus. The former originates from the transverse processes of the cervical vertebrae and the lateral aspects of the thoracic ribs, and the latter originates from the neural spines of the thoracic vertebrae; both muscles insert into the medial surface at the top position of the scapula (Fig. S7; Nickel et al. 1986; Russell & Bauer, 2008). Electromyographic analyses of the quadrupedal gait in various tetrapod taxa (Tokuriki, 1973, 1974; English, 1978; Tuttle & Basmajian, 1978; Jenkins & Weijs, 1979; Jenkins & Goslow, 1983; Yamaguchi, 1992; Fischer et al. 2010) have shown that both m. serratus ventralis and m. rhomboideus are activated during the stance phase of the forelimb. In this phase, the thoracic skeleton is subjected to an uplifting force at the origins of these anti‐gravity muscles (Preuschoft et al. 2007; Fujiwara et al. 2009).

In nature, the stance on one forelimb, together with the hindlimb(s), causes torsion of the axial skeleton along the longitudinal axis (Preuschoft et al. 2007; Hohn, 2011). However, to simplify the model, the uplifted body element is assumed to be a rigid body in this study that is allowed to rotate three‐dimensionally about the three rotational axes through the acetabular joint(s) – the roll, yaw and pitch axes (Fig. 3). The uplifted elements of the body accelerate downward at the centre of mass (COM) under gravity, and are subjected to a negative pitch moment caused by the force of gravity. The forces activated by the thoracic muscles on the forelimb in the stance lift up the anterior portion of the trunk, and the uplifted body element is subjected to a positive pitch moment against gravity to stabilize the posture (Fig. 3). However, the uplifted body element is simultaneously subjected to roll and yaw moments by the muscle activities, and is destabilized (Fig. 3).

In stable posture, the uplifted body element of the quadrupedal tetrapod should be subjected to negligible net pitch, roll and yaw moments by gravity and muscle activities. Assuming the presence of static equilibrium during the stance, the uplifted body is balanced between the net moment of the contractile force of the muscle fascicles and the moment of the gravitational force. The orientations and paths of the anti‐gravity muscle fascicles connecting the rib cage and scapula (m. serratus ventralis and m. rhomboideus) depend on the position of the scapula relative to the rib cage (Fig. S8). Therefore, the pitch, yaw and roll moments of the uplifted body element about the acetabulum vary according to the scapular position and the contractive force of each anti‐gravity muscle fascicle.

Other muscles connecting the forelimb and rib cage, such as m. pectoralis, m. brachiocephalicus and m. latissimus dorsi, may also contribute to sustain the body during the stance (Tokuriki, 1973, 1974; English, 1978; Tuttle & Basmajian, 1978; Jenkins & Weijs, 1979; Jenkins & Goslow, 1983; Yamaguchi, 1992; Fischer et al. 2010). However, unlike the serratus and rhomboideus muscles that insert at the top position of the scapula, these muscles insert at a different position far from the top position of the scapula and, therefore, the fascicle orientations of these muscles depend not only on the scapular position to the rib cage, but also on the scapular orientation and shoulder joint angle. To simplify the mechanical model that focuses on the positional relationship between the scapula and rib cage, these muscles were not considered in this study.

In addition, the origins of the m. serratus ventralis on the thoracic ribs are subjected to the uplift force of the muscle, whereas the vertebral column is also subjected to the downward gravity force, so the rib cage is subjected to dorso‐ventral compression during the stance phase (Fujiwara et al. 2009). The distortion of the rib cage must be minimized to avoid the risk of bone fracture. Therefore, the rib beneath the scapula is expected to be strengthened against dorso‐ventral compression.

For reasons described above, it can be hypothesized that the scapulae on the side of the supporting forelimbs in quadrupedal tetrapods is located: (i) where the net roll, yaw and roll moments of the uplifted body element produced by the muscles and body acceleration are almost negligible; and (ii) above the rib that has relatively enhanced strength against vertical compression. In this study, these hypotheses were tested using two different mechanical models – the rotation and distortion models.

Materials and methods

Three‐dimensional (3D) imaging of the specimens

The carcasses of a cat (Felis silvestris catus, Carnivora, Mammalia), a rat (Rattus norvegicus, Rodentia, Mammalia) and a Meller's chameleon (Chamaeleo melleri, Lepidosauria) were used to test the hypotheses (Table S1). These animals were selected because they use relatively little lateral undulation or vertebral torsion during walking, and the scapular positions during their stance phases are known from cineradiographic studies (Jenkins, 1974; English, 1978; Peterson, 1984; Boczek‐Funcke et al. 1996; Macpherson & Ye, 1998; Alaverdashvili et al. 2008; Fischer et al. 2010; Bonnan et al. 2016).

The carcasses were positioned in a posture of the walking phase, in which they were standing on the right forelimb and hindlimbs (Fig. S9). The cineradiographic studies of them walking (Jenkins, 1974; English, 1978; Peterson, 1984; Boczek‐Funcke et al. 1996; Macpherson & Ye, 1998; Alaverdashvili et al. 2008; Fischer et al. 2010; Bonnan et al. 2016) were used to estimate the angle of the trunk to the ground. The carcasses were scanned with X‐ray computed tomography (CT; Table S1; Fig. S9). The CT images were imported into 3D imaging software (Avizo 8.1, FEI Visualization Science Group, Burlington, USA). The following elements were then segmented, and exported as 3D polygons in STL file format: the uplifted body element (UB), including the head, trunk and the left forelimb (in the swing phase); the thoracic skeleton (TS); and the right scapula (RS; Fig. S9).

The left acetabulum was defined as the common pivot (P) of the UB and TS, because the left hindlimb supports more weight for a longer time than the right hindlimb during the swing phase of the left forelimb in the studied taxa (Manter, 1938; Peterson, 1984; Webb & Muir, 2002). The resolution of the CT scans was insufficient to detect local densities of bones and soft tissues. The outlier volumes of the bony elements [densities of the hard tissues (e.g. cortical bones: 2.06 g mm⁻³) and soft tissues (e.g. muscle: 1.06 g mm⁻³; Gans, 1982; Vogel, 2003) were small relative to the whole‐body volumes (Felis, 7.06%; Rattus, 2.72%; Chamaeleo, 7.67%). Therefore, the COM of the UB was estimated based on the assumption that the specific weights within the body were uniform (Figs 4 and S9).

Figure 4.

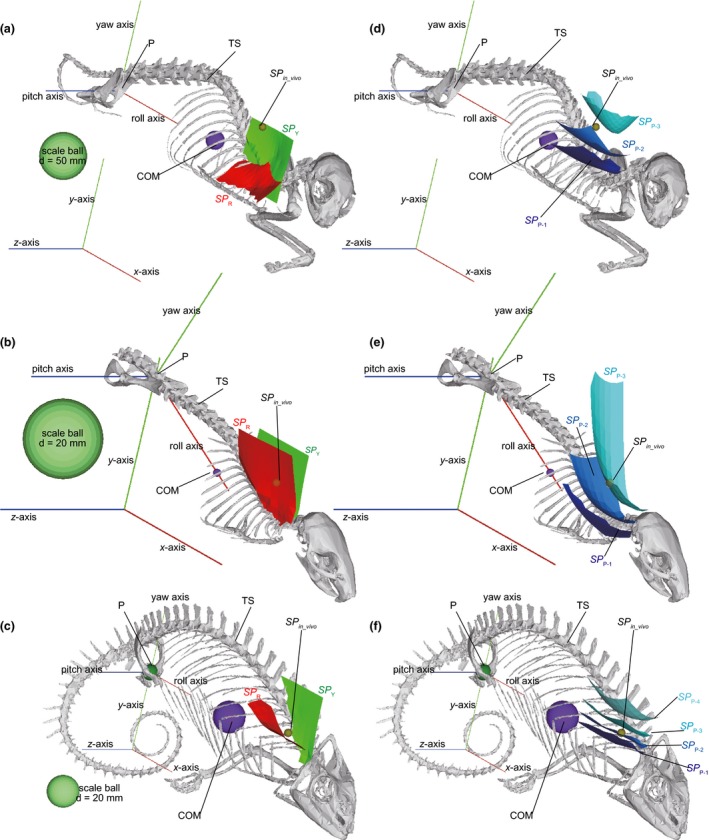
The appropriate scapular positions estimated for (a, b) Felis, (c, d) Rattus and (e, f) Chamaeleo in rotation models with the centre of mass (COM) accelerated vertically. (a, c, e) The scapular positions at which the net roll (SP_R) and yaw (SP_Y) moments generated by the contractive forces of the thoracic muscle fascicles (F _max) and the downward gravity forces (n × F_COM: n = 1, 2, 3, 4) applied to the fascicle origins and the centre of mass (COM), respectively, become zero; (b, d, f) The scapular positions at which the net pitch moment generated by the F _max and n × F_COM (SP _P−n: n = 1, 2, 3, 4) become zero. The results are shown in the oblique views in orthographic projection. COM, centre of mass of the uplifted body element (UB); P, a common pivot of the UB and TS about roll, yaw and pitch axes; TS, thoracic skeleton.

The origins and insertions of the thoracic muscle fascicles (Table S2) were determined by dissection conducted after the CT scan. The maximum contractive force of each fascicle of the thoracic muscles was estimated using the mean values for the length [l (mm)] and mass [m (g)]. The pennation angle (θ) of the muscle fibres was assumed to be zero because the muscle fibres were nearly parallel to the fascicle orientations. The physiological cross‐section area (PCSA) was then calculated for each muscle fascicle based on the equation (Table S2; Gans, 1982):

$$\text{PCSA}=(m\times cos\theta )/(\rho \times l)[{\mathrm{mm}}^2],$$

where ρ (g mm⁻³) is the density of the muscle.

3D rotation model

Three‐dimensional polygons of the UB, TS and RS were imported into a virtual xyz‐coordinate space (x, longitudinal; y, vertical; z, transverse) in software that constructs 3D musculo‐skeletal models (SIMM 6.0.3, Musculographics, Santa Rosa, USA). The common pivot (P) of UB and TS at the acetabulum was set on the y‐axis (Figs 3, S10 and S11). The SIMM models constructed for this study, which can be opened with SIMM 6.0.3, are available online as Appendices S1, S2 and S3.

A plane through point P parallel to the COM acceleration was defined as the reference plane of the body axis, and three rotational axes through point P were defined for the UB and TS – the axis on the reference plane through COM was defined as the roll axis of the UB and TS; the axis perpendicular to the roll axis on the reference plane was defined as the yaw axis; and the axis perpendicular to the reference plane was defined as the pitch axis (Fig. 3). If the COM acceleration vector directed ventrally, the reference plane corresponded to the median plane (Fig. 3a). The UB and TS were allowed to rotate about the roll, yaw and pitch axes in order in SIMM 6.0.3 (Fig. S10; Delp & Loan, 2000). These definitions of the common rotational axes of the UB and TS simplify the model, because the moment inertia of an object about an axis parallel to a certain orientation is minimized if the axis goes through COM (Paul, 1979), and also because the COM acceleration vector is on the plane through the roll and yaw axes. Therefore, the roll and yaw moments of the UB caused by the acceleration parallel to the reference plane on the COM can be neglected. The pitch angles of UB and TS about the horizontal (x–z) plane were taken from the posture during the stance phase determined from the cineradiographic records for these taxa (Fig. S3; Jenkins, 1971; English, 1978; Peterson, 1984; Boczek‐Funcke et al. 1996; Macpherson & Ye, 1998; Alaverdashvili et al. 2008; Fischer et al. 2010).

The RS was allowed to translate parallel to the x‐, y‐ and z‐axes, and to move independently from the rotations of UB and TS about point P (Figs S8 and S11). The top positions of the scapulae were defined as the ‘scapular positions (SPs)’ (Fig. S11). The paths of the fascicles of the thoracic muscles (e.g. m. serratus ventralis, m. rhomboideus) were modelled between the origin on TS and the insertion on RS (Fig. S11b,d,f). The insertions of the fascicles (m. serratus ventralis and m. rhomboideus) roughly correspond to scapular position. The muscle fascicles were modelled to wrap around the rib cage, not to penetrate the skeleton, in the model (Fig. S12; Delp & Loan, 2000).

The maximum possible contractive force (F _max) was estimated for each muscle fascicle using PCSA (Table S2; Powell et al. 1984), as a product of PCSA (mm²) and the specific tension [force per PCSA (N mm⁻²)] of the muscle. The specific tension was obtained from studies of the hindlimb muscles of therian mammals (2250–3120 N mm⁻²; Powell et al. 1984; Bodine et al. 1987; Brown et al. 1998), and the smallest tensile force (2250 N mm⁻²) was used in this study to ensure that the uplifting force produced by the thoracic muscle was not overestimated. The specific tensions of the therian hindlimb muscles were not the best choices for application to the models used in this study, but the specific tensions of the m. serratus ventralis and m. rhomboideus have not yet been determined for relatively small tetrapods. Future studies of their muscle architecture may resolve this problem.

The product of body acceleration (m s⁻²) and the body mass (kg) was defined as F _COM (N). The F _COM was applied to the COM (Figs 3 and S11a,c,e). If the gravitational acceleration (g = 9.80665 m s⁻²; vertical) was applied, F _COM corresponded to the body weight in the stand‐still posture (Fig. 3a). The total vertical reaction force on the supporting limbs in a walking cat or running rat can reach ~1.2 or < 2.0 times body weight, respectively (Manter, 1938; Webb & Muir, 2002). Therefore, the larger downward acceleration of the COM up to four times the body weight was considered as well (vertically accelerated models: F _COM = n × body weight, where n = 1, 2, 3 in Felis and Rattus; n = 1, 2, 3, 4 in Chamaeleo; Fig. 3a; Table S3a).

The COM acceleration can incline from the vertical during the stance phase, although the horizontal component is much smaller than the vertical component (Pandy et al. 1988; Schutt et al. 1997; Macpherson & Ye, 1998; Muir & Wishaw, 1999; Webb & Muir, 2002; Schmitt, 2003; Ahn et al. 2004; Witte et al. 2004; Schmidt, 2005; Ren et al. 2010). According to the gait analyses on Felis forelimb, the inclines of the vector from the vertical are less than 15° (Manter, 1938). Therefore, the models whose COM accelerations were inclined 15° from the vertical toward four different orientations (anterior, posterior, right and left) were taken into account as well (anteriorly, posteriorly, rightward and leftward accelerated models; Fig. 3b–e; Table S3b).

To simplify the model, all muscle fascicles were assumed to perform their maximum contractile forces to counteract the COM acceleration (Tables S2 and S3a,b). The roll, yaw and pitch net moments (N mm) of the UB about the pivot generated by the maximum contractive forces of these muscle fascicles (F _max) and the COM acceleration (n × F _COM; n = 1, 2, 3, 4) were estimated using SIMM 6.0.3 (Fig. S13). The scapular positions at which the roll and yaw net moments become zero were defined as the appropriate positions in terms of roll (SP _R) and yaw (SP _Y), respectively. The scapular position at which the net pitch moments become zero was defined as the appropriate scapular position in terms of the pitch moments (SP _P: SP _P−n corresponds to SP _P estimated for the downward force of n × F _COM, where n = 1, 2, 3, 4).

The above‐mentioned models assume that all the muscle fascicles perform their maximum contractile forces (Table S3a,b). However, the contractile force of each fascicle may not reach its maximum depending on the timing during the stance phase, although the forces in vivo are not fully understood (English, 1978; Jenkins & Weijs, 1979; Jenkins & Goslow, 1983; Yamaguchi, 1992). To test how the difference in contractile force of muscle fascicles affects the estimated scapular position, additional analyses were conducted for Felis models. In these models, the COM was subjected to vertical downward acceleration (n × F _COM), and the contractile forces of thoracic muscle fascicles (RHc, m. rhomboideus cervicis; RHt, m. rhomboideus thoracis; SVc, m. serratus ventralis cervicis; SVt, m. serratus ventralis thoracis) were conditioned as follows. In a model that relies more on the cranial fascicles (RHc‐SVc) than the caudal fascicles (RHt‐SVt; cranial fascicles‐dependent model), contractile forces of RHc, RHt, SVc and SVt were assumed to perform ×1, ×0.5, ×1, ×0.5 times F _max, respectively. Likewise, in a caudal fascicles (RHt‐SVt)‐dependent model, the four different fascicles, i.e. RHc, RHt, SVc and SVt, perform ×0.5, ×1, ×0.5, ×1 times F _max, respectively; in a dorsal fascicles (RHc‐RHt)‐dependent model, they perform ×1, ×1, ×0.5, ×0.5 times F _max, respectively; and in a ventral fascicles (SVc‐SVt)‐dependent model, they perform ×0.5, ×0.5, ×1, ×1 times F _max, respectively (Table S3c). The SP _R, SP _Y and SP _P−1 were estimated for these models. The solutions of SP _P−2 and SP _P−3 were not available for these models, because the net pitch moment did not exceed zero.

3D distortion model

The 3D polygons of the TS were imported into the software for a 3D stress analysis using the finite element method (Voxelcon 2014, Quint, Fuchu, Japan). The orientations of TS about the x‐, y‐, z ‐coordinates were set as in the postures in the 3D rotation models. The 3D polygon for each TS was replaced with blocks of ~100 000 small cubic voxels that reflected the shape of the TS. The sides of each voxel were perpendicular to the x‐, y‐, z‐axes.

The upward lifting force on each rib against gravity was assumed in this analysis. In the voxel blocks of TS, the translation of the vertebral column was fixed for the x‐, y‐, z‐axes, and the upward lifting force (1 N) along the y‐axis was applied to the origin of m. serratus ventralis on each rib (Fig. S14). Young's modulus and Poisson's ratio for TS were set to 18 GPa and 0.4, respectively, according to previously reported experiments on mammal bones (Vogel, 2003). The distribution of the von Mises stresses (N mm⁻²) on the TS block was calculated with Voxelcon 2014, and the maximum stress was estimated. The maximum stress is inversely proportional to the strength of the rib against vertical compression (Fujiwara et al. 2009). Therefore, the muscle fascicle origin at which the maximum von Mises stress on the rib was minimized is the rib most strengthened against vertical compression. The x,z‐position of this fascicle origin was defined as the appropriate scapular position against vertical compression (SP _V).

The appropriate scapular positions estimated from the rotation (SP _R, SP _Y and SP _P) and distortion (SP _V) models were compared with the positions in vivo (SP _{in_vivo}) based on cineradiographic records for these taxa [Felis (English, 1978; Boczek‐Funcke et al. 1996; Macpherson & Ye, 1998); Rattus (Jenkins, 1974; Alaverdashvili et al. 2008); Chamaeleo (Peterson, 1984; Fischer et al. 2010)].

Results

Appropriate scapular positions in the rotation model

In the vertically accelerated models, the appropriate scapular position in terms of the yaw moment (SP _Y) was distributed vertically near the reference plane in all the taxa studied (Figs 4a–c, S15–S17). As mentioned above, the reference plane corresponds to the median plane in the vertically accelerated model (Fig. 3a). The distribution of the appropriate position in terms of the roll moment (SP _R) was nearly parallel to the roll axis in all the taxa studied, although it was inclined latero‐ventrally in Felis, was more vertical in Rattus and was nearly horizontal in Chamaeleo (Fig. 4a–c).

The distributions of the appropriate scapular positions in terms of the pitch moment varied with the force applied to the COM [n × F _COM (N): n = 1, 2, 3, 4]. SP _P−1, SP _P−2, SP _P−3 and SP _P−4 were distributed nearly transversely and nearly parallel to, but above, the roll axis in all the taxa studied (Figs 4d–f and S15–S17). The dorso‐ventral heights were in increasing order: SP _P−1, SP _P−2, SP _P−3 and SP _P−4. SP _P−1, SP _P−2, SP _P−3 and SP _P−4 were convex ventrally above the anterior‐most portion of the rib cage and near the median plane. SP _P−4 was more deeply convex than SP _P−3, followed by SP _P−2 and SP _P−1, whose ventral convexity was shallowest among these limits (Fig. 4d–f). The distance between SP _P−1 and SP _P−3 in Rattus and Felis, or between SP _P−1 and SP _P−4 in Chamaeleo, was smallest at the point at which these surfaces were convex ventrally.

In all the taxa studied, the scapular position in vivo during the stance phase corresponded to the place at which the SP _R, SP _Y and SP _P−1−SP _P−4 (above the anterior portion of the rib cage, above the roll axis and near the median plane) came close to each other (Fig. 4; Jenkins, 1974; English, 1978; Peterson, 1984; Boczek‐Funcke et al. 1996; Macpherson & Ye, 1998; Alaverdashvili et al. 2008; Fischer et al. 2010). The SP _{in_vivo} was between SP _P−2 and SP _P−3 in Felis and Rattus, and between SP _P−1 and SP _P−2 in Chamaeleo. The SP _{in_vivo} corresponded to SP _R in Rattus and Chamaeleo, but was slightly higher than SP _R in Felis, although the distance was not great (Figs 4 and S15–S17).

In rotation models of Felis with the COM accelerated in different orientations (anteriorly, posteriorly, rightward and leftward; Table S3b), the scapular position at which the SP _Y, SP _R, SP _P−1 and SP _P−3 came close to each other was similar to the scapular position estimated in the vertically accelerated model (Fig. S18), although the orientations of the SP _R, SP _Y and SP _P distributions inclined depending on the orientations of the reference plane to the roll axis (Fig. S18d,e). Likewise, the scapular position at which the SP _Y, SP _R, SP _P−1 and SP _P−2 came close to each other in Felis models with different contractile forces of the thoracic muscles (RHc, RHt, SVc and SVt) were similar to the scapular position estimated in the vertically accelerated models as well (Fig. S19).

Appropriate scapular positions in the distortion model

The resistance of the rib against 1 N vertical compression was highest in the anterior‐most ribs in all the specimens studied (Fig. 5). In Felis, the maximum von Mises stresses were 8–12 MPa on the third to the ninth thoracic ribs (Fig. 5a: T8–12), whereas the stresses were 3–5 MPa on the first two thoracic ribs (Fig. 5a: T1–2). In Rattus, the maximum von Mises stresses were 190–260 MPa on the fourth to the sixth thoracic ribs, but decreased toward the anterior ribs, and were < 15 MPa on the first thoracic rib (Fig. 5b). In Chamaeleo, the fourth cervical rib had three fascicle origins of m. serratus ventralis, and the maximum von Mises stress distributed on the rib were smallest when the force was applied to the most proximal origin (< 15 MPa; Fig. 5c: C4p) rather than to the most distal origins (> 65 MPa; Fig. 5c: C4d).

Figure 5.

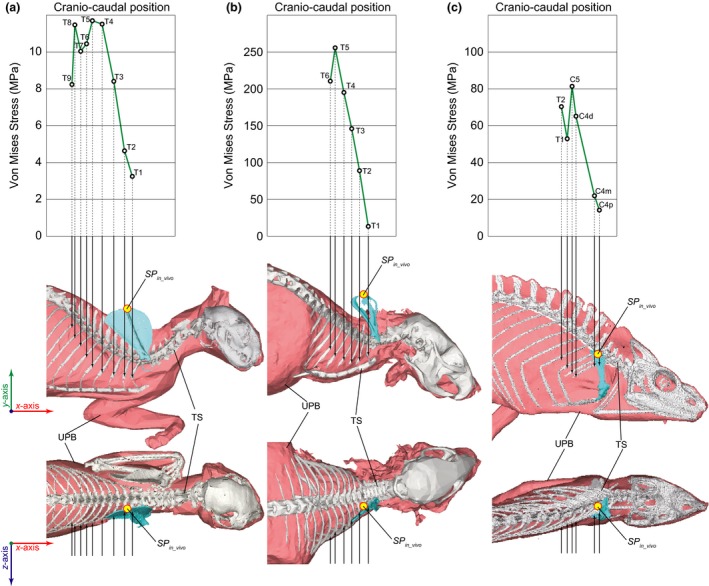
The appropriate scapular position against the vertical compression (SP_V): (a) Felis, (b) Rattus and (c) Chamaeleo. Graphs at the top show the relationship between the cranio‐caudal positions of the origins of m. serratus ventralis and the maximum von Mises stress distributed on the rib when each origin was subjected to upward lifting force (1 N) whereas the vertebral column was fixed to x‐, y‐, z‐axes. The uplifted body element (UB) and the thoracic skeleton (TS) were shown in the middle and the bottom, respectively, in the lateral and dorsal views in orthographic projections. The arrows on the images in the middle and the bottom indicate the positions on the rib cage where the vertical force was applied in the stress analyses, which correspond to the origins of the m. serratus ventralis. C4, the proximal (C4p), middle (C4m) and distal (C4d) origins of the m. serratus ventralis on the fourth cervical rib; C5, fifth cervical rib; Tn, nth thoracic rib.

SP _V was determined to be above the origin of the muscle fascicle on the anterior‐most rib in all the taxa studied (Fig. 5). The scapular positions in vivo were above the first two thoracic ribs in Felis and Rattus, but above the proximal muscle fascicle origin on the fourth cervical rib in Chamaeleo (Jenkins, 1974; English, 1978; Peterson, 1984; Boczek‐Funcke et al. 1996; Macpherson & Ye, 1998; Alaverdashvili et al. 2008; Fischer et al. 2010). Owing to the shapes of the rib cages, in which the medio‐lateral width narrows cranially, both the x,y scapular positions in vivo corresponded to SP _V in all the taxa studied (Fig. 5a–c).

Discussion

The top positions of the scapulae during the support phase (SP _{in_vivo}) in the taxa studied were above the anterior portion of the rib cage and near the median plane (Jenkins, 1974; English, 1978; Peterson, 1984; Boczek‐Funcke et al. 1996; Macpherson & Ye, 1998; Alaverdashvili et al. 2008; Fischer et al. 2010). The dorso‐ventral positions of SP _{in_vivo} were above the vertebral column in Felis and Rattus, whose rib cages are spread broadly posteriorly but narrowly anteriorly (Fig. 5a,b), whereas the position did not reach the top position on the trunk in Chamaeleo (Fischer et al. 2010), whose rib cage was narrow along its entire length (Fig. 5c). However, in all extant quadrupedal tetrapods, SP _{in_vivo} occurs at the position at which the width of the rib cage narrows (Jenkins, 1974; English, 1978; Peterson, 1984; Boczek‐Funcke et al. 1996; Macpherson & Ye, 1998; Alaverdashvili et al. 2008; Fischer et al. 2010). SP _{in_vivo} corresponded to the appropriate scapular position in both the rotation (SP _R, SP _Y, SP _P1−4) and distortion (SP _V) models (Figs 4 and 5). The estimated scapular position at which the SP _R, SP _Y and SP _P1−4 came close to each other did not largely depend on the orientations of the COM acceleration (Fig. S18) and the difference between contractile forces of the thoracic muscle fascicles (Fig. S19). This scapular position is shared by all non‐testudine quadrupedal taxa (see the Introduction). Therefore, the quadrupedal tetrapods seem to retain their scapulae in the appropriate positions for body support to avoid the risks of unsteadiness of the uplifted body element and bone fracture in the thoracic skeleton. This hypothesis could be further strengthened if healed micro stress fractures (McCaw & Bates, 1991; Burr, 1993) were found to be distributed on the weight‐bearing ribs beneath the scapulae in a future study.

The attachments to the skeletons and the fascicle PCSAs of the thoracic muscles are difficult to determine in fossils. Therefore, the analyses used in this study cannot be conducted for extinct taxa. However, if the number of case studies in which this method is applied to extant quadrupedal tetrapods increased, and the top positions of the scapulae/suprascapulae of the quadrupedal tetrapods were found to be common, the scapulae in extinct quadrupedal taxa could well be inferred to occur at similar positions, based on the assumption that the animal used quadrupedal locomotion with a symmetric gait.

Rib strength has been used to estimate the ability to walk on land in mammalian taxa that have shifted their eco‐space from land to water, such as cetaceans and sirenians (Ando & Fujiwara, 2016). Furthermore, the scapulae of some bipedal dinosaurs used to be reconstructed on the lateral aspect of the rib cage, mainly based on the preservations of the fossil occurrences, although their use of forelimbs for body support remains unclear [e.g. hadrosaurs (Galton, 1970); theropods (Stevens et al. 2008)]. The time when the ability of forelimbs to provide support on land was lost in these tetrapod lineages could be more precisely reconstructed if the appropriate scapular position for the terrestrial quadrupedal stance and the possible scapular position around the rib cage were determined for extinct taxa.

Limitations

The rotation and distortion models used in this study are quite new and constitute a useful approach to explaining why the scapular positions of terrestrial quadrupedal tetrapods are restricted. However, both the rotation and distortion models have several limitations. The first limitation is the uncertainties in the assumptions listed below, which were used in the models. The models assumed that each muscle fascicle exerts 100% or 50% of its maximum contractive force in proportion to the PCSA (Table S3), although the exact contractive force of each muscle fascicle during the stance is unknown. Furthermore, the models assumed that a static equilibrium was present between the forces generated by the muscle fascicles and body acceleration; however, the posture of uplifted body elements may not be fixed during the gait [e.g. Felis (Farrell et al. 2014); Rattus (Vidal et al. 2004)], which may cause a shift in the COM position. The models also assumed that only serratus and rhomboideus muscles were involved in supporting the body, although the other muscles connecting the forelimb and rib cage, such as m. pectoralis and m. latissimus dorsi, may also function to support the body (see Introduction). All these factors would affect the estimated appropriate scapular positions (SP _R, SP _Y, SP _P and SP _V). Future studies of these taxa that combine an electromyographic analysis of the fascicles of all the anti‐gravity muscles involved in body support and 3D kinematic analyses using force plates and cineradiography (Baier & Gatesy, 2013) would resolve these problems.

The scapular positions in vivo are not exactly consistent with SP _R in Felis (Fig. 4a). The roll moment on the uplifted body elements causes torsion about the body axis (Preuschoft et al. 2007; Hohn, 2011), although the roll moment is much smaller than the yaw and pitch moments. According to electromyographic studies of several terrestrial tetrapods, the axial muscles are activated during the gait [e.g. Varanus (Ritter, 1995), Rattus (Fischer, 1999), Felis (Macpherson & Ye, 1998; Wada et al. 2006), Ochotona (Schilling, 2005b)], and these muscles probably function to avoid the roll of the uplifted body elements caused by the thoracic muscles.

This study assumed a certain phase during symmetric walk, stance on a single forelimb and hindlimb(s), in quadrupedal tetrapods whose scapulae are flexible relative to the trunk. Likewise, the stance on the hindlimb(s) and non‐lead forelimb can occur during asymmetric gait as well (e.g. Ochotona; Fig. S3l; Gray, 1968; Gambaryan, 1974; Fischer & Lehmann, 1998; Rocha‐Barbosa et al. 2005), and the models in this study may explain the scapular positions in that case.

However, the timing when both forelimbs simultaneously support the body commonly occurs in both symmetric and asymmetric gaits (Fig. S3c,g,i,j,l,n,o). In stance on both sides of the forelimbs, which is the case assumed for the asymmetric gait, the roll and pitch moments generated by both sides of the anti‐gravity thoracic muscles could be balanced with each other about the roll and yaw axes, respectively (Fig. S10b–e). Therefore, the scapular positions that prevent roll (SP _R) and yaw (SP _Y) assumed for support on either side of the forelimb could not be critical for the support on forelimbs during the asymmetric gait.

On the other hand, both positive pitch moments generated by right and left thoracic muscles counteract the negative pitch moment generated by the COM acceleration (Figs 3 and S10f,g). The SP _Ps estimated for the stances on right and left forelimbs could be symmetrical with respect to the median plane, both of which could be distributed near the median plane and above the anterior portion of the rib cage (Figs 4 and S15–S17). The appropriate cranio‐caudal scapular position estimated in the distortion model (SP _V) does not largely depend on whether the animal supports itself on a single forelimb or both forelimbs (Fig. 5). Therefore, we could make rough estimates of appropriate scapular position in asymmetric quadrupedal gait to the similar position estimated for the symmetric gait. However, different analyses assuming the COM position and postures during the stance on forelimbs in asymmetric gait are required to test this.

In addition, further studies are required of the consecutive phases in many different gait patterns and styles of locomotion, such as trotting, galloping, vertical and suspensory gaits, in various taxa, including those whose scapulae are connected [e.g. lizards (Jenkins & Goslow, 1983) and monotremes (Jenkins, 1970; Pridmore, 1992)], to better understand the relationship between the scapular position and the rib cage morphology. The reason why quadrupeds share a similar scapular position relative to the trunk (Fig. S3) has not been explained completely in this study, because this study is based on a very complex assumption and also utilizes a limited sample size. However, this is the first study to reasonably estimate the 3D scapular positions in quadrupedal tetrapods using two different mechanical approaches, which have several advantages over previous approaches. This study is consistent with the skeletal reconstructions of extinct quadrupedal taxa in which the top positions of the scapulae/suprascapulae are positioned in the anterior portion of the rib cage, near the median plane, and high above the line connecting the acetabular joints and the COM.

Conclusion

Appropriate positions of the scapulae to the rib cage for body support on one forelimb and hindlimbs in quadrupedal tetrapods were estimated using two different mechanical models – rotation and distortion models. The former model estimated the net roll, yaw and pitch moments of the trunk generated by the gravity force and the anti‐gravity thoracic muscles. The latter model estimated the resistance of the rib to vertical compression by the downward gravitational force and the upward lifting force from the anti‐gravity thoracic muscles. According to the analyses in three different quadrupedal tetrapods that use symmetrical gait, i.e. Felis, Rattus and Chamaeleo, their scapular positions in vivo were consistent with the place at which the roll and yaw moments of the trunk are negligible, where the pitch moment is large enough to lift the body, and above the ribs having high strength against vertical compression.

Author contributions

All processes of this study, including the design of research, data processing, analyses and drafting the manuscript, were conducted by the author. The author declares no competing interests.

Supporting information

Fig. S1. Difference of the skeletal posture depending on the possible positions to the rib cage in Felis.

Fig. S2. Difference of the scapular positions among skeletal mounts of Triceratops (Ceratopsia, Dinosauria).

Fig. S3. Scapular position shared by extant non‐testudine quadrupedal tetrapods.

Fig. S4. Scapular positions in flying and obligate bipedal tetrapods.

Fig. S5. Scapular positions in semi‐aquatic and obligate aquatic tetrapods.

Fig. S6. Scapular positions of testudines.

Fig. S7. Muscular connection between the scapula and rib cage in Felis.

Fig. S8. The orientations of the muscle fascicles depending on the scapular positions.

Fig. S9. Posture of the CT scanned specimen (Felis).

Fig. S10. Definitions of the rotational (roll, yaw and pitch) axes of the uplifted body element in this study.

Fig. S11. Rotation models of Felis, Rattus and Chamaeleo.

Fig. S12. Paths of the muscle fascicles modelled in the rotation models.

Fig. S13. An example of the moment analysis in the rotation model.

Fig. S14. Boundary conditions of the distortion models in Felis, Rattus and Chamaeleo.

Fig. S15. The appropriate scapular positions in support on right forelimb in Felis (3D PDF).

Fig. S16. The appropriate scapular positions in support on right forelimb in Rattus (3D PDF).

Fig. S17. The appropriate scapular positions in support on right forelimb in Chamaeleo (3D PDF).

Fig. S18. The appropriate scapular positions estimated for Felis in rotation models with the COM accelerated in different orientations.

Fig. S19. The appropriate scapular positions estimated for Felis in rotation models with the thoracic muscles activated in different contractile forces.

Table S1. The specimens and CT scans used in this study.

Table S2. The forces applied to each muscle fascicle and to the COM of the uplifted body in the rotation model.

Table S3. The conditions of the moment analyses.

Appendix S1. Rotation model of Felis for SIMM 6.0.3.

Appendix S2. Rotation model of Rattus for SIMM 6.0.3.

Appendix S3. Rotation model of Chamaeleo for SIMM 6.0.3.