The human platelet antigen-1b (Pro³³) variant of α_IIbβ₃ allosterically shifts the dynamic conformational equilibrium of this integrin toward the active state

Abstract

Integrins are heterodimeric cell-adhesion receptors comprising α and β subunits that transmit signals allosterically in both directions across the membrane by binding to intra- and extracellular components. The human platelet antigen-1 (HPA-1) polymorphism in α_IIbβ₃ arises from a Leu → Pro exchange at residue 33 in the genu of the β₃ subunit, resulting in Leu³³ (HPA-1a) or Pro³³ (HPA-1b) isoforms. Although clinical investigations have provided conflicting results, some studies have suggested that Pro³³ platelets exhibit increased thrombogenicity. Under flow-dynamic conditions, the Pro³³ variant displays prothrombotic properties, characterized by increased platelet adhesion, aggregate/thrombus formation, and outside-in signaling. However, the molecular events underlying this prothrombotic phenotype have remained elusive. As residue 33 is located >80 Å away from extracellular binding sites or transmembrane domains, we hypothesized that the Leu → Pro exchange allosterically shifts the dynamic conformational equilibrium of α_IIbβ₃ toward an active state. Multiple microsecond-long, all-atom molecular dynamics simulations of the ectodomain of the Leu³³ and Pro³³ isoforms provided evidence that the Leu → Pro exchange weakens interdomain interactions at the genu and alters the structural dynamics of the integrin to a more unbent and splayed state. Using FRET analysis of fluorescent proteins fused with α_IIbβ₃ in transfected HEK293 cells, we found that the Pro³³ variant in its resting state displays a lower energy transfer than the Leu³³ isoform. This finding indicated a larger spatial separation of the cytoplasmic tails in the Pro³³ variant. Together, our results indicate that the Leu → Pro exchange allosterically shifts the dynamic conformational equilibrium of α_IIbβ₃ to a structural state closer to the active one, promoting the fully active state and fostering the prothrombotic phenotype of Pro³³ platelets.

Introduction

Integrins are heterodimeric cell-adhesion receptors formed of α and β subunits. Each subunit is divided into three parts: a large extracellular domain (ectodomain), a single-pass transmembrane domain, and a short cytoplasmic tail connecting the extracellular to the intracellular environment (1). In addition to their biomechanical role (2), integrins transmit signals allosterically (3) in both directions across the membrane (termed “outside-in” and “inside-out” signaling) by binding to intra- and extracellular components (4). In the present study, we focused on α_IIbβ₃ (5–8), which is expressed on the platelet surface and essential for platelet aggregation (8).

The ectodomain can be divided into two parts (9, 10) (Fig. 1). The “head” of the receptor is formed by the β-propeller and βA domains, and the “legs” are formed by the thigh and calf domains (α_IIb subunit) as well as EGF domains together with the β-tail domain (β₃ subunit) (4). The genu located between the thigh and calf-1 domain as well as the EGF-1 and EGF-2 domains in the α_IIb and β₃ subunits, respectively, forms a region of interdomain flexibility (11). Integrin structural dynamics is characterized by at least three states: a closed, bent, low-affinity state; a closed, extended, low-affinity state; and an open, extended, high affinity state (12). Although the magnitude of conformational changes has remained a matter of discussion (6, 10, 13), the majority of crystal structures of α_vβ₃ (14), α_IIbβ₃ (9), and α_xβ₂ (15) integrins show their ectodomain in a bent conformation (14, 16, 17). Here, the head is flexed toward the membrane at an angle of 135° (7) related to the legs, with the genu being the angle's vertex.

Figure 1.

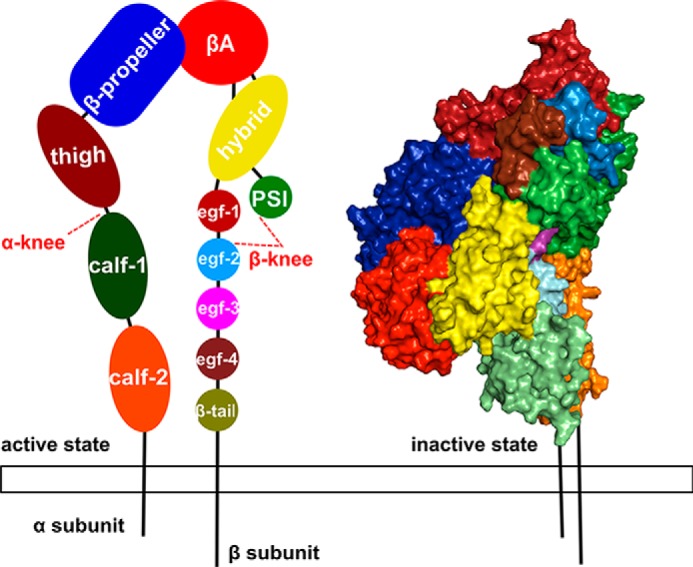
Representation of the domain organization of integrin α_IIbβ₃. On the left, the open conformation is depicted as a schematic with the α subunit divided into four different domains and the β subunit divided into eight domains. Each domain is colored and labeled. The knees of the protein are highlighted by red dashed lines and lie between the thigh and calf-1 domains and between the PSI and EGF-1/EGF-2 domains of the α and β subunits, respectively. On the right, the α_IIbβ₃ ectodomain starting structure (Protein Data Bank code 3FCS) in the bent conformation is depicted in surface representation (right) with domains colored as on the left.

According to current models, the genu plays a critical role in conformational transitions between the three structural states as a straightening in the genu region leads to a separation of the head from the legs and thus an unbending of the conformation. This motion is associated with reduced interactions between the two subunits, resulting in a spatial separation (“splaying”) of the α and β subunit legs (18). With respect to our study, the role of the plexin-semaphorin-integrin (PSI)⁴ domain, which is part of the β₃ genu (5), is of particular interest in integrin activation. Located >80 Å away from the extracellular binding site and >90 Å away from the membrane (estimated from Protein Data Bank code 3FCS), the domain's involvement in integrin activation has been demonstrated (19, 20). Specifically, the domain is believed to have a biomechanical role in the allosteric signal transmission across the structure (21).

The human platelet antigen-1 (HPA-1) polymorphism of the β₃ gene of α_IIbβ₃ arises from a Leu → Pro exchange at residue 33 of the mature β₃ subunit (22, 23), resulting in Leu³³ (HPA-1a) or Pro³³ (HPA-1b) platelets. This amino acid exchange, located within the PSI domain, leads to an inherited dimorphism that can be of clinical relevance (22). For example, the HPA-1b allele was significantly more frequent among young patients with acute coronary syndrome than among age-matched healthy subjects (24). In the Ludwigshafen Risk and Cardiovascular Health (LURIC) trial, an association study including more than 4,000 individuals, we documented that patients with coronary artery disease (CAD), who are carriers of the HPA-1b allele, experience their myocardial infarction 5 years earlier in life than CAD patients who are HPA-1b–negative (22, 23). In a prospective study on CAD patients undergoing saphenous-vein coronary-artery bypass grafting, we demonstrated that HPA-1b is a hereditary risk factor for bypass occlusion, myocardial infarction, or death after coronary-artery bypass surgery (25). These results suggest that the Leu → Pro exchange may modulate functional properties of α_IIbβ₃, resulting in a prothrombotic integrin variant. Prothrombotic properties are also displayed by Pro³³ platelets under flow-dynamic conditions (26). However, the molecular mechanism underlying the suggested prothrombotic phenotype of the Pro³³ (HPA-1b) variant has remained elusive.

We hypothesized that the Leu → Pro exchange allosterically shifts the dynamic conformational equilibrium of α_IIbβ₃ toward an active state. This shift, in turn, would facilitate reaching the fully active state in the presence of integrin ligands. To examine this hypothesis, we performed multiple microsecond-long all-atom molecular dynamics (MD) simulations of the ectodomain and Förster resonance energy transfer (FRET) measurements of α_IIbβ₃-transfected HEK293 cells expressing either the Leu³³ (HPA-1a) or Pro³³ (HPA-1b) isoform. Our MD simulations provide evidence that the Leu → Pro exchange weakens interdomain interactions at the genu and alters the structural dynamics of the integrin to a more unbent and splayed state, resulting in overall conformational changes that have been linked to integrin activation (18, 27). In accord with these results, FRET analyses of α_IIbβ₃ transfectants reveal that the Pro³³ (HPA-1b) variant in the resting state displays a significantly lower energy transfer than the Leu³³ (HPA-1a) variant.

Results

Platelet thrombus size in relation to α_IIbβ₃ HPA-1 isoforms under flow conditions in vitro

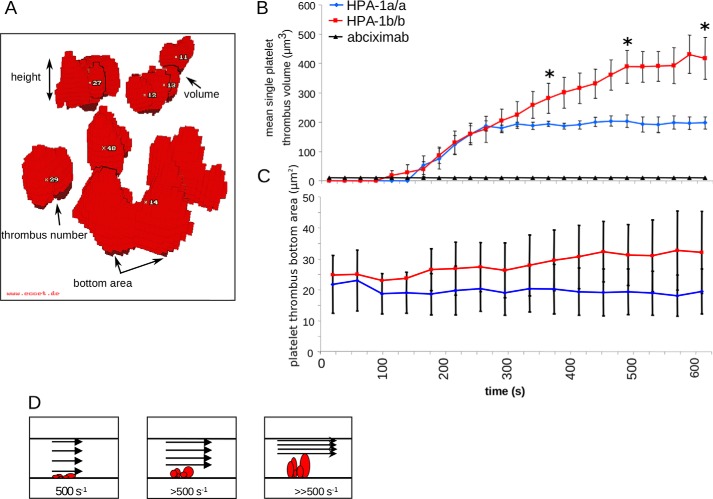
Given the prothrombotic phenotype of Pro³³ platelets, we initially focused on platelet thrombus formation under arterial flow conditions comparing Leu³³ (HPA-1a) with Pro³³ (HPA-1b) platelets. To study the dynamics of platelet thrombus formation, mepacrine-labeled citrated whole blood from healthy volunteers genotyped for HPA-1 of α_IIbβ₃ and α₂C807T of α₂β₁ (see supporting methods) was perfused at shear rates >500 s⁻¹ through a flow chamber coated with collagen type I. Image acquisition was achieved by a series of stacks corresponding to confocal sections from the bottom to the apex of forming platelet thrombi. For quantitation of thrombus formation in vitro, we applied a voxel-based method for 3D visualization of real time-resolved volume data using ECCET software (www.eccet.de)⁵ (28). As depicted in Fig. 2A, ECCET allows determination of the number, bottom area, height, and volume of single platelet thrombi formed in vitro.

Figure 2.

Dynamics and volumetric analysis of platelet thrombus formation under flow-dynamic conditions. A rectangular flow chamber coated with collagen type I (3 mg/ml) at the lower surface was perfused with mepacrine-labeled citrated whole blood for 10 min at an initial near-wall shear rate of 500 s⁻¹, simulating arterial flow conditions. Fluorescence signals were detected by confocal laser scanning microscopy, and digital imaging was processed as described under “Experimental procedures”. Volumetry of forming platelet thrombi was assessed by real-time 3D visualization. A, a reconstruction of formed platelet thrombi obtained from a stack of 30 images by confocal laser scanning microscopy and subsequent data processing by ECCET. B and C, initial platelet thrombus formation and subsequent thrombus growth were recorded in 25-s intervals for each single thrombus. Addition of abciximab (4 μg/ml), an inhibitory antibody to α_IIbβ₃, abrogated any platelet thrombus formation. B shows the mean single platelet thrombus volume, and C shows the corresponding thrombus bottom area. D, schematic illustrating the narrowing of the flow path within the perfusion chamber with a resulting increase in shear rates upon apical thrombus growth. Blue diamonds, homozygous Leu³³ (HPA-1a) platelets (n = 8); red squares, homozygous Pro³³ (HPA-1b) platelets (n = 8); black rectangles, control in the presence of abciximab (n = 2). Error bars indicate mean ± S.E. Asterisks indicate statistical significance (*, p < 0.05).

Using these tools, we detected that, upon perfusion over 10 min, platelets homozygous for Pro³³ (HPA-1b) formed single thrombi that were significantly higher than those of platelets homozygous for Leu³³ (HPA-1a) (Fig. 2B). This difference in mean single thrombus volume was due to an increased thrombus height, whereas the number and bottom area of thrombi (Fig. 2C) did not differ between the HPA-1 isoforms. Platelet adhesion and subsequent aggregate/thrombus formation under flow were abrogated by the monoclonal antibody LJ-Ib1 (a gift from Dr. Z. M. Ruggeri, La Jolla, CA) that completely inhibits binding of von Willebrand factor (VWF) to the platelet glycoprotein (GP) Ib-IX-V complex or by the monoclonal antibody 5C4 (a gift from Dr. M. Gawaz, Tübingen, Germany) that blocks the platelet collagen receptor GPVI (data not shown). As depicted in the schematic illustration (Fig. 2D), with increasing time, the flow path of the perfusion chamber becomes narrowed as the thrombi are growing. Consequently, shear rates gradually increase, and formed platelet thrombi, especially at their apex, are exposed to higher shear than initially applied. Thus, the difference in mean single thrombus volumes between the HPA-1 isoforms can be indicative of a higher thrombus stability of Pro³³ (HPA-1b) than Leu³³ (HPA-1a) platelets as reported before (29).

Structural variability of α_IIbβ₃ HPA-1 isoforms in MD simulations of the integrin ectodomain

To provide an atomistic view on the effect of the Leu → Pro exchange, the Leu³³ (HPA-1a) and Pro³³ (HPA-1b) isoforms were investigated by all-atom MD simulations using the respective integrin ectodomains in the bent conformation as starting structures. The quality of the crystal structure used as a starting structure for the Leu³³ isoform and to model the Pro³³ isoform was validated by MolProbity (30), yielding a percentile score of 1.70, equal to a 99th percentile rank, where a 0th percentile rank indicates the worst and a 100th percentile rank indicates the best structure among structures with comparable resolution (∼2.55 Å in the case of Protein Data Bank code 3FCS). For generating the Pro³³ isoform from the crystal structure, the Leu³³ side chain was mutated using the best rotamer of Pro at this position according to Swiss-PdbViewer (31). For this structure, the quality of the PSI domain in complex with the EGF-1 and EGF-2 domains (genu of the β₃ subunit) was assessed by MolProbity, yielding a percentile score of 1.30, equal to a 98th percentile rank.

Three independent MD simulations of 1-μs length each were carried out. The convergence of the MD simulations was tested by computing the root-mean-square deviation (RMSD) average correlation as described previously (32) (Fig. S1). The root-mean-square average correlation is a measure of the time scales on which structural changes occur in MD simulations. From the bumps in the curves, we can estimate that observed structural changes occur within ∼50–200 ns. For time intervals >200 ns, the curves are smooth, suggesting that no large structural changes happen during the investigation period.

In addition, we analyzed the overlap of histograms of principal component (PC) projections obtained in a pairwise manner from each simulation for a given isoform as a function of time (Fig. S2). The PC analysis was performed on the whole protein after a mass-weighted fitting on the β-propeller and βA domains. The results reveal that, overall, the Kullback-Leibler divergence between histograms of the respective first three PCs becomes small (<0.02) after ∼600 ns of simulation time, whereas values in the first 100 ns can be as high as ∼0.1. Hence, the analyses indicate that, in the given simulation times, rather similar conformational spaces were sampled by MD simulations of one isoform. However, in some cases, a small increase in the Kullback-Leibler divergence is observed toward the end of the simulation time; this behavior is not unexpected because the MD simulations were started from bent conformations of the isoforms that can relax to more open conformations (33). Given that, in the absence of force, the timescale of integrin activation is on the order of 10⁻³ (34) to 1 s (35), one cannot expect that the MD simulations are converged with respect to the bent-open conformational equilibrium of α_IIbβ₃ integrin. In total, differences in structural parameters between both isoforms that we report below relate to differences in the tendency of the ectodomains to go from a bent to an open state. Unless stated otherwise, all results of the MD simulations are expressed as arithmetic means calculated over time, and we considered only uncorrelated instances for S.E. calculations (see “Experimental procedures”).

The βA domain contains three metal ion–binding sites (Fig. S3). To assess their structural integrity during the MD simulations, we monitored the time evolution of distances between the SyMBS, MIDAS, and ADMIDAS metal ions and the respective coordinating residues (Table S3 and Fig. S3). The results reveal that during the production runs the distances remain almost unchanged with S.E. <0.1 Å in almost all cases. Thus, the local geometry of the metal ion–binding sites is well preserved throughout the MD simulations.

The structural similarity of the conformations obtained by MD simulations with respect to the starting structure was explored in terms of the RMSD of C^α atoms after mass-weighted superimpositioning. Similar to our previous MD studies performed on integrin α₅β₁ (18, 27), the simulations revealed minor structural changes of the single domains as mirrored by RMSD values that were largely below 3 Å with the exception of the calf-2 and EGF domains and the β-tail (RMSD up to 5 Å) (Table S4 and Fig. S4). Although the β-tail has been characterized as highly flexible (14), the larger RMSD of the calf-2 domain, in part, is due to the presence of long flexible loops (9); furthermore, the larger RMSD may result from simulating the ectodomain only; i.e. at the C-terminal ends of each subunit, the transmembrane domains are missing. As to the EGF domains, visual inspection of the MD trajectories revealed that the larger RMSD resulted in part from motions of the domains relative to each other.

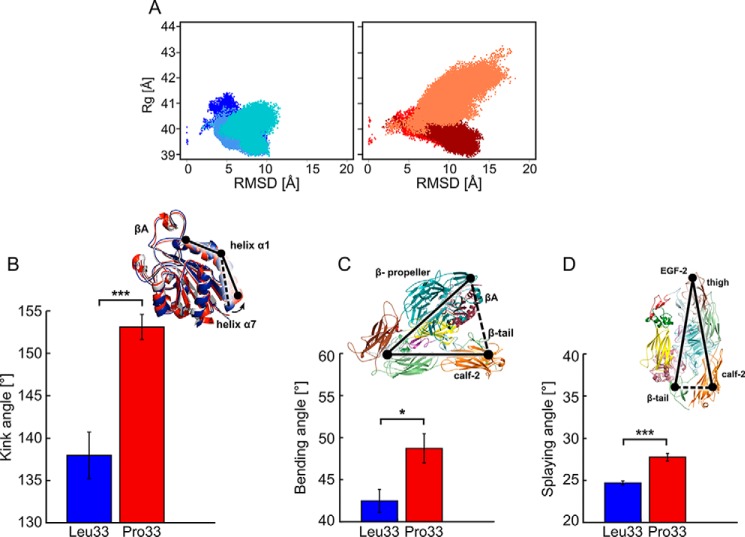
In contrast, when aligning only the head region, the mean RMSD increased up to ∼17 Å (Table S5 and Fig. S5) with the highest values found for the calf-2 and β-tail domains of the legs. Hence, these larger structural changes must arise from relative movements of the domains (or subunits) with respect to each other, considering that the single domains were structurally rather invariant. Comparing both isoforms of α_IIbβ₃, a larger mean RMSD (∼9.2 ± 0.34 Å) was found for Pro³³ than Leu³³ (∼6.6 ± 0.83 Å) (Fig. 3A). In accord with that, the mean radius of gyration (R_g) of the overall structure was larger for the Pro³³ (∼40.3 ± 0.22 Å) than the Leu³³ isoform (∼39.6 ± 0.09 Å) (Fig. 3A). Taken together, the sampled conformational space of both α_IIbβ₃ isoforms varied significantly with respect to the difference of the mean values of these structural parameters (Table S6). To conclude, the Pro³³ variant displayed significantly larger structural deviations from the bent starting structure and became less compact than the Leu³³ isoform during MD simulations.

Figure 3.

Conformational changes of the Leu³³ and Pro³³ isoforms of α_IIbβ₃ during MD simulations. A, two-dimensional histogram of the RMSD of C^α atoms of the entire ectodomain after mass-weighted fitting on the β-propeller and βA domains of the starting structure versus R_g for the ectodomains. Bluish colors represent the three MD simulations of the Leu³³ isoform, and reddish colors represent those of the Pro³³ variant. B–D, histograms of the kink, bending, and splaying angles averaged over three MD simulations with error bars showing the S.E. and asterisks indicating the statistical significance (*, p < 0.05; ***, p < 0.0001). Above the plots, the definitions of the angles are given: B, kink angles as black solid line connecting the three points (center of mass of C^α atoms of Lys¹¹² and Ile¹¹⁸, center of mass of C^α atoms of Gln¹¹⁹ and Lys¹²⁵, and center of mass of C^α atoms of Leu¹²⁶ and Leu¹³²) on both isoforms; C, bending angle as a black solid line connecting the three points (center of mass of the β-propeller and βA domains, center of mass of the PSI domain, and center of mass of the calf-2 and β-tail domains); D, splaying angle as a black solid line connecting the three points (center of mass of C^α atoms of Leu⁷⁸⁸ and Gly⁷⁹⁶ in the calf-2 domain, center of mass of the C^α atoms of Cys⁶⁰² and Cys⁶⁰⁸ in the thigh domain, and center of mass of C^α atoms of Glu¹⁵⁵⁷ and Val¹⁵⁶¹ in the β-tail domain).

Conformational changes of the ectodomains of α_IIbβ₃ HPA-1 isoforms toward a more open, extended conformation

To further characterize the structural differences between the α_IIbβ₃ isoforms, we monitored geometric parameters along the MD trajectories that have been linked with conformational changes of the ectodomain from an inactive to an active state (18, 27) (Fig. S6 and Table S7). First, we investigated possible variations in the region of the center of helix α1 and the N terminus of helix α7 (27, 37). This region was shown to form a “T-junction” upon activation (21, 27). We computed the kink angle of helix α1 (Fig. 3B), which revealed a mean value over three MD trajectories that is larger by 15° in the Pro³³ (∼153 ± 1.5°) than the Leu³³ isoform (∼138 ± 2.8°) (Fig. 3B). Hence, helix α1 straightens more in Pro³³ and thus shows a stronger tendency to form the T-junction than in Leu³³. The spread in the mean values found for Pro³³ (Table S7) resulted from a rapid and pronounced increase of the kink angle, which was initially ∼143° (calculated from Protein Data Bank code 3FCS), within the first 200 ns in two of the three MD simulations (Fig. S6A).

Second, we evaluated the unbending of the structure in terms of the separation of the head region and the terminal part of the legs (calf-2 domain and β-tail) (Fig. 3C). Furthermore, we monitored the spatial separation (splaying) of the integrin's legs (Fig. 3D). Similar parameters were successfully used previously (18). The bending angle was ∼7° larger in the Pro³³ (∼49 ± 1.8°) than in the Leu³³ isoform (∼42 ± 1.4°) (Fig. 3C, Fig. S6B, and Table S7). The splaying angle was ∼3° larger in Pro³³ (∼28 ± 0.5°) than in Leu³³ (∼25 ± 0.2°) (Fig. 3D, Fig. S6C, and Table S7). In the latter case, in two MD simulations, the time evolution of the splaying angle revealed a decrease of ∼22° within the last 200 ns of the simulation (Fig. S6C). The differences between angles in the Leu³³ and Pro³³ isoforms were significant in all cases (Table S7). As additional indicators of structural changes, we evaluated the opening of the structure in terms of changes in internal distances between the N and C termini of each subunit and between the C termini of the two subunits (Fig. S6D). All evaluated distances were larger in the Pro³³ than the Leu³³ isoform, and the differences between respective distances were significant in all cases (Table S8). To conclude, our results revealed significant differences in the conformational states of both α_IIbβ₃ isoforms with the ectodomain of Pro³³ displaying a stronger tendency to move toward the extended conformation with more splayed legs.

Experimental evidence for spatial rearrangements of the cytoplasmic tails of α_IIbβ₃ upon Leu → Pro exchange

To investigate a possible influence of the Leu → Pro exchange on the spatial separation of α and β subunits, we performed FRET acceptor photobleaching (APB) analyses in individual cells transfected with α_IIbmVenus and β₃Leu³³mCherry (HPA-1a) (Table S1) or β₃Pro³³mCherry (HPA-1b) (Table S2) plasmids, respectively. Using FRET, the spatial separation of the subunits is inferred from the amount of energy transferred between the fluorescent proteins mVenus and mCherry attached to the cytoplasmic tails of the subunits.

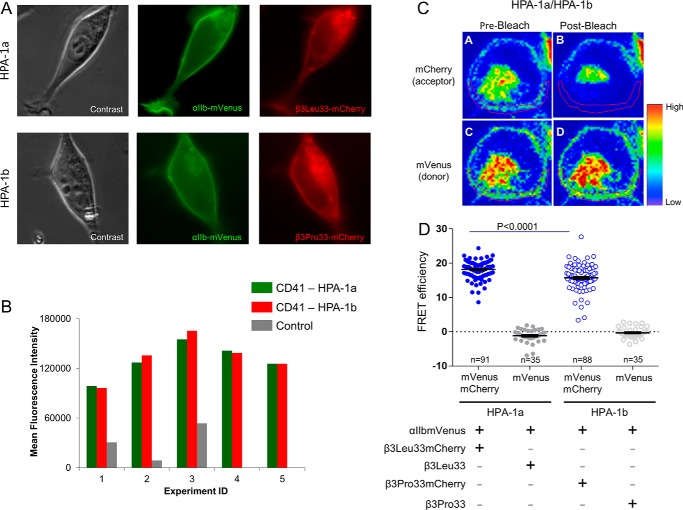
By fluorescence microscopy performed 48 h after transfection, we verified that both subunits were colocalized at the cell membrane (Fig. 4A). Concordant with the presence of the integrin at the plasma membrane, we detected the complete α_IIbβ₃ receptor (recognized by a complex-specific anti-α_IIbβ₃ antibody, anti-CD41, clone MEM-06) by flow cytometry. Functional integrity of both integrin isoforms and correct membrane insertion were documented by intact activation of α_IIbβ₃ in transfected cells upon phorbol 12-myristate 13-acetate–induced stimulation of protein kinase C and specific binding of Alexa Fluor 647-fibrinogen to α_IIbβ₃ upon inside-out activation (38). Notably, flow cytometry measurements of CD41 expression upon five independent transfection experiments indicated that the levels of α_IIbβ₃ expressing either the Leu³³ (HPA-1a) or the Pro³³ (HPA-1b) isoform did not differ more than 10% from each other (Fig. 4B).

Figure 4.

Transient expression of the complete α_IIbβ₃ receptor in HEK293 cells. A, phase-contrast and fluorescence microscopy images of a representative HEK293 cell transfected with α_IIbmVenus and β₃Leu³³mCherry plasmids (upper panel) and a representative HEK293 cell transfected with α_IIbmVenus and β₃Pro³³mCherry plasmids (lower panel). B, flow cytometric analyses of α_IIbβ₃ (CD41), expressing either isoform Leu³³ (HPA-1a) or Pro³³ (HPA-1b), performed 48 h after transfection in five independent experiments. Of note, the transfectants displayed less than 10% difference in α_IIbβ₃ expression of either Leu³³ (HPA-1a) or Pro³³ (HPA-1b) isoform. Values represent mean fluorescence intensity after staining of the transfectants with APC-conjugated CD41 antibody, a complex-specific anti-α_IIbβ₃ antibody. C, FRET-APB measurements in a representative HEK293 cell transfected with α_IIbmVenus and β₃Leu³³mCherry plasmids. D, results of FRET efficiency of fused individual Leu³³ (HPA-1a) or Pro³³ (HPA-1b) cells and respective donor controls. To determine the efficiency of energy transfer, the fluorescence of mVenus was measured in a defined region of the membrane (red circled) before and after photobleaching of mCherry at 561 nm (39, 40). Details are given under “Experimental procedures.” The error bars indicate mean ± S.E.

Using these transfectants, photobleaching of mCherry at 561 nm on a defined cellular region (region of interest) encompassing part of the cell membrane led to a complete loss of energy transfer and, consequently, to an increase in mVenus fluorescence intensity (Fig. 4C). For a control, cells were transfected with α_IIbmVenus and β₃Leu³³ or β₃Pro³³ plasmids (without mCherry), a condition that abrogated any energy transfer (data not shown). To focus on non-activated α_IIbβ₃ transfectants, as evidenced by absence of binding of Alexa Fluor 647-fibrinogen or PAC1, an activation-dependent anti-α_IIbβ₃ monoclonal antibody (data not shown), cells were left resting on chamber slides with culture medium for 24 h prior to FRET analyses, all of which were subsequently carried out with minimal manipulation of the cells to prevent any possible cellular activation.

FRET-APB analyses were performed in a total of 249 single cells: 91 Leu³³ cells, 88 Pro³³ cells, 35 Leu³³ donor control cells, and 35 Pro³³ donor control cells. FRET-APB efficiency was computed according to Equation 2 (see “Experimental procedures” and Refs. 39 and 40). Notably, FRET-APB efficiency between mVenus and mCherry in Leu³³ cells (mean ± S.E., 18.20 ± 0.276) was significantly higher (p < 0.0001) than in HPA-1b cells (15.74 ± 0.395) (Fig. 4D). This difference in energy transfer upon photobleaching of both α_IIbβ₃ isoforms suggested a larger spatial separation in the Pro³³ than the in Leu³³ isoform when both isoforms were examined in their bent conformation. This observation is indicative of a state more prone to activation as a consequence of the Leu → Pro exchange at residue 33 in the ectodomain of the β subunit of α_IIbβ₃.

Short- and mid-range structural, dynamics, and stability changes induced by the Leu → Pro exchange

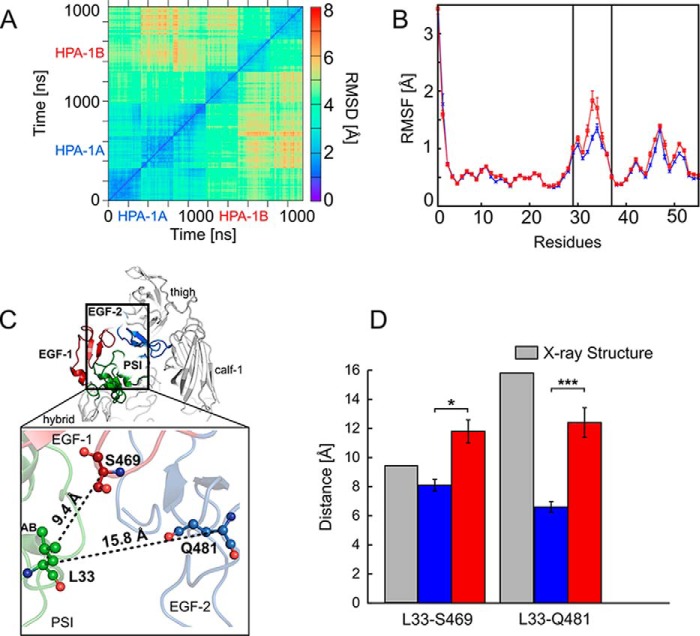
The two-dimensional (2D) RMSD of C^α atoms of the EGF-1/EGF-2/EGF-3 domains along the MD trajectories was computed after mass-weighted superimposition onto the respective starting structures of the domains. The 2D RMSD values indicated that the domains showed larger differences from the initial starting structure in the Pro³³ than in the Leu³³ isoform (see also Table S4) but also that the two isoforms adopted conformational states that largely deviated from each other (RMSD up to 8 Å) (Fig. 5A). Next, we computed the residue-wise root-mean-square fluctuations (RMSFs) of the PSI domain, a measure of atomic mobility, to identify differences in the conformational variations associated with the Leu → Pro exchange. The results revealed a marked increase in atomic mobility for residues Glu²⁹–Pro³⁷ of the loop between strands A and B in the PSI domain (Fig. 5B) with a ∼0.6-Å difference found at residue 33 (Leu or Pro). Beyond this region, the amino acid exchange did not affect the atomic mobility (Fig. 5B). Likewise, we did not detect significant differences in the secondary structure propensity of the AB loop residues between the Leu³³ and Pro³³ isoform except for a small decrease of the α-helix propensity in the helix C-terminal to the loop (Fig. S7). To conclude, in both isoforms, the PSI domain did not undergo marked changes in structure (see also Table S4) as a consequence of the polymorphism at residue 33 of the β₃ subunit. This was in contrast to the EGF domains, which revealed marked structural changes in Pro³³. However, the structural dynamics of the AB loop of the PSI domain increased in the Pro³³ variant.

Figure 5.

Short- and mid-range structural and dynamics changes induced by the Leu → Pro exchange. A, 2D RMSD plot calculated for the C^α atoms of the EGF-1, EGF-2, and EGF-3 domains after superimposing onto the respective domains. All trajectories accounting for an aggregate simulation time of 2 × 3 μs were considered together in the analysis, excluding the first 200 ns of each trajectory and extracting frames at intervals of 100 ns. B, residue-wise mean backbone RMSF of the PSI domain after a mass-weighted fitting onto the starting structure. Error bars denote S.E. Blue and red curves represent the Leu³³ and Pro³³ isoforms, respectively; the two black lines delineate the AB loop (residues Glu²⁹–Pro³⁷). C, α_IIbβ₃ is shown in schematic representation and colored in light gray (with the exception of the PSI domain (green), EGF-1 domain (firebrick), and EGF-2 domain (marine)). Domains are labeled. The enlargement shows the location of the Leu → Pro exchange in the PSI domain within the genu interface of the β₃ subunit. Black dashed lines indicate distances computed in D with the distance values of the starting structure reported next to them. Residues Leu³³ (PSI domain), Ser⁴⁶⁹ (EGF-1 domain), and Gln⁴⁸¹ (EGF-2 domain) are depicted in ball-and-stick representation. D, mean distances between the C^α atoms of Leu³³/Pro³³ as well as Ser⁴⁶⁹ (EGF-1) and Gln⁴⁸¹ (EGF-2) calculated for the Leu³³ isoform (blue boxes) and the Pro³³ variant (red boxes) and measured in the crystal structure (Protein Data Bank code 3FCS; gray boxes). Error bars indicate mean ± S.E., and asterisks denote a significant difference (*, p < 0.05; ***, p < 0.0001) between the two isoforms of α_IIbβ₃.

As this loop faces the EGF-1 and EGF-2 domains (41), the Leu → Pro exchange may also impact the structure, interactions, and stability of this interface. Therefore, we monitored the time evolution of the distance between the C^α atoms of residue Leu³³ or Pro³³ and Ser⁴⁶⁹ and Gln⁴⁸¹ to investigate the level of compactness of the interface between the PSI domain and the EGF-1/EGF-2 domains (Fig. 5C). In the bent conformation of α_IIbβ₃, the C^α atom at residue 33 is separated by 9.4 and 15.8 Å from the C^α atoms of Ser⁴⁶⁹ and Gln⁴⁸¹ (calculated from Protein Data Bank code 3FCS), respectively.

Comparing both isoforms of α_IIbβ₃, we found a mean value for the Leu/Pro³³···Ser⁴⁶⁹ distance that is smaller by ∼3.7 Å in Leu³³ (∼8.1 ± 0.40 Å) than in Pro³³ (∼11.8 ± 0.79 Å). A mean value smaller by ∼5.8 Å in Leu³³ (∼6.6 ± 0.37 Å) than in Pro³³ (∼12.4 ± 1.02 Å) was found for the Leu/Pro³³···Gln⁴⁸¹ distance. The differences between distances in the Leu³³ and Pro³³ isoforms were significant in all cases (Fig. 5D and Table S9). The pronounced decrease from the initial structure observed in the Leu³³ isoform (∼9 Å) for the Leu³³···Gln⁴⁸¹ distance is in line with the description of a contact area between these two domains in the closed, low-affinity, bent state (41). This contact is lost in the extended conformation (41). These results indicated that the interface between the PSI domain and the EGF-1/EGF-2 domains is more tightly packed in the Leu³³ than in the Pro³³ isoform.

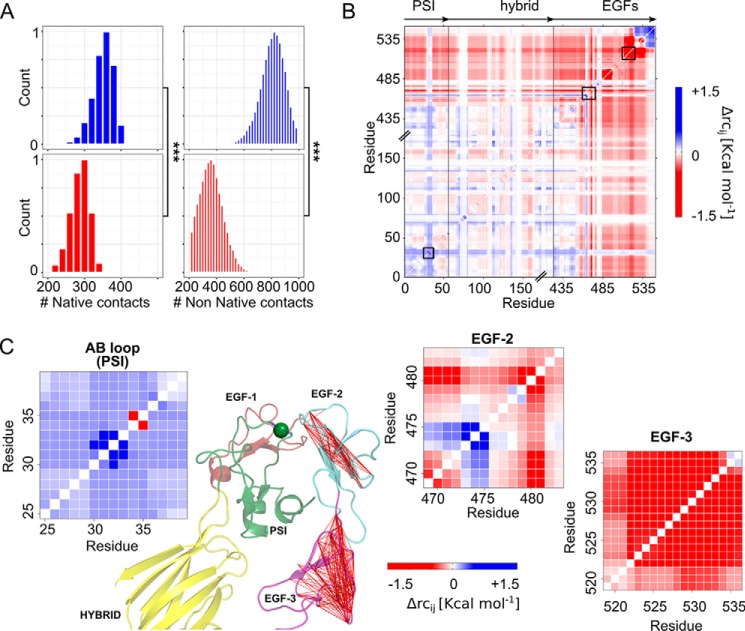
In addition, we computed the number of contacts present in the starting structure (“native contacts”) and those formed over the course of the MD simulations (“non-native contacts”). Contacts were evaluated between the nine residues of the AB loop and residues of the adjacent EGF-1 and EGF-2 domains, applying a distance cutoff of 7 Å between the side-chain atoms. In all three MD simulations of the Pro³³ variant, the total number of contacts was significantly lower than in the Leu³³ isoform (Fig. 6A and Table S10). This difference became even more pronounced when only non-native contacts were considered (2-fold decrease). The same holds true for specific interactions (hydrogen bonds and salt bridges) that were conserved in the Leu³³ isoform only (Fig. S8). In the segment connecting the EGF-1 domain with the EGF-2 domain, Gln⁴⁸¹ is hydrogen-bonded to Ser⁴⁶⁹ with a high occupancy (∼70% along the MD trajectories) and/or with Gln⁴⁷⁰ (∼27%). Additional stable intradomain hydrogen bond interactions (>60%) were found within the EGF-2 domain that involve Cys⁴⁹², which also forms a disulfide bridge with Cys⁴⁷³ of the EGF-1 domain (Fig. S8). To conclude, the Leu → Pro exchange leads to a less compact interface between the PSI domain and EGF-1/EGF-2 domains. Moreover, fewer interactions across the interface and within the EGF-1/EGF-2 domains were found in the Pro³³ variant compared with the Leu³³ isoform.

Figure 6.

Changes within the PSI/EGF domain interface and in the structural stability between the Leu³³ and Pro³³ isoforms. A, shown are the active contacts (left) and non-native contacts (right) formed between the AB loop (PSI domain) and all the side chains located within a distance range of 7 Å. Mean values were computed over three MD simulations of the Leu³³ isoform (blue histograms) and Pro³³ variant (red histograms). Asterisks denote a significant difference (***, p < 0.0001) between the two isoforms of α_IIbβ₃. B, difference stability map generated by CNA and averaged over three MD simulations showing the difference in structural stability between both isoforms, focusing on the β₃ genu region. The color gradient indicates residues with lower structural stability in the Leu³³ (blue) or Pro³³ isoform (red). C, enlargements of three areas highlighted within the difference stability map by black boxes (B) and corresponding to the AB loop (PSI domain), residues Ser⁴⁶⁹–Asp⁴⁸⁴ (loop connecting the EGF-1 domain to the EGF-2 domain), and residues Gly⁵¹⁹–Cys⁵³⁶ (EGF-3 domain), exemplifying changes in structural stability due to the Leu → Pro exchange. The results for the latter two regions are also displayed on the structure of the hybrid (yellow), PSI (green), EGF-1 (firebrick)/EGF-2 (light blue)/EGF-3 (purple) domains of α_IIbβ₃ (green sphere, C^α atom of residue 33) in terms of lines connecting residues whose mutual stability has decreased in the Pro³³ isoform (Δrc_ij > −1.5 kcal mol⁻¹).

Changes in structural stability of the EGF domains occur at long range from residue 33

To analyze changes in the structural stability of the interface between the PSI domain and EGF-1/EGF-2 domains resulting from the Leu → Pro exchange, we performed Constraint Network Analysis (CNA) on the β₃ leg (hybrid domain/PSI and EGF domains) of both α_IIbβ₃ isoforms, Leu³³ and Pro³³. In CNA (42), a molecular system is represented as a network of nodes (atoms) connected by constraints (non-covalent bonds). This network is analyzed applying rigidity theory (43), revealing rigid (i.e. structurally stable) clusters and flexible links in between (44). By rigidity analysis, long-range effects on the stability of distant structural parts due to a local structural change can be detected (45). Performing a constraint dilution simulation (46), a stability map (42), rc_ij (where i and j are residue numbers), is obtained that reports on the hierarchy of structural stability of the molecular system. The difference stability map calculated as rc_ij (Leu³³) − rc_ij (Pro³³) then reports on the influence on structural stability due to the Leu → Pro exchange (blue (red) colors in Fig. 6, B and C, indicate residues that were less stable in the Leu³³ (Pro³³) isoform, respectively). The AB loop showed a local increase in structural stability, which results from the overconstrained five-membered ring of Pro³³ compared with the flexible side chain of Leu³³ (48) (Fig. 6, B and C). By contrast, the loop connecting the EGF-1 to the EGF-2 domain and pointing toward the AB loop (21), which is >15 Å apart from residue 33, became less stable in the Pro³³ variant (Fig. 6, B and C; the segment formed by residues Ser⁴⁶⁹–Gln⁴⁸¹ is highlighted). The EGF-3 domain, although not directly interacting with the PSI domain, has been suggested to be important for keeping the integrin in its bent conformation (20). Residues Gly⁵¹⁹–Cys⁵³⁶ of the EGF-3 domain >30 Å apart from residue 33 became less structurally stable in the Pro³³ variant. To conclude, the Leu → Pro exchange leads to long-range decreases in the structural stability of the EGF domains.

Discussion

In this study, we provide evidence that indicates that the Pro³³ variant of α_IIbβ₃ allosterically shifts the dynamic conformational equilibrium of the integrin toward a more active state. This finding can provide an explanation for the prothrombotic phenotype of Pro³³ platelets that has been suggested in several clinical association studies (22–25) but also in experimental settings (26, 38, 49).

Both clinical and laboratory data regarding a possible impact of the HPA-1 polymorphism of α_IIbβ₃ on modulating platelet function have been discussed controversially. Specifically, it has been debated whether or not the Leu → Pro exchange at residue 33 of the β₃ subunit induces an increased thrombogenicity of Pro³³ platelets. We therefore initially studied the dynamics of platelet thrombus formation using a collagen type I matrix in an established perfusion system, simulating arterial flow conditions. Quantitation of thrombus growth in vitro demonstrated that the mean volume of single thrombi formed by Pro³³ platelets is significantly higher than that of the Leu³³ platelets (Fig. 2). The initial adhesion of circulating platelets with a collagen matrix is complex, involving platelet capture (“tethering”) by immobilized VWF via GPIbα of the platelet GPIb-IX-V complex, subsequent GPIb-IX-V–dependent signaling, and direct interaction with collagen via α₂β₁ and GPVI, the platelet collagen receptors, inducing platelet activation (50, 51). To block some of these interactions, we therefore used specific monoclonal antibodies such as LJ-Ib1 that completely inhibits VWF binding to the platelet GPIb-IX-V complex or 5C4 that blocks the platelet GPVI receptor (data not shown). The expression of α₂β₁ on the platelet surface is genetically controlled and modulated by nucleotide polymorphisms in the α₂ gene (52). Moreover, because the α₂807TT genotype of α₂β₁ has also been suggested to be a prothrombotic integrin variant (22), volunteers of this series of experiments were carefully selected by recruiting only carriers of the α₂807CC genotype.

A specific feature of the experiments summarized in Fig. 2 is that the difference in single thrombus volumes between Pro³³ and Leu³³ platelets is due to differences in apical thrombus growth (Fig. 2B). This is remarkable, especially because apical thrombus segments become exposed to increasing shear over time, exceeding an initial near-wall shear rate of 500 s⁻¹ (Fig. 2D). Our finding is indicative of a higher thrombus stability of Pro³³ than Leu³³ platelets as reported before (29). By contrast, considering the fact that neither the number nor the bottom area of formed thrombi differs between both isoforms of α_IIbβ₃, it appears rather unlikely that the initial adhesive interactions between the collagen matrix and platelets under flow had a significant effect on the results.

Assuming that the difference in thrombus volumes between both α_IIbβ₃ isoforms is indeed due to increased thrombus stability in the Pro³³ variant, it would be an attractive assumption that the Leu → Pro exchange has an impact on the mechanotransduction mediated by the integrin. Such a contention is in line with previous observations documenting a significantly more stable adhesion of Pro³³ than of Leu³³ platelets onto immobilized fibrinogen at shear rates ranging from 500 to 1,500 s⁻¹ (26). Moreover, it has been shown that the Pro³³ variant displays increased outside-in signaling (53). These findings suggest that the HPA-1 polymorphism of α_IIbβ₃ modulates the function and activity of the integrin.

However, the molecular nature underlying this modulation has remained elusive so far. In this context, a marked concern in the past has been that the point mutation at residue 33 of the β₃ subunit is located >80 Å away from relevant functional domains of α_IIbβ₃ such as extracellular binding sites or transmembrane domains. Conversely, due to its distant location, it appears quite appropriate to exclude that the Leu → Pro exchange would directly influence interactions with ligands at the extracellular or even intracellular binding sites. It is more likely that an increased activity of α_IIbβ₃ results from a change in the structural dynamics of the integrin. To probe this assumption, we performed microsecond-long MD simulations on the ectodomains of both α_IIbβ₃ isoforms, Leu³³ and Pro³³. The ectodomains of either isoform initially only differed in the side chains of residue 33.

Ectodomains of integrins have been successfully used by us (18, 27) and others (34, 54) in previous studies as model systems to explore possible influences of structure and solvent on integrin activation. For the MD simulations, we used established parameterizations for the solvent (55) and the protein (56, 57), which we had applied successfully in other integrin simulations (18, 27, 37), although we note that more recent protein force fields have become available (58, 59). The impact of force field deficiencies on our results is expected to be small due to cancellation of errors when comparatively assessing the two isoforms. Furthermore, we expect the deficiency of the ff99SB force field (56, 57) to destabilize helical structures (60) to not have a decisive influence on our results because the mutation site (residue 33) is located in a loop region. Finally, ff99SB was also shown to have some issues with side-chain torsions (61). As Leu³³ is located at the vertex of the AB loop, with the side chain facing away from the β₃ subunit, we do not expect imperfect leucine torsions to impact structural properties markedly however.

The present simulations were started from the bent conformation with closed legs as present in the crystal structure (62), representing a low-affinity, inactive state of the integrin (63). As depicted, our simulation findings reveal that the Pro³³ variant displays significantly larger structural deviations from the bent starting structure and becomes less compact than the Leu³³ isoform (Fig. 3). Furthermore, we evaluated geometric parameters within the βA domain (“T-junction formation” between helices α1 and α7; Fig. 3B) and variables characterizing the bending and splaying of the structure (Fig. 3, C and D), which had been used successfully in related studies to characterize inactive-to-active transitions (27, 37, 64). The results display significant differences in the conformational states of both isoforms of α_IIbβ₃ with the ectodomain of the Pro³³ variant showing a stronger tendency to move toward an open, extended conformation with more splayed legs than the Leu³³ isoform. We performed triplicate MD simulations for both isoforms, which allows probing for the influence of the starting conditions and determining the significance of the computed results by statistical testing and rigorous error estimation. As to the latter, we paid close attention to only consider uncorrelated instances for the S.E. calculations (Equations 1 and 2).

The results are consistent across three independent MD simulations for each isoform. This demonstrates the robustness of our approach. We are aware that the magnitudes of the changes of the bending or splaying angles do not correspond to those described for a fully open, extended ectodomain conformation (8). However, in consideration of the simulation times used here, this finding is in complete accord with the timescale of integrin activation in the absence of biomechanical forces, ranging from microseconds to seconds (34, 35).

As an independent approach to explore the impact of the Leu → Pro exchange on the structural dynamics of full-length α_IIbβ₃ integrin, FRET measurements on α_IIbmVenus and β₃Leu³³mCherry or β₃Pro³³-mCherry transiently cotransfected in HEK293 cells were performed (Fig. 4, A–C). HEK293 cells have previously been shown to be a suitable cellular model for functional studies involving α_IIbβ₃ (65, 66). The transfectants display a significantly higher efficiency of energy transfer between the α and β subunits in the Leu³³ than in the Pro³³ isoform. This difference is indicative of a smaller spatial separation between the cytoplasmic tails of the Leu³³ isoform in its resting state. Conversely, the lower energy transfer obtained in the Pro³³ variant reflects a larger spatial separation of its cytoplasmic domains that is already present in the resting state (Fig. 4D). A limitation of the FRET method is that it furnishes indirect information. However, the level of evidence is consistent, and the observation is in good agreement with the findings of the MD simulations. A direct study comparing activity and stability of both receptor isoforms using purified protein would provide complementary information about receptor conformations but was beyond the scope of the present work.

Taken together, both the MD simulations and FRET experiments reveal structural changes in the ectodomain of α_IIbβ₃ or the full-length integrin for the Pro³³ variant that relate to a conformational change from a closed, bent structural state with closed legs to a more open, extended state with splayed legs. According to current models (14, 16, 33), such a conformational change is required for integrin activation. Considering that in both the MD simulations and FRET measurements the integrin has been examined in the resting state, our results provide evidence that the Leu → Pro exchange can shift the dynamic conformational equilibrium of α_IIbβ₃ in such a way that a structural state more similar to the active conformation is present.

The effect of the Leu → Pro exchange appears to have some similarity to stimulatory monoclonal antibodies, which have been suggested to shift the dynamic conformational equilibrium in favor of those forms that lead to an increase in the proportion of a high-affinity integrin (62). As the effect induced by the amino acid substitution manifests in regions far away from the mutation site, the influence of the Leu → Pro exchange must be allosteric. Our results clearly go beyond a previous study (67) that used MD simulations of the β₃ subunit only to investigate possible effects of the HPA-1 polymorphism on the structure of the β₃ subunit.

To explore a possible mechanism of how the Leu → Pro exchange exerts an allosteric effect, applying MD simulations and rigidity analyses, we examined short- and mid-range structural, dynamics, and stability changes in the PSI domain and neighboring domains. Although the overall architecture of the PSI domain remains largely unchanged by the amino acid substitution, particularly the EGF domains show marked structural alterations in the Pro³³ variant (Fig. 5). The EGF-1 and EGF-2 domains, although sequentially distant from the mutation located at residue 33, are spatially close to the AB loop of the PSI domain in the bent state, which carries the HPA-1 polymorphism (5, 19, 21). Parts of the AB loop are markedly more mobile in the Pro³³ variant (Fig. 5B). Related to these changes, our analyses reveal that the Leu → Pro exchange leads to a less compact interface between the PSI domain and EGF-1/EGF-2 domains (Fig. 5, C and D). Specifically, fewer native and non-native contacts are formed across the interface and within the EGF-1/EGF-2 domains in the Pro³³ variant than in the Leu³³ isoform (Fig. 6A). These conformational and dynamic alterations are related to a change in the structural stability of the EGF-1 and EGF-2 domains that percolates from the interface region through these domains (Fig. 6, B and C).

Notably, similar changes in these regions have been related to integrin activation before. For example, the displacement of the PSI domain of about 70 Å, described to act as a mechanical lever upon outside-in signaling (21), alters the interface formed with the EGF-1 and EGF-2 domains (68). Furthermore, activating mutations have been identified in the N-terminal part of the PSI domain, the EGF-2 domain, and parts of the EGF-3 domain of α_xβ₂ integrin (20). These regions are thought to form the area of contact between α and β subunits in the bent conformation. Finally, when generating an integrin chimera by combining α and β subunits from different species, direct interactions between the subunits could not be formed, and the integrin no longer appeared locked in the closed conformation (20).

The results of this study provide an explanation for the prothrombotic phenotype of the Pro³³ variant of α_IIbβ₃. Specifically, the shift of the dynamic conformational equilibrium of the Pro³³ variant toward an active state may promote a fully active state in the presence of immobilized adhesive ligands such as fibrinogen or VWF and, consequently, favor outside-in signaling. This, in turn, may facilitate and accelerate platelet aggregation and subsequent formation of stable platelet thrombi. Thus, our results lend support to previous clinical (22–25, 29, 49) and experimental findings (26, 29, 38, 49) suggesting that the Leu → Pro exchange confers prothrombotic properties to α_IIbβ₃.

Experimental procedures

Blood collection

Blood was collected through a 21-gauge needle from 15 healthy, medication-free volunteers into vacutainer tubes (BD Biosciences) containing sodium citrate (0.38%, w/v). The volunteers were recruited by the Düsseldorf University Blood Donation Center. Written informed consent was obtained from the volunteers according to the Helsinki Declaration. The Ethics Committee of the Faculty of Medicine, Heinrich Heine University Düsseldorf, approved the study (study number 1864).

Parallel plate flow chamber

A custom-made rectangle flow chamber was used (flow-channel width, 5 mm; height, 80 μm; length, 40 mm). Glass coverslips forming the lower surface of the chamber were flame-treated, cooled, and coated with 0.04 μml/mm² collagen type S (concentration, 3 mg/ml) containing 95% type I and 5% type III collagen (Roche). The perfusion system was flushed and filled with PBS buffer (pH 7.3) containing 2% BSA to block unspecific adhesion onto the glass slides. A syringe pump (Harvard Apparatus Inc., Holliston, MA) was used to aspirate mepacrine-labeled citrated whole blood through the flow chamber for 10 min at a constant flow rate of 9.6 ml h⁻¹, producing an initial near-wall shear rate of 500 s⁻¹.

Labeling of platelets

Platelets were stained in whole blood by direct incubation with the fluorescent dye mepacrine (quinacrine dihydrochloride; 10 μm final concentration). Although this dye also labels leukocytes, these cells could be readily distinguished from platelets by their relatively large size and sparsity; moreover, leukocyte attachment to the surface tested was negligible under the conditions used. Mepacrine accumulates in the dense granules of platelets and had no effect on normal platelet function at the concentration used. Platelet secretion after adhesion did not prevent their visualization. Furthermore, mepacrine did not affect platelet adhesion or platelet aggregate/thrombus formation.

Picture acquisition and digital image processing

The fluorescence signal of mepacrine-stained platelets was detected by a Zeiss Axiovert 100 M/LSM 510 confocal laser scanning microscope (Jena, Germany). During the flow period of 10 min, 25 stacks of images were acquired. One stack consisted of 30 slices with a height of 30 μm. Digitized images had a standard size of 512 × 512 pixels and an optical resolution of 1 μm.

Volumetry of single platelet thrombi

The stacks were reconstructed three-dimensionally and analyzed with the custom-made software package ECCET (www.eccet.de).⁵ The software integrated the slices of every stack and divided the three-dimensional space into multiple “voxels” (three-dimensional equivalent to a pixel). All fluorescence signals were smoothed by a separate linear Gaussian filter in all three planes (filter σ2). Voxels with a gray value >10 were marked as thrombus; voxels with lower gray values were disregarded. Thus, background noise of fluorescence signals from adjacent focus planes and single platelets was suppressed. Thrombi were then categorized by volume, and only platelet aggregates exceeding the cutoff volume of 100 μm³ were assessed to avoid interference by non-stationary objects, e.g. moving platelets.

Starting structures for molecular dynamics simulations

The starting structure for MD simulations of α_IIbβ₃ in the bent, closed form representing the inactive state of the Leu³³ isoform was obtained from the coordinates of the X-ray structure of the ectodomain of α_IIbβ₃ integrin (Protein Data Bank code 3FCS) (9). In the Protein Data Bank entry, the α_IIb subunit contains two unresolved regions within the calf-2 domain (residues 764–774 (AB loop) and 840–873 (XY loop)), and the β₃ subunit has two unresolved regions within the EGF domains (residues 75–78 and 477–482). Residues unresolved in the α_IIb subunit were not included in the starting structures, consistent with our previous studies on integrin (18, 27). The apparently high flexibility of these residues implies that they will not contribute significantly to stabilizing the bent conformation of the α_IIbβ₃ integrin. The short regions of unresolved residues of the β₃ subunit were modeled and refined using the automatic loop refinement server ModLoop (69). The structure was finally refined by reverting the engineered residues Cys⁵⁹⁸ and Cys⁶⁸⁸ to the natural residues Leu⁵⁹⁸ and Pro⁶⁸⁸, respectively. MODELLER version 9.9 (70) was applied, allowing the modeling of the two Cys residues only. The Pro³³ variant was obtained by mutating residue Leu³³ to Pro³³, using Swiss-PdbViewer (31), without changing the coordinates of any of the other amino acids. As a final step, we capped the charges at the N-terminal residues Glu⁷⁶⁴ and Gly⁸⁴⁰ and the C-terminal residues Asp⁷⁷⁴ and Gln⁸⁷³ using the leap module of Amber 12 (71). All structural ions present in the protein were modeled as Mg²⁺ ions. Integrin sequence numbers used throughout this study are according to UniProt.

Molecular dynamics simulations

Each starting structure of the two HPA-1 isoforms, Leu³³ and Pro³³, was subjected to three replicates of all-atom MD simulations of 1-μs length each in explicit solvent summing up to 6 μs of aggregate simulation time for production. MD simulations were performed with the Amber 12 suite of programs (71) using the force field ff99SB, initially described by Cornell et al. (56) and modified according to Simmerling and co-workers (57). Parameters for the Mg²⁺ ions were taken from Aqvist (72). The total charge of the system was neutralized by adding eight Na⁺ counter-ions with the leap module of Amber 12 (71), and the solutes were placed into an octahedral period box of TIP3P water molecules (55). The distance between the edges of the water box and the closest atom of the protein was at least 11 Å, resulting in systems of ∼200,000 atoms. The particle mesh Ewald method (73) was used to treat long-range electrostatic interactions, and bond lengths involving bonds to hydrogen atoms were constrained using the SHAKE algorithm (74). The time step for integrating Newton's equations of motion was 2 fs with a direct-space, non-bonded cutoff of 8 Å. Applying harmonic restraints with force constants of 5 kcal mol⁻¹ Å⁻² to all solute atoms, MD simulations in the NVT (constant number of particles, volume, and temperature) ensemble was carried out for 50 ps, during which the system was heated from 100 to 300 K. Subsequent MD simulations in the NPT (constant number of particles, pressure, and temperature) ensemble were used for 150 ps to adjust the solvent density. Finally, the force constant of the harmonic restraints on solute atom positions was gradually reduced to zero during 100 ps of NVT MD simulations. Subsequently, we performed a 1-μs unrestrained simulation; the first 200 ns were discarded, and the following 800 ns were used for analysis with the programs ptraj/cpptraj (75) with conformations extracted every 20 ps. The production MD simulations were performed with the graphics processing unit (GPU) version of the program pmemd (76).

Analysis of the trajectories

For the analysis of the trajectories, ptraj/cpptraj (75) of the AmberTools suite of programs (71) were applied. For investigating structural deviations along the MD trajectories, the RMSD of all C^α atoms was computed after minimizing the mass-weighted RMSD of the C^α atoms of the βA and β-propeller domains with respect to the starting structure. In addition, to investigate the structural changes of a domain, the C^α atom RMSD of each domain was computed after superimposing the respective domain. To evaluate the level of compactness of the structure, the R_g was calculated with respect to the complete ectodomain. To examine atomic mobility, RMSFs were computed for the backbone atoms of the PSI domain. An analysis of the secondary structure of the PSI domain was carried out to monitor variations in the content of the two helices bordering the AB loop. Structural changes in the ectodomain were characterized as reported previously (18, 27). The kinking of the helix α1 was measured by the three points (center of mass of C^α atoms of Lys¹¹² and Ile¹¹⁸, center of mass of C^α atoms of Gln¹¹⁹ and Lys¹²⁵, and center of mass of C^α atoms of Leu¹²⁶ and Leu¹³²). The unbending of the structure was evaluated using the angle formed by the centers of mass of the β-propeller, βA, and PSI domains, and the splaying of the two legs was evaluated using the angle formed by the centers of mass of the calf-2, thigh, and β-tail domains. Changes in the β₃ genu region were first quantified by computing the distances between the C^α atom of residue 33 and the C^α atom of Ser⁴⁶⁹ (EGF-1 domain) and with the C^α atom of Gln⁴⁸¹ (EGF-2 domain). To identify a network of interactions keeping the interdomain interface stable, a maximal distance of 3.5 Å and a minimal angle of 120° were used as exclusion criteria to identify hydrogen bond formation.

The CNA software package was used to provide a link between structure and rigidity/flexibility of the HPA-1 isoforms (77). To derive information of the effect of Pro³³ on a local level, we first generated an ensemble of 400 equally distributed structures from the 200–1,000-ns intervals of each MD simulation, considering only the hybrid, PSI, and EGF block domains. Thermal unfolding simulations of the Leu³³ and Pro³³ isoforms were then carried out with CNA to identify differences in the structural stability within the β₃ genu region following established protocols (77). For each isoform, we generated three different stability maps and three different neighbor stability maps; from them we calculated the mean values used to build a final stability map and neighbor stability map for Leu³³ and Pro³³. Finally, a difference stability map was calculated as rc_ij (Leu³³ isoform) − rc_ij (Pro³³ isoform).

Statistical analysis

Results from three independent MD simulations are expressed as arithmetic means ± S.E. calculated over the time. The overall S.E. for each simulated system was calculated according to the law of error propagation (Equation 1),

$$\text{S}.\text{E}{.}_{\text{total}}=\sqrt{\text{S}.\text{E}.{\hspace{0.17em}}_1^2+\text{S}.\text{E}.{\hspace{0.17em}}_2^2+\text{S}.\text{E}.{\hspace{0.17em}}_3^2}$$ (1)

where the subscripts i = {1, 2, 3} indicate the three trajectories. S.E._i was computed following Ref. 78 and applying the multiple Bennett acceptance ratio method (79), which allows detecting the decorrelation time of an investigated variable along each MD simulation. From it, the effective sample size is established, and the S.E._i is derived.

In the case of hydrogen bond and contact analyses, S.E. is calculated from the S.D. of the three means of the three MD simulations according to Equation 2, assuming that the three MD simulations are statistically independent.

$$\text{S}.\text{E}.=\text{S}.\text{D}.\hspace{0.17em}/\hspace{0.17em}\sqrt{3}$$ (2)

Differences between mean values are considered statistically significant if p < 0.05 and p < 0.001 (indicated as * and **, respectively, in figures and tables) and highly statistically significant if p < 0.0001 (indicated as ***) according to the Student's t test for parametric testing. The statistical analysis was performed using R software (80) and the pymbar module for multiple Bennett acceptance ratio (79).

The FRET efficiency results obtained performing the FRET-AB experiments are expressed as means ± S.E. For statistical analysis, the unpaired t test was applied using GraphPad Prism version 6.00 for Windows (GraphPad Software, La Jolla, CA).

Figure preparation

The crystal structure of the α_IIbβ₃ integrin (Protein Data Bank code 3FCS) was used to represent the protein together with conformations extracted from the MD trajectories. PyMOL was used to generate molecular figures (36), and graphs were prepared using Gnuplot (47).

Live-cell imaging of α_IIbβ₃-transfected HEK 293 cells expressing either isoform Leu³³ or Pro³³

Live-cell imaging was performed to examine the cellular distribution of α_IIbβ₃-transfected HEK 293 cells expressing either isoform Leu³³ or Pro³³. 24 h after transfection, 3.7 × 10⁴ cells in complete culture medium were allowed to settle for more 24 h in individual chambers in a μ-slide 4-well ibiTreat chamber slide (Ibidi, Martinsried, Germany) previously coated with 50 μg/ml fibrinogen from human plasma (Sigma-Aldrich) in PBS without Ca²⁺ and Mg²⁺ for 1 h at 37 °C. Live-cell imaging was performed with an Axiovert S100 inverted fluorescence microscope (Zeiss) equipped with a 12.0 Monochrome without IR-18 monochromatic camera (Diagnostic Instruments, Inc, Sterling Heights, MI) and an LEJ EBQ 100 isolated lamp (Leistungselektronik Jena GmbH, Jena, Germany). Images were obtained with a 63× oil immersion objective lens using a 5,000-ms exposure time for mVenus, 100 ms for mCherry, and 300 ms for brightfield. Image acquisition was performed with MetaMorph software (version 7.7.7.0). Background subtraction and image processing were performed using Adobe Photoshop CS3 software (Adobe, San Jose, CA).

Flow cytometry

Transfected cells at 70–80% confluence were harvested 24, 48, and 72 h after transfection. Subsequently, cells were pelleted by centrifugation at 400 × g for 7 min and suspended again in 100 μl of Dulbecco's phosphate-buffered saline (PBS). Staining with allophycocyanin (APC)-conjugated mouse anti-human CD41 monoclonal antibody (clone MEM-06; Exbio, Praha, Czech Republic; 0.15 μg/ml) was performed for 30 min at room temperature protected from light. After staining, cells were washed once in Dulbecco's PBS and analyzed on a FACS Canto II flow cytometer (BD Biosciences) equipped with 488 and 633 nm lasers for excitation and FITC, phycoerythrin, and APC filters for detection of mVenus, mCherry, and APC, respectively. The collected data were analyzed with FACSDiva software version 6.1.3 (BD Biosciences). PAC1 was obtained from BD Biosciences, and Alexa Fluor 647-fibrinogen was from Thermo Fisher Scientific (Dreieich, Germany).

FRET measurements using APB

24 h after transfection, cells were harvested and seeded in a μ-slide 8-well ibiTreat chamber slide (Ibidi). Subsequently, 24 h later (48 h after transfection) and before measuring FRET efficiency, the culture medium was substituted by identical medium but containing phenol red–free Fluorobrite^TM DMEM (Thermo Fisher, formerly Life Technologies).

Live cells were examined with an LSM 780 (Zeiss) inverted microscope equipped with a C-Apochromat 40×/1.20 W Corr (from correction ring) M27 water-immersion objective lens, an AxioCam camera, and an HPX 120C lamp. FRET acceptor photobleaching experiments including image acquisition, definition of regions of interest for bleaching, and data readout were performed using the LSM software package ZEN 2012 (Zeiss). The chamber slide containing the live cells was mounted on a heating frame within a large incubation chamber (PeCon, Erbach, Germany) set to 37 °C. mVenus was excited with the 488 nm line of an argon multiline laser and detected between 513 and 558 nm using a gallium arsenide phosphide detector, whereas mCherry was excited at 561 nm using a diode-pumped solid-state laser and detected between 599 and 696 nm. The beam splitter was MBS 488/561/633. In total, a time series of 20 frames (128 × 128 pixels; pixel size, 0.33 μm) at a pixel time of 2 μs/pixel was acquired for each FRET experiment. The entire measurement including bleaching of mCherry was finished within 3.5 s. After the fifth frame, an area corresponding to half of a cell, with a constant dimension of 42 × 42 pixels (region of interest), was bleached by 30 iterations of the mCherry excitation wavelength (561 nm) using 100% laser power. After bleaching, 15 additional frames were recorded. The mean intensity of mVenus fluorescence at the cell membrane within the bleached area was extracted and analyzed according to Equation 3,

$$\text{FRET}\hspace{0.17em}\text{efficiency}=\frac{\left(I_{\text{after}}-I_{\text{before}}\right)}{I_{\text{after}}}\times 100$$ (3)

where I_before (intensity of mVenus before bleaching) and I_after (intensity of mVenus after bleaching) correspond to the mean intensity values of mVenus fluorescence of five images before and after bleaching within the bleached area at the cell membrane (39, 40).

Author contributions

G. P. and J. P. P. data curation; G. P., J. P. P., V. R. S., R. E. S., and H. G. formal analysis; G. P., J. P. P., and V. R. S. validation; G. P. and J. P. P. investigation; G. P. and J. P. P. visualization; G. P., J. P. P., and V. R. S. writing-original draft; G. P., J. P. P., R. E. S., and H. G. writing-review and editing; V. R. S., R. E. S., and H. G. supervision; A. B. software; A. B. methodology; R. E. S. and H. G. conceptualization; R. E. S. and H. G. funding acquisition; R. E. S. and H. G. project administration; H. G. resources.