Phylogenetic Quantification of Intratumor Heterogeneity

Abstract

As sequencing efforts continue to reveal the extent of the intratumor heterogeneity (ITH) present in human cancers, the importance of evolutionary studies attempting to trace its etiology has increased. Sequencing multiple samples or tumor regions from the same patient has become affordable and is an effective way of tracing these evolutionary pathways, understanding selection, and detecting clonal expansions in ways impractical with single samples alone. In this article, we discuss and show the benefits of such multisample studies. We describe how multiple samples can guide tree inference through accurate phasing of germline variants and copy-number profiles. We show their relevance in detecting clonal expansions and deriving summary statistics quantifying the overall degree of ITH, and discuss how the relationship of metastatic clades might give us insight into the dominant mode of cancer progression. We further outline how multisample studies might help us better understand selective processes acting on cancer genomes and help to detect neutral evolution and mutator phenotypes.

THE PROMISES AND CHALLENGES OF ITH STUDIES

In recent years, next-generation sequencing of tumors has revealed the extent of intratumor heterogeneity (ITH) in human cancers and we are slowly beginning to understand its functional consequences and implications for cancer treatment. As a result, targeted therapies have become a cornerstone of both translational cancer research and treatment. Although these therapies frequently show great initial success, they also frequently lead to resistance development in the treated cancers. For example, BRAF or MEK inhibitors for metastatic melanoma trigger impressive initial responses, but invariably the cancer develops resistance to the targeted treatment (Sun et al. 2014). In nonsmall cell lung cancer (NSCLC), activating epidermal growth factor receptor (EGFR) mutations can be targeted using tyrosine kinase inhibitors (TKI), but frequently (∼50% of cases) secondary EGFR mutation T790M leads to resistance (Chan and Hughes 2015). Such escape mutations can arise anew during treatment (acquired resistance), or as the result of clonal expansion of a resistant minor subclone already embedded in presentation disease (adaptive resistance) (Sharma et al. 2017). Unfortunately, many alternative genetic pathways are available for a cancer to achieve resistance. In NSCLC, the second most frequent way to prevent EGFR inhibition is MET amplification through mechanistic target of rapamycin (mTor) signaling, and at least half a dozen other mechanisms are known (Chan and Hughes 2015). Each such mechanism would require different targeted second line treatments, with the potential for further escape mutations. To this day, only few of these resistance pathways are understood, and specific treatments are available for even fewer. Understanding the mutational processes in cancer and the etiology of ITH in detail holds the promise of predicting cancer evolution and ultimately countering escape mutations through combination therapy of mutually exclusive mutations. Although we are not there yet, substantial progress is being made in understanding the patterns governing cancer evolution.

Further progress will require advances in data collection and management. Large-scale collections of cancer studies, such as The Cancer Genome Atlas (TCGA) and the International Cancer Genome Consortium (ICGC), largely consist of pairs of primary tumor and matched normal samples. Multiregion sampling, that is, the collection of multiple samples from the same patient, has many advantages. First, cancers frequently harbor a variety of different subclones with differing clonal frequencies and while deconvolution of these cancer subclones from deep bulk sequencing of a single sample is feasible, its resolution is limited and information about the spatial relationship of the subclones (spatial heterogeneity) is lost. Second, it is usually metastases that kill the patient and a systematic comparison between primary and metastatic samples from the same patient might shed light on the underlying genetics of the metastatic phenotype. However, multiregion genomic data is only slowly gaining popularity because of the high financial and computational costs as well as logistical difficulties.

Once multiregion genomic data has been acquired, we can infer the most likely course that tumor evolution followed through reconstruction of the phylogenetic tree of cancer within a patient. This problem is closely related to traditional phylogenetics: The evolutionary relationship of cells during cancer progression forms a tree and during metastasis tumor cells colonize new habitats. However, there are also new cancer-specific challenges, owing to normal admixture, subclonality and a high frequency of somatic copy-number aberrations (SCNA; for details see, e.g., Beerenwinkel et al. 2015) and overall chromosomal instability (CIN). Here, one encounters an ongoing debate between traditional evolutionary biologists and cancer researchers, in which the former often insist that “all has been done before” and that one simply needs to apply the existing methods, whereas the latter claim that “everything is different in cancer” and that existing methods are not applicable. It seems likely the truth may lie in the middle of these two views and the field would benefit from a closer interaction between the two communities.

After tree reconstruction, we can quantify ITH through summary statistics and compare characteristics of interest between patients. For example, total average tree length, the average number of mutations from the root of the tree to the leaf nodes, describes average mutational burden independent of the number of samples. Temporal or spatial heterogeneity describes the average evolutionary distance between treatment time points (biopsy vs. postchemotherapy vs. relapse) or how frequently the physical sites at which metastases were sampled cocluster in the evolutionary tree (a correlation between evolutionary distance and spatial proximity).

In this article, we will introduce our own efforts to derive such summary statistics. We will discuss how the overall shape of the phylogenetic tree (ladder-like vs. branched) is thought to relate to patient survival in the clinic and how it might be associated with selection pressure on the genomes. We will discuss if and how the phylogenetic relationship between metastases can be used to distinguish radial dissemination from the primary from metastasis-to-metastasis spread (parallel vs. linear modes of cancer progression). Finally, we will touch up on the ongoing debate about neutral evolution in cancer and what branch length distributions tell us about the existence of a molecular clock. We will address these questions mostly from the point of SCNAs and genomic rearrangements. However, much of what is discussed affects general evolutionary principles and is applicable to many different data types.

RECONSTRUCTION OF TUMOR EVOLUTION FROM COPY-NUMBER PROFILES

To test whether ITH is associated with resistance development in the clinic, we conducted the OV03/04 study on high-grade serous ovarian cancer (HGSOC) (Schwarz et al. 2015). HGSOC is a particularly aggressive disease with high tumor burden at presentation and frequently multiple metastases throughout the abdomen. Metastasis occurs through physical shedding of cells into the abdominal cavity, instead of typical lympho-vascular metastasis seen in other cancers. It is characterized by ubiquitous missense mutations in TP53, frequently in combination with a deletion of the second copy, and generally shows a high degree of CIN (Cooke and Brenton 2011). Patients usually respond well to a first round of platinum-based chemotherapy. However, relapse is frequent and often chemotherapy-resistant, with patients who relapse within the first 12 months showing a significant increase in the likelihood of resistance compared with slow responders who have more than 12 months free from progression (Cooke and Brenton 2011).

Because of the abundance of genomic rearrangements in ovarian cancer, we characterized ITH by whole genome SCNA profiles on Affymetrix SNP6 arrays, across a cohort of 20 patients with between 3 and 30 samples per patient taken at initial biopsy, interval debulking surgery, and relapse (Schwarz et al. 2015). We then processed the genomic data to reconstruct the evolutionary history of cancer within each patient (see Box 1) (van de Wiel and Wieringen 2007; Greenman et al. 2010; Van Loo et al. 2010), with the goal of investigating potential associations between ITH and the development of resistance and survival.

BOX 1. Allele-specific somatic copy-number aberrations (SCNA) profiles.

Both next-generation sequencing (NGS) and single nucleotide polymorphism (SNP) microarrays can be used for SCNA profiling. In both cases the analysis follows the same basic procedure. Array intensities of SNP probes or allele-specific read counts are used to determine total DNA content (log ratio/logR) and the B-allele frequency (BAF), defined as the number of reads mapped to the B allele divided by the total read count at that position. LogR and BAF are then used for segmentation using probabilistic models (e.g., PICNIC, [Greenman et al. 2010]) or piecewise constant linear functions (ASCAT, [Van Loo et al. 2010]), which transform raw data into allele-specific integer copy-numbers. Integer profiles can further be compressed using, for example, CGHregions (van de Wiel and Wieringen 2007) before evolutionary reconstruction with MEDICC (Schwarz et al. 2014) (see bitbucket.org/rfs/medicc).

Minimum-Event Distance

Reconstructing the evolutionary relationships between whole genome copy-number profiles brings its own unique challenges. Traditionally, pairwise Hamming, correlation or Euclidean distances were used (see, e.g., Navin et al. 2011), which treat genomic loci as independent. However, SCNAs typically cover genomic areas from a few hundred nucleotides up to whole chromosomes. This induces “horizontal dependencies” between adjacent genomic loci: an amplification (or deletion) of a locus drastically increases the probability that an adjacent locus is also amplified (or deleted). Methods that treat positions independently therefore are poor estimators of the true number of genomic events. To briefly illustrate this problem, consider three haploid genomes consisting of seven genomic segments each with respective copy-numbers (amplified regions in bold) c₁ = “1111111,” c₂ = “1211222,” and c₃ = “1222222.” Counting the number of different genomic loci (Hamming distance), we get pairwise distances d(c₁,c₂) = 4, d(c₁,c₃) = 6 and d(c₂,c₃) = 2. However, more likely, two independent genomic events happened between c₁ and c₂, but only one longer event between c₁ and c₃. Particularly in genomically unstable cancers, SCNA segments frequently overlap, where any successive duplication or deletion event starts within the boundaries of the previous, making deconvolution of individual events nontrivial. This is particularly relevant when a deletion event completely removes all copies of a genomic segment. Any overlapping amplification event cannot amplify this segment anymore (as the genetic material is lost), but can continue as normal on the surrounding segments.

To address these challenges in a unified framework, we developed MEDICC (Minimum Event Distance for Intra-tumor Copy-number Comparisons), an algorithm for computing evolutionary distances between genomes from copy-number profiles (Schwarz et al. 2014). MEDICC computes pairwise evolutionary distances based on a “minimum-event distance,” the minimum number of amplifications and deletions of arbitrary length needed to transform one genome into another. The output of MEDICC is a matrix of pairwise evolutionary distances (and reconstructed evolutionary tree and ancestral genomes) between the sample genomes of a cancer patient. Similar pairwise evolutionary distances can be computed using presence/absence data from somatic single-nucleotide variants (SNVs) or from full sequences using more traditional phylogenetic distance measures such as Jukes Cantor (Felsenstein 2003).

Phasing of Copy-Number Profiles

To get as accurate tree reconstructions as possible, phasing of SCNAs is highly recommended. Short-range phasing is traditionally performed using statistical phasing on the germline variants with methods such as IMPUTE2 (Howie et al. 2009) and SHAPEIT2 (Delaneau et al. 2012, 2013). Unfortunately, the genetic distance at which single nucleotide polymorphisms (SNPs) can be accurately phased is relatively low.

When sequenced, a diploid genome with two homologous copies of each chromosome has a theoretical 1:1 ratio of reads between reference and alternative alleles (B-allele frequency, BAF = 0.5) at a given site. SCNAs result in an unbalanced ratio of genetic material from the two homologous chromosomes at their genomic position (allelic imbalance). Distinguishing the two parental alleles in areas of clear SCNAs is straightforward, as the BAF frequency plots clearly show separation of the two alleles. Popular copy-number segmentation algorithms such as the Battenberg algorithm (Nik-Zainal et al. 2012a,b) take this into account by starting with statistically phased genotypes and “correcting” the statistical phasing when the haplotypes “switch” in the BAF frequency plot and give rise to the Battenberg patterns. The fundamental underlying assumption is that SCNAs are “greedy,” that is, in a region of allelic amplification it is always the same allele that is amplified.

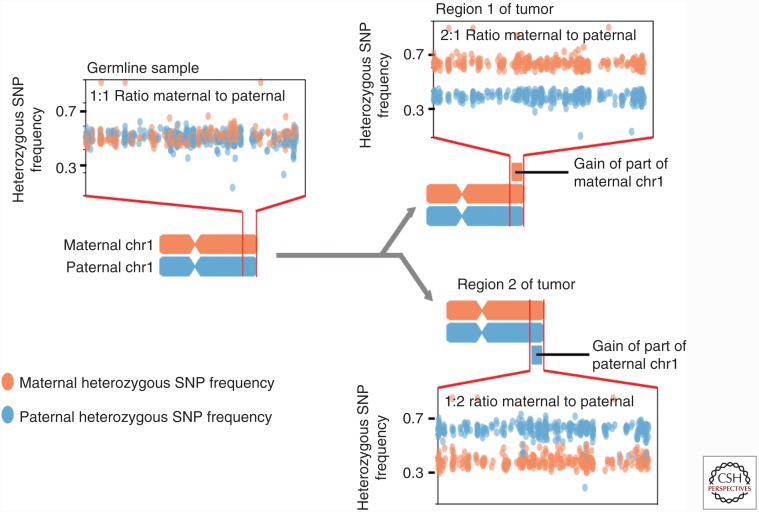
This “greedy” assumption is reasonable when used in the analysis of single samples from a tumor, as it is the most parsimonious explanation. However, as the cost of NGS has fallen, many groups have performed sequencing analyses on multiple spatially separate regions of the same tumor or of multiple spatially distinct tumor masses from the same patient (Gerlinger et al. 2012; McPherson et al. 2016; Jamal-Hanjani et al. 2017). Analyses of these multiregion or multisample studies that share the same original haplotypes can test the assumption that SCNAs occur on the same allele by comparing the frequencies of heterozygous SNPs across samples (Fig. 1). In the example, two regional amplifications of alternative alleles on the q arm of the hypothetical chromosome would normally be very likely to be considered the same event. Using Region 1 as a reference, we can color the SNPs of the two individual alleles differently, with the orange one being the amplified and the blue one being the wild-type haplotype. Applying the same coloring to Region 2 shows that the blue haplotype is amplified relative to the orange, allowing us to identify the amplifications as two separate evolutionary events.

Figure 1.

Schematic of copy-number events at similar genomic location distinguished by comparison of heterozygous single nucleotide polymorphism (SNP) frequencies in different regions of the same tumor.

We named such subclonal SCNAs occurring on opposite alleles mirrored subclonal allelic imbalance (MSAI). A statistical test for MSAI and an MSAI-based phasing procedure for genomic copy-number profiles is now part of the MEDICC software. MSAI events are suspected to be indicators of convergent structural evolution in cancer genomes, they have recently been extensively characterized in NSCLC as part of the TRACERx 100 cohort (Jamal-Hanjani et al. 2017).

Between Ladder-Like and Fully Branched Evolution—Quantifying ITH

ITH contributes to resistance development in the clinic by providing the variants on which selection can act on. Cancers explore the fitness landscape of the host through accumulation of somatic variants (Merlo et al. 2006). Different mutations have different fitness effects and (with the epistatic interactions between them) form the total fitness of a clone. Through positive selection and increased proliferation, fitter clones undergo clonal expansion and their relative frequency increases. The more subclones survive and expand, the faster this increase in diversity. It is hypothesized that cancers with high diversity have a higher chance to evade selective bottlenecks induced by chemotherapy or the immune system and lead to expansion of a therapy resistant clone (Merlo et al. 2006).

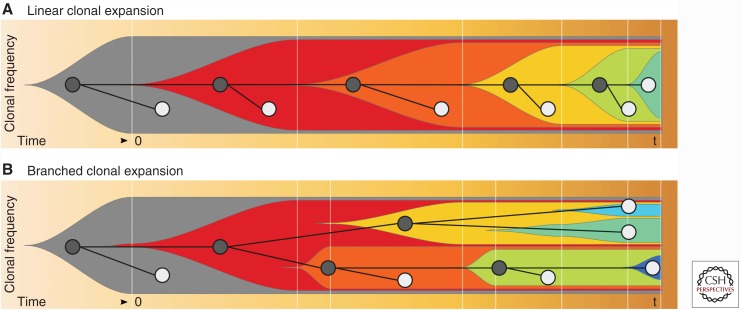
Arguably, two major types of tree topologies exist, depending on the rate at which new clones arise, and the selection pressure applied to those clones. If new variants arise under constant positive selection, successive clonal expansions will fixate these variants in the population. In this case, diversity increases linearly over time if the minor clones are not completely wiped out, and the resulting phylogenetic tree will show a ladder-like structure (Fig. 2A). In the case in which multiple subclones expand in parallel, either because of increased mutation rates or changes in selection pressure, trees will branch out and show distinct subclades (Fig. 2B). Both branched and ladder-like evolutionary trees have been found in ovarian (Schwarz et al. 2015) and other cancers, such as renal cell carcinomas (Gerlinger et al. 2012).

Figure 2.

Fishplots (Miller et al. 2016) of clonal frequencies over time. (A) Linear clonal expansion: Subclones emerge successively and diversity increases linearly over time. The resulting phylogeny is ladder-like. Because of dying out of subclones, diversity at the sampling time point t is relatively low. (B) Branched clonal expansion: Cancer subclones emerge and expand in parallel. Diversity increases quickly, leading to high diversity at the sampling time point (t). The resulting phylogeny is fully branched.

Bedford et al. (2011) analyzed the relationships between tree topology and selection pressure using extensive simulations as well as sequencing data on influenza. They concluded that the type of selection pressure imprints in the topology of phylogenetic trees. In general, both positive and purifying selections constrain tree topology and lead to more ladder-like trees than neutral selection. However, in contrast to constant positive selection, episodic positive selection induces branched clades during phases of low selection pressure, which themselves are connected in a ladder-like fashion, caused by evolutionary bottlenecks removing most of the previously existing taxa (see Figures 4–6 in Bedford et al. 2011). Although not directly targeted at cancer, the evolutionary scenarios considered in this work show many characteristics that make them relevant to our cause, such as rapid evolution, lack of genomic repair mechanisms, lack of recombination, quick adaptation to new environments, and constant attack by the immune system. We were therefore curious about whether different shapes of phylogenetic trees are associated with clinical end-points in cancer patients.

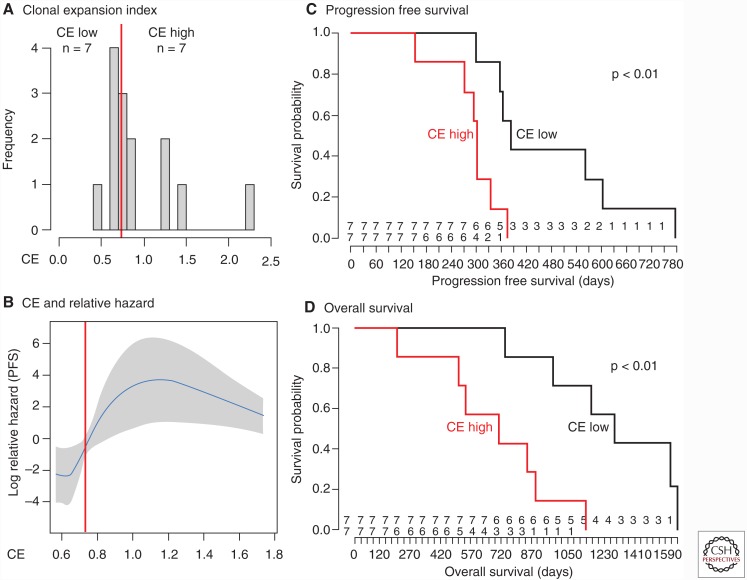
Figure 4.

Association between patient survival and ITH quantification using the CE index. (A) Stratification of patients into two groups through the clonal expansion clonal expansion (CE) index. (B–D) Patients stratified by the CE index show a significant difference in both progression-free (C) as well as overall survival (D) and an increased relative hazard (B).

The Clonal Expansion Index and Resistance Development in the Clinic

For the OV03/04 study, we sought a summary statistic that robustly distinguishes cancers with branched evolutionary patterns from those with ladder-like trees. Using principal component analysis (PCA), we can project sequences, whose pairwise distances were computed using MEDICC, onto a two-dimensional surface (Schwarz et al. 2014), a proxy for the evolutionary landscape. Because the more branched tree topologies have more clades with multiple taxa, these trees show stronger local spatial clustering on this landscape than ladder-like trees. The clonal expansion (CE) index (Schwarz et al. 2014) uses Ripley’s L statistic (Ripley 1977), which measures the degree of deviation from spatial uniformity in the surface, as a measure of the branched-ness of the evolutionary trees. Because the CE index is not a statistical test, but a quantitative readout to distinguish between ladder-like and branched evolutionary trees, it does not rely on this uniformity assumption as a null hypothesis, which might be violated because of “genealogical relatedness, finite time, and spatial structure” (Hong et al. 2015).

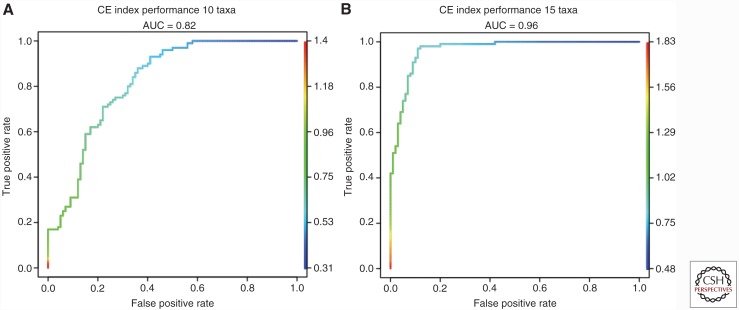
For sample sizes reasonably encountered in multiregion genomics studies, simple simulations show that the CE index is effective at distinguishing between these two scenarios (Fig. 3): 100 random nonultrametric branched 10 taxa (A) and 15 taxa (B) trees with uniformly distributed branch lengths were generated using R package APE (Paradis et al. 2007) and compared with 100 random ladder-like trees with equal number of taxa and uniform branch length distribution. CE indices were computed using MEDICCquant (Schwarz et al. 2014) and receiver operating characteristic (ROC) classifier performance was assessed and plotted using ROCR (Sing et al. 2005). The results show a very high classification accuracy (area under the curve [AUC] = 0.82) for n = 10 taxa that increases with increasing number of taxa (AUC = 0.96 for n = 15). One of the underlying assumptions of this approach is that the tumor has been sampled in an unbiased manner. In particular, spatial heterogeneity, i.e., a correlation between evolutionary and physical distance of the samples, can influence the distribution of samples in the evolutionary landscape. We found tumors with fewer samples to be more susceptible to such effects.

Figure 3.

Simulation-based validation of the clonal expansion (CE) index. Receiver operating characteristic (ROC) curves for the classification performance of the clonal expansion (CE) index for random trees with 10 (A) and 15 (B) taxa. The “area under the curve” (AUC) performance shows how the CE index distinguishes between ladder-like and branched phylogenies.

Using the CE index as implemented in (Schwarz et al. 2014), patients from the OV03/04 cohort were stratified into two groups with low and high CE index respectively. The two groups showed significant difference in both progression-free as well as overall survival (p < 0.01, Fig. 4) (Schwarz et al. 2015). It should be noted that, because of the low total sample size (17 patients), further studies will be required to validate these findings.

Distinguishing Different Modes of Tumor Progression

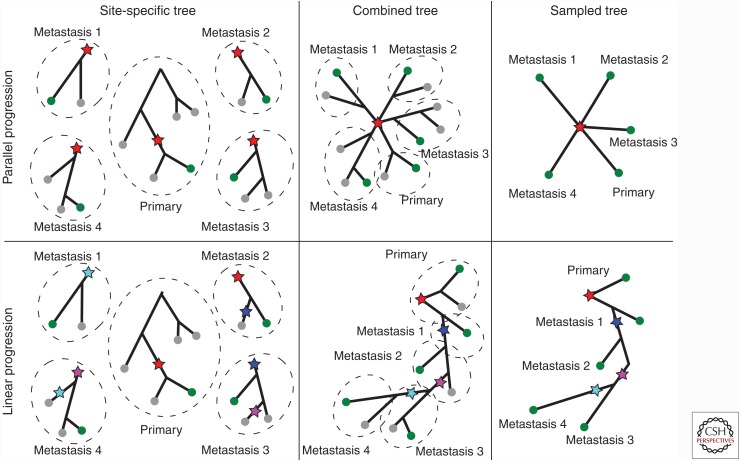
The discussion about the clinical relevance of branched vs. ladder-like evolution feeds into an important question in cancer research concerning the mode of tumor progression. Two main models are currently considered: the early dissemination of metastases from the primary tumor before it develops full malignancy (the parallel progression model), or the evolution of the tumor into a fully malignant cancer, followed by a metastatic cascade (the linear progression model). These two models have been extensively reviewed in recent as well as earlier literature (Klein 2009; Naxerova and Jain 2015). Although seemingly similar to the previously discussed question about clonal expansion patterns, the question here is about the origin of the metastases, and how the path to metastasis is related to the evolutionary tree (Fig. 5). We will first introduce the two models and then discuss how to distinguish between them given real data.

Figure 5.

Parallel (top) vs. linear (bottom) progression models. Sampled clones are marked in green, others gray. In the parallel scenario, metastases are established in quick succession compared with the overall time of disease development and then evolve independently (left and middle). After sampling one clone from each spatially separate metastasis the evolutionary relationship of the samples is a star (right). In the linear progression scenario, metastases give rise to other metastases (left, middle). After sampling one clone from each spatial location, the inferred tree is fully branched or ladder-like (right) as outlined in a previous paragraph. Branch lengths in the plot are maintained as far as possible.

Linear progression model

The basic assumption underlying the classic linear progression model is that the ability to colonize distant tissues requires the evolution of complex genomic changes and is one of the final stages of tumor progression. Metastases should appear therefore at around the time the primary tumor becomes detectable, leading to a relatively small evolutionary distance between primary tumor and metastases. In this model, metastases require a high growth rate and spread further to other tissues (metastatic cascade, metastasis-to-metastasis spread) (Weinberg 2008), which makes them more closely related to each other than to the primary tumor (Fig. 5).

Parallel progression model

The parallel progression model suggests that tumor cells disseminate and form metastases early before the primary cancer fully develops. Metastases are supposed to have growth rates similar to the primary cancer and become clinically relevant on their own, lagging behind their primary by the time it took them to become established. Metastases hence supposedly have large evolutionary distances between them. The parallel model allows for the metastatic phenotype to arise multiple times independently, but, because of the low proliferation rates, samples taken at a certain point in time will miss those that were not established early (Naxerova and Jain 2015).

It is likely that the actual mode of progression depends on the type of cancer and it is certain that accurately determining the mode of progression would be highly relevant for research and patient care alike. Despite this, there is no generally accepted experimental or statistical test to determine which mode dominates in a clinical sample.

McPherson and colleagues (2016) examined the subclonal architecture of in HGSOC and their intraperitoneal metastases using clustering of SNVs by their cancer cell fraction. The majority of the patients’ disease examined was found to be consistent with monoclonal spread whereas a minority showed polyclonal spread. These results could be interpreted as supporting linear progression in cases with monoclonal spread and parallel progression in those with polyclonal spread. We have argued that recurrent dissemination of metastases from the primary, indicative of the parallel progression model, would give rise to a star-like tree topology among spatially separate metastases (Schwarz et al. 2014). Many divergences will occur close together early in the overall progression. In contrast, if metastases seed other metastases (a dominant linear progression model), they would form non-star-like ladder-like or branched evolutionary trajectories.

The key observation is in the time that passes from the first to the last (sampled) metastatic event. In the case of the parallel progression model, metastases disseminate early and in a time span that is short compared with the evolutionary time over which they will grow and evolve. In other words, metastases are very dissimilar to each other and very dissimilar to the primary tumor, which has been observed by others. Naxerova and Jain (2015) write with regard to the parallel progression model: “Therefore, substantial genetic disparity between the primary tumor and its metastases, as well as between metastases in different anatomic locations, is expected.” A frequently used argument for the parallel model of cancer progression is the in-vivo observation that metastases often have similar proliferation rates and tumor volume doubling times (TVDT) as the primary tumor (Klein 2009). Although metastasis under the parallel model can be ongoing and continuous, late metastases would be too small to be clinically relevant, well below the detection threshold at presentation and would therefore not be sampled.

The linear model, in contrast, postulates metastatic cascades, or metastasis-to-metastasis spread. In this model, the metastatic phenotype is complex and metastasis is difficult. Metastases take a long time to establish, leaving ample time for evolutionary divergence between them. The metastasis-to-metastasis spread, together with divergent metastases, leads to a branched topology.

It is important to stress that adequate and homogenous sampling of the patient is key to such analysis. It takes at least three spatially separate metastatic sites in addition to a primary sample to test for deviation from the star model, another important advantage of multiregion studies over traditional sampling approaches.

In the OV03/04 study, each patient was sampled multiple times at distinct anatomic locations, across the primary tumor and different metastases. The tree for each patient consists of multiple, spatially distinct, metastatic samples, sometimes with a single primary sample as well (Schwarz et al. 2015). We used a statistical test for star topology between the metastatic clades to distinguishing between the two modes of cancer progression (see Box 2). We rejected the null hypothesis of parallel progression only in the case of compelling evidence for a linear progression model, which is the case in 8 out of 9 of the cases tested (Schwarz et al. 2015). We concluded that the linear progression model with late metastasis and ongoing metastasis-to-metastasis spread is the prevalent mode of progression in HGSOC.

BOX 2. Test for star topology for Poisson-distributed distance matrices.

From a given distance matrix D we extract the lower triangle as a vector p of pairwise distances between the n taxa (|p| = n(n-1)/2).

We set up a binary design matrix T of |p| rows and n columns. In a star topology, every pairwise distance is the sum of two branches and the number of branches equals the number of taxa n. Every row in T thus has exactly two ones for the two branches that have to be added for each pairwise distance in p.

Finding optimal branch lengths for our star topology is then equivalent to finding a least squares solution to the set of linear equations given by Tb = p, where b are the estimated optimal branch lengths for the star topology.

We assume the minimum-event distance as a count process to be Poisson-distributed with mean and variance equal to the true divergence “time” t. If we normalize the residuals (p—Tb)/sqrt(p), the sum of squared normalized residuals is chi-square distributed with |p|-n degrees of freedom (Schwarz et al. 2014).

It is worth noting that our approach of using a test for star topology does not involve the monophyly or paraphyly of the metastatic subclade, which itself would not be sufficient to determine the mode of cancer progression (Hong et al. 2015). It is the level of divergence between the metastatic clades that carries this information. If we do take branch lengths into account, a test for star topology is capable of separating the scenarios outlined in Hong et al. 2015, and makes it possible to reliably distinguish a metastatic cascade from parallel metastasis (Schwarz et al. 2015).

It is unlikely that the time between dissemination of the metastases in the parallel progression model is exactly equal to zero. If internal branch lengths are sufficiently large, there is a chance that the null hypothesis of a star topology will be wrongly rejected. A better model might be able to compensate for this effect. However, should the time between metastatic events be too large, these new metastases will never be sampled because they remain below the clinical detection threshold at diagnosis.

Will the star topology hypothesis always hold? No; it fails in the case in which there is no genetic basis for metastasis or under strong convergent evolution. It is, however, generally accepted that the propensity to shed and colonize distant tissues requires genetic change. Hence, metastases will share common genetic traits distinguishing them from other lineages of the primary tumor. This set of traits is a subset of the genetic traits all metastases have in common, and reconstruction of the last common ancestor (LCA) of all metastases does not define the metastatic phenotype, but a superset of it. However, the metastatic phenotype likely requires several genetic changes, which should make convergent evolution rare compared with inheritance of metastatic potential by descent.

We have shown in this section how accurate reconstruction of the evolutionary history, including branch lengths, gives us hints about the dominant mode of cancer progression. It is the relationship between spatially distinct metastases that allows us to align the metastatic to the evolutionary process. The evolutionary divergence of clones within a physical site can give us additional insights into the evolutionary processes, but including subclones from the same site will invalidate a global test for star topology.

Detecting Variable Evolutionary Rates

Evolutionary trees are asymptotically ultrametric under constant or no selection pressure and a constant mutation rate across all lineages (i.e., under a strict “molecular clock”), with distances from the root to all leaf nodes being identical (Felsenstein 2003). This molecular clock hypothesis is frequently violated in real world datasets, including cancer, in which mutator phenotypes (Bielas et al. 2006) can modulate the rate of evolution and subclones face changes in selection pressure as a result of treatment, the immune system and changing tissue microenvironments. On the other hand, finding markers that show a molecular clock is of great interest to time the onset of disease and estimate the time point of metastasis. For this, specific genomic loci such as microsatellites haven been proposed as neutrally evolving sequence elements in cancer (Shibata et al. 1996). Similar to our approach of a test for star topology (Box 2), we can use pairwise distance matrices between samples to test for a molecular clock by using the same Poisson assumption as used for the test for star topology. The vector p of distances from the root to each of the leaf nodes, after normalization (p − mean(p)) / sqrt(p), is then chi-square distributed with |p| degrees of freedom (Schwarz et al. 2014). We found certain nonclock like behavior in at least two of the patients in our OV03/04 study on ovarian cancer (Schwarz et al. 2015).

There are possible, sample-specific, factors that influence this analysis. SNV and CNV detection sensitivity depends on sequencing depth and sample purity. If some samples of the same patient have been sequenced at much higher depth or show much higher purity, a perceived increase in mutation rate might actually be an increase in detection sensitivity. In general, SNVs seem more prone to such effects. The multiregion SCNA phasing approach outlined in the previous section can help detect SCNAs in cases of low purity. As long as a sufficient number of reads over both parental alleles are available, SCNA segmentation works well even in cases with low-sequencing depth.

OUTLOOK

Many cancer evolution studies have focused on the phylogenetic relationship between subclones from a matched tumor–normal pair. In this article, we have seen how multiregion sampling strategies allow detailed insight into the modes of cancer progression. We have discussed how allele-specific copy-number profiles are an excellent readout to infer the tree of cancer evolution in the patient. This is particularly relevant for cancers such as HGSOC, in which ubiquitous deficiencies in homologous recombination inhibit the cells’ ability to repair double-strand breaks, leading to rapid and ongoing accumulation of SCNAs throughout evolutionary history. We have shown how reference phasing of SCNAs using information borrowed between different samples from the same patient allows the detection of convergent structural evolution. We have investigated how the overall topology of the phylogenetic tree, in terms of both shape and branch lengths between primary tumor and metastases, is a valuable source of information. It can tell us about the frequency and hierarchy of clonal expansions, the mode of cancer progression and about the existence of potential mutator phenotypes. More large-scale multisample cancer studies will need to be undertaken to exploit these sources of information, improve our understanding of the evolutionary processes shaping the cancer genome and ultimately allow us to fight metastasis, the main cause for cancer mortality.

We have seen that in the case in which metastatic samples are taken from spatially distinct sites, and assuming a genetic basis for metastasis, a test for star topology can be used to distinguish between the parallel and linear models of cancer progression. This test might be susceptible to an inflation of type I error, because even a scenario resulting from full parallel progression will leave positive lengths at some internal branches between dissemination points. We would like to see novel contributions to this field in the form of improved statistical testing methods for distinguishing between the two modes of cancer progression.

We have further established a method to distinguish between ladder-like and branched evolutionary trajectories, which might be indicative of episodic selective sweeps. It is too early to say whether the clinical relevance of this distinction, which we established in our prospective OV03/04 study, can be validated by larger sample sizes. In any case, the response of the cancer to selective sweeps and the propensity of a tumor to undergo clonal expansions, that is, to create a novel genotype with higher fitness that quickly gets fixated in the population, are essential to our understanding of cancer progression and adaptation. In this context, the question about the rate of mutation in human cancers is an important one, because the mutation and proliferation rates will allow us to calibrate our evolutionary models to reconstruct chronological events in the history of cancer, such as time of metastasis and disease onset.

Ultimately, the aim must be to understand metastasis as a complex phenotype and to find out which genetic, epigenetic, and regulatory changes are necessary for successful colonization of remote tissues. For this to work, the amount of data on multiple-sampled cancers has to be expanded significantly. We hope that the field will continue to move in this exciting direction and are hopeful that more light can be shed on understanding the complex relationship between healthy tissue, primary tumor, and metastases.