Evaluating the impact of varied compliance to lung cancer screening recommendations using a microsimulation model

Abstract

Background

The US preventive services task force (USPSTF) recently recommended that individuals aged 55–80 with heavy smoking history be annually screened by low-dose computed tomography (LDCT), thereby extending the stopping age from 74 to 80 compared to the national lung screening trial (NLST) entry criterion. This decision was made partly with model-based analyses from cancer intervention and surveillance modeling network (CISNET), which assumed perfect compliance to screening.

Methods

As part of CISNET, we developed a microsimulation model for lung cancer (LC) screening and calibrated and validated it using data from NLST and the prostate, lung, colorectal, and ovarian cancer screening trial (PLCO), respectively. We evaluated population-level outcomes of the lifetime screening program recommended by the USPSTF by varying screening compliance levels.

Results

Validation using PLCO shows that our model reproduces observed PLCO outcomes, predicting 884 LC cases [Expected(E)/Observed(O) = 0.99; CI 0.92–1.06] and 563 LC deaths (E/O = 0.94 CI 0.87–1.03) in the screening arm that has an average compliance rate of 87.9% over four annual screening rounds. We predict that perfect compliance to the USPSTF recommendation saves 501 LC deaths per 100,000 persons in the 1950 U.S. birth cohort; however, assuming that compliance behaviors extrapolated and varied from PLCO reduces the number of LC deaths avoided to 258, 230, and 175 as the average compliance rate over 26 annual screening rounds changes from 100 to 46, 39, and 29%, respectively.

Conclusion

The implementation of the USPSTF recommendation is expected to contribute to a reduction in LC deaths, but the magnitude of the reduction will likely be heavily influenced by screening compliance.

Introduction

Lung cancer (LC) is the leading cause of cancer-related death in the United States. Smoking is the strongest known risk factor for LC accounting for 80–90% of LC cases [1]. Recently national lung screening trial (NLST) showed that low-dose computed tomography (LDCT) is effective in reducing LC-specific mortality [2]. An individual aged from 55 to 74 years with at least 30 pack-years of smoking, and less than 15 years since smoking cessation (for former smokers), was eligible to participate in the trial, and each person enrolled was screened annually for 3 years either by LDCT or chest X-ray (CXR). The study showed that LDCT reduced LC-specific mortality by 20% compared to CXR.

The US Preventive Services Task Force (USPSTF) recently updated their national LC screening guidelines, recommending a person aged 55–80 years with at least 30 pack-years and less than 15 years since smoking cessation to be screened annually by LDCT. They extended the stopping age for screening from 74 to 80 compared to the NLST [3]. This decision was made partly based on the analyses provided by the cancer intervention and surveillance modeling network (CISNET) consortium [4, 5]. CISNET is an NCI-sponsored consortium that uses a comparative statistical modeling approach to estimate the population-level impact of cancer control strategies, and thereby help guide public health decision making.

As part of the CISNET lung group, we developed a microsimulation model that simulates LC initiation, progression, detection, and survival in the presence and absence of screening. This model was used to analyze the relative effectiveness of 576 lifetime LDCT screening strategies in the general US population and to aid the decision making of the USPSTF, together with four comparative simulation models [4, 5]. While high-level comparisons across the CISNET LC screening simulation models have been reported [4–6], the procedures and results of the calibration and validation of our individual microsimulation have not been fully described. Here we briefly describe these aspects of our model (with more details in the Supplement) then focus on the application of our model to an analysis of screening compliance. A limitation of previous CISNET analysis [4, 6] was the assumption of perfect compliance; the CISNET analysis assumed that every screen-eligible individual in the given population would comply with lifetime screening guidelines that could extend over 20 years. Violation of this assumption would likely impact the outcomes on the relative effectiveness among screening scenarios.

In this article, we apply our microsimulation model to study the impact of various compliance levels on the effectiveness of a lung screening program as recommended by the USPSTF. We compare the efficiency of the USPSTF recommendation to an “NLST-like” screening strategy, which stops screening at 74 instead of 80; this is a screening program based on NLST eligibility criteria extending three-year annual screenings to scheduled annual screenings between the ages of 55–74. Our analysis contributes to the evaluation of more realistic outcome of the recommended LC screening program in the US population by taking into account possible screening compliance changes over one’s lifetime. We provide insight into whether or not efforts would be needed to ensure high-risk individuals adhere to screenings in order to realize the relative benefits of the USPSTF-recommended screening program.

Methods

Microsimulation model

The purpose of our microsimulation model is to evaluate the population-level impact of LC screening. At the core of our simulation model, we simulate individual-level LC-related events including incidence age in the absence of screening, the tumor growth rate, and progression to lethal metastases and histologic subtype. We then impose a specific screening intervention to each individual and estimate individual-level survival outcomes. The individual-level outcomes are aggregated to estimate the population-level outcomes of the given screening strategy. We describe the key components of our microsimulation model for LC screening next.

Target population characteristics

Key inputs to the microsimulation model describe the target population at the individual level including sex, smoking history (e.g., pack-years and age for starting/quitting smoking), and age at entering a screening program. Supplemental Table S1 shows the example profiles of four individuals with different age, sex, and smoking histories.

Lung cancer incidence model

Given smoking history, sex, and age at entry, the annual hazard for LC detection in the absence of screening is predicted using the two-stage clonal expansion (TSCE) model, which is a commonly used model for investigating cancer incidence based on environmental risk factors [7–9]. The parameters of the TSCE model we used were estimated and validated on data from nurses’ health study/health professionals follow-up study (NHS/HPFS) [7]. However, multiple, potentially unmeasured, cohort-specific factors may influence LC risk providing somewhat different predictions for the different cohorts. Hence predictions based on this model were adjusted through calibrations (See “Model calibration to NLST”). This adjustment is a new feature to our model compared to the one used in the previous reports [4, 5]. Using annual hazards estimated from this model, the age-specific LC incidence in the absence of screening is predicted for each individual (See Supplemental Table S1 for example). We note that this incidence of LC in the absence of screening is due to detection promoted by symptoms (i.e., clinical detection) as opposed to screen detection that will be mentioned later in this section. For each LC case, a histologic subtype (namely, adenocarcinoma, squamous, large cell or small cell) was assigned by sampling from the observed proportions from SEER (See Supplemental Table S2).

Natural history model of lung cancer

The natural history model is used to predict individual’s tumor growth history over time conditioning on sex and histologic subtype and provides estimates of unobservable features including tumor volume doubling time, time for onset of metastasis, and observable features such as tumor size at clinical detection, and survival time [10]. More details of the natural history model are provided in Supplemental Material S1–2. The parameters of the natural history model were estimated using National cancer institute surveillance, epidemiology and end results (SEER) staging and survival data. Examples of these outputs of the natural history model are provided in Supplemental Table S1.

Modeling screening, follow-up, and treatment

Screening

For each individual, screening is imposed based on the type of screening program varying by duration, interval between screens, and screening mode (LDCT vs. CXR). To model the effect of screening, a screening detection threshold (for LDCT and CXR) is estimated, such that if the tumor size at a given screen time is larger than a given detection threshold, the tumor is screen detected (See example profiles in Supplemental Table S1). Concurrently, sampling the screen detection thresholds from a Weibull distribution introduces stochastic variability among individuals, as previously shown [11]. The mean screen detection threshold was expected to be in the range of 2–5 mm for LDCT and 20–25 mm for CXR based on previous trial data [12] and clinical expertise (AL), then calibrated to NLST data (See “Calibration to NLST”).

Diagnostic follow-up

For tumors that are screen detected but whose sizes are less than 10 mm, the Fleischner society guidelines are provided as a standard [13]. In our microsimulation model, we used a modified version of these guidelines in order to most closely capture observations in the NLST. We assumed that a patient with tumor (or nodule) size ≤4 mm is scheduled for next screening without being assigned diagnostic follow-up as in the NLST [2]. Moreover, we assumed that patients with a positive screening exam adhere perfectly to the follow-up strategy. While follow-ups are scheduled according to the Fleischner society guidelines, no final diagnosis is made until it reaches a certain size threshold that was determined by calibration to NLST data (See “Calibration to NLST”).

Treatment, survival, and death from other causes

Surgery is assumed for early-stage disease and surgery-related death rate is assumed to be 1% based on literature [14]; status of surgery-related death was assigned by sampling from 0 or 1 using this rate.

A survival time for each LC patient is predicted using the natural history model in the absence of screening (See Supplemental Materials S1). According to our natural history model, a patient can survive from LC if detection, diagnosis, and treatment of their tumor occur before the onset of lethal metastasis (called “cure threshold”; See Supplemental Materials S1 and Supplemental Table S1 for example). In this case, the age of death of this person is determined by other cause of mortality, which is predicted using a model developed by Meza [4], conditioned on smoking history and sex. We note that our model can also adequately handle the possibility that a patient may be cured from LC but suffer from a LC recurrence at a later data. This is possible because we used the survival data from SEER for estimating the parameters of our model, which include patients who have LC recurrence after their cancers are resected. Example profiles that include survival information are provided in Supplemental Table S1.

Aggregation and comparisons of screening strategies

After conducting a microsimulation to generate individual-level outcomes such as LC status, detection mode, survival time, and cause of death, we calculate study-level outcomes (when individuals are simulated for a specific clinical trial study) or population-level outcomes (when individuals are simulated for a general population) for a given screening program by aggregating individual-level outcomes. For example, LC-specific mortality rate of a certain screening program can be estimated by computing the number of individuals who died from LC divided by the total number of individuals simulated.

Calibration to NLST

While the main purpose of our microsimulation model is to evaluate the population-level outcomes of LDCT under various screening strategies for guiding health policy decision, model calibration to trial data is necessary for estimating screening-related practice patterns. Such calibration enables reliable extrapolation of clinical trial-level results to the population level. We conducted a calibration by systematically adjusting key screening-related parameters of our microsimulation model using the NLST data, which include CT detection threshold, CXR detection threshold, and tumor size threshold for diagnostic follow-up, LC clinical detection time adjustments (see Supplemental Table S4 and Supplemental Materials S3 for more details). A description for the NLST data is provided elsewhere [2]. The eligibility criteria for an enrollment of the NLST was based on age (55–74) and smoking exposure (≥30 pack-years and ≤15 years since quitting smoking for former smokers). Each enrolled individual received three annual screens using either LDCT (screen arm) or CXR (control arm) after randomization, and the screening results were followed up for 6 years.

Calibration method

The calibration method is based on a multivariate grid-search algorithm. A specified range of each calibration target parameter is partitioned into grids. We use each combination of grid points formed as input parameters and simulate the NLST comparing the model’s estimates with the observed NLST outcomes. A set of parameters that provides the best fit to the data is chosen as the final set of parameters to be used for the subsequent analyses.

Validation using PLCO

After a final set of calibration parameters was obtained using the NLST data, we validated our microsimulation model using PLCO data without any further adjustment of the parameters in the model. The full description of PLCO is provided elsewhere [15]. We conducted microsimulation analysis using all participants’ data from PLCO, as well as the subset of participants who meet the NLST smoking criteria (aka “NLST-eligible.”) For this validation exercise we used PLCO data from years 1 to 10. To measure goodness-of-fit to data, E/O ratio was calculated over study time along with its confidence interval, addressing parameter uncertainty and Monte Carlo error, calculated based on the Poisson distribution [16], where O is the observed count of LC incidence or mortality from data and E is the predicted count using our microsimulation model.

Evaluation of the USPSTF-recommended and the NLST-like screening program with lifetime screening and follow-up

After validating the microsimulation model using PLCO, we extrapolated our model by simulating the lifetime screening program recommended by the USPSTF in the general US population. Recall that USPSTF recommends a person aged 55–80 years with at least 30 pack-years and less than 15 years since cessation of smoking to be screened annually. We note that the screening and follow-up are based on an individual’s lifetime as the horizon in this simulation, which is different from that in the NLST simulation (3-year screening and 6-year follow-up) and the PLCO simulation (4-year screening and 10-year follow-up).

For the target population, we chose the 1950 US birth cohort because it was considered in the USPSTF report [3]. The lifetime smoking histories and other cause of mortality of 100,000 female and 100,000 male in this cohort were simulated using Smoking History Generator as input variables for microsimulations [17]. Our analysis focuses on individuals who are alive and without a cancer diagnosis at age 50. We follow each individual up to age 90 which translates into a time horizon of 40 years. In addition to simulating the USPSTF recommendation, we simulated an NLST-like program, which has the NLST eligibility criteria, but screening is extended from three annual screenings to lifetime screenings as long as smoking criteria is met. Another hypothetical scenario, namely “no-screen” scenario, was also considered as a control program, so that the effectiveness of the above two LDCT screening programs can be measured.

Screening compliance

We first conducted simulations under perfect screening compliance, meaning that anyone who meets the given screening criteria defined by age and smoking receives screening as scheduled. While perfect screening compliance was assumed in our previous analyses considered by the USPSTF [3, 4], it may not be realistic to assume that everyone attends annual screening for a long duration that ranges up to 20–26 years.

In order to conduct microsimulations under more realistic setting incorporating imperfect compliance, we estimated compliance probabilities using data from the PLCO, focusing on the NLST-eligible participants. The PLCO data were used because the duration of the PLCO trial was longer than the NLST (10 vs. 6 years), also providing more information on screening compliance with four annual screening rounds compared to three annual screening examinations in NLST. The screening attendance rate in PLCO was obtained for each screening round by calculating the fraction of individuals who received screening among those who are eligible for each screening round.

Markov model for screening compliance and estimation of transition probabilities using PLCO

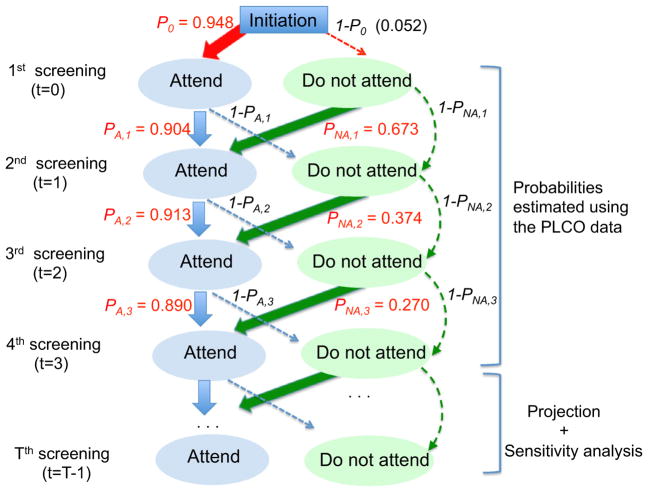
We develop a Markov model to simulate an individual-level status of screening compliance for each screening round (see Fig. 1 for an overview of this model). In this model, there are two possible states, “attend” or “not attend,” and a state is stochastically decided by the state of the previous year. More specifically, the attendance state of the first screening is decided by initial probability (p₀) that was estimated by calculating the attendance rate of the first screening in PLCO. The state of the second screening is then stochastically decided by the state of the first screening. We then estimated the transition probabilities (denoted by p_A,t and p_NA,t if a patient attend (A) or not (NA) screening at t-1, respectively, for screening round T = 1, 2, 3 using PLCO as shown in Supplemental Table S8.

Fig. 1.

Diagram for a Markov model for screening compliance. The numbers in red are the estimates of transition probabilities using the PLCO data. Note In this Markov model, there are two possible states, “attend” or “not attend” and these states are influenced by the states of the previous year. The state of the first screening attendance is decided by initial probability p₀ = 0.948 that is estimated using the attendance rate of the first screening from the PLCO data. The state of the second screening is then decided, informed by the state of the first screening. Among those who attended (A) the first screening, the attendance probability of the second screening is p_A,1 = 0.904 (PLCO estimation) and 1- p_A,1 (= 0.096) for probability of not attending the second screening. For those who did not attend (NA) the first screening, the attendance probability of the second screening is p_NA,1 = 0.673 (PLCO estimation). The states of the third through fourth screening are also decided by the states of the screening of the previous year. The PLCO data have only four screenings (T = 0, 1, 2, and 3), and hence transition probabilities estimated based on four years were extrapolated for T ≥ to be used for evaluating the impact of the lifetime USPSTF-recommended screen program and varied for sensitivity analysis (see Methods “Evaluation of the USPSTF-recommended and the NLST-like screening program with lifetime screening and follow-up”)

Projection of transition probabilities and sensitivity analysis varying the projection of compliance levels

The PLCO data have only four screening rounds (T = 0, 1, 2, and 3). In an attempt to evaluate the impact of the lifetime USPSTF-recommended screen program that has up to 26 screening rounds (age 55–80), we extrapolated the transition probabilities for screening round T ≥ 4. Log-transformed probabilities p_A = (p₀, p_A,1, p_A,2, p_A,3) and p_NA = (p₀, p_NA,1, p_NA,2, p_NA,3) estimated from the PLCO data were regressed on time T = 0, 1, 2, and 3, respectively, and the transition probabilities for T ≥ 4 were predicted from the two fitted regression models.

In order to take into account the parameter uncertainty raised from the crude projections that are based only on four data points, we conducted sensitivity analysis varying the levels of compliance probabilities. In particular, we obtained four different compliance levels by fitting log-transformed regressions considering, beyond the PLCO data points, an additional hypothetical data point at time T = 20 with varying values of 0.6, 0.7, 0.8, and 0.9 to establish four different compliance levels (denoted as Levels 1–4, respectively).

Results

Model calibration to NLST

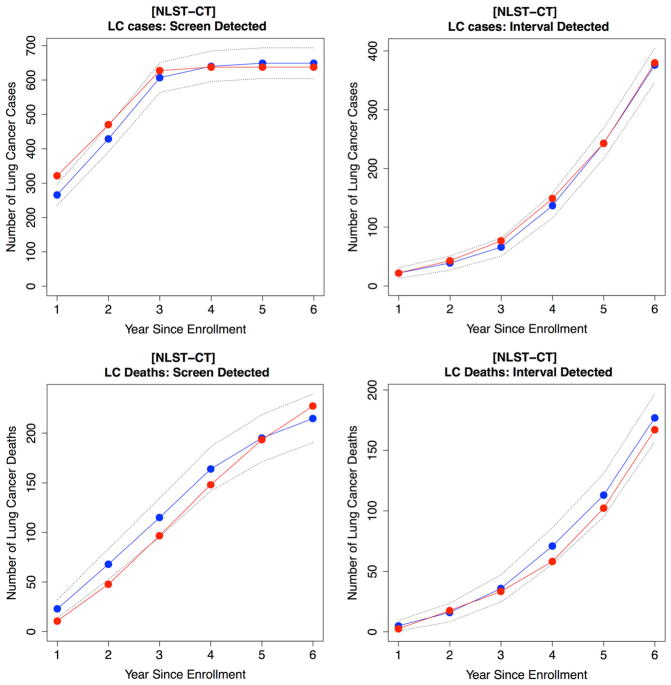
The calibrated parameters are shown in Supplemental Table S4. We used the calibrated microsimulation model to reproduce the outcomes of NLST. The comparisons of the predicted LC outcomes using the model versus observed outcomes from the NLST data are presented in Supplemental Table S5. Our model predicts 638 screen-detected (SD) cases as compared to 649 SD cases observed in the CT screening arm (E/O ratio: 0.98, 95% CI 0.91–1.06) with a 6-year follow-up. The CXR screening arm also had a reasonably good fit for LC incidence with E/O ratio 1.01 (0.9–1.14) for SD cases and E/O ratio 1.06 (0.98–1.14) for ID cases (see Supplemental Table S5). For LC-specific mortality, 227 LC deaths were predicted as compared to 215 observed deaths among SD cases in the CT arm (E/O ratio: 1.06 CI 0.93–1.2). Mortality reduction using CT compared to CXR using our model was 19.2% as compared to 18.6% from data (up to follow-up year 6). Cumulative incidence and mortality results are shown in Figs. 2 and Supplemental Figure S3 for CT and CXR arms, respectively.

Fig. 2.

Model calibration results using the NLST data for CT arm. Cumulative lung cancer incidence and mortality over study time. Observed data are in blue and predicted data are in red. Dotted lines are 95% confidence interval. First row is for lung cancer incidence and second row is for lung cancer death

Validation of the microsimulation model using PLCO

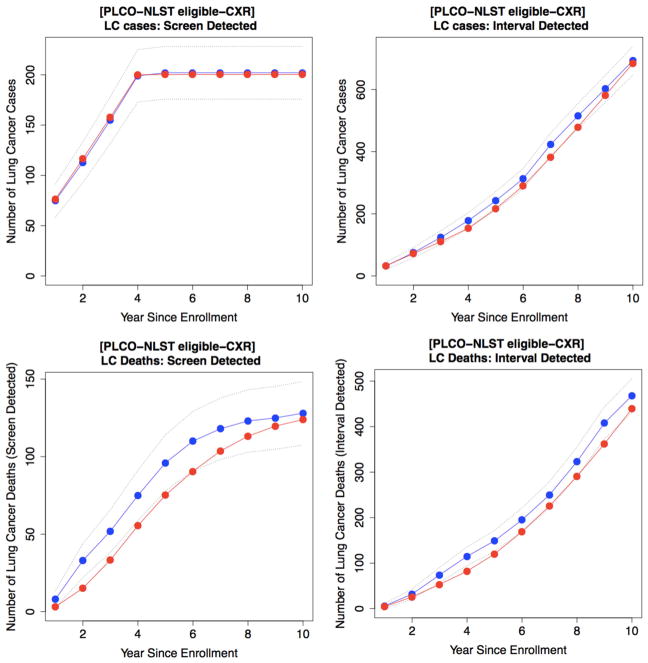
We validated our microsimulation model using data from PLCO (focusing on the NLST-eligible participants) without further adjustments of the model parameters (see Table 1). The prediction in the usual-care arm (no screening) shows that the model closely reproduces observations both for LC incidence (cumulative E/O: 1.03 CI 0.93–1.07) and mortality (cumulative E/O: 0.95, CI 0.88–1.03) with a 10-year follow-up. According to the results for the CXR arm, the model predicts 202 SD cases compared to 200 observed SD cases with E/O ratio = 0.99 (CI 0.86–1.13), and 683 ID cases compared to 693 ID cases with E/O ratio 0.98 (CI 0.91–1.06). Cumulative incidence and mortality results are shown in Fig. 3 and Supplemental Figure S4 for the CXR and usual-care arms, respectively. Similar results were observed for validating our model using data from all participants in PLCO (See Supplemental Table S6).

Table 1.

Model validation results using the PLCO data for NLST criteria eligible subjects

	Chest X-ray Arm									Usual-Care Arm
	Screen-Detected Cases					Interval Detected Cases				Clinical Detected Cases
	Time	O	E	E/O ratio	95% CI	O	E	E/O ratio	95% CI	O	E	E/O ratio	95% CI
Lung Cancer Incidence	1	75	76	1.01	(0.81–1.27)	32	33	1.03	(0.74–1.46)	65	65	1	(0.78–1.27)
	2	38	40	1.05	(0.77–1.44)	43	39	0.91	(0.66–1.24)	83	80	0.96	(0.78–1.20)
	3	42	41	0.98	(0.73–1.34)	49	39	0.8	(0.58–1.08)	85	80	0.94	(0.76–1.18)
	4	44	42	0.95	(0.71–1.30)	54	43	0.8	(0.58–1.06)	91	85	0.93	(0.76–1.16)
	5	3	0			64	63	0.98	(0.77–1.26)	97	89	0.92	(0.74–1.13)
	6	0	0			71	73	1.03	(0.82–1.30)	97	91	0.94	(0.76–1.15)
	7	0	0			110	93	0.85	(0.69–1.03)	84	94	1.12	(0.91–1.36)
	8	0	0			92	97	1.05	(0.87–1.29)	102	99	0.97	(0.79–1.18)
	9	0	0			88	103	1.17	(0.96–1.42)	98	103	1.05	(0.87–1.28)
	10	0	0			90	102	1.13	(0.94–1.38)	84	103	1.23	(1.01–1.49)
	Total	202	200	0.99	(0.86–1.13)	693	684	0.987	(0.91–1.06)	886	889	1.03	(0.93–1.07)
Lung Cancer Mortality	1	8	3	0.38	(0.13–1.19)	6	5	0.83	(0.3–1.89)	15	8	0.53	(0.28–1.10)
	2	25	12	0.48	(0.27–0.84)	26	21	0.81	(0.54–1.25)	43	37	0.86	(0.62–1.18)
	3	19	18	0.95	(0.61–1.52)	42	27	0.64	(0.44–0.94)	58	52	0.9	(0.68–1.17)
	4	23	22	0.96	(0.63–1.46)	41	29	0.71	(0.50–1.03)	62	58	0.94	(0.73–1.22)
	5	21	20	0.95	(0.60–1.46)	34	38	1.12	(0.81–1.53)	78	63	0.81	(0.63–1.04)
	6	14	15	1.07	(0.67–1.81)	46	49	1.07	(0.81–1.41)	63	69	1.1	(0.86–1.38)
	7	8	13	1.62	(0.95–2.82)	55	57	1.04	(0.79–1.33)	75	72	0.96	(0.77–1.22)
	8	5	10	2	(1.01–3.6)	73	65	0.89	(0.70–1.14)	78	75	0.96	(0.76–1.20)
	9	2	7	3.5	(1.51–7.03)	85	71	0.84	(0.67–1.06)	79	78	0.99	(0.80–1.24)
	10	3	4	1.33	(0.54–3.65)	60	77	1.28	(1.02–1.60)	68	81	1.19	(0.96–1.48)
	Total	128	124	0.96	(0.81–1.15)	468	439	0.93	(0.85–1.03)	619	593	0.95	(0.88–1.03)

Fig. 3.

Model validation results using the PLCO data for CXR arm. Cumulative lung cancer incidence and mortality over study time. Observed data are in blue and predicted data are in red. Dotted lines are 95% confidence interval. First row is for lung cancer incidence and second row is for lung cancer death

Evaluation of the USPSTF-recommended and the NLST-like screening programs under varied compliance to screening

Perfect compliance

Upon validation on PLCO, we used our model to simulate lifetime screening programs under the USPSTF-recommended and the NLST-like screening scenarios in the 1950 U.S. birth cohort. The population-level LC outcomes of the two screening programs are shown in Table 2 (second column), for which perfect compliance to screening was assumed, i.e., everyone in the cohort who meets the given screening criteria receives annual screening as scheduled. The NLST-like program saves 455 LC deaths per 100,000 persons in the cohort, with 9.27% LC-specific mortality reduction compared to the no-screen program. The benefit of extending the screening stopping age from 74 to 80 is shown in the USPSTF scenario, which has a 10.1% increase in LC deaths saved (455 vs. 501 LC deaths). The percent of early-stage (I–II) cases is also higher in the USPSTF scenario (49.11%) than the NLST-like (46.71%). Overall, the USPSTF screening program showed increased benefits on LC outcomes compared to the NLST-like under perfect compliance.

Table 2.

Impact of the USPSTF-recommended and NLST-like screening programs in the US population by varying screening compliance

Compliance level		Perfect		Imperfect1		Varying compliance level2
						Level 1		Level 2		Level 3		Level 4
Screening program		NLST3	USPSTF4	NLST	USPSTF	NLST	USPSTF	NLST	USPSTF	NLST	USPSTF	NLST	USPSTF
Screen results	Average compliance rate over screening rounds	1.00	1.00	0.36	0.29	0.47	0.39	0.52	0.46	0.61	0.56	0.72	0.70
	Percent of population screened (%)	19.69	19.80	19.52	19.64	19.57	19.68	19.57	19.69	19.59	19.70	19.59	19.71
	LC-Specific Mortality Reduction5 (%)	9.27	10.21	3.54	3.56	4.55	4.70	5.04	5.25	6.03	6.46	7.01	7.65
	Percent increase in mortality reduction in the USPSTF compared to the NLST-like (%)	10.1		0.57		3.13		4.1		7.13		9.01
Benefits	Number of lung cancer deaths avoided	455	501	174	175	223	230	247	258	296	317	344	375
	Percent of early stage (I–II) among cases (%)	46.71	49.11	34.69	34.75	37.16	37.48	38.45	38.98	40.45	41.53	42.44	44.16
	Number of CT screens	269,349	290,270	122,620	122,859	147,418	149,248	159,814	163,278	178,786	185,926	201,011	213,763
Harms	Number of overdiagnosed cases6	155	207	39	40	68	73	85	96	100	122	121	152
Benefits taking into account harms (BTIH)	Number of lung cancer deaths avoided per 100,000 CT screens	169	173	142	142	151	154	155	158	165	170	171	176

¹The compliance probability was estimated and extrapolated from PLCO data

²Transition probability p_A = Pr (attending screen at t = 20 given the person attended screen at t = 19) varied as 0.6, 0.7, 0.8, and 0.9 for Level 1–Level 4, respectively, where t is screen time (see Fig. 4)

³A person 55–74 screened annually with pack-years at least 30 and quit-years less than 15

⁴A person 55–80 screened annually with pack-years at least 30 and quit-years less than 15

⁵Comparison was made to “No-Screen” scenario

⁶Overdiagnosed case was defined as a person whose lung cancer was detected and diagnosed in a given screening program, but not in a hypothetical no screening program within one’s lifetime

Imperfect compliance

We further evaluate the impact of the lifetime screening programs under a more realistic setting, incorporating imperfect compliance. The annual screening attendance rates (compliance rates) of PLCO are 94.8, 89, 85.8, and 82.1% for the first, second, third, and fourth screening round, respectively (see Supplemental Table S7), supporting that the perfect compliance assumption may not be realistic, especially for programs with long active screening horizon.

The transition probabilities representing the likelihood of attending current screening based on the previous year’s attendance status (“attended” or “not attended”) are shown in Fig. 1 and Supplemental Table S8. We used the transition probabilities to simulate the compliance status of every individual in our simulation model. The rapid drop of p_NA (i.e., the probability of attending current screening given that the individual did not attend (NA) the previous year’s screening) is notable, where the probability is 0.673 for second screening round versus 0.270 for fourth round. This rapid drop of p_NA implies that the probability of attending screening decreases more rapidly among participants who do not attend the previous year’s screening compared to participants who attend the previous year’s screening (with 0.904 for second round and 0.890 for fourth round).

We conducted microsimulations under the imperfect screen compliance using the transition probability estimated using PLCO and projected for time T ≥ 4 (see the red curve in Fig. 4). The results in Table 2 show that the number of LC deaths avoided due to screening under the USPSTF programs decreases to 175 compared to 501 under perfect compliance. It is notable that assuming imperfect compliance also reduces the benefit of extending the screening stopping age from 74 to 80 in the USPSTF scenario versus the NLST-like (hence increasing the number of maximum screening rounds from 20 to 26). While the USPSTF program saves 10.1% more LC deaths compared to the NLST-like under perfect compliance, this rate drops down to 0.56% assuming imperfect compliance. This finding occurs because the attendance rate (proportion of attendants among eligible participants) becomes low as the programs run over 20–26 years (see Supplemental Figure S5) and hence the low attendance for screening after year 20 through year 26 does not contribute much to the benefits of extending the screening stopping age from age 74 to 80.

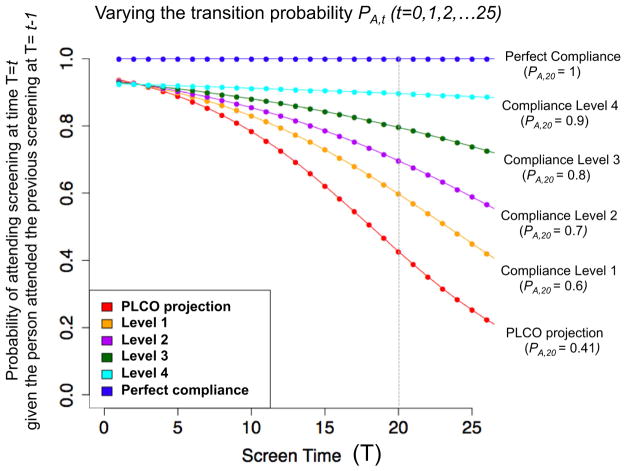
Fig. 4.

Varying the levels of transition probability p_{A, t} (t = 0, 1, 2,.., 25) in a Markov model for screening compliance for sensitivity analysis. The results on this sensitivity analysis are shown in Table 2. Note: P_{A, t} is the probability of attending the screening at each time T = t (t = 1, 2,…, 25) given the person attended the previous screening at time T = t-1(transition probability). The red curve is the transition probability (p_{A, t}) extrapolated based on the estimation using the PLCO data that have only four screenings (T = 0, 1, 2, and 3), and hence data points for T4 were predicted based on the log-transformed regression (see “Evaluation of the USPSTF-recommended and the NLST-like screening program with lifetime screening and follow-up”). In order to take into account uncertainty raised from this extrapolation, we conducted sensitivity analysis varying the levels of p_{A, t} over t. The orange curve obtained by fitting log-transformed regression by including one hypothetical data point at t = 20 with a value p_{A, 20} = 0.6 (increased from p_{A, 20} = 0.41 in the red curve for the PLCO projection). Similarly, Level 2, Level 3, and Level 4 curves were obtained by restraining the value of p_{A, 20} as 0.7, 0.8, and 0.9, respectively. Finally the top blue line is the transition probability under perfect compliance

Sensitivity analysis varying compliance levels

In order to take into account uncertainty raised from the crude extrapolation based on small number of data points, we conducted sensitivity analysis varying the levels of the transition probability (p_A) to Levels 1–4 (See Fig. 4). As shown in this figure, p_{A, 20} (i.e., the probability of attending the 20th screening round given the person attended the 19th screening) is around 41% based on the projection using the PLCO data (red curve), and it varied to 60, 70, 80, and 90% for Level 1, Level 2, Level 3, and Level 4, respectively (see Fig. 4). The microsimulations under these four scenarios in Table 2 show that the average attendance rates over 26 rounds of screening in the USPSTF scenario are 70, 56, 46, and 39% for Level 4–Level 1, respectively; these are lower than those under the NLST-like scenario (72, 61, 52, and 47%) that are based on 20 screening rounds, implying that the attendance rates after 20 screening rounds in the USPSTF scenario reduce the overall average attendance rates.

The results of sensitivity analysis in Table 2 show that the benefits of extending the screening stopping age from 74 to 80 in the USPSTF program versus the NLST-like is markedly influenced by levels of screening compliance assumed (p_A). In high level of compliance (Level 4), the percent increase of LC-specific mortality reduction is 9.01% compared to the NLST-like, and it drops to 7.13, 4.1, and 3.13% for Level 3, Level 2, and Level 1, respectively, as the compliance level decreases. The percent of early-stage (I–II) LC cases in the USPSTF program decreases from 44.2% to 41.5, 38.9, and 37.5% from Level 4 to Level 1, which shows that the benefits of screening are reduced as assumed compliance level decreases.

Discussion

In this report, our microsimulation model was used to assess the impact of the USPSTF-recommended screening program by varying screening compliance. Our analysis shows that while perfect compliance to the USPSTF recommendation saves 501 LC deaths per 100,000 persons in the 1950 US birth cohort, the number of LC deaths avoided reduces markedly as screening compliance decreases. In particular, as the compliance rate, averaged over 26 annual screening rounds, changes from 100 to 46, 39, and 29%, the number of LC deaths avoided drops from 501 to 258, 230, and 175 per 100,000 persons, respectively, implying that the long-term benefits of the USPSTF-recommended program heavily depend on screening compliance.

We compared the outcomes of the USPSTF-recommended scenario to those under the NLST-like screening program, which stops screening at 74 instead of 80. The results show that the benefits of extending the stopping age from 74 to 80 (and hence increasing the maximum screening rounds from 20 to 26) also substantially reduce as screening compliance level declines. Assuming perfect compliance, the USPSTF-recommended program prevents 10.1% more LC deaths compared to the NLST-like, whereas this benefit rate decreases to 4.1, 3.1, and 0.6% by assuming compliance rates of 46, 39, and 29%, respectively. Compliance among screen-eligible individuals would be expected to be lower among this older versus younger age groups, primarily due to increased comorbidity rates at older ages. Hence, extending the screening stopping age may not contribute much to the benefits of screening in the presence of comorbidity. Even though decreased compliance affects LC outcomes in both screening programs, by lowering the number of LC deaths prevented, it also reduces the “ratio” of the number of LC deaths prevented in the USPSTF versus the respective number in the NLST-like scenario. This implies that the relative loss from decreased compliance is larger in the USPSTF strategy compared to the NLST-like strategy. It is important to note however that, the compliance rate in the 75–80 age group is expected to be significantly higher in the early years of a screening program. That is due to the fact that many individuals from that age group (from various birth cohorts) would become screen eligible for the first time and seek screening. Therefore, our results, although specific to individuals with long screening history, may underestimate the effectiveness of the USPSTF program at the early years of implementation when individuals undergo screening for the first time. However, as the screening program matures our estimates should become more applicable.

We note that under perfect compliance, the LC-specific mortality reduction rate yield by the USPSTF program is around 10% (and 9% for NLST-like program), which is notably smaller than the 20% reduction rate observed from the NLST [2]. This difference can be explained by the difference in the target population for each calculation. In the NLST, the reduction rate is calculated among the participants who attended the trial, all of whom were screen eligible and hence screened at least once. However, for the USPSTF and the NLST-like programs in our analyses, this calculation is based on a cohort of 100,000 individuals from the general US population, only a subset of which—less than 20%—is screen eligible and hence screened. Therefore, the reduction rate based on the entire population is always smaller than the one that is based on only “screen-eligible” individuals. Indeed, our model estimates the mortality reduction among the screen-eligible individuals approximately at 19 and 17% for the USPSTF and NLST-like programs, respectively.

Overall, our calibration and validation analyses demonstrated reasonable LC incidence and LC-specific mortality estimates. Although our LC-specific mortality estimates lay on the lower boundary of the 95% confidence interval at the early years, we show that our estimates for the remaining study period, including the total sum, are reasonably close to the observed data. The discrepancy during the earlier time points can be associated with differences between sampling errors associated with low numbers of events at the early time period; these types of error are often reduced as the number of events increases, as happens over time in our analysis.

While the extension of our model to the population setting provides a mechanism to predict the effects of compliance on screening outcomes, our modeling approach has some limitations. One limitation of our microsimulation model is that it does not incorporate radiation effect to measure harms of LDCT screenings [18]. As a result, this may affect our mortality reduction estimates considering that a few fatal cancer cases (LC or other type) can be potentially caused from radiation exposure. Considering the prolonged active screening period implemented by the USPSTF strategy, we anticipate that the effect of radiation exposure would be slightly larger in the USPSTF strategy compared to the NLST-like strategy. Secondly, the Markov model for compliance is simple, for which the attendance is influenced simply by the attendance status of the previous screen even if the prior screen yielded a false positive. Moreover, the projection of the transition probability of the Markov model for screening compliance was based only on small number of data points from PLCO, which may not provide a reliable prediction for lifetime compliance behaviors. Ideally, a more complex model could be used to dynamically model compliance; however, this was beyond the scope of this study. To address the uncertainty surrounding our compliance estimates we used this projection as a hypothetical compliance level, rather than a true compliance behavior, and conducted a sensitivity analysis on the compliance levels. Finally, screening was performed in our model for any individual who meets the smoking and age criteria including individuals who may have high comorbidities. In particular, our analysis likely overestimates the number of individuals attending each screening exam by not taking into account the comorbidity of each individual. We assume that screen-eligible individuals will attend each screening exam with a certain probability, regardless of their overall health condition.

Our analysis focused on mortality reduction and not life-years saved or the balance between benefits and harms, such as overdiagnosis which was the focus of Han et al. [6]. Furthermore, in this analysis we do not account for the cost implications of LC screening nor for the year-over-year budget impact. A cost-effectiveness and budget impact analyses of LC screening could shed light and answer these questions. Hence, our findings should be cautiously generalized given that conclusions may be different from the aforementioned perspectives.

Our microsimulation model provides an analytical framework for evaluating the effectiveness of LDCT screening strategies by bridging between clinical trial results and decision-making processes for public health policies. Although the NLST showed the superiority of LDCT in terms of efficacy in reducing mortality compared to CXR, it may not indicate the optimal strategy at the population level. Different strategies with different starting/stopping ages, screening frequency, number of screening exams, or smoking criteria may lead to a larger mortality reduction and significantly affect the balance between harms and benefits associated with the screening program. Moreover, it has been shown that complementing LC screening with an adjunct smoking cessation program may amplify the effectiveness of the screening program [19]. Even though conducting many different clinical trials varying the aforementioned factors could help find solutions, this would be practically infeasible due to cost and time restrictions. Given these practical limitations on translating clinical studies into health policy, the approach of the proposed microsimulation model can be useful in predicting population-level outcomes under various screening strategies for guiding health policy decision-making processes through careful calibration and validation using all the available lung screening trial datasets.

Overall, our study shows that the implementation of the USPSTF recommendation is expected to contribute to a reduction in LC deaths, but the magnitude of the reduction will likely be heavily influenced by screening compliance. In particular, the effectiveness of extending the screening stopping age from 74 to 80 in the USPSTF-recommended program will likely depend on screening compliance levels. In order to maximize the targeted effectiveness of the screening program by USPSTF, efforts may be needed to encourage and support eligible individuals to attend screenings as scheduled especially at older ages.