Interpreting activation mapping of atrial fibrillation: a hybrid computational/physiological study

Abstract

Atrial fibrillation is the most common rhythm disorder of the heart associated with a rapid and irregular beating of the upper chambers. Activation mapping remains the gold standard to diagnose and interpret atrial fibrillation. However, fibrillatory activation maps are highly sensitive to far-field effects, and often disagree with other optical mapping modalities. Here we show that computational modeling can identify spurious non-local components of atrial fibrillation electrograms and improve activation mapping. We motivate our approach with a cohort of patients with potential drivers of persistent atrial fibrillation. In a computational study using a monodomain Maleckar model, we demonstrate that in organized rhythms, electrograms successfully track local activation, whereas in atrial fibrillation, electrograms are sensitive to spiral wave distance and number, spiral tip trajectories, and effects of fibrosis. In a clinical study, we analyzed n=15 patients with persistent atrial fibrillation that was terminated by limited ablation. In five cases, traditional activation maps revealed a spiral wave at sites of termination; in ten cases, electrogram timings were ambiguous and activation maps showed incomplete reentry. By adjusting electrogram timing through computational modeling, we found rotational activation, which was undetectable with conventional methods. Our results demonstrate that computational modeling can identify non-local deflections to improve activation mapping and explain how and where ablation can terminate persistent atrial fibrillation. Our hybrid computational/physiological approach has the potential to optimize map-guided ablation and improve ablation therapy in atrial fibrillation.

INTRODUCTION

Atrial fibrillation is an abnormal, rapid and irregular rhythm of the atria, the upper chambers of the heart. To restore normal heart rate and rhythm, medications are typically the first treatment of choice. An alternative to medication is atrial fibrillation ablation, a procedure that selectively scars or destroys specific regions of the atria to disrupt rhythm disorders⁴. Despite technical advances, mechanistic debate in atrial fibrillation continues to hinder major breakthroughs⁴⁷. A major confounding factor is that the observed fibrillation mechanisms—and with them the targets of ablation—are highly sensitive to the selected mapping approach. Optical mapping studies mostly reveal rotational drivers in animal models³² and human atria¹⁶. This work could explain clinical reports where local interventions terminate persistent atrial fibrillation^17,27. Conversely, traditional mapping techniques based on contour lines of electrogram onsets typically displays disordered activation patterns^1,23. Adding to the confusion, the same data reveal organized regions in human atrial fibrillation when analyzed using methods that avoid electrogram onsets^37,50. Moreover, far field noise, generated from distant electrical signals in the heart is captured by local electrograms, complicating the precise determination of activation times.

Here we hypothesized that far-field and other undefined components²⁸ of atrial fibrillation electrograms alter contour maps. However, these factors can be identified and filtered using computational techniques of wave propagation, tissue physiology, and electrode size. This hypothesis was motivated by evidence that electrode spacing, orientation, and size alter electrogram shape and impact mapping⁷, as do wavefront direction⁴³, wavefront number, signal type²⁶, and tissue factors including fibrosis¹⁰.

We used a physiologically motived, computational approach to map electrograms in atrial fibrillation in a cohort of patients with clinical endpoint in whom limited ablation in a defined zone terminated persistent atrial fibrillation prior to pulmonary vein isolation. This provides a mechanistically relevant mapping target, since termination of persistent atrial fibrillation by localized intervention¹⁷ is uncommon by random ablation⁴⁷. Our ultimate goal is to develop physiologically-tailored rules to map atrial fibrillation based on electrogram activation times.

METHODS

Clinical Study

We studied N=15 patients with persistent atrial fibrillation undergoing ablation for routine indications⁴. In these cases ablation at sites identified as potential fibrillation drivers terminated fibrillation to sinus rhythm or atrial tachycardia prior to pulmonary vein isolation. Persistent atrial fibrillation was defined as atrial fibrillation for >7 days without self-termination (n=13); longstanding persistent atrial fibrillation was defined as continuous for >12 months (n=2). Patients were recruited from Stanford University Hospital, Palo Alto, CA and University of California, San Diego, CA. The study was approved by both local IRBs.

Electrophysiological Study

Each patient in this series exhibited termination of persistent atrial fibrillation by ablating within a defined region, as a reference for computational analyses. Patients on anti-arrhythmic medications had these agents withheld for 5 half-lives (in patients previously on amiodarone: median 200 days, range 90–1980 days). Heparin was infused to maintain an activated clotting time >300 seconds. Endocardial baskets (64 poles; FIRMap, Topera, Inc) were advanced transvenously and positioned in right then left atrium for atrial fibrillation mapping, verified by fluoroscopy and 3-dimensional imaging (NavX, St Jude Medical, St Paul, MN; Carto, Biosense-Webster, Diamond Bar, CA). Mapping used a phasebased approach²⁷, which has been reported to identify fibrillation drivers in areas of 2–3cm² where ablation can eliminate atrial fibrillation^15,25,41,44. Radiofrequency ablation applied within these regions terminated fibrillation to sinus rhythm or atrial tachycardia.

Data Acquisition

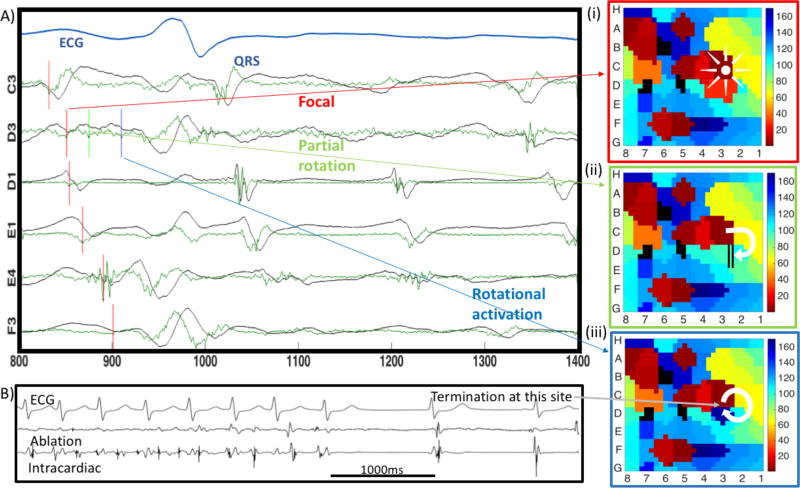
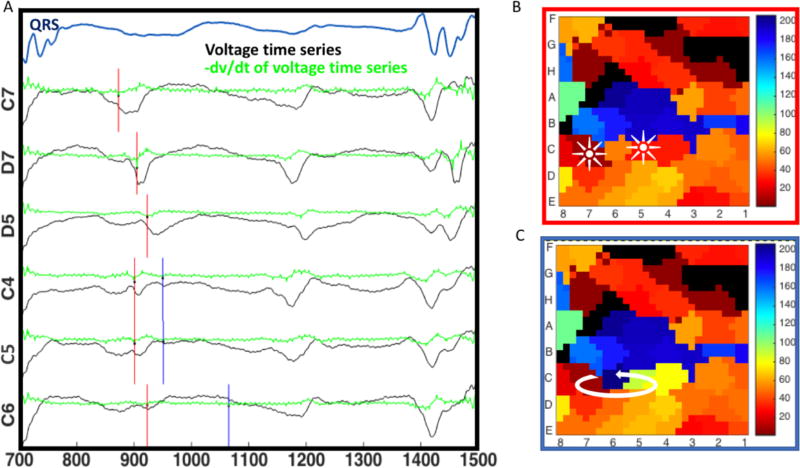
Electrograms in atrial fibrillation were recorded for 1 minute from 64-channel baskets (Bard LabSystem Pro, or GE Prucka Cardiolab) at 1000Hz sampling rate, filtered at 0.05 to 500Hz. The mapping epoch used prospectively to guide ablation was exported for analysis using tools developed specifically for this study. Analysis comprised creating contour maps of encompassing sites where ablation later terminated atrial fibrillation. We created maps using published methods for traditional mapping. Activation times were assigned using criteria of minimum dV/dt, i.e., maximum negative slope, within 50ms starting from the local absolute maximum of unipolar signals²⁰. We applied a 100ms blanking period to avoid analysis within repolarization²¹. Figure 1 shows a map in a patient with persistent atrial fibrillation prior to termination by localized ablation. Electrogram voltages are shown in black, with continuous dV/dt in green. The activation time of each electrogram is indicated by the local dV/dt minimum (vertical red lines), and indicates a rotational circuit where ablation terminated atrial fibrillation. Maps were analyzed to examine sites of termination. In this case, the signals are complex in the sense that there are multiple candidates to mark activation times in a window of 100 ms. This complexity can be caused by far field noise and/or the intricacy of the AF electrical waves, which obscures assignment of activation times. Depending on which deflection is selected for mapping, the apparent mechanism at the site of termination varies from a focal or partial reentry circuit to complete reentry. We thus turned to realistic computer modeling to explain the genesis of various electrogram deflections in atrial fibrillation. This tool is used to develop modified rules to assign deflections that reflect local activation for mapping.

Figure 1.

Mapped mechanisms at the site of atrial fibrillation termination by ablation depend on which electrogram deflection is selected. A) Four atrial fibrillation cycles are shown with annotations of voltages (black trace) in the selected cycle based on minimum negative dV/dt (green trace). D3 has 3 similar deflections. B) Localized ablation at this site terminated atrial fibrillation. Mechanisms at the site of termination vary for selection of i) first or ii) second deflections, which reveal a focal impulse or partial rotational circuits; iii) third deflection, which reveals a complete rotation.

Computational Model

To simulate spiral waves, we adopted the classical monodomain equations^9,12,14,18. This model is a particular case of the bidomain model, where the orthotropic conductivity ratios between the extra- and intra-cellular domains are equal. We implemented an explicit finite difference scheme, parallelized with OpenMP. For all simulations we used a time step size of 0.005ms and a mesh resolution of 0.1 mm. The conductivity value was set 0.13 mm²/ms. We employed the Maleckar model²⁴, a recent update of the Nygren model³⁰ to represent the membrane kinetics of human atrial cells. To represent the action potential in the electrically remodeled atria, we modified the conductances according to changes observed in myocytes subjected to AF^{8,31,39,45,46}: 70% reduction in L-type calcium current, 50% reduction in transient outward current, 50% reduction in ultra-rapid delayed potassium current and 100% increase in inward rectifier potassium current. We advanced all models in time using an explicit time integration⁴². We initialized the cellular model by pacing for 1000 cycles at cycle length of 500ms to establish steady state conditions. To initiate a spiral wave, we used a S1–S2 stimulus protocol: We applied an S1 stimulus in the left boundary of the domain with 5ms pulse duration, followed by an S2 stimulus in the lower left quadrant coupled at 215ms for the baseline model and 155ms for atrial fibrillation. We allowed 1000ms for the wave to stabilize before analyzing subsequent waves of activation and spirals.

Simulation of Electrograms

In contrast to prior modeling approaches based on theoretical point electrodes, we considered electrodes of varying finite size. We hypothesized that the electrode size is a major parameter to interpret clinical data. Human atrial fibrillation has been studied using electrodes with a diameter of 0.3mm and spacing from 2.25mm to 3.50 mm to approximate the scale of spiral wave trajectories and detect of far-field signals^1,2,11. In general, the potential ϕ_e of an electrode with coordinates x_e = [x_e, y_e, z_e] can be computed as a volume integral of the current sources I_m and a transfer function Z,

$${\varphi }_e({\mathit{x}}_e)={\int }_B{I}_m(\mathit{x})Z({\mathit{x}}_e,\mathit{x})\mathit{\text{dB}}\text{with }\mathit{x}=[x,y,z].$$

For the case of finite-size electrodes, we idealized the electrode as a plate with constant potential. Then, the analytical solution of the transfer function is¹⁹

$$Z({\mathit{x}}_e,\mathit{x})=\frac{1}{2\pi {\sigma }_e{d}_e}\text{arcsin}\left(\frac{d_e}{\sqrt{{(r-d_e/2)}^2+{z_e}^2}+\sqrt{{(r+d_e/2)}^2+{z_e}^2}}\right),$$

where $r=\sqrt{{(x-x_e)}^2+{(y-y_e)}^2}$, d_e is the electrode diameter and σ_e is the conductivity of the medium surrounding the tissue, which we assume to be equal to one. For comparison, we also computed electrodes using the common point electrode transfer function^6,40

$$Z({\mathit{x}}_e,\mathit{x})=\frac{1}{4\pi {\sigma }_e\sqrt{r^2+z_e^2}}.$$

Supplementary Figure 1 shows transfer functions for different electrode diameters. Transfer functions for plate electrodes are a plateau within the electrode diameter, meaning that all currents generated below the electrode are weighed equally. Point electrodes, however, weigh currents below the center of the electrode with a nearly infinite value, capturing only local activation. To avoid divergence, we assumed z_e equal to 0.001mm. We created an interactive software suite in Python to calculate electrograms. For interactive analysis, electrodes can be constructed at any position within the simulated domain, and the local action potential and corresponding electrogram are immediately calculated and displayed. This allows us to efficiently scrutinize electrograms in the vicinity of any feature including rotor tips.

Simulation of Fibrosis

We simulated fibrosis by growing an arbitrary region from the center of the patch using a breadth first search algorithm. Briefly, this algorithm first starts in a root cell and explores the neighboring cells first, then recursively explores the neighbors of all explored cells, until a maximum number of iterations has been reached. Without any modifications, this algorithm would create a squared region. To create an amorphously shaped region, each cell was explored randomly. Then, a fraction of the points within this region were randomly assigned as fibrotic, using a uniform distribution. We included the effect of fibrotic tissue at the cellular level using two different approaches: First, in all elements in the fibrotic region, we set the conductivity and the action potential source term equal to zero⁴⁸. In this case, fibrotic tissue acts as isolating barriers. Second, we considered patchy fibrosis interspersed with viable tissue, by simulating fibrosis as changes in action potential. We further remodeled the atrial fibrillation version of Maleckar model to replicate experimentally observed changes during fibrosis³³. We reduced the inward rectifier potassium current by 50%, reduced the L-type calcium current by 50%, reduced the sodium current by 50%, and decreased the conductivity in the fibrotic cells by 50%⁵².

Quantification of Electrogram Characteristics

To systematically characterize electrograms in the vicinity of spiral waves, we computed signals every 1mm in an area that included the entire trajectory of the spiral with a margin of 1mm, using electrode diameters of 0, 1, 3 and 5mm. For fibrotic cases, we defined this area as the patch with 1mm of margin. For these signals, we computed activation times automatically using minimum dV/dt³⁶. For more than one deflection in a window of 100ms, we chose the deflection with the minimum dV/dt to generate unique activation maps. We labeled these cases as multiple deflections and stored them for further analysis. We also defined the local activation time using the maximum dV/dt of closest cell’s action potential. We calculated the differences between activation times computed by electrograms and local activation times and related them to distance to the spiral tip at the time of activation and magnitude of dV/dt.

Statistical Analysis

We used the Welch’s t-test for independent samples to determine if there were significant differences between single and double deflection electrogram markings. We used a single group t-test to evaluate differences between electrodes sizes, by subtracting the errors for the same the activation. The null hypothesis is that the mean of the difference in errors is zero. For sample groups of size smaller than 20, we performed the Shapiro-Wilk test for normality before we used the t-test. We used Bonferroni correction to account for the multiple comparisons that we performed (n = 30). We then set the level of significance to 0.05/30 = 0.0016. We calculated the Pearson correlation coefficient to estimate a linear dependency between variables with its corresponding p-value to test the significance of the correlation. All statistics were performed in Python using the Scipy stats package.

RESULTS

Clinical Results and Mapping

Table 1 shows the characteristics of all subjects in the clinical study. In each patient, ablation at one localized source region alone terminated atrial fibrillation. Figure 1 indicates electrograms at the region of termination in a 54 year old man with persistent atrial fibrillation. In panel A, some channels show simple electrograms while others show multiple components and low amplitude. In panel B, ablation in the region producing these electrograms terminated atrial fibrillation to sinus rhythm. In panel C, the precise mechanism reported at the site of termination depends clearly on which electrogram component is marked for the map at site D3. Local activation is traditionally assigned at maximum– dV/dt. Marking (i) the first or (ii) second deflections at D3 made this site early consistent with a focal site or breakthrough or a map of partial reentry. Marking (iii) the third deflection at D3 pushed this site late, producing a map of complete rotation at the site of atrial fibrillation termination. Overall, five of 15 cases demonstrated rotational activity, which may explain atrial fibrillation termination at these sites. However, ten of 15 maps using activation timings revealed only partial rotations or disordered activation, which does not readily explain atrial fibrillation termination. We applied modeling to study whether ambiguities in assigning electrogram onset times could be improved by understanding the genesis of multiple signal components. Our goal was to study whether deterministic selection of local over non-local deflections may enable the development of novel rules for accurate mapping.

Table 1.

Patient demographics.

Patient Characteristics	Mean ± SD
Age (years)	62.0 ± 10.0
Gender (% male)	93
LA diameter (mm)	48.5 ± 8.4
AF history (years)	6.06 ± 4.23
LVEF (%)	53.9 ± 11.0
Hypertension (%)	87
BMI (kg/m2)	30.4 ± 5.3
CHADSVASc score	2.3 ± 1.4
Site of termination (%LA/RA)	86.7/13.3
Mode of termination (%SR/AT)	67/33

Simulated Tip Trajectories and Effects on Electrograms

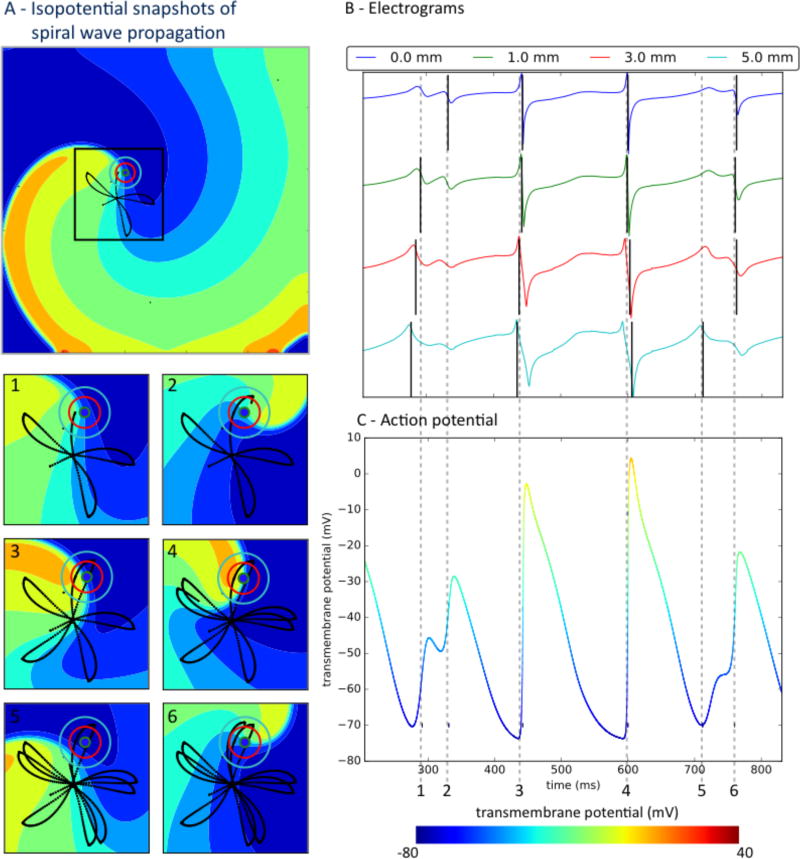
Electrograms were sensitive to spatial stability of the arrhythmia circuit. In organized atrial flutter, non-fibrillatory reentry in a fixed trajectory produced electrograms with regular shape throughout the domain, supplementary Figure 2. This was true for all electrode diameters, 0mm to 5mm. As expected, activation mapping of electrograms in atrial flutter robustly identifies similar mechanisms regardless of recording parameters. Conversely, spatially precessing waves and spiral tips in atrial fibrillation caused varying electrogram morphology and deflections, which could dramatically alter mapping. Figure 2 depicts a spiral wave in atrial fibrillation with tip precession in a “flower” trajectory⁵¹ (Fig. 2A, panels 1–6), with resulting irregular electrograms (Fig. 2B). Double deflections were detected (Fig. 2C), which often did not reflect local activation (phase 0, upstroke). Additional deflections varied with the size of the recording electrode, including far-field activation from nearby wave fronts and other effects.

Figure 2.

Precessing spiral wave trajectory causes variable atrial fibrillation electrograms; with similar local and far-field components on clinically sized electrodes. A) Isopotential snapshots of the spiral wave. Insets 1–6 show zoomed views with black lines representing spiral tip trajectory, at times referenced to electrograms. B) Electrograms for electrodes of diameters marked by concentric circles in panel A. Recorded activity depends on electrode size independent of spacing. C) Transmembrane action potentials. Time 1 indicates non-local activity from a passing wave, especially on larger electrodes. At time 2, low amplitude signals reflect tight turn of the spiral tip. At times 3 and 4, electrograms represent activation. Time 5 represents non-local activation from the nearby passing wave, which is difficult to separate from the next true activation at time 6. Vertical black lines mark onset (minimum dV/dt) in each electrogram.

Electrogram Sensitivity with respect to Electrode Diameter

Atrial fibrillation electrogram components reflected the capture of variable and complex propagation waves by variably sized electrodes. In Figure 2A, an advancing wave front of activation (warm colors, panel A1) inscribes a deflection which is small on the theoretical electrode (0mm) but larger on 1–5mm electrodes and distinct from local activation (time 1 versus action potential upstroke in panel C). The second deflection (time 2, panels B, C) represents activation from the tight turn of the wave tip. This is likely not part of repolarization because despite its comparable amplitude in the isopotential map (time 2, panel A), the wave is propagating forward. At times 3–4, panel A, the wave tip and wave tail produce simple activation with non-complex electrograms at the electrode site that reflect local activation (panel C). The fifth deflection (time 5 in panel B) represents the nearby passing wave (time 5, panel A and time 5, panel C) and is difficult to separate in larger electrodes from the next true activation at time 6 (panel C). We conclude that multiple electrogram deflections in atrial fibrillation may represent low amplitude depolarization and far field effects, which are particularly confusing for clinically sized electrodes and may contribute to the complex signals observed in human atrial fibrillation in Figure 1.

Electrogram Sensitivity with respect to Fibrosis and Electrode Size

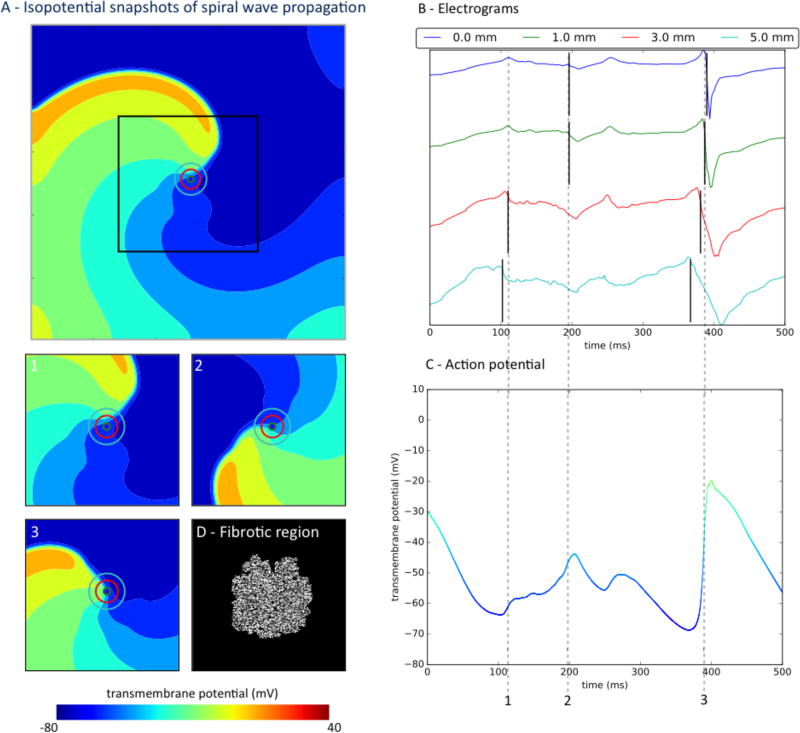
Structural remodeling, simulated as fibrosis, further increased spiral wave precession and electrogram complexity (Fig. 3, Supplementary Fig. 3). Figure 3 indicates exaggeration of timing errors in atrial fibrillation electrograms with fibrosis of 50%, despite relatively simple spiral wave activation, which is similar to Figure 2. Figure 3A portrays spiral wave snapshots (panels A1–3) through the fibrotic region (panel A4). In panel C, action potentials were impacted by the interaction between fibrotic and non-fibrotic regions with altered conductivity. Action potentials no longer present clear upstrokes at sites around which the spiral wave rotated. Electrograms from all electrode sizes were complex and irregular in time (panel B). At time 1, the 3 and 5mm electrodes capture the nearby passing wave front, but the 0 and 1mm electrodes capture a deflection that does not represent the spiral wave at time 2.

Figure 3.

Atrial fibrillation electrograms poorly represents timing of local activity in the presence of substantial fibrotic remodeling and for larger electrodes. A) Spiral wave propagates through fibrotic tissue, with electrodes of varying diameters marked by concentric circles. Panels 1–3 are isopotential snapshots at marked times; Panel D indicates fibrotic region. B) Atrial fibrillation electrograms generated by different electrodes sizes, with black lines marking minimum dV/dt. Large electrodes (3, 5mm) record a non-local deflection of the wave front that is passing nearby at time 1, whereas small electrodes (0, 1mm) record a deflection that is not a complete activation at time 2 (Panel A, time 2, light blue). C) Action potential at the electrode site is complex due to the interaction of fibrotic and remodeled tissue.

Supplementary Figure 3 shows a parallel analysis in the presence of 15 % fibrosis (panel A4). Permeation of the spiral wave through these regions exaggerated their trajectory and produced electrograms with multiple deflections. Compared to point electrodes (Fig. 3B), larger electrodes recorded electrograms that no longer time-aligned with local activation (action potential upstroke; Fig. 3B–C). The inaccuracy in electrogram timing worsened with electrode size, with the time difference between deflections being 31ms for a 3mm electrode and 38ms for a 5 mm electrode when compared to the point electrode (time point 2). Smaller electrodes produce lower errors for this time point (< 9ms), but still produced discrepancies due to action potential heterogeneity in fibrotic regions. Thus, electrograms are less accurate for local activation in atrial fibrillation with increasing fibrosis, even for relatively simple underlying wave dynamics.

Electrogram Accuracy and Clinical Recording Parameters

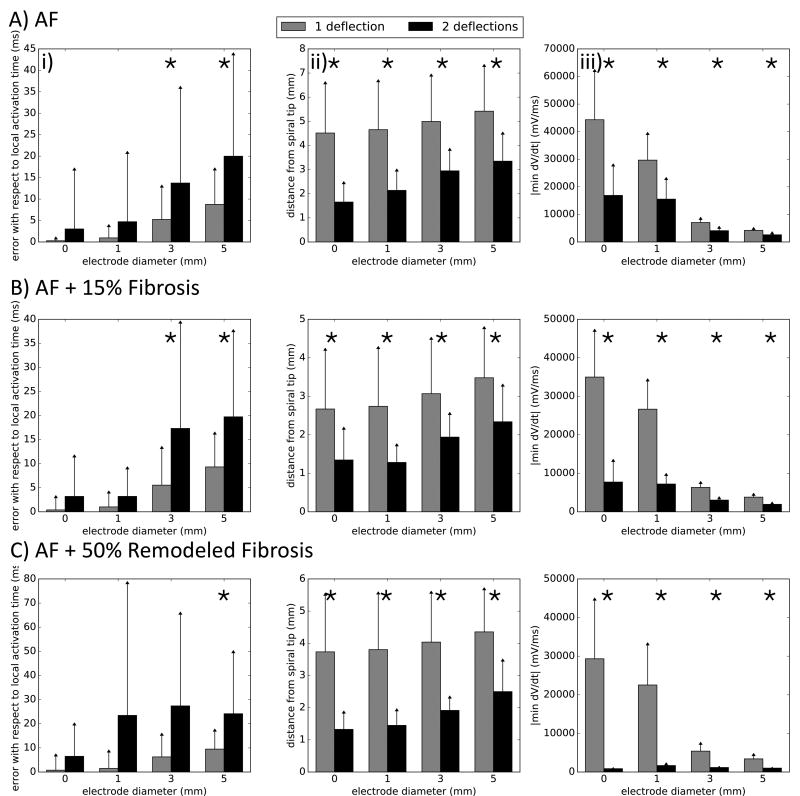
Figure 4 shows the accuracy of atrial fibrillation electrogram times for timing local activity based on the number of electrode deflections, dV/dt, distance of electrode to organized spiral wave core, electrode size and the impact of atrial fibrosis. The error between electrogram timing (dV/dt criteria) and action potential upstroke increased with electrode size, from 0.48 ± 3.92ms for a point electrode to 10.41 ± 13.11ms for a 5mm electrode (p < 0.001 between all electrodes). When comparing electrograms by morphology, we observe that signals with double deflections had, on average, higher error than single deflection signals for 3 and 5 mm electrodes (p < 0.001, Fig. 4 Ai). Signal characteristics also varied with distance of the electrode to the spiral core, and with electrode size. Multiple component electrograms were recorded, on average, closer to the spiral tip than single deflections (2.66 ± 1.20mm vs. 4.88 ± 2.07mm, p < 0.001, Fig. 4Aii), and were more prevalent in larger electrodes. Electrograms with 2 deflections showed smaller average dV/dt magnitude (Fig. 4Aiii), which depended on electrode size, with the reduction in deflection magnitude ranging from 62% for the point electrode to 38% for the 5 mm electrode (p < 0.001). These trends were exaggerated by increasing fibrosis to 15% (Fig. 4B) and 50% (Fig. 4C). Timing errors between electrograms and local action potentials increased with electrode size, ranging from 0.61 ± 4.64ms for the point electrode in the 15% fibrosis case to 12.11 ± 15.14ms for the 5mm electrode in the 50% remodeled fibrosis case when considering all deflections (p < 0.001, when comparing electrode sizes for each case). Complex electrograms were also more prevalent closer to the spiral tip (p < 0.001, Fig. 5B,Cii) with lower dV/dt magnitude (p < 0.001, Fig. 4B,Ciii).

Figure 4.

Errors in atrial fibrillation timing, number of electrogram deflections, and electrogram upstroke velocity varying with electrode size. For all simulations (panels A–C), electrograms with 2 deflections present increased error with respect to the local activation times, were further from the spiral tip and decreased dV/dt of the deflection. Significant differences are marked with (*).

Figure 5.

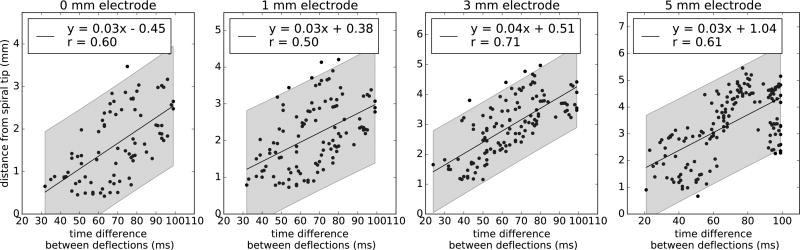
Estimation of distance to spiral tip based on time difference between electrogram deflections in atrial fibrillation. A linear trend (p < 0.001, n > 83 for all electrodes) was observed for each electrode size, with a positive correlation between the time interval between deflections and distance to the spiral tip at the time of the maximum negative dV/dt. 95% prediction intervals are shown in gray and have a range of 3mm for any given time difference.

Electrogram Deflections that Represent Local Activation

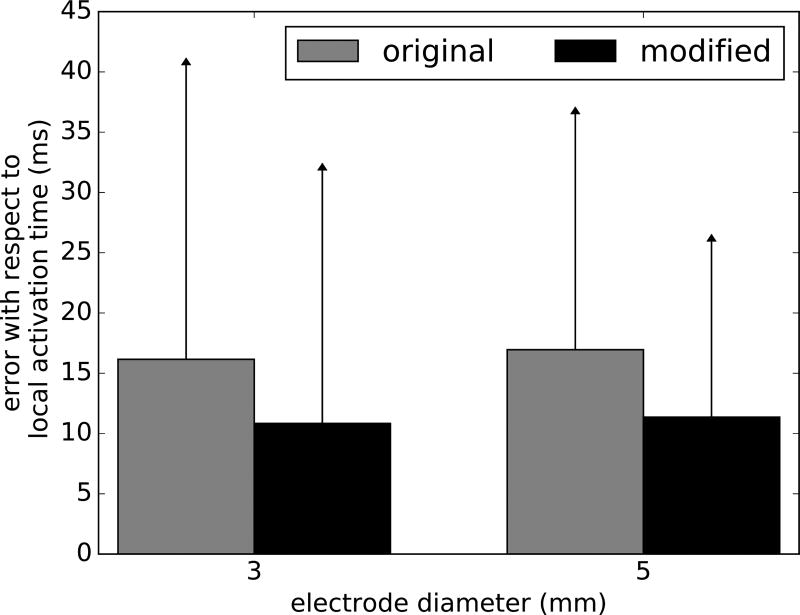
Figure 5 summarizes analyses to infer the distance from the electrode to a spiral tip core, using time spacing between deflections. These 2 variables showed a moderate linear correlation (r = 0.50 – 0.71, p < 0.001) with 95% prediction intervals shown for different electrodes sizes in gray. We systematically studied the impact of using the second electrogram deflection to indicate local activation rather than traditional minimum dV/dt. In 63% of cases for each electrode size of incorrect markings, the first deflection had a greater negative dV/dt than other deflections and was selected as activation time. Figure 2B illustrates this effect at times 1–2 for diameters > 1mm. The first deflection in these incorrect markings had a lower dV/dt magnitude than in cases of correct markings, in which the first deflection with highest negative dV/dt minimized the error with respect to local activation (p < 0.001 for electrodes of 3 and 5mm). We determined a dV/dt threshold to most accurately identify electrogram timings, i.e. that minimized the sum of false negatives and false positives in the set of simulated electrograms. Activation times where dV/dt exceeded threshold were considered accurate, while those with dV/dt below threshold were replaced by timings at the second deflection. We tested this methodology in a new set of electrograms with an offset of 0.5mm in both directions with respect to the original electrograms. Although this new set of data was obtained from the same simulation, it can be used to assess the validity of the method without losing the characteristic of the AF model. This new approach (Fig. 6) reduced the average timing error for local activation by 33% in electrodes of 3 and 5mm (p < 0.001), using thresholds of 2546.2 and 1468.4 mV/ms respectively, comparable to the error of single-deflection electrograms (Fig. 4Ai).

Figure 6.

Improved prediction of activation times in low dv/dt electrograms. By always selecting the second deflection as local activation time in cases of low dV/dt magnitude, we reduced the error to that seen in single deflection electrograms using clinically sized electrodes (independent t-test: p < 0.001, 3 mm electrode: n = 123, 5mm electrode: n = 149).

Adjusting Electrogram Timing

Figure 7 provides another example of how computational-physiological rules for marking electrograms from this study modified reported mechanisms in this series. This may resolve the ambiguity highlighted in Figure 1 where different timings alter interpretation of atrial fibrillation mechanisms at the termination site. In this 67 year old man with persistent atrial fibrillation, annotating the first electrogram deflection produces a map of multiple foci at sites C7 and BC5. Applying our modified rules to unipolar electrograms with low amplitude and patient specific dv/dt threshold of 0.7 mV/ms produced a map consistent with a complete rotational circuit at site CD56. Prospective ablation in the case at site CD56, identified by a separate method that did not require assignment of electrogram onset (phase mapping), terminated atrial fibrillation to sinus rhythm.

Figure 7.

Applying a second deflection criterion changes the detection of atrial fibrillation mechanisms. A) In this 67 years old man marking the channels by maximum negative dV/dt (red lines), gives a map with a focal pattern of atrial fibrillation B). However, in those channels with low dV/dt (C4, C5, C6), applying the proposed rule of taking the second plausible negative dV/dt reveals a rotational circuit C), where earliest activation (red) meets latest activation (blue). Ablation at this site terminated atrial fibrillation.

DISCUSSION

This study combines clinical mapping with computational modeling to improve mapping of human cardiac fibrillation. We established in silico simulations to identify physiological contributions to local and far-field atrial fibrillation electrograms. Our analysis revealed components from wave curvature and permeation through fibrosis, which were indistinguishable from local depolarization. We developed novel electrogram shape criteria to attenuate far-field components. In a series of clinical cases, we demonstrated how traditional rules may produce complex maps of atrial fibrillation at sites where ablation terminated persistent atrial fibrillation. At the same time, our novel combined computational approach revealed organized patterns including rotational activity in agreement with phase mapping at sites where ablation terminated atrial fibrillation. Future studies can build upon this approach to improve mapping of complex arrhythmias and ultimately guide therapy.

Electrograms Accuracy for Mapping Simple versus Complex Arrhythmias

This study is among the first to address why reported mechanisms for atrial fibrillation are highly sensitive to the underlying mapping technique. In organized, non-fibrillatory arrhythmias, where electrogram shape is regular across the mapped domain, this sensitivity is less pronounced which explains why, for example, atrial flutter circuits are revealed consistently by all electrode sizes and approaches with minimal differences. In atrial fibrillation, however, reported mechanisms vary dramatically with mapping method: Optical mapping consistently show localized drivers in human²² and other models of atrial fibrillation, where ablation can terminate fibrillation and explain clinical data^13,28. Conversely, traditional mapping shows mostly disorganized waves^23,24. Traditional mapping is more straightforward when repolarization data are available to filter far-field components, either with monophasic action potentials²⁶ or via optical mapping²². However, there are currently no mapping criteria to separate local from far-field activity in atrial fibrillation.

Identifying Local and Non-Local Activity in Electrograms

Here we established methods to separate far-field from local electrograms in atrial fibrillation, without the need for a reference channel of repolarization data²⁹ which is rarely available. First, we identified a bias in traditional mapping towards detecting earlier components than true local activation, particularly when using larger clinical electrodes. This may explain numerous reports of early ‘foci’ or ‘breakthroughs’. Simply selecting the second deflection—if electrograms on the first deflection had dV/dt below our determined threshold–improved accuracy of local activation time. Second, while atrial fibrillation electrograms from meandering rotor trajectories or fibrotic substrates are complex, double deflections may occur near a spiral wave tip with low amplitude and produce a large error in estimating local activation time. Third, our simulations suggest that it may be possible to infer the distance of a specific electrogram to a rotor core by considering the time interval between deflections, with narrower spacing indicating a closer proximity. These results may assist in accurately marking electrograms for mapping, and also for finding an ablation target.

Next Clinical Steps and Limitations

Rules proposed by our hybrid computational/physiological approach for improving atrial fibrillation mapping should be tested clinically. This could be done prospectively in patients undergoing ablation, or in blinded fashion retrospectively in patients where localized ablation terminates persistent atrial fibrillation, similar to this study.

This study has several limitations: First, we only simulated two-dimensional surfaces to represent the atria and we used a simplified fibrotic model. In future studies, we plan to create patient specific geometries and incorporate personalized fibrotic lesions from magnetic resonance images^3,5. This will allow us to characterize secondary effects of atrial fibrillation, e.g., mitral annular dynamics^34,35 and left ventricular function³. Second, we only simulated one spiral wave, as opposed to a more chaotic response observed clinically. However, it has been shown that many advanced electrophysiology models, such as the one used in this study, tend to be stable under atrial fibrillation⁵¹. Moreover, we have shown that even for a single source during a single cycle of fibrillation, there is considerable error, often up to 50ms when estimating local activity with electrograms. This has implications on mechanisms and their stability for each successive cycle and importantly will impact therapy delivery. Third, we have disregarded the mechanical contraction of the tissue^13,49. Tissue deformation could induce additional sources of fibrillation³⁸ and disease progression also alters the electro-mechanical properties of the tissue²². Fourth, clinically, our cohort was not prospectively studied; this is the focus of our current efforts.

CONCLUSION

In conclusion, we have identified physiological contributions to local and far-field fibrillatory electrograms in atrial fibrillation using computational simulations. Our simulations define novel rules to map atrial fibrillation. The major feature of these rules is to attenuate far-field contributions. Our pilot clinical study revealed that traditional rules were incapable of identifying sites where ablation terminated persistent atrial fibrillation. Our novel rules reliably identified rotational activation patterns, which were consistent with sites of successful ablation, and were concordant with phase mapping. Our study can serve as a scientific foundation for novel mapping strategies to guide ablation therapy.