Histogram-Based Features Selection and Volume of Interest Ranking for Brain PET Image Classification

Abstract

Positron emission tomography (PET) is a molecular medical imaging modality which is commonly used for neurodegenerative diseases diagnosis. Computer-aided diagnosis, based on medical image analysis, could help quantitative evaluation of brain diseases such as Alzheimer’s disease (AD). A novel method of ranking the effectiveness of brain volume of interest (VOI) to separate healthy control from AD brains PET images is presented in this paper. Brain images are first mapped into anatomical VOIs using an atlas. Histogram-based features are then extracted and used to select and rank VOIs according to the area under curve (AUC) parameter, which produces a hierarchy of the ability of VOIs to separate between groups of subjects. The top-ranked VOIs are then input into a support vector machine classifier. The developed method is evaluated on a local database image and compared to the known selection feature methods. Results show that using AUC outperforms classification results in the case of a two group separation.

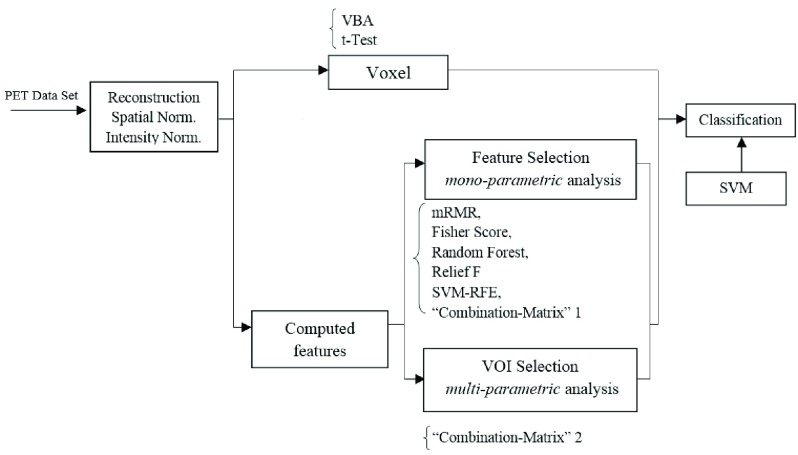
General scheme of region ranking and feature selection for computer-aided diagnosis of Alzheimer's Disease on PET images.

I. Introduction

Alzheimer Disease (AD) is a degenerative and incurable brain disease which is considered the main cause of dementia in elderly people worldwide. It is expected that 1 in 85 people will be affected by 2050 and the number of affected people will double in the next decades [1]. The diagnosis of this disease is done by clinical, neuroimaging and neuropsychological assessments. Neuroimaging evaluation is based on nonspecific features such as cerebral atrophy, which appears very late in the progression of the disease. Therefore, developing new approaches for early and specific recognition of AD is of crucial importance.

Several imaging biomarkers to identify AD are effective [2], including structural Magnetic Resonance Imaging (MRI) [3]–[7], Single Photon Emission Computed Tomography (SPECT) [8], electroencephalographic EEG rhythms [9], [10] and Positron Emission Tomography (PET) [11], [12]. In addition to these imaging bio-markers, biological biomarkers such as Cerebral Spinal Fluid (CSF) [6] have also been developed for AD diagnosis. It has been shown that PET functional imaging associated with FluoroDeoxyGlucose (18F-FDG) as a tracer is able to increase the confidence of neurodegenerative diagnosis [13]–[16].

Early detection of AD is important because it increases the chances of early treatment and may enable pre-emptive and even preventative therapies in the future.

The clinical diagnosis of AD uses a variety of tests including patient’s family history, physical examination, mini-mental state examination, and/or neuroimaging [17]. Recently, functional neuroimaging technologies, such as the Positron Emission Tomography (PET), has become a powerful tools in the diagnosis of AD since it is now possible to reveal pathophysiological changes before irreversible anatomical changes are present. 18F-Fluoro-deoxyglucose (FDG) is a widely used radioactive tracer in PET imaging. FDG-PET provides useful information about the cerebral glucose metabolic rate.

Studies have demonstrated reduced glucose metabolism in a small number of brain regions in AD patients comparing to normal subjects [18], [19]. As such difference becomes noticeable, researchers are increasingly interested in distinguishing AD patients from normal subjects by utilizing their brain images. As a non-negligible complementary way in the diagnosis of AD, PET imaging has high specificity and sensitivity, even a long period before the full-blown dementia has developed.

Visual evaluation of brain PET images is qualitative and deals with two problems: it is time consuming and operator dependent [20]. Visual method depends greatly on the observer’s experience and lacks a clear cut-off between normal and pathological finding. This has been highlighted in the imaging literature [16]. FDG-PET is today recommended and largely used to contribute to the diagnosis of AD in case of atypical presentations, especially in young patients, to distinguish AD from focal neurodegenerative diseases and from non-neurodegenerative diseases (encephalitis, psychiatric disorders). This evaluation is usually conducted on visual interpretation and depends on the experience of the physician. An automated classification method may contribute to improve the robustness and the reproducibility of the diagnosis across different centres, of course if this evaluation remains compatible with a clinical work-up in terms of time spending and necessary resources. Moreover, in the perspective of future disease modifying therapies in AD, early diagnosis at initial stages of the disease will be required to stop or slow down the disease before the diffusion of the brain lesions, with at this step a greater uncertainty of the visual PET interpretation because of possible limited abnormalities, which may increase the need of computer-aided methods. Computer-Aided Diagnosis (CAD) could bring a valuable tool to quantitatively evaluate brain disease such as AD.

Image processing techniques applied to PET images have been widely used for CAD purposes [21], including feature selection and extraction [12], [22]–[31], segmentation: Fuzzy C-Means [32], Gaussian Mixture Model [33], [34], Dynamic Neuro-Fuzzy technique [35], and K-Means clustering [36] and classification: Random Forest (RF) [23], Support Vector Machine (SVM) [22], [12], [11], [37], [38], K-Nearest Neighbour (KNN) [37], [39] and Neural Networks [25], [40]–[42].

The general scheme of analyzing PET images for classification purposes consists in acquiring and preprocessing images first, then applying a feature selection or extraction technique in order to reduce the amount of redundant information and finally input these chosen feature to a classifier. Many approaches have been used to tackle the problem of feature selection and extraction including Fischer Discriminates Ratio (FDR) [22], Non-Negative Matrix Factorization (NMF) [22], [30], Partial Least squares (PLS) [23], Gaussian Mixture Models (GMM) [12], Wavelets Packet Transform [25], Principal Component Analysis (PCA) [26]–[29] and Independent Component Analysis [31] (ICA).

The curse of dimensionality problem or the small sample size is a well-known problem encountered in neuroimaging where the features used for the classification process are higher than the sample used for the training process. This is the case of the Voxel-Based Analysis (VBA), where the brain is considered as a set of raw voxels, on which some statistical tests Student’s t-Test [43]–[45] or Mann-Whitney-Wilcoxon U-Test [46], [47] are computed and then input to a classifier. A lot of voxels are redundant and irrelevant for classification tasks and therefore feature selection is needed.

Feature selection methods focus on the selection of a subset of features that describes well the input data while reducing effect noise or irrelevant variables and still provides good classification results [48]. They can be broadly classified into three groups: filters, wrapper and embedded methods.

Wrapper methods evaluate the utility of feature subsets using the results of a specified classifier. These methods allow to detect the possible interactions between variables. A search procedure within the possible feature subsets space is done. As the number of subsets grow exponentially with the number of features, a heuristic or a sequential selection algorithms are used for search purposes [49]. The two main disadvantages of these methods are the increasing overfitting risk when the number of observations is insufficient and the significant computation time when the number of variables is large [50], [51]. In the context of AD diagnosis, Chyzhyk et al. [52] used a wrapper method with a genetic algorithm for optimal subset search.

Embedded methods reduce the computational time compared to wrapper methods by incorporating the feature selection in the training process of a classifier. These are very sensitive to the learning algorithm used to set feature subset. Support Vector Machine (SVM) approaches [53] or decision tree [54] algorithms are some examples of embedded methods. This approach has been used for MRI brain classification in the case of AD diagnosis [55].

Filter methods do not depend on any classifier but can be considered as pre-processing steps based on specific criterion to evaluate the relevance of features. One of the main disadvantages of these approaches is that they ignore the interaction between features and hence are unable to remove redundant features. The most proposed techniques are univariate, this means that each feature is considered separately, for instance on mutual information [56], Fisher discriminant ratio [30], [57], Pearson correlation coefficient [58], Laplacian score [59], gain ratio [60], [61], chi-square test [62], Relief [63]. On the other hand, some multivariate methods which can handle both irrelevant and redundant features have been used to take into account dependence between features. Minimal-Redundancy Maximal-Relevance (mRMR) proposed by Peng et al. [64] is a well-known method where the selection of the feature subset is based on mutual information. Other criteria have also been proposed including conditional mutual information [65] or the second approximation of the joint mutual information [66], clustering technique [67], Fast correlation based filter [68], [69] Relevance-redundancy feature selection [70]. More details can be found in a recent feature selection survey [71], in [72] for Alzheimer’s disease and in [73] in the general case.

There has been a growing interest in using the FDG rate for AD/HC classification [74]. Four main groups of methods have been studied: voxels as feature (VAF)-based [75], discriminative voxel selection-based [76], [77], atlas-based [78], [79], and projection-based methods [30].

A lot of radiomic methods exist and have been used on PET images especially for diagnosis, staging, prognosis and therapy responses assessment in oncology. The proposed method, based on statistical features extraction from histograms and described in our paper, derives from the expertise transfer that we obtained, when discussing with nuclear medicine doctors with whom we were working. In neurodegenerative diseases there is no particular tumour region in which a Standardized Uptake Value (SUV) could be computed. The main important features we need to compute, according to doctors, is the anatomical Volumes of Interest (VOI) uptake statistical properties (average, variance, and heterogeneity through skewness and asymmetry). These are the first order statistical moments extracted from regions’ histograms. The information being captured using histograms is the difference of FDG uptake across VOI, as it important for Alzheimer’s Disease to detect reduced glucose metabolism in some VOI in the brain.

In this paper a novel supervised filter-based feature selection is developed. It allows to select the best feature subset and rank them according to the “Area Under Curve” (AUC), a criterion based on Receiver Operating Characteristic (ROC) in the feature space. With a view to applying this approach on PET brain images, a brain mapping using an atlas is applied to segment PET into Volumes-Of-Interest (VOIs). Statistical moments of each VOI’s grey level histogram are computed and using the developed technique it was possible to rank the ability of a VOI or a subset of VOIs, characterized each by a subset feature vector, to distinguish between AD and Healthy Control (HC) brain images. The performance of the proposed method is compared with other well-known feature selection methods in terms of classification success rates using the feature subset selected by each method as an input to a Support Vector Machines (SVM) classifier. The evaluation is done on our own FDG PET image database and results show that the proposed approach is amongst the algorithms with the best results.

The rest of the paper is organized as follows. Section II gives a brief description of the developed approach. The main contribution on feature selection and region ranking is presented in section III. Section IV reports the obtained results, performance evaluation and comparison. Finally, a conclusion and future work are given in section V.

II. Proposed Method Description

A. Overview of the Proposed Method

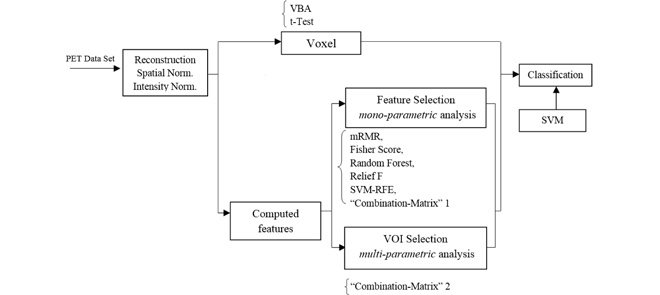
The flowchart of the proposed method is shown in Fig. 1. As for any CAD system, it consists in several important stages:

• 1.18F-FDG-PET data acquisition and preprocessing.
• 2.Computed features
• 3.Mono-parametric analysis feature selection.
• 4.Multi-parametric Volume-Of-Interest (VOI) selection and ranking.
• 5.Classification.

FIGURE 1.

Flowchart of the proposed CAD system.

The different stages appearing in this flowchart are detailed in the next sections.

B. Image Database

FDG PET scans were collected from the “La Timone” University Hospital, in the Nuclear Medicine Department (Marseille, France). The database was built up based on imaging studies of subjects that followed the standardized protocol of a hospital-based service. PET scans were performed using an integrated PET/CT camera (Discovery ST, GE Healthcare, Waukesha, USA), with 6.2 mm axial resolution, allowing 47 contiguous transverse sections of the brain of 3.27 mm thickness. 150 MBq of 18FDG were injected intravenously in an awake and resting state, with eyes closed, in a quiet environment. Image acquisition started 30 min after injection and ended 15 min later. Images were reconstructed using ordered subsets expectation maximization algorithm, with 5 iterations and 32 subsets, and corrected for attenuation using CT transmission scan. The local database image enrolled 171 adults 50–90 years of age, including 81 patients with AD and 61 HC and 29 MCI (Mild Cognitive Impairment). Their demographic characteristics are summarized in Table 1. HC were free from neurological/psychiatric disease and cognitive complaints, and had a normal brain MRI. Patients exhibited NINCDS-ADRDA [80] clinical criteria for probable AD.

TABLE 1. Demographic Details of the Dataset.

	HC	AD	MCI
Number	61	81	29
Male/female	(24/37)	(32/49)	(12/17)
Ages (Mean/[Min..Max])	68.18 [50..86]	70. 60 [50..90]	67.55 [50..85]

C. Image Preprocessing

Images were spatially normalized because of brain volume variation, shape and position from one patient to another. Spatial normalization consisted in applying deformations on volumes so that the whole-brain statistical analysis was performed at voxel-level using SPM8 software [43] (Wellcome Department of Cognitive Neurology, University College, London, UK). The data were spatially normalized onto the Montreal Neurological Institute atlas (MNI).This method assumes an affine generic model with 12 parameters [22] and a cost function which presents an extreme value when the image and a template that represents our ‘brain space’ correspond to each other. The spatial normalization is achieved by optimizing the quadratic difference between the template and each image. After this spatial normalization, the dimensions of the resulting voxels were 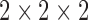mm and the resulting images of 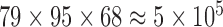voxels size. These images were then smoothed with a Gaussian filter (with different values (0, 4 and 8) of Full Width at Half Maximum (FWHM) to blur individual variations in gyral anatomy and to increase the Signal to Noise Ratio (SNR) [82]. The best FWHM appeared to be 8.

After spatial normalization, intensity normalization was required in order to perform direct images comparison between different subjects. Intensity normalization was necessary since global brain activity varies from one subject to another. Different normalization methods were tested [83] to determine the most appropriate one. The retained method consisted in dividing the intensity level of each voxel by the intensity level mean of the gray-matter global brain VOI.

III. Feature Selection and Volume of Interest Ranking

In this section, we present the main idea of both feature selection and VOI ranking. Brain images are segmented into 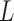VOIs according to AAL of WFU-Pickatlas tool, version 2.4. [84]. Each VOI, V_v, 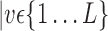is characterized by a set of features 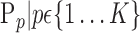. The main question that we want to answer is: how to quantify VOI ability to best distinguish between AD and HC?

Our approach in this work consists in selecting VOIs which best separate between AD and HC classes. Different parameter combinations for each VOI are used to select and rank VOIs according to the “Area Under Curve” (AUC) parameter, defined in the following. The top-ranked VOIs are then introduced into a SVM classifier.

A. Notation

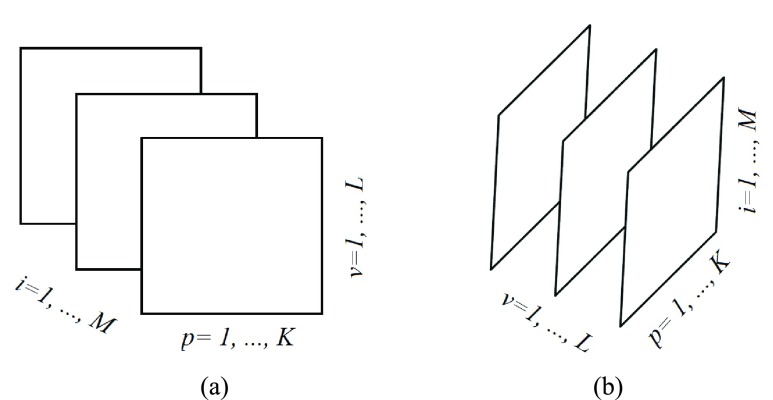
We consider a dataset 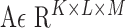. A is a 3-D tensor, where 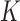denotes the number of parameters computed for each VOI among 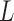VOIs and 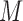is the number of acquired PET images. Let us consider their corresponding metricized version 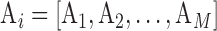and 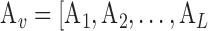]. As depicts in Fig. 2, each matrix A_i is of dimension 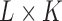and represents all regional parameters values for cortical VOIs for a selected simple 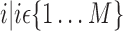. Each column of A_i is defined as volume parameter values computed for all VOIs on the selected simple 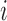. A_v is of dimension 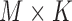and represents all simples with parameters values computed on a selected VOI, .

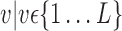FIGURE 2.

Frontal (A_i) and lateral (A_v) slices of the tensor A that are handled within PET images. (a) A_i matrix of the tensor A. (b) A_v matrix of the tensor A

B. Features Definition

The brain is mapped into 116 cortical VOIs according to AAL of WFU-Pickatlas tool (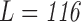). Five parameters (K = 5) 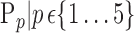are computed for Each VOI, 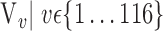. The first order statistics and the entropy were extracted from the histogram 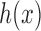of each VOI:

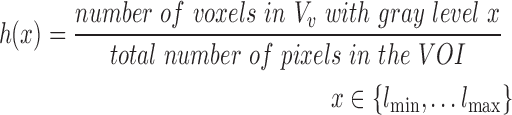where 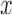is a gray level value of a voxel belonging to volume V_v 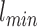and and 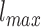are the minimum and the maximum gray level values in V_v respectively.

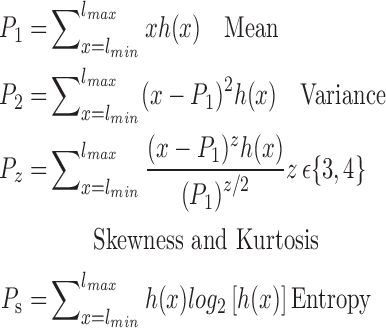C. Area Under Curve (AUC) Parameter

For each VOI, a set of parameters 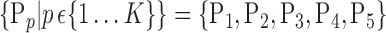is computed. In the following, we will use 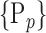instead of 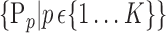for easier readability. HC and AD subjects are plotted in a N feature space, which represents a subset of 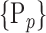, denoted 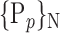, 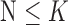among 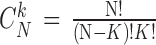subsets. An N-Dimensional sphere (N-D sphere) is created over the group of healthy subjects (HC) (N equals 1 for an interval, 2 for a disk and N is greater than 2 for a sphere). The N-D sphere’s center is the mass center of healthy subjects. At various radii of the N-D sphere, we compute the following parameters:

• •nb_HC_in, number of HC subjects inside the N-D sphere,
• •nb_AD_in, number of subjects with AD inside the N-D sphere.
• •nb_HC_in/nb_HC⁽¹⁾, True Positive Rate (TPR).
• •nb_AD_in/nb_AD⁽²⁾, False Positive Rate (FPR).

⁽¹⁾ number of HC subjects in the database ⁽²⁾ number of AD subjects in the database

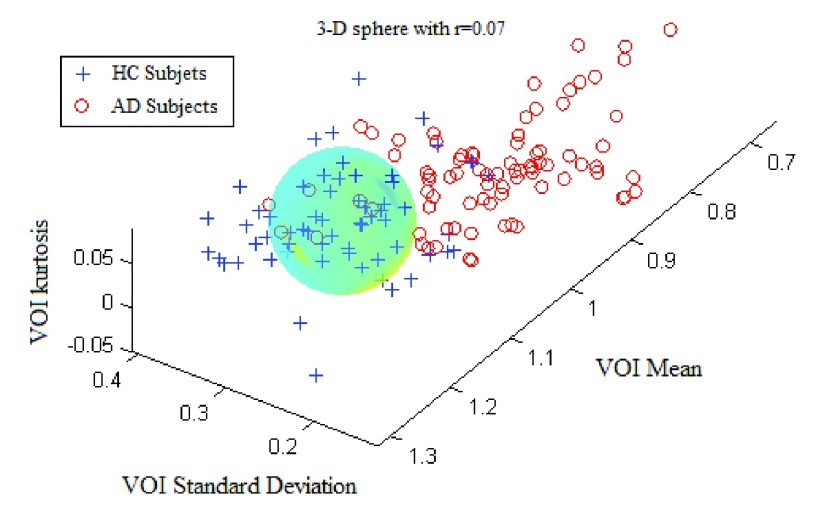
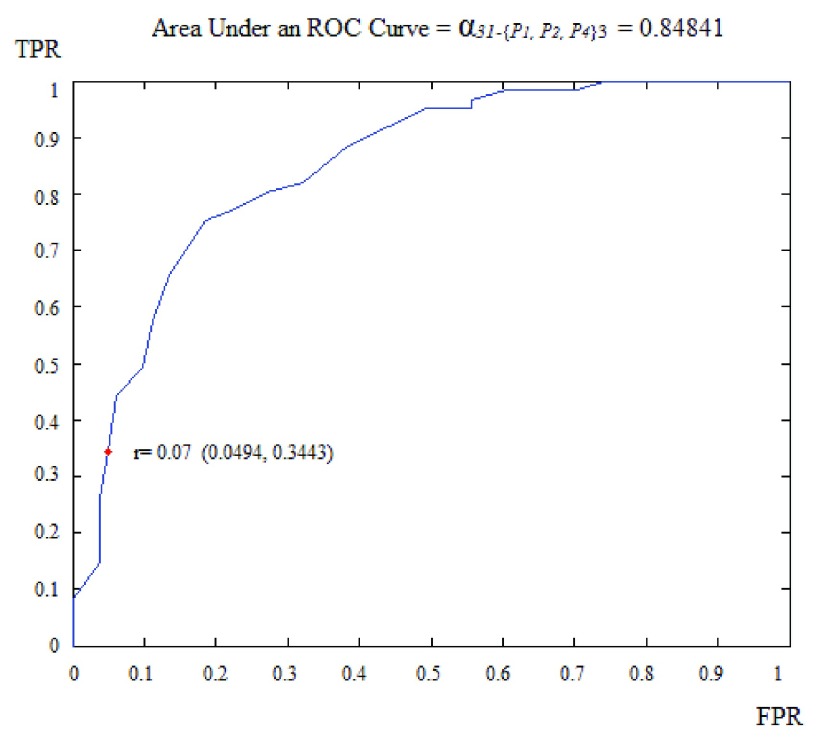
The ROC curve is created by plotting the true positives rate (TPR) (i.e. HC subjects well classified) vs. the false positives rate (FPR) (i.e. the AD subjects misclassified) for different radii of the N-D sphere. The AUC is defined as the Area Under ROC Curve (AUC) and is within the range [0, 1]. This AUC quantifies the ability of a given VOI, in a N-D feature space (N≤K) from a subset of K parameters, to separate between groups. This AUC value is all the more near 1 that the subset feature space on which the corresponding VOIs are plotted is able to separate well between AD and HC subjects. Fig. 3 shows the case of ‘Cingulum_Post_Left’ VOI based on three parameters: the mean, the standard deviation and the kurtosis (P₁, P₂ and P₄). The corresponding ROC curve is shown in Fig. 4.

FIGURE 3.

The separation between AD and HC groups relative to the region ’Cingulum_Post_Left with three parameters: the mean, the standard deviation and the kurtosis.

FIGURE 4.

ROC curve obtained for region ’Cingulum_Post_Left using three parameters: the mean, the standard-deviation and the kurtosis.

D. “Combination_Matrix” Analysis

For each VOI, we examine the combination of these parameters (noted P_p) with a length varying from 1 to 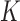. Therefore, we start by the combinations of length 1 (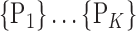), then those of length 2 ({P_j, P_q}, 1 ≤ j,q 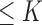, 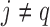), and so on until reaching the combination length of 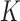parameters. Thereby, we create a “Combination_Matrix” of 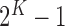columns.

For each column, which represents a subset 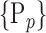_N, of N elements of , we compute the AUC (noted or 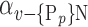) for each VOI, 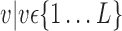, according to the N-D sphere. The “Combination_Matrix” has then 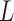lines and 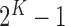columns.

• 1)“Combination_Matrix” 1: mono-parametric analysis Based on the “Combination_Matrix”, VOIs are ranked according to their higher values of AUC. Each VOI is characterized by its own combination parameters N that gives the highest AUC. The set of the top ranked VOIs (associated to the higher values of AUC) are selected to be used in AD/HC classification. This is a mono-parametric analysis, in which the selection of VOIs depends only on the combination of the parameters 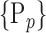_N for each VOI.

  Table 2 gives, for each VOI, the corresponding subset of parameters for which the highest AUC was obtained. The set of best ranked VOIs obtained using AUC approach (21 are given in Table 3 and shown in Fig. 5) are concordant with a recent review of the 18F-FDG PET literature about the positive diagnosis of AD, with VOIs involving the temporo-parietal cortex, including the precuneus and the adjacent posterior cingulate cortex [85].

• 2)“Combination_Matrix” 2: multi-parametric analysis Multi-parametric analysis for “Combination_Matrix” depends on both the combination of the parameters, (subset of 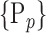), for each VOI, and the combination of the VOIs (subsets of 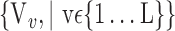). For easier readability, we use the expression 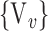instead of 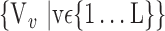. Depending on the “Combination_Matrix” 1, each VOI is characterized by its own combination of parameters, as it is presented in the Table 2. The procedure begins with the choice of the first two combination VOIs depending on all the possible combinations of VOIs of length 2 ({V_j, 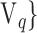, 1 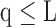≤ j, , j 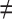q). Thereafter, a Sequential Forward Selection (SFS) [86] is used where we add one VOI at each step to a VOI list.

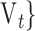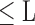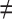  So, we start by the combinations of the two VOIs already selected in the previous step, then those of length 3 ({V_j, V_q, , 1 ≤ j,q,t , j q 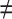t), and so on until reaching the combination length of L VOIs. At each step of the iterative procedure, HC and AD subjects are plotted in a new feature space by combination of parameters for that selection of VOIs. The AUC value based on this combination is named Cumulated AUC (CAUC). 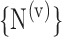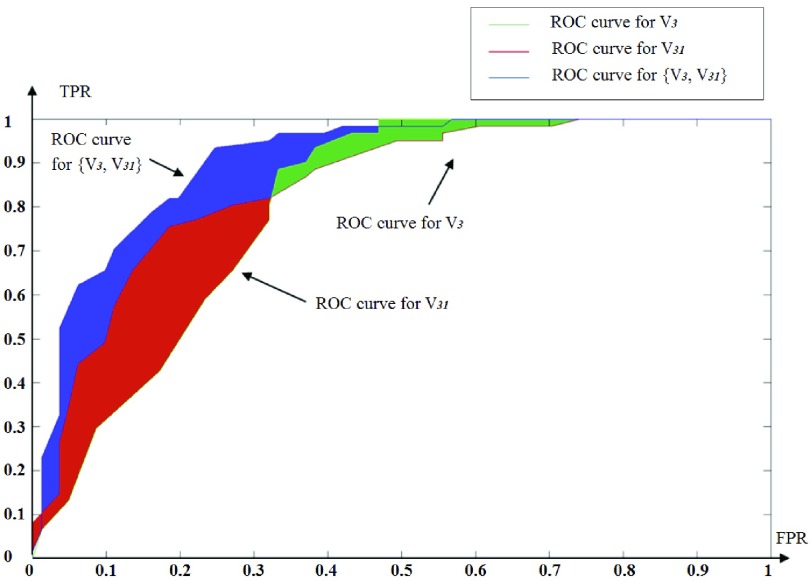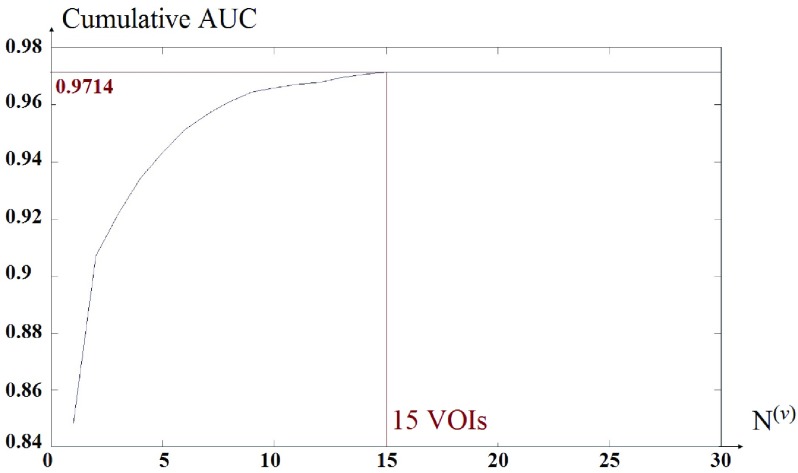For easier readability, we use instead of 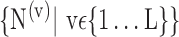. The VOIs that provide the best CAUC are then added to the final VOIs combination. Our algorithm stops when the same or a lower CAUC is obtained. Then, we select the feature combination with the lowest number of VOIs that achieves the highest CAUC. Fig. 6 shows that the cumulated AUC reaches 0.9071 value when combining V₃ and V₃₁, the AUC of which are respectively 0.8012 and 0.8484. The CAUC reached a limit value when more than 15 VOIs were added. This is depicted in Fig. 7.

TABLE 2. Each VOI 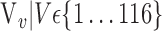is Caracterized By its Own Combination Parameters .

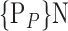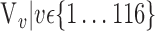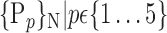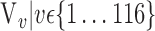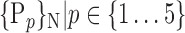1. ‘Amygdala_L’		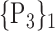59. ‘Insula_L’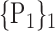
2. ‘Amygdala_R’		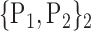60. ‘Insula_R’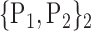
3. ‘Angular_L’		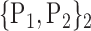61. ‘Lingual_L’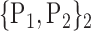
4. ‘Angular_R’		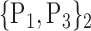62. ‘Lingual_R’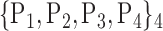
5. ‘Calcarine_L’		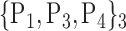63. ‘Occipital_Inf_L’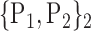
6. ‘Calcarine_R’		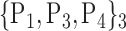64. ‘Occipital_Inf_R’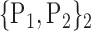
7. ‘Caudate_L’		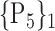65. ‘Occipital_Mid_L’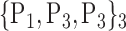
8. ‘Caudate_R’		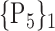66. ‘Occipital_Mid_R’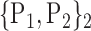
9. ‘Cerebelum_10_L’		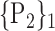67. ‘Occipital_Sup_L’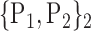
10. ‘Cerebelum_10_R’		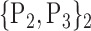68. ‘Occipital_Sup_R’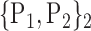
11. ‘Cerebelum_3_L’		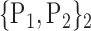69. ‘Olfactory_L’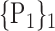
12. ‘Cerebelum_3_R’		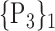70. ‘Olfactory_R’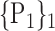
13. ‘Cerebelum_4_5_L’		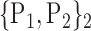71. ‘Pallidum_L’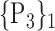
14. ‘Cerebelum_4_5_R’		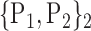72. ‘Pallidum_R’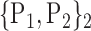
15. ‘Cerebelum_6_L’		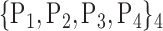73. ‘ParaHippocampal_L’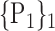
16. ‘Cerebelum_6_R’		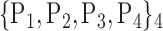74. ‘ParaHippocampal_R’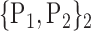
17. ‘Cerebelum_7b_L’		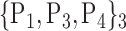75. ‘Paracentral_Lobule_L’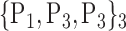
18. ‘Cerebelum_7b_R’		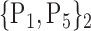76. ‘Paracentral_Lobule_R’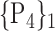
19. ‘Cerebelum_8_L’		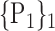77. ‘Parietal_Inf_L’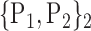
20. ‘Cerebelum_8_R’		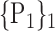78. ‘Parietal_Inf_R’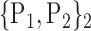
21. ‘Cerebelum_9_L’		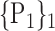79. ‘Parietal_Sup_L’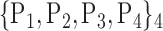
22. ‘Cerebelum_9_R’		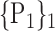80. ‘Parietal_Sup_R’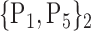
23. ‘Cerebelum_Crus1_L’		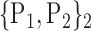81. ‘Postcentral_L’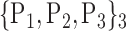
24. ‘Cerebelum_Crus1_R’		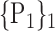82. ‘Postcentral_R’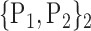
25. ‘Cerebelum_Crus2_L’		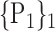83. ‘Precentral_L’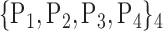
26. ‘Cerebelum_Crus2_R’		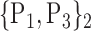84. ‘Precentral_R’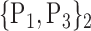
27. ‘Cingulum_Ant_L’		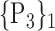85. ‘Precuneus_L’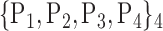
28. ‘Cingulum_Ant_R’		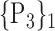86. ‘Precuneus_R’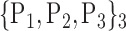
29. ‘Cingulum_Mid_L’		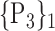87. ‘Putamen_L’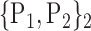
30. ‘Cingulum_Mid_R’		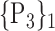88. ‘Putamen_R’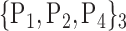
31. ‘Cingulum_Post_L’		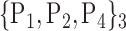89. ‘Rectus_L’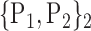
32. ‘Cingulum_Post_R’		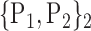90. ‘Rectus_R’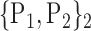
33. ‘Cuneus_L’		91. ‘Rolandic_Oper_L’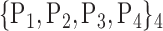
34. ‘Cuneus_R’		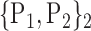92. ‘Rolandic_Oper_R’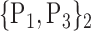
35. ‘Frontal_Inf_Oper_L’		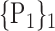93. ‘Supp_Motor_Area_L’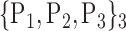
36. ‘Frontal_Inf_Oper_R’		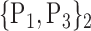94. ‘Supp_Motor_Area_R’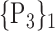
37. ‘Frontal_Inf_Orb_L’		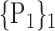95. ‘SupraMarginal_L’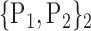
38. ‘Frontal_Inf_Orb_R’		96. ‘SupraMarginal_R’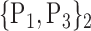
39. ‘Frontal_Inf_Tri_L’		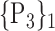97. ‘Temporal_Inf_L’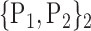
40. ‘Frontal_Inf_Tri_R’		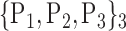98. ‘Temporal_Inf_R’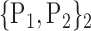
41. ‘Frontal_Med_Orb’		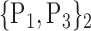99. ‘Temporal_Mid_L’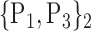
42. ‘Frontal_Med_Orb’		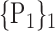100. ‘Temporal_Mid_R’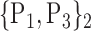
43. ‘Frontal_Mid_L’		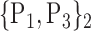101. ‘Temporal_Pole_Mid_L’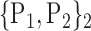
44. ‘Frontal_Mid_Orb_L’		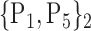102. ‘Temporal_Pole_Mid_R’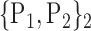
45. ‘Frontal_Mid_Orb_R’		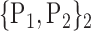103. ‘Temporal_Pole_Sup_L’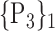
46. ‘Frontal_Mid_R’		104. ‘Temporal_Pole_Sup_R’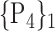
47. ‘Frontal_Sup_L’		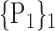105. ‘Temporal_Sup_L’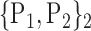
48. ‘Frontal_Sup_Medial_L’		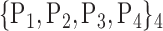106. ‘Temporal_Sup_R’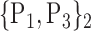
49. ‘Frontal_Sup_Medial_R’		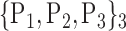107. ‘Thalamus_L’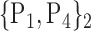
50. ‘Frontal_Sup_Orb_L’		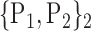108. ‘Thalamus_R’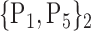
51. ‘Frontal_Sup_Orb_R’		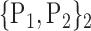109. ‘Vermis_10’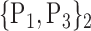
52. ‘Frontal_Sup_R’		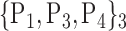110. ‘Vermis_1_2’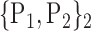
53. ‘Fusiform_L’		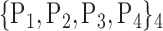111. ‘Vermis_3’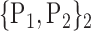
54. ‘Fusiforrm_R’		112. ‘Vermis_4_5’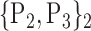
55. ‘Heschl_L’		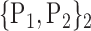113. ‘Vermis_6’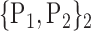
56. ‘Heschl_R’		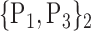114. ‘Vermis_7’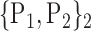
57. ‘Hippocampus_L’		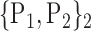115. ‘Vermis_8’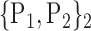
58. ‘Hippocampus_R’		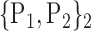116. ‘Vermis_9’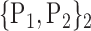

TABLE 3. The List of the Top Ranked VOIs Selected With the Best Parameters.

Name of the Top ranked VOIs		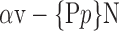AUC
‘Cingulum_Post_L’		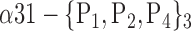0.8484
‘Angular_R’		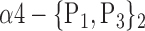0.8124
‘Cingulum_Post_R ‘		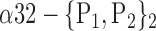0.8041
‘Angular_L’		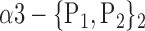0.8013
‘Parietal_Inf_L’		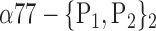0.7958
‘Temporal_Mid_L’		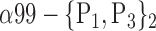0.7949
‘Cingulum_Mid_R’		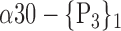0.7940
‘SupraMarginal_L’		0.7919
‘Precuneus_L’		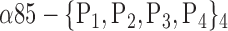0.7907
‘Rolandic_Oper_R’		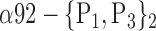0.7861
‘Temporal_Mid_R’		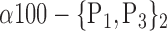0.7842
‘Precuneus_R’		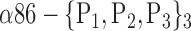0.7809
‘Cerebelum_6_L’		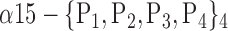0.7697
‘Parietal_Inf_R’		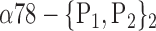0.7615
‘Cerebelum_6_R’		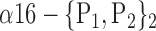0.7542
‘Postcentral_R’		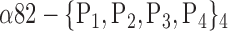0.7542
‘Temporal_Inf_L’		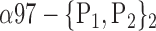0.7526
‘Temporal_Sup_L’		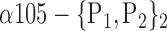0.7476
‘Fusiform_ L’		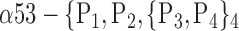0.7471
‘Cerebelum_8_L’		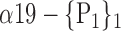0.7449
‘Postcentral_L’		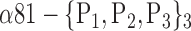0.7391
…	…	…

The AUC denoted 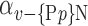is computed for a region 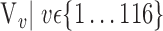depending on the contribution of the parameters .

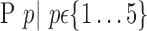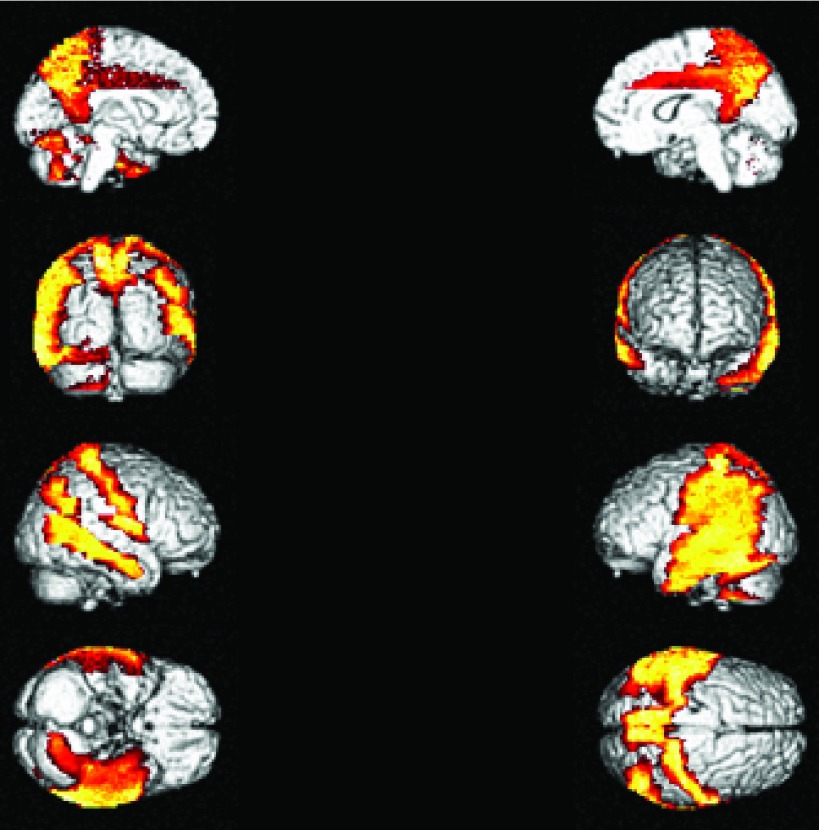
FIGURE 5.

The top VOIs (21 VOIs) selected are presented on a 3D brain image

FIGURE 6.

ROC curve obtained for V₃, V₃₁ and V₃, V₃₁.

FIGURE 7.

Cumulated AUC value based on the different combination of the VOIs, .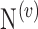

IV. Classification Results and Discussion

The result of the proposed algorithm is presented and assessed in this section. However, direct comparison with existing work is hard to achieve due to several factors such as the different datasets, sampling methods, and different features used. We focus on the development and performance of an algorithm as a whole, while exploring several potential features. In assessing the proposed framework, we provide performance comparison to other feature selection methods using the same local database. The normalized PET database is selected as input data for the CAD tool. PET image of each subject is of 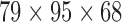voxels size, which yields voxels. In order to reduce the curse of dimensionality, the 116 VOIs are used first and then the most discriminative VOI among them are then selected. The resulting reduced feature vector obtained from the different PET images is finally taken for classification. In order to validate the effectiveness of the proposed method, we performed experiments using a comparison with the state-of-art of Feature Selection methods (FS) including Student’s t-Test analysis [39], Fisher score [86], [87], Support vector Machine feature elimination (SVM-RFE) [88], feature selection with Random Forest [86], [87], [89], minimum Redundancy Maximum Relevance (mRMR) [64], and ReliefF [63], [90], [91]. The Voxel Based Analysis (VBA), considered as a baseline classification approach is also used for comparison purposes. It consists in inputting to the classifier the whole brain voxels that represent metabolic activity in the gray matter for each subject.

For comparison purposes with feature selection methods but for VBA and Student’s t-Test, a 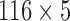matrix, whose lines are VOIs and column are histogram extracted features defined in section III was used. This matrix was input to each FS method in order to obtain the optimal set of features to be input to the SVM classifier.

A. Classification Results

Classification was performed using a Support vector machines (SVM) classifier. This classifier map pattern vectors to a high-dimensional feature space where a ‘best’ separating hyperplane (the maximal margin hyperplane) is built. SVM maximize the separation margin by the distance between a hyperplane and the closest data samples. A linear kernel is used our study [86], [87]. Several experiments were carried out to evaluate the “Combination_Matrix” feature selection process and the SVM classifier.

The reduced number of subjects (142 patients) suggests the adaptation of a leave-one-out (LOO) strategy as the most suitable for classification validation. It is a technique that iteratively holds out a subject for test, while training the classifier with the remaining subjects, so that each subject is left out once. Therefore 142 training and testing experiments are carried out. Parameter C is used during the training phase and tells how many outliers are taken into account in calculating Support Vectors. For large values of , the optimization will choose a smaller-margin hyperplane. Conversely, a very small value of 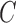will cause the optimizer to look for a larger-margin separating hyperplane, even if that hyperplane misclassifies more subjects. A good way to estimate relevant 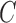value to be used is to perform it with cross-validation. As a result, the estimation value is fixed to 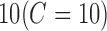depending upon database. In order to evaluate the developed CAD tool, which depends on the choice of 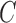, several values of 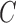are used. The soft-margin constant 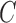of the optimal hyperplane uses a value range from 10⁻⁷ to .

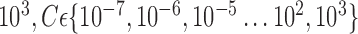Subsequently, performance is also tested using a permutation test [92], repeating the classification procedure after randomizing and permuting labels. The p-value is then given by the percentage of runs for which the score obtained is greater than the classification score obtained in the first case. The error of our results were estimated at 0.09% (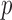-value) for a permutation number equal to 1000.

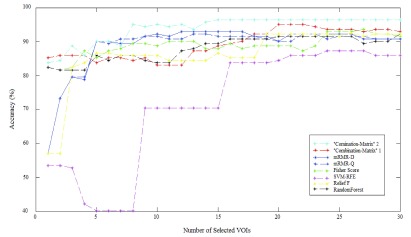
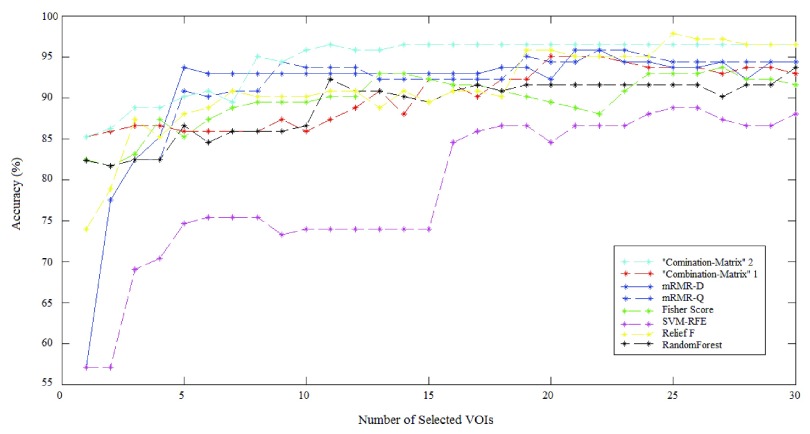
The results achieved using the proposed methods and the SVM are depicted in Fig. 8 and Fig. 9. It illustrates classification success rate with the different features selection methods outlined in previous sections. These figures show detailed cross-validation average accuracy results as a function of the number of selected VOIs input to the SVM classifier. For the whole Feature selection methods, good classification results (above 80% accurate classification rate) are obtained when inputting a low number of VOIs. When the number of VOIs input to the classifier is more than 20, classification results reach a value that remains constant. There is no way to increase classification results by injecting more VOIs. The best accuracy rate obtained by “Combination_Matrix” 1 equals 95.07% (with 19 VOIs), which is higher than the one obtained using VBA which equals 94.36% (see Table 4). The “Combination_Matrix” 2 achieved better results than all the other methods (96.47%) with a lower number of VOIs which are depicted in Fig. 10 (15 VOIs).

FIGURE 8.

Average Accuracy obtained with SVM classifier varying number of features for different VOI selection analyses and applying LOO cross-validation with estimation value .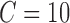

FIGURE 9.

Average Accuracy obtained with SVM classifier varying number of features for different VOI selection analyses and applying LOO cross-validation with estimation value .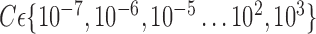

TABLE 4. Voxel Selection and VOI Selection Analyses To Discriminate Between Groups (AD, HC AND MCI).

Method	LOO cross-validation with a constant 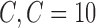.			LOO cross-validation with estimation value 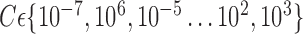.			Computati on Time
	AD vs HC	MCI vs AD	MCI vs HC	AD vs HC	MCI vs AD	MCI vs HC
VBA 182413 (voxels)	94.36%	86.36%	67.77%	94.36%	86.36%	67.77%	a day
T-test	93.66% 28.413 (voxels)	88.18% 32.982 (voxels)	77.77% 3.877 (voxels)	93.66% 28.413 (voxels)	88.18% 32.982 (voxels)	77.77% 3.877 (voxels)	few minutes
116 VOIs (mean)	91.54%	85.45%	68.88%	91.54%	85.45%	68.88%
116 VOIs (5 parameters)	92.95%	87.72%	67.77%	92.95%	87.72%	67.77%
SVM-RFE	88.02% {24} (VOIs)	76.36%	67,77%	91.54 {25} VOIs	80% {15} VOIs	67.77%	few seconds
RandomForest	91.54% {21} (VOIs)	88.18% {8} (VOIs)	76.66% {21} (VOIs)	92.25% {11} VOIs	90% {24} VOIs	77.77% {19} VOIs
mRMR	92.25% {13} (VOIs)	89.09% {11} (VOIs)	67.77%	95.77% {19}VOIs	91.81% {27} VOIs	67.77%
Score Fisher	93.66% {27} (VOIs)	89.09% {21} (VOIs)	74.44% {11} VOIs	93.66% {27} VOIs	91.81% {12} VOIs	76.66% {23} VOIs
ReliefF	90.84% {19} (VOIs)	73.63%	67.77%	97.88% {25}VOIs	87.27%	74.44%
“Combination_Matrix”1	95.07% {20, 21, 22} (VOIs)	88.18% {11} (VOIs)	75.05% {23} (VOIs)	95.07% {20, 21, 22} (VOIs)	89.09% {12} (VOIs)	75.05% {22} (VOIs)
“Combination_Matrix”2	96.47% {15} (VOIs)	-------------------	-------------------	96.47% {14} (VOIs)	-------------------	-------------------

FIGURE 10.

15 VOIs representation of the “Combination Matrix” 2 on a coronal plane (a), on a transverse plane (b) and on a sagittal plane (c).

B. Discussion

A novel approach of feature selection multi-parametric analysis is presented in this paper. The main innovative aspects of this approach rely on the ranking of each anatomical VOI according to its ability to distinguish between groups of subjects. This method could have been applied to any image data set where a feature selection and ranking is needed. It is also able to give a ranking of a set of VOIs according to their ability to separate groups of subjects. Our study explored two methods: voxel selection and VOI selection analysis applied to 18F-FDG PET data, as well as how to use the parameters in the former approach: mono-parametric or multi-parametric one. The results achieved using the proposed methods are depicted in Table 4. In the case of VBA and t-Test, we talk about voxel approach mono-parametric analysis (voxel is characterized by its intensity). In the case of other classical feature selection methods and “Combination_Matrix” 1, we used a VOI selection mono-parametric analysis. Each VOI was characterized with 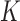parameters. When, we selected the most discriminant VOIs to discriminate between HC and AD patients, each VOI was characterized by one parameter 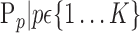or a set of parameters computed on it, .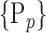

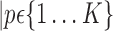In the context of our study, each feature is either a VOI with a combination of parameters computed on it (Combination Matrix 1) or a combination of VOIs, (Combination_Matrix 2). After selecting the relevant VOIs, the classification performance was tested by varying the features vectors dimension and summarized in Tab IV. Our study reduces considerably feature space and computational time. The number of VOIs was reduced to 15 thanks to “Combination_Matrix” 2 and the computation time was reduced to a few seconds rather than VBA which lasted a day computation time to analyze the whole database.

Even if the main results presented in this paper concern HC versus AD classification, we studied two other possibilities. To evaluate the discrimination of MCI (Mild Cognitive Impairment) and AD, we had only 29 patients. Discrimination of MCI from HC is more difficult in comparison to classification of AD from HC (or AD from MCI). We achieved a low performance in discrimination of these groups due to the small number of samples (67.77% with VBA). The best accuracy achieved for discriminating between MCI and AD was 88.18% with “Combination_Matrix” 1, which needs to be evaluated on a larger database. We notice that our approach increases the classification rate for each pair of groups compared to the VBA classification rate, unlike the various classical feature selection methods. ReliefF performed well in the classification between AD and HC, rather than in the case of MCI vs AD and MCI vs HC. The mRMR achieved high accuracy in the case of AD vs HC and MCI vs AD, whereas in the case of MCI vs HC, mRMR features selection achieved lower accuracy values. The obtained results using “Combination_Matrix” 2 for both “MCI” vs “HC” or “MCI” vs “AD” did not achieve good results. This is due to the small number of MCI patients and to the fact that VOIs, in these cases, are more correlated, which did not allow to choose an optimal set of VOIs. Moreover within MCI group we did not distinguish between progressive MCI (pMCI) and stable MCI (sMCI) due to the low number of subjects. Progressive MCI are subjects that are evolving to an AD state whereas sMCI are subjects that are not going to evolve. The less good results obtained in trying to compare AD to MCI and HC to MCI could be also explained by the fact that AD and pMCI, and also HC and sMCI, are subjects that are hard to distinguish due to the fact that these sub-groups are very close to each other.

VOIs identified and selected in the present work are classically involved in FDG-PET studies of AD, with a bilateral metabolic impairment of bilateral posterior associative cortices, especially of temporo-parietal regions including the precuneus, and also the posterior cingulate cortex [93].

These results show that the proposed classification results can improve the Computer-Aided Diagnosis of AD on PET images. Therefore, the proposed features selection “Combination_Matrix” is very effective providing a good discrimination between groups and in some cases (due to the small number of samples) comparable results with the various classical feature selection methods.

V. Conclusion

In this paper, a novel method for VOIs ranking is developed to better classify brain PET images. This ranking is obtained using ROC curves and quantifies the ability of a VOI to classify HC from AD subjects. A first combination matrix was proposed in order to select relevant features extracted from VOIs then a second combination matrix was able to define best VOIs association for classification purposes.

The Area Under Curve used in this paper could be easily computed for feature selection for any other medical image modality. The evaluation of this parameter was done on a local image database but needs to be evaluated on a larger database.

To go further in the computer aided-diagnosis tasks, other features like texture, gradient computed on VOIs have to be joined to first order statistical parameters in order to enrich information and obtain higher classification results.

Funding Statement

This work was supported in part by DHU-Imaging through the A * MIDEX Project funded by the “Investissements d’Avenir” French Government Program and managed by the French National Research Agency under Grant ANR-11-IDEX-0001-02, the region PACA, and Nicesoft.