A Detailed Model of Electroenzymatic Glutamate Biosensors to Aid in Sensor Optimization and in Applications in vivo

Abstract

Simulations conducted with a detailed model of glutamate biosensor performance describe observed sensor performance well, illustrate the limits of sensor performance, and suggest a path toward sensor optimization. Glutamate is the most important excitatory neurotransmitter in the brain, and electroenzymatic sensors have emerged as a useful tool for the monitoring of glutamate signaling in vivo. However, the utility of these sensors currently is limited by their sensitivity and response time. A mathematical model of a typical glutamate biosensor consisting of a Pt electrode coated with a permselective polymer film and a top layer of crosslinked glutamate oxidase has been constructed in terms of differential material balances on glutamate, H₂O₂ and O₂ in one spatial dimension. Simulations suggest that reducing thicknesses of the permselective polymer and enzyme layers can increase sensitivity ~6-fold and reduce response time ~7-fold, and thereby improve resolution of transient glutamate signals. At currently employed enzyme layer thicknesses, both intrinsic enzyme kinetics and enzyme deactivation likely are masked by mass transfer. However, O₂ dependence studies show essentially no reduction in signal at the lowest anticipated O₂ concentrations for expected glutamate concentrations in the brain, and that O₂ transport limitations in vitro are anticipated only at glutamate concentrations in the mM range. Finally, the limitations of current biosensors in monitoring glutamate transients is simulated and used to illustrate the need for optimized biosensors to report glutamate signaling accurately on a subsecond timescale. This work demonstrates how a detailed model can be used to guide optimization of electroenzymatic sensors similar to that for glutamate and to ensure appropriate interpretation of data gathered using such biosensors.

1. INTRODUCTION

The rapid and selective sensing of neurotransmitters including dopamine,^1–3 acetylcholine,^4–7 and glutamate^8–12 with high spatial resolution has demonstrated usefulness for the study of neurological disorders as well as normal brain function in a variety of systems.¹³ Electrochemical devices based on carbon fibers or on microelectrode arrays (MEAs) on silicon or ceramic microprobes have proven particularly well suited for selective neurotransmitter monitoring at subsecond resolution with less tissue damage than that associated with typical microdialysis probes, although not all analytes are amenable to facile electrochemical detection.^{3, 13–17} Nevertheless, the sensing of multiple analytes on MEAs in vivo promises to be a powerful approach for study of the neurochemistry underlying normal and abnormal brain function and associated behaviors. Yet, the optimal construction and use of the various sensing sites of differing modality on these MEAs will require adequate mathematical simulations both to guide sensor optimization and to interpret properly the data gathered with such sensors.

Glutamate (Glut) sensors, for example, most commonly are electroenzymatic biosensors operated in constant potential amperometry mode. Typically, glutamate oxidase (GlutOx) serves as the molecular recognition element that catalyzes the oxidation of Glut to α-ketoglutarate in the presence of molecular oxygen to give ammonia and H₂O₂.

$$\text{L-glutamate}+{\mathrm{H}}_2\mathrm{O}+{\mathrm{O}}_2\to \mathrm{\alpha }\text{-ketoglutarate}+{\text{NH}}_3+{\mathrm{H}}_2{\mathrm{O}}_2$$

This selective recognition event is transduced, usually by electrooxidation of H₂O₂ at a platinum electrode held at a constant positive potential, to provide a measurable current signal that is correlated to Glut concentration. However, a variety of species exist in brain extracellular fluid (ECF) that may be oxidized directly at a platinum electrode at positive potential, therefore one or more permselective polymer films are deposited underneath or in conjunction with the immobilized GlutOx to prevent electrooxidizable species other than H₂O₂ from accessing the electrode surface.^{10, 18–22} Such species, including ascorbic acid and dopamine, which typically are the most problematic for such Glut sensors, would otherwise cause a false current signal. A variety of polymeric materials have been used as permselective films including polypyrrole (PPY), polyethylenediamine (PPD), and Nafion.^{10, 18} GlutOx has been immobilized in or on these various polymer films through methods entailing dip coating, manual spreading, or electrodeposition.^{21, 23–25} Most commonly, GlutOx is immobilized on electrodes by spreading a mixture of enzyme and bovine serum albumin (BSA) on the electrode surface and crosslinking with glutaraldehyde.^{23, 24} However, the many variations of methods used produces layers of different thicknesses and compositions that directly affect the sensitivity, response time, stability, and selectivity of the sensor.

Synaptic neurochemical signaling is thought to occur on the millisecond timescale, which is much faster than the reported response times of Glut sensors to date, yet more responsive sensors would be important to correlate neurochemical signaling with action potentials. In addition, the ideal Glut sensor would be able to resolve Glut signals at much less than 1 μM in order to address the controversy regarding Glut concentrations in the brain and to enable use of smaller sensing sites similar in area to those used for electrophysiological recordings. These important sensor attributes must be exhibited by an implantable device that can operate with high selectivity in the complex chemical and biological environment of the brain. There is a clear need for detailed simulations of transient conditions that can establish the theoretical performance limits of an electroenzymatic Glut biosensor and that can facilitate its optimization.²⁶

Many mathematical modeling studies of electroenzymatic biosensors based on numerical solutions of a modified diffusion equation have been published,^27–41 although frequently these solutions rely on simplified kinetics or a partial analytical solution,^{33, 34, 37, 39} are limited to the steady state,^{27, 30–34} and/or do not include the detail necessary (e.g., an additional, enzyme-free permselective layer) to guide typical biosensor optimization.^{27, 30–35, 38} Further, we are aware of no published, detailed modeling efforts of electroenzymatic Glut biosensors in particular. Glut sensors for neuroscience applications should be optimized for sensitivity, detection limit, selectivity, stability, and response time. Fortunately, modern, commercially available software has made the solution of the applicable partial differential equations more straightforward.

A new transient model of an electroenzymatic Glut biosensor operated in constant potential amperometry mode has been formulated and is described here. The model incorporates an oxygen-dependent rate model for GlutOx and explicit H₂O₂ electrooxidation kinetics,⁴² as well as a description of internal and external mass transfer of Glut, oxygen and H₂O₂. In addition, the model describes the immobilized enzyme layer composition and thickness, and the effects of permselective films on Glut sensing performance. Detailed simulations using the model show the limits of sensor performance, the impact of controllable sensor design parameters on sensor attributes, and how the sensor response relates to actual external transients in Glut concentration. Finally, the mathematical model and accompanying assumptions show the contextual relevance of these results and can provide insight for similar electroenzymatic sensor devices.

2. RESULTS AND DISCUSSION

2.1. Model Simulates the Sensitivity and Response Time of Existing Glutamate Biosensors

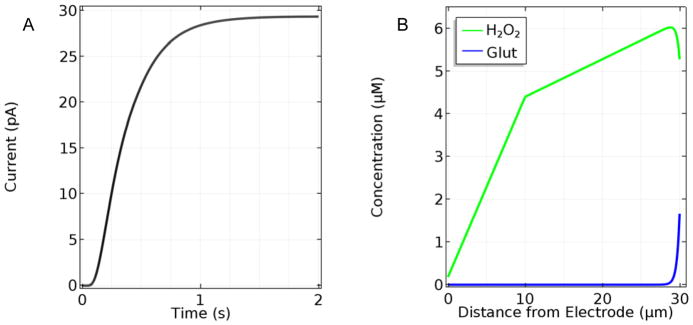
Numerical solutions of the linked sets of PDEs and boundary conditions that constitute the mathematical model (see below and Supporting Information for model details) provide the concentrations of Glut, O₂ and H₂O₂ at all points within the sensor surface coatings over chosen periods of time. This information can in turn be used to determine the response of the simulated sensor. To best represent recent Glut biosensor fabrication methods on arrayed microelectrodes,^{3, 18, 25} initial simulations were conducted to describe the response of base-case sensors (with a 10-μm-thick permselective layer, a 20-μm-thick enzyme layer, and a GlutOx protein mass fraction, f_glutox, in the enzyme layer equal to 0.5) to a 0 to 10 μM step in sample Glut concentration at time zero. Such conditions are common for in vitro calibrations. Fig. 1 shows the temporal current response and the steady-state (SS) H₂O₂ concentration profile. The model predicts a corresponding sensitivity of 60.7 nA/μM/cm², consistent with experimental values of 51.3, 63.2, and 152.1 nA/μM/cm² for sensors made using a Nafion layer, and enzyme immobilization using BSA and glutaraldehyde.^{24, 43, 44} The simulated response time, 0.73 s, also matches very closely with experimental response times (0.8 ± 0.2 s).²⁴ Here, response time was calculated as the time from the initial step-change in boundary concentration until the current reaches 90% of its steady-state (SS) value as is customary for these sensors used in neuroscience applications.

Figure 1.

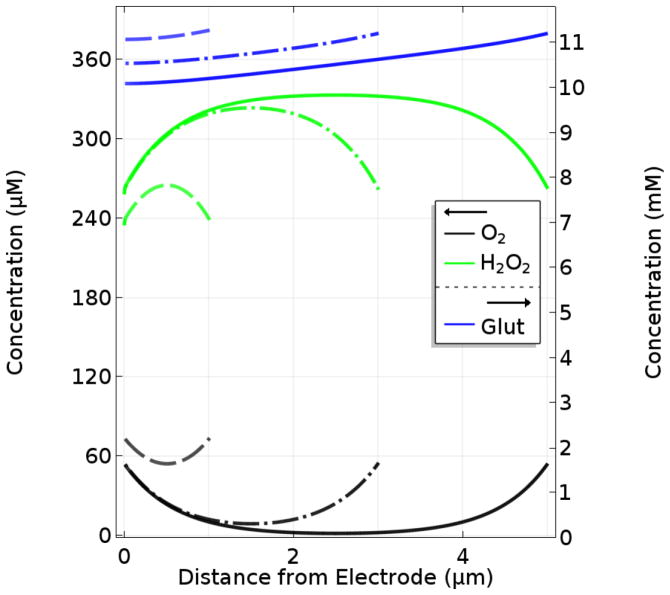
A. Temporal response of a base-case sensor (10 μm Nafion layer, 20 μm GlutOx layer) to a 10 μM step in bulk sample Glut concentration with sample O₂ concentration at 270 μM and B. the corresponding steady-state H₂O₂ concentration profile within the sensor layers. Note that the outer edge of the Nafion layer is at 10 μm and the outer edge of the sensor is at 30 μm.

These initial results also provided some important observations regarding the sensor response time and the efficiency of H₂O₂ capture at the electrode surface. As shown in Fig. 1A, there is a time lag in current response from when Glut is introduced at t = 0 until current begins to increase due to the time required for initial Glut turnover and penetration of H₂O₂ to the electrode surface. This time lag contributes significantly to the overall response time, which demonstrates that response time cannot accurately be determined from the current rise time alone.

In addition, the SS H₂O₂ concentration profile (Fig. 1B) shows that much of the H₂O₂ generated in the enzyme layer is lost back to the sample bulk solution. Calculations based on the flux toward the electrode surface compared to that toward the sample solution, indicate that only 3.6% of the H₂O₂ generated is electrooxidized at the electrode and contributes to the current signal. The concentration profile also shows that most H₂O₂ is produced within the first few microns into the enzyme layer. In agreement with this peak in the H₂O₂ profile near the sensor surface, the accompanying data for Glut shows that virtually all the analyte is consumed in the first few microns into the enzyme layer. These results strongly suggest that thinner enzyme layers could result in better performing sensors.

2.2. Thinner Permselective Films and Enzyme Layers Are Shown to Give Better Performing Sensors

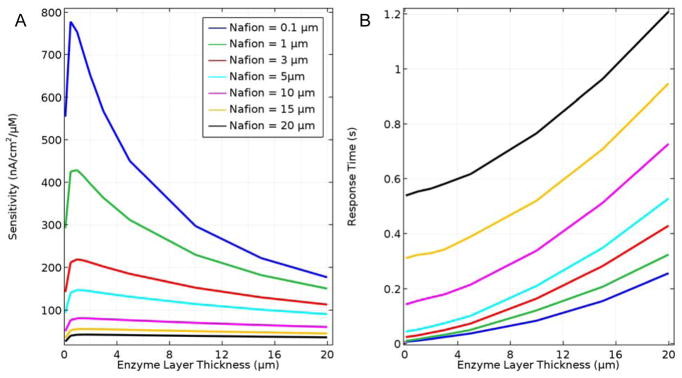
Optimization of sensor fabrication generally entails incorporating enough enzyme and permselective resistance to ensure high sensitivity and selectivity without applying coatings so thick that they cause elevated mass transfer resistance and long response time. Efforts to balance these effects have resulted in numerous enzyme immobilization procedures and variations of permselective coatings,⁴⁵ but a theoretical treatment considering both permselective and enzyme layer characteristics can illustrate how a given sensor construct may be expected to perform relative to its theoretical limits. Fig. 2 shows that by reducing the Nafion and enzyme layer thicknesses, the sensitivity and response time theoretically can be improved an order of magnitude or more from the base case. However, the results also show that the enzyme layer thickness goes through an optimum for the various Nafion film thicknesses investigated. In general, sensitivity drops sharply for enzyme layer thicknesses less than a micron, which corresponds to ~45 enzyme monolayers. This result is consistent with published experimental results showing that enzyme immobilization through electropolymerization of ultra-thin layers produces sensors with lower sensitivity.^{22, 46, 47} The decrease in sensitivity for thicker enzyme layers is consistent with the results shown in Fig 2 and is due to diffusional mass transfer limitations and the loss of the vast majority of H₂O₂ generated in the enzyme layer back to the sample solution.

Figure 2.

A. Sensor sensitivity based on steady-state response to a 10 μM Glut step change as a function of Nafion and enzyme layer thicknesses, and B. sensor response time (bottom) also as a function of layer thicknesses. In all cases, f_glutox = 0.5 and sample O₂ concentration equal to 270 μM.

Based on results displayed in Fig. 2 for an immobilized enzyme concentration corresponding to an f_glutox of 0.5, sensors with enzyme layer thicknesses less than ~5 μm show the greatest potential for improved sensitivity and response time. At ~5 μm and less, the sensitivity increases most sharply with reduced enzyme layer thickness, and the response times converge for Nafion layer thicknesses ranging from 0.1 to 5 μm. For what may be practical layer thicknesses of 1 and 3 μm (permselective layer and enzyme layer, respectively), the model predicts that sensitivity to Glut increases 6-fold over the base case and that the response time is reduced to 33 ms. The highest sensitivity (780 nA/μM/cm²) and fastest response time (10 ms) was observed for a sensor with a 0.1 μm thick layer of Nafion and a 0.5 μm thick layer of enzyme, although for layers this thin, assumptions concerning Nafion continuity (and ability to block interfering species such as ascorbate) and enzyme activity (see below) may need further consideration and experimental support. Based on a recent review article,²⁶ the best sensitivities achieved are in the vicinity of ~200 nA/μM/cm², which likely is due to a lack of experimental methods to generate very thin layers of active enzyme at high density on electrodes. The very fast theoretical response times for an optimized biosensor are consistent with characteristic times for enzyme-catalyzed reaction, based on k_cat, and for species mass transport, based on diffusivities and diffusion lengths; yet current experimental response times are in the ~1 s range, also due to overly thick enzyme and polymer layers. It is important to recognize here that these theoretical optima for sensitivity and response time are subject to the modeling assumptions described below and may not be experimentally attainable, however these simulation results do support the subjective conclusion that the performance of Glut biosensors can be improved significantly.

2.3. Effect of Enzyme Loading and Activity

Improvements to electroenzymatic glutamate sensors also have been accomplished through fabrication procedures that have increased the amount of enzyme deposited on the sensor sites, and efforts to do this have been analyzed experimentally through studies that measure enzyme loading and functionality indirectly.⁴⁸ The modeling approach used here enables direct investigation of the effect of deposited enzyme concentration on sensor performance and thereby shows what can be expected when enzyme loading has been optimized experimentally.

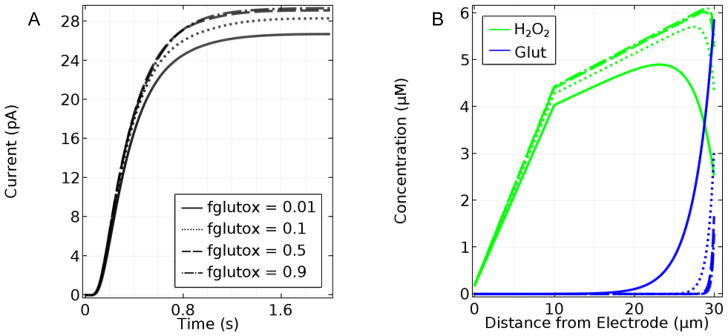
For existing sensor designs, an easy design modification to investigate a change in enzyme loading without impacting catalytic layer thickness would be to mix a different proportion of GlutOx with BSA, thereby increasing or decreasing f_glutox and producing a different enzyme concentration in the deposited layer. To test independently the effect of varied active enzyme concentration in the catalytic layer, f_glutox was varied from 0.01 to 0.9 for the base case sensor.

Interestingly, the current versus time plots in response to a 10 μM Glut step change show almost no difference over the broad range of f_glutox examined (Fig. 3A). The corresponding SS concentration profiles of Glut and H₂O₂ give insight into these results (Fig. 3B). As enzyme concentration decreases, more Glut diffuses farther into the enzyme layer before being oxidized to give H₂O₂, a phenomenon also observed in the simulation of similar glucose biosensors.³⁸ Even at low enzyme concentrations corresponding to f_glutox = 0.10, Glut is completely consumed within about 3 μm of the outer edge of the sensor, suggesting that the fraction of active enzyme has little to no effect for enzyme thicknesses much greater than a few microns. These results also suggest that the actual rate of GlutOx deactivation may be masked by mass transfer effects in sensors with thick enzyme layers,⁴⁹ since GlutOx deactivation essentially results in a decrease in f_glutox with time. If the lifetime of an implanted, electroenyzmatic Glut sensor is limited by GlutOx deactivation upon immobilization or by later exposure to H₂O₂, for example, these simulations also indicate that it may not be beneficial to construct sensors with the thinnest enzyme layers predicted to be optimal (Fig. 2).

Figure 3.

A. Current response to a 10-μM step change in Glut for sensors with 10-μm-thick Nafion and 20-μm-thick enzyme layers, where the f_glutox is varied from 0.01 to 0.9, and the sample O₂ concentration equals 270 μM. B. Corresponding plots of SS Glut and H₂O₂ concentration profiles in the Nafion and enzyme layers. Note that the outer edge of the Nafion layer is at 10 μm and the outer edge of the sensor is at 30 μm.

2.4. Mass Transfer Resistance and Oxygen Limitations Complicate Analysis of Immobilized Enzyme Kinetics

In the development of optimized electroenzymatic sensors, sensor performance is often tested over a range of substrate (i.e., analyte) concentrations, and the measured signal commonly follows a trend resembling Michaelis-Menten kinetics (the apparent K_m represents the concentration of analyte that produces half of the maximum response, and the apparent k_cat is related to the maximum response). Thus, sensor performance is often evaluated using apparent sensor Michaelis-Menten parameters. Mass transfer resistance and oxygen limitations may explain in large part (enzyme crowding, crosslinking and deactivation may also contribute) the observed differences between sensor and intrinsic enzymatic values for K_m and k_cat, although the detailed physical basis for these differences have not been fully explored. Nevertheless, it might be expected that the apparent kinetic parameters describing performance of an electroenzymatic sensor are shifted in a similar, straightforward manner away from the intrinsic, free solution values of the immobilized enzyme for all biosensors due to mass transfer effects and O₂ limitations, but the simulations of Glut biosensors shown below demonstrate that simple generalizations cannot be constructed. It is noteworthy here that the range of substrate concentrations that must be explored in order to estimate a sensor K_m typically extends up to an order of magnitude or more beyond that observed in vivo. Also, for these relatively high concentrations of Glut, levels of H₂O₂ near the electrode surface begin to affect the electrooxidation rate, further justifying the use of explicit electrooxidation kinetics in our model.

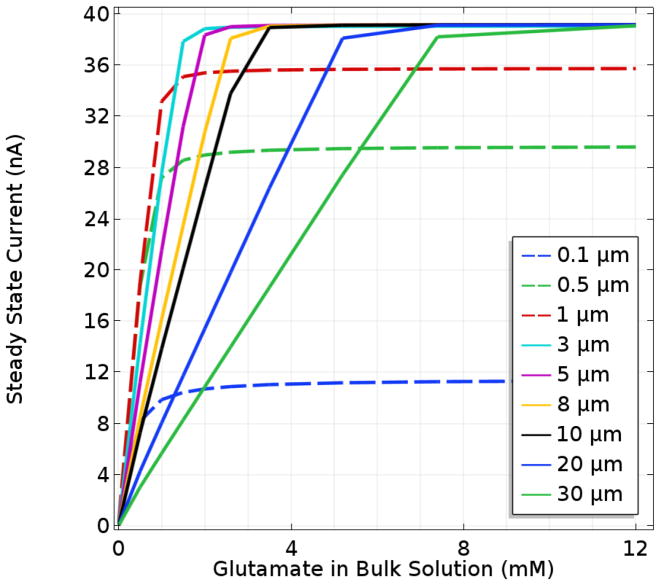
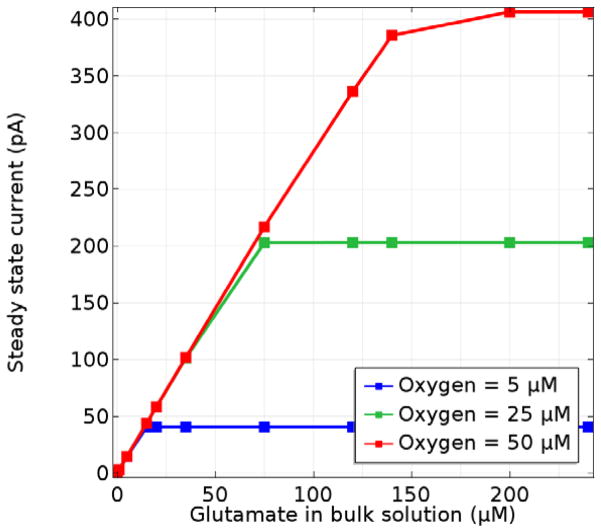
To investigate the apparent K_m of Glut biosensors and any complications due to mass transport resistance or O₂ limitations, the model was used to simulate the SS response to Glut ranging from 0.1 to 30 mM for biosensors with varied enzyme layer thicknesses. In order to highlight the effect of the enzyme coating, the permselective (Nafion) film was reduced to 10 nm in thickness so that its mass transfer resistance could be ignored.^{34, 50} It may be expected that a sensor with a thinner enzyme deposit (and therefore reduced mass transfer resistance) would display apparent kinetics that more closely correspond to the intrinsic kinetics of GlutOx. However, Fig. 4 shows that even for enzyme layers 1 μm thick, the sensor K_m (0.6 mM) is considerably larger than that reported for the free enzyme in oxygen-saturated solution (0.173 mM), and even for layers 0.1 μm thick, the sensor K_m is 0.3 mM. It is important to note that these K_m values were generated under conditions affected by oxygen concentration (since the O₂ concentration at saturation is well below the intrinsic K_m,O2 and do not represent intrinsic enzyme kinetics, although mass transfer influence and oxygen limitation are more evident for the immobilized enzyme. An additional consequence of the oxygen transport limitations is a reduced apparent k_cat, which further complicates analysis of the immobilized enzyme kinetics underlying biosensor performance. Construction of biosensors with thinner immobilized enzyme layers might be expected to bring apparent k_cat values more in line with the free enzyme, but sensors with the thinnest enzyme coatings display a further reduced apparent k_cat, since a greater fraction of the produced H₂O₂ is swept into the bulk solution due to shorter diffusion distances to the sensor surface.

Figure 4.

Modeled SS response of sensors with varied enzyme layer thicknesses and a permselective layer of negligible transport resistance. In all cases, f_glutox = 0.5 and the sample O₂ concentration equals 270 μM.

For thicker immobilized enzyme coatings, the sensor current response is linear to a higher Glut concentration until the maximum current at which O₂ becomes fully limiting (Fig. 4). The thickest layers, with a correspondingly greater mass transfer resistance, might be expected to have a lower maximum current response. However, since oxygen is produced at the electrode surface when H₂O₂ is electrooxidized, Glut that has diffused deep into the enzyme layer can be turned over to produce H₂O₂ much closer to the electrode surface. This mitigates the increased mass transfer resistance present in thicker deposits, and causes sensors to operate in a fundamentally different manner at high Glut concentrations. This is best understood by examining first the concentration profiles of O₂, H₂O₂, and Glut in the thickest enzyme layers (> ~3 μm) at saturating Glut concentration (Fig. 5). Under these circumstances, it is evident that O₂ does not penetrate from the bulk to the electrode surface and is essentially depleted to near zero in a broad zone in the center of the layer where the GlutOx-catalyzed reaction rate must be near zero as well. When the bulk Glut concentration is sufficiently high that the concentration at the inner edge of the enzyme coating is much greater than K_m,glut, the enzyme kinetics are independent of Glut concentration, and H₂O₂ and O₂ are cycled in a zone close to the electrode. This condition corresponds to the maximum current observed for sensors with thick enzyme layers and is identical for all these sensors, since the enzyme kinetics driving the sensor response are independent of Glut concentration. However, as the enzyme deposit is made thinner (but still greater than ~3 μm), the Glut transport resistance is reduced and higher currents at lower Glut concentrations are observed, which corresponds to lower sensor K_m values. For enzyme layers somewhat less than 3 μm in thickness (Fig. 5), increased H₂O₂ loss to the bulk with progressively reduced thicknesses limits both the maximum concentration of H₂O₂ attained in the enzyme layer and the maximum current, despite the fact that greater O₂ penetration is achieved such that Glut turnover occurs throughout the enzyme layer. Yet importantly, Glut transport resistance also is reduced, and optimal performance in terms of current signal at physiological Glut concentrations is observed (as described earlier). Based on this analysis, it should be clear that inferences about the state of the enzyme upon immobilization cannot be made straightforwardly based on sensor K_m and maximum current measurements alone, rather the influence of O₂ limitations and other mass transfer effects must be considered carefully as well.

Figure 5.

Concentration profiles of O₂, H₂O₂, and Glut for sensors with 1, 3, or 5 μm thick enzyme coating after reaching a steady state with saturating Glut (12 mM). In all cases, f_glutox = 0.5 and the sample O₂ concentration equals 270 μM.

2.5. Oxygen is Not Expected to Limit Glutamate Sensing in the Brain Under Normal Conditions

In brain extracellular fluid (ECF), Glut concentrations are expected to be ≤10 μM under normal circumstances where significant trauma has not occurred.⁵¹ Sensor response to this range of Glut concentrations in vitro should not be influenced by O₂ concentrations, since the saturating concentration of O₂ in water from air at 25° C is ~270 μM. However, O₂ concentrations in ECF can be far lower, commonly 5–50 μM.⁵² To investigate whether O₂ limitations would be a problem at the lower expected O₂ concentrations in vivo, simulations were generated using base-case thickness parameters (10 μm Nafion and 20 μm enzyme layers) and otherwise identical boundary conditions as those used for Fig. 4. The results presented in Fig. 6 show that sensors respond linearly, as expected, until O₂ is depleted within the enzyme layer, at which point a sensor cannot discern differences in Glut concentration and the response flattens. At the lowest O₂ concentration examined (5 μM), the sensors could discern differences in Glut concentration up to 15 μM, and for O₂ at 25 μM, they could differentiate between Glut concentrations well beyond expected ECF levels (Fig. 6). Improved sensors with thinner Nafion and enzyme layers behave similarly at the low O₂ concentrations expected in the brain. Thus, these Glut biosensors are expected to be useful at relatively low O₂ concentrations in vivo.

Figure 6.

Steady-state response of a base-case sensor to increasing Glut concentrations over the range of O₂ concentrations typical in brain ECF.

2.6. Mass Transfer Limitations Cause Distortion of Sensor Output Relative to Pulsed Glutamate Signal Input

One of the advantages of constant-potential amperometric methods as opposed to other methods of detection, including fast cyclic voltammetry, is its potential for near continuous sampling and very rapid response times as illustrated above.⁵³ However, the simulations above focused on sensor response to an instantaneous step change in Glut concentration, whereas for studies in vivo, the Glut signals commonly would take the form of signal pulses. A key issue, therefore, is the relationship between sensor output and the transient signal input. A further step, which is beyond the scope of this work, would additionally consider how release from synapses and diffusion through brain tissue results in a transient concentration at the surface of the sensor. As an illustrative preliminary investigation into the ability of the electroenzymatic Glut biosensor to track concentration transients in the brain, simulations were run to approximate the case where Glut release takes place right at the surface of a sensor (i.e., the outer edge of the enzyme layer). The results illustrate the ability of a sensor to describe a Glut signal input, and likely represent the best possible signal resolving ability to be expected for these sensors in vivo.

In this modeling study, the Glut concentration at the surface of the sensor was changed from zero to a maximum in a Gaussian-shaped pulse with respect to time, C_glut(t) = C_maxe^{−(t−t_p)2/2σ2}, where C_max is the maximum bulk sample concentration (taken as 10 μM), t_p is the center of the pulse (0.5 s), and σ is its standard deviation. The value of 4σ represents the approximate time that Glut is potentially measurable. The simulated distortion in the base-case sensor signal relative to the imposed concentration pulse at the sensor surface is shown in Fig. 7 for pulses of σ = 0.25 s and σ = 0.05 s with the pulsed Glut concentration normalized relative to its maximum and the sensor current signal normalized relative to its previously modeled, SS response to the maximum Glut concentration of the pulse, C_max. As expected, the peak sensor response is time shifted relative to that for the input Glut transient, which is representative of the sensor response time. The simulated sensor output also is broadened and skewed relative to the symmetric input peak, and the maximum current observed is well short of that expected for 10 μM Glut, based on the SS response. Thus, the base case sensor might not prove reliable for estimation of peak Glut concentrations in vivo based on SS calibration data in vitro. Also, the less steep and asymmetric output signal obtained relative to the input can make the use of such sensor data for determination of Glut release and uptake kinetics problematic. Similar issues have been described in a frequency response analysis of glucose biosensors.³⁸

Figure 7.

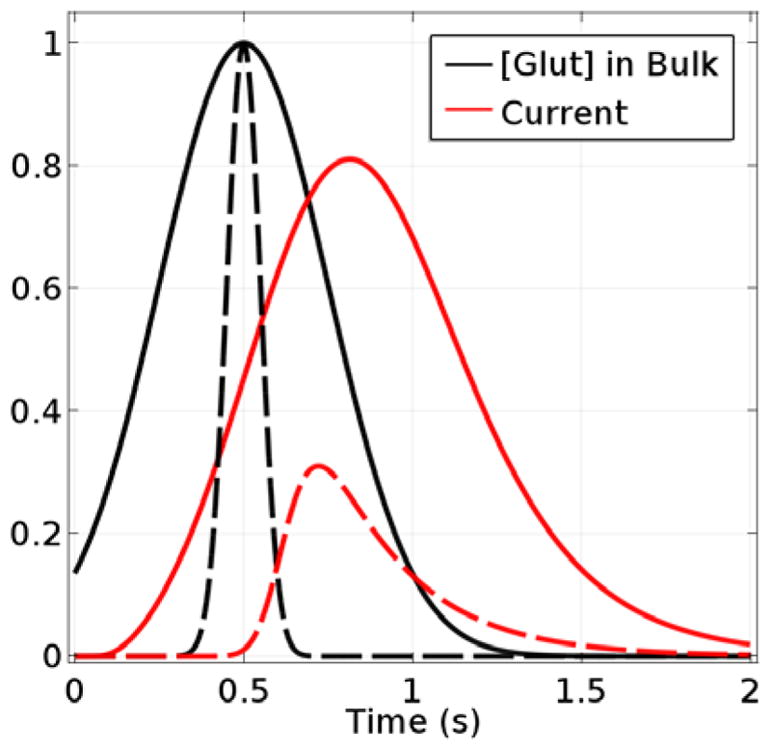
Glut concentration at sensor edge (relative to its maximum concentration) and observed current signal (relative to the SS current for the maximum Glut concentration). The solid curves correspond to an input pulse and output signal for a Gaussian input with σ = 0.25 s and C_max = 10 μM, and the dashed curves correspond to an input with σ = 0.05 s and C_max = 10 μM.

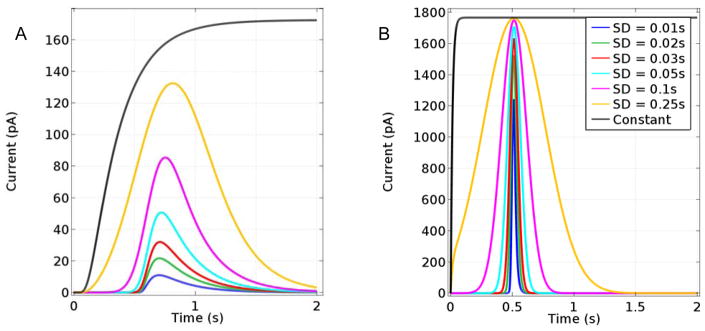
Fig. 8A shows the predicted response of the base-case Glut sensor to Glut concentration pulses (10 μM peak concentration) of varied σ centered at 0.5 s, as well as the response to a step change in Glut to 10 μM. The simulations show that if pulsed Glut is present in solution for less than 1 s (σ < 0.25 s), the sensor will show less than 75% of the maximum concentration reached. If the goal is to observe multiple Glut signals, maintaining full resolution of transients present for less than a second is ideal. Fortunately, simulations suggest that a sensor with thinner coatings (1 μm Nafion and 3 μm enzyme) and a response time of 0.03 s, would show little delay, distortion, or reduction of response relative to the input signal, and would be able to distinguish between instantaneous step changes in concentration as well as concentration pulses (Fig. 8B). These results indicate that sensors with thinner layers can not only have greatly increased sensitivities but also could be well suited to measure rapid Glut transients.

Figure 8.

A. Modeled base-case sensor response to a single pulsed Glut concentration reaching maximum glutamate concentration (C_max = 10 μM) at 0.5 s and with standard deviations ranging from 0.01–0.25 s and to a step change in bulk sample Glut concentration to 10 μM for reference. B. Responses of a sensor with 1 μm Nafion and 3 μm enzyme layers to the same inputs.

2.7. Mass Transfer Resistances Limit Resolution of Sequential Glutamate Signals

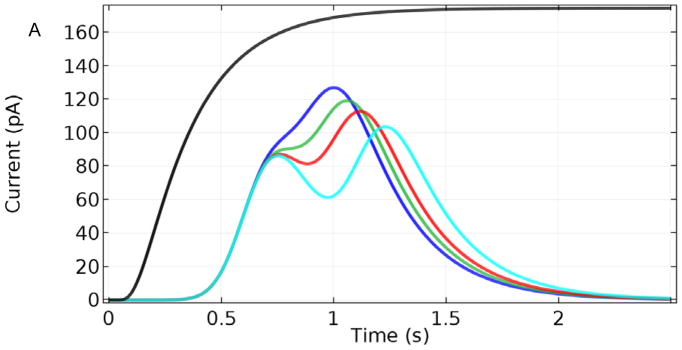
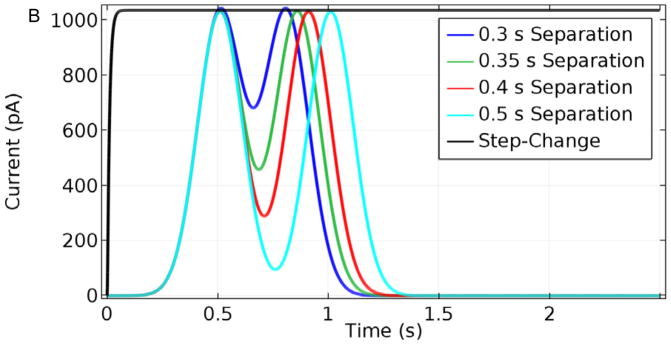
Based on the simulations above, the increased breadth of the base-case sensor output relative to the actual Glut pulse width is expected to be problematic for resolution of a rapid train of Glut signals in vivo. When considering this, it also is important to account for noise that can obscure currents within 1 pA^{16, 24} of each other. Fig. 9 shows how multiple pulses of σ = 0.1 s separated by 0.3, 0.35, 0.4, and 0.5 s (Fig. 9) would be reported by the base-case sensor (Fig. 9A). Based on these simulations, such concentration peaks in solution must be separated by at least 0.35 s seconds to be resolved clearly. In contrast, sensors with thinner coatings (1 μm Nafion and 3 μm enzyme), and thus faster response times, maintain clear resolution of the same pulses (Fig. 9B).

Figure 9.

Sensor response to a Glut concentration step change to 10 μM and to two Glut pulses of σ = 0.1 s and C_max = 10 μM, separated by 0.3, 0.35, 0.4, and 0.5 s. A. Base-case sensor response. B. Response of a sensor with 1 μm Nafion and 3 μm enzyme layers.

3. MATHEMATICAL MODEL

3.1. Differential Mass Balances and Boundary Conditions

The model was developed to represent existing electroenzymatic Glut sensors based on an immobilized GlutOx layer deposited on a permselective polymer film atop a Pt electrode held at constant potential (Fig. 10).²⁴ Three chemical species are of particular interest in modeling these Glut biosensors, Glut, H₂O₂, and O₂; and the rates at which they are transported and participate in reactions determine the limits of how well a sensor can function. Transport of and reactions involving each of these three species were modeled with time-dependent mass balance equations of the general form below,

Figure 10.

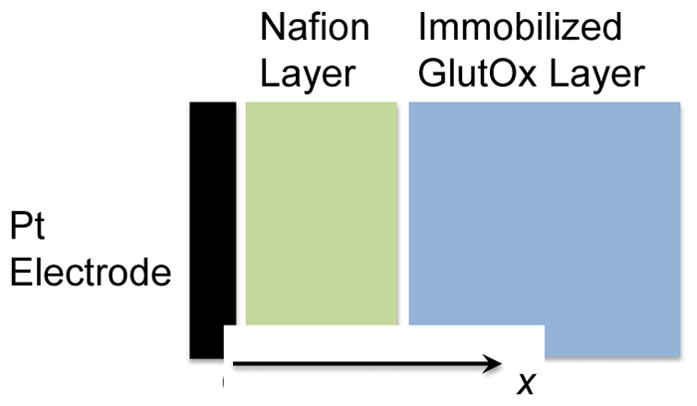
Schematic of the base-case Glut biosensor used in the model with a 10-μm-thick permselective Nafion layer and a 20-μm-thick immobilized GlutOx layer.

$$\mathrm{\epsilon }\frac{\partial C_i}{\partial t}=-D_{\mathit{eff}}\frac{{\partial }^2{C}_i}{\partial x^2}+r_i$$

where ε is the porosity of the enzyme or permselective layer; C_i is the pore concentration of each species (i), e.g., Glut, O₂ or H₂O₂; t is time; D_eff is the effective diffusivity; x is the distance from the Pt electrode surface; and r_i is the volumetric reaction rate, which is zero for all species in the permselective layer (see Supporting Information for a complete listing of mass balance equations, boundary conditions, parameters and parameter values). The enzyme and permselective polymer layers were modeled as separate mathematical domains where equality of fluxes as well as solute partitioning were described in appropriate boundary conditions at the interface between the layers. As described above, the enzyme layer typically consists of co-deposited GlutOx and BSA, which are crosslinked with glutaraldehyde. Although the permselective layer commonly consists of an electrodeposited film of polypyrrole (PPY) or of polyphenylenediamine (PPD) and a dip-coated layer of Nafion,²⁴ this model treated these coatings as one layer of Nafion, since the Nafion layer is generally much thicker and poses the dominant mass transfer resistance. At the Pt electrode surface, H₂O₂ electrooxidation kinetics were modeled explicitly in boundary conditions, equating species transport to the consumption and generation of H₂O₂ and O₂, respectively, since H₂O₂ electrooxidation results in the generation of O₂ as well as protons. In contrast, the Glut flux at this solid boundary was set equal to zero. At the outer edge of the enzyme layer, which is in contact with the sample environment, transport of the species was modeled using appropriate mass transfer coefficients (see below) or the concentration was described by a time-dependent function. Depending on the values of the mass transfer coefficients used or the imposition of a time-dependent expression for the concentration of species at the enzyme layer/sample interface, the model may be representative of a probe in a flow cell used to measure sensor response characteristics or of a probe implanted in brain tissue where transients in Glut concentration at the sensor surface might be expected. Finally, the current produced by the sensor was modeled based on the expression for H₂O₂ electrooxidation, which includes a parameter that accounts for reduced Pt surface area due to electrodeposited polymer and the influence of local O₂ concentration on the electrooxidation rate.⁴²

3.2. Modeling Assumptions and Parameter Values

The formulation of the model equations and the choices of parameter values rely on a number of assumptions and approximations. The following key assumptions were made in formulating the differential material balances for species in the enzyme and permselective layers:

1. One-dimensional mass transport

2. Solutions are dilute and layers are homogeneous such that Fick’s Law applies

3. The enzyme layer void space can be represented by a network of random pores such that the model for effective diffusivity of Wakao and Smith⁵⁴ applies

4. Enzyme kinetics are not changed by immobilization and can be described by a ping-pong, dual-substrate mechanism similar to that for other oxidases including glucose oxidase⁵⁵

5. No enzyme is deactivated during immobilization and enzyme deactivation is not important over the time course of the simulations

6. H₂O₂ electrooxidation kinetics⁵⁶ are not affected by species other than H₂O₂ and O₂

7. Ammonia production does not affect kinetics and its potential electrooxidation does not contribute significantly to the current signal

One-dimensional transport is a reasonable approximation for microelectrodes with characteristic dimension exceeding 25 μm,⁵⁷ which applies well to the ~40 μm × ~100 μm microelectrodes produced by us.²⁴ The second assumption regarding the applicability of Fick’s law is commonly applied in models of this type where concentrations are indeed relatively dilute. However, the enzyme and permselective polymer layers may not be homogeneous in reality, which necessitates the use of effective diffusion coefficients and average reaction rates.

The effective diffusivities of each species were based on their diffusion coefficients in water, D_i.⁵⁸ For the enzyme layer, the water diffusivity was multiplied by the square of the medium porosity to give the effective diffusivity in accordance with the random pore model,⁵⁴ while for the permselective layer a simple multiplier, α, was used to match published effective diffusivities in Nafion. Since a large range of diffusivities in Nafion have been reported,⁵⁹ the values used here for α were based on reported measurements of O₂ effective diffusivity at a temperature, pressure, and water content that resembles biosensor conditions.^{59, 60}

Conditions in the enzyme layer of the biosensor may alter enzyme kinetics significantly as a consequence of covalent crosslinking and the high protein concentration. Recent work on enzymes in intracellular environments, for example, has shown that enzymatic rates under such crowded conditions may be increased or decreased depending on the enzyme, the reactions catalyzed, and the nature of the enzyme microenvironment.^{61, 62} Many of these changes can be explained by considering the effects of reduced void space on mass transport,^63–65 which is accounted for through the effective diffusivities described above. However, for lack of applicable data, other influences on observed GlutOx kinetics were not included in the model. Also, it is known that glutaraldehyde can cause enzyme deactivation during immobilization, yet as discussed below, this may not be a significant concern for thicker enzyme deposits.

The rate equation for H₂O₂ electrooxidation was taken from a study conducted under conditions resembling the physiological, where the reaction has been shown to be phosphate-mediated.⁶⁶ More complex rate forms and slightly different rate constants than those used here have been generated to account for nonlinearities in the reaction rate due to influences of pH, chloride ion, temperature, electrode potential, and deficiencies in phosphate.⁶⁷ However, these alternative rate forms apply to conditions that generally are not expected in the brain.

The last assumption listed above may constitute a significant approximation, especially if the ammonia concentration reaches a level sufficient to overcome any buffering capacity in the enzyme layer and causes pH to rise significantly into the alkaline range. In this situation, enzyme activity may be affected and ammonia electrooxidation may occur; however this effect may be moderated by the production of protons at the electrode surface as H₂O₂ is electrooxidized. It is well known that ammonia, and to a lesser extent ammonium,⁶⁸ is electrooxidized on Pt under alkaline conditions; yet, we have not observed ammonia or ammonium ion electrooxidation currents above noise on bare Pt or on PPD/Nafion-coated Pt at the operating potential for Glut biosensors (0.7 V vs. Ag/AgCl) and at pH 7–11 (data not shown). Clearly, this model does not include a description of all phenomena of potential importance and does entail some important assumptions and approximations; regardless, it can serve as a useful tool to study the interplay of kinetics and mass transfer on biosensor performance and as a guide for device optimization as described below.

A full list of parameters, definitions and values is given in the Supporting Information. Parameter values were obtained directly from the literature, measured experimentally, or calculated from published experimental data. The thickness of a dip-coated Nafion layer on a microelectrode array site³ has been observed by us using scanning electron microscopy to range from 5 to 20 μm, thus the thickness of the permselective Nafion layer was modeled in the base case as 10 μm, but was also varied over the range of 0.1 to 20 μm when investigating the effects of Nafion layer thickness. The void fraction (i.e., porosity) of the enzyme layer was set at 0.5, whereas that for the permselective layer was chosen based on measured Nafion film void fractions.⁶⁹

Parameters related to the GlutOx concentration in the enzyme layer and GlutOx kinetics are discussed in detail in the Supporting Information. Although the reaction mechanism for GlutOx has not been established, the enzyme kinetics were modeled according to the common ping-pong reaction mechanism of oxidase enzymes.⁵⁵ Also, Glut concentrations in the brain before and after trauma have been measured to range from 1–50 μM,⁵¹ in accordance with our experimental sensor measurements,²⁴ which guided the range of Glut concentrations investigated.

Species transport from the sample space to the outer edge of the sensor enzyme layer was described in terms of mass transfer coefficients. Such a mass transfer coefficient has been measured for O₂ at a microelectrode surface in a flow field,⁷⁰ and experiments testing sensor response time have used flow cells with similar flow rates (~1 cm/s) and dimensions.²⁴ The mass transfer coefficients for Glut and H₂O₂ were estimated based on their molecular diffusivities relative to that for O₂ and the theoretical relationship between a species diffusivity and its mass transfer coefficient.⁷¹ The partition coefficient between the electronegative permselective film (Nafion) and the enzyme layer was assumed to be 1 for the charge neutral O₂ and H₂O₂ species and 10⁻³ for negatively charged Glut, thereby essentially excluding Glut from the permselective layer. The equation for the current generated at the electrode surface accounts for two electrons liberated with each oxidized H₂O₂ molecule, platinum electrooxidation kinetics based on the concentration of H₂O₂ and O₂ at the electrode surface (see Supporting Information),⁴² and an electrode surface area of 4800 μm² that is half covered with a polypyrrole permselective film as follows from its porosity, which was taken as 0.5.⁷²

3.3 Numerical Solution

The model was solved using COMSOL (v. 5.2a) using 1D coefficient form PDE physics and the standard finite element solver, with time steps as small as 0.1 ms in cases where the simulations reached a steady state very rapidly or as boundary conditions required. Each domain was given a coefficient form PDE with local variables and a global variable version to implement the partition coefficient. Advanced physics settings were required to specify the partitioned concentrations between layers without disrupting flux continuity. Error tolerances for all variables were set to 10⁻⁹. Solutions were verified to be mesh independent at the settings used, by first splitting the combined domains into 100 domain elements (between 6 nm and 0.3 μm in size, depending on overall sensor thickness) and then refining to 200 or 300 elements as needed. To smooth the solutions over the first few time steps, the bulk sample Glut concentration was stepped from 0 to the specified value over the first 0.01 s, or with further mesh refinement at domain boundaries. Use of the COMSOL software package enabled straightforward exploration of parameters representing experimentally controllable characteristics, including enzyme and permselective layer thicknesses, and enzyme loading, which might be optimized for improved sensor performance.

4. CONCLUSION

A detailed mathematical model of an electroenzymatic glutamate sensor that accounts for diffusion and reaction in an immobilized enzyme layer and diffusion across a permselective polymer layer to an underlying Pt electrode was constructed without any adjustable parameters. The model simulates well the performance of existing glutamate biosensors consisting of permselective polymer and enzyme layers of ~10 and ~20 microns in thickness, and illustrates a lag in biosensor current response that makes estimation of response time from current rise time problematic. These simulations also show that >95% of H₂O₂ generated in the thick enzyme layers characteristic of current biosensors is lost back to the sample environment, which suggests that biosensors constructed with much thinner polymer and enzyme layers would be optimal. A theoretically near-optimal biosensor with polymer and enzyme layers of 1 μm and 3 μm in thickness would result in several-fold improvement in response time and sensitivity to ~30 ms and ~365 nA/μM/cm²; yet these predictions might best be interpreted as qualitative, as they are subject to the modeling assumptions described. Interestingly, for enzyme layers greater than a few microns in thickness, the simulations also show that enzyme loading over the practical range has very little impact on sensor performance due to mass transfer effects unless much less than 1% of the enzyme is functional. This result suggests that enzyme deactivation, which was not included in the model, may also be masked by mass transfer effects. Mass transfer effects, including related O₂ limitations, also mask intrinsic enzyme kinetics such that the apparent sensor Glut K_m for GlutOx, even for a very thin 1 μm thick layer, is much higher than what is observed for the enzyme in free solution. Thus, care must be taken in inferring conclusions about the state of the immobilized enzyme from these sensor kinetic constants without support from simulations. Model simulations also showed that O₂ transport limitations are not expected to limit sensor performance in discerning glutamate concentrations up to 15 μM for sample O₂ concentrations as low as 5 μM. Finally, an analysis of biosensor response to subsecond glutamate pulses of the sort that may be representative of glutamate signals in the brain shows the limitations of existing glutamate biosensors and the promise of theoretically optimized biosensors in monitoring such signals.

The results presented here are specific to electroenzymatic Glut biosensors of the construction described, although they can be extended to other electroenzymatic sensors by adjusting enzyme layer parameters and those of permselective polymer film(s) as necessary. However, the limitations of the model to one spatial dimension makes it difficult to investigate the effects of electrode surface roughness, which has been shown to increase sensitivity by more than an increase in surface area alone would predict,⁷³ and makes it impossible to optimize electrode size or placement on microelectrode array probes. Extension of the model to three spatial dimensions is planned to address these issues and to enable incorporation of probe placement into a simulated brain region, where synaptic release and subsequent diffusion and uptake could also be modeled, so as to provide insights into operation in vivo of existing and theoretically optimized sensors.