Memory as perception of the past: Compressed time in mind and brain

Abstract

In the visual system retinal space is compressed such that acuity decreases further from the fovea. Different forms of memory may rely on a compressed representation of time, manifested as decreased accuracy for events that happened further in the past. Neurophysiologically, “time cells” show receptive fields in time. Analogous to the compression of visual space, time cells show less acuity for events further in the past. Behavioral evidence suggests memory can be accessed by scanning a compressed temporal representation, analogous to visual search. This suggests a common computational language for visual attention and memory retrieval. In this view, time functions like a scaffolding that organizes memories in much the same way that retinal space functions like a scaffolding for visual perception.

Outside of me, in space, there is never more than a single position of the … pendulum, for nothing is left of the past positions. Within myself a process of organization … of conscious states is going on… It is because I endure in this way that I picture to myself what I call the past oscillations of the pendulum at the same time as I perceive the present oscillation…. [S]uccession exists solely for a conscious spectator who keeps the past in mind and sets the two oscillations … side by side in an auxiliary space.

Henri Bergson, Time and Free Will, 1910

The analogy between time and space

Memory theorists have long proposed that memory relies on a representation of past events organized along a timeline [1, 2, 3]. Indeed, it can be shown that our experience of the passage of time requires the involvment of memory [4, 5, 6]. Consider Bergson’s description of a person observing a swinging pendulum (quoted at the beginning of this paper). Simultaneous information about both time points A and B is required to determine that A precedes B. Our experience of the passage of time requires that there be some neural code that represents the temporal relationship between events. Bergson postulated that this neural code is in some sense spatial, in analogy to the representation of physical space. Although Bergson, in 1910, made this postulate in the absence of almost any empirical data on neurobiology this paper reviews a growing body of evidence that suggests there is in fact a strong analogy between the neural representation for time and the neural representation for external space in the visual system and that this suggests a deep connection between the neural computations supporting memory and those supporting visual attention.

The visual system represents robust information about the location of objects in physical space and utilizes this information to support behavior. Neurons throughout the visual system respond preferentially to stimuli that appear in a circumscribed region of retinal space. These visual coordinates convey both ordinal and metric information about the location of objects. This information can be used to organize behavior. This paper pursues the hypothesis that memory is analogous to perception acting on a metric representation of time rather than on a representation of retinal space. In the next section, we review recent evidence that the mammalian brain maintains a temporal representation analogous to the spatial representation in the visual system. Then we review behavioral data suggesting that people can scan through time in much the same way they scan through retinal space in visual search experiments. If memory and vision share similar neural representations and if behavior manifests similar capabilities in accessing these forms of information, then computational mechanisms for accessing information in one domain could be recycled to access information in the other domain. In the last section we sketch out some of the computational requirements necessary to access and manipulate spatial representations.

Neural evidence for a compressed representation of time

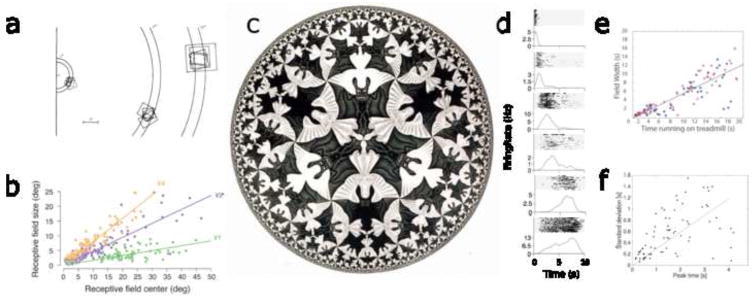
It has long been known that the visual system supports a compressed representation of visual space. Photoreceptors in the retina respond only to light that lands on a circumscribed region of the retinal surface; this spatial organization is reflected at least through early cortical regions (e.g., [12]). Receptive fields further from the fovea are larger than receptive fields closer to the fovea (Fig. 1a, [7]). Moreover, there are more cells with receptive fields centered closer to the fovea than there are with receptive fields further from the fovea (e.g., [13]). These observations led to the conclusion that the representation of the visual world is logarithmically compressed in the radial direction [14, 15, 16].

Figure 1.

Compressed neural representations of space and time. a. Visual receptive fields of single units from monkey V1. The size of each square indicates the spatial extent of the receptive field; the location of the square shows the preferred excentricity. The clusters of receptive fields were recorded within .1 mm of each other on the cortical surface. Visual receptive fields farther from the fovea average over larger regions of visual space. After [7]. b. Width of spatial receptive fields as a function of position in different regions of macaque visual cortex. After [8]. c. In this tiling by M.C. Escher, the spacing of the angels and devils becomes more compressed as one approaches the edge of the circle. If one samples a constant region of the image, the number of tilings grows larger as one approaches the edge. d. A sequence of hippocampal time cells firing during the 10 s delay interval of a memory task. Each panel gives rasters (top) and smoothed peristimulus time histogram (bottom). Units have consistent receptive fields that tile the delay. Temporal receptive fields later in the delay average over a wider range of time than temporal receptive fields early in the delay. After [9]. e. Width of temporal receptive fields as a function of peak time in rodent hippocampus (blue: CA1; red: CA3). After [10]. f. Width of temporal receptive fields as a function of peak time in rodent mPFC. After [11].

The compression of the visual world is roughly analogous to the compressed tilings in the work of M. C. Escher, an example of which is shown in Figure 1c). To see this, imagine that one is looking at a large, evenly-spaced tiling that covers the entire visual field. Receptive fields close to the fovea might cover only a part of an angel or a devil. Receptive fields further from the fovea average over a larger area might cover several angels and devils. If we constructed an image of the visual world appearing in each neuron’s receptive field in which neurons are evenly spaced (roughly analogous to the retinotopic map on the cortical surface), this image would roughly correspond to the compressed tiling.

Receptive fields in time

As reviewed below, a growing body of recent neural evidence suggests that the mammalian brain maintains a representation of time that is compressed in a way analogous to the compression of visual space [9, 92, 19, 20]. In much the same way that neurons in visual cortex have receptive fields that respond when a visual stimulus with appropriate properties is present in a circumscribed region of visual space [12], so-called time cells [17, 9] respond when a stimulus with appropriate properties was experienced during a circumscribed range of times in the past. Figure 1d shows an example of this phenomenon. In this study, simultaneously recorded hippocampal neurons were recorded during a memory experiment [9]. On each trial the animal sampled an object. After sampling the object the animal had to wait for 10 s before a test that required memory for the identity of the sampled object. Figure 1d shows the firing rate of different hippocampal time cells during the 10 s delay interval. Note that each time cell fires during a circumscribed period of time within the delay. We will refer to the range of times during which the time cell shows elevated firing as its temporal receptive field.

Compressed temporal representation

The time cells shown in Figure 1d exhibit properties of compression. Note that the width of the temporal receptive fields increases with the center of the temporal receptive field, in much the same way that the size of visual receptive fields increases with distance from the fovea. Also note from the trial rasters that this increase in the width is not simply an artifact of averaging over trials. The distance between the centers of time cells 1 and 2 is less than the distance between the centers of time cells 2 and 3. Although these are just three example neurons, both of these signatures of compression have been evaluated in many experiments (see e.g., Fig. 1e–f, [10, 11, 18, 19, 20]). In some experiments, time cells respond selectively to different stimuli that initiate the trial [9, 21, 22]. This conjunctive code for what and when is analogous to neurons in the visual system that show a conjunctive code for what and where. For instance, simple cells in primary visual cortex respond to gratings of a particular orientation that are also in a circumscribed region of retinal space.

Time cells exhibiting properties of compression have now been observed in a wide range of brain regions believed to be involved in various forms of memory. Hippocampal time cells were initially identified in region CA1 of the rodent [17, 9], which is believed to be of central importance in episodic memory. Time cells have subsequently been observed in closely-related brain regions, including hippocampal region CA3 [10] and the entorhinal cortex [18]. In addition, neurons with temporal receptive fields have also been observed in rodent medial PFC [11, 20], and rodent and macaque striatum [23, 24, 25, 19], regions typically thought to be preferentially involved in working memory and implicit memory respectively. It is worth noting that there is a broad diversity to the behavioral tasks performed by the animals in these studies. The observation of a temporal representation with similar properties in different brain regions during performance of very different tasks suggests that different forms of memory can be understood as different operations on a common form of representation [26].

Scale-invariant logarithmic compression

It has long been appreciated that logarithmic compression results in a scale-invariant representation. Put another way logarithmic compression like that seen in the visual system means that the difference between 10 and 11 is not the same as the difference between 100 and 101, but is instead equal to the difference between 100 and 110. This form of neural scaling leads naturally to the perceptual Weber Law, which states that the change in the perceptual difference associated with a change in a physical stimulus depends only on the proportional change in the stimulus. Similarly, the Fechner Law states that psychological scales are a logarithmic function of physical scales [27].

Cognitive scientists have long considered the possibility that both memory [28, 3, 29] and time perception [30, 31] rely on a scale-invariant representation of time. Although the empirical question of whether temporal representations are scale-invariant has not been quantitatively established to the degree of precision that it has been established for vision, there is good reason to suspect that scale-invariance is adaptive for all domains (see Box 1). Although constructing a scale-invariant representation of time is computationally non-trivial, much work has been work done on this topic (see Box 2).

Box 1. Convergent evolution of compressed representation.

In addition to retinal space and (arguably) time, there is also neural and behavioral evidence for logarithmic compression in the non-verbal numerosity system in both humans and animals [95, 96, 97]. Why is this mathematical form so ubiquitous? Perhaps this is a case of convergent evolution, when a property evolves through independent pathways because it’s adaptive. For instance, dolphins and sharks are not closely related, yet share many features (Fig. BI). One would expect that the developmental pathways that lead to the spatial distribution of photorecptors on the retina and the placement of “receptors” for time and numerosity ought to be largely independent.

If logarithmic compression is an example of convergent evolution, what principle leads to this convergence? Perhaps logarithmic compression is an optimal response to statistics of the world [98, 99]. This supposes that the statistics of the world are constant across domains and across different environments; these suppositions may not hold [100, 101]. An alternative hypothesis suggests that logarithmic compression is an adaptive response to uncertainty about the statistics of the world [102].

Imagine that the world contains a number of objects that have some specific size s when projected onto retinal coordinates. Suppose the receptors are spaced by a fixed resolution Δ. If Δ ≫ s we would not be able to resolve the boundaries of the objects. In contrast, if Δ ≪ s most of the receptors would have the same value and we would be wasting resources. If Δ ≃ s, the receptors would represent the object efficiently. Critically if s is not known in advance, any specific choice for Δ will lead to either an inability to resolve the objects or inefficient coding for almost all values of s.

It can be shown [102] that logarithmic compression is optimal in the sense that the set of receptors will convey the same information about a world composed of objects of any size s over a wide range of potential values. Thus, the logarithmic compression seen in the visual system (Fig. 1b, [7, 14]) can be understood as an adaptive response to an uncertain world. To the extent that the organism gains an evolutionary advantage from being able to work efficiently in diverse environments with different statistics, this could provide a principle for convergent evolution across different sensory systems in different species. Because the logic is extremely general, this argument would presumably apply to “cognitive” dimensions such as time (Fig. 1d) and numerosity as well.

Box 2. Constructing a compressed representation of time.

If sensory and cognitive dimensions share a common form of logarithmic compression, this raises the question of how compressed scales can be constructed and accessed. In the visual system, logarithmic compression in is ultimately attributable to the spatial distribution of receptors along the retina; whatever developmental process controls the placement of those cells is the mechanistic cause for logarithmic compression in the visual system. In the case of cognitive dimensions such as time (and numerosity, etc), the nature of the “receptors” is not so obvious. For instance, it is nontrivial to construct a “time receptor” that responds a fixed time after a stimulus is presented. The most obvious mechanism to construct time cells is to imagine a chain of neurons that fire sequentially [103, 104]. In addition to the limited flexibility of chaining models [105], it is also difficult to cause a chain to exhibit the correct form for temporal compression. If the links in the chain—presumably synapses–have the same transmission time, then the sequence of time cells would progress at a uniform rate and the number of cells with each time constant would be constant, in contrast to the compression that is empirically observed.

An alternative proposal is that time cells are not generated from a chain, but rather reflect a different form of computation ([79, 80], see [106, 107] for other non-chaining mechanisms). According to this proposal [79], external stimuli provide input to a set of units that respond to the input and then decay exponentially; each of these units decays with a slightly different time constant. It can be shown that at each moment the set of decaying units approximates the Laplace transform of the input function leading up to the present. A feed forward projection approximates the inverse Laplace transform, resulting in a set of units that activate sequentially. Each of these sequentially-activated units receives input only from a small number of decaying units. The time lag at which a sequentially-activated unit is activated depends on the time constants of the decaying units that provide it input. Because of this, choosing the compression of the sequentially-activated units amounts to choosing the distribution of the time constants of the decaying units [108, 109].

Behavioral evidence for a compressed timeline

The neural evidence for compressed representations of time and space is paralleled by behavioral evidence for compressed representations. These studies use RTs to estimate the time taken to access different pieces of information, suggesting the organization of the neural representation.

Scanning in visual search

In the visual system, space not only organizes receptive fields, but also shapes behavior. We can direct attention to regions of visual space, manifest as enhanced gain for receptive fields in the attended region [33] and also speeded identification of targets [34]. If memory is constructed from a temporal representation with the same properties as visual space, perhaps we can enhance access to information at selected temporal coordinates, resulting in characteristic behavioral effects. Indeed, scanning models, in which attention is sequentially directed to different regions, have a rich history in the study of both visual search [35, 36], where the regions are in visual space, and in the study of short-term memory for recency [37], where the regions are in a temporally-organized memory.

Scanning through time in memory

In memory scanning models, a probe is compared sequentially to the contents of memory. In self-terminating search models [37], the search terminates when a match is found. As a consequence, if scanning consistently follows the same sequence through the contents of memory, one can infer something about the structure and organization of the memory representation from response times.

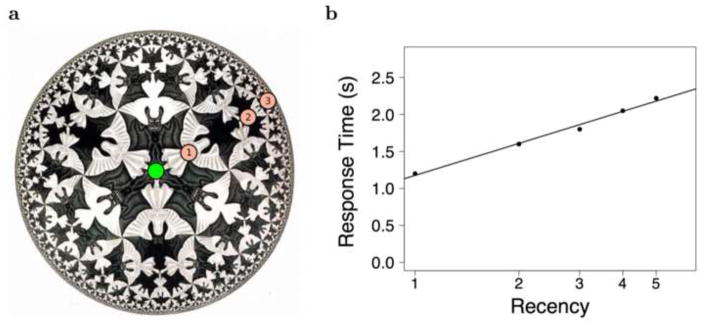
Consider the pattern of search times that would result if one scanned a compressed representation like that shown in Figure 2a along the radial direction, starting from the center (green dot). If the target of attention moves at a constant rate outward from the center towards the edge, this would sweep over larger and larger regions of the external image. That is, if attention moves at a constant rate across the surface of the disk, it would take less and less time to approach equally spaced locations (numbered red dots) as the search moves away from the center. As a consequence, the time to access a target would appear to decelerate when shown as a function of eccentricity. If the compression in the radial direction was logarithmic, then we would expect to see the time to access a target go up linearly with the logarithm of its eccentricity. Similarly, scanning through a logarithmically-compressed temporal representation would result in a linear increase in search time when plotted as a function of the logarithm of the probe’s recency.

Figure 2. Behavioral evidence for a compressed representation of time in memory.

a. In a compressed scale, the time to scan to a point is a decelerating function of objective distance. If the search starts at the green circle and proceeds radially, it takes longer to scan from point 1 to point 2 than it does to scan from point 2 to point 3. If the compression is logarithmic, one should observe a linear relationship to the logarithm of distance. b. Scanning in short-term memory. Participants compared two probes and selected the one presented more recently. This task has long been believed to be performed via a self-terminating search model in which a temporal representation is scanned from the present towards the past. RT to correctly choose a probe as a function of the number of time steps in the past at which the probe was presented. The plot is roughly linear on a logarithmic scale. After [32].

Scanning in short-term memory for recency

Memory scanning in short-term memory shows good evidence for this deceleration as a function of time. In the short-term judgment of recency (JOR) task, participants study a list of rapidly-presented stimuli. After the list, they are presented with two stimuli and asked to select the one that was presented closer in time to the present. The classical finding is that the time to select a probe depends on how far in the past that probe was presented, but not on the distance between the two probes [37, 32, 38]. This is what one would expect from a self-terminating search model that scanned sequentially through a temporal representation of the list (see also [39]).

The response time to find a probe in short-term JOR goes up the further in the past the probe one selects was. However, the increase in RT with increasing lag is not constant [37, 32, 39]. Figure 2b shows median response time as a function of lag on a logarithmic scale. If there is backward scanning of a temporal representation, this finding requires that the temporal representation is compressed. The data are also at least consistent with logarithmic compression.

It should be noted that not all short-term memory tasks show evidence for serial scanning models. For instance, short-term item recognition experiments [32, 40, 41, 42] do not show appear to show evidence for scanning even with superficially similar methods to short-term JOR experiments (Experiment 2 from [32] is an especially dramatic demonstration of this point). One account of these disparate findings is that participants have access to a compressed temporal representation for working memory, but they choose to access the representation differently in different tasks. For instance, when participants are instructed to instead choose the probe that came first in the list, the results resembled a scanning model in which particpants scanned forward starting at the beginning of the list [43]. This is analogous to a visual search experiment where the participant chooses to start the search at a different location and suggests that this search process in short-term memory is subject to strategic control.

Scanning in long-term memory

Although work on scanning in memory has focused on short-term memory, there are a number of findings from longer-term memory experiments that are consistent with scanning of a compressed temporal representation. Results from the JOR task over longer time scales are consistent with this hypothesis, despite the fact that the time scales in these experiments are sometimes several orders of magnitude greater than the time scales in the short-term JOR paradigm, in which the entire list is presented within a few seconds.

The authors who first introduced the JOR task conceived of JOR as a search process in which the participant sorts through “time tags” [44]. The finding was that the discriminability of a pair of probes separated by a particular delay decreases as the pair recedes into the past, much like the perceptual Weber law. Numerical judgments of recency are not linear functions of true recency but instead approximate a logarithmic function of actual recency, consistent with a Fechner scale for time ([45], see also [46]). In one classic JOR experiment participants were presented with the same stimuli at three different times, P1, P2 and P3 [47]. Participants rated the recency of the most recent presentation at both P2 and at P3. The key finding was that ratings at P3 depended a great deal on the lag between P2 and P3, but very little on the lag between P1 and P2. This is analogous to the results from short-term memory which suggest a self-terminating scanning model. Although none of these findings are uniquely predicted by a scanning model, all of these findings can be modeled using a backward self-terminating scan through a logarithmically-compressed representation of time [26].

Toward a common computational language for visual attention and memory retrieval

If vision and memory have representational and behavioral similarities, then perhaps this means that the neural representations are accessed using a similar computational language. Operations for accessing visual space could be recycled to access time, and perhaps even other domains (such as numerosity) with similar representational compression. In this view, time functions like a scaffolding that organizes memories in much the same way that retinal space functions like a scaffolding for visual perception.

The computational requirements for this view can perhaps be made more clear by analogy to how digital computers handle memory. In a digital computer, physical memory is associated with an address, which is distinct from the content stored at that address. For instance, in the C programming language, one can access and manipulate the contents of a memory stored at an address, or the address itself—a pointer. Critically, there is both an ordinal and metric structure to the address space, such that pointers can be incremented and the difference between addresses has some meaning [48]. That is, some addresses are close to one another whereas others are further apart such that the pointer space is equipped with a metric.

Retinal space as a pointer system for visual perception

There can be little question that in visual attention, retinal coordinates behave like a metric pointer system for the content of the visual display. We have already noted that the visual system can strategically direct attention to a specific part of the visual field. The content at those retinal locations becomes more accessible, with increased behavioral performance (e.g., [50]) and enhanced neural responses (e.g., [33]). We argue further that the pointer system must be equipped with a metric that can be utilized for directing visual attention.

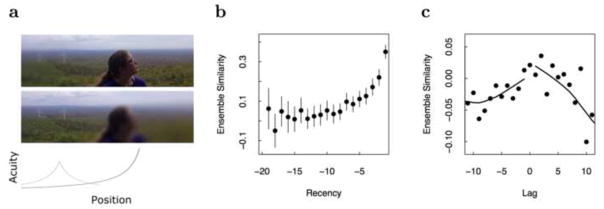
Consider the operations necessary to direct attention to a location in searching for some target object. The top panel in Figure 3a shows a scence with acuity decreasing with distance from the foveated face. In the periphery a large white object is barely visible. The location of this region captures attention, followed by a saccade in which the target location is foveated, revealing a pair of windmills. In order to trigger an appropriate eye movement, the content at the periphery must have conveyed information about its spatial address. In order to successfully direct a saccade of the right direction and distance, this coordinate must have been coded in a number system equipped with information about both direction and distance, i.e., it must be equipped with a metric.

Figure 3.

Analogy between shifting the focus of gaze and a jump back in time. a. Top: When the gaze is focused on the young scientist at the center, decreasing acuity with distance from the fovea makes objects in the periphery difficult to distinguish. One windmill can barely be discerned. Middle: If the gaze is shifted to the windmill, nearby objects (e.g., the windmill on the left) and their spatial relationships become distinguishable. Bottom: The gradient of acuity across the physical image changes as the gaze shifts. b. A neural recency effect. Ensembles of single units were recorded from human epilepsy patients during presentation of a list of pictures. The population vector at each moment was compared to population vectors from preceding moments. c. A neural jump back in time. When a picture from the list was presented the population vector was compared to the earlier population vectors as a function of the distance from the original presentation of the remembered picture (b and c after [49]).

The behavioral jump-back-in-time is analogous to gaze shift

In much the same way that acuity decreases with distance from the fovea, so too the precision of memory decreases with distance from the present. This recency effect is a fundamental property of memory and is observed behaviorally in all of the major memory paradigms and across a range of time scales [51, 52]. The recency effect is a natural consequence of the decrease in acuity for events further in the past that accompanies a compressed temporal representation.

The contiguity effect refers to the finding that when a stimulus is remembered, other stimuli that were presented close together in time to the remembered stimulus become increasingly available. Like the recency effect, the behavioral contiguity effect has been observed in all of the major memory paradigms [53] and has been observed across a range of time scales [52, 54, 55]. When a remote event is remembered, it brings to mind other stimuli that were close to it in time. Put another way, when a temporally-distant event is remembered, the “memory acuity” of other events nearby in time to the remembered event is enhanced. This is analogous to the increase in visual acuity in the neighborhood of a fixated region after a saccade.

A neurophysiological jump-back-in-time

A neural recency effect can be measured neurophysiologically. If one measures the population vector across neurons at a point in time and compares that to population vectors for the same neurons at earlier points in time, one finds that the present population vector overlaps more with vectors closer in time than with population vectors further in the past (see for instance Fig. 3b). This is what one would expect from a compressed representation of time; as stimuli are presented they trigger sequences of time cells. For stimuli further in the past, the time cells fire for longer periods of time, causing slow changes in the state of the population vector. Although it is not known if this gradual change is a consequence of a scale-invariant compressed temporal representation, gradual changes in population vectors have been observed over a range of time scales from seconds up to days with a range of different preparations [56, 57, 58, 49, 59, 60, 61, 62].

As predicted by the conception of episodic memory as “mental time travel” [63, 64, 65] and by models of free recall memory [66, 67], when an event is remembered, it causes recovery of a gradually-changing population vector (Figure 3c, [49], see also [68, 69]). It is not known whether the changing neural state is due to information slowly receding along a compressed temporal representation, nor whether the slowly-changing state that is recovered is a compressed temporal representation. However, the available data is consistent with that hypothesis. To the extent this is true, the jump-back-in-time associated with episodic memory is analogous to a saccadic shift of temporal attention. Perhaps memory retrieval also makes use of a cue to “shift temporal gaze” that includes information about the distance in the past to be targeted by retrieval.

Metric pointer systems and translation operators for vision and memory

There are obvious differences between a shift in gaze in vision and a “shift in temporal gaze” corresponding to the jump back in time that accompanies episodic memory. Whereas a shift in gaze in visual perception is accompanied by an influx of new information from the external world, a shift in “memory fixation” along the temporal dimension causes an influx of information that must be recovered from some internal memory store. Nonetheless, let us consider the implications of the hypothesis that the neural jump-back-in-time that accompanies memory retrieval is analogous to the change in the visual display that comes from shifting the gaze.

First, there is no question that in vision, metric information about distance from the current fixation is recovered and utilized as such by the visual system. The evidence for this comes from neural and behavioral data (for reviews see [70, 71, 72]). Neurons in the parietal cortex remap prior to a planned eye movement such that their firing is based on the image that will be in the receptive field after the planned eye movement [73]. Behavioral results show that visual aftereffects transfer to a location that is going to be fixated [74]. This pattern of neural and behavioral results has been hypothesized to reflect translation of a visual pointer system across retinal coordinates [75].

Predictive remapping seems to require that the visual coordinate system is equipped with a translation operator. A translation operator is a function that takes in a representation of the current state of the visual scene and a vector representing the planned eye movement, then generate as output the visual scene in the new spatial coordinates that will be observed after that movement is executed [76, 77]. Because there are many possible scenes and many possible movements, the correct output cannot be learned via a pairwise associative mechanism. The flexibility of this operation thus satisfies the requirements for symbolic processing [78].

If vision includes a translation operation along the radial direction, perhaps memory also makes use of a translation operation to implement scanning, prediction of the future and perhaps even facilitate a jump back in time. If the compressed representation of time is generated using the mechanism described in Box 2 [79, 80], then a translation operator can be readily implemented in time [81]. Scanning through a memory representation amounts to sequential translation. Translation towards the past would approximately “unwind” the change in the compressed representation as time unfolds, enabling examination of past events. In constrast, translation towards the future combined with an associative mechanism could be used to predict future states of the world [81, 82].

Translation may also be an important computational step in implementing the mechanism for jumping back in time. Consider the item recognition task (Figs. 2c, 3b,c). Let us suppose that the participant is presented with an old probe. We know that when old probes are remembered, there is a neural jump back in time (Fig. 3c, [83]) accompanied by a behavioral contiguity effect [84]. In vision, redirecting gaze is facilitated by a vector valued representation of the target location that includes metric information about its distance. Perhaps the neural jump-back-in-time that accompanies memory for the probe is also facilitated by metric information about the time at which the probe was experienced.

This account also goes some way towards making sense of the primacy effect in memory as analogous to a visual operation. The primacy effect refers to the finding that, all else equal, stimuli from the beginning of a list are better remembered than stimuli from the end of a list [85, 86]. In the free recall task, the primacy effect is almost entirely due to remote transitions to the very first position within a list, which is then followed by forward transitions to its neighbors in the forward direction [87, 88]. This pattern is reflected in models of free recall in which the very first stimulus in the list is preferentially available [87, 89]. Arranged along a timeline, the beginning of a list would appear as a boundary or edge between a region without words (the time before presentation of the first item) and a region with a series of words (starting with the first item in the list). Perhaps this edge or boundary is perceptually salient in much the same way a perceptual edge is more distinctive than a region within a boundary [3]. This perceptual analogy in time also provides a way to frame behavioral and neuroimaging work on event boundaries in memory [90, 91].

Concluding Remarks

Recent developments in neurophysiology and cognitive psychology suggest a potentially deep analogy between the representation of retinal space in vision and the representation of time in memory. While there are still important gaps in the empirical story, this convergence would create an opportunity for a general framework for cognitive computation operating on similar representations across domains. What might such a general framework look like?

We have suggested that memory and time have similar computational requirments—metric pointer systems equipped with translation operators for scanning and “saccadic” shifts of attention (Figure 3). Recent theoretical work has suggested that part of the solution is for the brain to construct a scale-invariant compressed representation via computation of the Laplace transform of past events (Box 2 , [79, 80]). Detailed computational models have been developed on the basis of this approach and applied to a range of cognitive [26] and neurobiological [92] findings.

The use of the Laplace transform has several desirable computational properties. First, because it is well-understood mathematically it can be shown that it is straightforward to generalize from representations of time to any other one-dimensional quantity for which we have access to the time derivative [92]. For instance, one can construct a compressed representation of allocentric spatial position using the same computational approach as used for a compressed representation of time if we have access to allocentric velocity, the time rate of change of position. This approach can be used to generate neural phenomena that resemble different properties of the hippocampal place code [92, 93]. Second, many nontrivial computations can be performed efficiently in the Laplace domain. For instance, given the Laplace transform of a function it is straightforward to write down a translation operator that gives the transform of a translated function [81]. The requirements of the translation operator suggest a strong correspondence to theta phase precession in the hippocampus and other regions [81]. Other operations that would be necessary for more general symbolic computations—such as an equality operator or a difference operator—can also be readily computed in the Laplace domain [94]. With a large enough repertoire of operators, one could imagine a common computational language that might make use of the flexibility and power of the Laplace transform for many sensory and cognitive domains that utilize logarithmically-compressed function spaces.

A correct theory of cognition will have to operate at several Marr levels simultaneously. To pursue the hypothesis described here will require closely coordinated research in cognitive psychology, neurophysiology, and theoretical/computational work (see Outstanding Questions). Although there is evidence suggesting that the brain maintains a representation of time in support of memory, more work will be needed to understand the behavioral and computational repertiore used to access and exploit this representation in different memory tasks.

Outstanding questions box.

• Is the temporal representation logarithmically compressed? Although the available data are consistent with this hypothesis, it is not known whether this holds quantitatively. In vision there is strong quantitative evidence for logarithmic compression.

• Do time cells persist across multiple presentations of stimuli? The available data comes from experiments in which there is presentation of a stimulus, then a delay period. In typical human list learning experiments, many stimuli are presented in sequence. It is not currently known whether each stimulus triggers overlapping sequences of time cells.

• Does the hippocampal place code, which is believed to be important in episodic memory, also show logarithmic compression? In order to answer this question, experiments must demonstrate control over place field position using a moveable landmark in order to estimate the distance associated with the place field.

• How much control do people have over temporal search in memory? Is it possible, for instance, to do a temporal analog of the Posner task?

• How does the brain implement a pointer system with metric relationships? If multiple domains share similar representational properties, knowing how the brain computes in one domain may generalize broadly to other domains of cognition.

Figure BI.

Convergent evolution. Dolphins and sharks are not closely related, but share many features. They both have dorsal fins and streamlined bodies which provide stability and good hydrodynamics. Many species have grey skin and countershaded markings, making them more difficult to see when lit from above. Moreover, dolphins have sonar and many sharks have well-developed electrical senses to facilitate finding prey in murky water.

Trends box.

• The brain contains time cells in many regions that code for the time since a stimulus was encountered.

• Time cells show compression analogous to the compression of retinal space in visual perception.

• In short-term memory, and perhaps long-term memory, memory retrieval may utilize scanning of a temporal representation, analogous to visual scanning.

• In memory the recency effect—a decrease in “memory acuity” with the passage of time—parallels the decrease in acuity with eccentricity in vision.

• In memory the contiguity effect—a boost in “memory acuity” for stimuli near in time to a remembered event—is accompanied by a neural jump back in time. This is analogous to the boost in acuity that comes from changing fixation in vision.

Glossary

Allocentric

A coordinate system that is fixed as an animal (or person) moves around in the world. Because they carry information about the animal’s location relative to environmental landmarks, place cells and grid cells are believed to code for allocentric space. This is in contrast to an egocentric coordinate system, which moves with movement of the body or a retinotopic coordinate system which moves with the retina.

Compressed representation

Neural representations of visual space and time do not show the same resolution for all parts of the scale. As retinal position moves from the fovea, and as temporal position moves further to the past, the neural resolution decreases.

Contiguity effect

The finding that, all else equal, memory for an event tends to bring to mind other events that were experienced close to that event. This term is typically used to refer to the temporal contiguity effect, but spatial and semantic contiguity effects are also observed.

Fechner Law

The Fechner Law refers to logarithmic psychological scales of physical dimensions: p = logx + C. Because the Fechner Law can be derived from the Weber Law (under certain assumptions), they are sometimes referred to collectively as the Weber-Fechner Law.

Laplace transform

The Laplace transform is a mathematical technique to transform a function f(t) into another function F(s). The Laplace transform is useful in memory. If f is a function over past time leading up to the present, the Laplace transform F contains information about the values of f in the past.

Scanning model

A behavioral model in which the observer gathers information from one “region” of a neural representation at a time. Scanning models have been proposed for both visual attention, in which the scan takes place along regions of retinal space, and memory, where the scan takes place along a temporal representation.

Scale-invariant representation

A scale-invariant neural representation of a variable x is one that preserves relative differences between stimuli with a rescaling of the variable. That is, if a stimulus is transformed by taking x → ax the neural response to that stimulus is simply translated. Note that the early visual system obeys this relationship outside of the fovea.

Recency effect

The finding that, all else equal, events that were experienced more recently are better remembered than events that were experienced further in the past.

Weber Law

The Weber Law refers to the finding that psychological discriminability depends on the inverse of a physical dimension