Classifying heatwaves: Developing health-based models to predict high-mortality versus moderate United States heatwaves

Abstract

Heatwaves are divided between moderate, more common heatwaves and rare “high-mortality” heatwaves that have extremely large health effects per day, which we define as heatwaves with a 20% or higher increase in mortality risk. Better projections of the expected frequency of and exposure to these separate types of heatwaves could help communities optimize heat mitigation and response plans and gauge the potential benefits of limiting climate change. Whether a heatwave is high-mortality or moderate could depend on multiple heatwave characteristics, including intensity, length, and timing. We created heatwave classification models using a heatwave training dataset created using recent (1987—2005) health and weather data from 82 large US urban communities. We built twenty potential classification models and used Monte Carlo cross-validations to evaluate these models. We ultimately identified several models that can adequately classify high-mortality heatwaves. These models can be used to project future trends in high-mortality heatwaves under different scenarios of a changing future (e.g., climate change, population change). Further, these models are novel in the way they allow exploration of different scenarios of adaptation to heat, as they include, as predictive variables, heatwave characteristics that are measured relative to a community’s temperature distribution, allowing different adaptation scenarios to be explored by selecting alternative community temperature distributions. The three selected models have been placed on GitHub for use by other researchers, and we use them in a companion paper to project trends in high-mortality heatwaves under different climate, population, and adaptation scenarios.

1 Introduction

A small percentage of heatwaves have extraordinary impacts. During these rare heatwaves, mortality rates soar, hospitals and emergency services are overwhelmed, and infrastructure is stressed (Anderson 2014). One example is the 1995 Chicago heatwave; while, on average, Midwest heatwaves increase mortality risk by about 6%, this heatwave more than doubled mortality risk (Anderson and Bell 2011). More common heatwaves have a more moderate effect on human mortality risk, but occur much more frequently, and so can lead to large cumulative effects distributed over many days.

Projections of future heatwave risks that give separate estimates of the frequency of and exposure to these two types of heatwaves could provide important information as cities develop plans to prepare for and respond to dangerous heat. Some of the responses that cities take to limit heat-related mortality during a heatwave (e.g., opening and providing transportation to air-conditioned shelters; Luber and McGeehin 2008; White-Newsome et al. 2015) have a cost proportionate to the number of days the response is undertaken. Some of these responses might be too costly per day to implement during all moderate heatwaves, but may be a reasonable expense during high-mortality heatwaves. Heat mitigation strategies, including efforts to reduce the urban heat island effect (Luber and McGeehin 2008), could provide a more continuous benefit for the cost and so prove a better use of city funding if most excess heatwave deaths are expected to occur during moderate rather than high-mortality heatwaves.

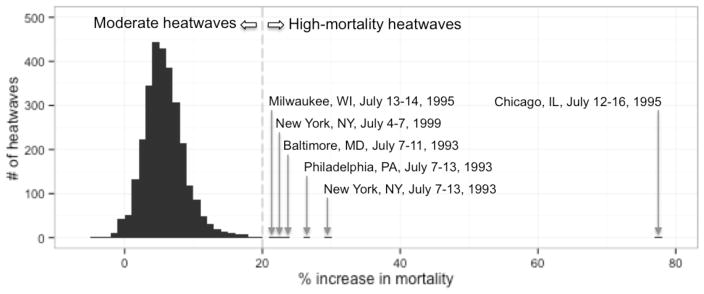
Here, we aimed to build classification models to predict whether a United States heatwave is high-mortality or moderate, where we define a “high-mortality” heatwave as one that increases mortality risk by 20% or more and define all other heatwaves as “moderate”. We selected this threshold to define a “high-mortality” heatwave because, among the observed mortality impacts in the US heatwaves used to build our models, it provided a reasonable boundary between the main distribution of moderate heatwaves and a skewed right tail of heatwaves with very extreme effects (Figure 1).

Figure 1. Distribution of the estimated heatwave effects (% increase in mortality), after hierarchical pooling, of all training set heatwaves (82 US communities, 1987–2005).

The vertical gray dotted line shows the division between moderate and high-mortality heatwaves, based on our definition (>20% increase in mortality for high-mortality).

We built these models with the aim of investigating trends in high-mortality and moderate heatwaves during a changing future. With climate change, heatwaves are expected to become more frequent and more severe (Meehl and Tebaldi 2004), and a critical potential effect of climate change is the health impact caused by increasing exposure to both high-mortality and moderate heatwaves. Some US cities already try to prevent heat-related mortality through community heat plans (White-Newsome et al. 2014). More detailed projections on expected exposure to dangerous heat, including the distribution of heatwave exposure between high-mortality and moderate heatwaves, could help cities optimize these plans. The models we develop here could be used in conjunction with near-term climate projections (e.g., decadal climate projections; Meehl et al. 2014) to explore expected exposure within a city to high-mortality and moderate heatwaves in the coming 10–30 years, to help plan effective use of heat planning / response budgets. The models could also be used with longer-term climate projections to explore the potential benefits of efforts to limit climate change.

Previous studies have projected death tolls from heat under climate change scenarios, but the methods used for these projections are constrained by a number of limitations. First, to measure impacts of heat under different climate change scenarios, most studies have projected death tolls (e.g., Hayhoe et al. 2004; Knowlton et al. 2007; Peng et al. 2011; Mills et al. 2014). This estimation of death tolls is subject to uncertainty from a number of sources beyond the uncertainty inherent in projecting future weather. Projecting death tolls requires estimates of future baseline mortality rates, which are governed by uncertainty in future population characteristics, including education, age-structure, and income, at a community-level resolution. In addition, projecting exact death tolls introduces uncertainty associated with considering mortality displacement (how many heatwave deaths represent deaths that would have occurred within the month regardless?), depletion of susceptible people under scenarios of very frequent extreme heat, and high-dose extrapolation of temperature-mortality models (O’Neill and Ebi 2009; Bell and Dominici 2010; Rocklov and Ebi 2012).

Second, most death toll projections have used models that assessed heat impacts using a single characteristic, usually a measure of temperature. There is evidence from epidemiologic studies that a variety of characteristics of heatwaves may influence their impacts on human health. For example, heatwaves tend to be associated with higher cardiorespiratory mortality risk if they are longer or occur earlier in the summer (Anderson and Bell 2011). Since trends in these heatwave characteristics are likely to evolve with climate change, it is important to project health impacts using a model that incorporates more of the characteristics that may influence health impacts.

We aimed to address these challenges to allow our models to provide information that complements and adds to existing projections of future risks to health from heatwaves. First, instead of developing models to project heat-related death tolls, we developed models to project trends in high-mortality heatwaves: how often will US communities face heatwaves, with high impacts per day, like Chicago in 1995,as climate changes, and how many people will be exposed to these heatwaves? Since these models project expected numbers heatwaves rather than excess mortality counts, they avoid much of the uncertainty that aggregates in projecting heat-related death tolls.

Second, we fit models that consider, as possible predictive variables, many heatwave characteristics that might influence whether a heatwave is high-mortality (Table 1). These models therefore allow a deeper exploration of scenarios of climate change, population growth, and adaptation than temperature-only models. For example, many heatwave characteristics besides temperature will change under different climate scenarios (e.g., projected heatwave length and timing depend on choice of climate scenario [Oleson et al. 2015]). Further, if population size or density influence whether a heatwave is high-mortality, changes in community populations could influence trends high-mortality heatwaves in US communities. Finally, adaptation to increasingly frequent heatwaves could mean that some heatwaves that would be high-mortality heatwaves today, based on their absolute temperatures, would not be in the future.

Table 1.

Heatwave characteristics considered as predictive variables in the models built to predict classification of heatwaves and their relative importance in models. Variable importance values are for each type of model built using ROSE to adjust for class imbalance in the training data. For the classification model, variables are either included or excluded from the model; included variables are indicated with an “x”. For bagging and boosting models, the value indicates the variable’s relative importance in reducing the model loss function, averaged across 500 trees fit for each ensemble model and normalized to sum to 100% for each model. Higher values indicate greater importance in classifying heatwaves. (Table continued on following page.)

		Relative importance in models
Category	Variable	Classification tree	Bagging	Boosting
Absolute intensity	Average of daily Tmean during the heatwave		0.01	<0.01
	Highest daily Tmean during the heatwave		0.01	<0.01
	Lowest daily Tmean during the heatwave		<0.01	<0.01
Relative intensity	Quantile of average daily Tmean		0.01	<0.01
	Quantile of highest daily Tmean	x	64.44	64.60
	Quantile of lowest daily Tmean		0.01	<0.01
Timing	Day of year the heatwave started		0.01	<0.01
	Month the heatwave started	x	34.51	35.26
	Whether the heatwave was the first in its year		0.02	<0.01
Length	Length in days		0.01	<0.01
	Number of days with Tmean > 80°F		0.02	<0.01
	Number of days with Tmean > 85°F		0.01	<0.01
	Number of days with Tmean > 90°F		0.01	<0.01
	Number of days with Tmean > 95°F		0.27	0.12
	Number of days with Tmean > 99th percentile	0.03	<0.01
	Number of days with Tmean > 99.5th percentile	0.01	<0.01
Community population	Community’s population	0.01	<0.01
	Community’s population density	<0.01	<0.01
Community climate	Community’s long-term average Tmean	0.29	0.01
	Community’s long-term average warm season Tmean	0.33	<0.01

For the models that we ultimately identified as useful, we have made R (R Core Team 2015) versions of the models available to other researchers through GitHub (https://github.com/geanders/HyperHeatwavePredictiveModels). We use them ourselves in a companion paper (Anderson et al., submitted) to project the avoided impacts of a more severe climate change scenario compared to a more moderate one, as part of a larger project, Benefits of Reducing Anthropogenic Climate changE (BRACE) (O’Neill and Gettleman in prep.). By making the models available, other researchers can apply them to perform their own projections of high-mortality and moderate heatwaves under future scenarios. We offer some guidelines for the use of these models both in the discussion and in a short tutorial available with the models on GitHub.

2 Materials and Methods

We used present-day weather and health data to build and evaluate predictive models to classify heatwaves as high-mortality or moderate, based on 20 heatwave characteristics. To do so, we:

1. Identified and measured characteristics of all heatwaves in 82 US study communities for 1987–2005 to create a training dataset of heatwaves;

2. Used epidemiologic methods to establish the classification of each heatwave in the training dataset as high-mortality (>20% increase in mortality) or moderate;

3. Used this training dataset to build multiple potential models to classify whether a heatwave is high-mortality or moderate, based on the heatwave’s characteristics; and

4. Evaluated each model to identify three useful models for research projecting future trends in high-mortality and moderate heatwaves.

Step 1. Identify and characterize heatwaves in present-day data to create a training dataset

We identified, characterized, and estimated mortality impacts for present-day heatwaves using an extended version of the National Morbidity, Mortality, and Air Pollution Study dataset, which includes daily measures of temperature and all-cause mortality counts for 108 US communities (each community comprises one or more counties) for 1987–2005 (Samet et al. 2000). We limited our study to communities in the contiguous US with populations >300,000, based on the 2000 US Census. We also excluded Colorado Springs, CO, because this community lacked future projections of urban heatwaves in the climate scenarios used in our companion papers (Anderson et al., submitted; Oleson et al., 2015). Within each community, we averaged daily maximum and minimum temperature to generate daily mean temperature (T_mean). Our final dataset included 19 years of daily temperature, mortality, and population data for 82 communities.

Within this dataset, we identified heatwaves as >2 days with T_mean >98^th percentile of community year-round T_mean (Anderson and Bell 2009; Oleson et al., 2015). For each heatwave, we measured characteristics that could be useful in classification models (Table 1). These included measures of heatwave length (total and how many days exceeded a certain absolute or relative temperature), timing, and temperature—both absolute and relative (i.e., in comparison to a community's long-term temperature distribution). We measured community population size and density (Table 1) using averaged population counts reported by the US Census Bureau over the training data study period (1987–2005).

Step 2. Establish whether each heatwave in the training dataset was high-mortality or less dangerous

For each heatwave in this training dataset, we used epidemiologic methods to determine whether the heatwave was high-mortality or less dangerous. We estimated mortality risk associated with each heatwave using a community-specific generalized linear model with a log link and over-dispersed Poisson distribution, fitting separate indicators for each heatwave. Models included age-specific intercepts and controlled for changes in community mortality rates associated with long-term trends, seasonal trends, and day of week (Anderson and Bell 2011).

Using this model, we estimated the percent increase in mortality for each heatwave in each community. We then pooled effect estimates from all heatwaves using a two-stage Normal hierarchical model (Everson and Morris 2000) and generated posterior effect estimates. This pooling/posterior step addressed the higher variability inherent in heatwave effect estimates from smaller-population communities by shrinking estimates in such communities towards the mean effect estimate. We used the posterior estimates to establish whether each heatwave was high-mortality (>20% increase in mortality) or less dangerous (<20%). A definition of a high-mortality heatwave that used a threshold that was substantially higher than 20% would not have included enough examples of high-mortality heatwaves to build a reasonable predictive model. A threshold that was much lower than 20% would be dominated in the “high-mortality” class by heatwaves very near the threshold cutoff. This would also make a model hard to fit as heatwaves labeled as high-mortality that just exceeded the threshold would be very similar to the heatwaves just below the threshold labeled as moderate. We tested sensitivity of our final predictive models to small changes in the classification threshold, exploring alternative thresholds of 19% and 21%.

Step 3. Build potential predictive models

With this training dataset, we created and tested multiple predictive models, aiming to find models useful in classifying heatwaves as high-mortality or moderate using the characteristics in Table 1.

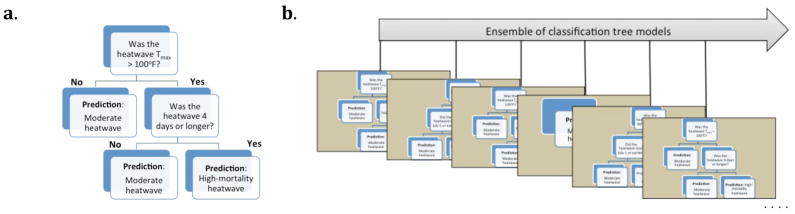
All the models we tested were classification trees or ensembles of classification trees. Classification tree models are structured as decision trees; a hypothetical example of the structure of such a model is shown in Figure 2a. To predict the classification of a specific heatwave from a classification tree model, the model proceeds from the top of the tree structure, using the characteristics of that specific heatwave, until reaching a final tree node with a prediction of either “high-mortality” or “moderate”. For example, for a three-day heatwave with a maximum daily mean temperature of 101°F, the model would follow the right branch of the hypothetical model shown in Figure 2a for the first split and then the left branch for the next split, resulting in a prediction that the heatwave is moderate. Any potential predictive variables that are considered when building the model, but that are not selected for the final model, would not be considered when making predictions.

Figure 2. Hypothetical examples of the structure of (a) a classification tree model and (b) a tree-based ensemble model.

The classification tree model fits and uses a single decision tree to predict heatwave classification, while ensemble-based models fit many different trees and then predict by generating a prediction from each tree and taking the majority vote across all trees in the model.

Some of the models we fit were ensembles of many classification trees (Figure 2b shows a hypothetical example of this structure). These ensemble models fit many different classification tree models, with each tree potentially different, because a different random sample of the data is used when fitting each tree. Ensemble models are generally lower-variance models than single-tree models, because they reduce overfitting to the training dataset by fitting many different trees to randomly drawn subsets of the full training dataset (James et al. 2013). Ensemble models predict by the majority vote across all trees (i.e., “high-mortality” is predicted if more than half of the ensemble trees predict “high-mortality”).

We fit five types of models. The first two were classification trees, which can be built using a variety of methods. Methods differ in how they choose (1) which variables to use to make splits in the tree; (2) at what value of that variable to split; and (3) when to stop splitting. We created our two classification tree models using two methods: deviance-based (referred to as the "classification tree" model throughout this paper) (Ripley 2015) and conditional inference-based ("conditional tree") (Hothorn et al. 2014).

In addition, we fit three ensemble models: a bagging model, a random forests model, and a boosting model. Bagging and random forests methods both bootstrap the training data when fitting each tree in the ensemble. The random forests method, however, limits to a random subset of predictor variables (here we considered six) when selecting a variable for each split (James et al. 2013). The boosting method builds multiple trees in a deterministic way, with results from the previous tree fit used to improve fit of the next tree in the ensemble (James et al. 2013). For model parameters, we selected standard default values (e.g., interaction depth of 4 and shrinkage value of 0.001 for bagging model), since tuning these parameters would require a larger training dataset than was available. We built random forests and bagging models using the randomForest R package (Liaw and Wiener 2014) and the gbm R package (Ridgeway 2013), respectively.

High-mortality heatwaves are rare, so our training dataset was imbalanced, with a very low percentage of high-mortality heatwaves. This imbalance introduces a number of problems when fitting and assessing classification models. In particular, the loss functions, which are used to build classification and ensemble models, perform poorly when there are only a few observations in one of the two classes (Kuhn and Johnson 2013; Lunardon et al. 2014).

To address this class imbalance, we tested models built using three different sampling methods: (1) over-sampling data from the rare class; (2) a combination of over-sampling from the rare class and under-sampling from the common class; and (3) generating synthetic data in the neighborhood of rare samples from the training data (Randomly over-sampling examples [ROSE]) (Lunardon et al. 2014). For all three methods, we used the ROSE R package (Lunardon et al. 2014). All three methods generated datasets as large or larger than the original training dataset, with equal balance between classes of heatwaves; this new dataset was then used to fit each model type.

In total, we built and tested 20 models: five types of models (classification tree, conditional tree, bagging, random forests and boosting), each built using four different adjustments for class imbalance (no adjustment, over-sampling, over- / under-sampling, and ROSE).

Step 4. Assess models to identify several good candidate models for future use

To assess models, we used Monte Carlo cross-validation (100 simulations) (Kuhn and Johnson 2013), with a two-thirds / one-third split into training and testing data. To ensure consistent class proportions across all simulations, we stratified sampling by class (Kuhn 2008).

We used three metrics to assess models: (1) sensitivity, (2) interquartile range of positive predictive value and (3) interquartile range of false omission rate. Sensitivity measures the percentage of high-mortality heatwaves that the model predicts correctly; ideally, a model would classify all or almost all high-mortality heatwaves correctly (i.e., few or no false negatives for the rarer class). Positive predictive value and false omission rate measure percentage of true positives and false negatives the model generates out of all positive and negative predictions, respectively. We ultimately use these rates to adjust estimates of the projected number of high-mortality and moderate heatwaves for the occurrence of false positives and negatives from the model, so we considered a model to be useful only if it had stable estimates of these rates (i.e., small interquartile ranges) across cross-validations.

We chose the best models based on criteria of higher sensitivity and low variability in positive predictive value and false omission rates. We then re-built these best models using the full dataset of heatwaves; the performance of these final models should be as good or better than that estimated via the Monte Carlo cross-validation. We have made all three of these best models available through GitHub for other researchers to use (e.g., for projecting trends in high-mortality and moderate heatwaves under near-term and long-term scenarios of climate change).

3 Results

Our training dataset included six high-mortality heatwaves (0.2% of all training heatwaves) and 2,974 moderate heatwaves (99.8%) in the 82 study communities for 1987—2005 (Figure 1). We tested and evaluated twenty models on this training dataset of heatwaves (Table 2). Models that used ROSE to adjust for class imbalance had the highest sensitivity (percent of high-mortality heatwaves correctly classified by the model). Among models with high sensitivity, three had small interquartile ranges for positive predictive value across simulations: the classification tree model, the bagging model, and the boosting model (highlighted in bold in Table 2). All models had low false omission rates and interquartile ranges, likely because high-mortality heatwaves are so rare. Based on our selection criteria of high sensitivity and low variability in positive predictive value and false omission rates, we therefore selected the three models highlighted in Table 2 to use for projections and re-built them using the complete dataset.

Table 2.

Evaluations of the twenty potential predictive models built using health and weather data from heat waves in 82 US communities, 1987–2005. Sensitivity: % of high-mortality heatwaves correctly identified; positive predictive value: % of heatwaves predicted as high-mortality heatwaves that really are; false omission rate: % of heat waves predicted as less dangerous that are really high-mortality. Also shown are precision and false omission rate inter-quartile ranges (IQR). The three best models based on this evaluation are shown in bold.

Model	Sensitivity (%)	Positive predictive value (%)	Positive predictive value IQR	False omission rate (%)	False omission rate IQR
No adjustment
Classification tree	18.5	29.3	50	0.2	0.1
Conditional tree	<0.1	--	--	0.2	<0.1
Bagging	2.0	12.9	<0.1	0.2	<0.1
Random forest	<0.1	<0.1	<0.1	0.2	<0.1
Boosting	50.0	0.2	<0.1	0.2	<0.1
Oversampling
Classification tree	31.0	23.0	33.3	0.1	0.1
Conditional tree	29.0	14.7	25.0	0.1	0.1
Bagging	14.0	22.5	50.0	0.2	0.1
Random forest	12.5	30.7	50.0	0.2	<0.1
Boosting	53.5	14.2	13.8	0.1	0.1
Over / under sampling
Classification tree	44.0	22.3	33.3	0.1	0.1
Conditional tree	33.5	13.3	20.0	0.1	0.1
Bagging	29.5	22.6	33.3	0.1	0.1
Random forest	21.0	33.0	50.0	0.2	0.1
Boosting	59.5	11.5	7.2	0.1	0.1
ROSE
Classification tree	94.0	2.6	0.7	<0.1	<0.1
Conditional tree	87.5	7.2	4.5	<0.1	<0.1
Bagging	94.0	2.6	0.6	<0.1	<0.1
Random forest	94.0	4.1	2.0	<0.1	<0.1
Boosting	94.0	2.3	0.5	<0.1	<0.1

These three models were similar in terms of which predictive variables were important (Table 1). The most important variable in all models was a measure of relative intensity: the quantile of the highest daily T_mean during the heatwave relative to the distribution of T_mean in the community. Another fairly important variable was the month in which the heatwave started. Other variables were minimally important in predicting whether a heatwave was a high-mortality heatwaves. We tested sensitivity of the results to the threshold for defining high-mortality heatwaves. Changing the threshold to >21% mortality increase did not change which heatwaves were identified as high-mortality in the training dataset and so had no effect on model building. When we set the threshold to 19%, two additional heatwaves were classified as high-mortality in the training dataset: 1988 heatwaves in Detroit, MI, and Rochester, NY. Under this new threshold, the same model types (classification tree, bagging, and boosting, all built using ROSE) performed best and so were selected, although all three models had lower sensitivity (72.5%, 73%, and 73%, respectively, for the classification tree, bagging, and boosting model) than the models defined using a 20% or 21% threshold. The models fit using the 19% threshold varied somewhat from the main models in terms of which variables were most important. For models fit using the 19% threshold, two variables–those characterizing (1) the number of days in the heatwave >95°F and (2) the quantile of the average T_mean during the heatwave–were much more important than in the original models. Another variable, the quantile of the highest T_mean during the heatwave, was somewhat less important than in the main models, and the month in which the heatwave started became much less important. These models, built with an alternative threshold to identify high-mortality heatwaves, can be used when exploring projections from the main models, to test sensitivity to this modeling choice of the threshold for high-mortality heatwaves. They are included on GitHub.

4 Discussion

Here we built classification models to predict if a United States heatwave is likely high-mortality or moderate, using a training dataset of heatwaves created from present-day health and weather data. Using Monte Carlo cross-validation, we found three suitable models (Table 2), all with high sensitivity (successful identification of high-mortality heatwaves) and stable positive predictive value and false omission rates over Monte Carlo cross-validations. These three models can be combined with climate projections to project how often high-mortality and moderate heatwaves are expected under near- and long-term scenarios of climate change. Further, they allow incorporation of different scenarios of adaptation to heat, as explained later in this section. All three models had high false positive rates; we address later in this section how projections using these models should be adjusted to account for this.

Interpreting the models

The predictive models developed here were dominated by a measure of relative intensity: the quantile of maximum daily mean temperature during the heatwave compared to the distribution of year-round mean temperatures in the community (Table 1). Online Resource Figure 1 shows the differences between high-mortality and moderate heatwaves in the training data for distributions of both this relative metric (Online Resource Figure 1a) and its absolute analogue (the heatwave’s maximum daily mean temperature; Online Resource Figure 1b). While high-mortality heatwaves tended to have notably high relative temperatures, they were not as unusual in terms of absolute temperature. This finding resonates with trends identified in heat-health epidemiology: heat effects depend on how extreme temperature is relative to community climate (Anderson and Bell 2009; Curriero et al. 2002). Further, the most devastating recent heatwaves in the US have occurred not in locations with extremely hot summer climates, like Arizona or Texas, but instead in milder locations like Illinois (Whitman et al. 1997), Pennsylvania (Wainwright et al. 1999), and California (Knowlton et al. 2009).

The model-fitting procedure also identified another variable as a useful predictor: the month in which the heatwave started. For example, the classification tree built with ROSE predicts a heatwave to be high-mortality only if it starts in July. The ensemble models (bagging and boosting) are not as restrictive, but also place a fairly high importance on heatwave starting month. Due to these concerns that models might be overfitting to the heatwave starting month (more discussion is included in the Online Resource), we specified a fourth, custom model—a simplified classification tree, based on the classification tree fit to our training data, but with starting month removed from the tree’s structure. We have included R code for this simplified custom model on GitHub. We include this model to be used to explore uncertainty across models, rather than as a primary model to be used in preference to the main models.

Most characteristics were not identified as useful predictors. For example, although epidemiologic studies have found that the health risks of heatwaves can be larger for heatwaves that last longer or occur earlier in the summer (e.g., Anderson and Bell 2011), the models selected here do not predict heatwaves with these characteristics as more likely to be high-mortality. This discrepancy may suggest that the defining features of high-mortality heatwaves differ from the characteristics that modify the risks associated moderate heatwaves, which are much more common and so would have dominated analysis of trends in the health risks associated with all heatwaves in present-day studies.

Although heatwave length and population size were not useful predictors of whether a heatwave was high-mortality or moderate, these characteristics will influence how many deaths occur during a high-mortality heatwave. Heat wave death tolls are the product of the increased mortality risk associated with the heat wave, the number of days that risk persists, and the baseline daily mortality count in the community, which is correlated with the size of the population exposed to the risk.

All the main models had a low positive predictive value, so although they found characteristics that were shared by all examples of high-mortality heatwaves (e.g., maximum daily mean temperature at or above the community’s 99.89^th percentile temperature in the classification tree model), there were many moderate heatwaves with the same meteorological characteristics that turned out to not have the same high impacts per day. It would be interesting in future research to explore what other characteristics, including community characteristics like age structure and poverty levels, as well as concurrent exposures like air pollution, help explain heatwaves with these extreme meteorological characteristics are high-mortality and which are moderate.

Applying the models

The models developed here can be used to project frequency of and exposure to high-mortality and moderate heatwaves under future scenarios. Each predictive model, when applied to a time series of heatwaves identified and characterized under a future scenario, will predict for each heatwave a classification of high-mortality or moderate. These heatwave-specific predictions can be added across all heatwaves in the time series to give the total number of heatwaves predicted to be high-mortality (H_ph) and the total number of heatwaves predicted to be moderate (H_pm). These values must be adjusted for the model’s rates of false positives and false omissions. The total number of high-mortality heatwaves in the time series (H_h) is the sum of high-mortality heatwaves correctly predicted and of heatwaves incorrectly predicted to be less dangerous, which can by estimated as:

$$H_h=P\ast H_{ph}+F\ast H_{pm}$$

where P is model positive predictive value and F is model false omission rate, both estimated from Monte Carlo cross-validation analysis of each model (Table 2). Similarly, the number of moderate heatwaves in a time series (H_m) can be estimated from model results as:

$$H_m=(1-P)H_{ph}+(1-F)H_{pm}$$

Person-days of exposure to high-mortality heatwaves (E_h) and moderate heatwaves (E_m) can be estimated using:

$$\begin{array}{c}{E}_h=P\sum _i(D_i{N}_{c,i})+F\sum _j(D_j{N}_{c,j})\\ E_m=(1-P)\sum _i(D_i{N}_{c,i})+(1-F)\sum _j(D_j{N}_{c,j})\end{array}$$

where P is model positive predictive value, i is a heatwave classified as a high-mortality heatwave, with the first summation summing over all high-mortality heatwaves, D_i is the length of heatwave i in days, N_c,i is the population of the community, c, in which heatwave i occurred, F is model false omission rate, j is a heatwave classified as a less dangerous heatwave, with the second summation summing over all less dangerous heatwaves, D_j is the length of heatwave j in days, and N_c,j is the population of the community, c, in which heatwave j occurred. An example of this process is given in the GitHub tutorial.

Applying these models to other heatwave time series assumes that the heatwaves in our training dataset are reasonably representative of heatwaves in the projected time series, both in terms of how the characteristics included in the model are related to heatwave classification and in terms of the distribution of characteristics not included in the model that might help explain whether a heatwave is high-mortality or moderate (e.g., age structure of the population). This model assumption is likely to be reasonable in the study communities for near-term projections (e.g., estimating a community’s expected exposure to high-mortality and moderate heatwaves in the next ten years), but may affect model performance when projecting heatwave classifications further into the future. If health and weather data could be collected over a longer time range, future work could explore the stability of models like those developed here when projecting over long time periods.

Exploring adaptation scenarios

Because these models include measures of relative temperature as predictions, they can be used to explore basic scenarios of adaptation for future projections. One critical question when projecting the future health impacts of heat is whether the same absolute temperature will bring the same health risk as that temperature becomes more common in a community. A few studies have explored adaptation scenarios when projecting future heat risks. Some have used temperature-mortality curves from analog cities (e.g., Kalkstein and Greene 1997; Knowlton et al. 2007), where analog cities are selected based on currently having a climate similar to the study city’s expected future climate. Others have assumed all communities will adapt to a certain absolute increase in temperature—all communities will react to, for example, 100°F in the future as they currently do to 97°F (e.g., Gosling et al. 2009).

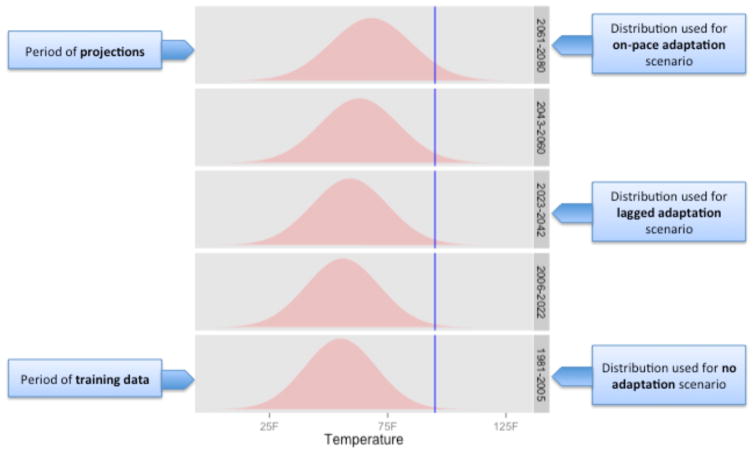
Here, our models include heatwave characteristics that are measured relative to the community’s normal temperature distribution, so scenarios of adaptation can be explored by changing the temperature distribution used to convert the absolute temperature of a heatwave into this relative value (illustrated in Figure 3). The models we create here can project health impacts under different adaptation scenarios by using the temperature distributions within a community at some lag prior to the projection period. This approach addresses this evolutionary nature of adaptation, since adaptation will likely depend on the pathway and pace with which climate changes in each community.

Figure 3. Illustration of adaptation scenario methodology.

This figure shows the changing temperature distributions for a hypothetical community between present-day (1981–2005) and an example future period (2061–2080) to be used in projections of climate change impacts. Temperature distributions (both mean and variance) may change with climate change; these different distributions can be modeled under different ensemble members of climate change scenarios for different time periods, as shown here. The blue line shows a hypothetical absolute measure of temperature for a heat wave (e.g., highest T_mean during the heat wave). To convert this absolute measure to a relative measure, the absolute value must be compared to a temperature distribution. Under the “no adaptation” scenario, the absolute temperature would be compared to the 1981–2005 temperature distribution; under the “lagged” scenario, to the 2023–2042 distribution; and under the “on-pace” scenario, to the 2061–2080 distribution. The same absolute temperature (e.g., 95°F) will therefore translate into a lower relative measure under the “on-pace” scenario (e.g., 90^th percentile) than under the “no adaptation” scenario (e.g., 99.5^th percentile).

Exploring variation introduced by model uncertainty

We explore and address model uncertainty in two ways. First, we evaluate and select models using Monte Carlo cross-validation. Of studies projecting the health impacts of future heat, only a few have used a similar validation approach to build, evaluate, and select models to use to project future impacts of heat on health (e.g., Gosling et al. 2007; Peng et al. 2011). Second, by developing and sharing multiple reasonable models, we allow researchers using these models to explore uncertainty from model choice in projections of high-mortality heatwaves. As part of this, we developed a simplified custom model in case the models developed here overfitted to unhelpful characteristics correlated with the heatwaves’ regional weather system (e.g., starting month), as well as models that used a slightly different threshold choice for identifying high-mortality heatwaves (19% increase in mortality; we also explored a 21% threshold, which generated identical models as the 20% threshold). If projections are sensitive to which of the models is used, we would expect large differences in projections across the predictive models for a given scenario. All these models are available, for this purpose, on GitHub.

Future extensions of this work

The models developed here project trends only in heatwaves of two or more days. Heat will likely cause deaths and other health impacts on single days of extreme heat; the models developed here aim to identify the most severe heatwaves, but would not identify all heat exposures that could impact health under future scenarios. Future work could explore building models based on ensembles of regression trees, with the aim of predicting relative risk of mortality on extremely hot days rather than the simpler metric of classification as high-mortality or moderate. A key challenge in this model development will be determining how to appropriately account for uncertainty in the initial estimates of excess heat-related deaths for each day in the training dataset.

Here, we created models that performed well in the metrics we chose to reflect the needs of predictive models of the frequency of and exposure to high-mortality and moderate heatwaves. However, there are other applications of predictive models of heatwaves, particularly high-mortality heatwaves, including for creating or improving community heatwave warning systems. These applications would prioritize different metrics. For example, for a community warning system, it would be critical to limit the number of false positives—if a community gives 30 false alarms for every one heatwave that truly is high-mortality, people are likely to disregard all such alarms.

There are other model building strategies that might be useful for building models with these goals. For example, predictive models can be tuned on parameters like interaction depth (Kuhn 2008; James et al. 2013). We were able to build satisfactory models for our purposes without extensive model tuning; it may be possible to build models with, for example, lower false positive rates through tuning, although it would require more extensive training data than was available here.

Further, there are likely many other factors that may help explain whether a heat wave is high-mortality or moderate, including measures of concurrent ambient exposures (e.g., humidity, wind speed, air pollution), community characteristics (e.g., poverty, age structure, access to air conditioning), and other concurrent risk factors (e.g., whether a power outage occurred during a heatwave). A model that includes these additional factors would introduce additional uncertainty in projections, because there would be some uncertainty in projecting each of these separate factors for future heatwaves. Because of this added uncertainty, a model with fewer predictive variables might prove more useful for longer-term projections, but in situations where these added factors could be forecast with less uncertainty (e.g., short-term heatwave warnings, nearer-term projections), added factors could prove helpful in predicting whether a heatwave is likely to be high-mortality or moderate.