Rapid global spread of wRi-like Wolbachia across multiple Drosophila

SUMMARY

Maternally transmitted Wolbachia, Spiroplasma and Cardinium bacteria are common in insects [1], but their interspecific spread is poorly understood. Endosymbionts can spread rapidly within host species by manipulating host reproduction, as typified by the global spread of wRi Wolbachia observed in Drosophila simulans [2, 3]. However, because Wolbachia cannot survive outside host cells, spread between distantly related host species requires horizontal transfers that are presumably rare [4–7]. Here we document spread of wRi-like Wolbachia among eight highly diverged Drosophila hosts (10–50 million years) over only about 14,000 years (5,000–27,000). Comparing 110 wRi-like genomes, we find 0.02% divergence from the wRi variant that spread rapidly through California populations of D. simulans. The hosts include both globally invasive species, D. simulans, D. suzukii and D. ananassae, and narrowly distributed Australian endemics, D. anomalata and D. pandora [8]. Phylogenetic analyses that include mtDNA genomes indicate introgressive transfer of wRi-like Wolbachia between closely related species D. ananassae, D. anomalata and D. pandora, but no horizontal transmission within species. Our analyses suggest D. ananassae as the Wolbachia source for the recent wRi invasion of D. simulans, and D. suzukii as the source of Wolbachia in its sister species D. subpulchrella. Although six of these wRi-like variants cause strong cytoplasmic incompatibility, two cause no detectable reproductive effects, indicating that pervasive mutualistic effects [9, 10] complement the reproductive manipulations for which Wolbachia are best known. “Super spreader” variants like wRi may be particularly useful for controlling insect pests and vector-borne diseases with Wolbachia transinfections [11].

Blurb

Turelli et al. document rapid spread of very similar strains of the endosymbiotic bacterium, Wolbachia, across eight Drosophila host species. Whole Wolbachia genomes indicate that the strains diverged less than 30,000 years ago, yet spread through Drosophila hosts that diverged 10–50 million years ago via horizontal transmission and introgression.

RESULTS

Wolbachia can spread rapidly within and among conspecific populations, aided by reproductive manipulations like cytoplasmic incompatibility [CI, 12], which causes embryo mortality when uninfected females mate with infected males, and through mutualistic effects such as increasing fecundity [13], protecting from parasitic microbes [9] and nutrient provisioning [10]. Interspecific horizontal Wolbachia transmission occurs [4–7] but is expected to be quite rare because Wolbachia are obligately intracellular. Within host species, there is typically concordance between mitochondrial and Wolbachia lineages, as expected with maternal transmission [14, 15].

Host species can acquire Wolbachia in three ways: cladogenically, with sister species inheriting Wolbachia during speciation [16, 17]; by hybridization and introgression from a closely related host species [16, 18]; or by horizontal transmission [4–7]. Determining the relative frequency of these alternative scenarios requires analyzing sequence data from Wolbachia and nuclear and mitochondrial genomes of closely related host species, especially sister species [16, 19, 20].

To quantify patterns of Wolbachia acquisition and coevolution with hosts, we have surveyed the melanogaster, montium, ananassae, takahashii and suzukii subgroups of the melanogaster species group of Drosophila, which includes about 190 identified species [21]. From 29 infected species, we discovered that 8 harbor Wolbachia very similar to wRi [22], first identified in a Riverside, California population of D. simulans [23].

Recent Horizontal Transmission

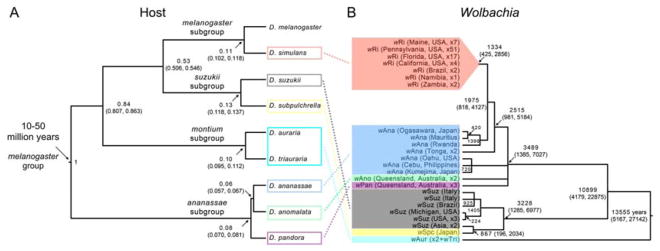
Discordance between the ages of the most recent common ancestor (MRCA) of 8 Drosophila host species [which diverged 10–50 million years ago, 24, Figure 1A] and the MRCA of 110 wRi-like Wolbachia genomes (~5,000–27,000 years ago, Figure 1B) indicates that these Wolbachia-host associations arose recently, mainly by horizontal transmission and introgression. The inferred time scale of Wolbachia divergence is an order of magnitude faster than Drosophila speciation [25], indicating that at most one of these Wolbachia was acquired cladogenically. This conclusion is robust to uncertainty concerning the rate of Wolbachia molecular evolution [20], which has been estimated by comparing rates of Wolbachia and mitochondrial co-divergence within D. melanogaster [15] and co-divergence of Wolbachia and nuclear genomes between species of Nasonia wasps [16] and Nomada bees [17] with cladogenic Wolbachia acquisition.

Figure 1. Hosts and their wRi-like Wolbachia.

(A) Bayesian chronogram with relative age estimates (medians and 95% credible intervals) of nodes in the phylogeny for the eight focal Drosophila host species, which span the melanogaster species group, plus D. melanogaster. The estimated age of the melanogaster species group (i.e., the age of the root node) is from [24]. (B) Bayesian chronogram with absolute age estimates (medians and 95% credible intervals) for 110 wRi-like Wolbachia genomes, based on a calibration of rates of Wolbachia divergence from [15]. The chronogram was estimated using complete sequences of 525 single-copy loci present in full length in all 109 draft genomes (506,307 bp), plus the wRi reference. Node ages (see Table S5) are provided only for nodes with posterior probabilities > 0.95 (we collapse nodes with lower probabilities into polytomies). The clade with an inferred age 3489 years (and 95% credible interval (1385, 7027)) includes all of the wRi-like sequences from D. simulans (wRi), D. ananassae (wAna), D. anomalata (wAno) and D. pandora (wPan). Its sister clade has an estimated age of 3228 (1285, 6977) years and includes only the Wolbachia from D. suzukii (wSuz) and D. subpulchrella (wSpc). The wRi sequences occur in a clade that includes eight diverse wAna, consistent with D. ananassae as the source for wRi in D. simulans. These data do not resolve the relationships among the wRi-like Wolbachia in the three ananassae subgroup species, D. ananassae, D. anomalata and D. pandora. The wSpc sequence from D. subpulchrella is nested within the wSuz sequences from its sister species, D. suzukii, suggesting horizontal Wolbachia transfer or introgression from Asian D. suzukii to D. subpulchrella. Our posterior estimate of the MRCA age for these 110 wRi-like variants is approximately 14,000 years, with 95% credible interval (5,000–27,000) years. See also Table S1.

At least two host species surveyed—D. simulans and D. pandora—harbor more than one Wolbachia strain [18, 26], and D. ananassae has both cytoplasmic Wolbachia and (partial) Wolbachia genomes integrated into its nuclear genome [27, 28]. Our analyses consider only cytoplasmic wRi-like Wolbachia, which we generally denote using the first three letters of the host species name [analogous to wMel, the Wolbachia in D. melanogaster, 29]. Strikingly, our most distantly related hosts, D. simulans and D. ananassae [far too divergent to produce fertile hybrids, 30], share sister wRi-like variants (Figure 1B), confirming horizontal transmission. The wRi from D. simulans are nested within paraphyletic wAna variants, suggesting D. ananassae as the donor of wRi [28], possibly through an intermediate host [5]. Although D. simulans evolved in Africa while D. ananassae originated in southeast Asia, these human commensals have probably co-occurred for many hundreds of years [30], consistent with the estimated MRCA age for wRi in D. simulans (Figure 1B). The three closely related ananassae subgroup species—D. ananassae, D. anomalata and D. pandora—harbor very similar Wolbachia—denoted wAna, wAno and wPan, respectively—whose phylogeny is unresolved. Our wAno and wPan data suggest that each is monophyletic, reflecting a single acquisition of wRi-like Wolbachia by each host. Joint analysis of mitochondrial and Wolbachia genomes below (Figure 2) suggests that introgression underlies the similarity of wAna, wAno and wPan.

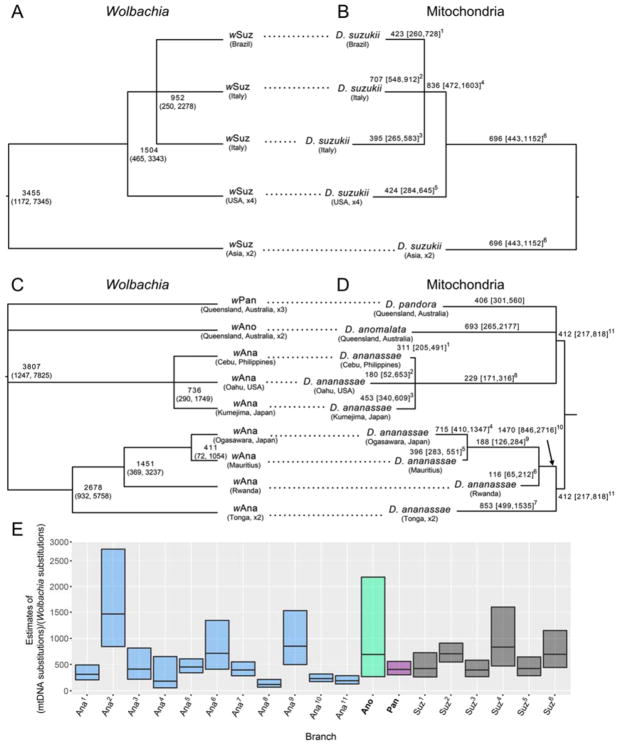
Figure 2. Wolbachia and corresponding mtDNA.

Wolbachia and corresponding mtDNA from infected D. suzukii and three ananassae subgroup species, D. ananassae, D. anomalata and D. pandora. (A) A Bayesian chronogram for wSuz with estimated node ages (medians and 95% credible intervals). Nodes with posterior probabilities less than 0.95 are collapsed into polytomies. The chronogram repeats a portion of Figure 1B. (B) A Bayesian phylogram, with branch lengths rendered proportional to average substitution rate, based on the protein-coding mtDNA from the isofemale lines that produced the wSuz sequences. For all nodes that can be confidently resolved, the phylogram is topologically identical to the corresponding chronogram, as expected with maternal transmission. Branches are labeled with the median of the posterior distribution of ratios of the substitution rates of mtDNA versus Wolbachia along the branch. (C) A Bayesian chronogram for our wAna, wAno and wPan genomes with estimated node ages and 95% credible intervals. Nodes with posterior probabilities less than 0.95 were collapsed into polytomies. This repeats a portion of Figure 1B. (D) A Bayesian phylogram based on the protein-coding mtDNA from the isofemale lines that produced the wAna, wAno and wPan sequences. The phylogram is topologically identical to the corresponding chronogram. As in (B), the branches are labeled with the posterior-median ratios of the substitution rates for mtDNA versus Wolbachia divergence along each branch. The fact that the branches leading to wPan and wAno do not show atypically large substitution-rate ratios is consistent with introgression of Wolbachia among the three ananassae subgroup species. (E) Medians and upper and lower quartiles of the posterior distributions for the substitution-rate ratios of mtDNA to Wolbachia along each branch in panels B and D. The superscripts in the branch labels correspond to the superscripts that appear in the interquartile range limits in (B) and (D). These estimates are based on specific resolutions of the polytomies. Table S7 shows that all possible resolutions of the polytomies produce comparable results. See also Tables S1 and S6.

The single wSpc sample from D. subpulchrella, which co-occurs with its sister species, D. suzukii, in China and Japan, falls within a well-supported clade of Asian wSuz haplotypes from D. suzukii, a recent cosmopolitan invader [20]. Based on a single wSuz haplotype—from the recent European invasion by D. suzukii—the divergence of wSuz and wSpc was estimated at 1000–9000 years ago [20]. Our more extensive sampling suggests that this wSpc haplotype diverged from Asian wSuz only 150–1700 years ago.

No Evidence for Non-maternal Transmission within Species

Discordance between intraspecific phylogenies for Wolbachia and host mtDNA can arise from rare paternal transmission of either mtDNA or Wolbachia [14] or non-sexual horizontal Wolbachia transmission. In contrast to the clear discordance of mtDNA and Wolbachia phylogenies found with limited molecular data in spiders [5] and wasps [7], no evidence of mtDNA-Wolbachia discordance was found using full genomes for 91 wMel-infected D. melanogaster [15]. Similarly, among the nodes that could be confidently resolved, we found no evidence of non-maternal transmission among 84 wRi-infected D. simulans [consistent with an independent sample of 161 lines and earlier analyses in California; 14, 31], 9 wSuz-infected D. suzukii (Figure 2A, B), and 8 D. ananassae with cytoplasmic wAna (Figure 2C, D). Maternal transmission in these species allows us to estimate relative substitution rates for Wolbachia and host mtDNA.

Introgression versus Horizontal Transmission between Closely Related Species

Closely related species that co-occur in nature and produce fertile female hybrids—such as the closest relatives in Figure 1A—can harbor very similar Wolbachia because of either horizontal transmission or introgression. These alternatives can in principle be distinguished by comparing Wolbachia and host mtDNA divergence times. Specifically, divergence times should coincide if Wolbachia are transferred via introgression; whereas horizontal transmission will produce more recent Wolbachia than mtDNA divergence. We qualitatively test this by estimating the relative substitution rates of Wolbachia versus mtDNA. Our informal approach first estimates relative rates of co-divergence within geographically widespread D. suzukii, then considers relative substitution rates of Wolbachia versus mtDNA across all three ananassae subgroup species.

The topologies of the wSuz and D. suzukii mtDNA phylogenies are congruent (Figure 2), as expected under joint maternal transmission. Moreover, the ratio of mtDNA to Wolbachia substitutions does not vary significantly across lineages (Figure 2B; Table S6). The median ratio of mtDNA substitutions to Wolbachia substitutions is 566 (first, third quartiles: 467, 706). Similarly, there is no topological discordance between the phylogenies of the three Wolbachia variants (wAna, wAno and wPan) and the associated mtDNA (Figure 2C). In this case, however, the ratio of mtDNA to Wolbachia substitutions varies markedly across lineages (Figure 2D, 2E; Table S6). For the ananassae subgroup species, overall median ratio of mtDNA substitutions to Wolbachia substitutions is 406. Although somewhat lower that observed within D. suzukii, the substitution ratios across branches in Figure 2B versus 2D are not significantly different (Mann Whitney, P > 0.2). Notably, the estimated ratios along the branches leading to D. pandora and D. anomalata (406 and 693, respectively) are not particularly large, but consistent with intraspecific estimates for both D. ananassae and D. suzukii (Figure 2E, Table S7), as expected under introgression. Our qualitative assessment cannot definitively exclude horizontal transmission within D. ananassae or among the three ananassae subgroup species; but with so few tips, co-divergence cannot be rigorously assessed without unsubstantiated assumptions about clock-like evolution for both mtDNA and Wolbachia (Methods).

Similarly, our data from two D. auraria strains and one D. triauraria cannot distinguish introgression from non-sexual horizontal transmission. Although the two wAur genomes are identical with one wTri over 506,307 bp, they are differentiated from wTri by a deletion that includes copies of two CI loci (Table 2). By contrast, mtDNA protein-coding genes from one D. auraria strain differ from the D. triauraria strain by only 4 bp (out of 11,178), whereas the D. auraria strains differ by 14 bp from each other. Unlike these mixed signals from Wolbachia and mtDNA, analyses of 20 nuclear loci clearly indicate that the two host D. auraria strains are conspecifics relative to D. triauraria (Methods).

Table 2. Differences among the CI Loci in wRi-like Wolbachia.

^a.

See also Table S2.

Locus (amino acid position)	wRi Codon (translation)	Alternative Codon (translation)	wRi Variants Affected b
WD0631c
28	ACT (Thr)	GCT (Ala)	wAur, wTri
216	AAG (Lys)	GAG (Glu)	wAur, wTri
363	AAA (Lys)	GAA (Glu)	wAur, wTri, wSuz, wSpc
473	AAA (Lys)	AGA (Arg)	wAur, wTri, wPan, wAna, wSuz, wSpc
WD0632 c
2	TCT (Ser)	CCT (Pro)	wPan
91	GGA (Gly)	GGG (Gly)	wSuz, wSpc
176	TAT (Tyr)	GAT (Asp)	wSuz, wSpc
213	TGA (STOP)	CGA (Arg)	wAno, wAur, wTri, wPan, wSuz, wSpc, wAna [Cebu, HNL0501, KMJ1 only]
905	CGA (Arg)	TGA (STOP)	wAna [Cebu, HNL0501, KMJ1 only]
1118	TTA (Leu)	TGA (STOP)	wSpc
WRi_006710 d
663	TAT (Tyr)	CAT (His)	wSuz, wSpc
WRi_006720 d
No SNVs

^aAdditional copy-number differences are reported for wSuz and wSpc in [20].

^bUnless otherwise noted, the single-nucleotide variants (SNVs) apply to all sequences examined in the host species.

^cTwo copies exist in the wRi reference, one copy each of WD0631 and WD0632 was lost in wAur, two copies each of WD0631 and WD0632 were gained in wAna_HNL0501.

^dMissing in wAur, wTri.

Low Wolbachia and mtDNA Variation in wRi-infected D. simulans

Table 1 shows conservative estimates of intraspecific variation (π, average pairwise difference per bp) for wSuz and wRi based on 525 Wolbachia genes with one-to-one homology across all 110 wRi-like draft genomes and 11 protein-coding mtDNA loci. For cytoplasmic wAna, we estimate π over the same 525 loci, then over larger stretches of the (more complete) wAna [28] and wMel [15] genomes. The nucleotide variation of wSuz is comparable to variation of cytoplasmic wAna and wMel in D. melanogaster. By contrast, wRi shows much lower variation (Table 1), consistent with the shorter residence time of wRi in D. simulans (Figure 1B).

Table 1. Variation of Wolbachia and mitochondrial genomes within host species.

We consider only individuals with cytoplasmic wRi-like infections. We compare the wRi-like infections to wMel from D. melanogaster. See also Table S1.

Wolbachia	N	L	π (Wolbachia)	L	π (mtDNA)
wRi	84	506,307	1.42×10−6	11,184	1.12×10−4
wSuz	9	506,307	2.07×10−5	11,178	5.31×10−3
wAnaa	8	506,307	3.48×10−5	11,184	4.06×10−3
wAnab	8	1,194,063	3.65×10−5	14,904	3.02×10−3
wMelc	91	1,209,286	1.06×10−5	14,492	5.34×10−4

N is the number of strains, L is the number of nucleotides analyzed, π is the average number of pairwise nucleotide differences per site.

^aData from [28] analyzed for only the 525 reference Wolbachia loci used in Figures 1 and 2 and only the mtDNA protein-coding data used in Figure 2.

^bData from [28].

^cData from [15].

Not All wRi-like Wolbachia Cause Cytoplasmic Incompatibility

Wolbachia can rapidly spread and reach high frequencies through CI [2]. But some strains that cause no detectable CI or other reproductive manipulations [32] still reach appreciable frequencies, presumably through mutualistic effects [3]. No reproductive manipulation has been associated with wSuz or wSpc [19, 33] despite their close affinity to wRi, so their frequencies are expected to depend on local Wolbachia fitness effects and maternal transmission fidelity [12, 34]. These infections occur at variable but intermediate frequencies in populations around the globe [19, 33, Table S3], as does wMel, which causes little CI in nature [29, 35]. By contrast, wAno and wTri cause intense CI in their native hosts (Table S4), comparable to wRi [23], wPan [26], wAur and wAna [36]. As expected at equilibrium under strong CI and high maternal transmission fidelity [29], wAno and wAur are at high frequencies in populations (>90%, Table S3), consistent with population data on wRi [3, 14], wAna [28] and wPan [26]. Strong versus weak CI may be caused by host or Wolbachia [12], motivating an analysis of molecular evolution at Wolbachia loci causing CI.

Evolution at CI Loci

Loci WD0631 and WD0632 in Wolbachia wMel cause CI [37–39]. In wRi, there are two paralogs of both WD0631 and WD0632, with identical WD0631-32 pairs contained in the two copies of prophage WO [37]. Two paralogs in wRi, WRi_006710 and WRi_006720, are outside WO. Table 2 presents single-nucleotide and copy-number differences at these loci across the eight wRi-like variants. Orthologs of WD0631-32 and WRi_006710-20 were found in all variants except wAur and wTri, which lack WRi_006710-20. This difference supports the sister relationship of wAur and wTri (Figure 1).

Because the CI loci (and phage WO) varied in copy number across the wRi-like variants, they were excluded from the 525 one-to-one homologs used for our phylogenetic analyses. In the wRi annotation [22], the WD0632 orthologs are marked as pseudogenes because of a premature stop codon (position 213). This is shared only with the five wAna lines that form a clade with wRi (Figure 1B), supporting our inference that wRi was introduced into D. simulans horizontally from D. ananassae. In the other three wAna variants, the stop codon is at position 905. By contrast, the analogous stop codon in wAno, wAur, wPan, wSpc, wSuz and wTri is at position 1174; this is presumably the ancestral condition given that it occurs in outgroups wMel and wPip [37].

The orthologs to WD0631 and WD0632 are enriched for single-nucleotide variants (SNVs), with 4 and 6 variable sites out of 1425 (0.28%) and 3522 bp (0.17%), respectively; whereas only 239 sites vary among the 110 wRi-like genomes across our 525 reference loci (506,307 bp, 0.05%). This difference is statistically significant (Fisher exact: P < 0.001). By contrast, variation at the orthologs to WRi_006710-20, with 1 and 0 SNVs respectively out of 2265 (0.04%) and 1371 bp, is consistent with our reference loci (P > 0.5). Overall, 349 of our 525 reference loci have 0 SNVs; whereas only 14/525 (2.7%) have more variation per site than WD0631 and 42/525 (8%) have more than WD0632 (Methods). Notably 3 of the 11 variable sites in the CI loci involve stop codons.

DISCUSSION

The radical discordance between the 110 wRi-like Wolbachia (MRCA about 5,000–27,000 thousand years ago, ≤0.02% sequence divergence) and their 8 host species (MRCA 10–50 million years ago, up to 12.34% divergence for 20 nuclear loci), indicates that many Wolbachia infections are relatively young. By contrast, in three systems with maternal/cladogenic Wolbachia acquisition—within D. melanogaster [15] and between species of Nasonia wasps [16] and Nomada bees [17]—Wolbachia genomes diverge at most two orders of magnitude more slowly than host nuclear genomes [20]. We document both horizontal transmission—as in the apparent acquisition of wRi by D. simulans from its distant relative D. ananassae—and plausible transfer via recent introgression, as with the three D. ananassae subgroup species. The recent acquisition of at least seven of these eight infections suggests that Wolbachia often displace each other, as observed with wRi displacing wAu in Australian D. simulans over the past 25 years [3].

Among Drosophila, hybridization is common during speciation [25] and introgression often occurs [40], facilitating Wolbachia transfer. By contrast, horizontal transmission remains mysterious, but parasitoids and mites are plausible vectors [5–7, 41]. The fact that Wolbachia have not been detected in about half of the melanogaster group species, despite co-occurrence with infected cosmopolitan species, such as D. simulans, D. ananassae, and D. melanogaster, suggests that successful horizontal transmission is rare, consistent with its apparent rarity within these species.

The strong CI observed in six hosts and no/low CI in two other hosts raises questions about the timescale and repeatability of Wolbachia-host coevolution. Hosts are selected to suppress CI [42]. D. melanogaster suppresses CI effects of both native wMel and transinfected wRi, whereas D. simulans shows high CI with both variants [43], which may reflect the greater age of the wMel-melanogaster association. The timescale and repeatability of Wolbachia-host coevolution, and the relative roles of host versus Wolbachia evolution, can be investigated using reciprocal transinfections of wRi-like variants.

Recent data suggest that natural Wolbachia infections are often intrinsically advantageous and tend to spread from arbitrarily low initial frequencies [3, 29, 34]. By contrast, Wolbachia transinfections from Drosophila into the disease-vector mosquito Aedes aegypti are deleterious to their new hosts. These transinfections tend to spread only once they become sufficiently common that their frequency-dependent advantage from CI overwhelms their deleterious effects. Release areas needed to establish spreading transinfections and the ensuing speed of spatial spread are both inversely proportional to transinfections’s deleterious effects [11]. “Super spreader” Wolbachia, like the wRi-variants considered here, may tend to be less deleterious in novel hosts and spread more readily. Although introduced Wolbachia may occasionally spread to unintended host species, the ubiquity of Wolbachia infections in nature suggests that these rare events are unlikely to be harmful [44].

STAR METHODS

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Biological Samples
Drosophila auraria, NGN11, Nagano, Japan, 2003	Ehime Stock Center, Cooper lab	E-11217 (Ehime)
D. auraria, SP11-11, Sapporo, Japan, 2011	Ehime Stock Center, Cooper lab	E-11230 (Ehime)
D. anomalata, A29, Cairns, Australia, 2014	Hoffmann lab	N/A
D. anomalata, CHC221, Townsville, Australia, 2014	Hoffmann lab	N/A
D. pandora, CHC1, Townsville, Australia, 2014	Hoffmann lab	N/A
D. pandora, CHG108, Cairns, Australia, 2014	Hoffmann lab	N/A
D. pandora, pl, Cairns, Australia, 2011	Hoffmann lab	N/A
D. simulans, I14-18, Irvine, California, 2014	Cooper lab	N/A
D. simulans, I14-19, Irvine, California, 2014	Cooper lab	N/A
D. simulans, LZV15_057, Zambia, 2014	Cooper lab	N/A
D. simulans, LZV15_058, Zambia, 2014	Cooper lab	N/A
D. simulans, NMB15_030, Zambia, 2015	Cooper lab	N/A
D. simulans, USP16.124, Sao Paulo, Brazil, 2016	Cooper lab	N/A
D. simulans, USP16.125, Sao Paulo, Brazil, 2016	Cooper lab	N/A
D. simulans, Y14_29, Yolo County, California, 2014	Cooper lab	N/A
D. triauraria, Tokyo, Japan	Drosophila Species Stock Center	14028-0691.01
Deposited Data
Illumina reads for the Drosophila lines listed above	This paper	GenBank SAMN08438540-08438555
RevBayes scripts and input sequences for all of our phylogenic analyses	This paper	DRYAD doi:10.5061/dryad.4kt079g
Software and Algorithms
ABySS	[45]	https://github.com/bcgsc/abyss
BCFtools	[46]	http://www.htslib.org/
Bonsai	[47]	https://github.com/mikeryanmay/bonsai
BUSCO	[48]	http://busco.ezlab.org/
BWA	[49]	http://bio-bwa.sourceforge.net/
ControlFREEC	[50]	http://boevalab.com/FREEC/
MAFFT	[51]	https://mafft.cbrc.jp/alignment/software/
Prokka	[52]	https://github.com/tseemann/prokka
RevBayes	[53]	https://revbayes.github.io/
Samtools	[46]	http://www.htslib.org/
Sickle	[54]	https://github.com/najoshi/sickle

CONTACT FOR REAGENTS AND RESOURCE SHARING

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Michael Turelli (mturelli@ucdavis.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

The Drosophila stocks used for new genomic analyses, and their availability, are described under Biological Samples in the Key Resources Table. These stocks were maintained on standard cornmeal medium without temperature controls.

METHOD DETAILS

Genetics and Genomics

Wolbachia genomes

Our analyses rest on the reference genome for wRi [22] and published draft genomes of wRi-like Wolbachia from D. ananassae [wAna, 28, 55], D. suzukii [wSuz, 56] and D. subpulchrella [wSpc, 20]. We generated draft wRi-like genomes from global samples of D. suzukii and D. simulans; from the montium subgroup sister species, D. auraria (wAur) and D. triauraria (wTri), and from two newly described ananassae subgroup species [8], D. pandora [wPan, 26] and D. anomalata (wAno).

Sequencing of wSuz, wAno, wPan, wRi, wAur and wTri

The new D. suzukii genome data were generated from a global sample of ethanol-preserved field-collected flies. Single-index libraries were produced from individual flies using the Kapa Hyper Plus library prep kit, with insert size about 300 bp. Libraries were sequenced by Novogene, Inc. (Sacramento, CA) using Illumina HiSeq 4000, generating paired-end, 150 bp reads.

Genome data for D. anomalata (strains A29, CHC221) and D. pandora (strains CHC1, CHG108, pl) were generated from stocks maintained in the Hoffmann lab. Genome data for D. auraria (strain SP11-11) and D. simulans (strains I14_18, I14_19, LZV15_057, LZV15_058, NMB15_030, USP16.124, USP16.125, Y14_29) were generated from stocks maintained in the Cooper lab. The libraries were constructed by Novogene, Inc. (Sacramento, CA) using the NEBNext® Ultra^™ II DNA Library Prep kit for 350 bp inserts. Libraries were sequenced at the Novogene Sequencing Laboratory at UC Davis Medical Center on an Illumina HiSeq X10, generating paired-end, 150 bp reads.

Genome data for D. auraria (strain NGN11) and D. triauraria (strain 14028-0691.01) were generated from stocks maintained in the Cooper lab. The libraries were constructed using the Illumina TruSeq DNA PCR-Free Library Prep kit for 350 bp inserts. Libraries were sequenced at the Vincent J. Coates Genomics Sequencing Laboratory at UC Berkeley on an Illumina HiSeq2000, generating paired-end, 100 bp reads.

Wolbachia de novo assembly for wPan, wAno, wAur, wTri and wAna

To assemble the Wolbachia from D. anomalata, D. pandora, D. simulans, D. auraria, D. triauraria and the eight D. ananassae lines with cytoplasmic Wolbachia [28], we cleaned and trimmed the reads with Sickle v. 1.33 [54] and assembled them with ABySS v. 2.0.2 [45]. K values of 51, 61…91 were tried. Scaffolds with best nucleotide BLAST matches to known Wolbachia sequences, with E-values less than 10⁻¹⁰, were extracted as the Wolbachia assembly. For each line, the best Wolbachia assembly (fewest scaffolds and highest N50) was kept.

To assess the quality of our draft assemblies, we used BUSCO v. 3.0.0 [48] to search for orthologs of the near-universal, single-copy genes in the BUSCO proteobacteria database. As a control, we performed the same search using the reference genomes for wRi [22], wAu [57], wMel [58], wHa and wNo [59].

Wolbachia alignment for wSuz and wRi

Reads for 197 D. suzukii lines were aligned to the D. suzukii reference [60] and the draft wSuz reference [56] with bwa v. 0.7.12 [49], requiring alignment-quality scores ≥ 50. To avoid losing genes due to low coverage, lines with average Wolbachia coverage less than 20 were dropped. Consensus Wolbachia sequences for the remaining eight lines were extracted with samtools v. 1.3.1 and bcftools v. 1.3.1 [46].

D. simulans reads from Machado et al. [61] were aligned to the D. simulans reference plus the wRi reference [22] with bwa v. 0.7.12 [49], requiring alignment-quality scores ≥ 50. Consensus sequences for the 75 lines with the highest average Wolbachia coverage (all above 20) were extracted with samtools v. 1.3.1 and bcftools v. 1.3.1 [46].

Wolbachia loci for phylogenetic and variation analyses

All of the Wolbachia sequences, plus the wSpc assembly [20] and the wRi reference [22], were annotated with Prokka v. 1.11 [52], which identifies orthologs to known bacterial genes. To avoid pseudogenes and paralogs, we used only genes present in a single copy and with identical lengths in all of the sequences. Genes were identified as single copy if they uniquely matched a bacterial reference gene identified by Prokka v. 1.11. There are 734 such genes in the wRi reference genome. By requiring all orthologs to have identical length in all of the wRi-like genomes, we removed all loci with indels. 525 genes, with combined length of 507,307 bp, met our criteria. These reference genes were extracted, aligned with MAFFT v. 7 [51], and concatenated.

Wolbachia assembly quality assessment

Out of 221 near-universal, single-copy orthologs in proteobacteria, our BUSCO v. 3.0.0 [48] analysis (Table S1) found effectively the same number of genes in all of our de novo assemblies as in the complete reference genomes (wRi, wMel, wAu, wHa, and wNo). The only exception was increased fragmentation in wAna_HNL0501. Although the wRi-like genomes are on the order 1.4 Mb [22], our phylogenetic analyses focus on 525 genes covering only 506,307 bp. Nevertheless, our BUSCO analyses indicate that our draft genomes are essentially complete, comparable to the draft wSpc genome described in [20].

Drosophila nuclear loci

Our host phylogeny (Figure 1A) was based on 20 nuclear genes: aconitase, aldolase, bicoid, ebony, enolase, esc, g6pdh, glyp, glys, ninaE, pepck, pgi, pgm, pic, ptc, tpi, transaldolase, white, wingless and yellow. Coding sequences were extracted from the annotated reference genomes for D. melanogaster [62], D. ananassae [63], D. simulans [64], and D. suzukii [60]. We used protein BLAST with the D. melanogaster coding sequences to extract the orthologs from one draft genome assembly of D. triauraria (strain 14028-0691.01), D. auraria (strain NGVII), D. anomalata (strain F23), and D. pandora (strains CHC_1). Coding sequences for esc and ptc in D. subpulchrella were obtained from [20] (sequences of the other 18 loci from D. subpulchrella are not yet publically available). The genes were aligned with MAFFT v. 7 [51].

mtDNA protein-coding loci

Reads from D. anomalata, D. pandora, D. auraria, D. triauraria, the eight D. ananassae lines with cytoplasmic Wolbachia [28], and the 500-bp-insert-size D. suzukii read archive used to make the D. suzukii reference [60] were trimmed with Sickle v. 1.33 [54]. (The D. subpulchrella mtDNA genome and nuclear reads are not yet publically available.) As the mitochondria did not assemble well with the full read sets, the reads were down sampled by a factor of 100, so that the nuclear genome would not assemble but the mtDNA, with much higher coverage, would. The down-sampled reads were assembled with ABySS v. 2.0.2 [45] with K values of 51, 61…91. We identified orthologs to the 13 D. simulans protein-coding mitochondrial genes in each assembly with protein BLAST, choosing the K value that produced the largest number of mtDNA genes on a single scaffold.

The mitochondrial protein-coding genes for the D. simulans lines [61] were extracted by aligning the reads to the D. simulans reference plus the wRi reference [22] with bwa v. 0.7.12 [49], requiring alignment-quality scores ≥ 50, then extracting the consensus sequences with samtools v. 1.3.1 and bcftools v. 1.3.1 [46].

The mitochondrial protein-coding genes for the other eight D. suzukii lines were extracted by aligning the reads to the D. suzukii reference [60] plus the D. suzukii mitochondrial assembly generated above and the wRi reference [22] with v. bwa 0.7.12 [49]. We required alignment-quality scores ≥ 50, then extracted the consensus sequences with samtools v. 1.3.1 and bcftools v. 1.3.1 [46].

The genes were aligned with MAFFT v. 7 [51] and concatenated.

Analysis of Wolbachia loci controlling CI

Beckmann et al. [39], Beckmann et al. [38] and LePage et al. [37] identified WD0631, WD0632, WRi_006710, WRi_006720, wPip_0294, and wPip_0295 as causing CI. We identified orthologs to these loci in our Wolbachia sequences with protein BLAST. No orthologs to wPip_0294 or wPip_0295 were found in any of the genomes. The remaining four genes—WD0631, WD0632, WRi_006710, WRi_006720—were aligned with MAFFT v. 7 [51] and examined for single-nucleotide variants (SNVs).

To look for copy-number variants (CNVs), we aligned the reads for each line to the wRi reference [22] with bwa v. 0.7.12 [49]. Normalized read depth for each alignment was calculated over sliding 1000 bp windows by dividing the average depth in the window by the average depth over the entire genome. The normalized read depth was plotted and visually inspected for CNVs in regions containing the CI loci. Putative CNVs were confirmed with the Kolmogorov-Smirnov test implemented in ControlFREEC v. 8.0 [50]. As WD0631 and WD0632 have two copies in the wRi reference genome [22], the genome was treated as diploid for putative CNVs involving them. The genome was treated as haploid for putative CNVs involving WRi_006710 and WRi_006720. The results are reported in Table S2.

Wolbachia frequencies in natural populations

We estimated infection frequencies in samples of D. ananassae from Cairns (N = 13) and from Townsville (N = 1), Australia; D. anomalata from Cairns (N = 7) and from Townsville (N = 1), Australia; D. auraria (N = 21) from Japan; and D. subpulchrella (N = 50) and D. suzukii (N = 80) from several sites in China (Table S3). All of our non-Chinese samples are isofemale lines, the Chinese samples were ethanol-preserved flies from nature. For D. ananassae, D. anomalata, and D. pandora, DNA was extracted using the 5% Chelex method outlined in Richardson et al. [26]. Wolbachia infection status was determined using standard polymerase chain reaction (PCR) with the gatB primers from the Multilocus Sequence Typing System (MLST) for Wolbachia [28, 65]. PCR conditions began with 3 minutes at 94°C followed by 37 cycles of 30 seconds at 94°C, 45 seconds at 54°C and 90 seconds at 72°C. A final extension for 10 minutes at 72°C completed the assay. To confirm infection status, we also screened a subset of samples using the Wolbachia-specific validation primers wsp_val [3, 66] with the cycling regime outlined above for gatB, and an annealing temperature of 59°C. For D. auraria, we extracted DNA using a standard ‘squish’ buffer protocol [67] and determined infection status using PCR with primers for the wsp gene [65, 68]. A second reaction for the arthropod-specific 28S rDNA [69] served as a positive control. PCR conditions for these assays began with 3 minutes at 94°C followed by 34 rounds of 30 seconds at 94°C, 30 seconds at 55°C, and 1 minute and 15 seconds at 72°C. The profile finished with one round of 8 minutes at 72°C. PCR products were visualized in 1% agarose gels with a molecular-weight ladder.

We estimated the frequency (p) of wRi-like Wolbachia infections in D. ananassae, D. anomalata, D. auraria, D. pandora, D. subpulchrella, and D. suzukii. All sampled lines of D. ananassae, D. anomalata, D. auraria, and D. pandora were Wolbachia infected. By contrast, both D. subpulchrella (p̂ = 0.62) and D. suzukii (p̂ = 0.83) samples contained infected and uninfected individuals. The D. suzukii infection frequencies in China are significantly higher than the most frequencies observed in North America [19], which are generally 10–25%. Higher frequencies, comparable to those in China, have been observed in European D. suzukii populations [33]. Data and statistical analyses are presented in Table S3.

Cytoplasmic Incompatibility (CI)

Screening for CI

When Wolbachia cause CI, crosses between uninfected females and infected males (denoted UI) produce lower egg hatch than do the reciprocal crosses between infected females and uninfected males (IU). To determine if wRi-like Wolbachia cause CI in D. anomalata, D. auraria, D. pandora, and D. triauraria hosts—as wRi does in D. simulans—we first generated Wolbachia-uninfected lines of each species by allowing Wolbachia-infected lines to develop from egg to adult in tetracycline-supplemented (0.03%) cornmeal medium. Curing was required to screen for CI because all available lines of these host species were Wolbachia infected. In all cases, flies were cleared of Wolbachia within two generations of tetracycline treatment according to the PCR assays.

We reciprocally crossed Wolbachia-infected D. anomalata, D. auraria, D. pandora, and D. triauraria lines to their tetracycline-treated conspecifics to screen for CI. Virgins were collected from each line and held for at least 48 hours. To initiate both UI (D. anomalata, N = 43; D. auraria, N = 17; D. pandora, N = 24; and D. triauraria, N = 17) and IU (D. anomalata; N = 30; D. auraria; N = 18; D. pandora; N = 23; and D. triauraria; N = 16) crosses, males and females from each line were paired individually in vials containing a small spoon with cornmeal medium and yeast paste. After 24 hours, D. auraria and D. triauraria pairs were aspirated to spoons in new vials. This process was continued for a total of five days. D. anomalata and D. pandora pairs remained together until mating was observed, after which males were removed and females were aspirated to spoons in new vials every 24 hours until a minimum of 10 eggs had been laid [23]. The proportion of eggs that hatched on each spoon was scored between 24 and 48 hours after the adults were removed. During preliminary trials, we confirmed that these times sufficed for all eggs to hatch for all species assayed. We excluded from our analyses replicate crosses that produced fewer than 10 eggs and those for which mating was not observed (or inferred from egg hatch).

Estimated levels of CI

We screened wRi-like infected D. anomalata, D. auraria, D. pandora, and D. triauraria for CI by comparing the egg hatch of UI and IU crosses within each host species. We found that UI egg hatch was significantly lower than IU egg hatch for D. anomalata (UI egg hatch = 0.047 ± 0.168, IU egg hatch = 0.698 ± 0.247, P < 0.001), D. auraria UI egg hatch = 0.344 ± 0.184, IU egg hatch = 0.899 ± 0.093, P < 0.001), D. pandora (UI egg hatch = 0.009 ± 0.027, IU egg hatch = 0.778 ± 0.294, P < 0.001), and D. triauraria (UI egg hatch = 0.144 ± 0.167, IU egg hatch = 0.886 ± 0.093, P < 0.001). The statistically significant CI observed for D. anomalata, D. auraria, and D. pandora is consistent with their high infection frequencies in nature (p = 1.0 for each host). Data and statistical analyses are presented in Table S4.

QUANTIFICATION AND STATISTICAL ANALYSIS

Phylogenetic Analyses

We performed a series of Bayesian phylogenetic analyses on several different alignments, with the data partitioned as described below. For some analyses, we inferred phylograms, where the branch lengths are proportional to the expected number of substitutions per site (averaged over the data partitions); for other analyses, we inferred chronograms, where the branch lengths are proportional to absolute or relative time. We performed extensive MCMC diagnosis to confirm that our analyses adequately approximated the joint posterior probability distribution of the model parameters. For each analysis, we performed posterior-predictive simulation [70] to confirm that the model adequately describes the process that generated our data (i.e., to assess the absolute fit of the assumed model to our data). We describe the details of each step of our analyses below. All of our phylogenetic analyses were performed using RevBayes v. 1.0.5 [53]. (All RevBayes scripts used are available in the data archive listed in the Key Resources Table. We refer readers to those scripts for details regarding hyperparameters and MCMC settings.)

Data partitions and substitution models

For our Drosophila nuclear data, we partitioned the coding sequences by gene and by codon position to accommodate potential variation in the substitution process among genes and among the three codon positions within each protein-coding gene. For host mtDNA and Wolbachia alignments, we partitioned only by codon position (because levels of sequence variation appeared too low to justify additional partitions). We assumed that each data partition evolved under an independent GTR substitution model [71]. To accommodate variation in the substitution rate across the sites of each data partition, we used a discrete-Gamma model with four rate categories [i.e., GTR+Γ, 72]. We accommodated variation in the overall substitution rate among data partitions by assigning a rate multiplier, σ, to each data partition. We used flat, symmetrical (α = 1) Dirichlet priors both on the stationary frequencies, π, and the relative-rate parameters, η, of the GTR substitution model. We used a Gamma hyperprior on the shape parameter, α, of the discrete-Gamma model [adopting the conventional assumption that the rate parameter of this Gamma distribution, β, is equal to α, so that the mean rate is 1; 72]. (The gamma distribution, Γ(α,β), is parameterized so that the mean and variance are α/β and α/β², respectively.) The prior we used for the substitution-rate multiplier for the i^th data partition, σ_i, differs between our unrooted (phylogram) and rooted (chronogram) analyses; we describe these priors in their respective sections below.

Phylogram analyses

For our unrooted phylogenetic analyses, we assumed a discrete uniform prior on the unrooted tree topology, Ψ, and a flat symmetrical Dirichlet prior on the branch-length proportions, ν. We allowed each data partition to draw a substitution-rate multiplier, σ_i, from an exponential distribution with mean of 1 (i.e., Γ(1,1)). We rooted our Wolbachia phylograms using the outgroup wHa rather than wMel [which was used as the outgroup in Conner et al. 20], as wHa is more closely related to the wRi-like Wolbachia.

Under our parameterization, the proportional branch lengths sum to 1, since they are drawn from a Dirichlet distribution. The expected number of substitutions per site for data partition i on branch j is equal to σ_i × ν_j, where ν_j is the proportional branch length, so that the expected number of substitutions per site (across all the branches) for data partition i is simply σ_i. If we were to use a Γ(2n – 3, λ) prior on σ_i, this would be equivalent to the conventional Bayesian prior model, where each of the (2n – 3) branch lengths (in an unrooted tree with n species) is drawn independently from an Exponential(λ) prior. However, this conventional branch-length parameterization is known to be pathological [73, 74], motivating our use of a less informative exponential prior on the rate multiplier. When summarizing our phylogenetic estimates, we collapsed any internal branches that were not well supported (i.e., with a posterior probability < 0.95).

We used this procedure both to estimate the mtDNA phylograms depicted in Figures 2B and 2D, and also to estimate the relative rates of substitutions for mtDNA versus Wolbachia in Figures 2B and 2D.

Chronogram analyses

To estimate trees with a (relative or absolute) time scale, we used Bayesian strict-clock models. For the node-age prior model, we assumed a constant-rate sampled-birth-death process, which specifies the prior distribution on the tree topology and node ages, Ψ [75]; in this prior model, τ_i is the length of branch i in units of (relative or absolute) time. As in our unrooted-tree analyses, we assigned a rate multiplier, σ_i, to each data partition. We assigned a diffuse Γ(0.001, 0.001) prior on the data-partition-specific substitution-rate multipliers, σ. This diffuse prior is uninformative and is known to be well behaved over a wide range of datasets (Andrew Rambaut, pers. comm.).

The constant-rate, sampled birth-death process model has four parameters: the speciation rate, λ, which determines the rate at which species arise; the extinction rate, μ, which determines the rate at which species go extinct; the sampling probability, ρ, which specifies the fraction of extant species included in the sample; and the age of the root, T. For our Drosophila analyses, we used ρ = 9/190, the fraction of the currently described melanogaster-group species that we studied. (Our initial analysis for Figure 1A assumed that ρ = 9/336, based on an inflated estimate of the number of species in the melanogaster species group [cf. 8, 21]. Redoing the analysis with ρ = 9/190 produced no differences in either the medians or the credible intervals to two significant digits.) For the wRi-like Wolbachia, we used ρ = 0.1 and 0.5, as plausible values concerning the fraction of the wRi-like variants in the melanogaster group that we have discovered. Given our uncertainty regarding ρ, we also estimated divergence times under the uniform node-age prior [76]. We specified empirical lognormal hyperpriors on the net-diversification rate (speciation – extinction) and extinction rate. Specifically, we used empirical information to specify the means of these distributions so that the prior expected number of species under the birth–death process is equal to the known number of species in the group (we refer readers to our RevBayes scripts for the mathematical details). We fixed the root age to 1, since we do not have fossil calibrations that would provide an absolute time scale and are mainly focused on relative rates and times.

Results of our chronogram analyses are depicted in Figures 1, 2A and 2C, with additional results reported in Table S5.

Wolbachia divergence times

To estimate chronograms with an absolute (rather than relative) time scale, we require either information on the absolute age of one or more nodes (e.g., a fossil-calibration prior), or information on the absolute substitution rate [i.e., a substitution-rate calibration prior; 77]. To estimate absolute divergence times for Wolbachia (Figure 1B), we used a legacy substitution-rate calibration prior based on empirical estimates in Richardson et al. [15]. To that end, we fit our substitution-rate prior distribution to the substitution-rate posterior distribution for the third-position sites inferred by Richardson et al. [15]; specifically, we used a Γ(7,7) × 6.87×10⁻⁹ as our substitution-rate prior (we chose parameters α = β = 7 for our substitute-rate prior so that the upper and lower credible intervals of the prior distribution matched the corresponding posterior distribution estimated by Richardson et al. [15], which we normalized by the median, i.e., 0.42 and 1.88).

Note that the expected number of substitutions on a branch is equal to r × t, where r is the substitution rate per unit time, and t is the branch length in units of time; for our relative chronogram analyses, time is arbitrarily scaled so that the age of the root is 1. Given an empirical estimate of the absolute substitution rate, r_a, we can rescale the branch length t such that the expected number of substitutions remains the same:

$$r_r{t}_r=r_a{t}_a,$$

where the subscripts r and a indicate the relative and absolute values, respectively. If the absolute and relative substitution rates, r_r and r_a, and the relative branch lengths, t_r, are known, then we can solve for the branch length on an absolute timescale: t_a = r_rt_r/r_a. We can use this relationship to rescale relative chronograms to an absolute timescale when the rate of substitution is known.

To estimate the Wolbachia chronogram with an absolute timescale, we first estimated a posterior distribution of relative chronograms as described in the previous section, then rescaled these relative chronograms as follows. For the i^th relative chronogram in the posterior distribution, we drew an empirical substitution rate, r_a,i, from the empirical rate distribution derived from Richardson et al. [15]. Next, we computed the ratio of the relative third-position substitution rate for the i^th chronogram, σ_3,i, to the empirical substitution rate, r_a,i. Finally, we multiplied the branch lengths of the i^th relative chronogram by σ_3,i/r_a,i to generate a chronogram with an absolute timescale. The absolute root ages of the Wolbachia trees under the alternative node-age prior models are listed in Table S5.

Wolbachia chronogram

The estimated number of third-position substitutions per site from the root to the tip of Figure 1B is 9.29×10⁻⁵ with 95% credible interval (7.06×10⁻⁵, 1.16×10⁻⁴). Hence, using the Richardson et al. [15] median estimate of 6.87×10⁻⁹ substitutions per third-position site per year, we can approximate the root age as 1.35×10⁴ years, consistent with the chronogram in Figure 1B. As discussed in Conner et al. [20], the Richardson et al. [15] Wolbachia calibration from D. melanogaster is consistent with independent estimates derived from Nasonia wasps [16] and Nomada bees [17].

Table S5 explores the robustness of the node-age estimates presented in Figure 1B to alternative models for the node-age prior in RevBayes. As indicated, the quantitative predictions are robust. In Figure 1B, we present the results for ρ = 0.1 simply because they are intermediate, representative and consistent with the intuitive prediction discussed above.

Drosophila relative chronogram

Our estimate of the relative divergence times for the Drosophila host species (Figure 1A) is based on analyses of the 20 nuclear loci described above for all species but D. subpulchrella, for which only esc and ptc sequences were available.

An unpublished analysis of about 30 species from the montium subgroup indicates that the two D. auraria strains are sisters relative to D. triauraria, details will be provided on request. Given the many uncertainties in calibrating rates of Drosophila molecular evolution, we have chosen to indicate the variability in current estimates as summarized by Obbard et al. [24].

Drosophila mtDNA phylograms

Our estimates of phylograms for the Drosophila mtDNA, Figures 2B and 2D, are based on analyses of mtDNA protein-coding genes, partitioned by codon position, for D. suzukii (Figure 2B) and for D. ananassae, D. anomalata and D. pandora (Figure 2D).

Estimating relative substitution rates in host mtDNA and Wolbachia

The relatively recent divergence times of the wRi-like Wolbachia compared to their Drosophila hosts precludes a cladogenic origin for this association (Figure 1B). Accordingly, the wRi-like Wolbachia must have been acquired either by introgression (which predicts proportional substitution rates in host mtDNA and Wolbachia, as they would have diverged for equal durations under this scenario), or by non-sexual horizontal transmission (which predicts disproportionately high substitution rates in mtDNA compared to those in Wolbachia, as the mtDNA would have had more time to diverge under this alterative scenario). We tested these predictions by estimating the relative substitution rates of Wolbachia versus host mtDNA with separate analyses for D. suzukii and the three ananassae subgroup species.

We estimated the relative substitution rates of host mtDNA versus Wolbachia sequences using two general classes of unrooted phylogenetic models. The first class assumes shared branch-length proportions for the host mtDNA and Wolbachia alignments (this is consistent only with introgression), the second class assumes independent branch-length proportions for the host mtDNA and Wolbachia alignments (this can occur with either introgression or non-sexual horizontal transmission). For both of these general model classes, we evaluated two candidate substitution models for a total of four candidate phylogenetic models. Specifically, the two shared branch-length models, Models 1 and 3, assume that the mtDNA and Wolbachia alignments share a common set of branch-length proportions, and assume four data partitions—one for the entire Wolbachia alignment, and one for each of the three codon positions of the host mtDNA alignment—with an independent GTR+Γ substitution model assigned to each data partition. The two independent branch-length models, Models 2 and 4, assume that the mtDNA and Wolbachia alignments have independent branch-length proportions, and assume six data partitions—one for each of the three codon positions of the Wolbachia alignment, and one for each of the three codon positions of the host mtDNA alignment—with an independent GTR+Γ substitution model assigned to each data partition. In all four candidate models, the host and Wolbachia sequences were assumed to share a common tree topology, which is supported by our independent analyses of the individual host and associate alignments. All remaining aspects of the substitution models and priors were identical to those described above for “Phylogram analyses.”

Empirical studies commonly adopt phylogenetic models to accommodate various sources of substitution-rate variation. For example, most phylogenetic analyses accommodate variation in substitution rates across the sites of an alignment (e.g., by using ASRV models that specify site-specific substitution-rate multipliers). Similarly, most models accommodate differences in the overall substitution rate between data partitions (e.g., by using partitioned-data models that specify partition-specific substitution-rate multipliers). Moreover, many analyses accommodate variation in the overall substitution rate across branches (e.g., by using relaxed-clock models that specify branch-specific substitution-rate multipliers). Although all of these common models accommodate various types of substitution-rate variation, they all nevertheless assume that there is a single set of branch-length proportions that are shared by all sites/data partitions.

By contrast, evaluating our hypotheses regarding the origin of wRi-like Wolbachia demands that we adopt models that accommodate differences in the branch-length proportions between data partitions; this is related to the phenomenon of heterotachy, in which the relative rates of evolution for different data partitions vary across branches [e.g., 78]. Specifically, the non-sexual horizontal transmission hypothesis corresponds to a model in which the mtDNA and Wolbachia alignments have independent branch-length proportions. Conversely, the introgression hypothesis corresponds to a model in which the mtDNA versus Wolbachia alignments may or may not share common branch-length proportions, depending on the constancy of the relative rates of evolution for mtDNA versus Wolbachia. We can assess the relative fit of each of these models to our data to test the corresponding hypotheses: the introgression hypothesis would be strongly supported if the shared branch-length proportions model was preferred by our interspecific data. Even if we reject the shared branch-length proportions model, however, introgression and prosaic heterotachy may be sufficient to explain the data. When the model with independent branch-length proportions is preferred—as indicated for our data (Table S6)—we can take the additional step of informally evaluating whether the estimated substitution-rate ratio differs markedly along the branches leading to D. anomalata or D. pandora in the ananassae subgroup (the suspected points of horizontal transmission).

To select among our four competing models, we computed the set of marginal likelihoods (Table S6), which represent the average fit of a given model to the data [e.g., 79]. We estimated the marginal likelihood of each candidate model using stepping-stone simulation [79,80], with 50 stones for each simulation, and performing four replicate simulations for each model to assess the reliability of our marginal-likelihood estimates. For each of our stepping-stone analyses, we assumed a fixed tree topology. Specifically, our analyses of the D. suzukii data iteratively fixed the tree topology to one of the three possible resolutions of the polytomy depicted in Figures 2A and 2B (involving the Wolbachia and mtDNA found in D. suzukii from two Italian samples and Brazil). Similarly, our analyses of the data for the ananassae subgroup iteratively fixed the tree topology to one of the three possible resolutions of the polytomy depicted in Figures 2C and 2D (involving the Wolbachia and mtDNA found in D. anomalata, D. pandora and three strains of D. ananassae; Table S6). Finally, we assessed the relative fit of the four candidate models by computing Bayes Factors, defined as: BF₀₁ = P(X | M₀)/P(X | M₁), where X represents the data and P(X | M_i) is the marginal likelihood of model i; Bayes Factors > 1 indicate that model M₀ provides a better description of the data than model M₁ [81].

mtDNA phylograms and comparison with Wolbachia chronograms

The topology for the D. suzukii mtDNA variants was concordant with the Wolbachia chronogram derived from the same lines, i.e., both analyses agreed on which nodes had very strong posterior support (P > 0.999) and which nodes had ambiguous support (P < 0.95).

With one exception, analogous results were obtained for D. ananassae, D. anomalata and D. pandora, i.e., both the mtDNA phylogram (Figure 2D) and the Wolbachia chronogram (Figure 2C) agreed. The single exception is that the mtDNA phylogram (which involves a higher rate of substitutions) resolves a clade uniting the mtDNA from three D. ananassae lines with those from D. anomalata and D. pandora (this is part of a polytomy based on Wolbachia data alone). We used the more-resolved topology in our analysis of relative rates of mtDNA versus Wolbachia divergence.

As shown in Table S6, for both the Wolbachia and mtDNA data and all three plausible topologies in the ananassae subgroup, the six-partition models (3 and 4) fit the data better than the four-partition models (1 and 2). This demonstrates significantly different rates of evolution for the three Wolbachia codon positions, unlike the analysis of wMel within D. melanogaster [15] and the divergence of wSpc from a European isolate of wSuz [20] that showed equal rates of evolution for all three Wolbachia codon positions. In the Wolbachia chronogram (Figure 1B), the estimated substitutions per site (and 95% credible intervals) from tip to root by position are: 1st, 1.03×10⁻⁴ (7.90×10⁻⁵, 1.27×10⁻⁴); 2^nd, 6.94×10⁻⁵ (5.15×10⁻⁵, 9.00×10⁻⁵); 3^rd, 9.29×10⁻⁵ (7.06×10⁻⁵, 1.16×10⁻⁴). So while the first and third positions have essentially identical rates of substitution, the second position is slightly slower.

For D. suzukii, Models 3 and 4 were equally likely. This is consistent with constant relative rates for mtDNA and Wolbachia evolution across the maternal lineages in this species. By contrast, for all plausible ananassae subgroup topologies, there was greater estimated variation in relative rates for mtDNA versus Wolbachia among our ananassae subgroup lineages, and Model 4 fit the data significantly better than Model 3. However, as shown in Figure 2E, the branches leading to D. anomalata and D. pandora do not stand out as particularly long. Hence, despite relative-rate heterogeneity, the data are consistent with introgressive transfer of Wolbachia among the three ananassae subgroup species.

MCMC simulation and diagnosis

We used MCMC simulation to estimate the joint posterior probability density of the model parameters for each unique analysis in our study. We ran each MCMC simulation for 100,000 iterations, thinning the chains by sampling every 20^th iteration. (Note that, unlike other Bayesian phylogenetic MCMC programs, RevBayes performs a large number—equal to the sum of the proposal weights for all parameters—of Metropolis–Hastings proposals per MCMC “iteration”. Therefore, the total number of MCMC iterations for a given simulation is the chain length multiplied by the sum of the proposal weights for all parameters. We refer readers to our RevBayes scripts for the full details of our MCMC settings). We ran four independent, replicate MCMC simulations for each unique analysis to assess convergence.

We diagnosed MCMC performance using bonsai [47]. We verified that each continuous model parameter satisfied the Geweke’s diagnostic [82] and mixed adequately according to the effective sample size [ESS; 83]. We visually confirmed that the clade posterior probabilities agreed among replicate runs using compare-trees plots [84]. We re-ran any chains that failed according to any of these diagnostics until they passed the MCMC diagnostics.

Assessing model adequacy

We used posterior-predictive simulation to ensure the adequacy of all models used in our analyses [that is, to assess the absolute fit of each model to the corresponding dataset; Bollback 70]. Posterior-predictive simulation is based on the following principle: if the assumed model provides an adequate description of the process that generated our observed data, then we should be able to use that model to simulate data that are “similar” to our observed data (where the data are simulated from the posterior inferred under that model from the original data). Conversely, if data simulated under the posterior are not “similar” to our observed data, then the model does not realistically capture the true process that generated our observations. We do not expect inadequate models to provide reliable estimates of the phylogeny and branch lengths; therefore, we should not trust inferences based on inadequate models.

Following Bollback [70], we simulated 1000 partitioned sequence datasets from the joint posterior distribution of each model. We computed the standard multinomial test statistic described by Goldman [85], T(X), for each data partition. We next computed the same statistic for each simulated data partition to generate a posterior-predictive distribution of the statistic, T’(X), for that partition. If the observed statistic lies outside of the 95% probability interval of the corresponding posterior-predictive distribution, then the model does not provide an adequate description of the generating process. All of our Wolbachia and mtDNA partitions passed this test in all analyses; 3 of the 60 nuclear partitions were outside of the 95% interval, as expected by chance.

Wolbachia frequencies in natural populations

We estimated exact 95% binomial confidence intervals, assuming a binomial distribution, for the infection frequencies of each host species. All analyses were implemented in R version 3.1.3 [86].

Screening for CI

Differences in egg-hatch success between UI and IU crosses was assessed using one-tailed Mann-Whitney U tests.

DATA AND SOFTWARE AVAILABILITY

Raw genome reads for our Wolbachia-infected Drosophila are available through GenBank under accession number SAMN08438540-08438555. The scripts used for all phylogenetic analyses and the specific sequence data used in those analyses can be found in the DRYAD repository doi:10.5061/dryad.4kt079g.

Highlights.

• Closely related Wolbachia spread across eight diverse Drosophila

• Spread was extremely rapid, over less than 30,000 years

• mtDNA analyses indicate no horizontal transmission within these species

• Only six of the eight Wolbachia strains cause detectable reproductive manipulation