Resource-driven changes to host population stability alter the evolution of virulence and transmission

Abstract

What drives the evolution of parasite life-history traits? Recent studies suggest that linking within- and between-host processes can provide key insight into both disease dynamics and parasite evolution. Still, it remains difficult to understand how to pinpoint the critical factors connecting these cross-scale feedbacks, particularly under non-equilibrium conditions; many natural host populations inherently fluctuate and parasites themselves can strongly alter the stability of host populations. Here, we develop a general model framework that mechanistically links resources to parasite evolution across a gradient of stable and unstable conditions. First, we dynamically link resources and between-host processes (host density, stability, transmission) to virulence evolution, using a ‘non-nested’ model. Then, we consider a ‘nested’ model where population-level processes (transmission and virulence) depend on resource-driven changes to individual-level (within-host) processes (energetics, immune function, parasite production). Contrary to ‘non-nested’ model predictions, the ‘nested’ model reveals complex effects of host population dynamics on parasite evolution, including regions of evolutionary bistability; evolution can push parasites towards strongly or weakly stabilizing strategies. This bistability results from dynamic feedbacks between resource-driven changes to host density, host immune function and parasite production. Together, these results highlight how cross-scale feedbacks can provide key insights into the structuring role of parasites and parasite evolution.

This article is part of the theme issue ‘Anthropogenic resource subsidies and host–parasite dynamics in wildlife’.

1. Introduction

The evolution of parasite traits presents a unique challenge to both basic and applied biology [1,2]. On the one hand, traits such as virulence (e.g. parasite-induced mortality) and transmission drive the invasion, spread and severity of disease [3]. Virulence evolution, in particular, frequently undermines targeted control strategies (e.g. vaccines, diet) [4–7]. On the other hand, these same traits govern the structuring role of parasites in natural systems. For instance, parasite-induced virulence can stabilize host dynamics [8] while virulence that reduces host reproduction has a destabilizing effect [9]. Changes in the stability of host populations, in turn, govern ecological interactions (e.g. resource use) in ways that should also influence within-host processes (e.g. immune function), between-host processes (e.g. density-dependent transmission [10]) and consequentially, parasite evolution. Yet, evolutionary studies typically assume that parasite and host populations remain constant and focus on either within- or between-host processes [11]. Few studies, however, have examined the potential connections between environmental factors that drive both population stability and cross-scale feedbacks (reviewed by [12]).

Here, we examine how a key environmental factor, resources, influences parasite evolution under both stable and unstable conditions. Resources could influence parasite evolution through two main pathways. First, resources can influence processes within infected hosts that can either promote or inhibit the production of parasites [13–15]. For instance, resource enrichment can support a more robust, energetically expensive immune response, helping hosts combat (resist, clear or control) parasites once infected and thus, reduce parasite fitness and transmission [16–18]. However, because parasites steal resources from hosts, resource enrichment can also promote parasite development and replication within hosts, increasing parasite fitness [13,15,19,20]. Such resource antagonism between hosts and parasites makes it challenging to determine the net effect of resources on the within-host processes that drive the evolution of virulence [21].

Resource enrichment (e.g. via anthropogenic resource subsidies) can also influence the density and stability of host populations in ways that directly influence between-host transmission (and thus, virulence). For instance, resources can destabilize the host/consumer-resource system via the ‘paradox of enrichment’ [22,23]. This resource-stability link arises because hosts with more resources can produce more (often susceptible) offspring. Higher fecundity then increases host density (at least until hosts overshoot their resources). Host density, in turn, strongly governs parasite fitness and the evolution of key traits such as virulence [24,25]. For example, classic R₀ expressions used to predict both parasite emergence and evolution often include the density of susceptible hosts [26,27]. However, while dynamic feedbacks between host density and resources form the cornerstone of ecological studies, links between resources and host density are rarely incorporated into evolutionary models, which typically assume that host density remains at equilibrium [3,28]. Yet, these key connections may provide crucial insight into parasite evolution and help guide management practices in natural populations where host populations inherently fluctuate (e.g. seasonal fluctuations, consumer-resource cycles [29,30]; in part due to parasite-driven changes to stability [8,10,31–34]). Moreover, parasites (or more broadly, pathogens) are often used to manage pest populations during extremely unstable outbreaks [35,36]. Hence, accounting for host population dynamics could improve our ability to accurately predict and manage parasite evolution [37].

We combine classic consumer-resource and epidemiological theory to model a disease system where changes in resources alter the stability of the host population [31]. We use adaptive dynamics to characterize the evolutionarily stable strategy (ESS) for parasite life history in this classic ‘non-nested’ model (which assumes a trade-off between virulence and transmission). We also consider a ‘nested’ model (sensu [38]) where the population-level epidemiological parameters are determined by an explicit model of within-host processes [11]. This nested model allows us to study how dynamic feedbacks between individual-scale and population-scale processes shape the ES life-history strategies of parasites (figure 1). Our results illustrate that resource-driven changes in the stability of host population dynamics drive the evolution of parasite virulence and transmission, but only when accounting for both within- and between-host processes.

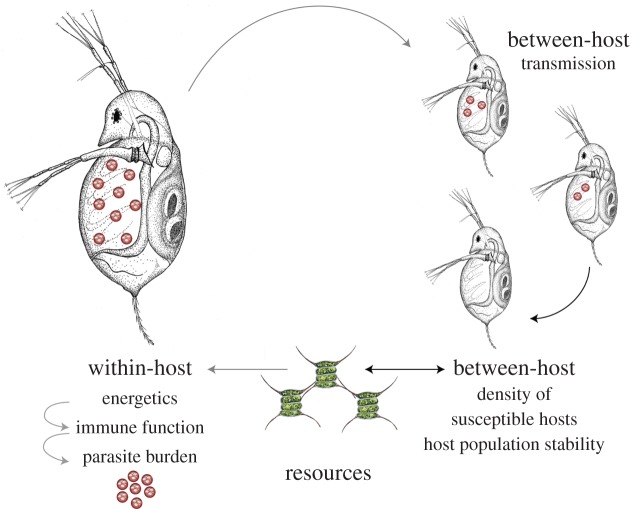
Figure 1.

Conceptual diagram showing the pathways that link resources to parasite evolution in the ‘non-nested’ model (black arrows) and the ‘nested’ model (black arrows plus the grey arrows). Note, we use this host–parasite–resource system for illustrative purposes; the model is quite general and can be applied to a diversity of hosts and parasites. Daphnia illustration credit: Julia Ferguson. (Online version in colour.)

In both models, parasite-induced mortality stabilized host population dynamics (relative to the disease-free conditions), preventing or reducing the amplitude of population cycles. However, the nested model revealed complex effects of host population dynamics on parasite evolution, including regions of evolutionary bistability. In these regions, evolution could push parasites towards strategies that strongly stabilize the host population or less-stabilizing strategies where parasites ‘ride the cycles’ of their hosts. The stabilizing strategy is identical to the ESS in the non-nested model and prevents host population cycling by sharply reducing the abundance of susceptible hosts. The second ‘cycle-riding’ strategy, on the other hand, depends on feedbacks between resource-driven changes to host density, host immune function and parasite production.

These results illustrate how dynamic feedbacks between resource-driven changes to individual-level (within-host parasite burden) and population-level (stability, transmission) processes can drive the evolution of key parasite traits (figure 1). More specifically, the nested model reveals strong cross-scale and bidirectional feedbacks that link resources and host population dynamics (density and stability) to the evolution of parasite life-history traits (e.g. virulence). These results indicate that accounting for feedbacks between within-host (individual-scale) and among-host (population-scale) processes may be particularly important during unstable dynamics. Together, these results provide an important guidepost for future studies seeking to use mathematical theory to predict and manage parasite evolution.

2. Material and methods

(a). The models

We compare non-nested (classical) and nested models across resource conditions that drive both stable and unstable host dynamics. Both models begin with the Rosenzweig–MacArthur model of consumer-resource dynamics [39]. This model provides a good starting point because varying either the background mortality rate of the consumer, d, or the carrying capacity of resources, K, generates equilibrium and non-equilibrium dynamics. The Rosenzweig–MacArthur model assumes logistic growth of the resource (R), with type II functional responses for the consumer. To capture the epidemiological dynamics, we consider both susceptible (S) and infected (Q) consumers. We assume that all hosts are born susceptible and that birth and background mortality rates for both susceptible and infected hosts are identical. We further assume that there are two strains of parasites circulating in the population, termed the resident, Q, and the mutant, Q_m. These strains differ in virulence (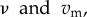 respectively) and per capita transmission rates; for the non-nested model we assume that per capita transmission rates are functions of virulence (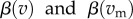, respectively). (We present the nested model below, in §2c.) We explain all model parameters and their biological inference in table 1.

2.1

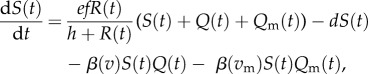2.2

2.3

2.4

Table 1.

List of state variables and parameters in the classic ‘non-nested’ and ‘nested’ models.

parameter/variable	description	non-nested	nested
R	density of resource	—	—
S	density of susceptible hosts	—	—
Q(Qm)	density of hosts infected with the resident (mutant) parasite	—	—
E	within-host energetics	—	—
I	within-host immune function	—	—
P	within-host parasite burden	—	—
t	time (population-level/between-host)	—	—
τ	time (individual-level/within-host)	—	—
ρ	resource maximum growth rate	1.0	1.0
K	resource carrying capacity	0.5–15	0.5–15
f	consumer (host) resource ingestion rate	1.0	1.0
h	resource ingestion half-saturation constant	1.0	1.0
e	consumer (host) conversion efficiency	0.5	0.5
d	consumer (host) background mortality rate	0.05–0.3	0.05–0.3
β0	max per-host transmission rate	15	15
βh	parasite transmission half-saturation constant	—	100
v(vm)	virulence rate of resident (mutant)	determined	—
v0	per-parasite virulence rate	—	0.01
r	rate of host energy use for non-parasite purposes	—	1.0
aB	baseline energy allocation rate to immunity	—	0.1
aI	induced energy allocation rate per parasite killed by the immune response	—	0.1
fI	killing rate, per immune cell	—	0.1
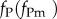	energy exploitation rate, per resident (mutant) parasite	—	determined
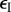	cost of producing immune cell	—	0.1
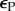	cost of producing pathogen	—	0.1
mI	immune cell background mortality rate	—	0.1
mP	parasite background mortality rate	—	0.01

(b). Evolution of parasite virulence: non-nested model

We analyse parasite evolution using an adaptive dynamics approach, which evaluates whether the mutant parasite Q_m can increase from rarity—that is, can it invade a system where R, S and Q are at the mutant-free (Q_m = 0) dynamical attractor [12,40]. The mutant can invade if the invasion fitness, 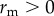. For this system, the mutant-free system approaches either a stable equilibrium or limit cycle. If the system approaches a stable equilibrium, r_m is 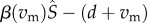, where 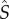is the equilibrium abundance of susceptible hosts in the mutant-free system. However, when the system cycles, the invasion fitness, r_m is

2.5

where T is the period of the limit cycle and is the average abundance of susceptible hosts over the cycle. Thus, r_m is the average per capita growth rate of the mutant parasite over the cycle [41,42].

Potential ES virulence strategies are given by the roots of the fitness gradient:

2.6

If the mutant-free system goes to an equilibrium, the singular strategies are given by the solutions to the equation 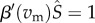. Whether these roots (termed singular strategies) are ES (that is, a population using this strategy cannot be invaded) depends on the sign of the derivative 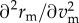. Detailed model derivation and analysis can be found in electronic supplementary material, appendix A. We performed all analyses using Mathematica 11.1 [43].

(c). The nested model: feedbacks between individual- and population-level processes drive parasite evolution

In the nested model approach, within-host (individual-level) dynamics interact with between-host (population-level) dynamics to influence the evolution of parasite traits (figure 1). This method works by connecting transmission rate and virulence to within-host variables, specifically parasite burden, ‘nesting’ the within-host model into the between-host model [11,38]. That is, we assume that transmission rate, β, and virulence, v, are both functions of parasite burden, P, and that the value of P is determined by the outcome of the model of within-host processes. Our model captures the dependence of within-host processes on host resources by assuming that the dynamics of both immunity, I, and parasites, P, depend on within-host energy, E, and that the dynamics of E depend on ingestion of host resources from the environment. Thus, the model becomes (see [21] for a detailed description of the model derivation and table 1 for an explanation of model parameters):

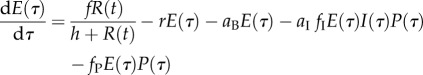2.7

2.8

2.9

Note that τ represents the time scale for within-host processes, whereas t represents the time scale for between-host processes. To facilitate analysis, we employ a separation of time scales argument by assuming that the within-host dynamics (equations (2.7)–(2.9)) are fast, relative to the between-host dynamics 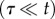. Hence, the within-host model instantaneously reaches the equilibrium 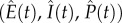. We write this within-host equilibrium as a function of t because changes in the abundance of host resources (equation (2.1)) will instantaneously change the within-host parasite burden and thus, transmission rate and virulence. This standard assumption [11] allows us to assume homogeneity of the infected class and facilitates theoretical tractability without the need for more complicated physiologically structured models.

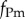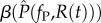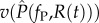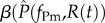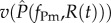We assume that the resident and mutant parasite strains differ in their exploitation rates, f_P and . Transmission and virulence are thus time-varying and resource-dependent functions: and for the resident parasite strain and ) and for the mutant. This resource-dependence of key parasite life-history traits creates dynamic feedbacks between within-host (individual-scale) and between-host (population-scale) processes. In other words, resource dynamics drive individual-level dynamics within hosts, which drive epidemiological dynamics, which in turn drive resource dynamics (figure 1).

(d). Evolution of parasite exploitation: nested model

The analysis of the nested model follows the same procedure as the non-nested model, by investigating when the mutant parasite strain can invade the (R, S, Q) system at its dynamical attractor (stable equilibrium or limit cycles). In this model, the parasite's virulence and transmission are determined by the dynamics of parasite burden within hosts (P), which is itself set by the exploitation rate (f_P). The mutant invasion fitness is

2.10

Again, the above equation is the average per capita growth rate of the mutant parasite at the attractor of the resident-only system. If this system approaches an equilibrium, then the invasion fitness is 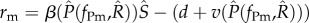. The singular strategies are given by the roots of the fitness gradient,

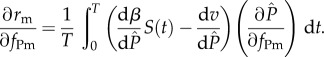2.11

Note that this equation cannot be simplified further because the derivatives of transmission and virulence with respect to 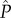are time-varying and thus cannot be factored out of the integral.

(e). Defining parasite transmission: non-nested and nested models

Again, in both models, we looked for singular strategies over gradients of the resource carrying capacity (K) (and the background mortality rate (d); see electronic supplementary material, figures S1 and S2)—parameters known to affect the stability of the host population dynamics [22]. For the non-nested model, we found singular strategies of virulence, whereas for the nested model we found singular strategies of exploitation rate (which then determined virulence). In order to explicitly find these singular strategies, we must specify the functional relationships between transmission and virulence (in the non-nested model) and between parasite burden and transmission and virulence (in the nested model). In the non-nested model, we assume that transmission is a saturating function of virulence, an assumption required for the existence of an ES virulence strategy [12]. Specifically, we assume that 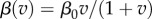. In the nested model, to facilitate comparison with the non-nested model, we assume that virulence is a linear function of 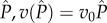, whereas transmission is a saturating function of .

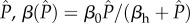3. Results

Before delving into the results, it is worth considering the effect of parasites on system stability. For the choice of parameters here, the underlying consumer-resource system is unstable for K > 1.75. Because parasites induce mortality in their hosts, they act to stabilize the consumer-resource system [8] and for any given K value, if virulence (in the non-nested model) or exploitation (in the nested model) is high enough, the parasite can fully stabilize the system (i.e. there will be a stable equilibrium). However, such a strategy may not be ES. As such, in the ensuing discussion of results, we will refer to equilibrium population ES strategies as those that fully stabilize the system and cyclic population ES strategies as those that dampen, but do not stabilize, the underlying consumer-resource cycle.

For both the non-nested and nested models, we find that the equilibrium population ESS maximizes the lifetime transmission potential of the parasite (electronic supplementary material, appendix A). For the non-nested model, lifetime transmission potential is 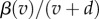and for the nested model, it is 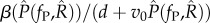. For the non-nested model, we show analytically that the virulence, v, which maximizes this quantity is 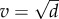, and that this virulence is ES. For the nested model, we show analytically that the ES exploitation rate (f_P) is such that the within-host equilibrium parasite burden satisfies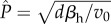; that is, virulence is 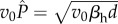. For the choice of parameters in table 1, 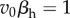, and the ES virulence is identical in the nested and non-nested models (figure 2). For both the non-nested and nested model, this high exploitation strategy leads to a high per capita transmission rate, but a low abundance of susceptible hosts. These results are consistent with the analytical result that maximizing lifetime transmission potential is mathematically equivalent to minimizing the abundance of susceptible hosts (electronic supplementary material, appendix A). In both models, the ESS strongly stabilizes the dynamics: in the absence of parasites, the consumer-resource system is unstable for K > 1.75, whereas with parasites, the system remains stable until K ≈ 9.53.

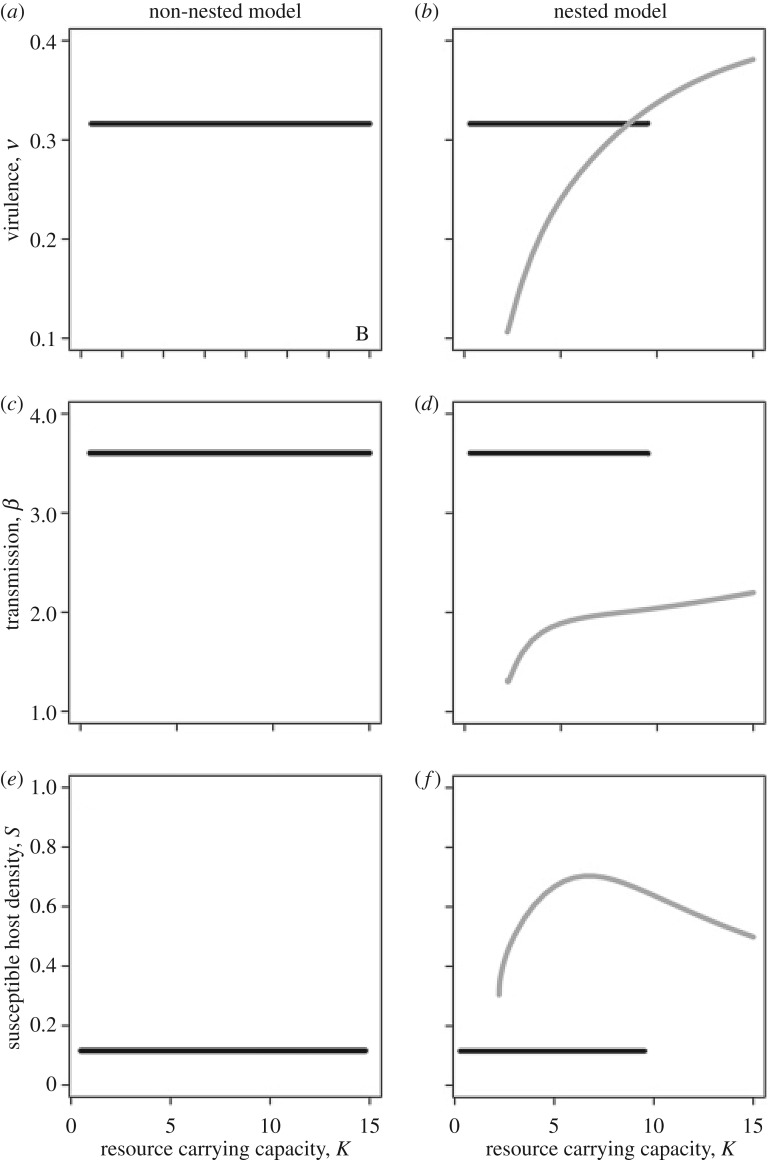
Figure 2.

Results from the non-nested and nested models reveal key differences between the model predictions across a resource gradient where host populations transition from stable to unstable dynamics. (a–d) The average evolutionarily stable (ES) transmission rate, β, and virulence, v, across a gradient in resource carrying capacity, K. (e–f) The average density of susceptible hosts under different ES strategies. For the nested model, the black line shows these averages for the ES strategies that strongly stabilize host population dynamics. The grey line shows these averages for the ES strategies that ‘ride the cycles’ of host density.

The two models predict disparate outcomes for virulence and transmission evolution for the cyclic population ES strategies. In the non-nested model, host dynamics do not influence the ES virulence or transmission (figure 2); that is, 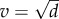remains an ESS for K > 9.53. In electronic supplementary material, appendix A, we show analytically that this result arises because the average density of susceptible hosts over the limit cycle is identical to the equilibrium density of susceptible hosts (i.e. 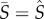). Hence, evolution again maximizes the lifetime transmission potential of the parasite at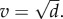

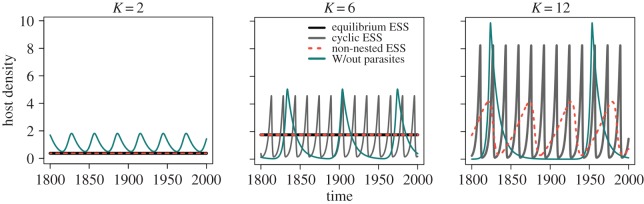
In the nested model, feedbacks between individual-level and population-level processes permit a second ES value for parasite exploitation (f_p) rate (figure 3). This second strategy does not fully stabilize the dynamics (although the cycles are of lower amplitude relative to the disease-free case; figure 4). This ESS exists both within and beyond the parameter ranges over which the stabilizing ESS exists, implying evolutionary bistability (figure 3). In these regions of bistability, evolution can shift the parasite towards either: (i) a high exploitation strategy that strongly stabilizes host population dynamics by minimizing the number of susceptible hosts or (ii) a low exploitation, less-stabilizing strategy where parasite burden responds dynamically to the various feedbacks that drive the cycles of the host. Here, average virulence over the cycle may be lower or higher than observed by the strongly stabilizing strategy (figure 2b) because the average per-host transmission rate and average virulence depend on how parasite burden changes over the cycle.

Figure 3.

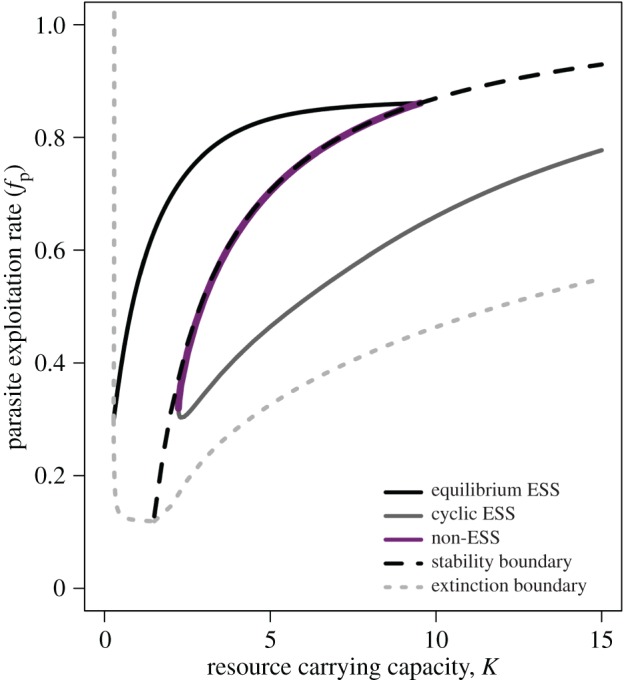
Singular parasite exploitation rate (f_P) strategies across a gradient in resource carrying capacity, K. The dotted grey line shows the parasite extinction boundary (for f_P below this line, the parasite cannot invade the host-only system). The dashed black line shows the stability boundary (Hopf bifurcation; for f_P above this line, the equilibrium of the system is stable). The solid black line shows the equilibrium population ES exploitation rates; the solid grey line shows the cyclic population ES exploitation rates that ‘ride the cycles’ of host density; the solid magenta line shows the non-ES singular strategies that are evolutionary repellors in this system—evolution will push the parasite population away from these strategies. The apparent overlap between the stability boundary and line of evolutionary repellors is coincidental—see electronic supplementary material, figure B2 for a case where these two lines do not overlap (here, the non-ES singular f_P values are actually slightly smaller than the boundary f_P values). (Online version in colour.)

Figure 4.

Comparison of the population dynamics of the parasite-free model (cyan line), the non-nested model at its ESS (red-dotted line), the nested model at the equilibrium ESS (black line) and the cycling ESS (grey line) for several values of resource carrying capacity, K. Parasites are always partially stabilizing, reducing the amplitude of population cycles and bounding the host population away from zero. (Online version in colour.)

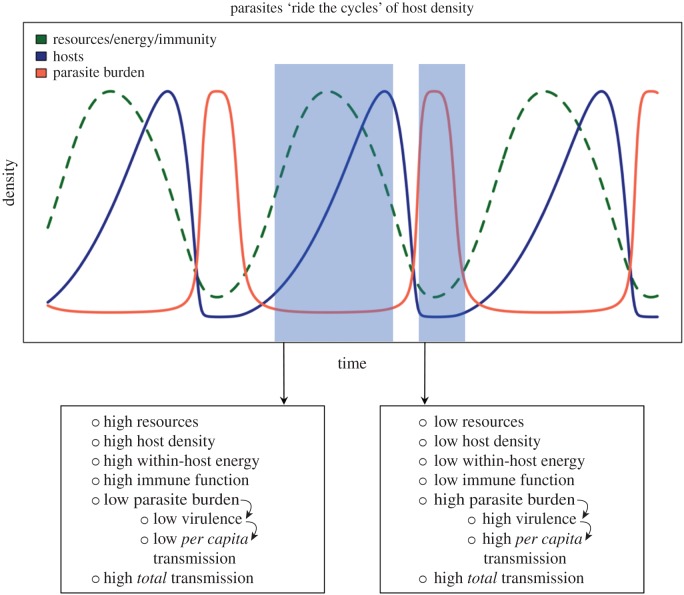
The existence of the second ESS emerges due to resource-driven feedbacks between within-host (individual-level) and between-host (population-level) processes (figure 5; electronic supplementary material, figure S3). During periods of high resources, host density increases. Here, hosts also have plenty of resources, leading to abundant within-host energy that fuels a strong immune response that suppresses parasite production, resulting in low within-host parasite burden and hence, low virulence and low per capita transmission rate. However, because host density is relatively high, the parasite has access to more hosts leading to a high total transmission rate (figure 5; electronic supplementary material, figure S3). This strategy continues until hosts overshoot their resources and begin declining. As resources decline, the immune response becomes resource-limited (i.e. low within-host energetics), resulting in high parasite burden within hosts and thus high virulence. However, high parasite burden also leads to a high per capita transmission rate, allowing the parasite to sustain itself when hosts are rare. The phases of high virulence are relatively short compared to the high resource phases because this strategy causes host density to drop quickly, such that the troughs in resources and host density occur almost simultaneously. As resources increase, hosts again begin to increase and the cycle continues (until the next cycle peak where hosts again overshoot their resources and become resource-limited). Together, these results illustrate how resource-driven feedbacks between with- and among-host processes allow parasites to ‘ride the cycles’ of their hosts.

Figure 5.

The time series of resources, susceptible host density and within-host burden from the nested model illustrates why a strategy emerges that ‘rides the cycles’ of host density. Within-host energy and immunity, although not plotted separately, closely mirror resource dynamics. Parasite burden within hosts (red line) is linearly related to virulence. Shaded regions highlight differences between within- and between-host dynamics under both high and low resource phases of the cycle. (Online version in colour.)

4. Discussion

Our results indicate that resource-driven changes in host population stability carry key consequences for parasite evolution (and vice versa). In the nested model, non-equilibrium host conditions resulted in a variety of novel and unanticipated predictions, including regions of evolutionary bistability (figure 3). In these regions, evolution could shift parasites towards high or low exploitation strategies (figures 2 and 3). These strategies, in turn, altered the stability of host populations; high exploitation strategies were strongly stabilizing while low exploitation strategies allowed parasites to ‘ride’ the cycles of the host (figure 5). However, classical non-nested models that do not account for feedbacks between individual- and population-scale processes missed these important links between host ecology and parasite evolution. These results also reveal key insight into the structuring role of parasites and further suggest that the stability of host populations may carry underappreciated implications for parasite evolution. Our results also suggest that when host populations fluctuate, accounting for such cross-scale feedbacks may prove particularly crucial to accurately predicting the evolution of parasite traits.

Under fluctuating population dynamics the nested model revealed regions of evolutionary bistabilty that the non-nested model did not (figures 2 and 3). These regions arose due to feedbacks between resource-driven changes in (i) processes within individual hosts (energetics, immune function and parasite production) and (ii) processes among hosts at the population level (host density, stability, transmission) that ultimately determined the parasite's lifetime potential for transmission (figure 5). As seen in other studies [44,45], virulence evolution tended to maximize lifetime transmission potential (electronic supplementary material, appendix A). Moreover, this maximum occurred at intermediate levels of within-host parasite burden (electronic supplementary material, figure S2). The nested model was necessary to capture these results because the production of parasites within individual hosts depended sensitively on host energetics and immune function, which depended on resource levels. Resource levels, in turn, depended on the dynamics of the host population. Together, these results illustrate how host resources could drive unexpected variation in parasite evolution.

Studies increasingly highlight that host resources play a prominent role in host–parasite interactions (e.g. [13,14,20,46–48]). Indeed, a number of papers in this special issue have highlighted how increased access to resources impacts immunity [48,49] and epidemiology [50,51]. However, studies that consider feedbacks between host ecology and parasite evolution remain surprisingly rare (but see, [1,19,44–46]). The framework developed here extends existing theory by combining three largely separate bodies of work: consumer-resource theory, classical epidemiological theory and adaptive dynamics [3,30,40] to explicitly account for resource antagonism between hosts and parasites [11,21]. The novelty of this study is its focus on resources as a mechanism that fully links processes at the within- and between-host scale, creating ‘essential’ nesting (sensu [11]). Most other nested models include parasite growth as a mechanism linking within- to between-host processes, but there is no link from between- to within-host. However, these links could be further strengthened. In the model used here, for example, to keep population dynamics comparable between the non-nested and nested models, host reproduction was decoupled from within-host processes; host reproduction depended only on resource ingestion.

Modifying the within-host model to couple energetics to both immune function and demography (e.g. making host birth rate a function of E rather than R) could yield important insight into links between host energetics, immune function and reproduction. Empirical studies that quantify these relationships remain rare and present a ripe area for future research. Moreover, the within-host model used here is just one among many possible models of within-host processes [21,52,53], chosen to maximize the potential for resource conflict between host and parasite. Other models could reveal alternative dynamical patterns (e.g. the parasite could peak in abundance when resources are abundant rather than rare), though we expect that resource-driven dynamical feedbacks will still allow alternate evolutionary strategies when the host population cycles. Slight adjustments to this existing framework could also examine how resource-immune links (‘bottom-up’ processes) determine co-infection dynamics [37,54]. Hence, our general yet mechanistic model could be applied to a diverse array of host–parasite systems and can also be used to examine links between other environmental factors and parasite evolution.

How and why virulence evolves poses a fundamental challenge to both basic and applied biology [55]. Recent theory illustrates that accounting for feedbacks between within-host viral load and between-host transmission can improve predictions of the evolutionary epidemiology in, for example, influenza, avian flu and HIV (reviewed in [12]). Our results extend existing theory by addressing bidirectional feedbacks between individual- and population-level processes [56,57]. These results also provide a guidepost for future studies investigating parasite evolution. First, the more complex nested models may only be necessary when host populations fluctuate. Second, the general theoretical framework here could be integrated with empirical data. To do so requires a concerted effort to quantify relationships between key environmental factors, immune function, parasite burden within hosts and total transmission potential at the population level. Such data-theory integration could bolster intervention strategies and provide a more complete understanding of host–parasite ecology and evolution [11,58].

Data accessibility

Electronic supplementary material, appendix A contains the mathematical analysis of the non-nested and nested model, including derivations of the invasion fitness and analysis of the singular strategies. It also contains the Mathematica code used to find singular strategies for the nested model under cycling conditions. A full, editable Mathematica notebook containing all of the analysis used to produce the data shown in the main text and electronic supplementary material, appendix B is available in the Dryad Digital Repository (https://doi.org/10.5061/dryad.7d60f) [59].

Authors' contributions

J.L.H. and C.E.C. designed the study and performed the analysis. J.L.H. wrote the initial draft of the manuscript and both J.L.H. and C.E.C. edited the manuscript.

Competing interests

We have no competing interests.

Funding

This research was supported by funding from the University of Nebraska-Lincoln.