Consequences of resource supplementation for disease risk in a partially migratory population

Abstract

Anthropogenic landscape features such as urban parks and gardens, landfills and farmlands can provide novel, seasonally reliable food sources that impact wildlife ecology and distributions. In historically migratory species, food subsidies can cause individuals to forgo migration and form partially migratory or entirely sedentary populations, eroding a crucial benefit of migration: pathogen avoidance through seasonal abandonment of transmission sites and mortality of infected individuals during migration. Since many migratory taxa are declining, and wildlife populations in urban areas can harbour zoonotic pathogens, understanding the mechanisms by which anthropogenic resource subsidies influence infection dynamics and the persistence of migration is important for wildlife conservation and public health. We developed a mathematical model for a partially migratory population and a vector-borne pathogen transmitted at a shared breeding ground, where food subsidies increase the nonbreeding survival of residents. We found that higher resident nonbreeding survival increased infection prevalence in residents and migrants, and lowered the fraction of the population that migrated. The persistence of migration may be especially threatened if residency permits emergence of more virulent pathogens, if resource subsidies reduce costs of infection for residents, and if infection reduces individual migratory propensity.

This article is part of the theme issue ‘Anthropogenic resource subsidies and host–parasite dynamics in wildlife’.

1. Introduction

Land use change and urbanization increasingly lead to overlap between wildlife and areas of high human population density [1]. Wildlife that are able to persist at the wildlife–human interface often do so by capitalizing on novel food resources provided unintentionally, e.g. through crop-raiding or scavenging of human trash, via exotic fruiting or flowering plants planted ornamentally or occurring as widespread invasives, and intentional feeding in parks and gardens. Food subsidies alter many components of life history, for instance by increasing breeding duration, breeding success and survival during harsh seasons [2], and by decoupling predator–prey relationships [3,4]. As a result, wildlife often spend more time and attain high densities in provisioned areas, but with unintended negative consequences such as increased pathogen pressure [5,6] and risk of spillover of zoonotic pathogens [7–9].

Anthropogenic food sources tend to be more spatially and seasonally predictable than food encountered in natural habitats [10], causing many animals to change their distributions and movement patterns (e.g. [11,12]). In particular, animals that undergo seasonal, long-distance migrations between breeding and nonbreeding habitats have been shown to adopt novel migratory routes and shorter migrations [13,14], or even to abandon migration altogether and form sedentary populations [15–17]. In combination with range-wide threats of climate change and habitat loss, provisioning that reduces migratory propensity may contribute to declines in migratory behaviour across taxa, and loss of important ecosystem services provided by migratory animals (e.g. [18,19]).

In migratory species where some individuals are able to abandon migration and form sedentary populations, food abundance is one critical mechanism that can affect the proportion of residents to migrants [20]. In historically partially migratory populations, the ability to capitalize on novel food sources may be particularly flexible. For example, individuals that migrate to escape harsh overwinter conditions are able to escape competition for scarce resources and move to more climatically favourable conditions, while those that remain resident have the advantage of being able to compete for and secure territories before migrants arrive [21,22]. In these cases, residents benefit from reproductive success while migrants benefit from increased overwinter survival. With resource supplementation, however, residents are more likely to survive over winter and have a competitive advantage in spring, potentially outweighing the life-history benefit of maintaining migrants in the population, and outcompeting migrants.

A reduction in migratory propensity in response to food supplementation would seem beneficial for populations that no longer need to migrate to track seasonal resources or escape inhospitable environmental conditions [23]; these populations in theory avoid migration-caused mortality. A reduction in migratory propensity, however, could mean loss of a major benefit of migration: escape from predation [24,25] and pathogen pressure [26]. Mathematical models have been useful for exploring the mechanisms by which migrants experience reduced pathogen impacts, including seasonal escape from sites of high transmission potential by all migrants [27] or by highly susceptible host stages [28], disproportionate mortality of infected individuals during costly migrations [29], and recovery from infection on nonbreeding grounds [30]. In areas where food provisioning or other external forces increase sedentary behaviour in partially migratory or formerly fully migratory populations, however, these benefits of migration may be lost, leading to enhanced transmission and potential maintenance of more virulent pathogens.

Mathematical models have been developed to explain the evolution and maintenance of partially migratory populations [31–33] and the consequences of resource provisioning for local and spatial pathogen transmission [34,35]. We lack, however, synthetic studies that explore pathogen dynamics in partially migratory populations. Increases in resource availability and more favourable overwinter climates that increase nonbreeding season survival across taxa make such studies particularly timely. Here, we explored how increased nonbreeding resident survival, one potential direct consequence of resource supplementation, affects the persistence of migration and a shared pathogen in a partially migratory population where the breeding location is shared. Since residents frequently find mates and establish breeding territories before migrants return [36], we make the simplifying assumption that residents and migrants do not interbreed. We assume that offspring adopt the same strategy as their parents, and further assume that migrants and residents do not switch strategies, except in the case in which costs of infection cause migrants to adopt a resident strategy with some probability. These are reasonable assumptions given that residents tend to outcompete migrants for resources and territories, individuals often maintain a given migratory strategy over time, both facultative and obligate migration strategies can exist within a population, and in cases where switching occurs, it is more often migrant to resident than vice versa [37–40].

We explore the possibility of switching migratory strategies upon infection because infected individuals may have delayed migratory departure and shorter migrations [41,42], which could ultimately lead to residency. We expect reverting back to a migratory strategy to be less likely in the avian system with which we parametrize our model because infected individuals are unlikely to recover (e.g. from avian malarias [43]), and the likelihood of switching strategies multiple times is low given a relatively short lifespan in the wild [44]. In addition, with resource supplementation, we expect that individuals that are delayed from departing should benefit from abandoning migration, given high costs of infection on migration [45]. We do not here model fecundity costs of infection, and thus migrants that become resident due to infection have the same reproductive success as residents if they survive the nonbreeding season.

Our mathematical modelling framework explores how increased nonbreeding resident survival, our proxy for increases in resource provisioning, alters disease risk in partially migratory populations, and the role of migration in mediating pathogen prevalence. For a partially migratory population where the majority of individuals migrate prior to resource supplementation, we expected that (1) long-distance migration would minimize infection prevalence through migratory culling and seasonal escape from infected biting vectors in the breeding region; (2) increases in nonbreeding season survival of individuals that forgo migration would reduce the proportion of migrants in the population; and, therefore, (3) increasing residency, presumably induced by resource supplementation, would increase infection prevalence by eroding the population-level benefits of migration for reducing pathogen impacts.

2. Material and methods

We present a modelling framework for a partially migratory host population and a pathogen that is transmitted by a biting vector in the host breeding range. We focused on the case of ‘nonbreeding partial migration’, whereby individuals breed in the same location but spend the nonbreeding season apart [21]. We assumed that the major fitness effect of resource supplementation was to increase survival of residents during the nonbreeding season; this is consistent with increasing numbers of primarily migratory songbirds overwintering at north-temperate latitudes in gardens and cities, where they capitalize on provisioned food such as seeds and suet, and ornamental plantings that provide fruit, flowers or evergreen foliage that supports invertebrate prey [46,47]. The goal of our model was, therefore, to analyse how increased nonbreeding season survival in the breeding region, a likely consequence of resource supplementation [46,48], influences the coexistence of migrants and residents, and invasion and persistence of pathogens. The model was motivated by, and parametrized for, a partially migratory passerine bird for which migration distances have become increasingly shorter, but its general structure may be adapted for other partially migratory host taxa.

(a). Disease-free model

Let N = N(Y, τ) be the population size of the partial migrant in year Y and within-year time τ. For model tractability, we assumed a perfectly heritable migration strategy, with the number of migratory and resident individuals given by N_M and N_R, respectively. The breeding ground has a favourable season beginning at within-year time τ = τ₀, and ending at τ = τ₁, during which conditions are suitable for breeding, and migrants and residents experience the same per capita mortality rate, μ_b. We assumed that residents initiate breeding at the beginning of the favourable season, but that migrants initiate breeding with a small delay δ (i.e. at within-year time τ = τ₀ + δ) due to constraints of migration timing. Migrants and residents cease breeding at τ₁ and migrants depart, experiencing relatively high migratory mortality (μ_mig > μ_b) during a one-way migration of duration T_mig, followed by relatively low mortality at their wintering site (μ_w ≈ μ_b) for the duration of overwintering, T_w. In the unfavourable season (i.e. nonbreeding season, T_nb, of within-year duration T_nb = 1 − (τ₁ − τ₀)), residents experience relatively high nonbreeding mortality (μ_nb > μ_b) that declines with increasing resource supplementation.

Migrants and residents compete for resources on the breeding ground, and so the population is regulated by density dependence in offspring production. To avoid offspring contributing to reproduction in their hatch year, resident and migrant fecundity is proportional to the number of residents surviving the winter (N_RB), and the number of returning migrants (N_MB), respectively. We describe the population dynamics of migrants and residents through an annual cycle by systems of differential equations for each of the breeding and nonbreeding phases. When both migrants and residents are breeding (τ₀ + δ < τ < τ₁), the dynamics are given by

2.1a

and

2.1b

where the subscripts M and R refer to the migrant and resident populations, respectively, b₀ and b₁ are the density-independent and density-dependent reproductive rates, and μ_b is mortality during the breeding season. Prior to the arrival of the migrants (τ₀ < τ < τ₀ + δ), the residents' breeding dynamics are given by equation (2.1b), where N in the density-dependent reproduction term is simply N_R because no migrants are present.

Outside of the breeding season, we assumed that migrants and residents experience density-independent mortality at rate μ_j, where j = [mig, w, nb], during periods of migration, migrant overwintering and resident nonbreeding (each with respective duration T_j). The probability that migrant or resident individuals survive each of these periods is therefore

2.2

Equation (2.2) can be used to relate the number of breeding migrants and residents in the current year to the respective number of residents and migrants at the end of the previous breeding season:

2.3a

and

2.3b

Together, equations ((2.1)–(2.3)) describe the interannual dynamics of the system.

(b). Host–pathogen dynamics

We followed Hall et al. [29] and assumed the focal pathogen is transmitted by a biting vector at the partial migrant's shared breeding ground whose activity period coincides with the favourable season (figure 1). Because we are modelling a vector in a temperate system, we describe the seasonal vector emergence rate, E(τ), by a quadratic function with peak emergence E_max in the middle of the favourable season:

2.4

and vectors experience per capita mortality at rate μ_v. Following Hall et al. [29], we further assumed that the partially migratory host species is the primary competent reservoir for the pathogen, such that infection of vectors depends only on the number of infected residents and migrants, and that the vector distributes bites among a larger community of vertebrates such that the biting rate per host is independent of the host's population size. Thus, the transmission rate from hosts to vectors and vice versa is described by two constants, β_hv and β_vh, respectively.

Figure 1.

Overview of vector, resident and migrant population dynamics throughout the annual cycle (a), and associated timing for each period (b). (a) Schematic of the population and infection dynamics of a partially migratory host population, where resident and migratory populations share their breeding grounds with a disease-causing vector. Each large rectangle represents the breeding, migratory and wintering range of the migrant. Squares represent the populations of susceptible (S) and infected (I) migrant and resident (subscripts M, R respectively) hosts, and circles represent susceptible and infected vectors (subscript V). Solid arrows represent transitions between states resulting from births, deaths and infection; dashed arrows indicate variables influencing transmission rates. (b) Seasonal presence of residents, migrants and vectors throughout the migratory range. Grey shaded regions represent the timing of habitat use by the migrant, black lines indicate seasonal presence of migrants, residents and adult vectors during their breeding (thick lines) or nonbreeding (thin lines) period. Solid grey vertical lines represent the timing of migratory departure and arrival, and the grey dashed line denotes the onset of breeding in resident hosts and vectors.

We modelled costs of infection to the host as proportionate increases in mortality rates, which may vary through the annual cycle for residents and migrants; the mortality rate of infected individuals in stage j is μ_j/(1 − c_j), where c_j in [0, 1] is the magnitude of the associated cost. Additionally, we considered the case where infection may cause migrants to abandon migration and join the resident population with probability p ≥ 0. Vectors do not incur costs of infection, but we accounted for any vector mortality between the vector acquiring the pathogen and becoming infectious by the probability of the vector surviving the latent period, θ.

Denoting the susceptible and infected populations of migrants, residents and vectors as S_k and I_k, where k = [M, R, V], the host–pathogen dynamics when residents and migrants co-occur with vectors (i.e. when τ₀ + δ < τ < τ₁) are described by the system of equations

2.5a

2.5b

2.5c

2.5d

2.5e

2.5f

where I = I_M + I_R, N = S_M + S_R + I. The number of breeding adult migrants and residents at the beginning of their respective breeding seasons (N_MB, N_RB) is obtained by calculating the number of susceptible and infected individuals that survive their nonbreeding period (i.e. the product of their population sizes at the end of the breeding period and their nonbreeding survival), such that

2.6a

and

2.6b

The nonbreeding survival of migrants (partitioned into survival at the overwintering site and two rounds of migration) and residents are defined in equation (2.3), with survival of infected individuals modified by the cost of infection to migration or overwintering mortality. Before the migrants return to the breeding site (τ₀ < τ < τ₀ + δ), the resident-vector–pathogen dynamics are described by (2.5a,b) with N replaced by N_R, and by (2.5e,f) with I replaced by I_R. We summarize the model structure in figure 1, and provide a list of model parameters, their definitions, and default values in table 1.

Table 1.

Summary of model variables, parameters, definitions and their initial or default values (for those parameters that were varied, the range is shown in brackets). All times are in units of years and rates in units of years⁻¹.

symbol		definition	value
variables	SM	susceptible migrants	450
	IM	infected migrants	50
	SR	susceptible residents	450
	IR	infected residents	50
	SV	susceptible vectors	0
	IV	infected vectors	0
phenology	τ0, τ1	start and end of favourable season at breeding site (breeding period for residents and vectors)	0.29 (≈mid-late Apr), 0.74 (≈mid-late Aug)
	δ	delay between τ0 and migrant arrival	0.042 (≈2 weeks)
	Trb	duration of resident breeding (= τ1 − τ0)	0.45 (5.4 months)
	Tnb	duration of resident nonbreeding (= 1 − Trb)	0.55 (6.6 months)
	Tmb	duration of migrant breeding (= Trb − δ)	0.41 (4.9 months)
	Tmig	duration of one-way migration	0.092 (1.1 months)
	Tw	duration of migrant wintering (= 1 − Tmb − 2Tmig)	0.41 (4.9 months)
demography	b0	density-independent reproductive rate	3.7
	b1	density-dependent reproductive rate	3.7 × 10−3
	μb	breeding season resident and migrant mortality rate	0.075
	σnb	resident nonbreeding survival probability	0.49 [0.35–0.6]
	σmig	migration survival probability (one-way)	0.74
	σw	migrant overwintering survival probability	0.97
	Emax	maximum vector emergence rate	3.65 × 105 (100/day)
	μv	vector mortality rate	20 (≈18 day lifespan)
infection	βhv	transmission rate from host to vector	0.02
	βvh	transmission rate from vector to host	0.02
	cb	cost of infection to breeding survival	0.3
	cnb	cost of infection to resident nonbreeding survival	0.3 [0.1–0.8]
	cmig	cost of infection to migration survival	0.8 [0.3–0.8]
	cw	cost of infection to migrant overwinter survival	0.3
	p	probability infected migrant becomes resident	0 [0–0.5]
	θ	probability of vector surviving latent period	0.67

(c). Parametrization

We parametrized our models using American Robins (Turdus migratorius) as an example because many now remain resident in urban areas at more northerly latitudes, they are known to be fed on seasonally by arthropod vectors (mosquitoes, blackflies and ticks) that transmit pathogens including avian malaria, and they are competent reservoir hosts for zoonotic pathogens of human health concern, including West Nile virus and Lyme disease [49–51]. We provide default parameter values in table 1, and details of the parameter derivation in the electronic supplementary material.

(d). Analysis

As noted above, we assumed that the effect of resource supplementation was primarily to increase nonbreeding survival of the resident portion of the population. First, we varied resident nonbreeding survival to examine how the population sizes of migrants and residents, and migratory propensity (the fraction of the population that migrates, N_M/N), respond to resource supplementation in the absence of pathogens, and in the presence of pathogens that inflict different costs on survival across the annual cycle. When pathogens were present, we also recorded infection prevalence in the host population (I/N) and in migratory and resident hosts (I_M/N_M, I_R/N_R, respectively).

We considered the following scenarios for pathogens with differing costs of infection to compare to disease-free scenarios:

• (i) Baseline: moderate costs of infection for both migrants and residents (infected individuals experience a 30% reduction in expected lifespan) distributed proportionally through the seasonal mortality rates; c_j = 0.3 for j = [b, mig, w, nb], and all infected migrants attempt migration (p = 0);

• (ii) Migratory virulence: elevated costs of infection for migrants during migration (c_mig varied up to a maximum of 0.8, representing a pathogen too virulent to persist in a wholly migratory population);

• (iii) Nonbreeding tolerance: the cost of infection on nonbreeding resident survival is reduced by resource supplementation (c_nb varied down to 0.1);

• (iv) Nonbreeding virulence: harsh environmental conditions in winter cause elevated costs of infection for resident nonbreeding survival (c_nb varied up to 0.8, representing a pathogen too virulent to persist in a wholly resident population); and

• (v) Disease-induced residency: infected migrants abandon migration and become resident with probability p ≤ 0.5.

We ran all models in R [52] using the deSolve package [53]. Where maximum and minimum values are output in models, for simplicity we present minimum host population sizes, minimum migratory propensity, and maximum host infection prevalence. We chose these cases because we consider them of most relevance to conservation, allowing us to identify potential conditions under which food-subsidized sedentary populations could lead to undesirable outcomes such as loss of migration or increased risk of zoonotic spillover.

3. Results

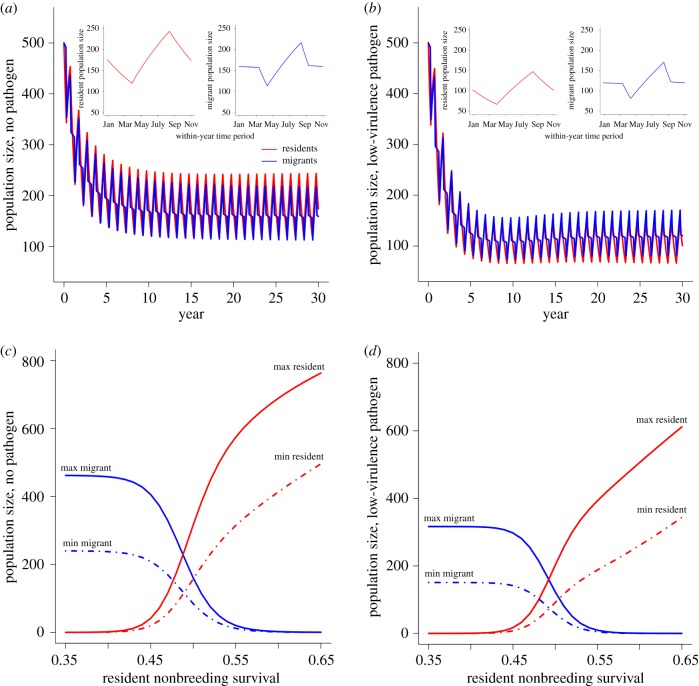
After an initial transient phase of approximately 20 years, host and pathogen dynamics settled into an annually repeating pattern (henceforth referred to as ‘equilibrium’) in which population size increased during the breeding season and declined across the nonbreeding portions of the year (figure 2a,b); provided at least some residents, migrants and pathogen were present initially, the equilibrium pattern was independent of initial conditions. In the disease-free case, when resident nonbreeding survival was increased from low values that prevent long-term persistence of resident populations (σ_nb ≈ 0.35), the migratory population declined and the resident population increased until migrants were competitively excluded (at σ_nb ≈ 0.6; figure 2c).

Figure 2.

Resident and migrant population sizes (red and blue lines, respectively) for disease-free (left column) and infection with a low-virulence pathogen (c_all = 0.3, right column). (a,b) Population trajectory over a 30-year period, showing dynamics settling into an equilibrium annually repeating pattern; insets show within-year resident and migrant population sizes at equilibrium. (c,d) Maximum (solid lines) and minimum (dot-dashed lines) resident and migrant population sizes at equilibrium as a function of resident nonbreeding survival (σ_nb).

(a). Scenarios

(i). Baseline (c_j = 0.3 throughout the annual cycle)

In the presence of a moderately virulent pathogen that reduced both resident and migrant survival equally across the annual cycle, the range of values of resident nonbreeding survival (σ_nb) for which residents and migrants coexisted was similar to the disease-free case (figure 2c,d). The maximum and minimum population sizes of residents and migrants, however, were lower (figure 2d). Maximum and minimum host population sizes through the equilibrium annual cycle responded in a qualitatively similar way to increases in σ_nb, justifying our inclusion in the results of only cases that we consider of most relevance for conservation: minimum host population sizes, minimum migratory propensity and maximum host infection prevalence.

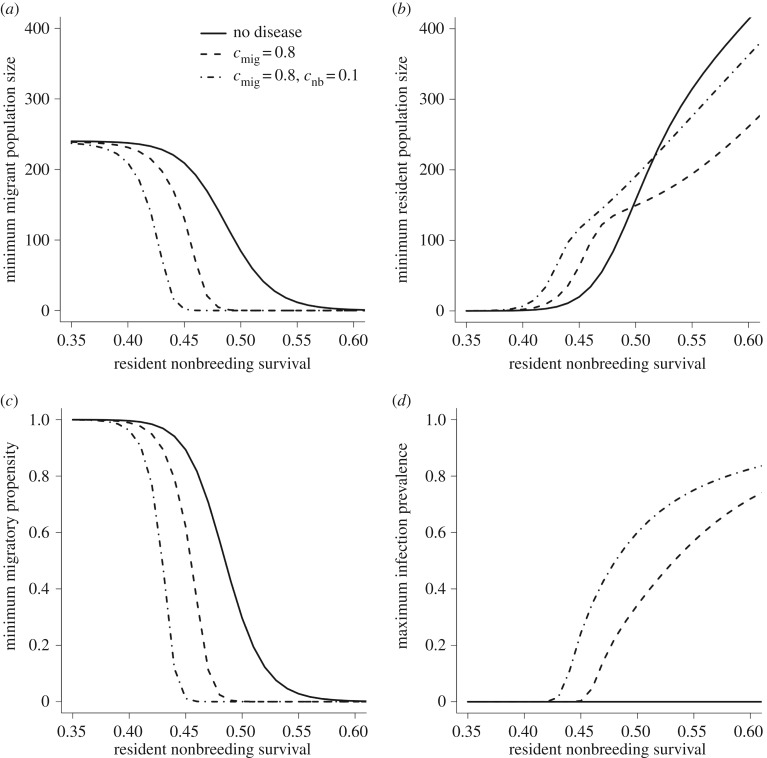
(ii). Migratory virulence (c_mig > baseline)

When the cost of infection on migration was high and resident nonbreeding survival was too low for resident populations to persist, the pathogen was unable to establish, maximizing migrant population size (figure 3). Increasing nonbreeding season survival allowed resident hosts to establish and sustain parasite transmission, and migration was lost from the population at lower values of resident nonbreeding survival than in the baseline or disease-free cases (figure 3a,c and electronic supplementary material, figure S1a). Infection prevalence increased quickly with σ_nb as the number of migrants declined, and the role of migratory culling in reducing prevalence was diminished (figure 2d). At modest increases in nonbreeding survival, resident population sizes were high relative to the disease-free case, due to disease-induced mortality in migrants reducing breeding-season competition; however, at higher levels of σ_nb where the host population was dominated by residents, equilibrium resident population sizes were lower than the disease-free scenario (figure 3b).

Figure 3.

Minimum population size of (a) migrants and (b) residents, (c) minimum fraction of the population that migrates (i.e. migratory propensity) and (d) maximum infection prevalence across a range of resident nonbreeding survival values, σ_nb. Results are shown for three model scenarios: disease-free (solid lines); infection induces high survival costs during migration only (c_mig = 0.8; dashed lines); and infection causes high migratory mortality and food provisioning lowers costs of infection for residents in the nonbreeding season (c_mig = 0.8, c_nb = 0.1; dotted-and-dashed lines). All other parameter values are listed in table 1.

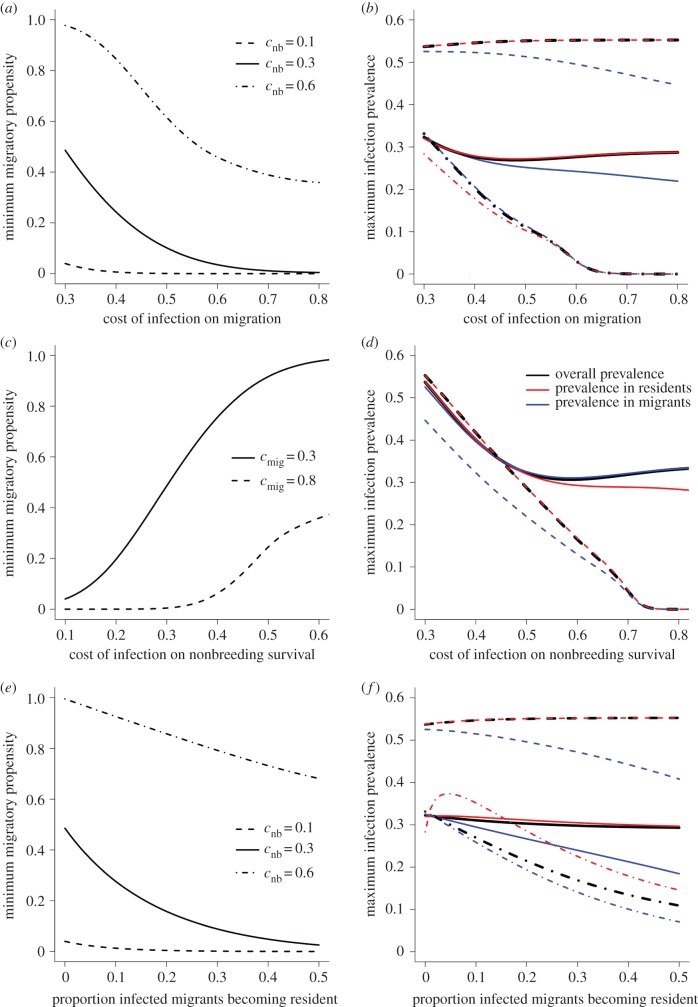
For a fixed value of nonbreeding survival that permitted disease-free coexistence of residents and migrants (σ_nb = 0.49), the proportion of the population that migrates declined as the cost of infection on migration increased (figure 4a). When costs of infection to nonbreeding survival were moderate (c_nb = 0.3), infection prevalence across all hosts was minimized at intermediate values of migratory virulence, reflecting the switch from a decreasing relationship between prevalence and virulence when the host population was dominated by migrants, to an increasing but saturating relationship as the resident population increased (figure 4b, bold lines).

Figure 4.

Minimum fraction of the population that migrates (i.e. migratory propensity) and maximum expected infection prevalence for (a,b) varying levels of costs of infection on migration, c_mig, (c,d) varying levels of costs of infection on nonbreeding resident survival, c_nb, and (e,f) when a proportion of infected migrants forgo migration. Resident nonbreeding survival, σ_nb, = 0.49 in all cases, and all c values not shown in figure = 0.3.

(iii). Nonbreeding tolerance (c_nb < baseline)

When we reduced the cost of infection on resident nonbreeding survival, a potential consequence of resource supplementation, residents established at lower values of σ_nb and migrants were lost from the population (electronic supplementary material, figure S1a,b). This effect was exacerbated when the pathogen caused high migratory virulence, and the range of σ_nb values for which coexistence of migrants and residents occurred was lower (figure 3a–c). Migratory populations were generally smaller (figure 3a), and overall infection prevalence was higher (figure 3d) when overwinter survival of infected residents was higher; this is the result of larger resident populations (figure 3b) negatively impacting migrants both through direct competition and through disease-mediated apparent competition.

(iv). Nonbreeding virulence (c_nb > baseline)

When nonbreeding survival of infected residents was low, reflecting that infected individuals may be particularly vulnerable to harsh environmental conditions such as cold snaps, formation of persistent resident populations only occurred at substantially lower levels of natural overwinter mortality (i.e. the population was wholly migratory for larger values of σ_nb relative to the baseline; electronic supplementary material, figure S1a–c). For a fixed value of σ_nb permitting disease-free coexistence, migratory propensity increased with higher costs of infection on nonbreeding resident survival (figure 4c). For a pathogen causing moderate migratory virulence, infection prevalence was minimized at intermediate nonbreeding virulence; a weak positive relationship between overall prevalence and high resident nonbreeding virulence is explained by a feedback between disease-induced mortality of residents releasing the migratory population from competition, allowing elevated pathogen transmission in migrants that spills over into residents (figure 4d). Pathogens causing high virulence during migration and the resident nonbreeding season were typically unable to persist (figure 4b,d)

(v). Disease-induced residency (p > 0)

When infection made migrants more likely to forgo migration and become resident, migratory propensity was typically lower (figure 4e), and migrants were lost from the population at lower values of resident nonbreeding survival (electronic supplementary material, figure S1c). The net effect of disease-induced residency on population sizes and infection prevalence in migrants and residents depended on nonbreeding costs to infected residents. When we assumed that provisioning would reduce nonbreeding virulence, migrant population size and infection prevalence decreased, while resident population size and prevalence increased, with increasing probability of infection-induced residency (electronic supplementary material, figure S1a,b; figure 4f). For pathogens causing high nonbreeding virulence in residents, when nonbreeding survival was low (σ_nb < 0.45), disease-induced residency increased migrant population sizes by reducing infection prevalence (and associated migratory culling) in the migrant population (electronic supplementary material, figure S1a,d). When nonbreeding resident survival was increased, competition with residents reduced migrant population size, but overall infection prevalence remained low as increasing numbers of infected migrants recruited to the resident population and experienced high nonbreeding virulence (electronic supplementary material, figure S1a,d; figure 4f).

4. Discussion

We investigated mechanisms by which anthropogenic resource subsidies can influence migratory propensity and infection prevalence in a partially migratory population in which individuals have a shared breeding location and spend the nonbreeding season apart. We found that improved nonbreeding survival of residents, a potential consequence of food subsidies, can cause declines in migrant populations. Our results emerge via disease-induced and density-dependent declines that play out in the real world through increased competition for breeding resources and elevated exposure to pathogens. Increased pathogen exposure in migrants can occur as a result of the loss of key mechanisms of pathogen avoidance in migratory populations: migratory escape (seasonal departure from transmission sites reducing seasonal overlap with disease-causing agents) and migratory culling (high mortality of infected individuals during migration, or of individuals that abandon migration and succumb to harsh environmental conditions in the unfavourable season). The benefits of migratory escape are diminished by provisioning, however, because residents experience an extended pathogen transmission season relative to migrants and improved overwinter survival, resulting in higher infection prevalence in biting vectors when migrants return to their breeding grounds. Migratory culling or abandonment of migration by infected individuals can fail to reduce infection prevalence in migrants because provisioned resident populations can reach relatively high abundance and sustain transmission of pathogens, including those that would be too virulent to be maintained in wholly migratory populations.

Our work suggests several non-exclusive mechanisms by which resource supplementation can result in high disease burdens in partially migratory populations: (i) extended overlap of residents with a seasonally transmitted pathogen that increases the transmission window; (ii) increased resident population sizes that support more transmission; and (iii) increased survival of infected residents (and migratory ‘dropouts’) between transmission seasons to initiate seasonal epidemics. Several other lines of theoretical and empirical evidence support provisioning increasing host–pathogen overlap. In monarch butterflies (Danaus plexippus), planting of non-native milkweeds that do not die back in winter leads to year-round monarch breeding and ingestion of infective spores of the protozoan Ophryocystis elektroscirrha by their larvae; the resulting sedentary populations experience higher infection prevalence than migratory populations [15,54]. Additionally, increased aggregation of wildlife in food-provisioned areas has been demonstrated theoretically to increase pathogen transmission [34], and may be associated with larger outbreaks of Hendra virus in urban-living flying foxes (Pteropus spp.) [16]. Finally, food supplementation has been proposed to modulate costs of infection through improved immune defense in urban-feeding kit foxes (Vulpes macrotis mutica) [55] and provisioned house finches (Haemorhous mexicanus) [56]. Such mechanisms could also be important for transmission of potentially zoonotic pathogens in migratory waterfowl where infection reduces migratory propensity (e.g. [41]), but which successfully overwinter at more northerly latitudes in response to agricultural subsidies [57].

We modelled our framework for investigating vector-borne disease dynamics after a food-supplemented avian partial migrant. Given the assumptions underlying our model, the qualitative results that migrants declined, residents increased and overall prevalence increased when provisioning increased resident nonbreeding survival were not entirely surprising. We did not, however, have clear quantitative predictions about the magnitude of effects of differential costs of infection through the annual cycle of residents and migrants, or migratory dropout, and we did not a priori expect the nonlinear relationships between these variables and infection prevalence (e.g. figure 4). Ours is the first study to our knowledge to outline general predictions for resource supplementation altering migratory propensity and pathogen impacts, and to verify these with a mathematical model. This framework could readily be adapted and applied to other partially migratory taxa for which resource supplementation may affect migratory behaviour (e.g. [58]) and vector-borne parasites (e.g. ungulates and tick-borne diseases), to interacting residents and migrants of different species, and to scenarios where residents, migrants and parasites overlap in one or more parts of the migratory range. Our findings may also apply more generally to other modes of long-distance animal movement that may emerge in populations that also exhibit resident and migratory strategies, such as nomadism [59], or to directly or environmentally transmitted pathogens, provided that migrants and residents only aggregate at densities permitting transmission at their shared breeding site. Patterns of increased infection risk associated with sedentary behaviour have been attributed to other anthropogenic or environmental drivers of reduced migratory propensity; for example, climate change that results in shortened migrations and longer transmission windows [28] and barriers to migration [29].

In our model, we focused on effects of resource subsidies on residents during a temperate-latitude nonbreeding period (improvements to survival and reductions to costs of infection). We assumed that harsh environmental conditions prior to provisioning were most likely to limit establishment of resident populations and survival of infected individuals, and that availability of natural (i.e. non-supplemented) resources was the primary driver of breeding success and higher survival during the favourable season. Given that partial migration is a naturally occurring phenomenon, however, the mechanism by which we model it is likely independent of the potential for increases in pathogen prevalence with higher resident nonbreeding survival. Negative effects of food subsidies on migratory population size may not occur if both residents and migrants experience benefits from food subsidies during the breeding season, if migrants experience additional carryover effects that offset the delay in breeding initiation relative to residents [48], or if food subsidies in other parts of the migratory range improve survival away from the breeding sites. In cases where supplemental feeding stimulates explosive breeding in hosts, or where the cost of infection for both migrants and residents is low, and is even lower for nonbreeding residents with food supplementation (e.g. c_nb = 0.1, all other c = 0.3, unpubl. simulations), population cycles for a highly transmissible, highly virulent pathogen might be expected. In addition, the relationship between food subsidies and increases in nonbreeding survival could saturate or lead to population cycles if resources or increased population sizes attract predators. Nevertheless, these positive effects of food supplementation may still be associated with increases in infection prevalence that may be relevant to zoonotic spillover [34].

We considered a pathogen that causes lifelong infection, as is often seen in short-lived songbirds infected by haemospiridian parasites [60]. Food subsidies could reduce infection prevalence if associated improvements to host immune defense allow them to recover more rapidly [34]. Alternatively, sedentary behaviour promoted by provisioning could erode another proposed benefit of migration: migratory recovery from infection [30]. Our model does not account for interannual variability in the harshness of environmental conditions in the nonbreeding season, or for the possibility of frequent extra-pair mating interfering with the temporal separation of mate acquisition, even in otherwise highly monogamous species. If food subsidies promote the formation of sedentary populations and draw in infected individuals from migratory populations, occasional climatic extremes such as cold snaps could extirpate resident populations and reduce pathogen transmission. However, if ephemeral resident populations also have a large negative effect on migrant abundance following mild winters, resource subsidies could threaten the persistence of the partial migrant and, therefore, act as an ecological trap.

In sum, our work suggests that animal migration, already considered to be a threatened phenomenon [18], may be negatively impacted through elevated transmission of virulent pathogens associated with food subsidies that allow resident populations to form. In extreme cases, this could lead to the irreversible loss of migratory phenotypes, with unforeseen consequences for ecosystem services [19]. Since food supplementation can increase infection prevalence of low-virulence pathogens in residents and migrants, it has the potential to influence zoonotic spillover risk not only at food-provisioned sites, but throughout the migratory range [35]. Our work presents a valuable framework for ecologists, highlights important consequences for wildlife managers, and motivates further empirical research on how food subsidies influence migratory decisions, survival, pathogen exposure risk and costs of infection in imperilled migrants and partial migrants that are known reservoirs for zoonoses.

Data accessibility

A version of the R code that can be used to run all models is included in this article's electronic supplementary material.

Authors' contributions

L.M.B. and R.J.H. contributed equally to conception and execution of the ideas, models and code for this manuscript, and drafted and revised the final manuscript.

Competing interests

The authors declare no competing interests.

Funding

This work was supported by a National Science Foundation (NSF) Postdoctoral training grant no. 1402287 in Mathematical Biology to L.M.B., and a NSF Ecology and Evolution of Infectious Disease grant no. DEB-1518611 to R.J.H.