Intrinsically Disordered Protein Exhibits Both Compaction and Expansion under Macromolecular Crowding

Abstract

Conformational malleability allows intrinsically disordered proteins (IDPs) to respond agilely to their environments, such as nonspecifically interacting with in vivo bystander macromolecules (or crowders). Previous studies have emphasized conformational compaction of IDPs due to steric repulsion by macromolecular crowders, but effects of soft attraction are largely unexplored. Here we studied the conformational ensembles of the IDP FlgM in both polymer and protein crowders by small-angle neutron scattering. As crowder concentrations increased, the mean radius of gyration of FlgM first decreased but then exhibited an uptick. Ensemble optimization modeling indicated that FlgM conformations under protein crowding segregated into two distinct populations, one compacted and one extended. Coarse-grained simulations showed that compacted conformers fit into an interstitial void and occasionally bind to a surrounding crowder, whereas extended conformers snake through interstitial crevices and bind multiple crowders simultaneously. Crowder-induced conformational segregation may facilitate various cellular functions of IDPs.

Introduction

It is now well recognized that more than one-third of proteins are intrinsically disordered or contain disordered regions, and the disorder is essential for signaling, regulation, and other cellular functions (1, 2, 3, 4). Characterizing the conformational ensembles of intrinsically disordered proteins (IDPs) is challenging but crucial for gaining deeper understanding of their cellular functions (5). For IDPs, their conformational malleability allows them to respond in a variety of ways to interactions with other molecules. In particular, disorder-to-order transition upon binding to specific targets is a common mechanism for signaling and regulation. In cellular environments, IDPs also experience nonspecific interactions with many bystander macromolecules (or crowders), and these interactions are expected to alter the conformational ensembles of the IDPs. Indeed, many studies have demonstrated significant effects of macromolecular crowding on the thermodynamic and kinetic properties of protein binding, folding, and conformational transitions (6, 7, 8, 9, 10, 11, 12, 13). Earlier studies have focused on the effects of steric repulsion by macromolecular crowders, given their generic nature, but recently the effects of weak favorable interactions, or soft attraction, have gained increasing attention. The aim of this study was to dissect the effects of steric repulsion and soft attraction by synthetic polymer and protein crowders on the conformational ensemble of the IDP FlgM, using small-angle neutron scattering (SANS) in combination with circular dichroism (CD) spectroscopy and coarse-grained simulations.

A variety of experimental techniques have been used to study the effects of macromolecular crowding on the ensembles of IDPs and unfolded proteins. Bulk and single-molecule fluorescence resonance energy transfer have revealed conformational compaction of an IDP and an unfolded protein by synthetic polymers (14, 15). Compaction of the IDP α-synuclein by both the synthetic polymer Ficoll and the protein bovine serum albumin (BSA) as crowders and in crowded cellular environments has also been observed in NMR studies (16, 17, 18). Whereas these and other studies using CD, fluorescence, and NMR spectroscopy indicated persistence of disorder under in vitro and in vivo crowding (19, 20, 21, 22), at least one study suggested crowding-induced gain of structure, in the case of FlgM (see below) (23).

By masking the signals of crowders through contrast matching (24), SANS is uniquely suited to study conformations of a tracer protein in crowded environments. As a prelude to biological applications, a SANS study showed compaction of polyethylene glycol (PEG) in Ficoll as a crowding agent (25). A recent SANS study on the homodimer of superoxide dismutase showed modest compaction of this structured protein complex under crowding by PEG (26). Most relevant to this study, Goldenberg and Argyle (27) used SANS to determine the size, i.e., the radius of gyration (R_g), of an IDP under crowding by globular proteins and found minimal crowding effects, in contrast to conformational compaction expected from steric repulsion by crowders. It has been argued that any compaction due to steric repulsion could be offset by the effect of soft attraction with the crowders (27, 28). In the foregoing studies, the SANS data were analyzed using the traditional Guinier (29) or indirect Fourier transform method (30, 31). In these methods, the scattered intensity I(q) as a function of the magnitude, q = 4πsinθ/λ (θ is the half-angle between incident and scattered beams; λ is the wavelength of the incident beam) of the scattering vector, is either plotted (on a log scale) against q², with the slope at low q yielding R_g, or Fourier-transformed into real space to yield the distance distribution function p(r) between scattering centers. A more recent method, the ensemble optimization method (EOM) (32, 33), which searches for the optimal conformational ensemble for matching the scattering data, has been employed for α-synuclein bound to lipid membranes (34). This SANS data analysis showed that similar R_g values could arise from two distinct conformational populations.

Computational studies of the conformational ensembles of IDPs under crowding by repulsive crowders have provided theoretical support for the compaction of IDPs in many experimental studies. Coarse-grained simulations of an IDP chain in repulsive crowders showed significant decreases in the radius of gyration of the IDP under crowding, suggesting steric repulsion by crowders as a common cause for chain compaction observed in experimental studies (35). Similar results were reported in two subsequent studies (36, 37). The second of the latter studies was of particular interest because the IDP was modeled as a heteropolymer instead of a homopolymer, hence allowing the incorporation of sequence information. In stark contrast, all-atom simulations of a small IDP (47 residues) in PEG and protein crowders revealed much more variable crowding effects (38). Although PEG, itself an extended polymer chain, induced the IDP into extended conformers with only modest secondary structure, interactions with the protein crowders forced the IDP into relatively compact conformers with well-defined α-helices.

It is abundantly clear that our knowledge about how IDPs respond conformationally to macromolecular crowding is far from complete. Although conformational compaction due to steric repulsion by macromolecular crowders has been emphasized in previous studies, potential effects of soft attraction by crowders are largely unexplored. For a generic polymer interacting with a generic solvent environment, it is expected that repulsive polymer-solvent interactions (poor solvent) lead to polymer chain compaction, with the Flory exponent ν < 0.5 in the scaling of R_g with respect to N, the number of residues, whereas attractive polymer-solvent interactions (good solvent) lead to polymer chain expansion, with ν > 0.5. However, IDPs are far more complex than a homopolymer, with propensities for residual secondary structure and possibly sequence-dependent preferential tertiary contacts, and the presence of macromolecular crowders does far more than merely modulate the quality of the solvent. Therefore, the effects of IDP-crowder soft attraction are hard to predict and expected to depend on many factors such as the sequence and length of the IDP, and the size, chemical nature, and concentration of the crowders.

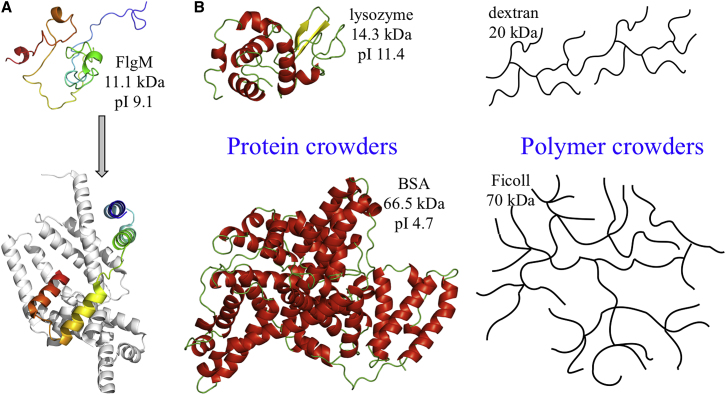
The IDP studied here is FlgM from Salmonella typhimurium, with 97 residues and a molecular mass of 10.6 (or 11.1 upon perdeuteration) kDa (amino-acid sequence shown in Fig. S1). FlgM is a transcriptional regulator involved in the ordered synthesis of proteins for bacterial flagellar assembly (39). During the expression of class 2 genes, FlgM binds to and thereby inhibits the flagellum-specific sigma subunit, σ²⁸, of the RNA polymerase. After assembly of the transmembrane flagellar base by the class 2 gene products, FlgM unbinds from σ²⁸ and is exported through the lumen of the flagellar base, henceforth releasing σ²⁸ to direct the expression of class 3 genes for completion of flagellar assembly. In dilute solution, FlgM was disordered, but with transient helix formation in the C-terminal half (40, 41). Upon binding σ²⁸, the C-terminal half became structured, as indicated by disappearance or significant reduction in intensity for NMR peaks of residues in the C-terminal half (40). Similarly, in 400 mg/mL BSA as a crowding agent or when overexpressed in Escherichia coli, NMR crosspeaks of the C-terminal residues were broadened beyond detection, which was interpreted as indicating gain of structure (23). The structure for the complex between thermophilic homologs of FlgM and σ²⁸ has been determined by x-ray crystallography, showing an extended conformation for FlgM, with two N-terminal helices tucked at one subsite on the σ²⁸ surface and two C-terminal helices sandwiching a σ²⁸ helix at a distant subsite (Fig. 1 A) (42).

Figure 1.

The disordered protein and the crowders in this study. (A) FlgM is shown as undergoing disorder-to-order transition upon binding σ²⁸. The sequence from the N- to the C termini is indicated by a coloring scheme from blue to red. (B) Four types of crowders are shown with molecular masses and isoelectric points (for protein crowders) indicated. To see this figure in color, go online.

Here we report SANS data on FlgM in both protein and polymer crowders (Fig. 1 B) over concentration ranges up to 400 mg/mL, which is the upper bound of macromolecular concentrations in bacterial cytoplasm (43). Using perdeuterated FlgM, the crowders were contrast-matched to observe only the scattering from FlgM. Overall the dependence of FlgM mean R_g on crowder concentration exhibited a biphasic behavior, with an initial reduction followed by an uptick. Moreover, EOM analysis indicated the existence of two distinct conformational populations under protein crowding, one compacted and the other extended. Coarse-grained simulations showed that the compaction occurs when IDP conformers are localized in an interstitial void between crowders (and occasionally bind to a surrounding protein crowder), whereas expansion occurs when conformers snake through interstitial crevices and bind multiple protein crowders at the same time.

Materials and Methods

Sample preparation

To maximize contrast for this study, fully deuterated FlgM was prepared. First, the FlgM gene was inserted into the pET-13b expression vector and the resulting plasmid was transformed into BL21(DE3) cells. Expression of perdeuterated FlgM was carried out following a previously developed protocol (44) using deuterated minimal media prepared with 99.8% D₂O and D8-glycerol (45). After adapting the cells to D₂O, fed batch cultivation was carried out in a Bioflo 310 system equipped with a 2.5 L bioreactor vessel (Eppendorf, Hamburg, Germany). Approximately 40 h after inoculation, FlgM expression was induced for ∼15 h by addition of 1 mM IPTG. Centrifugation (4000 × g, 30 min, 4°C) yielded ∼60 g of perdeuterated cell paste, which was suspended in lysis buffer (16 g/L NaOAc, 5.9 g/L KOAc, 1 mM PMSF, 0.05% BME) and disrupted using an EmulsiFlex-C3 homogenizer (Avestin, Ottawa, ON) at 4°C. FlgM was then purified as previously described (40, 46). Briefly, the cell lysate was centrifuged (30,000 × g, 30 min, 4°C) and polyethyleneimine was added to the supernatant at a final concentration of 0.1%. After stirring on ice for 30 min, the mixture was subjected to centrifugation (30,000 × g, 30 min, 4°C), heat treatment of the supernatant (80°C, 30 min), and further centrifugation (30,000 × g, 30 min, 4°C). The final supernatant was dialyzed against a low-salt buffer (50 mM NaOAc, 5 mM TCEP, pH 5) and further purified via a combination of cation-exchange (HiTrap SP FF; GE Healthcare, Chicago, IL) and size-exclusion chromatography steps (Sephacryl S-100; GE Healthcare) on an ÄKTA chromatography system (GE Healthcare). Purified perdeuterated FlgM was exchanged to a sample buffer (10 mM PO₄, 10 mM NaCl, 0.02% NaN₃, pH 6.2) and concentrated using Amicon Ultra-15 centrifugal filters (Sigma-Aldrich, St. Louis, MO) to a working stock of 50 mg/mL, as estimated via a Lowry assay. Throughout the expression and purification, FlgM presence and purity were tracked via SDS-PAGE.

Crowder solutions were made at the desired concentration and deuteration levels using hydrogenated and deuterated sample buffers. Crowders used and concentrations prepared were lysozyme (L6876; Sigma-Aldrich) at 75, 130, and 190 mg/mL; BSA (A2153; Sigma-Aldrich) at 120, 220, and 320 mg/mL; dextran 20 (5510 0020 8007; Pharmacosmos, Holbæk, Denmark) at 150, 250, and 400 mg/mL; and Ficoll70 (17-0310-50; GE Healthcare) at 100, 250, 320, and 400 mg/mL.

SANS

SANS data were acquired using the Extended Q-range SANS diffractometer at Oak Ridge National Laboratory (47). Samples were loaded into quartz banjo cells with the instrument configured to a 2.5-m sample-to-detector distance and 2.5–6.4 Å wavelength band. Samples were exposed to the beam for either 30 or 60 min, and azimuthally averaged 2D scattering data were background-subtracted in the software MANTiD (48) to obtain 1D scattering profiles that were then placed on absolute scale using a calibrated standard (49). The final reduced data is presented as intensity I (in cm⁻¹ units) as a function of q. For each type of crowder, the required D₂O level for contrast matching was determined by plotting [I(q)]^1/2, which is directly proportional to scattering length density (SLD) for the crowder, at 0, 20, 40, 60, 80, and 100% D₂O, and interpolating to the % D₂O at zero SLD. These match points were determined to be 26% for dextran 20, 36% for Ficoll, 40% for BSA, and 42.5% for lysozyme. Each sample was estimated to contain ∼5 mg/mL FlgM.

SANS data analysis

Data were analyzed in three ways for cross-validation. The first was indirect Fourier transform using the GNOM program (31), which converts the I(q) data to the distance distribution function p(r), yielding

$$p\left(r\right)=\frac{r^2}{2{\pi }^2}\underset{0}{\overset{\infty }{\int }}I\left(q\right)\frac{\text{sin}\left(qr\right)}{qr}{q}^{2}dq.$$ (1)

The mean radius of gyration can then be calculated from

$$R_g^2=\frac{1}{2}\frac{{\int }_0^{r_{\text{max}}}{r}^{2}p\left(r\right)dr}{{\int }_0^{r_{\text{max}}}p\left(r\right)dr},$$ (2)

where r_max is the maximum distance between two scattering centers. A p(r) curve was considered satisfactory if it exhibited the following characteristics: nonnegative and a smooth decay to 0 at r = r_max, minimal oscillations, and a low χ² in reproducing the experimental I(q). For all cases but three, r_max was fixed at 1.09 times the mean D_max from EOM. Two exceptions were for BSA at 220 and 320 mg/mL, where the mean D_max did not capture well a minor population of highly extended conformations; accordingly, we increased the r_max values from the initial 81.4 and 93.3 Å to 103 and 105 Å, respectively, at the two BSA concentrations. The last exception was for 400 mg/mL dextran, where r_max was reduced from 1.09D_max (or 92.5 Å) to 89 Å, to produce a satisfactory p(r) curve.

The second method was EOM (32, 33), in which an ensemble of conformations is generated to match the experimental scattering profile. In brief, EOM started with the generation of an initial pool of 20,000 structural models (Cα only) from the sequence of an IDP (FlgM in our case), with a scattering profile simulated for each model. Subsets of models were then sought to minimize χ² (the deviation of the subset average of simulated scattering profiles from the experimental one). The process started with a zeroth generation of 50 subsets, each composed of 20 models randomly selected from the initial pool. For each subset, 10 models were randomly selected for exchange, five with those in another subset and five with those in the pool. Twenty crossing operations then followed, each creating a new subset by mixing a random selection of models from two existing subsets. From the resulting total of 120 subsets, the 50 with the lowest χ² were chosen as the next generation. This process was propagated to the 1000th generation (with successively decreasing χ²), at which point a single optimal subset was chosen and the values of R_g and D_max (the largest distance between any two Cα atoms) of the models within were saved. In the default setting, EOM was run once, consisting of repeating the foregoing process 50 times, with the saved R_g and D_max values for the 50 optimal subsets used to calculate the distribution of R_g and mean values of R_g and D_max. In addition, the structural models (of which typically only 5–10 were distinct) in the subset with the lowest χ² among the 50 optimal subsets were output for potential usage. In our hands, we generated 100 EOM runs (all using the same initial pool of 20,000 models) for each experimental scattering profile, with both the distribution of R_g and the mean R_g and D_max further averaged over the 100 runs. Moreover, the structural models output from all the runs were pooled to calculate a distance distribution function, in the form of a histogram at 1 Å intervals. As a measure of the uncertainty in the mean R_g determined by EOM, we used the standard deviation of the mean R_g values calculated on the 100 lowest-χ² subsets of models from the 100 EOM runs.

In theory, mean R_g can be determined by fitting I(q) to the Guinier approximation at small qR_g $\equiv \sqrt{x}$ (29),

$$I\left(q\right)\approx I\left(0\right)e^{-x/3}.$$ (3)

However, as found in previous studies (50, 51), for unfolded and disorder proteins (in contrast to globular proteins), the q range over which Eq. 3 is valid is too narrow to yield reliable estimates for R_g. Instead, the Debye approximation (52),

$$I\left(q\right)\approx 2I\left(0\right)\frac{x-1+e^{-x}}{x^2},$$ (4)

derived for polymer chains, extends the range of validity to a higher q range for unfolded and disorder proteins. We used fitting to Eq. 4 as a third method to determine mean R_g for FlgM. Very recently, Riback et al. (53) used coarse-grained simulations to generate a molecular form factor, as a function of qR_g and the Flory exponent ν, for fitting SANS data. This model putatively extends the range of validity to an even higher q range for IDPs in buffer. We also tried this model on our SANS data.

To test for possible FlgM oligomerization, the forward scattered intensity I(0) determined via the Debye approximation was used to estimate the protein concentration with the equation (54)

$$c=\frac{I\left(0\right)N_{\text{A}}}{M\Delta {\rho }^2{\upsilon }^2}.$$ (5)

Here N_A is Avogadro’s number, M is the molecular mass of the protein, υ is the partial specific volume (typically 0.73–0.74 mL/g) of the protein, and Δρ is the difference in SLD between the protein and solvent. The SLDs for protein and solvent were estimated using the online tool MULCh (55), which requires input of solvent D₂O level (|Δρ| decreases with increasing % D₂O), protein deuteration level (between 0.8 and 1.0 for our FlgM), and fraction of protons accessible by the solvent (typically 0.9 and 1.0 for proteins). We used the lowest and highest estimates for Δρ to determine the range in which the protein concentration fell.

CD spectroscopy

CD data were acquired on a model No. 410 CD spectrometer (AVIV Biomedical, Lakewood, NJ) over a wavelength range of 210–240 nm, using a 1-mm path length, at 25°C. Ellipticity at each wavelength was measured for 5 s and data were averaged over three full sweeps of the wavelength range. FlgM CD spectra were measured in buffer and in crowded conditions (at dextran and Ficoll concentrations comparable to those used in the SANS experiment). FlgM concentrations were determined by a Bradford assay and were comparable to those estimated by a Lowry assay (FlgM is free of any tryptophan, rendering concentration determination by UV absorbance unsuitable). CD data were analyzed using the CDPro software package and the software Excel (Microsoft, Redmond, WA). The fraction of helical content was estimated as −(MRE₂₂₂ + 2340)/30,300, where MRE₂₂₂ is the mean residue ellipticity at 222 nm (56).

Coarse-grained simulations

The simulation protocol was as described previously (35), except for the addition of the second term in the interaction energy between an IDP residue and a crowder, turning it from a repulsive potential to the Lennard-Jones potential. The parameter ξ for the IDP internal interactions was chosen to be 0.7; the corresponding crowder-free mean R_g was 45.2 Å.

Access to data

The raw SANS data, the R_g distributions from EOM analysis, the p(r) results from EOM and GNOM analyses, and the R_g distributions from coarse-grained simulations can be retrieved from the web at http://pipe.rcc.fsu.edu/SANS/.

Results

We collected SANS data on FlgM both in buffer and in either protein crowders (lysozyme up to 190 mg/mL and BSA up to 320 mg/mL) or polymer crowders (dextran and Ficoll up to 400 mg/mL; all data plotted in Fig. S2). These were complemented by CD data in the polymer crowders and by coarse-grained simulations to gain deeper physical insight into the effects of the crowders on the conformational ensemble of FlgM.

Cross-validation of indirect Fourier transform and EOM analyses of SANS data

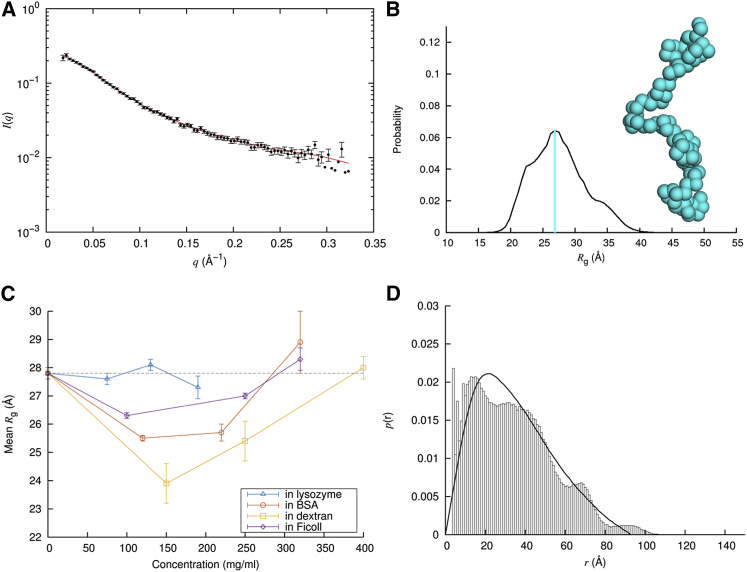
We analyzed each scattering profile (i.e., I(q) versus q curve; Fig. 2 A) in two ways: indirect Fourier transform as implemented in GNOM (31), and the EOM (32, 33). Both methods use the full scattering profile to determine the radius of gyration, and therefore provide cross-validation. EOM searches for an optimal conformational ensemble to match the scattering profile. Instead of only a mean R_g value as in GNOM, EOM generates, from the selected conformational ensemble, a distribution of R_g and representative Cα-only models (Fig. 2 B), as well as a mean value for D_max, the largest distance between any two Cα atoms. We calculated the distance distribution function p(r) from these Cα models and compared the result with that determined by GNOM, thereby gaining a second level of cross-validation.

Figure 2.

SANS data and analysis for FlgM. (A) Shown are the experimental scattering profile (dots) and the EOM fit (red curve). EOM introduced a small (−0.007) baseline subtraction from the experimental I(q). (B) The R_g distribution is shown with peak R_g indicated by a cyan bar. A structural model with R_g at the peak value is also shown. (C) Mean R_g values in buffer and for the four crowder at concentrations up to 400 mg/mL are shown. (D) Comparison is shown of distance distribution functions calculated from EOM structural models and generated by GNOM. Except for (C), the results are for FlgM in buffer. To see this figure in color, go online.

GNOM requires input of an r_max value above which p(r) = 0. Because of the disordered nature of FlgM, a range of r_max values all allowed an acceptable determination of p(r). We used EOM results for FlgM in buffer as a guide in choosing a unique r_max for GNOM analysis. Specifically, we chose an r_max that allowed GNOM to match the mean R_g, 27.8 Å, determined by EOM for FlgM in buffer. The ratio of that r_max to the mean D_max (the EOM equivalent to r_max), 1.09, was then used to choose r_max values for GNOM analysis on SANS data of FlgM under crowded conditions. The mean R_g values determined by GNOM and EOM essentially all agree with each other within determination uncertainties (Figs. 2 C and S3; Table S1).

As another measure of cross-validation, we also obtained mean R_g by fitting the scattering profiles to the Debye approximation (Eq. 4) over q between 0.025 and 0.051 Å⁻¹ (Fig. S4). The resulting R_g values (Table S1) agree with those determined by GNOM and EOM within errors for most of the cases. One exception is for 120 mg/mL BSA, where GNOM and EOM R_g values were 26.0 ± 0.5 and 25.5 ± 0.1 Å, respectively, but Debye fitting yielded 29.3 ± 0.7 Å. The Debye approximation, developed for polymer chains (52), has been found to model well scattering profiles of unfolded and disordered proteins (50, 51). For FlgM, with the parameters obtained from fitting over the above q range, the Debye approximation agrees reasonably well with the experimental scattering profiles even up to q = 0.1 Å⁻¹. This means that the choice of the upper bound for fitting has only a tempered effect on the resulting R_g. In contrast, the more commonly used Guinier approximation (Eq. 3) has a very narrow range of validity, below qR_g = 0.6 (50), for polymer chains and, by extension, IDPs. This upper bound corresponds to q ∼ 0.021 Å⁻¹, within which we had only a single data point, which was noisy and possibly affected by inter-FlgM interference. If one insists on fitting to the Guinier approximation (Fig. S4), the resulting R_g is not only erroneous but also highly sensitive to the range of q selected. Using the same q range as for the Debye fitting, Guinier fitting underestimated R_g values by ∼10% when compared to Debye fitting. The model of Riback et al. (53) fitted the FlgM data in buffer reasonably well, yielding R_g = 29.0 ± 0.3 Å and ν = 0.517, but the fit deteriorated for the data under crowding (Fig. S5; see below).

In addition to the cross-validation in mean R_g among GNOM, EOM, and Debye fitting, the Cα-Cα distance distribution functions for FlgM both in buffer and in the four types of crowders also match well between GNOM and EOM (Figs. 2 D and S6). Note that an apparent discrepancy at r ≤ 5 Å is due to the fact that the GNOM p(r) is a (virtually) continuous curve starting at r = 0, but the EOM p(r) was a histogram at 1 Å intervals, calculated from C_α-only structural models where the shortest C_α-C_α distances, between adjacent residues, fell into the bin at r = 4 Å.

Biphasic behavior in the dependence of mean R_g on crowder concentration

Fig. 2 C displays the mean R_g values determined by EOM for FlgM as a function of the concentrations of the protein and polymer crowders; the GNOM results showed similar trends (Fig. S3). In buffer, the mean R_g was 27.8 ± 0.2 Å. This value agrees closely with a value of 27.7 Å predicted by a scaling relation, R_g = 2.54 N^0.522 Å (with N = 97 for FlgM), that was compiled from a list of IDPs (57). FlgM in buffer thus has a size typical of IDPs. Crowding at the lowest concentrations (ranging from 75 to 150 mg/mL) led to a reduction in R_g for all the crowders. The reduction was the largest for dextran, down to 23.9 ± 0.7 Å, or by 14%, but miniscule for lysozyme; the extent of this R_g reduction had the appearance of correlating with the crowder concentration. However, upon further increases in crowder concentration, the mean R_g exhibited a steady uptick for BSA, dextran, and Ficoll but not for lysozyme. In the latter case, the mean R_g showed only small variations with crowder concentration.

The initial reduction in R_g could be attributed to steric repulsion, as expected from coarse-grained simulations with repulsive crowders (35). Indeed, all theoretical and simulation studies predict that repulsive crowders lead to larger reductions in R_g at higher crowder concentration, reaching as much as 10 and 30%, respectively, at 150 and 300 mg/mL crowders (35, 36, 37). Therefore, the uptick in R_g at higher crowder concentrations is opposite to what is expected from repulsive crowders and implicates crowder soft attraction toward FlgM. However, first we have to rule out crowder-induced FlgM oligomerization, which in theory could also lead to an apparent increase in R_g. To test for that possibility, we used the forward scattered intensity, I(0), which is proportional to the product, Mc, of the FlgM molecular mass M and concentration c (54). Oligomerization corresponds to an increase in M (e.g., dimerization leads to doubling in M) without affecting c, and hence a higher than expected I(0). Therefore, oligomerization is manifested by a higher than actual value of c when deduced from I(0), assuming a monomeric molecular mass. This test ruled out FlgM oligomerization in all the conditions studied except for 400 mg/mL Ficoll, where the deduced FlgM concentration was two-to-three times the actual value of ∼5 mg/mL. The latter data point was not further considered. For the other crowding conditions, soft attraction stands as he most likely reason for the uptick in R_g.

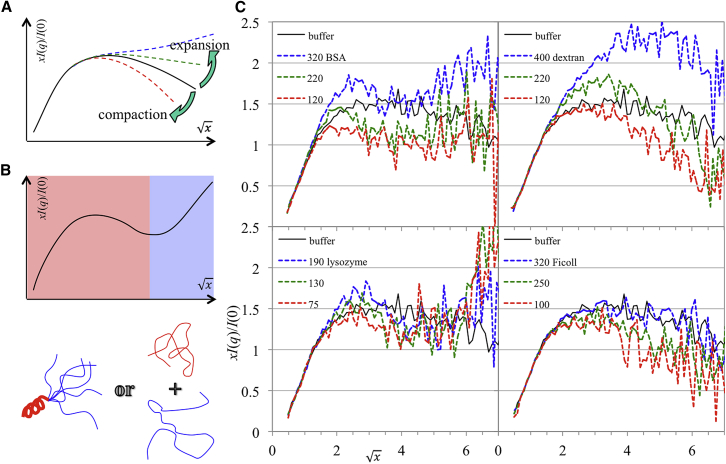
Distinct features of compaction and expansion in Kratky plots under crowding

Kratky plots, where q²I(q) is plotted against q (or xI(q)/I(0) versus $\sqrt{x}\equiv$ qR_g in dimensionless form) is useful for qualitatively identifying disordered states as well as the degree of compactness. Whereas globular proteins show a bell curve peaking at $\sqrt{x}=\sqrt{3}$, for disordered proteins the curve on the higher q side, depending on the degree of expansion, shows a downward drift, then plateaus, or plateaus and then rises (Fig. 3 A) (58, 59). When a protein has both a structured domain and a disordered region (51), or when the conformational ensemble contains both a compact population and an extended population, the Kratky plot shows a peak and a later rise separated by a dip (Fig. 3 B).

Figure 3.

Kratky plots of scattering profiles. (A) Typical Kratky plots of IDPs are shown with different degrees of compactness. (B) A Kratky plot is shown with signs for both compaction (red shading) and expansion (blue shading). The mixing of compaction and expansion can occur in the same molecule (lower-left cartoon) or in two populations of molecules (lower-right cartoon). (C) Kratky plots are presented for FlgM in buffer and under protein crowding or polymer crowding. I(0) and R_g values from GNOM were used for making the abscissa and ordinate dimensionless. Crowder concentrations in mg/mL are indicated in the legends. To see this figure in color, go online.

With this background information, we present the Kratky plots of our scattering profiles in Fig. 3 C. The plot for FlgM in buffer showed only a modest decline on the higher q side, indicating a disordered state with a typical degree of compactness. In the presence of both BSA and lysozyme, a dip in the Kratky plots developed between $\sqrt{x}$ = 3 and $\sqrt{x}$ = 5 and became more prominent at increasing concentrations of the protein crowders. This dip suggests some type of mixing of highly compacted and highly extended conformers.

In the presence of the polymer crowders, no dip was discernible, but a change in the degree of compactness was quite apparent. At the lowest concentrations of the two crowders, FlgM was clearly compacted. The compaction lessened at the intermediate crowder concentrations. Finally, at the highest crowder concentrations, FlgM was considerably expanded in the presence of dextran and modestly expanded in the presence of Ficoll. These qualitative features evident from the Kratky plots are in line with the mean R_g trends in Fig. 2 C.

The model of Riback et al. (53) failed for our FlgM data under protein crowding because it predicts a monotonic Kratky plot on the higher q side, thus missing the dip (Fig. S5). For Ficoll crowding, the fits themselves (up to q = 0.15 Å⁻¹) were acceptable but the extrapolation to higher q showed much greater deviations from data than those for buffer. For dextran crowding, the fits were poor. These deviations of the SANS data from the model of Riback et al. (53) reinforce the notion that the macromolecular crowders studied here do far more than merely change the Flory exponent by modulating the quality of the solvent.

In short, the Kratky plots indicated that, with increasing crowder concentrations, FlgM first compacted and then expanded under polymer crowding, but exhibited growing signs of mixed compaction and expansion under protein crowding. This mixing could be in the same FlgM molecule, which would mean structure formation in a segment of the sequence, or in two different populations of molecules. It is difficult to envision how growing structure formation in one segment of the protein is accompanied by growing expansion of another segment. On the other hand, as shown by the EOM and coarse-grained simulation results below, the scenario of population mix can be easily rationalized. Although presently we favor this scenario, we cannot rule out the scenario of structure formation.

FlgM conformational ensemble in buffer

For IDPs, EOM yields both R_g distributions and representative structural models. With the caveat that EOM can fit a given experimental scattering profile but cannot rule out alternative interpretations, we now present the EOM results.

As shown in Fig. 2 B, R_g values of individual members in the conformational ensemble of FlgM in buffer spanned a broad range, from <18 Å to >40 Å, consistent with its disordered nature. The R_g distribution is continuous, unimodal, and skewed. Compared to the left side of the peak, the right side extended to a greater range but had lower frequencies, such that the peak R_g value, 26.9 Å, was only modestly less than the mean R_g of 27.8 Å. Next, we use the R_g distributions in the protein and polymer crowders to provide further information on how crowding changed the mean R_g of FlgM.

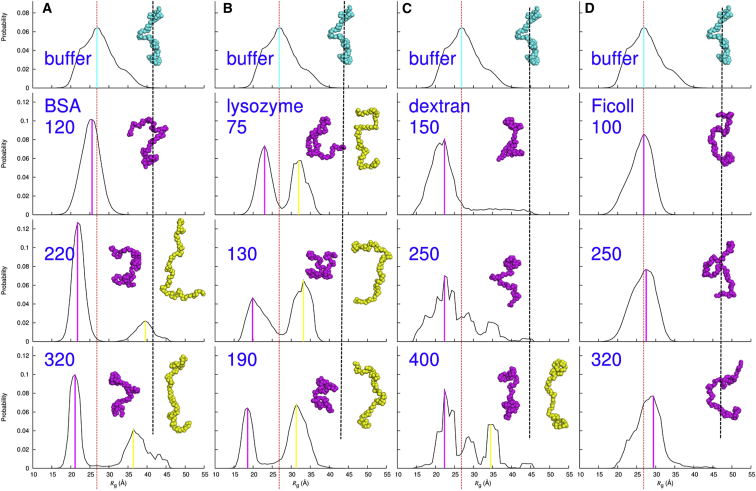
FlgM conformational ensembles in protein crowders

BSA at 120 mg/mL (the lowest concentration studied; Fig. 4 A) effectively suppressed the more extended conformations of FlgM, with vanishing frequencies for structural models with R_g exceeding 34 Å, leading to a narrowing and symmetrization of the R_g distribution. The peak R_g value also reduced slightly, to 25.6 Å. These two trends both contributed to conformational compaction, and together led to the decrease in mean R_g to 25.5 Å from 27.8 Å. Note that simultaneous occurrence of leftward shift in peak R_g and narrowing of R_g distribution was previously observed in coarse-grained simulations of an IDP in repulsive crowders (35).

Figure 4.

R_g distributions in buffer and under crowding. The top row shows the results in buffer (same as in Fig. 2B); the next three rows show the results in the four crowders at the concentrations (in mg/mL) indicated. (A) BSA. (B) Lysozyme. (C) Dextran. (D) Ficoll. A red vertical dash indicates the peak R_g in buffer; magenta and yellow bars indicate peak R_g values under crowding. Structural models with R_g at the peak values are also shown, with their positions relative to a black vertical dash approximating their R_g values relative to that in buffer. To see this figure in color, go online.

As the BSA concentration was increased to 220 mg/mL (Fig. 4 A), the R_g distribution, intriguingly, became bimodal. The low-R_g population continued the compaction seen at 120 mg/mL BSA, again with both leftward shift in peak R_g (now at 21.8 Å) and narrowing in R_g distribution, but a small high-R_g population emerged. The latter population peaked at R_g = 39.6 Å and extended to >45 Å, a region not sampled by the FlgM conformational ensemble in buffer. At 320 mg/mL BSA, the low-R_g population further compacted whereas the high-R_g population grew in abundance (Fig. 4 A). Although the population-averaged R_g exhibited a slight uptick at 220 mg/mL BSA relative to that at 120 mg/mL, the mean R_g at 320 mg/mL BSA, as a result of the growth in the high-R_g population, increased substantially to 28.9 Å—greater even than the value in buffer.

The R_g distributions in lysozyme further strengthened the finding of segregation between compacted and extended populations (Fig. 4 B). Even at the lowest concentration, 75 mg/mL, there was already a split in the FlgM R_g distribution, although the low-R_g and high-R_g populations together spanned approximately the same overall range of R_g as the ensemble in buffer. As the lysozyme concentration increased to 130 mg/mL and then to 190 mg/mL, the low-R_g population compacted more and more whereas the high-R_g population grew into the majority. These two trends have opposite influences on the population-averaged R_g, and the net effect was that the latter exhibited small variations instead of a systematic dependence on crowder concentration.

As one more measure of validation, we checked whether the bimodality remained when models with high R_g were removed from the initial pool. As illustrated in Fig. S7 when all models with R_g > 30 Å were removed, the R_g distributions under protein crowding remained bimodal. This is especially striking for BSA at 320 mg/mL, where the entire high-R_g population in the original R_g distribution had R_g > 30 Å, and hence was now completely removed from the initial pool. The new high-R_g population moved to the R_g range between 25 and 30 Å. Expectedly, the χ² increased significantly, by 10%.

FlgM conformational ensembles in polymer crowders

According to mean R_g, dextran at 150 mg/mL was the most effective in compacting the FlgM ensemble (Fig. 2 C). The R_g distribution (Fig. 4 C) revealed that this strong decrease in mean R_g, to 23.9 Å, came about due to both promotion of conformations too compact to be seen in the ensemble in buffer and suppression of the more extended conformations in the latter ensemble. Interestingly, even as the mean R_g indicated strong compaction, there was a minor population of expanded conformations, with R_g values extending beyond those observed in buffer. As the dextran concentration increased to 250 mg/mL, conformations with higher R_g grew in abundance. With a further increase in dextran concentration to 400 mg/mL, this shift in FlgM population continued. There was now a hint of segregation between low-R_g and high-R_g populations, but the data under this crowding condition were too noisy (as indicated by a 60% higher χ² than for the other crowding conditions) to be conclusive.

Among all the four types of crowders, Ficoll had the least effect on the FlgM ensemble (Fig. 4 D). At 100 mg/mL, Ficoll induced a narrowing of the R_g distribution although the peak position was unchanged, accounting for a slight decrease in mean R_g (to 26.3 Å). With the Ficoll concentration increasing to 250 mg/mL and then to 320 mg/mL, the peak R_g gradually albeit slightly shifted to higher values. It is possible that more of the extended FlgM conformations might appear at even higher Ficoll concentrations, but data analysis there was complicated by possible FlgM oligomerization.

Just as with the protein crowders, removing models with high R_g from the initial pool did not change the modality of the R_g distributions for the polymer crowders (Fig. S7).

Gain in FlgM helical content in polymer crowders

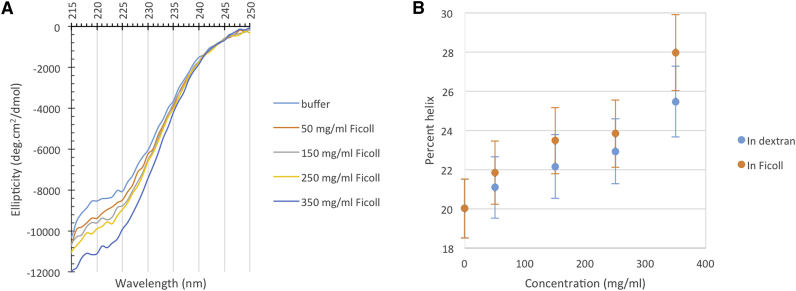
SANS data give rich information on sizes of FlgM conformations but are silent on the effects of macromolecular crowding on secondary and tertiary structures. As noted in the Introduction, NMR data have been interpreted as indicating gain of structure for the C-terminal half of FlgM in 400 mg/mL BSA (23). The latter study also showed that FlgM gained helical content in glucose, which is a known structural stabilizer although more by increasing water surface tension and hence strengthening the hydrophobic effect and less by steric repulsion (60). Because the polymer crowders, in contrast to protein crowders, do not generate CD signals at the wavelengths (∼222 nm) most indicative of secondary structure, we measured the CD spectra of FlgM in dextran and Ficoll to assess how the polymer crowders affected the secondary structure of FlgM (Fig. 5). The CD data indicated that, at increasing concentrations of the polymer crowders, the helical content of FlgM increased steadily though modestly, from ∼20% in buffer up to 25–28% at 350 mg/mL of crowders.

Figure 5.

CD spectra and helical contents of FlgM in buffer and under crowding. (A) Shown here are mean residue elliipticities in buffer and in Ficoll at four concentrations. (B) Changes in helical content are presented at increasing concentrations of dextran and Ficoll. To see this figure in color, go online.

Effects of IDP-crowder steric repulsion and soft attraction from coarse-grained simulations

Although the initial reduction and subsequent uptick in mean R_g potentially implicated steric repulsion and soft attraction, respectively, by crowders, the SANS data by themselves did not provide a direct probe of IDP-crowder interactions. To complement the SANS study, we carried out coarse-grained simulations of a homopolymer model of a 99-residue IDP in spherical crowders (30 Å radius). The simulations were similar to those in our previous study (35), but with one important difference. Instead of a purely repulsive potential, the IDP residues, each modeled by a single bead (3.15 Å radius), interacted with the crowders via a Lennard-Jones potential,

$$\left(r_{i\alpha }\right)=\epsilon \left[{\left(\sigma /r_{i\alpha }\right)}^{12}-{\left(\sigma /r_{i\alpha }\right)}^6\right],$$ (6)

where r_iα is the distance between residue i and crowder α, −ε/4 is the minimum energy, and σ is the nominal contact distance. This interaction potential consists of both steric repulsion (at r_iα < σ) and soft attraction (at r_iα > σ). We studied a range of ε-values, to mimic possible differences between protein and polymer crowders.

In Fig. 6 A we compare the mean R_g values of the model IDP in Lennard-Jones crowders with ε at 0.1 kcal/mol (termed “slight attraction”) and 0.5 kcal/mol (termed “moderate attraction”) against those in repulsive crowders. With slightly attractive crowders, the IDP was steadily compacted at increasing crowder concentration, although at a pace less than that for repulsive crowders. With the moderately attractive crowders, the mean R_g exhibited a dip at low crowder concentrations and then increased steadily at higher crowder concentrations. This apparent biphasic behavior qualitatively resembles that observed for FlgM in the SANS study.

Figure 6.

Coarse-grained simulation results for a model IDP under crowding. (A) Shown here are mean R_g values in repulsive and slightly and moderately attractive crowders. The symbol ϕ denotes crowder volume fraction; ϕ = 0.1 roughly corresponds to a concentration of 100 mg/mL. (B) Given here are R_g distributions in the absence and presence of slightly attractive crowders. (C) Given here are R_g distributions in the absence and presence of moderately attractive crowders. (D) Representative snapshots from the simulations are given. The IDP R_g values in the snapshots are, from left to right, 23, 36, and 55 (top row) or 65 (bottom row) Å. Crowders are shown as gray spheres, and the IDP is shown as a chain of beads in green or red; the latter color indicates close contact (within 2.85 Å of contact distance) with a crowder. Data for the crowder-free and repulsive-crowder cases were taken from Qin and Zhou (35). To see this figure in color, go online.

At increasing concentrations of the slightly attractive crowders, the R_g distribution gradually narrowed and the peak R_g shifted to lower values, as high-R_g conformations were suppressed and low-R_g conformations were promoted (Fig. 6 B). In contrast, for the moderately attractive crowders (Fig. 6 C), at low concentrations the R_g distribution narrowed from both sides, although to a greater extent on the high-R_g side than on the low-R_g side. As the crowder concentration increased, the R_g distribution steadily shifted toward higher R_g values.

Snapshots from the simulations shed light on how compacted, intermediate, and extended conformers were accommodated in their crowder environments (Fig. 6 D). For slightly attractive crowders at the highest concentration, the compacted conformers were localized in an interstitial void between crowders; the intermediate conformers were more open but with their bulk still localized in a void though with termini or loops reaching into nearby crevices; and the extended conformers snaked through interstitial crevices. The latter scenario was postulated in theoretical studies of polymer chains inside repulsive crowders (61, 62). The situations with moderately attractive crowders are similar, but with one important difference: the conformers now closely wrapped around one or more crowders. The nonspecific binding to multiple crowders was especially important for stabilizing the extended conformers.

Discussion

Our SANS study of FlgM in protein and polymer crowders has revealed evidence for both conformational compaction and expansion under crowding. Intriguingly, the data analysis suggested a segregation of FlgM conformations under protein crowding into a compacted population and an extended population. However, the effects of crowding vary not only for the four types of crowders but also for different concentrations of a given crowder. Below, by incorporating results from coarse-grained simulations and CD spectroscopy, we discuss physical mechanisms for and broad implications of these observations.

Generation of IDP conformational ensembles from SANS data

In dealing with SANS data of IDPs, the Guinier analysis (29), Debye analysis (52), and indirect Fourier transform method (30, 31) all have limitations. These methods all show sensitivity to input parameters; the Guinier analysis is particularly sensitive to the range of q chosen for fitting. The information provided is also limited. The first two methods yield only the mean R_g, which tells very little about the vast conformational ensemble of an IDP. The third method further yields the distance distribution function, which does not provide a unique interpretation of the conformational ensemble. Recently developed ensemble generation methods such as EOM (32, 33) are very suited for analyzing SANS data for IDPs. Here we have cross-validated EOM against the indirect Fourier transform method implemented in GNOM (31). The distance distribution functions calculated from EOM structural models agree well with those obtained by GNOM when r_max was chosen according to EOM mean D_max. However, although EOM can fit a scattering profile, it cannot rule out alternative interpretations.

Segregation of FlgM conformations under crowding

The EOM analysis revealed two distinct populations with low and high R_g, most evident for protein crowders at high concentrations. For lysozyme, the population split was prominent even at 75 mg/mL, and resulted in a nearly constant mean R_g at different crowder concentrations. It is of interest to note that Goldenberg and Argyle (27) also obtained a near-constant mean R_g for their IDP under crowding by globular proteins. These authors used Guinier analysis only, so it is unknown whether a population split occurred in their case.

Compared to the protein crowders in our study, the extended conformations were much less populated in the polymer crowders. The extended conformations did grow with increasing concentrations of dextran, but there was only a hint that they might split from the compact conformations. Our CD data also indicated a modest increase in helical content with increasing concentrations of the polymer crowders. It may be tempting to associate the increase in helical content with the increase in extended conformations. However, both conformational compaction and nonspecific binding to crowders can potentially increase the FlgM helical content, as they result in interactions with water being replaced by intra-FlgM or FlgM-crowder interactions, making water less likely to disrupt backbone hydrogen bonds in α-helices.

Effects of crowder size, chemical nature, and concentration

It is well known that steric repulsion leads to compaction of IDPs and the effect is greater for smaller crowders than for larger crowders. The latter outcome arises from the fact, at the same total volume fraction, larger crowders leave more voids for an IDP to occupy than smaller crowders. Our SANS results on the compacted FlgM conformations under crowding agree well with these theoretical predictions. In particular, at 250 mg/mL, Ficoll, with a molecular mass of 70 kDa, had little effect on the R_g distribution, but dextran, with a molecular mass of 20 kDa, shifted the peak R_g to a much smaller value (Fig. 4, D and C). Similarly, for the protein crowders, the smaller lysozyme (14.3 kDa) induced much greater compaction of the FlgM ensemble than BSA (66.5 kDa) at comparable concentrations (130 and 120 mg/mL, respectively; Fig. 4, A and B).

If steric repulsion can only lead to compaction of an IDP, then the crowding-induced expansion revealed by our SANS data must be attributed to soft attraction. Whereas crowder size is a determinant for the effects of steric repulsion, the chemical nature of crowders plays a major role in dictating the effects of soft attraction. As already noted, the protein crowders in our study were much more effective than the polymer crowders in inducing extended FlgM conformations, consistent with the expectation that, to a probe protein, protein crowders are generally sticky whereas polymers like dextran and Ficoll are nearly inert. That extended conformations could be induced to a modest extent by dextran at high concentrations suggests that even this polymer crowder is slightly attractive to FlgM. Synthetic polymer chains can interpenetrate at high concentrations, but it is not clear whether or how this distinction from protein crowders contributes to their dissimilar crowding effects. Differences in soft attraction between the two protein crowders are implicated by the fact the extended population was already prominent at 75 mg/mL lysozyme but first appeared only at 220 mg/mL BSA. Between the two polymer crowders, dextran was able to induce conformational extension whereas Ficoll was not. It is not clear whether crowder size has a role in this difference, although, at a given concentration, crowder size certainly affects the mean distance between crowder molecules (see next paragraph). Both FlgM and lysozyme are basic proteins whereas BSA is acidic, indicating that any electrostatic contribution to soft attraction is more influenced by interactions between short sequences of FlgM and surface patches of the crowder protein than by their net charges. Other experimental techniques, including NMR spectroscopy, are being applied to further probe protein-crowder interactions.

Lastly, we note that, for both the protein and polymer crowders, extended conformations could be promoted at high crowder concentrations. At high concentrations, crowder molecules are positioned close to each other. It is therefore likely that the promotion of extended conformations comes about because FlgM can nonspecifically bind to multiple crowders simultaneously.

Disparate stabilization mechanisms for compacted and extended conformers

From the foregoing discussion and the coarse-grained simulations, we can conclude that the compacted conformers are driven by steric repulsion. They fit into an interstitial void, with stability modulated by internal interactions and contributed to by weak binding to a surrounding protein crowder (Fig. 6 D). In contrast, the extended conformers snake through interstitial crevices, with simultaneous binding to multiple crowders providing essential stabilization. Our coarse-grained simulations did not directly demonstrate conformational segregation, perhaps due to imbalance of internal and external interaction parameters and absence of sequence-dependent interactions.

Broad implications

The data presented here and in previous studies suggest that conformational malleability allows IDPs to respond agilely to their crowded cellular environments, including conformational compaction, conformational expansion, persistent disorder, and induced structuring. Importantly, these responses can occur in different subpopulations and are therefore not necessarily mutually exclusive. It is entirely possible that cellular functions of IDPs take advantage of such varied conformational response to their crowded cellular environments. For FlgM, compacted conformations may be adopted for exporting through the lumen of the flagellar base, whereas extended conformations may be adopted for interacting with its cellular target σ²⁸.

Author Contributions

A.B. and H.-X.Z. designed the research. A.B., S.Q., K.L.W., and C.B.S. performed the research and analyzed the data. A.B. and H.-X.Z. wrote the manuscript.

Editor: Amedeo Caflisch.