Characterization of Cell Boundary and Confocal Effects Improves Quantitative FRAP Analysis

Abstract

Fluorescence recovery after photobleaching (FRAP) is an important tool used by cell biologists to study the diffusion and binding kinetics of vesicles, proteins, and other molecules in the cytoplasm, nucleus, or cell membrane. Although many FRAP models have been developed over the past decades, the influence of the complex boundaries of 3D cellular geometries on the recovery curves, in conjunction with regions of interest and optical effects (imaging, photobleaching, photoswitching, and scanning), has not been well studied. Here, we developed a 3D computational model of the FRAP process that incorporates particle diffusion, cell boundary effects, and the optical properties of the scanning confocal microscope, and validated this model using the tip-growing cells of Physcomitrella patens. We then show how these cell boundary and optical effects confound the interpretation of FRAP recovery curves, including the number of dynamic states of a given fluorophore, in a wide range of cellular geometries—both in two and three dimensions—namely nuclei, filopodia, and lamellipodia of mammalian cells, and in cell types such as the budding yeast, Saccharomyces pombe, and tip-growing plant cells. We explored the performance of existing analytical and algorithmic FRAP models in these various cellular geometries, and determined that the VCell VirtualFRAP tool provides the best accuracy to measure diffusion coefficients. Our computational model is not limited only to these cells types, but can easily be extended to other cellular geometries via the graphical Java-based application we also provide. This particle-based simulation—called the Digital Confocal Microscopy Suite or DCMS—can also perform fluorescence dynamics assays, such as number and brightness, fluorescence correlation spectroscopy, and raster image correlation spectroscopy, and could help shape the way these techniques are interpreted.

Introduction

Due to the popularity of confocal laser scanning microscopes, fluorescence recovery after photobleaching (FRAP) has emerged as a prominent technique to measure protein mobility, and throughout the past decade has appeared in over 150 publications annually (1). During a typical FRAP experiment, a cell expressing a fluorophore of interest is subjected to a high intensity laser pulse that permanently abolishes the fluorescence properties of the fluorophore—a process called photobleaching. This laser pulse is specifically localized to a predetermined region of interest (ROI) inside the cell, and over time fluorophores not subjected to the bleach move into the ROI, leading to a recovery of the local fluorescence.

The rate and directionality of this fluorescence recovery can then be used, via a model, to determine an array of important characteristics of the molecule of interest, diffusion coefficients, binding kinetics, and the number of dynamic states of the fluorophore. These properties are important for a wide array of biological questions. What is the contribution of diffusion in the transport of proteins? Is a protein part of a complex that changes its mobility? Is the protein associated with the cytoskeleton or other structures that could change its dynamics states? What are the in vivo kinetics of specific protein-protein interactions?

To obtain a physical constant, such as the diffusion coefficient, which can help answer these questions using FRAP, a model must be used. The two most commonly cited FRAP models are by Axelrod et al. (2) and Soumpasis (3), and they use an analytically calculated recovery profile of a 2D ROI inside a cell with an infinite boundary. Although these models are frequently used—over 650 combined citations to date—more recent studies have included and explored additional relevant FRAP parameters such as the finite confocal scan rate during photobleaching (4, 5, 6, 7, 8, 9), arbitrary photobleaching profiles (10), confocal imaging (5), and cell shape (11, 12, 13, 14). Despite this wealth of analytical models, as well as algorithmic approaches (10, 13, 15, 16, 17, 18, 19), it remains unclear whether these models can yield accurate estimates of the diffusion coefficients, for instance, when applied using realistic optical settings in actual cellular geometries. A simple thought experiment (described in detail in the Supporting Material, and shown in Fig. S19) based on a 1D FRAP model shows that geometric effects can produce a factor-of-four difference in the apparent diffusion coefficient under ideal conditions. Determining such quantities accurately is important, as this improves the significance of the biological conclusions derived from modeling of the cellular processes that are studied.

To provide more accuracy in analyzing FRAP recovery, interactive solutions such as the VirtualFRAP tool (part of VCell environment) (13) and simFRAP (10) have been developed, allowing the calculation of diffusion coefficients in arbitrary 2D geometries. Although these algorithmic approaches make fewer assumptions than existing analytical models (2, 3), they still rely on the timescale invariance of the process, which is not necessarily true in the case where the bleaching and imaging durations are not instantaneous. Without a comprehensive model that incorporates all the relevant aspects of FRAP, it remains a challenge to determine if a particular analytical or algorithmic method is appropriate to measure diffusion coefficients or identify dynamic states for a specific case.

Although it has been shown in silico that cellular geometry can influence FRAP (12), this effect is often not taken into account when analyzing recovery curves obtained from arbitrary 3D cellular geometries. When analytical models are unable to quantitatively describe these geometric effects, oftentimes multiexponential fitting is used to make qualitative conclusions about the inherent dynamics. This introduction of spurious dynamic states—potentially interpreted as multiple diffusing species, active transport systems, or diffusion/binding reactions—as a result of the fitting process can further confound the problem, leading to misinterpretations of the underlying biology. These conclusions can further be reinforced by an excellent goodness of fit, regardless of the underlying physical meaning.

Given the widespread use of FRAP, there is a need for a rigorous approach incorporating optical, geometric, and diffusive effects that would allow accurate model selection for any cell type. Here, we developed an experimentally validated particle-based diffusion model that allows us to conduct not only FRAP, but also other fluorescence fluctuation-based analyses on a wide variety of 3D cellular geometries. We then quantitatively demonstrate that cell shape is one of the predominant factors that can influence FRAP recoveries, and affect measured diffusion coefficients for commonly used FRAP models. Because there is a rich parameter space that influences fluorescent recovery, it would be misleading to make absolute conclusions about FRAP recoveries in a given system. To help remedy this challenge, and to make predictions for specific experimental setups and systems, we provide a free, user-friendly, cross-platform, and GPU optimized version of our software, namely Digital Confocal Microscopy Suite (DCMS), to the readers (20).

Materials and Methods

FRAP model in DCMS

To accurately measure the diffusive dynamics of a given molecule in complex cellular geometries, we created a particle-based simulation that consists of noninteracting Brownian particles, with a constant diffusion coefficient (21). Particles are contained within a region defined by a boundary surface with reflective boundary conditions (see the Supporting Material). This surface can be any triangulated mesh representing the cell boundary of interest; however, when possible, we used an analytical description of the cell shape (e.g., hemisphere-capped cylinder for moss) to reduce computational cost. In all of the production runs used for analysis here, we used 10⁶ particles within this simulation volume.

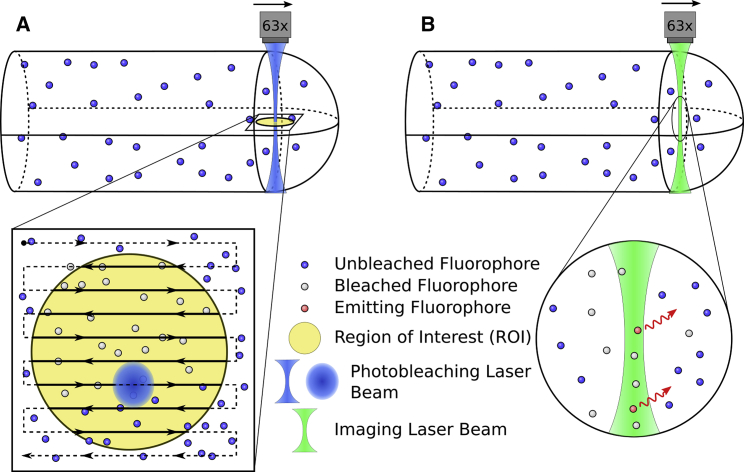
The simulation also incorporates properties of the optical system (i.e., imaging and bleaching, as illustrated in Fig. 1), finite scan rates of the confocal microscope, the PSF, and ROI size and shape-related effects, as described in detail in the Supporting Material. Briefly, imaging is performed by scanning across the region corresponding to the output image, using a squared Gaussian beam point spread function (PSF). The experimental PSF is measured (see the Supporting Material) and used to determine the parameters for the squared Gaussian. Photobleaching is performed by scanning across the ROI, and stochastically photobleaching fluorophores within the beam (see Fig. S5 and Movies S1 and S2).

Figure 1.

Illustration of FRAP process on the scanning confocal microscope in three dimensions. (A) Raster photobleach scan interacting with confined particles. Arrows indicate the bleaching pattern of the Gaussian photobleaching laser beam within the yellow circular region. (B) Particle excitation and emission. Here the green diffraction limited laser scans across the image and locally excites fluorophores that emit red light. Images are not to scale. To see this figure in color, go online.

Furthermore, the DCMS simulations can also conduct reversible photoswitching during imaging acquisition and bleaching events. If this reversible photoswitching is neglected, especially for 3xmEGFP, it can lead to overestimates in measured diffusion coefficients (22). However, because the kinetics of this process can be dependent on laser power (22) (see Fig S9 B), it would add additional model parameters. To increase the accuracy of our results, and avoid a large parameter scan, we experimentally measured and performed the necessary corrections for acquisition photobleaching (see the Supporting Material) and reversible photoswitching (see the Supporting Material).

Additionally, although it was not utilized in this article, DCMS also supports a number of other choices, such as alternative PSF forms, acquisition photobleaching and photoswitching, and binding kinetics (20).

Cell culture and sample preparation

FRAP experiments were conducted on the caulonemal cells of the moss Physcomitrella patens; moss tissue was cultured on cellophane placed on top of the solidified agar. Microscope samples were prepared in QR-43C chambers (Warner Instruments, Hamden, CT) as follows. First, 25-mm bottom coverslips were plasma-treated for 3 min to yield a hydrophilic surface. A solution of 0.8% type VII agarose in PpNO₃ medium (refer to (23) for details) was melted, then added directly to the coverslips. A small cellophane square (1 cm²) with moss tissue, grown for seven days after subculturing, was inverted and placed onto the agarose. To obtain flat cultures, a second untreated coverslip was placed on top of the cellophane and flattened using a blunted syringe. Agarose was solidified by placing the cultures onto a surface at 12°C. Once the agarose solidified, the top coverslip was gently removed from the top of the preparation. The remaining preparation was submerged in PpNO₃ and the cellophane was removed. With the moss firmly adhered to the agarose, the entire coverslip was added to the QR chamber. The chambers were capped with 18-mm coverslips and connected to silicone tubing with inner and outer diameters of 0.03 in and 0.065 in, respectively. The tubing was connected to a peristaltic pump and liquid PpNO₃ was perfused through the chambers overnight. Liquid PpNO₃ was made 2 days before perfusion and was filter-sterilized immediately before its use. During Latrunculin B treatment, a solution of 10 μM Latrunculin B in PpNO₃ was perfused through the chamber for 20 min.

Confocal imaging

FRAP experiments were conducted using a Leica TCS SP5 Scanning Confocal Microscope and the Leica FRAP Wizard (Leica Microsystems, Wetzlar, Germany). To conduct FRAP experiments, a 63× objective was used with a numerical aperture (NA) of 1.4. In the software settings, the pinhole was set to 2.00 Airy disks and the camera zoom was set to 9. Images of 256 × 256 pixels were acquired with a depth of 12 bits. To visualize 3xmEGFP, the Argon laser was set to 75% power with a bidirectional scanning speed of 2800 Hz and the 488 nm laser line was set to 10% power in the FRAP wizard. The emission bandwidth for 3xmEGFP was set between 499 and 546 nm. During bleaching events, all laser lines were set to 100%.

FRAP postacquisition processing and analysis

Several confounding factors that can influence the interpretation of FRAP results were examined, namely, image acquisition-induced photobleaching/reversible photobleaching (Supporting Material), reversible photobleaching after intentional photobleaching (Supporting Material), confocal detector linearity (Supporting Material), and the effects of imaging and photobleaching away from the medial cell plane (Supporting Material). We then constructed the FRAP processing scheme depicted in Fig. S6. This flowchart illustrates how the experimental and simulated FRAP images were processed and analyzed to yield the diffusion coefficients and highlight experimental boundary effects. Briefly, images from FRAP experiments, saved as tiff stacks, were converted into fluorescence recovery curves by averaging the intensity of the pixels within the ROI. Replicate experiments were then averaged and divided by acquisition bleaching controls. After processing the recovery curves, we used an argument minimization scheme to find the best fit simulation parameters (Supporting Material). Confidence intervals for the best fit parameters were found via Monte Carlo simulations (Supporting Material). To analyze the directionality of fluorescence recovery spatially the photobleaching ROI was cropped, corrected for the limited available volume at the cell tip (Supporting Material), and subjected to Fourier analysis (see the Supporting Material). A flow chart depicting this analysis can be found in Fig. S12.

Experimental measurement of the point spread function

To experimentally measure the point spread function (PSF) of the confocal microscope, beads were used from the Invitrogen PS-Speck Microscope Point Source Kit P7220 (Thermo Fisher Scientific, Waltham, MA). Preparations were made by adding 5 μL of $0.01\text{\%}$ polylysine and 5 μL of bead solution to a dry microscope slide. A coverslip was then placed directly onto the slide and sealed with wax. Beads were visualized and measured with the Leica TCS SP5 scanning confocal microscope (Leica Microsystems), using the settings described in the Supporting Material. Green fluorescent beads were used to match the 3xmEGFP fluorophore, and z-stacks of the 175 nm beads were taken. From these z-stacks, a 3D reconstruction of the bead’s intensity profile was created as shown in Fig. S5 a. These profiles were then used to determine the 3D functional form and parameters of the PSF, following the procedure defined in the Supporting Material.

GPU accelerated computation

Due to the high computational cost associated with the motion of many particles, we wrote a parallel simulation code to take advantage of general-purpose graphics processing unit computing. To provide a general-purpose tool, available to a wider audience, we made a graphical-user-interface-based simulation tool (DCMS). This interface was written in Java, using the cross-platform AMD APARAPI library (24) to use OpenCL computation whenever possible. This also allows the software to efficiently use general-purpose graphics processing unit computing when available, and fall back to CPU computing if it is not, in a cross-platform manner. Our standard production runs, using the moss geometry and 161-image, 2-bleach sequence, take approximately half an hour to run (on an AMD RX 480 GPU; Advanced Micro Devices, Sunnyvale, CA). More modest simulations, using fewer particles, fewer imaging steps, or simpler (fewer polygon) geometries, for example, can be performed in a few minutes.

To more effectively perform the large number of runs required for our library fitting approach used in the Supporting Material, we also wrote a version of the software using NVidia’s CUDA platform. Combined with some platform-specific optimizations, as well as using an analytical form of the ideal moss geometry rather than a triangulated mesh, our run-time was reduced by approximately a factor of 10 (i.e., to 140 s on an NVidia GTX 780Ti). See (25) for computational details.

Results

Cell shape influences fluorescence recoveries in vivo

To study the influence of cell shape and boundaries on fluorescence recovery in vivo, we conducted FRAP experiments in the moss P. patens, at two different ROI locations, one at the cell edge and another at the center of the cell (as depicted in Fig. 2 B). We processed the curves to correct for acquisition and reversible photobleaching, and ensured that our experiments were in the linear range of the detector (see the Supporting Material). Additionally, recoveries at the cell edge exhibited a slower rate of recovery and higher fluorescence plateau when compared to the center. To ensure that these observations were not due to filamentous actin localization at the cell edge, we performed the same analysis in the presence of an actin depolymerization agent, latrunculin B at 10 μM (Supporting Material). Latrunculin B treatment, which has been shown to completely depolymerize the actin cytoskeleton at this concentration (26), had no influence on the observed fluorescence recovery (Fig. S18).

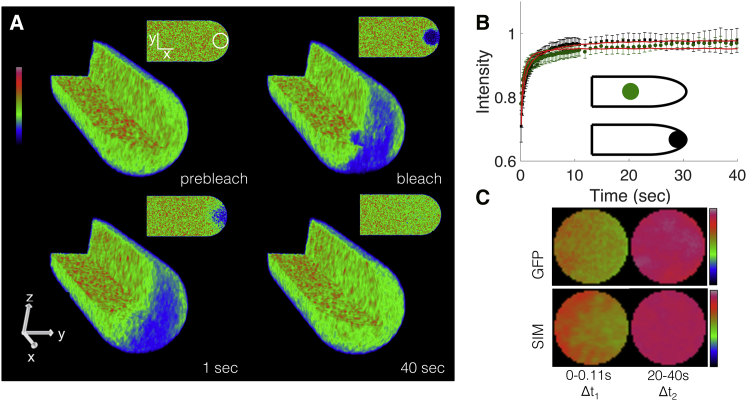
Figure 2.

Cell shape influences fluorescence recovery in vivo and in silico. (A) Three- and two-dimensional rendering of simulated scanning confocal photobleaching and recovery. Artificially fast (instantaneous) imaging scan rates were used to illustrate 3D properties of the simulation. The full animated form of this panel can be found in Movies S1 and S2. (B) Fluorescence recovery of 3xmEGFP cells at the edge (black squares) and center (green circles). Best fit simulation curves indicated in red. n = 14 and 7 for the edge and center, respectively. Error bars represent standard deviation. (C) Cropped and frame-averaged photobleaching ROI at the cell edge of 3xmEGFP cell line (top) and simulation (bottom). Time intervals for frame averaging are Δt₁ = 0–40.11 s and Δt₂ = 20–40 s, with n = 14 and 50, respectively. ROI is 4 μm in diameter. Image intensity is denoted with rainbow lookup table. To see this figure in color, go online.

To determine if a single diffusion coefficient could reproduce the different rates of recovery observed at the edge and the center, we simulated FRAP recovery curves at the edge and center for a range of diffusion coefficients using the model described in the Supporting Material and Fig. S1. In our fitting routine (Supporting Material), we used one diffusion coefficient to fit recovery at both the edge and the center, which yielded a value of D = 8.25 ± 0.358 μm² s⁻¹. This diffusion coefficient is within the expected range for 3xmEGFP under physiological conditions (27), and using the Einstein-Stokes relation can be used to estimate an effective viscosity of the moss cytoplasm—approximately one order-of-magnitude higher than that of water in this case. The simulations at the cell edge exhibited both a slower rate of recovery and higher fluorescence plateau when compared to the center, recapitulating experimental recoveries. The slower recovery at the cell edge is due to geometrical constraints provided by the apical plasma membrane, i.e., proteins cannot flow in or exchange in all directions as they can at the center of the cell. The higher plateau at the cell edge is caused by photobleaching fewer particles at the cell edge because the 3D Gaussian laser beam extends outside of the cell volume at the edge, in contrast to the fully encased beam at the cell center.

Fourier analysis of the spatial fluorescence recovery further supports the claim that cell shape can influence the interpretation of FRAP curves (Supporting Material). Specifically, experimental and simulated fluorescence concentration gradients are recovered in the same way, as characterized by the first mode of the Fourier series representation of the spatial recovery profile (Fig. S13 a and Movie S3). Our simulation results in conjunction with experiments highlight the strong influence of boundaries on recovery, and shows that erroneous conclusions about the fraction of bound molecules and fluorescent mobility at the edge and center can be made if such geometric effects are not taken into account. It is important to note that boundary effects are masked by the additional effects (such as scan speed) associated with a fast recovery, and become more apparent at lower diffusion coefficients (Fig. 3). In the limit of a fast scan speed, each imaging or photobleaching event happens at a single point in time, and the curve is well sampled during recovery. However, with a slower scan speed—or a faster recovery—each image scan spans a large amount of the recovery time, and the resultant recovery is undersampled, affecting the apparent fluorescence recovery.

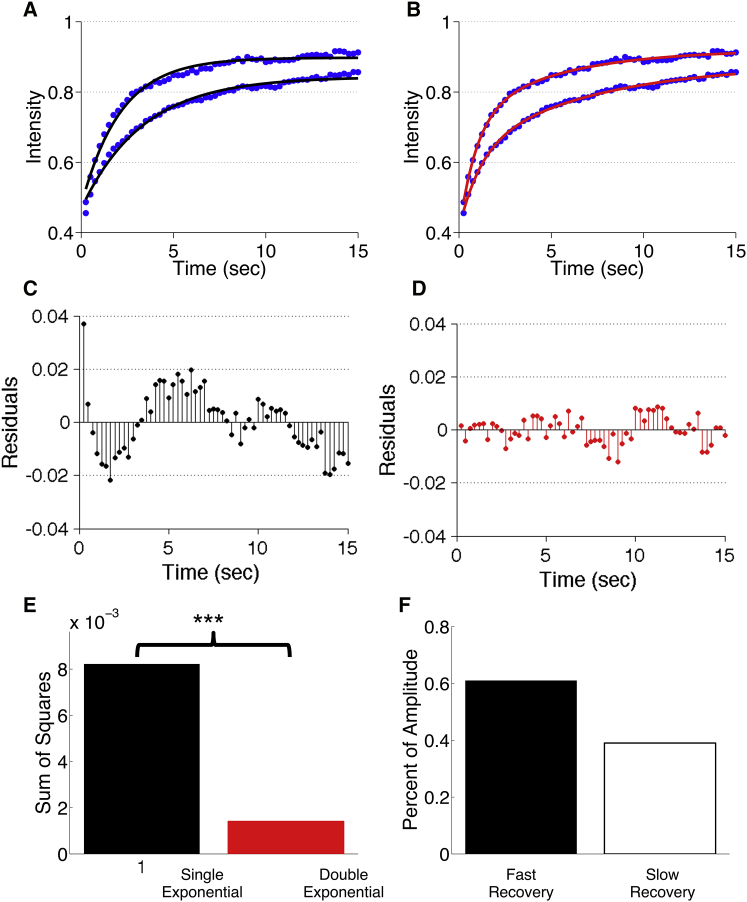
Figure 3.

Single and double exponential fits cannot evaluate the number of dynamic states of a fluorophore. (A) Simulated moss fluorescence recovery (blue circles) with corresponding single exponential fits (black lines), D = 1 μm² s⁻¹. Photobleaching was performed at the cell edge (bottom) or in the middle of the cell (top). (B) Simulated moss fluorescence recovery (blue circles) with corresponding double exponential fits (red lines), D = 1 μm² s⁻¹. Photobleaching was performed at the cell edge (bottom) or in the middle of the cell (top). (C) Residuals for the single exponential fit to simulated moss recovery away from the cell boundary. (D) Residuals for the double exponential fit to simulated moss recovery away from the cell boundary. (E) Sum of squares for the single exponential (black) and the double exponential (red) fits. Fits were performed on the simulated moss recovery at the middle of the cell. ^∗∗∗ indicates p value < 0.001 of “extra sum of squares” F-test. (F) Percent of fluorescence recovery dictated by the fast (black) and slow (white) terms in the double exponential fit. Fit was performed on moss recovery in the middle of the cell. To see this figure in color, go online.

Exponential fitting does not necessarily reflect the underlying dynamics

When a proper analytical model is not available to describe a given fluorescence recovery, a common practice is to fit the recovery data to a series of exponentials; the number of exponentials needed to fit the recovery has been interpreted as the number of “dynamic states” of the fluorophore (28, 29, 30, 31, 32, 33). In this context, having multiple dynamic states refers to the various modes by which a fluorophore recovers during a FRAP experiment. These modes can include multiple diffusion coefficients, chemical reactions, and active transport, or any combination of the three. Specific examples would include: the presence of more than one diffusion coefficient in a reaction-diffusion system; two modes of fluorescence recovery in an active transport and diffusion-based system; and two unique reaction rates in a reaction dominant FRAP experiment.

Fundamentally, exponential fitting should only be used to identify unique reaction rates in a reaction-dominant FRAP experiment (34). This is because diffusion-based fluorescence recovery asymptotically behaves as a power law, and neither a single, nor a double exponential can fundamentally reproduce this behavior at long times (see the Supporting Material and Fig. S20). Hence, there is no theoretical justification for fitting a single or double exponential to a diffusion-based recovery.

The divergence between asymptotic behavior and the exponential functional form often occurs at times longer than those that are experimentally practical, however, one may still want to consider using it to fit early times in a recovery curve. Although it may appear to provide an adequate fit in early recovery, as we will demonstrate below, using a proof-by-contradiction approach, exponential fitting fails to capture the underlying dynamics and is not able to predict the number of dynamic states in a diffusion-based recovery. To start, we analyzed simulated fluorescence recoveries of a fluorophore with a single input diffusion coefficient, D = 1 μm² s⁻¹, in the moss geometry. Simulations were conducted at the cell center and the cell edge. At both regions, a fit to the single exponential model exhibits periodic over- and undershooting (Fig. 3 A), whereas the double exponential model exhibits less periodicity for either location (Fig. 3 B). Residual plots demonstrate periodic errors in the single exponential fit and the lack thereof in the double exponential fit (Fig. 3, C and D). To determine if the models predict the trends of the fluorescence recovery, we performed a Wald-Wolfowitz runs test. This test determines if the residuals of the fit are random, where increased randomness suggests a better fit. The results of this test suggest (for this diffusion coefficient and given morphology) that neither the single nor the double exponential fits exhibited random residuals (null hypothesis of random residuals, p values = 2 × 10⁻⁸ and 0.027, respectively). However, there is an improvement in fit quality with the double exponential function. In addition, other morphologies show an improvement for the double exponential fit that becomes significantly random (see Table S4). Sum of squared differences between the simulation and exponential fitting demonstrated that the single exponential fit exhibits an eightfold-higher sum of squared difference compared to the double exponential fit (Fig. 3 E). Lastly, to determine if the single- or double-exponential model should be used, we performed an F-test to compare the change in sum of squares and the change in number of parameters between the two models. The results of this test predicted that the double exponential fits best with a p value < 0.001 (35), for this morphology and diffusion coefficient.

Table S4 further shows that similar results hold for other cell shapes and diffusion coefficients between 0.1 and 10 μm² s⁻¹. Because the double exponential fit is composed of two recovery phases, it is important to note how much each phase contributes to the recovery. For the curve generated at the cell center, the fast mode contributed to roughly 60% of the recovery whereas the slow mode contributed to ∼40% (Fig. 3 F), indicating that contributions from both modes are significant. Based on the results of this fitting procedure, one could naively conclude that the molecule simulated here has at least two dynamic states and that it must have two different modes of recovery. Such a conclusion would be incorrect, as we simulated only one diffusion coefficient.

As illustrated, at short times, exponential fitting inadequately describes the dynamic behavior of a FRAP curve, whereas at long times it diverges from the expected asymptotic limit. When examining diffusion-based processes, we suggest that exponential forms should only be used to make comparisons of the relative rate of fluorescence recovery between different curves.

Model selection should consider boundary effects, dimensionality, and initial conditions

To explore the predictions made by existing analytical FRAP models (see the Supporting Material), we simulated fluorescence recovery experiments for six different cellular shapes—nuclei, filopodia, and lamellipodia of mammalian cells, budding yeast, Saccharomyces pombe, and tip-growing plant cells (moss)—for a range of biologically relevant diffusion coefficients (Fig. 4, A and B, and Movies S4, S5, S6, S7, and S8). We used three notable analytical models (2, 3, 36) to fit to our simulated recoveries. Because of their substantial citation history, we selected both the analytical models from Axelrod et al. (2) and Soumpasis (3). For its simplicity, and because it incorporates boundaries, we selected a 1D analytical solution with reflective boundary conditions (36). Once the simulated recoveries were fit with these models, we measured the percent difference between the simulated input diffusion coefficient, D_true, and the model predicted diffusion coefficient, D_model, i.e., |(D_true – D_model)/D_true| × 100.

Figure 4.

Simulations of different 3D cell shapes. (A and B) Medial section of simulated fluorescence recoveries with photobleaching at the middle (A) or edge (B) of the cell. Postbleach image is 16 s after photobleaching. Fluorescence intensity is indicated by the rainbow lookup table. Scale bars, 5 μm. To see this figure in color, go online.

The analytical models from Axelrod et al. (2) and Soumpasis (3), most accurately predicted diffusion coefficients when photobleaching was conducted at the cell center. As expected, both models failed to predict diffusion coefficients reliably in long thin tubular geometries (with percent differences >50% for most cases), i.e., S. pombe and filopodia, as shown in Table 1. These models also exhibited similar failings in the remaining cell shapes when FRAP was conducted at the cell edge (with percent differences >50% for most cases). Further evidence for this spatial effect was demonstrated by conducting photobleaching and model fitting at a varying distance away from the cell edge. Consistent with strong boundary effects, as the bleaching event (ROI) was moved further from the cell edge, we observed an increased rate of fluorescence recovery and improved model predicted diffusion coefficients (see Fig. 5). This cautions against indiscriminately using analytical models that make infinite boundary assumptions in complex cellular geometries. These boundary effects can be further illustrated using the method of images in a 1D strip FRAP model that incorporates boundaries. This model predicts that bleaching at the boundary should recover with an effective diffusion coefficient four-times slower than would be measured with a centered bleach (see the Supporting Material).

Table 1.

Best Fit Diffusion Coefficients for the Four Analytical Models and the VCell VirtualFRAP Tool

Cellular Geometry		Diffusion Coefficient (μm2/s)
		Input D	Axelrod et al. (2)	Soumpasis (3)	1D FRAP	Virtual FRAP
B Yeast	E	1	0.123 ± 0.001	0.103 ± 0.001	0.820 ± 0.004	1.22 ± 0.01
B Yeast	C	1	1.95 ± 0.02	1.82 ± 0.02	3.98 ± 0.02	0.908 ± 0.004
B Yeast	E	10	3.16± 0.03	2.90 ± 0.02	9.44 ± 0.04	11.7 ± 0.1
B Yeast	C	10	96.7 ± 1.8	84.5 ± 0.3	44.4 ± 0.7	8.42 ± 0.13
Lamellipodia	E	1	0.534 ± 0.007	0.530 ± 0.007	6.18 ± 0.08	1.03 ± 0.01
Lamellipodia	C	1	0.962 ± 0.010	0.942 ± 0.010	3.54 ± 0.05	1.02 ± 0.01
Lamellipodia	E	10	2.16 ± 0.04	2.33 ± 0.04	25.1 ± 0.4	9.95 ± 1.29
Lamellipodia	C	10	12.8 ± 0.6a	12.1 ± 0.5	65.6 ± 1.3	10.0 ± 0.2
Nucleus	E	1	0.358 ± 0.008	0.351 ± 0.008	3.48 ± 0.07	1.03 ± 0.02
Nucleus	C	1	1.56 ± 0.02	1.55 ± 0.02	7.18 ± 0.14	1.01 ± 0.01
Nucleus	E	10	3.17 ± 0.05	3.38 ± 0.05	23.3 ± 0.3	13.9 ± 0.2a
Nucleus	C	10	81.7 ± 0.7	46.4 ± 0.4a	83.3 ± 1.4	6.36 ± 0.13a
Pombe	E	1	0.152 ± 0.001	0.135 ± 0.002	1.39 ± 0.02	1.05 ± 0.01
Pombe	C	1	0.374 ± 0.002	0.359 ± 0.002	1.17 ± 0.01	0.948 ± 0.004
Pombe	E	10	0.994 ± 0.005	0.999 ± 0.005	11.6 ± 0.1	11.3 ± 0.1
Pombe	C	10	6.94 ± 0.12	6.13 ± 0.08	37.3 ± 0.2	10.1 ± 0.1
Moss	E	1	0.467 ± 0.012	0.469 ± 0.014	5.68 ± 0.19	1.10 ± 0.02
Moss	C	1	1.06 ± 0.03	1.07 ± 0.03	4.31 ± 0.15	1.05 ± 0.02
Moss	E	10	2.26 ± 0.27	2.43 ± 0.29	32.7 ± 3.8	12.1 ± 0.2
Moss	C	10	6.62 ± 0.24	6.98 ± 0.23	52.9 ± 2.0	7.81 ± 0.14
Filopodia	E	1	0.147 ± 0.001	0.108 ± 0.001	1.09 ± 0.01	1.03 ± 0.01
Filopodia	C	1	0.420 ± 0.003	0.402 ± 0.003	1.12 ± 0.01	1.03 ± 0.01
Filopodia	E	10	0.982 ± 0.027	0.978 ± 0.030	9.56 ± 0.26	10.3 ± 0.1
Filopodia	C	10	8.30 ± 0.05	7.66 ± 0.04	32.0 ± 0.2a	10.3 ± 0.1

ROI is either at the cell edge (E) or center (C). The symbol “±” represents standard error of 10 simulations. Bolded text indicates cases where the model produced an answer within 25% of the true D value. Note that similar results for D = 0.1 μm² s⁻¹ are given in Table S3. To quantify the effects of confocal scan speed, we present results for D = 10 μm² s⁻¹, with a 280 kHz scan speed, in Table S5.

^aIndicates cases in which switching to a faster scan speed brought the measured value to within 25% of the true D value.

Figure 5.

ROI positional dependence. (A) Black squares, purple triangles, and blue circles indicate ROI position at center, intermediate, and edge positions, respectively. (B) Best fit diffusion coefficients for the simulated recoveries in (A) when fit to the model of Soumpasis (3). Smaller dots are intermediate points, not depicted in (A). To see this figure in color, go online.

The 1D strip FRAP model was found to be the most accurate (with percent differences <25% in most cases; see Table 1) in both S. pombe and filopodia, where the geometries closely resembled a long thin tube relative to the imaging ROI. Furthermore, because the model accounts for boundaries, it accurately predicts diffusion coefficients at the ends of the cells. Although moss is also a long tubular cell, the strip FRAP model could not accurately measure diffusion within this cell type. This is because moss is large relative to the PSF, allowing fluorophores to recover in both x- and y dimensions during the short times we fit. We further explore this effect in the Supporting Material. The 1D strip model failed to measure diffusion coefficients accurately for the remaining more complicated cell shapes (see Table 1).

Lastly, we chose the VirtualFRAP tool (part of VCell environment) (13) as an algorithmic example because it incorporates the cellular boundaries, albeit in two dimensions, and calculates a diffusion coefficient after an iteration procedure. Note that the VirtualFRAP tool is a 2D continuum approach that is best suited for low NA lenses. This low NA is necessary to bleach a cylindrical region encompassing the height of the cell. The algorithmic VCell VirtualFRAP tool accurately estimated diffusion coefficients (within a 25% difference; see Table 1) for all morphologies with the exception of the nucleus at D_true = 10 μm² s⁻¹ (explored below). This level of accuracy is consistent with our simulated bleached region being close to a cylinder, as shown in the Supporting Material. It also indicates that incorporating the 2D geometry is a good approximation for many cell types and our measured optical settings.

The inaccuracy of VirtualFRAP on the nucleus when D_true = 10 μm² s⁻¹ was consistent with a trend observed across all the models, specifically that the models mostly predicted inaccurate diffusion coefficients at the high diffusion coefficient. This inaccuracy is the product of the finite scan rate used during photobleaching and image acquisition, and can be attenuated at artificially fast scan speeds, as shown in Table S5. At $2800$Hz, a fluorophore diffusing at 10 μm² s⁻¹ is expected to travel roughly 80 nm during a single line scan. Given our 100-nm line spacing, this suggests that diffusion is too fast for our acquisition speed. Furthermore, this demonstrates that at the upper scan speed of our confocal system ($2800$Hz), we cannot reliably measure fast diffusion coefficients >10 μm² s⁻¹, and highlights how the finite scan speed of the confocal must be considered as a limiting factor in performing FRAP experiments.

Membrane FRAP

FRAP analysis of molecules associated with the plasma membrane has been used extensively to characterize their dynamics (37, 38, 39, 40, 41). Compared with intracellular molecules, using FRAP to estimate diffusion coefficients in membranes is simplified due to the 2D nature of the membrane, as well as the slower dynamics of the molecules. To explore the influence of membrane curvature on fluorescence recovery, we simulated photobleaching experiments inside a 200-nm-thick moss shell (Fig. 6 A). The shell was oriented such that the imaging plane was parallel to the flat circular surface of the cylinder (Fig. 6 B). Imaging and bleaching were then conducted on the flat circular surface of the cylinder or the extreme cell apex, as shown in Fig. 6, A and B. To simulate typical membrane diffusion, D = 0.1 μm² s⁻¹ was chosen. Analysis of our simulation results showed an increase in fluorescence recovery at the cell apex (Fig. 6 B). When fit with the Soumpasis model (3) (see also the Supporting Material), we found the measured diffusion coefficients to be D = 0.11 ± 0.01 and 0.13 ± 0.01 μm² s⁻¹ at the base of the cylinder and the cell apex, respectively. This reduction in predicted diffusion coefficient can be attributed to performing a planar bleach scan on a curved membrane. During this planar scan, the membrane curvature exposes more bleachable surface area, creating a larger effective ROI. We expect this effect to become more dramatic in instances where both the ROI and membrane curvature are large.

Figure 6.

Membrane FRAP. (A) Simulated fluorescence recovery images of the moss cell membrane, at the base of the cell (top) or the extreme cell apex (bottom) with bleaching and imaging planes perpendicular to the long axis of the cell. Scale bar, 3 μm. (B) Simulated fluorescence recovery curves at the base of the cylinder (green) or the extreme cell apex (black). n = 10, error bars indicate standard error. Dashed lines represent fits to the model of Soumpasis (3) (see also the Supporting Material). (C) Simulated fluorescence recovery images of the moss cell membrane, with bleaching and imaging planes parallel to the long axis of the cell. Scale bar, 5 μm. (D) Simulated fluorescence recovery curves at the base of the moss cell cylinder (red) or the extreme cell apex (black). n = 10, error bars indicate standard error. (E) Simulated fluorescence recovery images of the budding yeast membrane, with bleaching and imaging planes parallel to the long axis of the cell. Scale bar, 3 μm. (F) Simulated fluorescence recovery curves at mother cell (red) and the daughter cell (black). n = 10, error bars indicate standard error. To see this figure in color, go online.

To investigate the effects of FRAP on membranes in other cellular orientations, we simulated imaging and bleaching planes that were parallel to the long axis of the moss cell (Fig. 6, C and D). Simulations were then subjected to photobleaching at the base of the cylinder or the extreme cell apex. At early times, fluorescence recoveries at both locations appeared identical, but at long times we observed separation between the curves (Fig. 6 D). This is because photobleaching in this orientation bleached more molecules at the base of the cylinder when compared to the apex.

To explore FRAP in a cellular geometry often used to study membrane dynamics, we simulated photobleaching on the membrane of the budding yeast (Fig. 6, E and F). We found that photobleaching at the daughter or the mother cell had little-to-no influence on fluorescence recoveries. Once cell orientation and effective ROI sizes are accounted for, membrane curvature has minimal influence on fluorescence recoveries, consistent with earlier modeling work (41).

Discussion

In this article, we experimentally showed, to the best of our knowledge for the first time, the influence of cell boundaries in FRAP recovery. Our results were recapitulated using a comprehensive FRAP model that not only takes into account 3D cellular geometry, but also confocal microscope optical properties. We observed that when performed close to boundaries, for instance when studying tip growing cells, fluorescence recovery is significantly slowed even though a molecule’s diffusion coefficient remains the same. As we have also demonstrated with an analytical model in the Supporting Material, this results in a smaller effective diffusion coefficient. Therefore, whenever possible, we recommend avoiding performing FRAP closer than one ROI distance from the edge of the target volume. In addition, when FRAP is conducted close to the cell boundary, the 3D point spread function of the laser beam may extend into the area outside of the cell volume and, as a consequence, bleach fewer fluorophores than photobleaching experiments performed at the cell center. These results suggest that comparison of bound fractions of molecules near cellular boundaries should be performed with caution.

The FRAP models we used from Axelrod et al. (2) and Soumpasis (3) give very similar results and are useful to obtain diffusion coefficients in flat structures such as lamellipodia and membranes. These models can also be useful for larger structures, such as plant tip growing cells or other cylindrical structures, as long as appropriately fast image acquisition rates are used for the diffusion coefficient in question. Our results show that for thin and elongated structures, similar to a filopodium, S. pombe, or an elongated fungal hypha, a simple 1D FRAP model could be sufficient, as long as it incorporates boundaries. For more complex morphologies, sophisticated approaches are necessary, such as the VCell VirtualFRAP tool. We found that the VirtualFRAP tool, an algorithmic approach, performs well in all of our simulated cases when an appropriately fast scan rate is used, with <25% error in the estimation of the diffusion coefficient. Importantly, VirtualFRAP performs well at boundaries, but when two-dimensionality cannot be approximated (i.e., when high NA is required), it might become necessary to apply a full optical and geometrical simulation method such as the one presented in here. This level of accuracy, however, is often times adequate, and will also allow for the estimation of the effective viscosity, and can provide further insight into the cytoplasmic forces.

Overall, we found that the analytical models considered in this article can generally fail if the underlying assumptions do not match the cellular geometry or confocal optical properties that were used. Although this is expected, given the misuse of these models in the literature, we recommend that they should not be used naively without consideration of the experimental setup. This caveat also applies to our DCMS software, as it makes assumptions about the properties of the system (diffusion model, PSF shape, finite fluorophore reservoir, etc.), as well as requiring that the researcher knows and inputs the parameters of their experimental setup.

In addition, we find that extraneous recovery states resulting from fitting a series of exponentials can be explained by the geometrical and optical properties of the system, rather than an underlying biological mechanism. Moreover, when using analytical FRAP diffusion/binding kinetics models, we expect these effects to influence binding and dissociation constants. A detailed analysis of these effects is beyond the scope of this work, and is left for future studies.

Although our analysis showed how boundary and optical effects can confound FRAP analysis, these conclusions cannot be generalized to every experimental setup, and further validation across additional models is required. To make this model validation process more accessible for experimentalists using existing models or theorists developing new analytical models, we developed an interactive graphical interface for the Java-based version of our simulation, the Digital Confocal Microscopy Suite. This tool allows the users to simulate specific experimental conditions—cell type, microscope settings, and diffusion coefficient—and easily generate simulated recovery curves. Any given model (analytical or algorithmic) can then be fit to these simulated recovery profiles to calculate the model predicted diffusion coefficient. The difference between the model predicted and input (to the simulation) diffusion coefficients can then be used to determine the validity of the model of interest. DCMS can also serve as a useful and freely available (20) teaching tool, not only to explore optical and boundary effects in FRAP, but also to demonstrate how scanning confocal microscopes can be used in fluorescence dynamics techniques, such as raster image correlation spectroscopy (42), number and brightness (43, 44), and fluorescence correlation spectroscopy (45).

Author Contributions

J.L.K. developed the simulations. J.P.B. performed the experiments. J.L.K. and J.P.B. analyzed the data and wrote the manuscript. Z.C., X.H., and J.L.K. contributed to the initial CUDA implementation of the simulations. C.U., S.I.M., and J.L.K. developed DCMS APARAPI implementation. S.I.M. wrote the corresponding Java Graphical User Interface (GUI) for DCMS. E.T. and L.V. conceived the study, wrote the manuscript, and supervised the overall study.

Editor: Jochen Mueller.

Supporting Citations

References (46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57) appear in the Supporting Material.

Supporting Material

Movie S1. Simulation of FRAP at the Moss Cell Edge

3D (upper left) and 2D (upper right) renderings of simulated scanning confocal photobleaching and recovery are shown. Fluorescence intensity is indicated by the rainbow lookup table. Total fluorescence intensity measured in the ROI (4 μm, located at the edge of the cell) is shown as a function of time, focusing on the overall recovery (bottom) and photobleach (inset). Artificially fast imaging scan rates (instantaneous image capture at 1000 fps) and parameters (D = 1 μm² s⁻¹, 500 × 500-pixel resolution) were used to illustrate 3D properties of the simulation.

Movie S2. Simulation of FRAP at the Moss Cell Center

3D (upper left) and 2D (upper right) renderings of simulated scanning confocal photobleaching and recovery are shown. Fluorescence intensity is indicated by the rainbow lookup table. Total fluorescence intensity measured in the ROI (4 μm, located at the center of the cell) is shown as a function of time, focusing on the overall recovery (bottom) and photobleach (inset). Artificially fast imaging scan rates (instantaneous image capture at 1000 fps) and parameters (D = 1 μm² s⁻¹, 500 × 500-pixel resolution) were used to illustrate 3D properties of the simulation.

Movie S3. Analysis of Spatial Recovery of 3xmEGFP at the Moss Cell Edge

Cropped and frame averaged photobleaching ROI at the cell edge for 3xmEGFP cell line (left). Corresponding angular intensity profiles of 3xmEGFP at the cell edge (right). The first mode of the Fourier series, f1, is overlaid in blue, with its magnitude, a1 shown in the inset. n = 14; ROI is 4 μm in diameter. Mean subtracted image intensity is denoted with the rainbow lookup table.

Movie S4. Fluorescence Recovery in the Budding Yeast

Medial confocal slice of simulated fluorescence recovery of budding yeast after photobleaching of the daughter cell is shown. Simulations were run with a diffusion coefficient of D = 1 μm² s⁻¹.

Movie S5. Fluorescence Recovery in the Nucleus

Medial confocal slice of simulated fluorescence recovery of the nucleus after photobleaching at the cell edge is shown. Simulations were run with a diffusion coefficient of D = 1 μm² s⁻¹.

Movie S6. Fluorescence Recovery in the Filopodia

Medial confocal slice of simulated fluorescence recovery of filopodia after photobleaching at the cell edge is shown. Simulations were run with a diffusion coefficient of D = 1 μm² s⁻¹.

Movie S7. Fluorescence Recovery in S. pombe

Medial confocal slice of simulated fluorescence recovery of S. pombe after photobleaching at the cell edge is shown. Simulations were run with a diffusion coefficient of D = 1 μm² s⁻¹.

Movie S8. Fluorescence Recovery in the Lamellipodia

Medial confocal slice of simulated fluorescence recovery of lamellipodia after photobleaching at the cell edge is shown. Simulations were run with a diffusion coefficient of D = 1 μm² s⁻¹.