Five Alternative Myosin Converter Domains Influence Muscle Power, Stretch Activation, and Kinetics

Abstract

Muscles have evolved to power a wide variety of movements. A protein component critical to varying power generation is the myosin isoform present in the muscle. However, how functional variation in muscle arises from myosin structure is not well understood. We studied the influence of the converter, a myosin structural region at the junction of the lever arm and catalytic domain, using Drosophila because its single myosin heavy chain gene expresses five alternative converter versions (11a–e). We created five transgenic fly lines, each forced to express one of the converter versions in their indirect flight muscle (IFM) fibers. Electron microscopy showed that the converter exchanges did not alter muscle ultrastructure. The four lines expressing converter versions (11b–e) other than the native IFM 11a converter displayed decreased flight ability. IFM fibers expressing converters normally found in the adult stage muscles generated up to 2.8-fold more power and displayed up to 2.2-fold faster muscle kinetics than fibers with converters found in the embryonic and larval stage muscles. Small changes to stretch-activated force generation only played a minor role in altering power output of IFM. Muscle apparent rate constants, derived from sinusoidal analysis of the chimeric converter fibers, showed a strong positive correlation between optimal muscle oscillation frequency and myosin attachment kinetics to actin, and an inverse correlation with detachment related cross-bridge kinetics. This suggests the myosin converter alters at least two rate constants of the cross-bridge cycle with changes to attachment and power stroke related kinetics having the most influence on setting muscle oscillatory power kinetics.

Introduction

The evolution of a wide variety of types and isoforms has enabled myosin to contribute to a diverse range of cellular functions. In muscle fibers, it is well known that expression of different myosin isoforms is critical for setting the functional diversity of muscle types (1, 2). This diversity enables muscles to power a wide variety of locomotor tasks. However, our understanding of how myosin functional variation is set by differences in cross-bridge cycle biochemistry and, particularly, structural regions is fairly limited.

The first investigations into muscle myosin structural regions focused primarily on flexible loop regions, such as loops 1 and 2 (3, 4, 5, 6, 7). These chimeric myosin experiments led to some insights, especially for smooth muscle myosin (8, 9), but the limited work on skeletal and cardiac muscle myosin isoforms into important regions for setting isoform differences was mostly inconclusive (3, 10, 11). A major reason for inconclusive results was that although the chimeric myosins sometimes caused a myosin property value change, such as ATPase rate and actin velocity, the changes mostly did not correlate with the values of the myosin isoforms that were the sources of the flexible loops. Our investigations using the Drosophila system have revealed other regions besides the flexible loops are critical for setting myosin and muscle functional properties (12, 13, 14, 15).

We have utilized the unique expression pattern of the single muscle myosin heavy chain gene (Mhc) in Drosophila to explore structure-function relations (16). Transcripts from Mhc are alternatively spliced to generate at least 15 MHC isoforms found in a variety of muscle types (17). There are four alternatively spliced regions in the catalytic domain, alterative exons 3, 7, 9, and 11. To test these regions for functional importance, we and our collaborators systematically exchanged the alternative versions of these four regions between two Drosophila myosin isoforms, the very fast indirect flight muscle (IFM) myosin isoform (IFI) and a slower embryonic myosin isoform (EMB). The resulting eight chimeric myosins were transgenically expressed in Drosophila IFM, and we measured the resulting changes to myosin and muscle functional properties (12, 13, 14, 15).

A major finding of this previous comprehensive study of the alternatively spliced myosin regions was that the converter (Fig. 1) had the largest impact on myosin and muscle functional properties compared with the other three alternatively spliced regions in the myosin catalytic domain (12, 18, 19). The EMB myosin converter region, when exchanged into IFI (Fig. 1; 11d replaced 11a), decreased IFM power generation and displayed a much lower frequency at which maximum power was produced. Surprisingly, the animals could still fly despite these detrimental changes to IFM mechanical performance. Another surprise was that the converter exchanges did not alter ADP release in a way that correlated with the changes in muscle speed or actin velocity in the motility assay (20). ADP release is typically thought to be rate limiting for velocity (21). Thus, our results suggested a unique rate-limiting step for fast Drosophila myosin isoforms and likely very fast myosins found in other species (22). This rate-limiting step that the converter modifies to alter muscle kinetics remains to be determined.

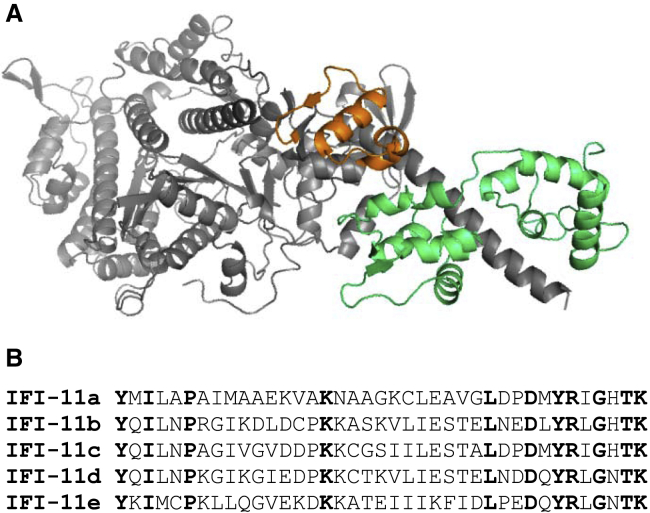
Figure 1.

Drosophila myosin S-1 fragment and five converter sequences. (A) Structure of the Drosophila myosin S-1 region (Drosophila EMB isoform, Protein Data Bank: 4QBD). The converter domain is shown in orange, the essential light chain (ELC) in green, and the rest of the MHC S-1 domain in gray. The regulatory light chain is not part of this crystal structure. (B) Sequences of the five Drosophila converters. Bold amino acids are identical. To see this figure in color, go online.

Another unanswered question about muscle function is the mechanism behind stretch activation (SA) and what role(s) myosin plays in this mechanism. SA is a delayed increase in force after stretch of a calcium-activated muscle that transiently boosts force to a higher level than that achieved by calcium activation alone (23, 24). Almost all muscle types display some amount of SA, which is generally lowest in skeletal muscle, moderate in cardiac muscle, and most prominent in insect asynchronous IFM. Rather than contracting once per motor nerve action potential, asynchronous muscles such as the IFM contract more often than the motor nerve action potential firing rate by utilizing the delayed SA force increase. The delay is timed to occur during the shortening portion of a contraction cycle, resulting in higher work and power output. Efficiency is increased in asynchronous IFM because calcium is not pumped out during the relaxation phase of each contraction cycle. We have previously shown that myosin isoforms can vary the amount of SA force generation between muscle types with minimal and moderate SA (25). However, it is not known which domain(s) of myosin are critical for this variation. The converter might be responsible because it is one of the four myosin catalytic domains that differ between the isoforms that we found to vary SA force generation (25).

Further insights into converter function would increase our understanding of the mechanisms behind myosin based myopathies. For example, the converter is a hotspot for hypertrophic cardiomyopathy (HCM) mutations that have severe phenotypes and poor prognoses (26, 27). HCM is the most identifiable cause of sudden death in young adults and the leading cause of death in competitive athletes (28). At least 25 HCM mutations have been localized to the converter, but we have only begun to learn how these mutations alter muscle function (27, 29).

The wide variety of Drosophila muscle types and the five naturally occurring alternative versions of the converter expressed from the Mhc gene present us with a unique opportunity to explore a potentially large variation in functional properties from alterations to a single muscle MHC domain (Fig. 1 B). Two of the converters are found in the adult fast musculature: 11a is expressed only in IFM, whereas 11c is found in the jump muscle and some direct flight muscles. 11d and 11e are primarily found in the slower external, intermediate, and internal embryonic and larval body wall musculature. 11d is also found in adult direct flight muscle 52, which is used for steering and fine tuning wing beat frequency (WBF) and wing stroke amplitude (WSA) (30), and the esophagus musculature. 11e is also found in the pharyngeal muscle which is used for ingesting food. A complementary DNA transcript containing 11b was found in a screen of an embryonic complementary DNA library, but it has yet to be localized to specific embryonic muscle types (31).

We examined the impact of all five converters on muscle and myosin function by creating five transgenic fly lines. Each line expressed myosin with a single converter substituted into the IFM myosin background. We found that the five converters enabled variation of optimal IFM power output by 2.8-fold and kinetics (e.g., f_max) 2.2-fold. Sinusoidal analysis suggested the kinetic differences were due primarily to changes in steps associated with myosin attachment rate to actin rather than detachment rate. The converters also influenced SA amplitude, suggesting that SA contributes to at least some of the changes seen in work and power generation. These changes in muscle properties caused decreased flight ability in all four non-native converter lines (11b–e). We attributed this decrease to slower WBFs, but some of the lines likely compensated for the slower WBF by increasing WSA.

Materials and Methods

Creation of transgenic Drosophila lines

PwMhc2, which is a wild-type Drosophila Mhc gene cloned into the P element vector pCaSpeR4 (32), was used to create four new converter lines: IFI-11a, IFI-11b, IFI-11c, and IFI-11e. IFI-11d was made previously (previously referred to as IFI-EC) (12). The entire exon 11 coding region and flanking introns of PwMhc2 were replaced with one of the alternative exons using standard PCR, restriction enzyme digestion, and ligation techniques. The resulting constructs were injected into Drosophila yw embryos (Bestgene, Chino Hills, CA) and integrated into the Drosophila genome using P element-mediated transformation (33). The transgenic lines were crossed into the Mhc¹⁰ background, which lacks myosin expression in IFM (34), to generate Drosophila lines that expressed a single converter variant in their IFM. Flies were raised at 25°C on a 12 h light/dark schedule.

Flight assays

All flight assays were conducted on 2–3 day old females at 15°C to allow for direct comparison with the muscle mechanics experiments performed at 15°C. Flies were acclimated to 15°C for at least 1 h before testing. Flight ability was determined by observing whether a fly is capable of flying up (U), horizontally (H), down (D), or not at all (N) when released in a Plexiglas flight chamber (35). Flight index equals 6U/T + 4H/T + 2D/T + 0N/T, where T is the total number of flies tested (36). For WBF, monofilament fishing line was adhered to the fly’s head and measured using an optical tachometer as previously described (37). WSA was captured using a digital SLR camera as previously described (19). Each flight assay used a separate set of flies.

IFM muscle mechanics

IFM skinned fiber preparation from a 2–3 day old female fly was performed as previously described (38). The fiber was bathed in relaxing solution (pCa 8.0, 12 mM MgATP, 30 mM creatine phosphate, 600 U/mL creatine phosphokinase, 1 mM free Mg²⁺, 5 mM EGTA, 20 mM N,N-Bis(2-hydroxyethyl)-2-aminoethanesulfonic acid (BES) (pH 7.0), 200 mM ionic strength, adjusted with Na methane sulfonate, 1 mM dithiothreitol (DTT)) at 15°C on the mechanics apparatus. Activation of the fiber to pCa 5.0 was accomplished by partial exchanges of the relaxing solution with activating solution (same as relaxing solution except with pCa 4.0).

Small amplitude sinusoidal analysis

Sinusoidal analysis was performed as previously described (Swank (38)). In brief, a sinusoidal length change of 0.125% muscle length (ML) and a frequency set from 0.5 to 650 Hz was applied to the fiber to measure elastic and viscous moduli, work, power, and apparent muscle rate constants. Work (J/m³) was calculated as πE_v (ΔL/L)², and power (W/m³) was calculated as πfE_v (ΔL/L)², where f is the frequency (Hz) of the length perturbations, E_v is the viscous modulus at f, and ΔL/L is the amplitude of the sinusoidal length change divided by the length of the fiber. The muscle apparent rate constants 2πb and 2πc, and amplitudes A, B, and C were obtained by fitting Nyquist plots of the elastic modulus versus viscous modulus with the equation: Y(f) = A(2π if/α)^k – Bif/(b + if) + Cif/(c + if), where f is the applied frequency of oscillation (0.5–650 Hz), i is the square root of −1, α is defined as 1 Hz, and k is a unitless exponent (38, 39, 40). The first term (A) reflects the viscoelastic properties of passive structures within the fiber, and the second and third term (B and C) reflect cross-bridge dependent processes (changes in dynamic stiffness moduli due to the strain-sensitivity of cross-bridge states) that are exponential in the time domain. Processes B and C appear as hemispheres in the Nyquist plot with characteristic frequencies b and c. In the time domain, these frequencies correspond to rate constants 2πb and 2πc. See Fig. S4 for how these rate constants relate to steps of the myosin cross-bridge cycle.

SA

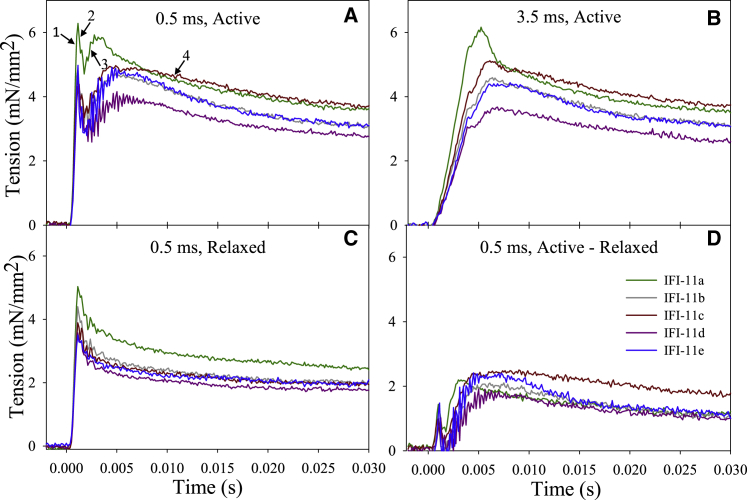
SA was measured at pCa 5.0, 15°C, by applying a 1% ML step stretch over 0.5 ms, the fastest rate that can be applied on our mechanics apparatus, and 3.5 ms, the estimated time over which the Drosophila IFMs lengthen during flight (41, 42). A 1% ML increase was chosen because our previous measures on skinned IFM showed that 1% is optimal for power generation (42, 43). The fibers were held at the new length for 300 ms then slowly returned to their original length (over 500 ms). Total stretch-activated tension (A_SA) was calculated by subtracting the isometric tension value immediately before the stretch from the delayed increased tension peak (Fig. 3, phase 3) after the stretch. A_SA was determined by averaging the tension trace points (sampled at 8 kHz) over 1 ms at each fiber’s peak of phase 3. The phase 3 peak typically occurred between 4.5 and 5.5 ms poststretch for IFI-11a, IFI-11d, and IFI-11e and between 3 and 4 ms for IFI-11b and IFI-11c. We also measured the SA response for a slower step, over 3.5 ms, which is closer to what occurs during flight (42). For 3.5 ms length steps, the peak occurred between 6 and 7 ms for IFI-11a, IFI-11d, and IFI-11e and between 4.5 and 5.5 ms for IFI-11b and IFI-11c. The fiber was relaxed by replacing the bathing solution with relaxing solution (pCa 8.0) and the same length step increases were repeated to determine passive stretch tension (P_SA). Subtracting P_SA from A_SA yielded the increased tension due to active stretch F_SA (corrected active stretch tension, F_SA = A_SA − P_SA) (42).

Figure 3.

SA characteristics of all fiber converter lines. (A) Representative tension traces from fibers stretched by 1% ML over 0.5 ms at pCa 5.0. Numbers and arrows indicate the classic four phases of the response to a rapid step increase. (B) Representative tension traces from fibers stretched by 1% ML over 3.5 ms at pCa 5.0, and (C) over 0.5 ms at pCa 8.0 (relaxed tension traces). (D) Corrected tension traces after subtracting the 0.5 ms, pCa 8.0 relaxed tension traces from the 0.5 ms, pCa 5.0 active tension traces. To see this figure in color, go online.

The SA tension redevelopment rate following stretch (k₃) was obtained by fitting phases 2–4 (44) of the corrected active tension trace to the sum of three exponential curves: F(t) = a₂exp(−k₂t) + a₃[1−exp(−k₃t)] + a₄exp(−k₄t) + C, where constants a₂, a₃, and a₄ are amplitudes; k₂, k₃, and k₄ are rate constants; k₃ is the rate constant of phase 3; and C accounts for nonzero starting values.

Results

Transgenic fly lines

We generated at least two independent fly lines for each of the converters, except for the IFI-11d line which was made previously (12). The majority of the experiments described in this article were performed on both fly lines to make sure the results were due to the converter exchanges and not secondary effects, such as the P element landing in a gene important for IFM function. If the two lines produced different experimental results, we tested a third line and used the results from the lines that were in agreement. Tables S1–S4 contain results of the experiments showing that two lines for each converter produced values that were not statistically different. For presentation clarity, we only include the results from one of the two lines for each converter in the tables and graphs in the body of this article.

Protein expression levels

We confirmed that the amount of myosin produced in the transgenic fly lines was comparable to wild-type myosin production. The converter constructs were injected into yw, which was used as the positive control. There were no significant differences in the amount of myosin protein produced in the fly thoraces between the yw positive control line and any of the transgenic lines (Table S1). No significant differences were observed between any of the transgenic lines. Mhc¹⁰ is included as a negative control because it does not produce myosin in its IFM or jump muscle, the primary muscle groups of the thorax (34). The very small amount of myosin detected in Mhc¹⁰ is probably from the direct flight muscles that are also located in the fly thorax.

Myofibril structure

To ensure that the mechanics and flight tests results were due to the converter exchange rather than an indirect effect due to damaged muscle ultrastructure, we imaged the skinned IFM fibers using electron microscopy. PwMhc2, a fly line expressing a full-length genomic version of Mhc in the yw background, was used as the control for the myofibrillar structural analysis. Micrographs of all five lines at 3 days of age appeared indistinguishable from the PwMhc2 control line (Fig. S1). None of the lines showed any missing filaments, abnormal thin/thick filament ratio, or any other signs of development or degradation problems.

Once we determined that all protein levels and sarcomere structures were the same as wild-type and PwMhc2, the best control for the remainder of the experiments was IFI-11a rather than PwMhc2. Although the PwMhc2 and IFI-11a constructs both result in the native 11a converter being expressed in IFM, the constructs differ in how this is accomplished. The PwMhc2 genomic construct includes the entire converter encoding region (all five exons and six introns) and relies on the native IFM splicing machinery to express 11a, whereas IFI-11a only contains exon 11a. All other converter region exons and introns were removed. Because the four non-native converter lines were designed the same way as IFI-11a, IFI-11a is the correct control.

Flight characteristics

Free-flight assays revealed that all of the converter lines were able to fly, but not as well as the control, IFI-11a (Table 1). Flight index values were at least 20% lower than the IFI-11a control value and spanned a 2.6-fold range, with a relative order of (best to worst) IFI-11a > IFI-11d ≥ IFI-11e ≥ IFI-11c > IFI-11b. WBF of all lines were 6–15% lower than the control, with a relative order of IFI-11a > IFI-11c, IFI-11b, IFI-11d, and IFI-11e. IFI-11d and IFI-11e WSA average values were higher but not statistically different than IFI-11a. The unadjusted ANOVA P values of 0.025 and 0.018, respectively, suggest that there is a substantial possibility that they are actually different. Plus, as aerodynamic power is proportional to WSA cubed, very small changes to WSA have a large effect on flight performance. In contrast, IFI-11c WSA was 5% lower than IFI-11a WSA.

Table 1.

Flight Characteristics

	Flight Index	WBF (Hz)	WSA (Degrees)
IFI-11a	3.18 ± 0.10b,c,d,e [107]	156.01 ± 1.42b,c,d,e[23]	319 ± 4c [16]
IFI-11b	1.56 ± 0.14a,c,d,e [100]	138.84 ± 1.27a [30]	327 ± 5c [15]
IFI-11c	2.11 ± 0.16a,b [104]	142.53 ± 1.42a,e [18]	301 ± 4 a,b,d,e [15]
IFI-11d	2.51 ± 0.11a,b [106]	138.14 ± 2.85a [15]	331 ± 2c [15]
IFI-11e	2.24 ± 0.06a,b [108]	135.33 ± 1.65a,c [20]	333 ± 3c [13]

Flight index, wing beat frequency (WBF), and wing stroke amplitude (WSA) were measured from 2 to 3 day old female flies at 15°C. All values are mean ± SE. Superscript letters after values in the tables indicate a statistically significant difference between that line and the converter line indicated. One-way ANOVA with Holm-Sidak pairwise multiple comparisons was used (SigmaPlot v11.0) with P < 0.05 as significant. Brackets indicate number of flies tested.

Work and power measurements

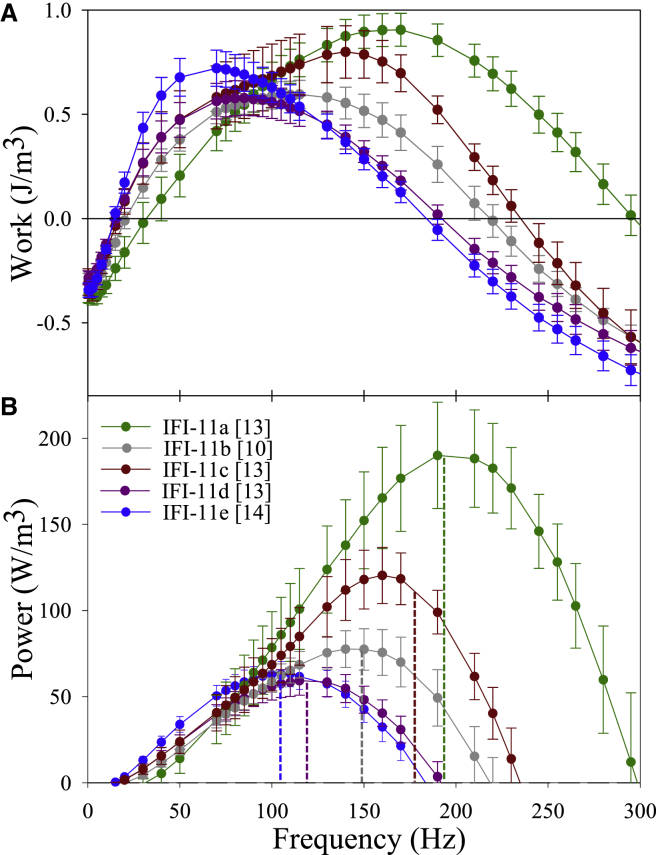
We used two methods to assess the impact of the five converters on IFM work and power generation. The first method was small amplitude (0.125% ML) sinusoidal analysis. This allows for a wide range and number of oscillation frequencies to be explored because the small amplitude does not damage the fiber. Maximum work (Fig. 2 A; Table 2) varied over a 1.6-fold range of values, with the highest and lowest values, IFI-11a and IFI-11d, being significantly different. Maximum power (Fig. 2 B; Table 2) exhibited a 2.8-fold range of values, with IFI-11a and IFI-11c displaying significantly higher values than IFI-11b, IFI-11d, and IFI-11e.

Figure 2.

Small amplitude work and power production by IFM fibers from the five converter lines. (A) Work and (B) power generation from 0 to 300 Hz measured by small amplitude, 0.125% ML, sinusoidal analysis at pCa 5.0 and 15°C. Error bars are mean ± SE. Brackets indicate number of fibers tested. To see this figure in color, go online.

Table 2.

Small Amplitude Power and Work

	Work (J/m3)	fwmax (Hz)	Power (W/m3)	fmax (Hz)	Ee (mN/mm2)
IFI-11a [13]	0.96 ± 0.08d	160 ± 9b,d,e	177 ± 20b,d,e	196 ± 6b,c,d,e	402 ± 21b,c,d,e
IFI-11b [10]	0.64 ± 0.07	118 ± 9a,c,d,e	88 ± 11a,c	150 ± 7a,c,d,e	267 ± 23a
IFI-11c [13]	0.82 ± 0.07	150 ± 4b,d,e	138 ± 10b,d,e	179 ± 3a,b,d,e	296 ± 29a
IFI-11d [13]	0.60 ± 0.08a	85 ± 5a,b,c	62 ± 8a,c	120 ± 5a,b,c	239 ± 20a
IFI-11e [14]	0.73 ± 0.09	69 ± 4a,b,c	63 ± 7a,c	107 ± 4a,b,c	218 ± 16a

Power was measured under small amplitude conditions, 0.125% ML. Work values are for the run that generated maximum power. E_e is elastic modulus values at 150 Hz, the IFI-11a WBF. f_wmax is the ML oscillation frequency that generated maximum work. f_max is the ML oscillation frequency that generated maximum power. All values are mean ± SE. Superscript letters after values in the tables indicate a statistically significant difference between that line and the converter line indicated. One-way ANOVA with Holm-Sidak pairwise multiple comparisons was used (SigmaPlot v11.0) with P < 0.05. Brackets indicate number of fibers tested.

The frequencies that generated maximum power (f_max) and work (f_wmax) exhibited a 1.8-fold and 2.3-fold range of values, respectively, and the majority of the lines were significantly different from each other (Fig. 2; Table 2). IFI-11a fibers (control fibers) had the highest f_max values, followed by IFI-11c at 9% lower, and IFI-11b at 24% lower. IFI-11d and IFI-11e had the lowest f_max and f_wmax values, ∼60% lower than IFI-11a. The upper frequency limits at which the fibers could still generate positive work varied by ∼1.7-fold: IFI-11e and IFI-11d could generate net positive work up to ∼180 Hz, IFI-11b up to ∼220 Hz, IFI-11c up to ∼240 Hz, and IFI-11a up to 300 Hz (Fig. 2). The lower limit of net positive work ranged from 18 to 30 Hz.

Our second method for measuring power generation was to optimize the ML change and the oscillation frequency until the maximum amount of power an individual fiber could produce was found using the work loop technique (38). This is closer to how the muscle functions in vivo than sinusoidal analysis where ML change is fixed at 0.125%. The fibers displayed a 2.8-fold range in power values and a 2.2-fold range for work (Fig. S2; Table 3). IFI-11a and IFI-11c generated the most power, followed by IFI-11b, IFI-11d, and IFI-11e. The optimal frequency for power generation (f_pmax) was highest for IFI-11a followed by IFI-11c, IFI-11b, IFI-11d, and IFI-11e (Table 3), and varied 2.2-fold. The relative order of f_pmax values for optimized work loops was the same as for small amplitude f_max.

Table 3.

Work Loops

	Power (W/m3)	fpmax (Hz)	Work (J/m3)	%ΔML
IFI-11a [12]	878 ± 174b,d,e	163 ± 10b,c,d,e	6.60 ± 1.93	1.00 ± 0.14
IFI-11b [11]	435 ± 75a	98 ± 9a,c	4.99 ± 0.97	1.40 ± 0.16
IFI-11c [12]	654 ± 79	135 ± 5a,b,d,e	4.98 ± 0.71	1.08 ± 0.08
IFI-11d [12]	312 ± 81a	88 ± 7 a,c	4.05 ± 1.26	0.98 ± 0.10
IFI-11e [13]	454 ± 80a	75 ± 5a,c	6.07 ± 1.03	1.33 ± 0.04

Maximum work and power generated by fibers when f_pmax and ML change are optimized for power generation. f_pmax is the ML oscillation frequency which generated maximum power. All values are mean ± SE. Superscript letters after values in the tables indicate a statistically significant difference between that line and the converter line indicated. One-way ANOVA with Holm-Sidak pairwise multiple comparisons was used (SigmaPlot v11.0) with P < 0.05. Brackets indicate number of fibers tested.

SA

Fibers from all the converter lines displayed the classic four phase stretch-activated response to a 1% ML rapid increase in length (Fig. 3 A). The delayed force increase (phase 3) is also referred to as A_SA. There were no significant differences in the passive component for both stretch durations (Fig. 3 C; Table 4), and only one significant difference in the active component, F_SA (Fig. 3 D; Table 4). IFI-11a fibers generated 2.1-fold greater F_SA than IFI-11d fibers when the 3.5 ms step duration protocol was performed.

Table 4.

Stretch-Activated Tension and k₃

	0.5 ms Length Step			3.5 ms Length Step			0.5 ms
	ASA	PSA	FSA	ASA	PSA	FSA	k3
IFI-11a [13]	5.59 ± 0.68	3.18 ± 0.33	2.41 ± 0.39	5.49 ± 0.63	3.18 ± 0.33	2.31 ± 0.33d	1625 ± 61b,d,e
IFI-11b [9]	4.62 ± 0.44	2.79 ± 0.27	1.83 ± 0.19	4.65 ± 0.45	2.85 ± 0.28	1.80 ± 0.19	1129 ± 37a,c
IFI-11c [12]	4.90 ± 0.43	2.69 ± 0.24	2.21± 0.31	4.70 ± 0.41	2.79 ± 0.20	1.92 ± 0.23	1492 ± 46b,d,e
IFI-11d [10]	3.94 ± 0.27	2.66 ± 0.19	1.29 ± 0.15	3.78 ± 0.26	2.70 ± 0.19	1.08 ± 0.15a	1038 ± 53a,c
IFI-11e [11]	4.77 ± 0.39	2.68 ± 0.33	2.08 ± 0.17	4.54 ± 0.39	2.71 ± 0.34	1.83 ± 0.16	1112 ± 53a,c

A_SA, total active stretch tension (pCa 5.0), P_SA, passive stretch tension (pCa 8.0), F_SA, corrected active stretch tension (F_SA = A_SA − P_SA), k₃, rate of tension development for phase 3. The units for k₃ are s⁻¹, and all other units are mN/mm². All values are mean ± SE. Superscript letters after values in the tables indicate a statistically significant difference between that line and the converter line indicated. One-way ANOVA with Holm-Sidak pairwise multiple comparisons was used (SigmaPlot v11.0) with P < 0.05. Brackets indicate number of fibers tested.

The relative order of k₃ (rate of SA) values was identical to sinusoidal f_max values except IFI-11d and IFI-11e were switched (compare Table 4 and Table 2). The adult muscle lines, IFI-11a and IFI-11c, had significantly higher k₃ values than IFI-11b, IFI-11d, and IFI-11e. We do not report k₃ values for 3.5 ms steps because the very brief duration of phase two prevented accurate equation fitting (Fig. 3 B). Examples of the equation fits to the 0.5 ms step are shown in Fig. S3.

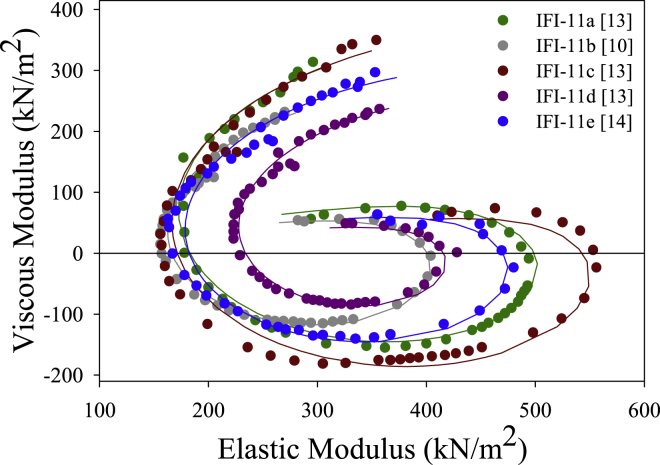
Muscle apparent rate constants

By fitting our small amplitude sinusoidal data Nyquist plots (Fig. 4) with a three-term equation, we derived apparent muscle rate constants and amplitudes (39). IFI-11a’s 2πb rate constant was the fastest, followed by IFI-11c, IFI-11b, IFI-11d, and IFI-11e (Table 5). All lines were statistically different, except IFI-11d compared to IFI-11e, resulting in a four-fold range of values. For 2πc there was a two-fold range of values, IFI-11e and IFI-11d were the fastest, followed by IFI-11b, IFI-11c, and IFI-11a. B and C are amplitudes proportional to work produced and work absorbed, respectively. Thus, similar to the work values we measured using the work loop technique (Table 3), IFI-11a and IFI-11c fibers had the highest B and C values, whereas IFI-11d and IFI-11e had the lowest values.

Figure 4.

Representative IFM Nyquist plots fitted with the complex modulus equation. Each fiber was oscillated through frequencies from 0.5 to 650 Hz at a ML change of 0.125%. The resultant force and length traces were used to generate the viscous and elastic modulus. A three-term equation was fit to each fiber’s Nyquist plot to determine muscle apparent rate constants and amplitudes (see Materials and Methods and Table 5). To see this figure in color, go online.

Table 5.

Muscle Apparent Rate Constants for the Converter Line Fibers under Conditions that Generated Maximum Small Amplitude Power

	A (kN/m2)	k (unitless)	B (kN/m2)	2πb (s−1)	C (kN/m2)	2πc (s−1)
IFI-11a [10]	268 ± 23	0.137 ± 0.006d,e	3219 ± 312b,c,d,e	1996 ± 79b,c,d,e	3041 ± 296b,c,d,e	2780 ± 56d,e
IFI-11b [10]	277 ± 25	0.125 ± 0.005c,d	1053 ± 153a,c	987 ± 113a,c,d,e	888 ± 156a,c	3425 ± 443d,e
IFI-11c [12]	217 ± 24	0.147 ± 0.005b,d,e	2186 ± 251a,b,d,e	1729 ± 120a,b,d,e	2125 ± 261a,b,d,e	3228 ± 231d,e
IFI-11d [13]	315 ± 37	0.100 ± 0.005a,b,c	563 ± 68a,c	651 ± 42a,b,c	587 ± 64a,c	5452 ± 432a,b,c
IFI-11e [14]	321 ± 33	0.116 ± 0.005a,c	635 ± 70a,c	509 ± 22a,b,c	485 ± 40a,c	5553 ± 410a,b,c

All values are mean ± SE. Superscript letters after values in the tables indicate a statistically significant difference between that line and the converter line indicated. One-way ANOVA with Holm-Sidak pairwise multiple comparisons was used (SigmaPlot v11.0) with P < 0.05. Brackets indicate number of fibers tested.

Discussion

We have expanded our exploration of the importance of the converter domain to myosin and muscle function by examining how all five Drosophila converters vary IFM mechanical properties. We had previously focused on how an embryonic version, IFI-11d, influenced IFM performance, but we now include all converter domains that are found in the wide variety of Drosophila muscle types. Here we focus on work, power, and SA because these are the most critical properties for the IFM’s functional role, powering flight by oscillating the thorax cuticle which moves the wings via a specialized hinge mechanism (30). IFM power generation is possible because of the extremely rapid IFM myosin kinetics (22) and its exceptionally high SA (24). In general, the three converters found in the embryonic and larval musculature, IFM-11b, IFM-11d, and IFM-11e caused IFM to produce lower amounts of work and power with slower optimal ML oscillation frequencies, whereas the two adult converters, IFI-11a and IFI-11c, displayed higher power production with faster optimal frequencies.

The embryonic and larval stage converters

The three converters found in the embryonic and larval musculature, 11b, 11d, and 11e, slowed IFM kinetics. For example, f_max was decreased to ∼110 Hz for IFI-11b fibers. The slower kinetics corroborate previous findings that the two embryonic myosin isoforms, EMB and EMB-3b, which we previously expressed in IFM, decrease f_max to be around 20–35 Hz (13). However, as the chimeric lines tested here did not slow f_max all the way to EMB’s or EMB-3b’s values, at least one other alternative exon that differs between the embryonic isoforms and the IFM isoform must also be involved in functionally converting IFM myosin to these two isoforms. Converters 11b, 11d, and 11e decreased maximum work production by ∼30%, but this was not nearly as much as power, which decreased ∼60%. The body wall musculature, composed mainly of supercontractile muscle types that shorten to over 50% of their length (45), likely produce a relatively high amount of work. The antagonistic and coordinated contraction of the longitudinal and oblique larval body wall muscles generate the peristaltic contractions that power larval locomotion (46). However, the muscle contractions are not nearly as rapid as IFM or the jump muscle, thus less power generation is needed.

Of the three slow converters, only 11d had a statistically significant impact on stretch activation amplitude (F_SA) compared to the control. We have previously shown that some myosin isoforms can vary F_SA to a modest degree (25). The EMB myosin isoform expressed in the jump muscle transformed it from a muscle type with minimal F_SA to one with moderate F_SA. The converter could be responsible for EMB’s higher F_SA because it is one of four regions in the head that differ between the EMB and jump muscle isoforms. The EMB isoform contains 11d whereas the jump expresses 11c (31). Although IFI-11d F_SA was significantly different from IFI-11a, our results do not support the converter being responsible for the jump muscle transformation because IFI-11d and IFI-11c did not differ in F_SA (Table 4). Another of the EMB specific alternative exon regions is likely responsible or is needed in conjunction with the 11d converter to increase F_SA. In contrast, the 11d and other two larval converters definitely contributed to changing SA kinetics to the slower speeds that would be required for effective SA in embryonic, larval and other slower muscle types because we observed substantial decreases in their k₃ values.

All three slower converters substantially decreased flight index. Decreased flight ability was most likely caused by the lower WBF they all exhibited. Despite large drops in f_pmax, 163 to 75–98 Hz, WBF only dropped from 156 Hz to ∼138 Hz. Clearly, these three fly lines are beating their wings at a higher than optimal IFM oscillation frequency, which decreases the amount of power from the IFM and thus impairs flight. These WBF frequencies probably cannot be dropped to optimal f_pmax without eliminating flight ability, and we are likely observing the minimum WBF necessary for producing enough aerodynamic power for flight in Drosophila, ∼138 Hz. IFI-11b, IFI-11d, and IFI-11e are also likely increasing their WSA, partially compensating for the lower WBF as aerodynamic power generation is proportional to both WBF and WSA cubed (47, 48). The increase in WSA correlates well with the increase in work loop percent ML change that helped increase IFI-11b and IFI-11e IFM power generation. However, whether these lines actually increase their IFM length changes during in vivo contraction is not known.

The two adult muscle converters

The higher power generating and faster converters, 11a and 11c, are found predominantly in the adult musculature, with 11a being restricted to the IFM whereas the 11c converter is found in the jump muscle and direct flight muscle 51 (31). We presumed 11c would likely alter IFM properties to be more like the jump muscle. The jump muscle needs to shorten rapidly, ∼6 ML/s, to power flight takeoffs (49), but not nearly as fast as the IFM extremely rapid sinusoidal oscillations, which occur over a much shorter length change to power a ∼155 Hz WBF at 15°C (12). The IFM requires very high F_SA whereas the jump muscle has very low F_SA (25, 50). The jump muscle’s primary function of jumping would gain no benefit from SA as it is likely not significantly stretched before takeoff. The IFI-11a and IFI-11c lines are both capable of producing large amounts of oscillatory work and power; however, this occurred at significantly different frequencies (Tables 2 and 3). The IFI-11c converter f_max, f_pmax, and k₃ values were ∼20% lower than IFI-11a. At the IFI-11a WBF, IFI-11c produced 70% of the power generated by IFI-11a. The f_max values of the fiber types positively correlated with estimated in vivo myosin speeds. Myosin is moving actin during jumping in the jump muscle at ∼9.5 μm/s at 15°C (50) whereas during flight, IFM myosin is moving actin ∼15 μm/s during the shortening portion of its oscillatory cycle (51).

No differences were observed in F_SA when 11c (found in the jump muscle) was exchanged into IFM. This result is in agreement with our previous work in which we expressed the IFM myosin converter in the jump muscle and found it did not significantly alter F_SA (52). Jump muscle SA only increases tension 12% above calcium activated isometric tension, whereas IFM SA increases tension two-fold above isometric tension (25). Because exchanging the converters between the two muscles failed to produce significant changes in F_SA, we can conclude that the converter alone is not responsible for IFM SA. At this time, we think that an alternative mechanism, perhaps a thin filament-based mechanism (53, 54), is likely responsible for the very high F_SA produced by IFM.

Myosin isoforms, however, do play a role in setting the SA kinetic differences between IFM and the jump muscle. The IFI-11a fiber k₃ average value was greater than the IFI-11c k₃ value (52). The proper phase 3 rate (k₃) is important for timing the delayed response of the force increase to match the contraction speed of the muscle type. The increase in force must occur during the shortening portion of the contraction cycle where it is beneficial to increase tension. This results in greater positive work and power production. If the timing is mismatched, tension might instead be boosted during lengthening causing higher work absorption, and perhaps net work absorption, which would result in no useful power being produced.

The jump muscle myosin and IFM myosin also differ in their essential light chain (ELC) isoforms. The IFM possesses its own specific isoform, whereas all other muscles use the same ELC isoform. These two isoforms differ in their last 14 amino acids through alternative splicing (55). If we had also transferred the jump ELC into the IFM, it is possible there would have been more changes to muscle mechanical properties. This would be especially interesting to investigate as myosin structures show that the converter directly interacts with the ELC and this interaction is likely critical for both the forward and reverse power strokes (56, 57).

IFI-11c fibers are not able to power flight as well as the control IFI-11a fibers as seen by the decreased IFI-11c flight index. Similar to the other chimeras, a lower WBF contributed to the decreased flight ability. However, the WBF decrease was not as great as the slower larval converters. This might be due to muscle kinetics as the IFI-11c line f_max and f_pmax did not decrease as much as the three larval converter lines. Further, the IFI-11c line decreased WSA, which contrasted to no change or an increase in WSA by the other lines. Increasing WSA would have increased IFI-11c fly’s aerodynamic power and offset its slower WBF. Perhaps IFI-11c WSA could not be increased because this might have caused the IFM ML change to be increased. This would decrease IFM power, as we observed that increasing IFI-11c %ML amplitude decreased work loop power rather than the increase seen for some of the larval converters (Fig. S2; Table 3).

We have previously hypothesized that changes in WBF due to alterations in IFM mechanical performance are more influenced by muscle stiffness than muscle kinetics (13). The IFMs do not directly move the wings, but instead cause fast resonant oscillations of the entire thorax, which is converted into wing beating by a complex wing hinge mechanism (30). The stiffness of the thoracic cuticle, IFM, and other system components can potentially alter the optimal resonance frequency of the thorax and hence, WBF. From our sinusoidal analysis, we determined the elastic modulus (stiffness) values at the WBF of the flies, ∼150 Hz (E_e in Table 2). Although only IFI-11a E_e was statistically different from the other lines, the elastic modulus average values followed that exact order of the WBF values. The f_max and f_pmax values also showed this same order. Thus, it is difficult to determine from this study if one parameter has more influence than the other on WBF or if both stiffness and muscle kinetics are important for setting WBF.

Mechanisms behind the converters influence on power

Overall, we found that the converters varied IFM power over a 2.8-fold range when measured at both short and optimized length changes. Changes in IFM work, SA, and muscle kinetics all contributed to the differences in power. The variation in work (2.3-fold) at the fixed short ML oscillations (0.125%) suggests changes to force production as W = force × length change. Variation in muscle force arises from changes to myosin step size, duty ratio, myosin stiffness, and sarcomere geometry (29). Electron microscopy confirmed that sarcomere geometry was normal. Step size is likely unchanged in these chimeras, as we previously did not observe a difference between IFI-11d and wild-type step size (18) and also between EMB and IFI isoforms (51). Duty ratio is likely contributing to the differences we observed in work production. Duty ratio is the amount of time spent strongly attached to actin (producing force) divided by the total cross-bridge cycle time and is set by the rate constants of the cross-bridge cycle. Some of our kinetic measurements suggested that the duty ratio is higher for the slower converter chimeras: the lower f_max, k₃, and 2πb values. If so, this should have caused an increase in force and work production. However, we did not observe an increase. In contrast, the higher 2πc values, which are most influenced by work absorbing steps of the cycle (39), measured from the slower chimeric fibers, suggest less time spent in the ADP and rigor strongly bound states. This would decrease duty ratio and presumably decrease force and work production. Because we only observed decreases in work, this suggests that either the steps associated with 2πc are having a greater influence on duty ratio, or if duty ratio is higher, then it would have to be offset by a decrease in another force altering parameter, such as myosin stiffness, to account for the drop in work production. A measure of active myosin stiffness, the elastic modulus at 150 Hz, suggests that the slower converter myosins have a lower stiffness (Table 2). The ability of the converter to alter myosin stiffness has been shown by the Brenner and Kraft group’s studies of point mutations in the β-cardiac myosin converter known to cause HCM (29). However, we cannot rule out that the change in stiffness is a secondary consequence due to changes to other myofibril proteins.

Differences in force and work levels between chimeric converter fibers, during cyclical muscle contractions, could also be due to changes in F_SA. Greater F_SA increases positive work relative to negative work which leads to greater net work and power. The converter is capable of varying F_SA because we observed that the 11d converter decreased F_SA. However, only observing one change suggests that setting F_SA is not a major role of the converter and is likely not very important in altering power production.

Power was highly influenced by changes to optimal muscle oscillation frequency (power = work × frequency), i.e., muscle kinetics. Sinusoidal analysis revealed a two-fold range in f_max, which correlated well with small amplitude power. When power was maximized under optimal conditions using work loops, the correlation was not as strong (Tables 2 and 3). This is likely due to the addition of a second variable, ML change. The ability to change length allowed for the speed at which myosin and actin slide past each other to be varied indirectly. A longer length change at the same frequency equals faster sliding. The longer length change can also add variation to the amount of strain/stress on the myosin, which is known to alter cross-bridge rate constants (58).

Cross-bridge rate constants

Changes to IFM’s optimal contraction frequency induced by the converter substitutions suggest substantial alterations to underlying cross-bridge kinetics. The muscle apparent rate constants derived from sinusoidal analysis allow for insight into likely alterations to rates of the cross-bridge cycle (Fig. S4). The apparent rate constant 2πb was decreased by all of the nonnative converters (Table 5). According to the six-state model of Kawai and Brandt (59), 2πb is most influenced by work producing steps of the cycle: attachment and power stroke related steps. Thus, decreased 2πb suggests that the rate of at least one of these steps has been slowed by the converters. Conversely, 2πc is most influenced by work absorbing steps of the cycle: steps after the power stroke (39). According to Palmer et al. (60), 2πc is inversely related to attachment time. By either model, this would mean 2πc is most influenced by transitions involving strongly bound steps, such as ADP release and ATP-induced myosin detachment from actin. All of the nonnative converters increased 2πc, suggesting that the rate of at least one of these steps of the cross-bridge cycle is being sped up by these “slower” converters. In fact, 2πc values of the fiber types inversely correlated with general measurements of overall muscle kinetics, e.g., f_max and k₃, whereas 2πb positively correlated with f_max, f_pmax, and k₃ (Tables 2 and 5). As slower rate constants have more influence on the overall rate at which myosin moves through strongly bound states of the cross-bridge cycle, this suggests that attachment and/or power stroke related steps, those influencing 2πb, have the most influence on overall muscle kinetics under loaded conditions.

That detachment associated rates were increased whereas values such as f_max were decreased is contrary to results for most muscle types where detachment kinetics and, more specifically, ADP release rate are thought to be rate limiting (61). However, we have previously observed that the fast Drosophila myosins appear to have a different rate-limiting step than slower myosins under high load conditions (22, 40). Our results suggested that Pi-release might be rate-limiting or ATP-induced detachment if ATP is <12 mM in fly muscle. Solution kinetic studies also suggest ADP release is not rate-limiting (20). Our collaborators found that the ADP release rate for four Drosophila myosins did not correlate with velocity in the actin motility assay (20). This included the slower IFI-11d chimeric myosin where ADP release actually increased compared with the faster IFM myosin (IFI-11a). Further, the conformational changes of these Drosophila myosins’ active sites when ADP is bound do not correlate with velocity (62).

ADP release not being limiting has also been suggested for fast myosins from other organisms. Work by the Geeves’ laboratory on myosin isolated from a range of fast mammalian muscles found ADP release was sometimes too fast to limit velocity (21). This includes the fastest human isoform, extraocular myosin, which has the same ADP release rate, ∼4000/s, as Drosophila IFM myosin (63). Recently, Brizendine et al. (64) proposed an attachment-limited model for setting muscle velocity rather than a detachment-limited model. Thus, our current chimeric converter results bolster the argument that ADP release is not always rate-limiting. Instead, a step before ADP release, perhaps Pi-release, may be the limiting step for muscles containing very fast muscle myosin isoforms.

Author Contributions

D.M.S. conceived experiments; B.M.G., S.R., M.P., D.S., J.T.P., and L.A.R. performed and analyzed experiments; B.M.G. and D.M.S. interpreted experiments and drafted and edited the manuscript.

Editor: David Warshaw.