Motor Adaptive Remodeling Speeds Up Bacterial Chemotactic Adaptation

Abstract

Bacterial chemotaxis is a canonical system for the study of signal transduction. One of the hallmarks of this system is its robust adaptive behavior. However, how fast the system adapts remains controversial. The adaptation time measured at the level of the kinase activity was tens of seconds, whereas that measured at the level of the flagellar motor was <10 s. The flagellar motor was recently shown to exhibit adaptive remodeling, its main physiological function being to provide a robust match between the chemoreceptor output and the motor input, whereas its adaptation timescale was thought to be too slow to contribute much to the overall adaptation timescale of the chemotaxis system. Here, through theoretical modeling of the motor adaptive remodeling and experimental tests, we show that this motor adaptation contributes significantly to speeding up the overall chemotactic adaptation, thereby resolving the previous inconsistency.

Introduction

The chemotaxis system allows bacteria to sense and respond to changes in concentrations of chemical attractants or repellents in the environment (1, 2). Receptor clusters process input (1, 2, 3), with signal relaying to the flagellar motor to generate output (4). Binding of the chemicals to receptors modulates the activity of an associated histidine kinase, CheA, thereby changing the level of phosphorylation of a small diffusible protein, CheY. Phosphorylated CheY (called CheY-P) binds to FliM, a component of the switch complex at the base of the flagellar motor, and modulates the direction of motor rotation (5, 6, 7). A phosphatase, CheZ, dephosphorylates CheY-P. The chemotaxis system exhibits robust, perfect adaptation (8, 9, 10). After a stepwise stimulus, the system output, measured by the CheY-P level or the directional bias of the motor rotation, changes abruptly before slowly readapting to its pre-stimulus level. Adaptation at the receptor level is mediated by receptor methylation and demethylation by the corresponding enzymes (CheR and CheB).

The adaptation time, measured using the CheY-P level or the motor rotation directional bias as the system output, has been controversial. The measurements performed by monitoring the motor-rotation directional bias led to an adaptation time ranging from 4 to 9 s in a wild-type Escherichia coli cell at room temperature (11, 12, 13), whereas measurements performed by monitoring the CheY-P level resulted in an adaptation timescale of ∼20 s (14). Recently, the flagellar motor was shown to exhibit adaptive remodeling (15). Thus, the chemotaxis system exhibits a tandem architecture of adaptation at the receptor and motor levels (16). An intuitive guess would be that the motor adaptation contributes to the difference between those two types of measurement: whereas adaptation time measured at the level of CheY-P concentration results from receptor-level adaptation, that measured at the level of motor-rotation directional bias results from receptor-level adaptation and an additional contribution of motor adaptive remodeling. However, the motor-adaptation timescale was thought to be in the range of 1 min, too long to play a critical role in the overall adaptation timescale (15). Here, by investigating the dynamics of motor adaptive remodeling, we will show that it surprisingly contributes significantly to speeding up the overall chemotactic adaptation.

Materials and Methods

Experiments to measure overshoot phenomenon

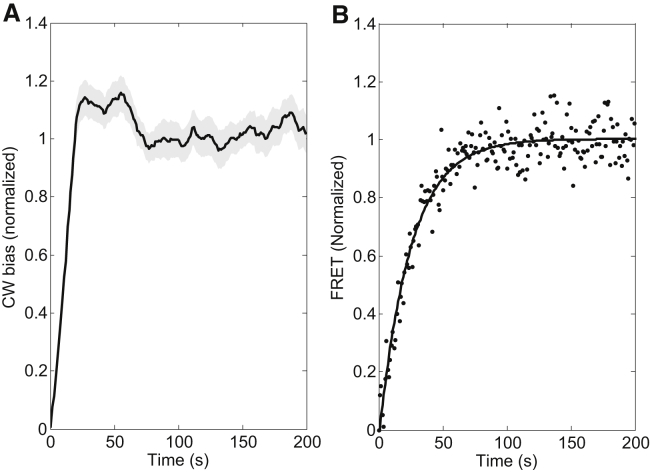
HCB316 [Δ(5201(tar-tap) and Δ7021(tsr))], were derived from E. coli K12 strain RP437. The filament gene fliC was further deleted from HCB316, yielding CZ1. The plasmid pFD313 constitutively expresses sticky filament FliC^st (17). The plasmid pLC113 expresses Tar under a salicylate-inducible promoter. CZ1 transformed with pFD313 and pLC113 was used in the experiment. Cells were grown, and the bead assay was carried out in a procedure described previously (13). During cell growth, 1 μM salicylate was used to induce Tar expression to a level approximating that in wild-type cells. In the experiments, 2.5 μM MeAsp was used as the attractant. Twenty experiments were performed, and the mean and standard deviation were plotted in Fig. 1 A. The clockwise (CW) biases were normalized by dividing by the average pre-stimulus value.

Figure 1.

Responses of cells with a single type of receptor (Tar) subjected to a stepwise stimulus of 2.5 μM MeAsp at time 0. (A) The overshoot phenomenon observed at the level of motor CW bias with a bead assay. The solid line is the average of 20 measurements and the shaded area represents the standard deviation. (B) There is no overshoot at the level of CheY-P concentration measured by FRET between CheZ-eCFP and CheY-eYFP. The solid line is a fit with 1 − exp(−t/τ), where τ is the fitting parameter.

Förster resonance energy transfer measurements

The experimental setup is similar to that described previously (18). cheZ and cheY were further deleted from HCB316. CheZ-eCFP and CheY-eYFP were expressed from pVS88, a plasmid that encodes both fluorescent fusion proteins under control of an isopropyl β-D-thiogalactopyranoside-inducible promoter (19). The setup was based on a Nikon Ti-E microscope with a 40× 0.60 NA objective. The illumination light was provided by a 75 W xenon lamp through an excitation bandpass filter (FF02-438/24-25, Semrock, Rochester, NY) and a dichroic mirror (FF458-Di02-25x36, Semrock). The epifluorescent emission was split into cyan and yellow channels by a second dichroic mirror (FF509-FDi01-25x36, Semrock), and collected through emission bandpass filters (FF01-483/32-25 and FF01-542/32-25, Semrock) by two photon-counting photomultipliers (H7421-40, Hamamatsu, Hamamatsu City, Japan). Signals from the two photomultipliers were recorded at a sampling rate of 1 Hz using a data-acquisition card installed in a computer (USB-1901(G)-1020, ADlink, New Taipei, Taiwan). The ratio of the signals from the yellow and cyan channels was used to represent the fluorescence resonance energy transfer (FRET) value. The FRET value is normalized by subtracting the lowest FRET value reached after attractant addition and then dividing by the average pre-stimulus value (Fig. 1 B).

Stochastic simulations of motor adaptive remodeling

The simulations started with a steady-state CheY-P level, Y, of 2.90 μM and a corresponding steady-state CW bias, B. At t = 0 s, the motor is in the counterclockwise (CCW) state, switching randomly between the two states. The rate of switching from CCW to CW is B/0.11 s⁻¹, and the rate of switching from CW to CCW is (1 − B)/0.11 s⁻¹, as measured previously (20). The rate of change with time in the number of FliM molecules followed Eq. 1, and was different for the CCW and CW intervals. The instantaneous CW bias was calculated using Eq. 3. The time step in the simulations was 0.01 s. For simulation of the overshoot response in Tar-only cells with intact receptor-level adaptation, at t = 100 s, the CheY-P level abruptly reduces to 2.60 μM, and then recovers back to 2.90 μM with a timescale, τ_m, of 20 s: Y = 2.60 + 0.30 × (1 −exp(−(t − 100)/τ_m) for t > 100 s. For the simulation to reproduce the motor partial adaptation, at t = 100 s, the CheY-P level rapidly reduces to 2.6 μM according to Y = 2.60 + 0.30 × exp(−(t − 100)/τ_A), with a time constant, τ_A, of 8 s, mimicking the time it takes for medium exchange in a typical motor adaptation experiment with a stepwise addition of attractant. For the simulation of response to a small stepwise stimulus, at t = 100 s, the CheY-P level dropped abruptly from the initial value of 2.90 to 2.82 μM, and then recovered to the initial value with a timescale, τ_m, of 20 s: Y = 2.82 + 0.08 × (1 − exp(−(t − 100)/τ_m) for t > 100 s. For the simulation of the spontaneous fluctuation of motor rotation direction in a steady state, the fluctuation of CheY-P level was described using the Langevin equation (21): $dY/dt=-\left(Y-Y_0\right)/{\tau }_{\text{m}}+\eta \left(t\right)$, where τ_m is the relaxation time, the same as the timescale of receptor methylation/demethylation, and η(t) is a Gaussian white noise with zero mean and $\langle \eta \left(t\right)\eta \left(t^{\prime }\right)\rangle =2{\sigma }_Y^2/{\tau }_Y\delta \left(t-t^{\prime }\right)$. The deviation, δY, of the CheY-P level from its steady-state value was updated using the Ornstein-Uhlenbeck formula (20, 22):

$$\delta Y\left(t+\Delta t\right)=\delta Y\left(t\right)\times e^{-\Delta t/{\tau }_Y}+{\sigma }_Y\times \sqrt{1-e^{-2\Delta t/{\tau }_Y}}\times n\left(\mathrm{0,1}\right)$$

where n(0,1) is the standard normal distribution with zero mean and unit variance, σ_Y is the standard deviation of the fluctuation of CheY-P level, and τ_Y is equivalent to τ_m.

Results

Experimental observation of overshoot response in cells with a single type of chemoreceptor

In studying the dynamics of motor adaptive remodeling, we observed an overshoot phenomenon in the step response of E. coli cells with only one type of chemoreceptor and intact receptor-level adaptation. We used a Tar-only strain and studied its response to a stepwise stimulus of 2.5 μM α-methyl-DL-aspartate (MeAsp). The motor CW bias (the probability of the motor rotating clockwise) was used as the indicator of chemotactic output, and its kinetics was monitored with a bead assay. After the stepwise stimulus of attractant at time 0, the motor CW bias dropped abruptly, after which it slowly recovered but overshot to a higher level and then returned back to its pre-stimulus level (Fig. 1 A). Four examples of the raw data (un-normalized) are shown in Fig. S1.

The overshoot phenomenon has been observed before, but only in the step response of wild-type E. coli cells with multiple types of chemoreceptors (23, 24). This was due to methylation cross talk in cells with multiple types of receptors, as suggested by a recent model for the dynamics of receptor clusters (25). Therefore, it was surprising to observe the overshoot response in the Tar-only strain, as there is no methylation cross talk. As the model dealt with the chemotactic output at the level of CheY-P concentration, we tested to see whether the overshoot phenomenon exists at the level of CheY-P concentration. We used a FRET measurement between CheZ-eCFP and CheY-eYFP to monitor the kinetics of the CheY-P concentration, finding that the FRET value (a linear function of the CheY-P level) dropped after the stepwise stimulus of 2.5 μM MeAsp, and afterward recovered monotonically to the pre-stimulus level (Fig. 1 B). The raw data (un-normalized) are shown in Fig. S2. Therefore, there is no overshoot at the level of CheY-P concentration. The overshoot phenomenon observed in the Tar-only strain at the level of motor rotational bias must be due to motor adaptive remodeling. We then sought to build a theoretical model of motor adaptive remodeling.

Model for motor adaptive remodeling

We used the Monod-Wyman-Changeux (MWC) model of allostery (26) to describe the ultrasensitive response of the motor to the intracellular CheY-P level. According to recent studies of motor adaptation (15, 27), FliM molecules are coming on and off the motor switch complex, and the number of FliM molecules in a motor at steady state is dependent on the directional bias of the motor rotation. The FliM molecules in the switch complex exist in two different stability states: one is an unstable exchanging state, with a timescale for FliM exchange of 1/k_off ∼ 50 s (where k_off is the off rate), and the other is a stable non-exchanging state (27). The number of FliM molecules in the non-exchange state is denoted as N_NE, which adopts different values depending on the motor rotational direction, with 34 in the CCW direction and 12 in the CW direction. The rate of change of the number of FliM molecules in a motor is

$$\frac{\text{d}N}{\text{dt}}=k_{\text{on}}\left(M-N\right)-k_{\text{off}}\left(N-N_{\text{NE}}\right),$$ (1)

where M is the maximum number of sites for the FliM molecules in a motor, and k_on and k_off are the on and off rate constants, respectively, both ∼0.02 s⁻¹. The value of N_NE depends on the motor rotational direction. As the CW/CCW intervals (∼1 s) are much shorter than the adaptation timescale of the FliM molecules (1/k_off ∼ 50 s), a quasi-equilibrium approximation can be used. Under this approximation, N_NE in Eq. 1 can be defined as the average FliM number in the non-exchange state, and written as a function of the CW bias (the probability of the motor rotating in a CW direction): $N_{\text{NE}}=B\times 12+\left(1-B\right)\times 34,$ where B is the CW bias. Inserting the equation for N_NE into Eq. 1 leads to

$$\frac{\text{d}N}{\text{dt}}=k_{\text{on}}\left(M-N\right)-k_{\text{off}}\left(N-\left(B\times 12+\left(1-B\right)\times 34\right)\right).$$ (2)

Further discussion about Eqs. 1 and 2 is presented in the Supporting Material.

The motor CW bias (B) is ultrasensitive to the CheY-P level (Y), and the dependence can be expressed using an MWC model:

$$B=\frac{1}{1+{\text{e}}^{N\times G\left(Y\right)+\epsilon }},$$ (3)

where ε denotes the energy difference for the CW and CCW states when no CheY-P binds to the switch complex, and G(Y) is a function of the CheY-P level (28):

$$\text{G}\left(Y\right)=\text{ln}\left(\frac{1+Y/K_2}{1+Y/K_1}\right),$$ (4)

where K₁ and K₂ are the dissociation constants of CheY-P binding to FliM in the CW and CCW states, respectively. According to a previous measurement (6), K₁ and K₂ satisfy $\sqrt{K_1{K}_2}=3.1\mu \text{M}$. The ultrasensitive dependence of B on Y was measured previously for motors at two fixed N values, that is, with two adapted CW biases, B, of 0.5 and 0.8 (29). Using the relationship between the number of FliM molecules in a motor in steady state (N_s) and the CW bias measured previously (30),

$$N_{\text{s}}=34\times \left(B+\left(1-B\right)\times 1.32\right),$$ (5)

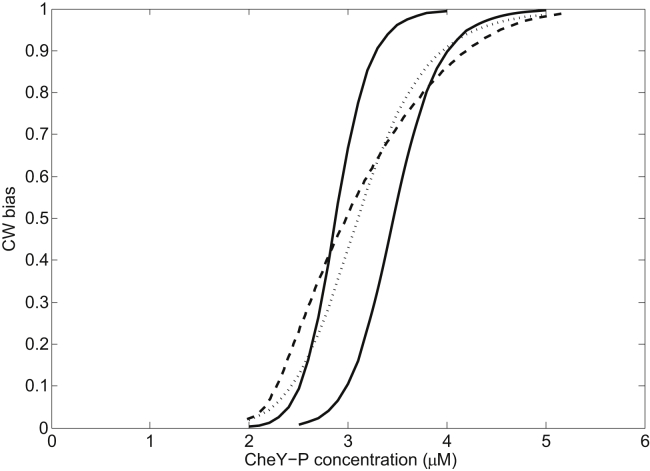
we could determine the number of FliM molecules for those two ultrasensitive curves (N = 36 and 39 for adapted B of 0.8 and 0.5, respectively). We fit both curves simultaneously using Eq. 3 with K₁ and ε as two free parameters. The results of fitting are K₁ = 1.28 ± 0.11 μM and ε = 33.65 ± 3.41 k_BT. Using these fitted parameters and Eqs. 3 and 5, we can obtain the relationship between the CW bias and the CheY-P level for adapting motors with varying N. For each value of B, the steady-state number of FliM molecules (N_s) was obtained from Eq. 5. Replacing N with N_s in Eq. 3, the corresponding Y can be extracted from the value of B. Changing B from 0 to 1 and repeating the process of extracting Y, the curve of B versus Y can be obtained, which is shown in Fig. 2 as the dashed curve, similar to that measured by Cluzel and co-workers (6). This curve was constructed from a family of ultrasensitive curves with different steady-state numbers of FliM molecules (N_s) ranging from 34 to 45, as determined from Eq. 5. Thus its slope was shallower than the ultrasensitive curves with a fixed number of FliM molecules.

Figure 2.

Dependence of motor CW bias on CheY-P level calculated by the model of motor-adaptive remodeling. The solid curves are for motors with a fixed number of FliM molecules (39 and 36 for the solid curves on the left and right, respectively), the dotted line is the Hill curve determined by Cluzel and co-workers, and the dashed curve represents adapted motors with varying number of FliM molecules ranging from 34 to 45.

The model explained the overshoot response in cells with a single type of receptor

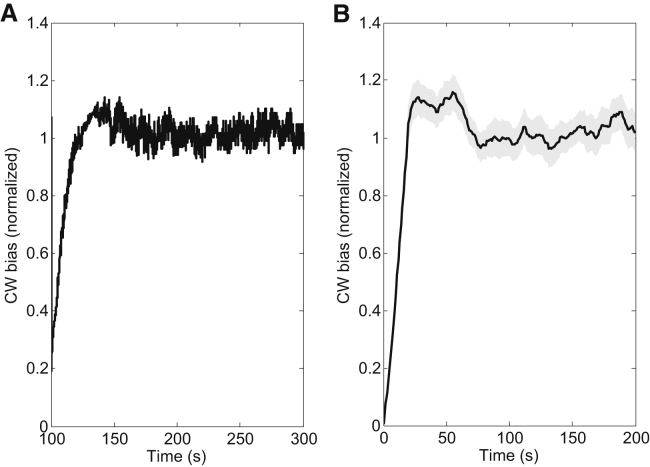
We performed stochastic simulations of our theoretical model for cells with a single type of receptor and intact receptor-level adaptation. Details of the simulation are presented in Materials and Methods. Briefly, the simulations are initialized at time 0, with a CheY-P level of 2.90 μM and a motor at an initial steady-state CW bias and containing N_s FliM molecules (as determined by Eq. 5). At t = 100 s, the CheY-P level abruptly reduces to 2.60 μM, and then recovers to the initial value with a timescale, τ_m, of 20 s: Y = 2.60 + 0.30 × (1 − exp(−(t − 100)/τ_m) for t > 100 s, mimicking the response to a stepwise stimulus. Motor switching traces were generated using a rate of switching from the CCW to the CW state of B/0.11 s⁻¹, and a rate of switching from the CW to the CCW state of (1−B)/0.11 s⁻¹, as measured previously (20). The number of FliM molecules changes with time according to Eq. 1 for each CCW or CW interval. The motor CW bias as a function of time was simulated for 300 s using our model of motor adaptive remodeling, and the simulation was repeated 30 times. The average of the 30 simulation traces is shown in Fig. 3 A and is consistent with our experimental observations shown in Fig. 3 B.

Figure 3.

Comparison of simulations and experimental observations for the overshoot phenomenon for cells with a single type of receptor subjected to a stepwise stimulus. (A) Stochastic simulation with the model of motor-adaptive remodeling. (B) Experimental measurements (same as Fig. 1A).

The overshoot phenomenon can be intuitively understood as follows. After a stepwise addition of attractant, the CheY-P level Y drops abruptly and gradually adapts back to the pre-stimulus level. As the steady-state number of FliM molecules only depends on the CW bias, B, and the pre-stimulus B value equals the value after adaptation, the pre-stimulus N should also be equal to the value after adaptation. After the stepwise addition of attractant, B abruptly drops, so that N initially increases (Eq. 2). Therefore, N must exhibit a peak in its relationship with time. As B shows monotonic dependence on both N and Y (Eq. 3), and Y increases monotonically with time as it adapts, B also exhibits a peak in its relationship with time when it adapts, that is, an overshoot. The magnitude of the overshoot depends on specific values of the parameters.

The model reproduced the motor adaptation behavior in cells with no receptor-level adaptation

To also test whether our model could quantitatively reproduce motor adaptation behavior, we carried out stochastic simulations of motor dynamics as the CheY-P level decreases in a step without recovery, mimicking the behavior of a mutant strain without receptor-level adaptation that was typically used in a motor-adaptation experiment. The simulations are initialized at t = 0 s, with a CheY-P level of 2.90 μM and a motor at an initial steady-state CW bias and containing N_s FliM molecules. At t = 100 s, the CheY-P level rapidly reduces to 2.60 μM with a time constant of 8 s, mimicking the time it takes for medium exchange in a typical motor-adaptation experiment with a stepwise addition of attractant. The motor CW bias as a function of time was simulated for 300 s, and the simulation was repeated 10 times. The average of the simulations is shown in Fig. S3, exhibiting the partial adaptation behavior, consistent with that measured previously by Yuan et al. (15).

Contributions of receptor-level adaptation and motor adaptation to the overall adaptation of the chemotaxis system

After establishing the theoretical model for motor-adaptive remodeling, we asked how receptor methylation/demethylation and motor-adaptive remodeling contribute to the overall adaptation of the chemotaxis system. The adaptation time is the characteristic relaxation time of the system when subjected to a very small step of stimulus. We used the motor CW bias, B, as an indicator of the system output. After a very small step of stimulus, B changes with time as the CheY-P level (Y) and the number of FliM molecules (N) change:

$$\frac{\text{d}B}{\text{dt}}=\frac{\partial B}{\partial Y}\times \frac{\text{d}Y}{\text{dt}}+\frac{\partial B}{\partial N}\times \frac{\text{d}N}{\text{dt}}.$$ (6)

As the deviation from the steady state is very small, all relevant equations can be linearized around the relevant steady-state values. Using a coarse-grained model of the dynamics of the receptor cluster, and also linearizing the righthand side of Eq. 2 at the steady-state values (N₀ and B₀), Eq. 6 can be written as the combination of contributions from receptor-level adaptation and motor adaptation:

$$\frac{\text{d}B}{\text{dt}}\approx -\left(\frac{1}{{\tau }_{\text{m}}}+\frac{1}{{\tau }_{\text{N}}}\right)\times \left(B-B_0\right),$$ (7)

where τ_m is the adaptation timescale due to receptor methylation/demethylation, B₀ is the steady-state CW bias, and τ_N is the adaptation timescale due to motor adaptation:

$${\tau }_{\text{N}}=-\frac{1}{\text{G}\left(Y_0\right)B_0\left(1-B_0\right)\times 22\times k_{\text{off}}}.$$ (8)

Details of the derivation are given in the Supporting Material.

Therefore, both τ_m and τ_N contribute to the overall adaptation timescale, τ_T:

$$\frac{1}{{\tau }_{\text{T}}}=\frac{1}{{\tau }_{\text{m}}}+\frac{1}{{\tau }_{\text{N}}}.$$ (9)

τ_m was measured to be ∼20 s. At a steady-state CW bias, B₀, of 0.33, the steady-state CheY-P level Y₀ is 2.90 μM according to the relationship between CW bias and CheY-P level for adapted motors measured by Cluzel and co-workers (6). From Eq. 8, τ_N was calculated to be 11.8 s. Thus τ_T was ∼7.4 s, consistent with previous measurements of the adaptation timescale using motor rotational bias as the indicator of the system output. The contribution of the motor-adaptive remodeling timescale to the overall adaptation, 11.8 s, is much faster than what was thought previously (1/k_off ∼ 50 s). This is due to the large difference in the number of non-exchanging FliM molecules for a motor in the CCW and CW states (∼22) and to the high sensitivity of motor CW bias to the change in the number of FliM molecules in the motor.

Stochastic simulation of the response to a small stepwise stimulus

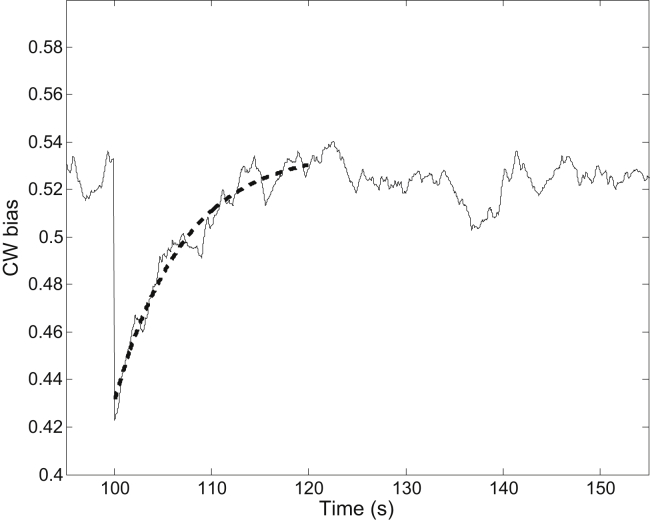
To compare to the analytical calculations above, we also performed stochastic simulation of the response to a small stepwise stimulus, from which the overall adaptation timescale was extracted. Details of the simulation are presented in Materials and Methods. Briefly, after a small stepwise stimulus at t = 100 s, the CheY-P level dropped from the initial value of 2.90 μM to 2.82 μM, and then recovered to the initial value with a timescale, τ_m, of 20 s: Y = 2.82 + 0.08 × (1 − exp(−(t − 100)/τ_m) for t > 100 s. The motor CW bias as a function of time was simulated for 1000 s using the model of motor-adaptive remodeling, and the simulation was repeated 10 times. One of the simulation traces is shown in Fig. 4. The simulated trace was fit with the function B = a + b × (1 − exp(−(t − 100)/τ_T) for t > 100 s with a, b, and τ_T as fitting parameters, resulting in an average τ_T of 7.1 ± 0.4 s for the 10 simulations, consistent with our analytical result.

Figure 4.

One example trace generated by the stochastic simulation of response to a small stepwise stimulus (at t = 100 s). The dashed line is the fit with the equation B = a + b × (1−exp(−(t − 100)/τ_T) to extract the adaptation time, τ_T.

Stochastic simulation of the spontaneous fluctuation of motor-rotation direction in a steady state

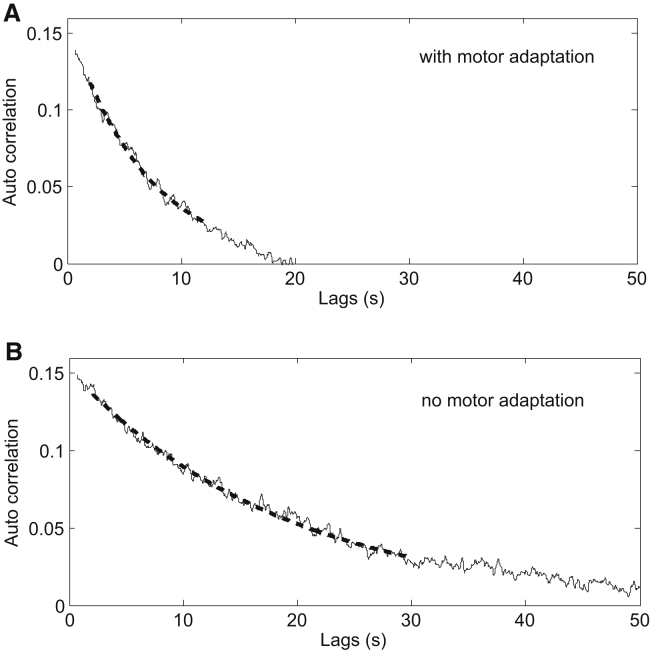
Another way of extracting the adaptation time is to calculate the correlation time of the spontaneous fluctuation of motor-rotation direction for an un-stimulated wild-type cell in a steady state (12, 13), originating from fluctuation of the steady-state CheY-P level. We simulated this spontaneous fluctuation with or without motor-adaptive remodeling. The fluctuation of CheY-P level was introduced into the simulation using a Langevin equation with a characteristic relaxation time of 20 s (20). The trace of motor-rotation direction was simulated for 10,000 s and repeated 10 times with or without motor-adaptive remodeling. The autocorrelation for each trace was calculated, and one example for each case (with/without motor adaptive remodeling) is shown in Fig. 5. The adaptation time was extracted as the decay time of the autocorrelation curve by fitting with an exponential decay function. The average adaptation time without motor adaptive remodeling is 19.7 ± 0.9 s, consistent with the relaxation time of the fluctuation of CheY-P level. The average adaptation time with motor-adaptive remodeling is 7.0 ± 0.6 s, consistent with the analytical result and the result from simulations of response to very small stepwise stimuli.

Figure 5.

Two example traces from stochastic simulations, one with motor adaptation (A) and the other without (B), of the spontaneous fluctuation of motor-rotation direction in a steady state. Autocorrelations of the motor-rotation direction were calculated. The dashed lines are fits with exponential decay to extract relaxation times, yielding 7.0 and 19.7 s with and without motor adaptation, respectively.

Discussion

To explain previous contradictory measurements, where the adaptation time measured using CheY-P level as an indicator of system output was ∼20 s and that measured using the motor-rotation direction as system output was in the range 4–9 s, we built a theoretical model for the motor-adaptive remodeling using an MWC model for the ultrasensitive response of the motor CW bias to the CheY-P level, and the previously measured rates for FliM molecules coming on and off the motor switch complex. The model explained the overshoot response observed experimentally in cells with a single type of chemoreceptor. We further validated the model by stochastically simulating the model and reproducing the motor partial adaptation phenomenon observed previously. Linear-relaxation analysis with our model showed that motor-adaptive remodeling contributes significantly to speeding up the overall chemotactic adaptation, to a much larger degree than previously thought. This is due to two factors that were neglected in previous analysis: the large difference in the number of non-exchanging FliM molecules for a motor in the CCW and CW states (∼22), and the high sensitivity of motor CW bias to the change in the number of FliM molecules in the motor switch complex. Stochastic simulations of the response to small stepwise stimuli and of the spontaneous fluctuation of motor-rotation direction in a steady state further confirmed our analysis.

Ultrasensitive response of the motor to the intracellular CheY-P level has been modeled with equilibrium models such as a thermal isomerization model (17), an MWC model (28), or a conformational spread model (31). Detailed molecular mechanisms of the ultrasensitivity partly come from non-equilibrium effects (32, 33), as does the torque dependence of the motor response (33). As we do not deal with load dependence in this study, and as the MWC model can effectively describe the ultrasensitive response and is also amenable to parameterization and analytical formulization, we adopted the MWC model for the ultrasensitive response here.

In the tandem feedback architecture of adaptation of the bacterial chemotaxis system, the relatively slow adaptation at the receptor level is attributed to the attenuated feedback strength near the steady state (14) inducing large fluctuation of the steady-state CheY-P level, which was shown to increase chemotactic sensitivity (20, 34, 35). The motor-adaptive remodeling not only allows the motor to operate in its most sensitive region (15), but also speeds up the overall chemotactic adaptation to provide a quick enough response, thereby ensuring an optimal memory range between 1 and 10 s (36, 37). Therefore, the tandem feedback architecture of adaptation allows both a beneficial signaling noise (fluctuation of the CheY-P level) and a fast enough adaptation speed. Considering the ubiquity of adaptation in biological networks, similar tandem adaptation mechanisms should exist in other biological systems.

Author Contributions

J.Y. and R.Z. designed the work. J.Y. conceived the model and performed the analytical calculations. C.Z. and R.H. performed the experiments and simulations. J.Y. and R. Z. wrote the manuscript with input from other authors. C.Z. and R.H contributed equally to this work.

Editor: Dennis Bray.