Structural Transitions in Ceramide Cubic Phases during Formation of the Human Skin Barrier

Abstract

The stratum corneum is the outermost layer of human skin and the primary barrier toward the environment. The barrier function is maintained by stacked layers of saturated long-chain ceramides, free fatty acids, and cholesterol. This structure is formed through a reorganization of glycosylceramide-based bilayers with cubic-like symmetry into ceramide-based bilayers with stacked lamellar symmetry. The process is accompanied by deglycosylation of glycosylceramides and dehydration of the skin barrier lipid structure. Using coarse-grained molecular dynamics simulation, we show the effects of deglycosylation and dehydration on bilayers of human skin glycosylceramides and ceramides, folded in three dimensions with cubic (gyroid) symmetry. Deglycosylation of glycosylceramides destabilizes the cubic lipid bilayer phase and triggers a cubic-to-lamellar phase transition. Furthermore, subsequent dehydration of the deglycosylated lamellar ceramide system closes the remaining pores between adjacent lipid layers and locally induces a ceramide chain transformation from a hairpin-like to a splayed conformation.

Introduction

The main function of skin is to present a barrier between the body and the environment. It prevents water loss from the body and protects against penetration of exogenous substances into the body. The barrier property is located in a lipid structure situated in the intercellular space of the superficial-most layer of the skin, the stratum corneum (1, 2, 3, 4, 5, 6). The lipid structure consists of a mixture of saturated long-chain ceramides and free fatty acids together with cholesterol, in an ∼1:1:1 molar ratio (7). It is formed via secretion into the intercellular space of glycosylceramide-based bilayers, tightly folded in three dimensions with cubic-like symmetry (unpublished data).

After secretion, the glycosylceramide-based bilayers with cubic-like symmetry are reorganized into ceramide-based stacked lamellae (unpublished data). Concomitantly, the glycosylceramides are deglycosylated (8, 9) and dehydrated (10, 11, 12). This has led to the suggestions that deglycosylation might facilitate the release of lipid material out of the stratum granulosum cells (13), and that a combined deglycosylation and dehydration may create a driving force for a cubic-to-lamellar transition of the glycosylceramide-based bilayers (unpublished data). Here, we investigate the effect of glycosylation and hydration upon human glycosylceramide- and ceramide-based bilayers with cubic symmetry, using molecular dynamics (MD) simulation.

The presented MD simulations display a striking difference in behavior between human skin glycosylceramides and ceramides. The simulated systems of human skin glycosylceramides maintain a bilayer structure with cubic symmetry. In contrast, the simulated systems of human skin ceramides are unable to stabilize a bilayer structure with cubic symmetry, and transform into a bilayer structure with stacked lamellar symmetry as the water content is gradually reduced. Deglycosylation of a stable glycosylceramide-based cubic phase triggers a transition into a stacked lamellar phase with remnant connections between adjacent layers. In the ceramide systems, strong interactions between the hydrophobic tails drive the transition into a bilayer structure with stacked lamellar symmetry. In the glycosylceramide systems, the interactions between the glycosylceramide headgroups are stronger, which enable them to maintain the bilayer structure with cubic symmetry. Additionally, based on the simulation models, it appears likely that ceramides may locally cluster together and transform from a hairpin to a splayed-chain conformation as the bilayer structure with cubic symmetry relaxes into a bilayer structure with stacked lamellar symmetry.

Taken together, our results support the hypothesis that deglycosylation and dehydration of the lipid material in the uppermost stratum granulosum facilitate a structural transition that is important for the formation of the human skin barrier.

Methods

The sizes of the membrane systems required for this study made an all-atom representation of the ceramides and water unfeasible, since the computational cost would be too high to reach the relevant timescales. Therefore, we decided to use a coarse-grained approach with the MARTINI force field (14), which applies a 4:1 mapping of heavy atoms (carbon, oxygen, nitrogen, and phosphorus; see also Fig. S1) and thereby reduces the model system’s total amount of particles roughly by an order of magnitude. Naturally, this will have an effect on the accuracy (in quantitative terms) of the interactions within the simulated systems. However, for qualitative properties such as the difference between models, coarse-grain modeling has the advantage of allowing for direct observation of the actual transitions of the systems not only at the level of individual molecules but also at the mesoscale level of molecular assembly. Further, the rougher interaction landscape used in the MARTINI force field, compared to an all-atom simulation, increases the kinetics of the simulated systems. For water, this usually means that a scaling factor of 4 has to be used to attain correct experimental diffusion rates (14). Herein, although we discuss some kinetic properties in absolute terms, we foremostly consider relative differences between simulations. Due to the time acceleration coupled to coarse graining, we follow the convention set by Marrink and co-workers (14, 15) and use a factor of 4 scaling of the raw time coordinate in the simulations.

Construction of lipid models

The construction of a folded bilayer structure with cubic symmetry is a non-trivial task due to the complex geometry of the system. The literature of previous simulation studies of lipid bilayer structures with cubic symmetry is limited (16, 17, 18, 19, 20), and no general method for the construction of these structures is presently available. The cubic membrane structures that we simulated in this study were constructed by first rendering a gyroid isosurface (21) in a cubic unit cell with a side length of 15, 17.5, 20, 22.5, or 25 nm, using the Marching cubes method (22) implemented in the VTK framework (23). For each triangle used in the rendered surface, its area was multiplied by a preset density parameter, λ, resulting in an area parameter, α, which was used to evaluate the placements of the ceramides at each triangle:

• α < 1: No ceramide was placed.

• 1 < α < 2: A pair of oppositely oriented ceramides in hairpin conformation were placed in the center of the triangle, with their long axes perpendicular to the triangle surface.

• α > 2: The triangle was split in half along its longest edge and the new triangles were evaluated separately, using α as before.

The initial cubic structure constructed for the ceramide (ceramide NS, the most abundant ceramide in human skin (24)) simulation, with cell side length 20 nm, can be seen in Fig. 1 c.

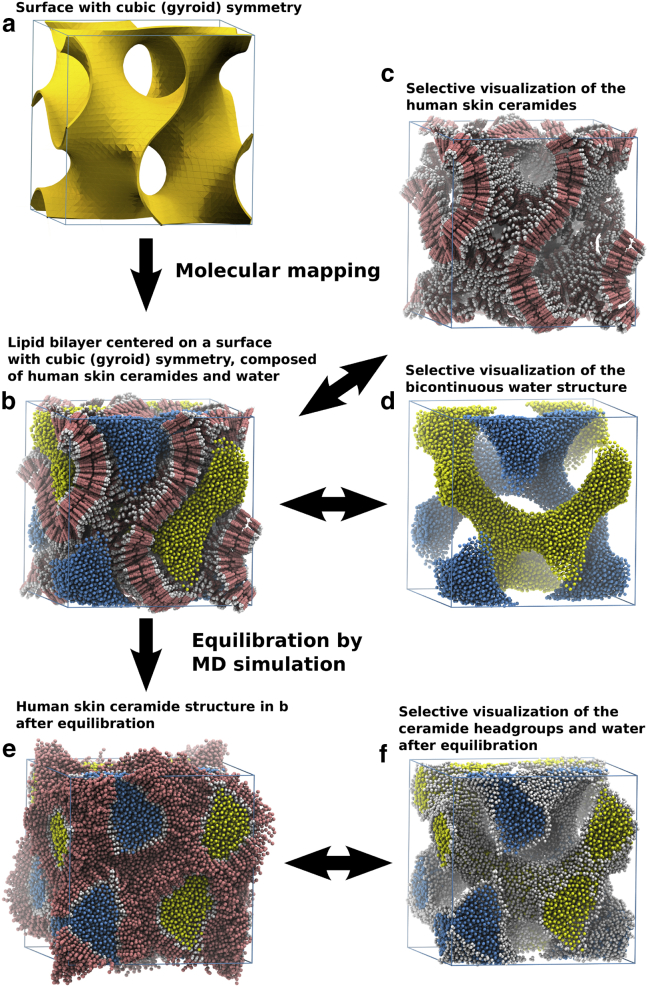
Figure 1.

Creation of the initial cubic structure in the ceramide simulation. (a) The ceramide starting structures were created by first rendering a periodic gyroid surface in a cubic box (shown here is the surface used in the ceramide simulation with a hydration of ∼14.5 waters/lipid). (b) The cubic ceramide structure was created by placing ceramide molecules across the gyroid surface, with the ceramide headgroups pointing along the positive and negative surface normals, and thereafter was solvated with water inside the channels. (c and d) Selective visualization of the ceramides (c) and water (d). (e) Before the MD simulations, the starting structure was energy minimized and equilibrated to minimize positional artifacts from the schematic placement of all particles in the system. (f) To make it easier to visualize the structural changes in the system, only particles from the headgroups and water will be shown in most of the images. (cf. Movie S1). To see this figure in color, go online.

After this, the structures were solvated with water particles in the empty space between the ceramide headgroups (Fig. 1 d), creating systems with ∼11.5, 12.5, ∼14.5, ∼18, and ∼23 waters/lipid (using the fact that each MARTINI water corresponds to four water molecules). One of the resulting water structures can be seen in Fig. 1 d. The simulations were performed with the MARTINI force field using the parameters of Sovová et al. (25) for ceramide NS, and the parameters from López et al. (26) for the glycosylceramides. The starting structures (15, 17.5, 20, 22.5, and 25 nm side length) in the ceramide simulations were built using λ equal to 0.026, 0.03, 0.046, 0.039, and 0.04 and contained 2218, 3528, 4664, 5544, and 7726 ceramide molecules, 5374, 9623, 14,863, 22,269, and 38,513 water particles, and 812, 1428 2208, 3289, and 5722 MARTINI anti-freeze particles. The glycosylceramide simulations were constructed with λ equal to 0.0317, 0.03, 0.045, 0.038, and 0.038 and contained 2086, 3528, 4344 5104, and 7360 glycosylceramides, 5374, 9626, 13,614, 19,263, and 38,513 water particles, and 812, 1428, 2029, 2879, and 5722 MARTINI anti-freeze particles. λ-values were chosen to maintain a similar hydration between the ceramide and glycosylceramide systems with equal box side length, as well as to maintain an adequate surface density of the ceramides in the respective systems. Furthermore, the investigated hydration range corresponds to between 26 and 64% water by weight. This compares well with the total water content of the uppermost stratum granulosum cell, which is ∼70% w/w (11), considering that not all water will be present in the cubic lipid structures.

MD simulations

The starting structures were first energy minimized for 5000 steps using a steepest-descent algorithm. After this, all structures, except those with side length 25 nm, were equilibrated in two steps, first for 80 ns using a time step of 2 fs, and then by an additional 4 μs using a time step of 20 fs (the equilibrated structure for the ceramide system with side length 20 nm can be seen in Fig. 1 e). During the equilibration, the waters were restrained to their positions using a force of 1 kJ/mol/nm² to maintain the network of water channels in the structure (Fig. 1 d). For the systems with side length 25 nm, restraints on just the water structure were not enough to prevent small ruptures at the ceramide/water interface during the initial equilibration steps, and therefore, these simulations were equilibrated in three steps, first for 80 ns using a time step of 2 fs, where the ceramides were restrained using a force of 5 kJ/mol/nm²; then by an additional 80 ns where both the ceramides and waters were restrained using a force of 1 kJ/mol/nm², and finally for an additional 4 μs using a time step of 20 fs and the same restraints as for the other systems.

Non-bonded parameters were set according to the updated MARTINI recommendations (27) for simulations with the Verlet cutoff scheme in GROMACS (28, 29). During equilibration, the pressure was isotropically maintained at 1 bar with the Berendsen barostat (30) using a coupling constant of 5 ps and a compressibility of 3.0e⁻⁵ bar⁻¹. The temperature was set to 303 K using separate velocity-rescale thermostats (31) for water and ceramides. After equilibration, the structures were simulated for an additional 40 μs with a time step of 20 fs. Pressure was coupled anisotropically to 1 bar using the Parrinello-Rahman barostat (32) with τ = 12 ps.

After 12 μs of simulation, the glycosylceramide structure with a hydration of 14.5 waters per lipid (i.e., the system with side length 20 nm) was transformed into a ceramide structure by a superposition of the three ceramide headgroup particles onto the five headgroup particles of the glycosylceramides. The hydration level was kept constant during this transformation. The resulting structure was first energy minimized for 5000 steps using a steepest-descent algorithm and then equilibrated for 80 ns using a time step of 2 fs, with the waters restrained to their positions using a force constant of 1 kJ/mol/nm². After this the system was simulated for an additional 20 μs using the same parameters as described above for the 40-μs-long simulations.

After this, a series of simulations were performed in which the water content of the transformed ceramide system and original glycosylceramide system was gradually reduced by randomly removing a number of water molecules corresponding to either 15 or 10% of the water content in the starting systems. Since the overall structure of the glycosylceramide system did not change much after 12 μs (the point at which the transformation to a ceramide structure was performed), this structure was also used as a starting point for the water removal. After the random removal of water at each step, the systems were equilibrated for 800 ns with the ceramides/glycosylceramides restrained to their positions using a force constant of 10 kJ/mol/nm². This was then followed by a production run of an additional 4 μs. In total, the series of production runs for each system consisted of four iterations in which 15% of the water was removed in each step (60% in total), followed by four additional steps where 10% was removed in each step. For all the other simulated systems, the same water removal procedure was applied starting from their final conformation after 40 μs of simulation.

All simulations were performed with GROMACS 5.1.2 (28, 29), and the molecular visualizations were created using VMD 1.9.2 (33, 34). Fig. 1 a was created using Blender 2.76 (35). The software utilized in the construction of the cubic structures is available at https://github.com/alinar/cubic_membrane, and also requires the Molar package available at https://github.com/alinar/Molar.

Curvature and lipid mobility calculations

To study the geometric properties of the lipid/water surface at a particular frame in the MD simulations, the surface must be extracted from the coordinate and trajectory files. The MDAnalysis toolkit (36, 37) was used to access the coordinates in the simulation and the VTK framework (23) was used to implement the three-dimensional space calculations. A scalar field in the form of a voxel grid (size 32 × 32 × 32) was produced with the voxel attributed values equal to the voxel distance to the closest bead of a tail group of any lipid molecule. A cutoff distance of 4.0 Å was chosen to outline the isosurface separating the tail from the head and the water beads. The Marching cubes method (22) was used to extract the mesh of the isosurface from the scalar field, and the surface was smoothed with a Laplacian smoothing filter to obliterate small ripples. The value of the local curvature (mean and Gaussian) was then calculated for the mesh. The “vtkMarchingCubes,” “vtkSmoothPolyDataFilter,” and “vtkCurvature” built-in class methods were used to extract and smooth the surface and to calculate the curvature values.

The lipid mobility in the simulations was calculated as an average of the total three-dimensional displacement of each simulation particle in each ceramide molecule. The average displacement was calculated and stored for each frame in the simulation, and the final mobility was calculated as a moving average over three consecutive frames.

The visualizations of the curvature and lipid mobility were created using VMD 1.9.2 (33, 34). The software utilized in the curvature calculations is available at https://github.com/alinar/cubic_membrane, and also requires the Molar package available at https://github.com/alinar/Molar.

Cryo-electron microscopy simulations

The all-atom structures used in the cryo-electron microscopy (cryo-EM) simulations were generated from the glycosylceramide structure with a hydration of 14.5 waters per lipid (i.e., the system with side length 20 nm) after 40 μs using the method backward (38), which does a geometric reconstruction of the all-atom structure followed by energy minimization and short equilibration. Simulated images from the generated all-atom structures were created with an EM simulation program developed by Rullgård et al. (39). The software is freely available at http://tem-simulator.sourceforge.net. Simulated electron micrographs of the equilibrated molecular dynamics models of the cubic glycosylceramide-based phase (Fig. 6 e), as well as of the pure water solution (Fig. 6 f), were generated at a defocus of −1.75 μm, a section thickness of 30 nm, a magnification corresponding to a pixel size of 1.88 Å, and an electron dose of 3,300 eV/nm². For the MD models of the stacked lamellar phase, simulated EM images were generated at a defocus of −2.50 μm, a section thickness of 50 nm, a magnification corresponding to a pixel size of 4.35 Å and an electron dose of 13,000 eV/nm².

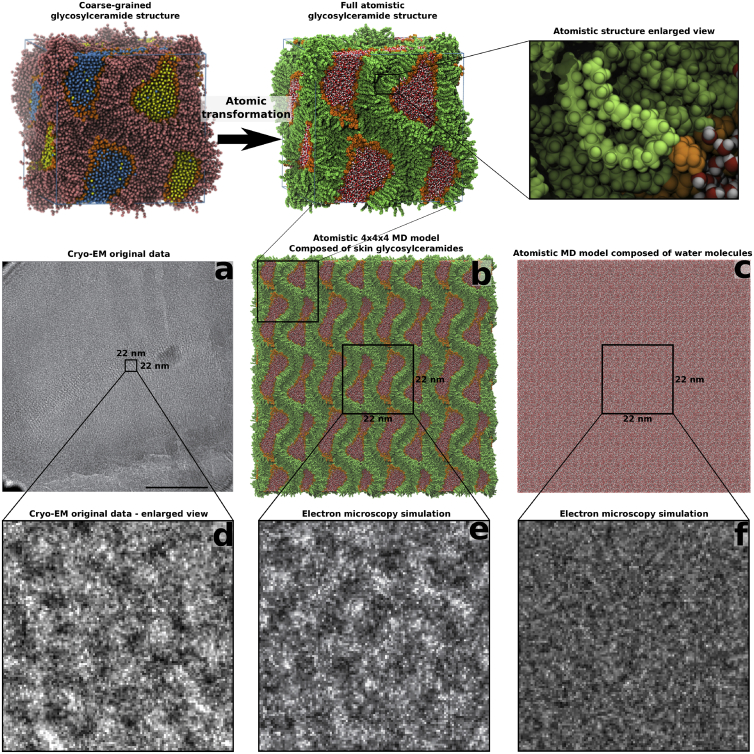
Figure 6.

Transformation of a coarse-grained cubic-phase glycosylceramide structure into an all-atom structure enables comparison to original cryo-EM data. The glycosylceramide structure with a hydration of ∼14.5 waters/lipid was transformed into an all-atom structure (top). To compare to experimental cryo-EM data (a), the unit cell of the all-atom structure was extended in three dimensions (b) and subjected to a cryo-EM simulation. Features from selected parts of experimental cryo-EM images (d) can then be compared to features present in the simulated cryo-EM images (e), or toward a negative control such as water (c and f). (a and d) adapted from Norlén, unpublished data, with permission. To see this figure in color, go online.

Results and Discussion

The formation of the stacked lamellar structure in the intercellular space of the stratum corneum likely takes place through a cubic-to-lamellar transformation of glycosylceramide-based bilayers with gyroid symmetry (unpublished data). The general form of this lipid structure is that of a bicontinuous water-channel network, separated by a folded lipid bilayer (Fig. 1, b–d). Fig. 1 a shows a surface with cubic (gyroid) symmetry, which was used as a template for constructing the simulated ceramide structures in this work. A completed ceramide structure can be seen in Fig. 1 b, together with selective visualizations of either the ceramide bilayer structure (Fig. 1 c) or the bicontinuous water structure (Fig. 1 d). Finally, the ceramide/water structure after an initial 4 μs equilibration by MD simulation can be seen in Fig. 1 e, and a selective visualization of the ceramide headgroups and water channels can be seen in Fig. 1 f.

Due to the relatively complex geometry of lipid bilayer structures with cubic symmetry, the structural changes within the simulated systems are difficult to visualize using a space-filling model for all particles, which is evident from Movie S1 or by comparison of Fig. 1, e and f. Therefore, the majority of the images (and videos) discussed from here on only show the simulation particles that represent water together with the simulation particles that represent the glycosylceramide- or ceramide headgroup regions (more details about the particle representation, as well as the colorization utilized online, are available in the Supporting Material).

Selection of simulated models

Due to the hydration-dependent behavior of lipid cubic phases, and the fact that the utilized MARTINI models are parametrized to reproduce properties of a flat lipid bilayer rather than a folded cubic bilayer phase, the choice of a suitable system configuration is a non-trivial task. We constructed five different models of ceramide and glycosylceramide systems with hydration levels between 11.5 and 23 waters per lipid, corresponding to simulation box sizes with a side length between 15 and 25 nm, and each system was initially simulated for 40 μs (Fig. 2; Figs S3–S6). As the aim of this study was to study the effect of deglycosylation on cubic ceramide systems with gyroid symmetry, the systems with a hydration level of ∼11.5 (Fig. S3) and ∼23 (Fig. S6) waters per lipid were given less emphasis during the analysis. The ceramide and glycosylceramide systems simulated at a hydration of ∼11.5 waters per lipid both quickly transitioned into a cubic inverted micellar phase, which might be an interesting entry point for future work but further analysis of which is beyond the scope of this study. Furthermore, an inverted micellar phase with cubic symmetry gives a cryo-EM pattern that is absent at the interface between stratum corneum and stratum granulosum (unpublished data). The ceramide and glycosylceramide systems with a hydration of ∼23 waters per lipid both transitioned into stacked lamellar structures, a behavior we believe to be an indication of an oversaturation of water in the systems that likely prevents the formation of a stable cubic phase.

Figure 2.

Snapshots of the cubic structures with a hydration of ∼14.5 waters/lipid after 0, 6, 12, and 40 μs of simulation time. In the ceramide system (a–d), there is a large structural rearrangement with a complete disconnection of two water channels. There is an overall rearrangement of the original gyroid bilayer structure into a structure resembling a lamellar bilayer. In the glycosylceramide system (e–h), the gyroid geometry is maintained throughout the simulation. The starting (a and e) and final structures (d and h) are displayed using a full representation of all simulation particles. (cf. Movies S1 and S3). To see this figure in color, go online.

For the other three simulated system compositions, with hydration levels of 12.5, ∼14.5, and ∼18 waters per lipid (Fig. 2; Figs. S4 and S5), a similar behavior was observed for systems with the same lipid (ceramide or glycosylceramide), but a distinct difference was observed when comparing the ceramide systems with the corresponding (same hydration level) glycosylceramide systems.

Due to the similar behavior of the systems with hydration levels of 12.5, ∼14.5, and ∼18 waters per lipid, most of the next sections will focus on the systems (ceramide or glycosylceramide) with a hydration level of ∼14.5 waters per lipid as a discussion point, although data from the other systems will also be presented wherever suitable. In the next section, we first discuss the initial 40 μs simulations of the cubic glycosylceramide and ceramide lipid bilayer structures, and the effect of glycosylated headgroups on the stability of a ceramide cubic phase. Thereafter, we discuss the effect of dehydration, and finally compare some of the obtained lipid structures with experimental cryo-EM data from human skin.

We have tried to select appropriate snapshots from the simulations to display the events we discuss in the text. However, we strongly encourage the reader to utilize Movies S1, S2, S3, and S4, since some structural details are difficult to convey in two-dimensional images.

Human skin glycosylceramides stabilize a folded bilayer structure with cubic-like symmetry

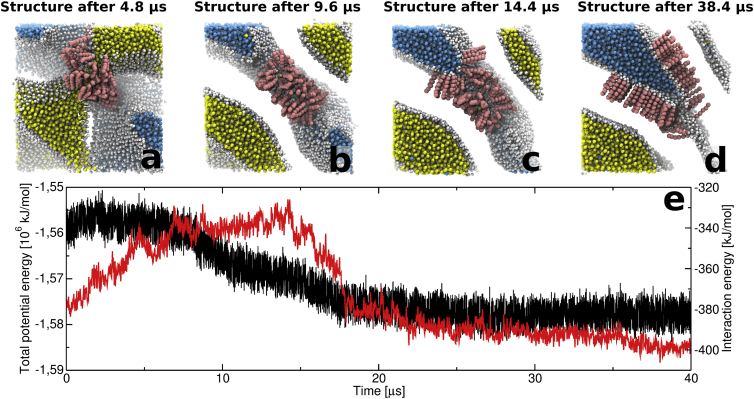
The evolution of the initial ceramide system (∼14.5 waters per lipid) during the first 12 μs of simulation time can be seen in Movie S1, and snapshots of the system after 0, 6, 12, and 40 μs can be seen in Fig. 2, a–d. During this time the system gradually changes from its original cubic symmetry (Fig. 2 a) into a structure similar to stacked bilayers separated by water (Fig. 2, c–d). This transition includes a complete disconnection of two of the water channels, with the intermediate structures displayed in Fig. 2, a–c resembling the inverse of the lamellar-to-cubic phase transition described by Tang and co-workers (Fig. 5 in (40)). This conformational change appears to be driven by the hydrophobic interactions in the system, as the structural rearrangements (from Fig. 2, a–d) lead to a tighter packing of the ceramide hydrocarbon chains and thus the formation of a gel-state phase. This strong propensity of the ceramides to adopt a gel phase destabilizes the cubic phase, and drives the system toward a lamellar geometry. Movie S2 displays this effect during the disconnection of one of the channels in Fig. 2, a–d, and four snapshots from the full simulation are displayed in Fig. 3 together with the total potential energy in the simulated system (black curve) and the average interaction energy for the fully visualized ceramides (thin curve). The favorable interaction energies coupled to the tighter packing of the ceramide tails can be seen from the interaction energy for the visualized ceramides (Fig. 3 e) as the structure transforms from the cubic phase, with fluid hydrocarbon tails, into the gel-state lamellar phase at the end of the simulation. The combined conformational changes in the whole system drive the locally situated ceramides, visualized in Fig. 3, a–d, toward less favorable ceramide-ceramide interactions (Fig. 3 e, thin curve) as the diameter of the water channel (Fig. 3 a) gradually decreases. After 6 μs the water structure becomes divided into two separate entities, with the space previously occupied by the water channel now filled by disordered ceramides (Fig. 3 b). After this, the disordered region gradually shrinks as its ceramides integrate into the surrounding bilayer structure. For a majority of the visualized ceramides this happens between 14 and 18 μs (Fig. 3, c and d, respectively), simultaneous with the formation of a larger gel-state region in the ceramide structure that can be observed through the shift in the total potential energy of the system (black curve at ∼15 μs). At the end of the simulation, the local geometry of the region originally occupied by a water channel has changed into a lamellar structure with ordered ceramides in the gel state (Fig. 3 d).

Figure 3.

Full disconnection of one water channel in the ceramide structure in Fig. 2 over 40 μs of simulation. The structural changes within the ceramide system lead to a gradual decrease of the diameter of the original water channel (a) as the simulation progresses. (b) The channel disconnects completely after ∼6 μs, and leaves a disordered structure of ceramides, and a few waters, behind. (c and d) Eventually, the disordered ceramides arrange into a bilayer structure. (e) The total potential energy in the system is shown in black, and the interaction energy for the visualized ceramides (calculated as a per-molecule average) is shown in thin. (cf. Movie S2.) To see this figure in color, go online.

For the simulated glycosylceramide system (hydration ∼14.5 waters/lipid), the evolution during the first 12 μs can be seen in Movie S3, and snapshots taken after 0, 6, 12, and 40 μs can be seen in Fig. 2, e–h. In contrast to the ceramide system, the glycosylceramide system maintains the cubic lipid bilayer phase throughout the duration of the 40 μs simulation despite the propensity for glycosylceramides to form bilayers in the gel state at the simulated temperature (303 K) (26). The formation of these gel-state bilayer structures is, as for the ceramide system, driven by the increased amount of favorable interactions coupled to the tight packing of the hydrocarbon chains. In the glycosylceramide system, the gel-state-driven disconnection of water channels, as observed in the ceramide system, appears to be prevented, and the overall cubic-like structure is maintained throughout the simulation, although local formations of gel-state bilayers can be observed in the cubic structure. One explanation for this behavior might be the stronger interactions between the glycosylceramide headgroups (displayed as a fraction relative to the tail region interactions for all simulated systems in Fig. S2). To further test this hypothesis, the glycosylceramide system was chemically transformed into a ceramide system by an exchange of the headgroup particles of the glycosylceramide structure after 12 μs simulation (Fig. 4, b and c). The transformed ceramide structure was then simulated for 20 μs (Fig. 4, b–e) during which it displayed a structural transformation into a lamellar structure similar to the original ceramide system (cf. Fig. 2 d).

Figure 4.

The combined simulations of the cubic-to-lamellar phase transition. The simulated glycosylceramide structure (with a hydration of ∼14.5 waters/lipid) (a) was alchemically transformed into a ceramide structure (b and c) by exchanging its headgroup particles after 12 μs of simulation. Although the original glycosylceramide structure retained its cubic geometry over an additional 28 μs, the transformed ceramide structure displayed a cubic-to-lamellar transition (c–e) during the first 20 μs after the transformation, indicating the importance of the headgroup interactions for the stability of the cubic phase. Dehydration of the ceramide system (f–h) resulted in a fully lamellar structure (i). The simulation box is outlined in blue. To see this figure in color, go online.

The results from Fig. 2 together with those from the deglycosylated ceramide system indicate that to maintain a cubic-like structure, the interactions between the headgroups need to be strong enough to counteract the hydrophobic interactions in the hydrocarbon chain regions that locally drive the systems toward the gel state. This suggests that glycosylceramides are critical for the stabilization of folded bilayers with cubic-like symmetry in human skin.

Furthermore, using the analysis tools available in the GROMACS simulation package (28, 29), we calculated the water diffusion coefficient during the first and last 4 μs of the simulation time in all systems (Table S1). Diffusion coefficients are calculated using a linear fit through the mean-square displacement of the water particles in the simulations. The error estimates are obtained as the difference between diffusion coefficients calculated from the first and second halves of the fitting intervals. For the systems with low hydration (∼11.5 waters/lipid), the quick transition to an inverted micellar phase greatly reduces the diffusion of water in these systems, resulting in diffusion coefficients an order of magnitude below those of the other systems.

The other, more hydrated systems all display an increase in the diffusion coefficient for water with increasing system size. This is most likely attributed to the increased volume of water inside the channels as well as to the reduced friction experienced from water interacting with the lipid headgroups. The diffusion coefficient in the ceramide system with a hydration of 23 waters/lipid (0.4393 × 10⁻⁵ cm²/s) is not far off from the self-diffusion of coarse-grained water, which has been calculated to 0.5 × 10⁻⁵ cm²/s (15), at 300 K. For the simulations with a gyroid cubic symmetry, we otherwise see a reduction of the diffusion by a factor of ∼1.5–2 compared to self-diffusion in bulk conditions. This agrees qualitatively well with a previous study (20) where the water diffusion coefficient in a diamond cubic phase was reduced by a factor of 3.

Additionally, the glycosylceramide systems all display a lower diffusion coefficient (compared to the ceramide systems) during the first 4 μs where all the systems have a cubic geometry. This might be due to the more hydrophilic headgroups of the glycosylceramides, which increase the friction experienced by the water in the channels. During skin barrier formation, this effect might facilitate water evacuation from the ceramide-based folded bilayer structure with cubic-like symmetry during its transition into a non-water-containing stacked lamellar structure.

On a more mesoscopic scale, we can also look at the molecular mobility of each ceramide (calculated from the displacement of each atom in each ceramide, averaged in a 72 ns moving window from the simulation), and correlate that molecular mobility to the local mean and Gaussian curvatures at the ceramide/water interface. In Figs. S12 and S13, we show this for the systems with a hydration of ∼14.5 waters/lipid. During the first 12 μs in the ceramide system, we see a local increase of the molecular mobility (red intensity level) and the mean curvature (green intensity level) in the regions adjacent to the disconnected water channels and a decrease in the Gaussian curvature (yellow intensity level) in the flattened stacked lamellar regions. Accordingly, those regions that have transitioned into a lamellar structure are characterized by low molecular movement and low mean and Gaussian curvatures (Fig. S12). By contrast, in the glycosylceramide system, where there is no disconnection of the water channels and the cubic geometry is maintained throughout the simulation, the lipid mobilities (like the local mean and Gaussian curvatures) appear to be homogeneously distributed across the whole structure (Fig. S13). Furthermore, the relatively low mobility of the lipids in the simulation (average displacement of ∼5–7 Å over the 72 ns window in Figs. S12 and S13) should limit the effect of any potential artificial lipid movement coupled to the use of periodic boundary conditions.

As water content is reduced, the human skin ceramide folded bilayer structure transforms into a stacked lamellar structure

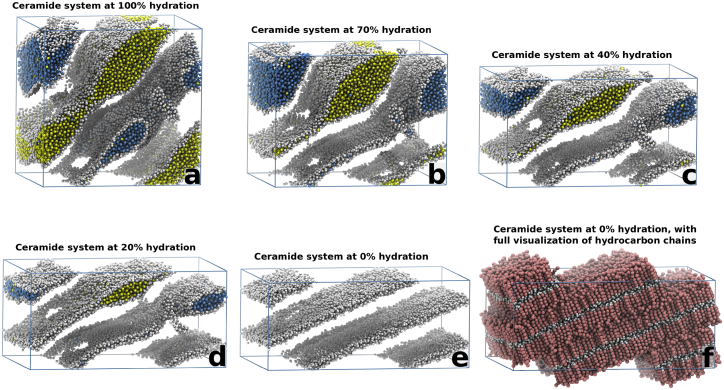
Although it is theoretically possible to perform simulations in grand canonical ensembles to gradually reduce the concentration of a molecule, this is not supported in normal simulation programs. Instead, the structure from the deglycosylated ceramide system in Fig. 4, c–e, had its water content reduced in a step-wise series of 4-μs-long simulations. The water was reduced in four steps of 15% (relative to the starting structure) followed by four steps of 10% (relative to the starting structure), until there was no water left in the systems. Comparatively small structural transformations were observed upon the stepwise water removal in the ceramide system (displayed in Movie S4), compared to the larger structural transformations observed during the first 20 μs of simulation (Fig. 4, c–e). Due to this, we believe that the stepwise reduction in water content is able to reproduce the different behaviors of the ceramide system adequately. Movie S4 displays the combined trajectories from all simulations in the dehydration series of the ceramide system. Fig. 5 shows the ceramide structure after the simulations at the steps with 100, 70, 40, 20, and 0% water remaining from the starting structure.

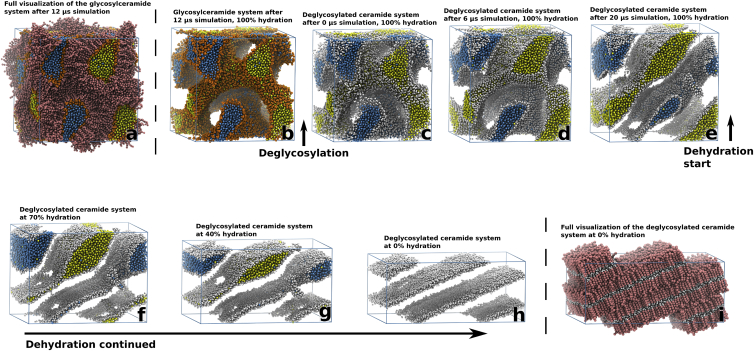
Figure 5.

The final structures of the ceramide system with an original hydration of ∼14.5 waters per lipid, at a water content (compared to the original system) of 100, 70, 40, 20, and 0% (a–f). As water is removed from the system, a transition into a fully lamellar structure is observed. Some areas with disordered ceramides can be seen as holes in the headgroup structure, but the majority of these areas eventually relax into the same bilayer conformation as the surrounding ceramides. The full representation of the 0% water system (f) clearly demonstrates the final lamellar structure. The simulation box is outlined in blue (cf. Movie S4). To see this figure in color, go online.

Going through the steps in the series of dehydration simulations (Fig. 5, a–e), the ceramide structure transitions into a stacked lamellar bilayer structure (Fig. 5 f). During this transition some parts of the structure remain distorted, with the locally disordered ceramide chains oriented approximately parallel to the surrounding bilayer structure (e.g., Fig. S14 a), and these irregularities seem to stem from the large local conformational changes that occur during the closure and disconnection of the water channels in the simulation of the starting structure (Fig. 2, a–d). Almost all of these distorted regions eventually disappear, and only a few persist at the end of the dehydration series (Movie S4).

One interesting observation from these distorted regions is that the ceramides tend to cluster together in the splayed-chain conformation, orienting their oppositely directed sphingoid and fatty acid moieties along the bilayer normal in a seemingly alternating fashion, as the system relaxes into a non-water-containing stacked lamellar structure (Fig. S14 b). Speculatively, this finding could be of relevance for the formation of the stacked lamellar bilayer structure based on splayed ceramides present in the stratum corneum intercellular space (unpublished data; 10).

In addition to the ceramide system in Fig. 4, c–e, we also performed the same dehydration procedure with the corresponding glycosylceramide system, starting from the structure after 12 μs (Fig. 2 g), and the results can be seen in Fig. S7. The glycosylceramide system retains the cubic-like structure as the water content is reduced, with its original bi-continuous structure being conserved throughout the simulation series. At greatly reduced water contents (0% water content in Fig. S7 e), there are some local lamellar bilayer structures present (as shown in Fig. S7 f), but the overall architecture of the final dehydrated system is still far from lamellar (Fig. S7 e).

Furthermore, the systems simulated at other hydration levels were subjected to the same water removal procedure, starting from their structure after the initial 40 μs simulation, and snapshots from these simulations at 70, 40, and 0% hydration can be seen in Figs. S8–S11. Starting with the systems with a hydration of 12.5 (Fig. S9) or ∼18 (Fig. S10) waters/lipid, the structure in the respective ceramide simulations at 0% hydration resembles that of a stacked lamellar lipid bilayer, whereas the glycosylceramide simulations appear to preserve the gyroid network present in the original system. There are some irregularities in the bilayer structure displayed in Fig. S9 c (visualization of the whole structure displays two bilayer formations situated at an angle against each other), but it still follows the same pattern as observed in the previously discussed simulation, with a clear transition toward a lamellar organization for the ceramide system. For the glycosylceramide systems, there is a tendency toward a lamellar structure for the system with a hydration of ∼18 waters per lipid (Fig. S10 f), although remnants of the old channel structure are still present in the same way as for the system in Fig. S7 e. The system with a hydration level of 12.5 waters/lipid displays a clearly non-lamellar structure (Fig. S9 f). Additionally, splayed-chain ceramides similar to those in Fig. S14 also appear in the simulated ceramide systems with ∼12.5 and ∼18 waters/lipid.

In the simulations with a starting hydration of ∼11.5 waters/lipid (Fig. S8), the ceramide system displayed no cubic-to-lamellar phase transition, and the final system instead contained a disorganized mixture of ceramides with no apparent structure. The final conformation of the corresponding glycosylceramide structure once again preserves the channel structure, as observed in the other glycosylceramide simulations (Figs. S7, S9, and S10).

For the highly hydrated systems (Fig. S11) there is a transition into a stacked lamellar structure observed in both simulations, although the glycosylceramide systems still contain remnants of the old channel structure, similar to Fig. S10 f. These results, taken together with the results from the starting simulations (Fig. 2; Figs. S3–S6), strengthens the notion that the glycosylceramides are able to stabilize a three-dimensional folded bilayer structure with gyroid cubic symmetry, whereas gyroid cubic ceramide structures appear to transition into stacked lamellar bilayers. Unless they were highly hydrated, glycosylceramide systems displayed no transition into a stacked lamellar system. A deglycosylation of the glycosylceramide headgroups reduces the inter-headgroup interaction strength (Fig. S2) and ultimately leads to a loss of the cubic symmetry in a previously stable glycosylceramide system (Fig. 4, b–e). A dehydration of the deglycosylated ceramide structure promotes a full transition into a stacked lamellar structure (Fig. 4, f–h).

Molecular transformation to all-atom structures enables validation against cryo-EM data

The size of the structures studied in this work required us to utilize a coarse-grained approach to be able to reach the timescales relevant for the structural transitions that occurred during the simulations. Validation of the simulated models against experimental data from human skin is thus a non-trivial task. In previous publications, we presented a methodology (10) that utilizes simulated cryo-EM images to identify molecular models yielding patterns compatible with cryo-EM patterns observed in human skin. A natural extension of this method would be to utilize the thermodynamically equilibrated structures obtained from MD simulations as input structures for EM simulation. However, since EM simulations require structures with an all-atom representation, to get the correct electron density distributions, the simulated structures presented in this work first have to be transformed into all-atom structures (38). This methodology is described in Figs. 6 and 7, which show the simulated cryo-EM images from the MD-simulated cubic (hydration ∼14.5 waters/lipid) and corresponding lamellar structure after deglycosylation and dehydration, respectively.

Figure 7.

Transformation of a lamellar coarse-grained ceramide structrure into an all-atom structure enables comparison to the original cryo-EM data. The lamellar ceramide structure with a hydration of ∼14.5 waters per lipid (Fig. 4f) was transformed into an all-atom structure (top). To compare to experimental cryo-EM data (a), the unit cell of the all-atom structure was extended in three dimensions (b) and subjected to a cryo-EM simulation. Features from selected parts of the experimental cryo-EM images (c) can then be compared to features present in the simulated cryo-EM images (d). Images (a) and (c) are adapted from Norlén, unpublished data, with permission. To see this figure in color, go online.

The coarse-grained-to-all-atom transformation of the glycosylceramide structure after 40 μs of simulation is shown at the top of Fig. 6, and the corresponding transformation of the final lamellar structure at the top of Fig. 7. After transformation, the all-atom unit cell is replicated in three dimensions (Figs. 6 b and 7 b) to reduce possible edge effects in the EM simulation, and the resulting simulated image (Figs. 6 e and 7 d) can then be compared with the original cryo-EM data (Figs. 6 d and 7 c).

Despite the simplified models used in this work (only one ceramide or glycosylceramide component, no cholesterol, and no free fatty acids), the simulated cryo-EM images of the cubic phase (Figs. 6 e) compare favorably with the granular pattern obtained from the continuous membrane region of the topmost stratum granulosum cell (Norlén, unpublished data, with permission.) (Fig. 6 a). As a negative control, an EM simulation image of a pure water solution obtained under the same conditions is shown in Fig. 6 f. Likewise, simulated electron micrographs of the dehydrated stacked lamellar structure (Fig. 7 d) correspond closely with the lamellar cryo-EM patterns found in skin (Fig. 7 c).

Conclusions

Skin barrier formation likely takes place through a cubic-to-lamellar lipid transition (unpublished data). Through this process, a three-dimensionally folded cubic-like lipid bilayer structure transforms into a stacked lamellar structure at the interface between the stratum granulosum and stratum corneum. A change in lipid composition, from being dominated by glycosylceramides (41, 42, 43) in the stratum granulosum to becoming completely replaced by ceramides (8, 9, 41, 42, 44, 45) in the stratum corneum, has been suggested as the driving force for this cubic-to-lamellar transition (unpublished data; 10).

The MD simulations provided here cast, to our knowledge, new light on the molecular properties of these processes and indicate that glycosylceramides are able to stabilize a cubic-like bilayer structure. Furthermore, simulations of ceramides lead to a collapse into a stacked lamellar structure. The main driving force seems to be the hydrophobic interactions between the ceramides, which at the simulated temperature form bilayers in the gel state. The stronger interactions between the glycosylceramide headgroups enable them to maintain the cubic-like bilayer geometry in the glycosylceramide system, whereas interactions between the hydrophobic tails are the main cause of the structural changes in ceramides. These observations suggest that glycosylceramides are important for the stability of the cubic-like lipid bilayer structure present in the stratum granulosum, and that β-glucocerebrosidase-mediated cleavage of their sugar moieties might be important for its collapse into the stacked lamellar structure present in the stratum corneum (unpublished data; 10).

A more realistic model of skin barrier formation should account for the complex mixture of ceramides, free fatty acids, and cholesterol that is present at the stratum-granulosum-stratum-corneum interface. However, the simplified models studied here, based on pure skin ceramides and glycosylceramides, reveal striking differences in the simulated properties between the two systems that are in agreement with available experimental human skin data. The simplified models may thus provide mechanistic insight into the basic features of skin barrier formation at the molecular level.

Furthermore, we show that a molecular transformation of simulated coarse-grained structures into their all-atom counterparts enables us to obtain simulated EM images of the equilibrated structures. The simulated electron microscopy data obtained from the MD models can then be compared to the original cryo-EM data from native skin to validate the structural information obtained from the MD simulations. This approach presents, to our knowledge, a novel way of obtaining structural information from biological tissues through the combination of cryo-EM, MD simulation, and electron microscopy simulation.

Author Contributions

The starting structures were created by C.L.W., A.N., and M.L.. The MD-simulations and analysis were performed by C.L.W. The cryo-EM simulations were performed by A.N., who also helped with the analysis, together with M.L. The study was designed and written by, C.L.W., L.N., and E.L. C.L.W., A.N., M.L., and L.N. have stock options in ERCO Pharma AB. C.L.W., A.N., and M.L. are employed by ERCO Pharma AB.

Editor: Andreas Engel.

Supporting Material

Movie S1. Cubic Ceramide System

The evolution of the ceramide system with hydration ∼14.5 waters per lipid during the first 12 μs of simulation time. The biocontinuous water structure is displayed in blue and yellow, the ceramide headgroup region in white, and the hydrocarbon tail regions in pink. The simulation box is outlined in blue.

Movie S2. Water Channel Disconnection in Ceramide NS System

Disconnection of a water channel in the simulated ceramide structure with hydration ∼14.5 waters per lipid. The bicontinuous water structure is displayed in blue and yellow, the ceramide headgroup region in white, and the hydrocarbon tail regions in pink.

Movie S3. Cubic Glycosylceramide System

The evolution of the glycosylceramide system with hydration ∼14.5 waters per lipid during the first 12 μs of simulation time. The bicontinuous water structure is displayed in blue and yellow, the glycosylceramide headgroup region in orange, and the hydrocarbon tail regions in pink. The simulation box is outlined in blue.

Movie S4. Dehydration of Ceramide System

Stepwise removal of water from the transformed ceramide-system in Fig. 4, C–E. The bicontinuous water structure is displayed in blue and yellow, the ceramide headgroup region in white, and the hydrocarbon tail regions in pink. The simulation box is outlined in blue.