Anticooperative Nearest-Neighbor Interactions between Residues in Unfolded Peptides and Proteins

Abstract

Growing evidence suggests that the conformational distributions of amino acid residues in unfolded peptides and proteins depend on the nature of the nearest neighbors. To explore whether the underlying interactions would lead to a breakdown of the isolated pair hypothesis of the classical random coil model, we further analyzed the conformational propensities that were recently obtained for the two guest residues (x,y) of GxyG tetrapeptides. We constructed a statistical thermodynamics model that allows for cooperative as well as for anticooperative interactions between adjacent residues adopting either a polyproline II or a β-strand conformation. Our analysis reveals that the nearest-neighbor interactions between most of the central residues in the investigated GxyG peptides are anticooperative. Interaction Gibbs energies are rather large at high temperatures (350 K), at which point many proteins undergo thermal unfolding. At room temperature, these interaction energies are less pronounced. We used the obtained interaction parameter in a Zimm-Bragg/Ising-type approach to calculate the temperature dependence of the ultraviolet circular dichroism (CD) of the MAX3 peptide, which is predominantly built by KV repeats. The agreement between simulation and experimental data was found to be satisfactory. Finally, we analyzed the temperature dependence of the CD and ³J(H^NH^α) parameters of the amyloid β_1–9 fragment. The results of this analysis and a more qualitative consideration of the temperature dependence of denatured proteins probed by CD spectroscopy further corroborate the dominance of anticooperative nearest-neighbor interactions. Generally, our results show that unfolded peptides—and most likely also proteins—exhibit some similarity with antiferromagnetic systems.

Introduction

The classical view of the unfolded state of proteins and peptides—the so-called random coil model—is based on the assumption that individual amino acid residues sample the entire sterically accessible conformational space in the Ramachandran plot irrespective of the conformational motions of respective neighboring residues (1). This is generally called the isolated pair hypothesis. Although still invoked in the scientific literature, recent experimental, computational, and bioinformatics studies have shown that different backbone rotamers are not isoenergetic, that their conformational sampling is more restricted than assumed (2, 3, 4, 5, 6, 7, 8, 9), and that it depends on the steric and electrostatic properties of their nearest neighbors (10, 11, 12, 13). Though the influence of nearest neighbors on propensity distributions of residues can now be considered as firmly established (12, 13), the specifics of the underlying nearest-neighbor interactions (NNIs), their significance for conformational manifolds of statistical coils, and their role in the protein folding processes have yet to be established. It is particularly unclear whether NNIs depend predominantly on the conformations of the nearest neighbors or whether they mostly reflect their steric and physicochemical properties. In the former case only, the potential function of a given residue i depends on the φ,ψ angles of residues i−1 and i+1, and the isolated pair hypothesis breaks down. If this happens, the Gibbs energy and the entropy of unfolded peptides or proteins can no longer be calculated as a sum of individual residue contributions, which is still assumed to be the case in estimations of solvation energies of proteins (14).

Some important work that explicitly addresses the conformational dependence of NNIs must be acknowledged in this context. Pappu et al. provided computational evidence for anticooperative interactions between neighboring residues adopting right-handed helical and β-strand structures, respectively (15). Avbelj and Baldwin studied the influence of different amino acid residues at a distinct position of a polypeptide chain on the solvation free energies of their alanine neighbors by computational means. They showed that the replacement of an alanine residue by valine reduces the solvation free energies of adjacent alanines (11).

In an effort to examine the effects of conformational structure versus side chain moiety, Sosnick and coworkers (3, 10) analyzed (truncated) coil-library-derived distributions for NNI-induced changes. The authors were able to identify different NNI effects being caused by upstream and downstream neighbors. If the former adopts a helical conformation, the β-strand fraction of the target residue increases at the expense of polyproline II (pPII), with the strongest effects induced by alanine, valine, and isoleucine as neighbors. These observations are apparently at variance with the results for Pappu et al. (15). Aromatic downstream neighbors in the pPII state were found to increase the β-strand content of the target residues, whereas those with branched side chains were found to have a very limited overall influence. The relevance of conformational-dependent NNIs for the calculation of the folding-induced loss of conformational entropy of ubiquitin was subsequently demonstrated by Baxa et al. (16).

A recent conformational analysis of selected GxyG tetrapeptides in water by Toal et al. (13) has shed some light on how NNIs depend on the type of amino acid residue. The study showed that the high preference of alanine for pPII is substantially reduced if an adjacent glycine is substituted by serine or aspartic acid on the N-terminal site or by valine on the C-terminal site. The presence of similar neighbors on the C-terminal side of protonated aspartic acid stabilizes pPII at the expense of turn-like conformations. NNIs were found to have a lesser effect on K and V and a nearly negligible influence on the propensities of L (17). However, in the latter case, NNIs induce changes of local free energy minima position in the Ramachandran space.

The current study is aimed at extracting conformation-dependent NNIs from a comparison of the conformational propensities of x and y guest residues in GxyG peptides (13) with corresponding propensities in GxG peptides (8, 9, 18, 19). GxG tripeptides have been used previously as tools to determine intrinsic conformational propensities of the guest amino acid x, as the glycine environment provides a zero-point reference for the further quantification of NNIs. The use of GxyG peptides then allows one to probe NNIs produced by either an N-terminal or a C-terminal neighbor. An investigation of the combined influence of these two NNIs and the identification of possible synergetic effects would require the use of GxyzG-type pentapeptides. Such data are not yet available. The use of model peptides in water rather than coil library data is motivated by recently reported evidence for the capability of the former to serve as suitable reference systems for elucidating ideal statistical coil structures of unfolded and intrinsically disordered proteins (17). Generally, conformational distributions of short peptides contain less helical content than coil-library-derived distributions (18). The term “statistical coil,” which was introduced by Scheraga and coworkers (20), implies the absence of any residual structure. It is different from an ideal random coil in that its applicability is not confined to peptide/protein-solvent systems close to the θ-point. The term can therefore be used for unfolded proteins under folding conditions, thermally unfolded proteins, and unfolded proteins under denaturing conditions. The conformational distribution of a statistical coil can depend on residue-specific backbone-solvent interactions, side-chain-solvent interactions, and NNI effects. In addition to analyzing NNI effects at room temperature, we use the thermodynamic data of GxyG (13) to calculate propensities at the high temperatures (353 K) at which many proteins are thermally unfolded. This step is motivated by the observation that enthalpic and entropic differences between pPII and β-strand conformations of individual residues are much larger than their respective Gibbs energies at room temperature (13, 21). Finally, we use the results of our analysis to predict the temperature dependence of circular dichroism and ³J(H^NH^α)-values of the low-complexity MAX3 peptide and the more heterogeneous amyloid fragment Aβ_1–9. With regard to the influence of NNIs, we focus on the changes of propensities and ignore the (sometimes significant) changes of the (ϕ,ψ) positions of subdistributions in the Ramachandran plot. For a discussion of the latter, we refer the reader to our recent work (17).

Results and Discussion

This chapter is organized as follows. First, we identify and compare NNI-induced changes of the Gibbs energy difference, ΔG_pPIIβ, between pPII and β-strand conformations of x and y residues in GxyG peptides by utilizing their earlier-reported conformational propensities (13). Second, to identify the pattern of these NNIs, we investigate these conformational propensities for correlations between changes of pPII and β-strand propensities. We ignore NNIs involving right-handed helices and turn structures because their total fraction seldom exceeds 0.2. Third, based on the results of this analysis, we construct a simple model that explains NNI-induced changes of ΔG_pPIIβ of the central GxyG peptide residues solely in terms of the conformations adopted by nearest neighbors. Fourth, the insight from this analysis is used to construct a Zimm-Bragg/Ising-type transfer matrix formalism for polypeptide chains (22), which accounts for both cooperative and anticooperative interactions between nearest neighbors. In a fifth step, we compare the predicted temperature dependence of spectroscopic data of two unfolded peptides with experimental data reported in the literature.

Temperature dependence of nearest-neighbor-induced free energy changes

We used the Gibbs free energy difference between pPII and β, ΔG_pPIIβ, as well as the corresponding enthalpy (ΔH_pPIIβ) and entropy (ΔS_pPIIβ) (Fig. S1) values of GxyG (13) and the corresponding single guest GxG peptides (8, 9, 18, 19) to calculate the difference between ΔG_pPIIβ values of a distinct residue in GxG/GyG and GxyG. These thermodynamic parameters were derived from conformational propensities derived from spectroscopic data as briefly described in the Supporting Material. Whereas the ΔG_pPIIβ derived from GxG are used as a reference system to define the zero level of NNI energies, ΔG_pPIIβ derived from residues within GxyG are subjected to NNIs from either an N- or a C-terminal neighbor. Hence, the NNI-induced Gibbs energy changes are written as follows:

$$\delta \Delta G_{ij}=\Delta G_{pPII\beta ,i\left(j\right)}-\Delta G_{pPII\beta ,i},$$ (1)

where i = 1,2 indicates the target residue and j = 2,1 the nearest neighbor. In our numbering scheme, x and y are represented by 1 and 2, respectively.

It is customary in the field to compare differences between Gibbs energies with the thermal energy RT_room at room temperature (20, 23). We term a change $\delta \Delta G_{ij}$ large if it exceeds RT_room, moderate if it lies between 0.5 and 1 RT_room, and weak if it is below 0.5 RT_room. As shown in Fig. S2, the obtained nearest-neighbor-induced Gibbs energy changes are mostly moderate or weak at room temperature, with the exception of the changes obtained for A in GAVG. At 353 K, the energy landscape is substantially different. Four $\delta \Delta G_{ij}$ values (of V in GDVG, GSVG, GAVG, and GKVG) exceed RT_room by a substantial amount. These changes reflect large differences between respective entropic contributions to the Gibbs energy in GVG (21) and GxVGs (13). Also noteworthy are the large positive values for S and K in GSKG and A in GAVG. Thus, our data clearly indicate that the influence of NNIs on propensities increases significantly with temperature.

Correlation between propensity changes

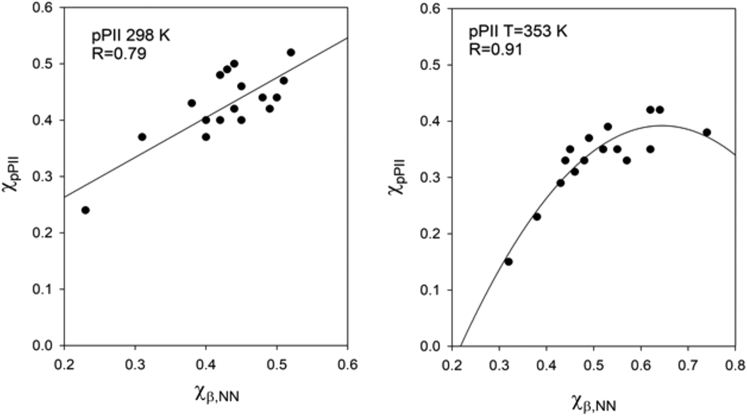
If the NNI depended on the conformation of adjacent residues, one would expect a correlation between their conformational propensities. Therefore, we checked whether the pPII fraction of residues x or y (χ_pPII) exhibits a correlation with the β-strand fraction of its respective neighbor y or x (χ_βN). We a priori considered the possibility that it might exist only for a subset of our data. We will justify this approach a posteriori below after we have performed a statistical thermodynamics analysis of our data. To identify the subset of correlating data pairs, we calculated the average χ_pPII/χ_βN ratio of all 28 residues investigated and identified the residues that deviated less than the standard deviation from this value. We found that the χ_pPII/χ_βN ratio of most residues lies within this region. By considering only the residues lying within the 1 σ interval, we eliminated 9 pieces of data from the room temperature set and 11 pieces of data from the 353 K data set. Fig. 1 shows the correlation plots for the remaining 19 and 17 data points, respectively. For room temperature, the pPII/β_N data then showed a rather strong positive correlation with R = 0.79. Interestingly, the reduced 353 K data set, which spread over a much larger region, could best be fitted by assuming a quadratic relation (R = 0.91), which was positive up to χ_βN values of 0.5. A linear fit with a somewhat lower correlation coefficient (R = 0.8) and a positive slope could be obtained by further eliminating the four data points with the highest χ_pPII-values. We also checked to what extent β-strand correlates with β_N propensities and found the correlations to be weak (R = 0.33) at room temperature and on an intermediate level (R = 0.51) at 353 K (Fig. S3). Correlation plots with the complete, unreduced data set are shown in Fig. S4.

Figure 1.

Correlation plot relating the mole fraction of x- and y-residues of a reduced set of earlier-investigated GxyG peptides at T = 298 K (left) and T = 353 K (right). The y-axis gives the pPII (χ_pPII) fraction of a residue x or y versus the β-strand fraction (χ_βNN) of its respective neighbor; the x-axis gives the β-strand fraction of its respective neighbor (χ_βN). Solid lines result from the regression analysis described in the text.

Most of the GxyG peptides taken out of the room temperature pool contain either an alanine or a valine. For the high temperature set, a majority of excluded peptides contain A or K. As shown below, the magnitude of data scattering in the correlation plots of Fig. 1 reflects residue-specific differences between NNI energies. Overall, we take the obtained correlations as suggesting that some anticooperative NNIs between x and y residues of GxyG exist.

The rather large difference between the two Pearson correlation coefficients obtained for χ_pPII/χ_βN and β/β_N plots is surprising. An explanation of this observation is given below, where we perform a model-dependent analysis of correlations between nearest neighbor propensities.

Exploring the cooperative and anticooperative character of NNIs

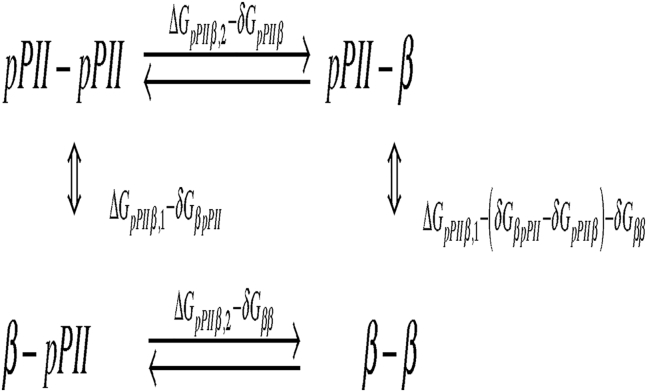
The model that is outlined in this section assumes that the differences between the propensities of an amino acid residue in GxyG and in corresponding tripeptides GxG (GyG) can be described exclusively in terms of interaction Gibbs energies between x and y in different conformations. Fig. 2 depicts a thermodynamic cycle that illustrates the considered NNIs. Herein $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ denote the interaction energies in xy-heterodimers in which x adopts pPII (β) whereas y samples β (pPII). $\delta G_{\beta \beta }$ is the interaction energy in an xy-homodimer, in which both residues adopt β-strand-type conformations. The homodimer with both residues in pPII is considered the zero-energy ground state of the system. The three interaction energies completely describe the system if we ignore possible interactions with turn- and helix-like states.

Figure 2.

Thermodynamic scheme representing the energetics of the four conformational states pPII-β, β-ppII, and β-β relative to the pPII-pPII ground state.

As known from helix $\rightleftarrows$ coil theory (24), the partition sum of polypeptides with NNIs can be calculated by utilizing an Ising-type transfer matrix. For the present case, the latter can be written as follows:

$$G_{ji}=\left(\begin{array}{ccc}{\langle P2|P2\rangle }_{ji}& {\langle P2|\beta \rangle }_{ji}& {\langle P2|t\rangle }_{ji}\\ {\langle \beta |P2\rangle }_{ji}& {\langle \beta |\beta \rangle }_{ji}& {\langle \beta |t\rangle }_{ji}\\ {\langle t|P2\rangle }_{ji}& {\langle t|\beta \rangle }_{ji}& {\langle t|t\rangle }_{ji}\end{array}\right),$$ (2)

where i, j label different residues (in this case nearest neighbors). The matrix elements ${\langle l|k\rangle }_{ji}$ represent the (conditional) probability for the jth residue to adopt conformation l, provided that the ith residue is in conformation k. t denotes turn conformations. The partition sum of a polypeptide chain can now be written as follows:

$$Z=q_N·\prod _{i=1}^{N-1}{G}_{i+1i}·q_i,$$ (3)

where q₁ and q_N are the state vectors of the terminal residues. For GxyG, N is equal to two.

We expressed the transfer matrix and state vectors as follows:

$$G_{ij}=\left(\begin{array}{ccc}1& \exp \left(\left(\Delta G_{p2\beta ,j}+\delta G_{P2\left(i\right)\beta \left(j\right)}\right)/RT\right)& \exp \left(\Delta G_{P2t,j}/RT\right)\\ \exp \left(\delta G_{\beta \left(i\right)P2\left(j\right)}/RT\right)& \exp \left(\Delta G_{p2\beta ,j}+\delta G_{\beta \beta }/RT\right)& \exp \left(\Delta G_{P2t,j}/RT\right)\\ 1& \exp \left(\Delta G_{p2\beta ,j}/RT\right)& \exp \left(\Delta G_{P2t,j}/RT\right)\end{array}\right)$$ (4)

and

$$q_N=\left(\begin{array}{ccc}1& \exp \left(\mathrm{\Delta }{G}_{pPII\beta ,N}/RT\right)& \exp \left(\Delta G_{pPIIt,N}/RT\right)\end{array}\right)$$

$$q_1=\left(\begin{array}{c}1\\ \exp \left(\mathrm{\Delta }{G}_{pPII\beta ,1}/RT\right)\\ \exp \left(\mathrm{\Delta }{G}_{pPIIt,1}/RT\right)\end{array}\right).$$ (5)

For the sake of consistency with earlier studies, the above formalism uses negative Gibbs energies as indicators of a conformation that is destabilized relative to pPII-pPII dimers. This is obvious because N = 2 for GxyG, i = 1(x), and j = 2(y) in Eq. 4. For our calculations, we utilized the $\Delta G_{pPII\beta }$ values of corresponding GxG peptides (8, 9, 18, 19). To determine the NNI parameters $\delta G_{pPII\beta }$, $\delta G_{\beta pPII}$, and $\delta G_{\beta \beta }$—indices have been dropped for the interaction parameters in the following—we would have to utilize three independent, experimental pieces of information. Unfortunately, only two experimentally obtained values usable for this purpose are available, namely the molar fraction ratios $R_1={\chi }_{\beta 1}/{\chi }_{\beta 1}$ and $R_2={\chi }_{\beta 2}/{\chi }_{\beta 2}$. As we will demonstrate below, $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ correlate strongly with $\delta G_{\beta \beta }$, which suggests that the former parameters are sufficient for a characterization of the NNIs in the investigated GxyG. Therefore, while keeping $\delta G_{\beta \beta }$ in the general formalism outlined below, we will first set it to zero so that we can calculate $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ by using available R₁ and R₂. In a second step, we will explore how $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ change if $\delta G_{\beta \beta }$ is varied within a reasonable range.

Interactions between residues in turn-like and pPII/β-strand structure are considered only indirectly by allowing the corresponding Gibbs energies $\Delta G_{P2t,i}$ (i = 1,2) of the GxyG residues to differ from those of the corresponding tripeptides. Their values were adjusted to reproduce the total fraction of turn-like structures reported by Toal et al. (13).

To express $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ as functions of R₁ and R₂, we carried out a tedious but straightforward calculation that yielded the following (c.f. Supporting Material):

$$\delta G_{pPII\beta }=RT·\ln \left[\begin{array}{l}{R}_2\left(1+R_1\right)-\left(R_2+1\right)\exp \left\{\left(\mathrm{\Delta }{G}_{pPII\beta ,1}+\mathrm{\Delta }{G}_{pPII\beta ,2}+\delta G_{\beta \beta }\right)/RT\right\}\\ \frac{-R_2\exp \left\{\left(\mathrm{\Delta }{G}_{pPII\beta ,1}+\mathrm{\Delta }{G}_{pPIIt,2}^{\ast }\right)/RT\right\}-\exp \left\{\left(\mathrm{\Delta }{G}_{pPII\beta ,2}+\mathrm{\Delta }{G}_{pPIIt,1}^{\ast }\right)/RT\right\}}{1-R_1{R}_2}\end{array}\right]+\mathrm{\Delta }{G}_{pPII\beta ,2}.$$ (6a)

This can be used in the following equation:

$$\delta G_{\beta pPII}=RT·\ln \left[\begin{array}{l}{R}_1\left(1+\exp \left\{\left(\mathrm{\Delta }{G}_{pPII\beta ,2}+\delta G_{pPII\beta }\right)/RT\right\}+\exp \left\{\mathrm{\Delta }{G}_{pPIIt,2}^{\ast }/RT\right\}\right)\\ -\exp \left\{\left(\mathrm{\Delta }{G}_{pPII\beta ,1}+\mathrm{\Delta }{G}_{pPII\beta ,2}+\delta G_{\beta \beta }\right)/RTT\right\}-\exp \left\{\left(\mathrm{\Delta }{G}_{pPPII\beta ,1}+\mathrm{\Delta }{G}_{pPPIIt,2}^{\ast }/RT\right)\right\}\end{array}\right]+\mathrm{\Delta }{G}_{pPII\beta ,1}.$$ (6b)

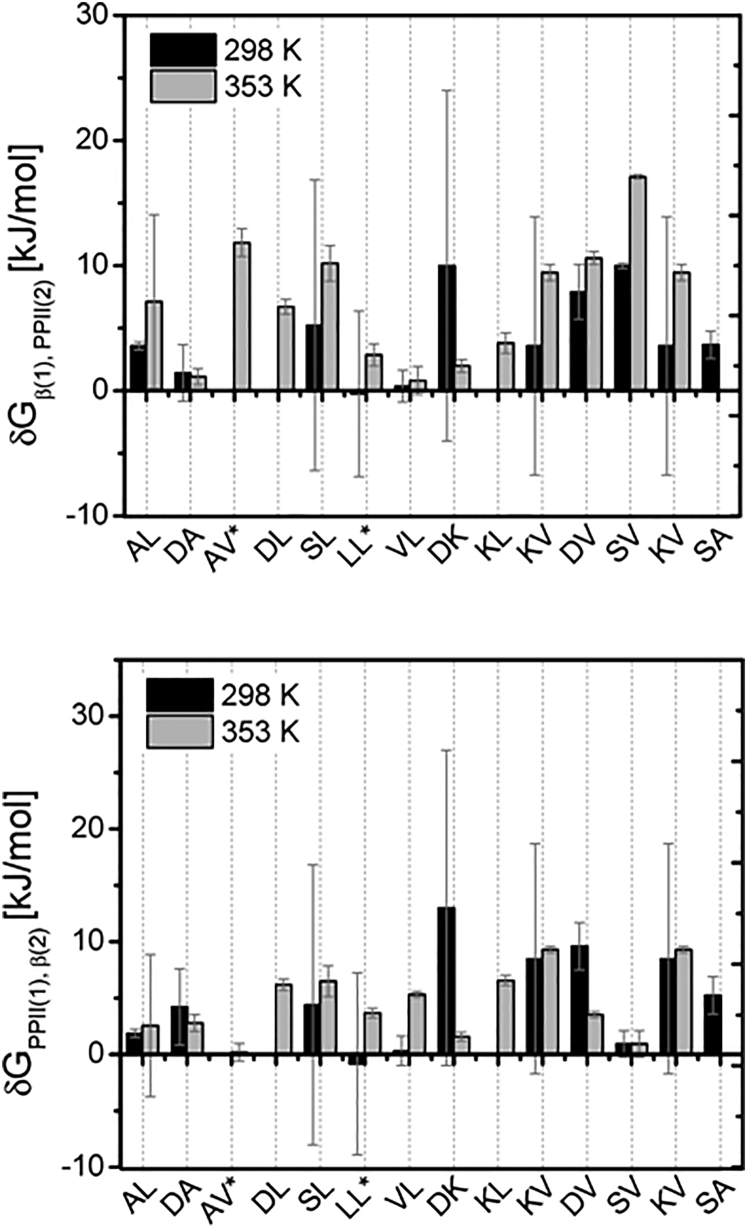
In a first step, we used (6a), (6b), (6a), (6b) a and b with the respective GxG Gibbs energies and the experimental mole fractions R₁ and R₂ of the considered GxyG peptides to calculate $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ for two different temperatures (i.e., 298 and 353 K). $\delta G_{\beta \beta }$ was set to zero. The respective R_i values for the latter temperature were calculated using the $\Delta H_{pPII\beta ,i}$ and $\Delta S_{pPII\beta ,i}$ values of GxyG (13). For 298 K, this procedure yielded real solutions only for 11 of the 14 investigated peptides. Imaginary numbers emerged for GDAG, GAVG, and GSLG. On the contrary, respective calculations for 353 K produced real solutions for all GxyG peptides investigated. Imaginary numbers were caused by negative arguments of the logarithmic functions in (6a), (6b), (6a), (6b). The obtained real and physically meaningful parameter values are listed in Table S1 and plotted in Fig. 3. Since the variation of $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ values among peptides and even with temperature is very large, we wondered about their statistical significance. Therefore, we estimated the statistical errors of R₁ and R₂ based on the uncertainties of corresponding propensity values of the investigated GxyG peptides described in the Supporting Material and used Gaussian error propagation to calculate the corresponding standard deviations of $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ (the utilized algorithm is derived in the Supporting Material). Indeed, some of these statistical errors (Table S1) are very large and sometimes even exceed the values of the obtained thermodynamic parameters. The reason for this error amplification lies in the very steep slope of the respective logarithmic function in the region where the argument is smaller than one.

Figure 3.

Graphic representation of conformation-dependent NNI interaction Gibbs energies $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ obtained from experimental ΔG_pPIIβ values of GxG and corresponding GxyG peptides for the indicated temperatures as described in the text. The error bars are the result of a Gaussian error propagation calculation.

The mostly positive signs of the obtained NNI-Gibbs energies (Fig. 3) indicate that mismatched states of residue pairs with one residue in pPII and the other one in β-strand are stabilized relative to states in which both residues are either in pPII or β-strand. The underlying NNIs are thus anticooperative. A negative sign implies a stabilization of matched residue states (pPII or β-strand) and thus positive cooperativity. The estimated statistical errors are very large for some room temperature parameters (SL, DK, KV). The relative errors of the δG-values obtained for 353 K are generally smaller, with those derived for AL as the sole exception. For a vast majority of tetrapeptides, statistically reliable $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ values strongly suggest an anticooperative character of NNIs.

To explore how the consideration of the thus-far neglected ββ-parameter could actually influence $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$, we recalculated these parameters for $G_{\beta \beta }$, varying between 5 and −5 kJ/mol for GKVG. This peptide was selected for its substantial positive coupling energies and for its importance in our exploration of the influence of NNIs in a disordered peptide containing KV repeat units (vide infra). The results of the calculations carried out for 298 and 353 K are visualized in Fig. S5. In each case, obtaining real solutions required $G_{\beta \beta }$ -values of −1 kJ/mol and larger. Both $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ scale nearly linearly with $G_{\beta \beta }$. This result suggests that if ββ-type interactions exist, the respective interaction energy is likely to be positive, indicating cooperative interactions between neighbors in β-type conformations. However, the concomitant increase of $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$, which are always larger than $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ (Fig. S5), indicates that the overall NNI remains anticooperative so that pPII-β and β-pPII dimers are still stabilized over β-β ones. What the occurrence of positive ββ-interactions would do is a stabilization of β-β over pPII-pPII. One can therefore conclude that the explicit consideration of $G_{\beta \beta }$ does not change the general picture that we obtained with the truncated interaction model.

We were wondering whether the addition of $G_{\beta \beta }$ would yield real solutions for those peptides for which our two-parameter model produced only imaginary numbers. Indeed, we obtained real solutions for GAVG if $G_{\beta \beta }$ exceeded 2 kJ/mol. For GDAG and GSLG, we had to assume negative $G_{\beta \beta }$ -values (−5.0 and −3.0 kJ/mol, respectively). The $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ values obtained thus are listed also in Table S2. Interestingly, with the exception of the $\delta G_{pPII\beta }$ value of GAVG, they are all positive. The results of these calculations thus suggest that for these peptides, the heterodimer (pPII-β and β-pPII) and homodimer interactions (β-β) are both anticooperative.

What are the structural implications of anticooperative interactions between neighboring peptides in pPII and β-strand conformations? To illustrate their significance, Document S1. Supporting Materials and Methods, Figs. S1–S8, and Tables S1 and S2, Document S2. Article plus Supporting Material a displays the mole fractions of all GxyG conformations that we calculated for 353 K by explicitly taking into account the above conformation-specific NNIs. The utilized formalism is detailed in the Supporting Material. Note that xy-sequences with a common residue are grouped together so that one and the same pair appears in different figures. A plot of corresponding statistically reliable room temperature data is shown in Fig. S6 b. To assess the specific impact of NNIs on individual mole fractions, these values have to be compared with corresponding mole fractions derived directly from the $\Delta H_{pPII\beta ,i}$ and $\Delta S_{pPII\beta ,i}$ values of individual residues of GxyG (Fig. S1) (13). These mole fraction values, which are also plotted in Fig. S6 a, would correctly represent conformational sampling if the involved NNIs were conformation independent. Apparently the consideration of conformation-specific NNIs enhances the pPII-β and β-pPII hybrids at the expense of homogeneous pPII-pPII and β-β conformations for a vast majority of the investigated peptides. The exceptions are GVLG and GLLG, for which differences between the mole fractions of hybrids are less pronounced.

One might wonder to what extent our NNI model is consistent with the (linear) correlations inferred from the data in Fig. 1. To address this issue, we calculated the pPII mole fraction of residue x (i = 1) and the corresponding β-strand mole fraction of y (i = 2) as a function of $\Delta G_{P2\beta ,2}$ value for different values of $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$. In each case we obtained linear relationships between the pPII fraction of x and the β-strand fraction of y (Fig. S7 a). The slope of the respective linear plots depends on the choice of the NNI energies: the larger the considered $\delta G$ values, the larger the slope. In a second step, we calculated both propensities as a function of $\Delta G_{P2\beta ,2}$ and varied the $\delta G$ -values stochastically within intervals of different length. Although we still obtained a linear correlation, the data points simulated thus were now scattered (Fig. S7 b). As one would expect, the scattering increases with increasing $\delta G$ variations. Finally, we allowed uncorrelated statistical variations of $\delta G_{pPII\beta }$, $\delta G_{\beta pPII}$, $\delta G_{\beta \beta }$, $\Delta G_{pPIIt,1}$, and $\Delta G_{pPIIt,2}$. Fig. S7 c shows that these lead to much stronger scattering of ${\chi }_{\beta }/{\chi }_{\beta NN}$ values compared with ${\chi }_{pPII}/{\chi }_{\beta NN}$ scattering, which is in agreement with what we observed experimentally (Fig. 1). Thus, our calculations verify the validity of the obtained correlations and explain the observed scattering as reflecting the variability of $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ values.

Predicting the temperature dependence of unfolded peptides

The question arises as to whether insights about NNIs in short model peptides are of relevance for understanding the longer unfolded peptides. To address this issue, we utilized the above transfer matrix algorithm to incorporate the conformation-specific NNIs into the partition sum of longer peptides. In a subsequent step, we calculated the temperature dependence of circular dichroism data of unfolded peptides and compare them with published experimental results. Details of the utilized algorithm are given in the Supporting Material.

To employ our NNI values in a quantitative way, we consider the so-called MAX3 peptide of Pochan et al. It has the following amino acid sequence: (VK)₄V^DPPTKVKT(KV)₂-NH₂. The authors showed that this peptide can fold into a hairpin structure and subsequently self-assemble into a hydrogel at pH 9 and high temperatures. They reported the temperature dependence of the molar ellipticity $\Delta {\epsilon }_{218}$ of this peptide measured at 218 nm; the data were measured before the onset of the aggregation process. The corresponding dichroism values (in M⁻¹ cm⁻¹) taken from (25) are plotted in Fig. 4. The error bars reflect the uncertainty associated with reading the data points from the respective figure in Pochan et al. (25) To reproduce these data with our model, we proceeded as follows. First, we assumed that we could use the thermodynamic parameters of GKVG for all KV pairs in MAX3 (i.e., $\Delta G_{pPII\beta ,V},\Delta G_{pPII\beta ,K},\text{δ}{G}_{pPII\left(V\right)\beta \left(K\right)},\text{δ}{G}_{\beta \left(V\right)pPII\left(K\right)},\Delta G_{pPIIt,V}$, and $\Delta G_{pPIIt,K}$). Owing to the similarity between V and T (21), we used the same parameters for TK pairs. For P, we substituted G_ij by $P_{i+1,i}^{P2}$. Since we were not interested in the details of the actual conformation in terms of dihedral angles, we could treat ^DV like V, thereby keeping in mind that the dominant conformations reside in the lower right quadrant of the Ramachandran plot so that the corresponding dichroism values carry signs that are opposite to those of V. We used (6a), (6b), (6a), (6b) a and b to calculate $\delta G$ values for different temperatures. Subsequently, we used those values for which the calculated uncertainty was less than the values themselves in linear regression fits, the result of which we utilized to calculate statistical weights of sequences and the partition sum (Eqs. S12 and S13). Hence, we defined the partition sum and the mole fractions without using any free parameters. The theoretical $\Delta \epsilon \left(T\right)$ graph was then calculated by using the following expression:

$$\Delta \epsilon \left(T\right)=\frac{\sum _{\{k^{\prime }]}\left(\sum _k\left(n_k\Delta {\epsilon }_k\right)q_N\prod _{j=0}^{N-1}{S}_{j+1j}^{\left\{k^{\prime }\right\}}\right)}{N·Z}$$ (7)

The index k in Eq. S12 labels the residue conformation (k = pPII, β, and t), whereas {k′} represents a sequence of N residues. Hence, the choice for $P_{i+1,i}^{\left\{k^{\text{'}}\right\}}$ depends on the specific conformation of the sequence k’ at the position j. The statistical weight of each conformation is multiplied with the number n_k of residues that adopt the conformation k in the sequence. For $\Delta {\epsilon }_k$, we used the respective $\Delta {\epsilon }_{215}$ values for pPII and β-strand that Toal et al. obtained from their analysis of the circular dichroism (CD) spectra of GKG, GVG, and GTG (21), as well as the earlier reported value for proline and calculated average values for each conformation (26). The very small differences between ellipticities measured at 215 and 218 nm can be neglected for our calculations. Since we do not have reliable information about the respective $\Delta {\epsilon }_t$ values, which could represent our manifold of turn-like structures, we allowed this parameter to vary between 0.1 and −0.2 M⁻¹ cm⁻¹ residue⁻¹ to minimize the difference between simulation and experimental data. This interval was chosen based on the assumption that contributions from mixtures of turn-like structures with different chiralities should not be expected to be substantial at 218 nm (21). Hence, $\Delta {\epsilon }_t$ was the only free parameter used for our calculation. Since the total turn fraction of the peptide can be expected to exhibit only a very weak temperature dependence (21), changing this parameter solely shifts the calculated $\text{ Δ}\epsilon \left(T\right)$ curve without changing its slope. The calculations were carried out with a MATLAB program that utilized Eqs. S12 and S13. It deserves to be mentioned in this context that our model contains a simplification in that we assume that NNIs from the N- and C-terminal neighbor are identical, which implies that we put KV and VK on the same footing. A more sophisticated modeling would require the availability of data for GKVG and GVKG.

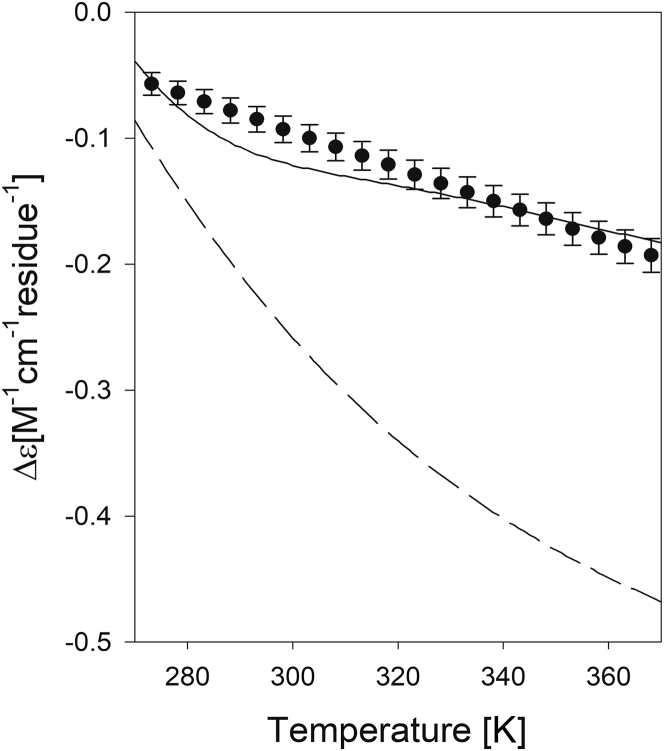
Figure 4.

Experimental and calculated Δε₂₁₈ (solid line) of the MAX3 peptide plotted as a function of temperature. The experimental data were retrieved from Pochan et al. (25). The calculation is described in the text. The dashed line results from a calculation for which the interaction parameters Gibbs energies $\delta G_{pPII\beta }$ and $\delta G_{\beta pPII}$ were set to zero.

The result of the above calculation is shown as a solid line in the upper panel of Fig. 4. In view of some of the employed simplifications and the statistical error associated with the interaction parameters, the agreement between experiment and simulation is impressive. To demonstrate the significance of our result, we also calculated $\Delta \epsilon \left(T\right)$ for a scenario for which we only used the thermodynamic parameters $\Delta H_{pPII\beta }$ and $\Delta S_{pPII\beta }$ reported for GxyG to calculate $\Delta G_{pPII\beta }$ for K and V in MAX3. Again, we assumed the turn fraction to be temperature independent (13). Such a model reflects a scenario in which the conformational propensities of x and y solely depend on the residue type but not on the actual conformation of the respective neighbor. The result of this simulation is shown as a dashed line in Fig. 4. Compared with the experimental data, the temperature dependence of $\Delta \epsilon$ is now clearly overestimated. Hence, this comparison between theory and experiments lends strong support to the notion that the conformational manifold of MAX3 is indeed governed by the anticooperative interactions between K and V residues.

The influence of anticooperativity is illustrated in Fig. S8, which shows the temperature dependence of the mole fractions of pPII, β-strand as well as of pPII-β and pPII-β-pPII-β segments. The formalism for their calculation is given in the Supporting Material. The results of these calculations reveal a very weak temperature dependence of the pPII and β-strand fractions and substantial contributions of segments with alternating pPII and β-strand conformations. Note that the pPII-β-pPII-β-pPII-β and pPII-β fractions are not mutually exclusive: the former actually contains the latter.

It should be mentioned that the computed $\Delta \epsilon \left(T\right)$ values are rather insensitive to changes of the NNI parameters within a range of ±10% of the respective values used for the calculations. The reason for this lies in the magnitude of the interaction parameters even at room temperature, which ensures a preponderance of pPII-β and pPII-β segments even upon the considered variation of the NNI parameters, particularly at high temperatures.

As a second check of the applicability of our NNI model, we analyzed the temperature dependence of the CD spectra of the monomeric Aβ_1–9 fragments reported by Danielsson et al. (27) These authors measured the CD spectra and several ³J(H^HN^α) constants of this peptide as a function of temperature. Fig. 5 depicts the temperature dependence of Δε₂₂₀ and of the ³J(H^HN^α) constants of the residues E3 and H6. It is noteworthy that contrary to the former, the latter does not exhibit a monotonous temperature dependence as was generally observed for short peptides (21). To check whether our theoretical approach could actually describe these experimental data, we used Eq. 7 and the associated formalism to simulate Δε₂₂₀. This simulation had to be based on some simplifying assumptions since we do not have any specific information about the Gibbs energies of NNIs for most of the residue pairs of Aβ_1–9. However, we considered it useful to check whether our NNI model could at least qualitatively account for the rather different temperature dependence of Δε₂₂₀ and ³J(H^HN^α). To this end, we used the respective Gibbs energies reported for GxG peptides $\Delta G_{P2\beta ,i}$ and $\Delta G_{P2t,i}$ and the corresponding Δε_pPII and Δε_β values obtained from their CD spectra (21). The representative dichroism for turn conformations was varied within the above limits employed for the MAX3 simulation. With regard to interaction Gibbs energies, we varied them over a broad range in the positive and negative region by changing the parameters $\delta G_{pPII\left(i\right)\beta \left(i+1\right)}^0$ (and $\delta G_{\beta \left(i\right)pPII\left(i+1\right)}^0$) and $m_{pPII2\left(i\right)\beta \left(i+1\right)}$ ($m_{\beta \left(i\right)pPII\left(i+1\right)}$) of the following linear equations:

$$\delta G_{pPII2\left(i\right)\beta \left(i+1\right)}=\delta G_{pPII\left(i\right)\beta \left(i+1\right)}^0\left(T_0\right)+m_{pPII\left(i\right)\beta \left(i+1\right)}\left(T-T_0\right)$$ (8a)

and

$$\delta G_{\beta \left(i\right)pPII\left(i+1\right)}=\delta G_{\beta \left(i\right)pPII\left(i\right)}^0\left(T_0\right)+m_{\beta \left(i\right)pPII\left(i+1\right)}\left(T-T_0\right),$$ (8b)

where the reference temperature T₀ was set to 278 K (i.e., the lowest temperature for which Danielsson et al. (27) reported experimental data). To simultaneously calculate the J-coupling constants, we utilized the following equation:

$${}^{3}J_j\left(T\right)=\frac{\sum _{\{k^{\prime }]}\left({}^{3}J_j^k{q}_N\prod _{i=j+1}^{N-1}{G}_{i+1i}{P}_{j+1j}^k\prod _{i=0}^{j-1}{G}_{i+1i}\right)}{Z}.$$ (9)

Herein, ³$J_j^k$ is the ³J(H^HN^α) value of the jth residue in the kth conformation. We calculated these values from the earlier reported conformational distributions of GxG peptides (8, 9, 18, 19). This is another simplification, since it does not take into account that, e.g., the pPII and β-strand subdistributions can shift in (ϕ, ψ) space as a consequence of NNIs (17).

Figure 5.

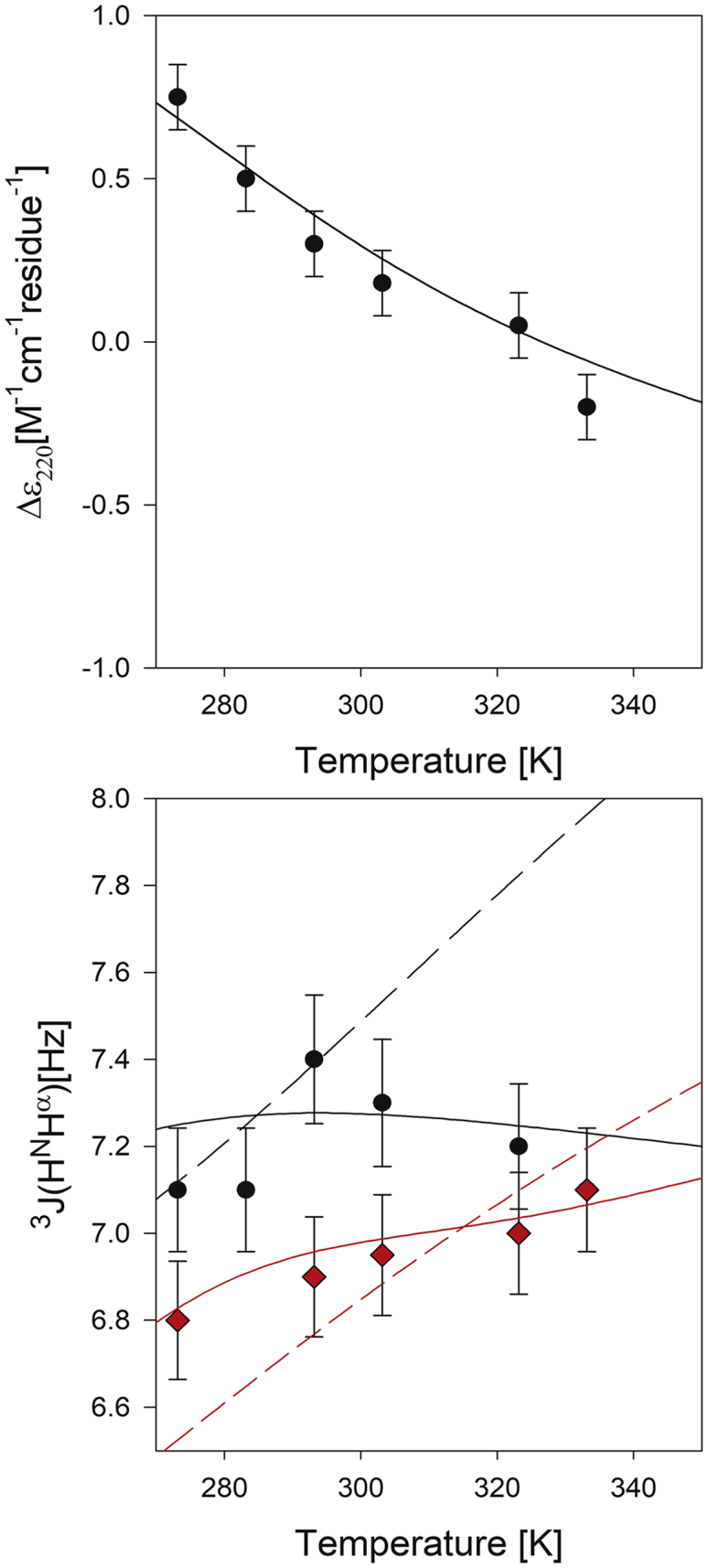
The upper panel gives experimental and calculated Δε₂₂₀ (solid line) of the Aβ_1–9 peptide plotted as a function of temperature. The lower panel gives the experimental and calculated ³J(H^NH^α) (solid lines) values of the E3 (black) and D7 (red) residue. The dashed lines result from a calculation for which the NNI parameters associated with the E3 and D7 residues have been set to zero. The experimental data were retrieved from Danielsson et al. (27) The calculation is described in the text. The solid line results from the calculation with the NNI model described in the text. To see this figure in color, go online.

In a first step, we set the NNI parameters to zero and utilized the $\Delta G_{pPIi\beta ,i}$ and $\Delta G_{pPIit,i}$ values of GxG peptides (21). The simulation yielded Δε₂₃₀(T) values that are significantly more negative (by ∼1 M⁻¹ cm⁻¹ residue⁻¹) and exhibited a more pronounced temperature dependence than the experimental values (data not shown). There could be two explanations for the systematic difference between experiment and simulation: the pPII-fraction could be higher than predicted—which would be consistent with the analysis of Danielsson et al. (27), who attributed a rather high pPII fraction to this peptide—or the Δε_pPII, Δε_β, or Δε_t values of the residues differ from those of the respective GxG peptides. A closer look at the ³J(H^HN^α)-values (vide supra) informed us that they are inconsistent with the former option. In view of the observation that in particular the Δε_pPII value of residues can vary between 0 and 4 M⁻¹ cm⁻¹ residue⁻¹ depending on the nearest neighbor (28, 29), we heuristically increased all Δε_pPII by the same factor to minimize the difference between simulation and experimental data. To account for the reported temperature dependence of Δε₂₃₀ (T), we introduced NNIs and varied the parameters of (8a), (8b) until we observed the result shown in Fig. 5. The same parameters $\delta G_{pPII\left(i\right)\beta \left(i+1\right)}^0=\delta G_{\beta \left(i\right)pPII\left(i+1\right)}^0$ = 1.5 kJ/mol and $m_{pPII\left(i\right)\beta \left(i+1\right)}=m_{\beta \left(i\right)pPII\left(i+1\right)}=0.02kJ/mol·K$ were used for all residues. They therefore have to be considered as representative. Obviously, the resulting NNI-Gibbs energies are positive, thus reflecting anticooperativity.

Next, we calculated the ³J-coupling constants for E3 and D7, using the above parameters for Eq. 9. The values calculated thus were in the range of the experimental data at low temperatures. To minimize the differences between simulation and experimental data, we modified the NNI parameters in Eq. 9 for these two residues. This modification did not impair our simulation of $\Delta {\epsilon }_{230}$ (T). Moreover, we made very slight adjustments of the ³J(H^HN^α)-values for pPII, β-strand, and turn-like structures for E3. These parameter values are all listed in Table S2. As depicted in Fig. 5, the agreement between simulation and experimental data is quite satisfactory. To demonstrate the relevance of NNI coupling, the dashed line in Fig. 5 also depicts the ³J(H^HN^α) plot calculated by setting all NNI energies to zero. The agreement between experiment and simulation is still good at room temperature, but major discrepancies appear at higher temperature.

Comparison with denatured proteins and Intrinsically Disordered Proteins

Finally, we relate the findings of this study to some CD-based investigations of the temperature dependence of denatured proteins on a more qualitative level. Yang et al. (30) measured the far ultraviolet CD spectra of several mutants of the N-terminal 6–85 fragment of the lambda repressor in the presence of 6M GuHCl as a function of temperature. If the denatured proteins were describable as ideal random coils, their ultraviolet CD spectra would be nearly temperature independent. However, the authors observed spectral changes with increasing temperatures that are very similar to those reported for several short peptides, namely a decrease of the negative amplitude below 200 nm and a concomitant increase of negative values above 210 nm (6, 13, 21, 31). The CD spectra exhibit isodichroic points, which are indicative of two-state transition. The authors interpreted their data as reflecting an increasing β-strand population at high temperatures. Of particular interest in the context of the current study is the fact that the observed ellipticity changes at 222 nm are actually rather modest. If converted into changes of molar absorptivity, they lie in the region of changes reported for MAX3 (between 0 and −1.0 M⁻¹ cm⁻¹ residue⁻¹). The corresponding dichroism of the denatured N-terminal domain of UIA (102 residues) varies between 0 and −1.3 M⁻¹ cm⁻¹ residue⁻¹. Among the proteins examined by Yang et al. (30), only phophoglycerate kinase departs from this behavior, in that its CD exhibits changes between ∼−0.6 and −2.5 M⁻¹ cm⁻¹ residue⁻¹. Kjaergaard et al. (32) used CD to investigate the temperature dependence of three intrinsically disordered proteins, namely the activation domain of the thyroid hormone activator and the C-terminal distal tails of the human sodium-proton exchanges 1(hNHE1cdt) and the S-phase delayed protein (Spd1). For all three proteins, they observed spectroscopic changes diagnostic of a changing two-state pPII $\rightleftarrows$ β equilibrium. Changes observed at 220 nm fall again into range between 0 and −1 M⁻¹ cm⁻¹ residue⁻¹, which seems to be indicative of anticooperative interactions between pPII and β-strand conformations.

Conclusions

This study was aimed at exploring whether the earlier-obtained context dependence of conformational propensities of amino acid residues in unfolded peptides result from specific interactions that depend on the conformation of downstream and upstream neighbors. Such conformation-dependent NNIs have been predicted based on computational and bioinformatic studies (2, 11). An analysis of conformational propensities of guest residues in GxyG peptides revealed a positive correlation between pPII and β-fractions of x and y, respectively. The correlation is more pronounced at high temperatures, where the influence of NNIs on conformational properties is larger than at room temperature owing to the closer proximity of the latter to the enthalpy-entropy compensation temperature (13). The results of our correlation analysis prompted us to construct a model that explains the difference between pPII and β-strand propensities of residues in GxG and GxyG solely in terms of interactions in pPII-β and β-pPII pairs. For most of the investigated pairs, the interaction energies are positive, which is in line with the results of our correlation analysis reflecting anticooperativity between pPII and β. To explore whether our findings are of any relevance for longer peptides, we applied our model and the parameters obtained for GKVG to the unfolded MAX3 peptide, which is basically comprised of two segments of KV repeats connected by a turn-forming element (V^DPP). We were thus able to quantitatively reproduce the temperature dependence of CD measured at 222 nm. An analysis of the conformational distribution of this peptide revealed a preference for pPII-β, β-pPII, and even pPII-β-pPII-β pairs, which reflects the rather large anticooperative NNIs between residues in pPII and β conformations. The significance of anticooperative NNIs for unfolded peptides was further corroborated by our analysis of $\mathrm{\Delta }{\epsilon }_{230}\left(T\right)$ and ³J(H^HN^α)(T) data from the Aβ_1–9 fragment.

Although our analysis reveals the occurrence of anticooperative NNIs at both room temperature and the high temperatures generally used for thermal unfolding of proteins, results clearly focus on the predictions for the latter case. For most of the considered peptides, NNIs are found to be weaker at room temperature. One might therefore debate their direct biological relevance. As pointed out by Toal et al. (13), nearest-neighbor-induced changes of propensities affect some residues more than others. Although alanine and protonated aspartic acid exhibit rather significant changes if neighboring glycines are replaced by residues with bulkier side chains, such effects are less pronounced for V and K and even less for L. In the latter cases, NNIs change positions of subdistributions rather than affecting their statistical weight (17). This selective influence on, e.g., A and D is also reflected by the respective $\delta G_{P2\left(i\right)\beta \left(j\right)}$ - and $\delta G_{\beta \left(i\right)P2\left(j\right)}$ -values of these peptides discussed herein (Fig. 2; Table S2; values obtained for nonvanishing $\delta G_{\beta \beta }$ should be taken into account here). The involvement of K also seems to promote anticooperative NNIs. In view of the general abundance of alanine in all proteins and the higher-than-average appearance of K and D in disordered proteins, anticooperative NNIs could well be relevant even at low temperatures depending on sequence (33).

One might wonder about the mechanism that underlies the obtained anticooperative interactions between adjacent residues. At present, a definite answer cannot be given. However, we like to emphasize that several lines of earlier-reported evidence suggest that the intrinsic propensities of amino acid residues are predominantly determined by peptide-solvent and solvent-solvent interactions (21, 34, 35, 36). NNI-induced changes of the enthalpy-entropy compensation for the pPII-β equilibrium in GxyG peptides led us to conclude that these changes are communicated through peptide-solvent interactions as well. This notion is corroborated by theoretical predictions that suggest NNIs caused by the substitution of V for A in a polyalanine chain are produced by the change of backbone solvation (11). Recent density functional theory calculations for trialanine complexed with 22 water molecules by Lanza and Chiacchio (37) have also revealed very strong evidence for the role of peptide hydration in stabilizing pPII. They calculated the internal energies—in this case identical with enthalpies—of the residue pair formed by the central and C-terminal alanine for pPII-pPII, pPII-β, β-pPII, and β-β conformational sequences. The energies were obtained by combining geometry optimizations with single point calculations on a higher level of theory. In addition to the 22 water molecules, the outer hydration shell was considered implicitly with a polarization continuum model. Corresponding entropies were calculated as well. If one takes these energy and entropy values, calculates the corresponding free energies, and uses pPII-pPII rather than β-β as a reference point, one obtains −5.8 kJ/mol for β-pPII, −12.9 kJ/mol for pPII-β, and −31.3 kJ/mol for β-β (note again that in our formalism, negative energies mean destabilization). It is apparent that the total negative free energy of the hybrids (−18.7 kJ/mol) does not add up to the free energy of β-β. This indicates that the hybrids are substantially more stabilized over β-β than one expects for independent noninteracting residues. Thus, the results of Lanza and Chiacchio (37) are very much in line with those of this study. Interestingly, they also showed that this discrepancy between the hybrids and the β-β conformation depends significantly on the number of explicitly considered water molecules. In the gas phase, the free energy differences between all conformations becomes very small.

The anticooperative model that we invoke to explain the context dependence of conformational propensities in unfolded polypeptides is of course reminiscent of the Ising model for a one-dimensional antiferromagnetic system (38). In the absence of an external magnetic field, the two spin orientations in a chain of identical spins on a one-dimensional lattice have the same energy if there is no spin-spin interaction. In the presence of this interaction, the system becomes either ferromagnetic (positive interaction energy) or antiferromagnetic (negative interaction energy). In the case of the latter, the ground state of the system features alternating spins. In the presence of a magnetic field, which favors parallel spins, the system becomes initially more entropic, and the correlation length of opposite spin pairs is reduced. Only in high magnetic fields do all spins overcome the nearest neighbor interactions and line up with the magnetic field. In our case, the Gibbs energy difference between conformational states plays the role of the magnetic field. If pPII and β-strand conformations are isoenergetic, the peptide will constantly switch between pPII-β-pPII-β-pPII-β- and β-pPII-β-pPII-β-pPII- sequences.

The influence of positive NNI energies on the entropy of unfolded peptides and proteins is likely to depend on the intrinsic Gibbs energy differences $\mathrm{\Delta }{G}_{pPII\beta ,i}$ of individual residues. If the differences are small compared with the NNI energies, both the conformational and the combinatorial entropy will be low. With increasing $\mathrm{\Delta }{G}_{pPII\beta ,i}$, the system will certainly become more entropic because more configurations with the same overall pPII/β-strand content become thermodynamically accessible. However, if $\mathrm{\Delta }{G}_{pPII\beta ,i}$ significantly exceeds the NNI energies, the persistence length of either pPII or β-strand (depending on the sign of $\mathrm{\Delta }{G}_{pPII\beta ,i}$) will increase, and the conformational as well as the combinatorial entropy will decrease. In the extreme cases (low or high $\mathrm{\Delta }{G}_{pPII\beta ,i}$), the conformational entropy will be practically additive. In the in-between region, this approximation breaks down, and more elaborate formalism must be applied to calculate the entropy of unfolded peptides and proteins, as demonstrated by Baxa et al. (16).

Author Contributions

R.S.-S. has designed the theory presented in the article and wrote a first draft. The final product is a collaborative effort between S.E.T. and R.S.-S. Both authors produced the final description of the theory. S.E.T. produced most of the figures.

Editor: Monika Fuxreiter.