Tissue-Specific Optical Mapping Models of Swine Atria Informed by Optical Coherence Tomography

Abstract

Computational models and experimental optical mapping of cardiac electrophysiology serve as powerful tools to investigate the underlying mechanisms of arrhythmias. Modeling can also aid the interpretation of optical mapping signals, which may have different characteristics with respect to the underlying electrophysiological signals they represent. However, despite the prevalence of atrial arrhythmias such as atrial fibrillation, models of optical electrical mapping incorporating realistic structure of the atria are lacking. Therefore, we developed image-based models of atrial tissue using structural information extracted from optical coherence tomography (OCT), which can provide volumetric tissue characteristics in high resolution. OCT volumetric data of four swine atrial tissue samples were used to develop models incorporating tissue geometry, tissue-specific myofiber orientation, and ablation lesion regions. We demonstrated the use of these models through electrophysiology and photon scattering simulations. Changes in transmural electrical conduction were observed with the inclusion of OCT-derived, depth-resolved fiber orientation. Additionally, the amplitude of optical mapping signals were not found to correspond with lesion transmurality because of lesion geometry and electrical propagation occurring beyond excitation light penetration. This work established a framework for the development of tissue-specific models of atrial tissue derived from OCT imaging data, which can be useful in future investigations of electrophysiology and optical mapping signals with respect to realistic atrial tissue structure.

Introduction

Atrial fibrillation (AF), the most common cardiac arrhythmia, remains complicated by the complexity of atrial structures and heterogeneity of AF across patient populations (1, 2, 3). Furthermore, the development of techniques for monitoring successful radiofrequency ablation (RFA) therapy, a common treatment for AF that currently has variable success (4), is an active area of research. For these reasons, three-dimensional (3D) imaging of atrial-specific structure, and correlation to function and treatment, is an important challenge. Currently, magnetic resonance imaging (MRI) (5, 6, 7, 8, 9) and computed tomography (10) are often used for the detailed, nondestructive imaging and modeling of the atria. However, limitations remain in terms of resolution for complete characterization of tissue features, particularly in thin atrial regions. Additionally, these modalities may have long acquisition times (9) or the need for exogenous agents for sufficient tissue contrast (10).

Optical coherence tomography (OCT), a fast, nondestructive imaging modality with micrometer resolution and a typical imaging depth of 2–3 mm (11, 12), can be used in conjunction with other imaging techniques to image the atria. OCT has been shown to be able to image important features of cardiac tissue, including myofiber orientation (13, 14, 15, 16), the Purkinje network (17), regions of ablation lesions (18), and varying tissue types within the heart wall (19). Although imaging significant portions of the atria may require a larger field of view than is typical of a single OCT image volume, this can be mitigated by image stitching of multiple OCT volumes (20, 21). To investigate structure-function dynamics with OCT, structural information from OCT has also been used in combination with optical mapping, an experimental technique for investigating cardiac electrophysiology using voltage-sensitive dyes that emit fluorescent light proportional to changes in transmembrane potential (22). In a study by Hucker et al. (23), tissue-specific structure identified by OCT imaging was correlated to multilayer electrical conduction and the location of reentry cores during arrhythmia. Different fiber orientation patterns seen at different depths of the tissue, as imaged by OCT, could be correlated to the electrical activation patterns observed from optical mapping. Additionally, the location of optically mapped reentry cores was associated with tissue regions where shifts in dominant fiber angle distributions were identified at different tissue depths by volumetric OCT imaging. Thus, structural information from OCT has been demonstrated to assist in the interpretation of optical mapping signals.

The correspondence between optical mapping measurements and OCT structural information motivates the development of OCT-informed computational models for optical mapping simulation, which may enable more precise correlations of experimental two-dimensional optical mapping data to 3D imaging data. Owing to scattering of fluorescent light, optical mapping signals can be distorted compared with their corresponding electrical signals, including elongated optical action potential upstrokes and differences in repolarization morphology (24). Interpretation of optical mapping signals may be further complicated by interactions with heterogeneous tissue structure (25, 26). Thus, tissue-specific, computational modeling of optical mapping has been developed to enable a deeper understanding of the influence of structural heterogeneities on the formation of optical mapping signals. Previous modeling studies have investigated the effects of ventricular tissue thickness, fiber orientation, and tissue geometry on optical mapping signals. The influence of varying tissue thickness on optical signal morphology in slab models ranging from 2.5 to 10 mm thickness as well as in models simulating trabeculation of the ventricular endocardium have been previously investigated (27, 28, 29). The effect of ventricular fiber orientation patterns has been analyzed in slab models (24, 27, 30) and cylindrical models (28). Whole rabbit ventricular models, with ventricular anatomy and fiber orientation informed by serial sectioning, have been used to assess the effect of tissue structure on optical signal morphology during pacing, arrhythmia, and defibrillation (25, 31, 32). Additionally, a model of a rabbit ventricular wedge, using high-resolution MRI to inform tissue geometry and histologically informed fiber orientation, has been developed to investigate the effect of tissue structure, specifically vein cavities, on the optical signal (26). To the authors’ knowledge, there are currently no optical mapping models focusing on atrial structure or utilizing the high-resolution 3D structural information that can be offered by OCT.

In this study we present, to our knowledge, the first use of high-resolution OCT volumetric data to develop tissue-specific atrial models. We developed atrial models including tissue-specific fiber orientation extracted from OCT imaging and ablation lesions that utilized OCT to determine the lesion boundaries within the tissue geometry. Four different swine atrial samples were used to demonstrate the incorporation of OCT-derived structural features into optical mapping models. Finite element electrophysiology simulations were combined with Monte Carlo simulations of photon scattering to simulate optical mapping and analyze the effects of tissue structure on the modeled signals.

Methods

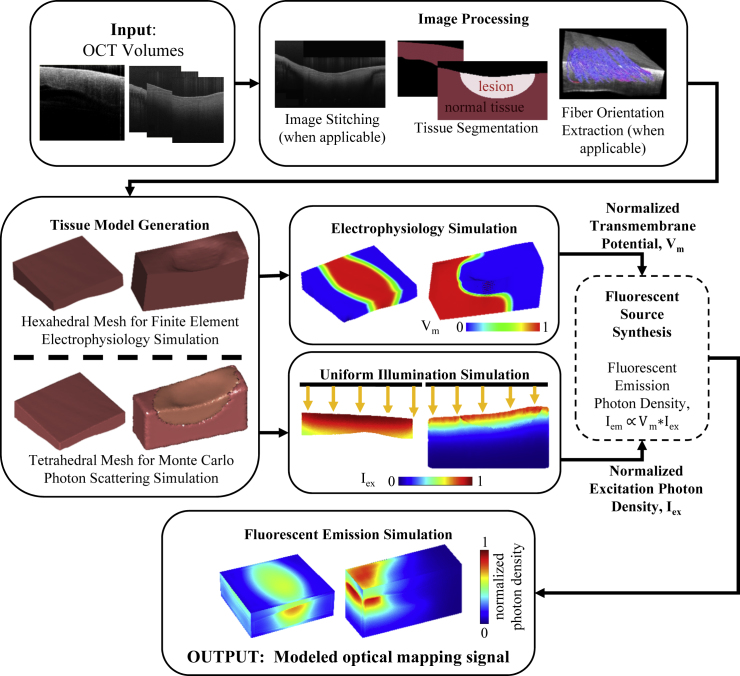
The workflow for simulating optical mapping in OCT-characterized atrial models is depicted in Fig. 1. First, structural features, including fiber orientation and the location of ablation lesions, were extracted from the OCT volumetric data of the tissues and used to develop the tissue-specific models. After construction of the models, electrophysiology and excitation photon scattering were simulated, and the resulting transmembrane potential and excitation photon density data were used to generate the fluorescent sources that produce the optical mapping signal. In the final step, fluorescent light propagation was simulated to produce the optical mapping signal in the atrial tissue models. In this study, four models were developed incorporating the tissue geometry and extracted structural features: 1) a model of left atrial tissue with tissue-specific fiber orientation and tissue geometry as extracted from OCT; 2) a model of left atrial tissue from a larger stitched region, including an area of sharp myofiber orientation change; 3) a model of right atrial tissue with a nontransmural lesion region; and 4) a model of right atrial tissue with a transmural lesion region. For simplicity, these models will be referred to as the 1) left atrium-1 model, 2) left atrium-2 model, 3) the nontransmural lesion model, and 4) the transmural lesion model. The left atrium-1 and left atrium-2 models were developed to investigate the influence of OCT-derived, tissue-specific fiber orientation on the transmural electrophysiological propagation and corresponding optical signal. The lesion models were developed to investigate the behavior of the optical mapping signal within lesions areas.

Figure 1.

Flow diagram for optical mapping modeling of atrial tissue as derived from OCT images. V_m is normalized transmembrane potential, I_ex is normalized excitation photon density, and I_em is fluorescent emission photon density. To see this figure in color, go online.

Imaging of atrial tissue

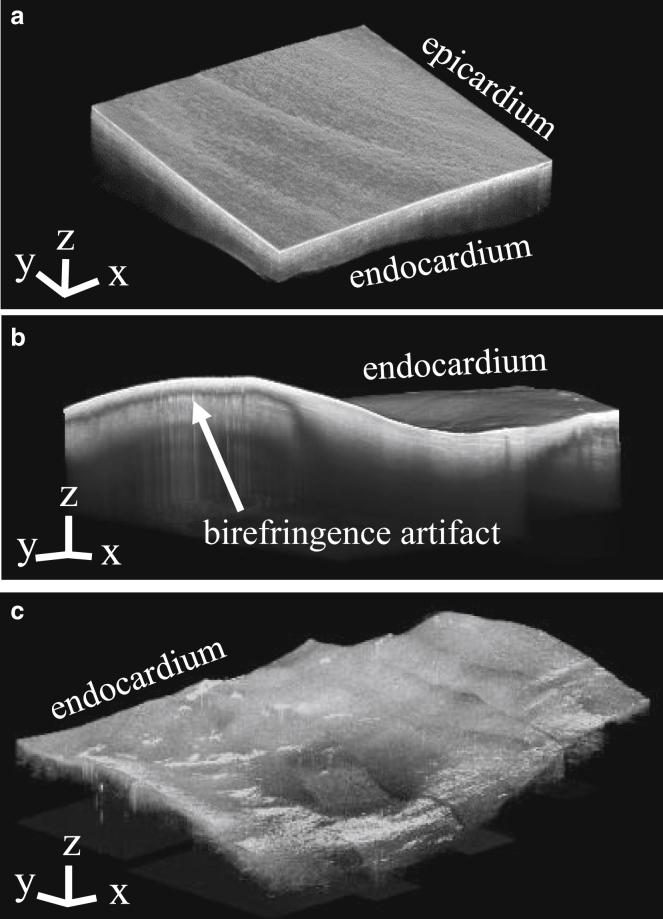
Volumetric OCT image sets were acquired from four swine atrial samples, ex vivo. The atrial tissues had been dissected from healthy swine hearts and laid flat for imaging. The tissue samples for the left atrium-1 and left atrium-2 models were acquired from the left atrium and imaged using the commercial spectral domain OCT system, TELESTO (Thorlabs GmbH, Dachau, Germany). The TELESTO OCT system has a 15 and 6.5 μm lateral and axial resolution in air, respectively, and a 2.51 mm imaging depth. The left atrium-1 data set was acquired from the epicardial side, whereas the left atrium-2 data set was acquired from the endocardial side. For the lesion models, two right atrial tissues were first ablated on the endocardial surfaces using the commercial RFA system, Stockert 70 (Biosense Webster, Irvine, CA). The image sets for the radiofrequency-ablated tissues were then acquired from the endocardial side using a custom-built ultrahigh resolution OCT system, with 5.52 and 2.72 μm lateral and axial resolution in air, respectively, and 1.78 mm imaging depth (33). This OCT system was used for imaging the ablated tissues because the TELESTO system did not capture the birefringence artifact that could be used to detect the ablation lesion in the OCT images, as will be described in further detail in Extraction of Ablation Lesion Region.

Multiple overlapping image volumes were acquired to cover larger regions of tissue for the left atrium-2 and lesion models. When necessary, the overlapping image volumes were histogram matched to equalize the contrast between separate volumes and stitched together manually. Consecutive stitched B-scans were averaged by three to improve the visualization of tissue features. When necessary, stitched image volumes were downsampled by three to reduce the computational load during image processing. Trichrome histology and triphenyltetrazolium chloride staining were carried out on the ablated tissue samples to reveal lesion characteristics beyond the sampling depth of the OCT system. Fig. 2 shows the OCT image volumes used to inform the left atrium-1, nontransmural, and transmural lesion models, displaying the tissue geometry of the data. For the left atrium-2 data, the surface farthest from the OCT lens was not within the OCT system’s imaging depth, and fiber orientation could only be observed within a limited region of myocardium underneath the endocardial surface. Therefore, the tissue geometry was not included in the left atrium-2 model and only an electrophysiological simulation was carried out on the left atrium-2 model.

Figure 2.

OCT imaging of swine atrial tissues. (a) Left atrial tissue OCT image volume for the left atrium-1 model is shown. (b) Right atrial tissue OCT image volume with a nontransmural lesion for the nontransmural lesion model is shown. (c) Right atrial tissue OCT image volume with a transmural lesion for the transmural lesion model is shown. The axes and scale bars indicate 0.5 mm.

Extraction of atrial tissue structure

Image processing to extract the fiber orientation, tissue geometry, and lesion location from the OCT volumetric data was implemented in MATLAB (The MathWorks, Natick, MA). Full details of the fiber orientation extraction algorithm can be found in the paper by Gan et al. (15) but will be briefly described here. Fiber orientation in three dimensions was extracted from fresh tissue samples without optical clearing. We used an automated algorithm that first detected the fiber angles in the en face plane and then projected them to 3D form based on the detected tissue surface orientation. Identification of the fiber angles in the en face images was carried out by determining the dominant gradient within small subregions spanning each en face image. Afterwards, the tissue surface was detected from the OCT B-scans, and for each voxel, the en face fiber angle was projected onto a plane parallel to the tissue surface. The fiber orientation data was median filtered by a 3 × 3 kernel to smooth the angles before fitting to the models. The extraction of the tissue geometry as well as ablation lesion regions for the ablated samples is described in further detail below.

Extraction of tissue geometry

The surfaces of the cardiac tissues were detected semiautomatically from the OCT B-scans to extract the tissue geometry. Surface detection consisted of image smoothing to reduce the effect of speckle noise and then detection of the maximal gradient magnitude in the axial direction. Filtering parameters were tuned manually between data sets or different tissue regions because of varying image quality caused by saturation artifacts, distance of the varying tissue topology from the imaging surface, use of different imaging systems, or image-stitching artifacts. The steps are summarized below, with further detail on the image processing parameters and extent of manual corrections provided in the Supporting Material. For the left atrium-1 and left atrium-2 data set, the upper surfaces of the tissues were detected by first applying a median filter to reduce speckle noise, then computing and detecting the maximum of the gradient magnitude in the axial direction. The endocardium in the left atrium-1 data set, because of being located further from the image focus, was additionally processed with histogram equalization to enhance contrast along with an additional series of median filtering and morphological opening and closing to extract the less visible lower tissue boundary. The lower boundary of the left atrium-2 data set was not visible within the OCT system’s imaging depth. For detection of the endocardial surface in the ablated tissue data sets, median filtering was applied to reduce speckle noise along with morphological opening with a rectangular structuring element to reduce the effect of vertical streak-like artifacts. The image gradient magnitude was then computed and thresholded to detect the tissue surface. For the ablated tissue data, the tissue surface farthest from the OCT lens was outside of the OCT system’s imaging depth. Therefore, a flat bottom surface for the ablated tissue data was assumed. The maximal thicknesses of the ablated tissues were approximated from histology or white light images of the gross specimen cross section.

Extraction of ablation lesion region

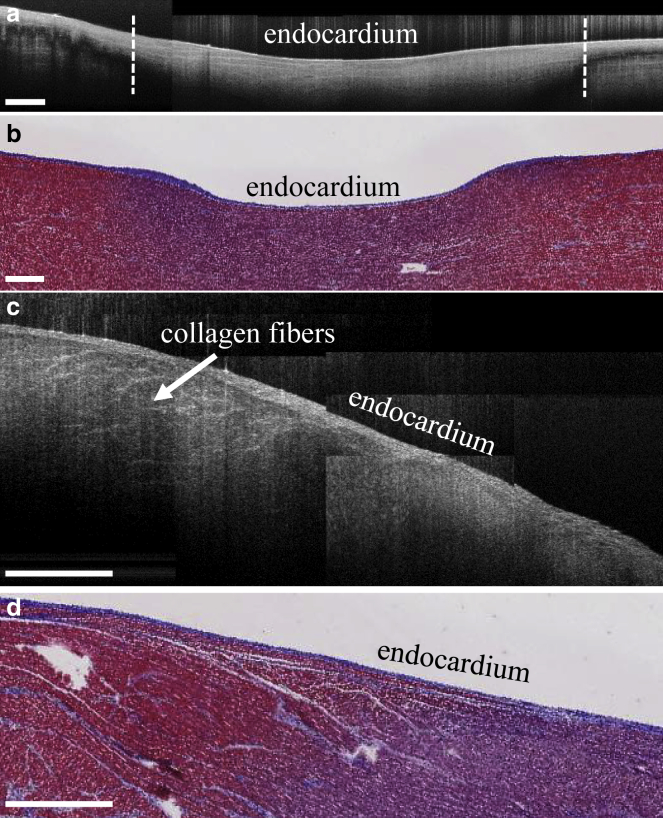
The boundaries of the ablation lesions were identified by the appearance of the birefringence artifact as well as by changes in the tissue features as visualized by OCT. The birefringence artifact appears as a dark band underneath the tissue surface in OCT images of unablated tissue but is not present in ablated tissue (18, 34, 35), as seen in Fig. 3, a and b. By detecting the presence or absence of this artifact within each B-scan, the lateral positions of the lesion boundaries could be identified. A method based on that described in (18) was used. The image processing steps are described in further detail within the Supporting Material. In the OCT image volume of the transmural lesion, the birefringence artifact could not be seen in this particular data set. In this case, the decreased contrast between the endocardium and myocardium as well as the disappearance of collagen fibers within the lesion was used as a marker for the boundary of the lesion, as shown in Fig. 3, c and d. The lesion boundary was segmented manually through visual inspection. Since the depth of the lesions could not be extracted from the OCT images, the maximal depth of the lesions was approximated from histology and triphenyltetrazolium chloride staining. Afterwards, elliptical curves were fit to the lesion location data to approximate the lesion contours in depth.

Figure 3.

Visualization of ablation lesions in OCT. (a) Representative stitched B-scan from ablated right atrial tissue with birefringence artifact is shown. Dotted white lines indicate the boundaries of the lesion as detected by the falloff of the birefringence artifact. (b) Corresponding trichrome histology of ablated right atrial tissue is shown. Purple indicates necrotic tissue, whereas red indicates healthy tissue. (c) Representative stitched B-scan from ablated right atrial tissue is shown, in which the ablation lesion can be observed by the loss of collagen fiber structure and decreased contrast between the myocardial and endocardial layers. (d) Corresponding trichrome histology is shown. The scale bars indicate 0.5 mm. To see this figure in color, go online.

Electrophysiology simulation

With the tissue geometry, fiber orientation, and RFA lesion location extracted from the images, the atrial structural data were used to generate finite element models of the tissues for electrical propagation and light scattering simulations. The multiscale modeling finite element package Continuity 6 (36), distributed by the National Biomedical Computation Resource, was used to carry out the electrophysiology simulations. The validation of the Continuity 6 software for electrophysiological simulations has been described in a previous study (36).

Mesh generation for electrophysiology simulation

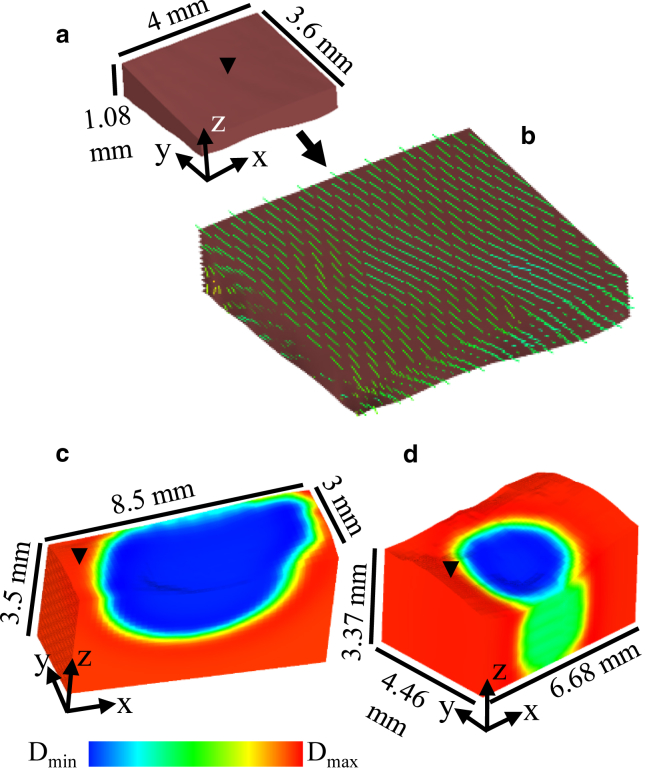
For the left atrium-1 and lesion models, 3D hexahedral finite element models corresponding to the tissue geometry were generated from the OCT-derived structural data as seen in Fig. 4. The spatial discretization for all models was Δx = Δy = 0.1 and Δz ≤ 0.1 mm. For the left atrium-1 model, the fiber orientation was fitted to the model using the fitting module within Continuity 6, which uses a least-squares fitting approach. For the lesion models, conduction was assumed to be isotropic as the fiber orientation could not be extracted throughout the tissue, limited by imaging depth or interference from the birefringence artifact. For the lesion models, the location of the lesions was also fitted to the geometric model via the fitting module in Continuity 6.

Figure 4.

Finite element, hexahedral models for electrophysiological simulation, generated from OCT data of atrial tissues. (a) Shown is the left atrium-1 model, which is shown enlarged in (b) to show fitted fiber orientation superimposed on the model. (c) Nontransmural lesion model is shown. (d) Transmural lesion model is shown. For the lesion models, the fitted ablation lesion region is shown by a color map of assigned diffusivity (D) parameters. Black arrows on the models indicate location of stimulus. To see this figure in color, go online.

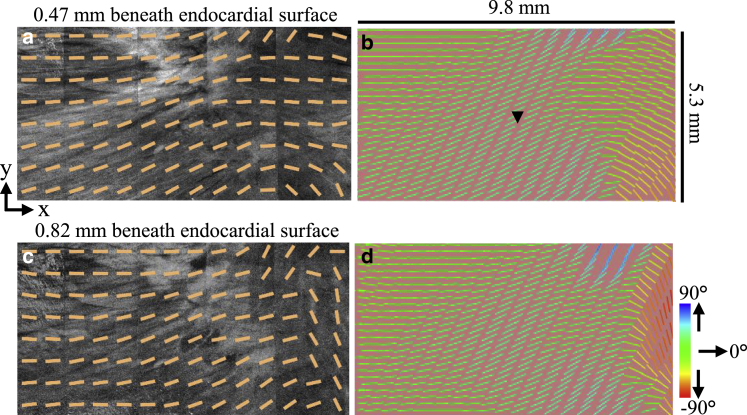
For the left atrium-2 model, a slab tissue geometry with uniform thickness was assumed but incorporated the fiber orientation data within a 9.8 × 5.3 × 0.35 mm volume of myocardium. This volume of myocardium was extracted from the image volume starting 0.47 mm underneath the endocardial tissue surface to ensure extraction of information from the myocardium and not the endocardium. Representative images of the extracted fiber orientation data from OCT and the fiber orientation fitted to the model are shown in Fig. 5. Because of the simplistic geometry used, interpolation of the fiber data to the nodal locations of the model was deemed sufficient to fit the fiber angles to the model.

Figure 5.

Left atrium-2 slab model incorporating fitted fiber orientation as extracted from a 9.8 × 5.3 × 0.35 mm volume of myocardium imaged by OCT. En face OCT images with superimposed, extracted fiber angles at depths of (a) 0.47 mm and (c) 0.82 mm from the tissue surface are shown. Corresponding fiber fields from (a) and (c) are shown fitted to the model in (b) and (d), respectively. Black arrow indicates location of stimulus. To see this figure in color, go online.

To investigate the influence of detailed OCT-derived fiber orientation, two simplified variants of the left atrium-1 and left atrium-2 models were developed with less fiber complexity. First, the left atrium-1 and left atrium-2 models were developed without depth-resolved changes in fiber orientation, hereafter called transmurally uniform fiber orientation. For these models, the fiber orientation in the uppermost layer of elements on the model’s stimulated surface was assigned to all layers underneath, thus retaining the spatial fiber orientation heterogeneity in the lateral dimensions but creating homogeneous fiber orientation transmurally. Second, the left atrium-1 and left atrium-2 models were simplified to a uniform fiber orientation. To generate uniform fiber orientation, all fiber angles were aligned to the y axis in the left atrium-1 model and to the x axis in the left atrium-2 model. This was based on which axis was closer to the dominant fiber orientation direction within each model. Additionally, to investigate the effect of tissue geometry on the electrical and optical signals, a uniform thickness model was developed with the same lateral dimensions as the left atrium-1 model and with a uniform thickness equal to the average thickness of the left atrium-1 model.

Electrophysiology model and simulation parameters

The Fenton Karma ionic model with atrial parameters (37, 38) was used with the monodomain model for all electrophysiology simulations. For the left atrium-1 and left atrium-2 models—including their variants—anisotropic diffusivity was assigned such that the ratio of the longitudinal to the transverse conduction velocity was ∼1.8, based on previous literature (39, 40). For the ablated tissue models, isotropic conduction was assigned. The longitudinal conduction velocity was adjusted to 0.75 m/s (41), with diffusivity set to 0.1331 mm²/ms. The transverse conduction velocity was adjusted to 0.42 m/s, with diffusivity set to 0.0411 mm²/ms. For isotropic conduction, a conduction velocity of 0.75 m/s was used. For the ablated tissue regions, the diffusivity and Fenton Karma ionic model excitability parameter, g_fi, were reduced to a minimum of ∼0.1% in the lesion region to induce the nonconducting property of the lesion. For all electrophysiology simulations, point stimulation was applied on the upper surfaces of the models. The location of stimulus is shown on the models in Figs. 4 and 5.

Light scattering simulation

The transmembrane potential data from the electrophysiology simulations are coupled with simulated excitation photon density data and then used as input to a fluorescent light scattering simulation to model the optical mapping signals. The Tetrahedron-Based Inhomogeneous Monte Carlo Optical Simulator (TIM-OS) (42), which has been validated (43) and utilized for optical mapping models in previous studies (26), was used to compute light scattering in tetrahedral meshes corresponding to the tissue or rectangular geometry.

Mesh generation for light scattering simulation

A tetrahedral mesh must be input to TIM-OS for the Monte Carlo simulation of photon scattering. Therefore, tetrahedral meshes were generated from the tissue segmentation images with iso2mesh (44) and corresponded to the same tissue geometry as the hexahedral models. The tetrahedral meshes are shown in Fig. S1. The tissue meshes were modeled to be surrounded by a rectangular region of perfusate as shown in Fig. S1 d. The optical parameters of the perfusate were set such that the light was not absorbed within the perfusate region and was only scattered forward in a straight line, with the anisotropy coefficient g = 1, as has been done in previous optical mapping models using TIM-OS (26). The refractive index of atrial tissue was set to 1.4, or 1.46 if within the ablation lesion region to approximate structural changes such as increased collagen content (45, 46). The refractive index of the perfusate region was set to 1.3. The models also included a region of air surrounding the perfusate that had a refractive index of 1. The mean element edge lengths for the left atrium and uniform thickness models were ∼0.06 mm, whereas the mean element edge lengths for the nontransmural and transmural lesion models were ∼0.09 and 0.07 mm, respectively.

Simulation of tissue illumination

During optical mapping, the tissue is first illuminated to excite the fluorescent dye. To simulate the illumination process, a uniform beam of collimated light was propagated from the flat upper surface of the perfusate layer to the upper surface of the tissue within each model. The area of the illumination beam covered the entire tissue upper surface for each model. The resulting photon density within the tetrahedral elements represented the illumination intensity within the tissue. The excitation wavelength, 488 nm, was chosen to match the wavelength of light used to excite the commonly used voltage-sensitive fluorescent dye, Di-4-ANEPPS (Thermo Fisher Scientific, Waltham, MA). The optical parameters (absorption coefficient μ_a, scattering coefficient μ_s, and anisotropy coefficient g) used in the models for 488 nm are shown in Table 1. An approximation of the optical parameters of ablated and unablated tissue was obtained experimentally by diffuse reflectance measurements of swine atrial tissue samples and an inverse Monte Carlo procedure as described in (47). To investigate the change in excitation photon density distribution caused by the lesion optical properties, an illumination simulation was also run for the nontransmural lesion model with the entirety of the model having the optical parameters of unablated tissue only.

Table 1.

Optical Properties of Swine Tissue Models at Excitation Wavelength 488 nm

Tissue Type	μa (mm−1)	μs (mm−1)	g
Myocardium	0.62	17.2	0.95
Ablation lesion	0.68	19.2	0.95

Simulation of fluorescence emission

After illumination, the fluorescence of the voltage-sensitive dye must be simulated to synthesize the optical mapping signal. The intensity of fluorescent emission is proportional to the amount of excitation light and the change in transmembrane potential. To simulate the fluorescence emissions, photons were emitted in an isotropic fashion from each tetrahedron in the mesh. The photon density of emission from each tetrahedron was calculated by scaling a maximal photon density by the normalized excitation photon density and normalized transmembrane potential within that tetrahedron. The emission wavelength, 669 nm, was chosen to match the wavelength of light commonly measured with the voltage-sensitive fluorescent dye, Di-4-ANEPPS. The optical parameters used in the models for 669 nm are shown in Table 2 and were obtained with the same method used to obtain the optical properties at the excitation wavelength.

Table 2.

Optical Properties of Swine Tissue Models at Emission Wavelength 669 nm

Tissue Type	μa (mm−1)	μs (mm−1)	g
Myocardium	0.075	13.6	0.95
Ablation lesion	0.104	16.2	0.95

Data analysis and computational resources

Activation time, transmural activation time, action potential upstroke duration, and fractional level of maximum upstroke velocity were computed to quantify the simulated electrical and optical action potentials. Activation time was computed as the time of the upstroke’s maximal derivative (48). Total activation time was defined as the latest activation time. Transmural activation time was defined as the difference between the activation times on the stimulated surface of the model from the activation times on the opposing surface of the model. Specifically, the transmural activation time at a particular x-y coordinate was computed by subtracting the activation time at the x-y point on the stimulated surface of the model from the activation time at the point on the opposite surface of the model with the same x-y coordinates. Action potential duration was calculated as the time between 10 and 90% depolarization. The action potential upstroke duration is reported as mean (±1 SD). The fractional level of maximum optical upstroke velocity, V_f^∗, is a parameter that has been established in past optical mapping studies (28, 30) in which it was used to describe changes in optical upstroke morphology with respect to direction of electrical propagation. The parameter quantifies the time of the maximum upstroke velocity and ranges from 0 to 1. A higher value of V_f^∗ indicates the location of the maximum upstroke velocity is near the apex of the upstroke, whereas a lower value indicates the maximum upstroke velocity is near the foot of the upstroke (28, 30). V_f^∗ was detected within the 10 to 90% depolarization interval. To compute the derivatives of the upstroke, the upstrokes were first interpolated with piecewise cubic polynomials to a discretization of ∼6.5 μs before a first order, one-sided finite difference method was applied. Simulations were run on Columbia University’s Yeti Shared High Performance Computing Cluster and the Rocce cluster from the National Biomedical Computation Resource.

Results

Electrophysiology results

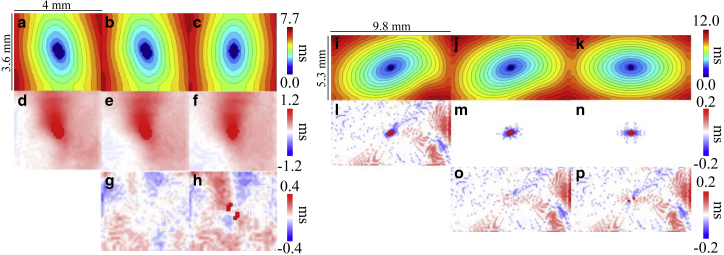
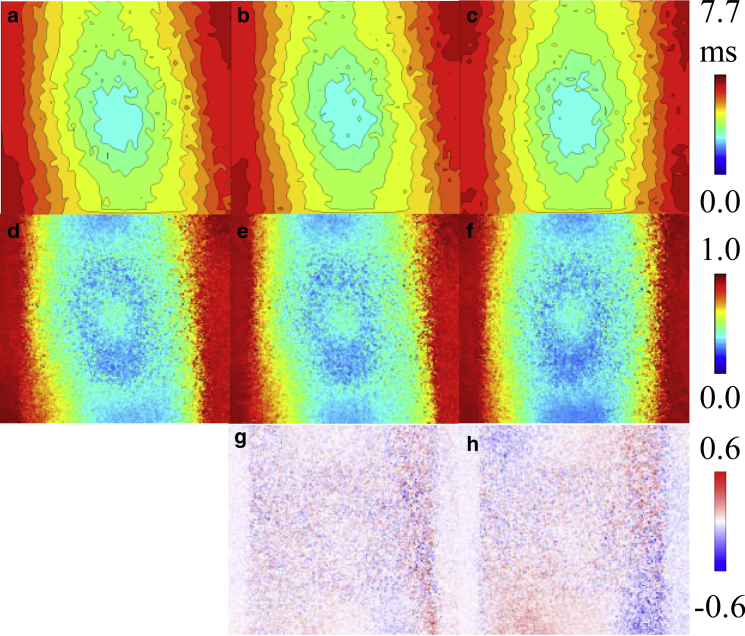
Electrical activation maps, transmural electrical activation maps, and differences between transmural electrical activation maps for the left atrium-1 and left atrium-2 models are given in Fig. 6. The difference in surface electrical activation pattern with tissue-specific fiber orientation compared to activation with uniform fiber orientation is apparent when comparing Fig. 6, a and c, and Fig. 6, i and k. As expected, the surface activation between the tissue-specific and transmurally uniform fiber orientation models were nearly identical, as seen in Fig. 6, a, b, i, and j. Total activation time tended to increase with increasing complexity of fiber orientation. The left atrium-1 model had a total activation time of 7.7 ms with tissue-specific fitted fiber orientation, 7.6 ms with transmurally uniform fiber orientation, and 7.3 ms with uniform fiber orientation. For the left atrium-2 model, the total activation time of the model with tissue-specific fitted fiber orientation and transmurally uniform fiber orientation were the same, with a total activation time of 12.0 ms. The total activation time of the left atrium-2 model with uniform fiber orientation was 11.2 ms. For the left atrium-1 model, subtle differences can be observed between the transmural activation maps of the model’s variants, as shown in Fig. 6, d–f. To more clearly show these differences, Fig. 6, g and h show the transmural activation times of the simplified fiber models subtracted from the transmural activation times of the tissue-specific fiber model, showing differences up to ∼0.4 ms. For the left atrium-2 model, the transmural activation times were low because of the thinness of the mesh. However, the tissue-specific fiber orientation induced nonzero transmural activation time up to ∼0.2 ms, as seen in Fig. 6 l, whereas the transmurally uniform and uniform fiber orientation models had zero transmural activation time throughout the majority of the model, as shown in Fig. 6, m and n. Accordingly, the difference maps of Fig. 6, o and p closely resemble the transmural activation time map from the fully fitted left atrium-2 model of Fig. 6 l.

Figure 6.

Electrical activation maps, transmural electrical activation maps, and differences between transmural electrical activation maps for the left atrium-1 model, left atrium-2 model, and their variants. Isochronal activation maps of the stimulated surface for left atrium-1 model with (a) tissue-specific fitted fiber orientation, (b) transmurally uniform fiber orientation, and (c) uniform fiber orientation are shown. Black isolines indicate 0.5 ms intervals. Transmural activation maps for the left atrium-1 model with (d) tissue-specific fitted fiber orientation, (e) transmurally uniform fiber orientation, and (f) uniform fiber orientation are shown. Shown is the difference in transmural activation times between the left atrium-1 model with tissue-specific fiber orientation and (g) transmurally uniform fiber orientation and (h) uniform fiber orientation. Isochronal activation maps of the stimulated surface for left atrium-2 model with (i) tissue-specific fitted fiber orientation, (j) transmurally uniform fiber orientation, and (k) uniform fiber orientation are shown. Black isolines indicate 0.5 ms intervals. Transmural activation maps for the left atrium-2 model with (l) tissue-specific fitted fiber orientation, (m) transmurally uniform fiber orientation, and (n) uniform fiber orientation are shown. Shown is the difference in transmural activation time between the left atrium-2 model with tissue-specific fiber orientation and with (o) transmurally uniform fiber orientation and (p) uniform fiber orientation. To see this figure in color, go online.

Illumination results

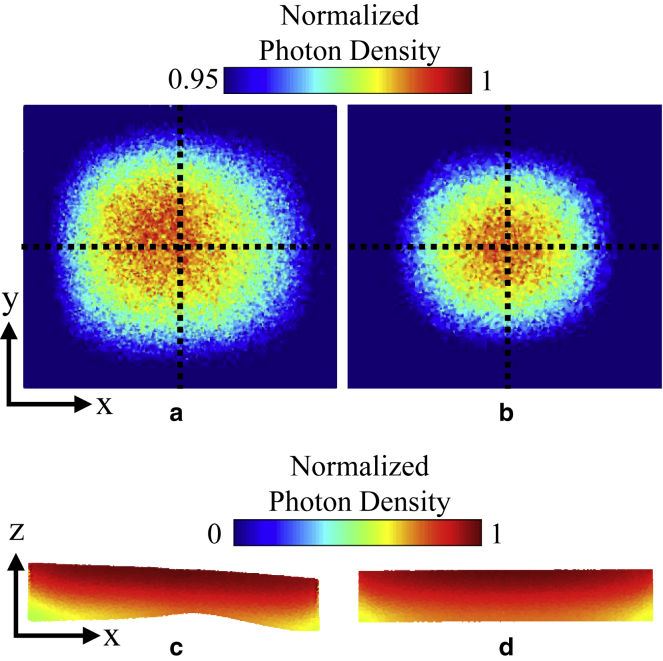
The distribution of excitation photon density was slightly different between the left atrium-1 model containing tissue geometry and the uniform thickness model. In the epicardial distributions of excitation photon density as shown in Fig. 7, a and b, the photon density distribution in the tissue-specific model was greater toward the left region of the model, whereas it was more symmetric in the uniform thickness model. In transmural cross sections, the illuminating light was not fully attenuated through the thin tissues upon reaching the endocardial surface of the pictured cross sections, as illustrated in Fig. 7, c and d.

Figure 7.

Excitation photon density on the left atrium-1 model and uniform thickness model. The photon density is normalized with respect to the maximum density in each model, exempting values on the lateral boundaries of the models due to boundary effects. (a) Epicardial map and (c) cross-sectional view at y = 1.8 mm on the left atrium-1 model are shown. (b) Epicardial map and (d) cross-sectional view at y = 1.8 mm on the uniform thickness model are shown. The epicardial map color values are shown starting from 95% of the maximum photon density to enhance the contrast of the surface photon density distribution. Cross-hairs on the epicardial maps depict the center of the surface. To see this figure in color, go online.

For the nontransmural lesion model, the excitation photon scattering was simulated with and without the lesion region to determine the effect of the lesion optical properties on the penetration of excitation light. The difference between the excitation photon density within the model with and without the lesion, scaled to the maximal excitation photon density in the model without the lesion, is shown in Fig. 8. The inclusion of the lesion region, which had increased scattering and absorption compared to unablated tissue, caused a slight increase in the excitation photon density close to the ablated tissue surface and a decrease throughout the rest of the lesion area.

Figure 8.

Cross-sectional view of the difference between the excitation photon density in the nontransmural lesion model with and without the lesion region included is shown at y = 1.5 mm. The difference is scaled to the maximal excitation photon density in the model without the lesion. To see this figure in color, go online.

Fluorescent emission results

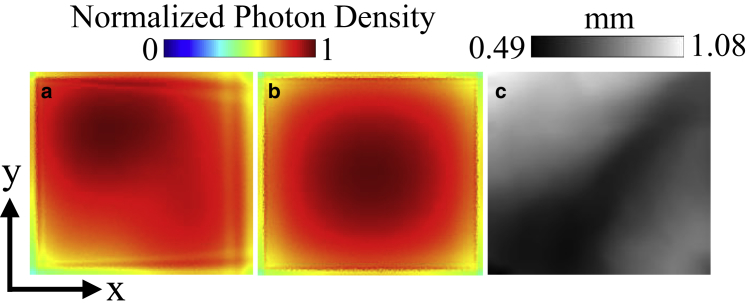
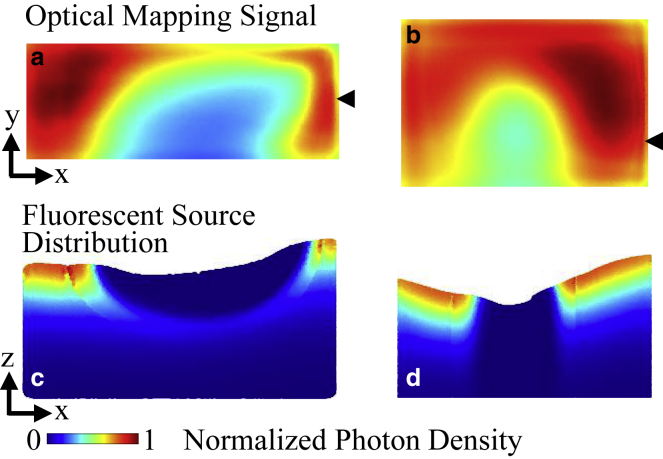
As in the illumination simulation, the optical mapping signal amplitude between the tissue-specific left atrium-1 model and the uniform thickness model had different distributions, reflecting the influence of the thin tissue geometry. The epicardial maps of the optical mapping signals in Fig. 9, a and b show the asymmetric distribution within the tissue-specific model in contrast to the uniform thickness model. In comparison to the tissue thickness map shown in Fig. 9 c, the signal amplitude in the tissue-specific model was generally lower within approximate regions of thinner tissue and higher around thicker regions.

Figure 9.

Tissue thickness and optical mapping signal distribution for the left atrium-1 model and uniform thickness model. (a) Epicardial distribution of the optical mapping signal in the left atrium-1 model at t = 9 ms is shown. (b) Epicardial distribution of the optical mapping signal in the uniform thickness model at t = 9 ms is shown. (c) Tissue thickness of the left atrium-1 model. The photon density is normalized to the maximum photon density on the top surface of the model. To see this figure in color, go online.

Optical activation time maps and distributions of the fractional level of maximal upstroke velocity V_f^∗ for the left atrium-1 model are shown in Fig. 10. The trends of optical activation time seen in Fig. 10, a–c correspond to that of the electrical activation times shown in Fig. 6, a–c. The fractional level of maximal upstroke velocity is a parameter that has been used in previous studies to characterize the correlation between the optical upstroke morphology and the angle of propagation of the subsurface electrical wave front with respect to the tissue surface (28, 30). In agreement with past studies, the values of V_f^∗ increased from the point of stimulation. The pattern of V_f^∗ followed the surface activation pattern from the electrophysiological simulation. Differences in V_f^∗ up to ∼60% were observed between the V_f^∗ maps of the tissue-specific fitted fiber model when compared to the V_f^∗ maps of the transmurally uniform fiber model or uniform fiber model. These differences were especially apparent at the areas where the propagation of the electrical wave front transitioned from moving away from the stimulated surface to an angle moving toward the stimulated surface. Differences were minimal at regions where V_f^∗ had reached a maximum. Comparing Fig. 10, g and h to Fig. 6, g and h, the correlation of the differences in V_f^∗ between the different fiber distributions to the differences in transmural activation times was not apparent.

Figure 10.

Optical activation and V_f^∗ maps for the left atrium-1 model and its variants. Isochronal optical activation maps of the stimulated surface for (a) tissue-specific fitted fiber model, (b) transmurally uniform fiber model, and (c) uniform fiber model are shown. Black isolines indicate 0.5 ms intervals. V_f^∗ maps for (d) tissue-specific fitted fiber model, (e) transmurally uniform fiber model, and (f) uniform fiber model are shown. Difference in V_f^∗ between tissue-specific fitted fiber model and (g) transmurally uniform fiber model and (h) uniform fiber model is shown. To see this figure in color, go online.

For the lesion models, the blurring of optical signals into regions that were electrically inactivated could be observed. As seen within the optical mapping signal snapshots shown in Fig. 11, a and b, the minimal normalized optical mapping signal amplitude was higher within the transmural lesion. To better understand the relative contribution of fluorescent signal throughout the tissue, Fig. 11, c and d show the density of emitted fluorescent photons for the same time points as the optical mapping snapshots in a transmural cross section of the tissue. The density of emitted photons is weighted by the distribution of excitation photon density and transmembrane potential, and the absence of emitted photons within the electrically inactivated lesion area can be seen by the darkened regions near the upper tissue surface. The density of emitted photons can also be seen to decrease with depth because of the decay of excitation intensity. As seen in Fig. 11 c, electrical propagation occurring underneath the nontransmural lesion did not contribute heavily to the fluorescent signal because of the low intensity of illumination at that depth.

Figure 11.

Optical mapping results in the lesion models. (a) Endocardial map of optical mapping signal distribution and (c) transmural cross section of emitted fluorescent photon density distribution at y = 1.5 mm and t = 23 ms in the nontransmural lesion model is shown. (b) Endocardial map of optical mapping signal distribution and (d) transmural cross section of emitted fluorescent photon density distribution at y = 1.2 mm and t = 21 ms in the transmural lesion model is shown. The optical mapping signal photon density is normalized to the maximal photon density on the top surfaces of the models. The emitted fluorescent photon density distribution is normalized to the maximal photon density within the cross section. Black arrows indicate the location of the transmural cross sections along the y axis. To see this figure in color, go online.

Optical upstroke prolongation was observed. For the left atrium-1 model, the electrical upstroke duration was 1.1 (±0.3) ms, whereas the optical upstroke duration was 3.1 (±0.3) ms. Upstroke duration was not computed for the lesion models because of complications with differentiating electrically activated from inactivated regions.

Discussion

To the authors’ knowledge, this study demonstrated the first OCT-derived atrial tissue models for electrophysiology and optical mapping simulations. Four different models were developed containing tissue structural characteristics extracted from OCT imaging, including tissue geometry, fiber orientation, and ablated tissue location. The effects of the incorporated tissue structure on the simulated electrical and optical signals were analyzed. Our objective for developing tissue-specific atrial models is to facilitate deeper investigation of the relationship between atrial electrophysiological function and detailed tissue-specific structure to improve the understanding and treatment of atrial fibrillation.

OCT offers depth-resolved, micrometer-scale information on fiber orientation, which can be useful when considering transmural electrophysiological dynamics. Depth-resolved variation in fiber orientation led to changes in transmural activation time. This was observed in the left atrium-1 and left atrium-2 models by the differences in transmural activation time between the tissue-specific fitted fiber orientation models and their simplified fiber variants. With recent interest in the difference between epicardial and endocardial electrical activation during atrial fibrillation (49), high resolution and depth-resolved fiber orientation information offered by OCT may be helpful in understanding arrhythmia dynamics.

We also investigated the ability of optical mapping signals to reflect such changes in electrophysiological transmural activation. Optical mapping simulations and experimental studies by Hyatt et al. (30) demonstrated that the subsurface orientation of the propagating electrical wave front with respect to the tissue surface is correlated to the optical upstroke morphology. However, it has been demonstrated in anatomic optical mapping models (25, 26) and experiments (28) that patterns of electrical propagation and consequently extracted V_f^∗ can become more complex because of tissue heterogeneities and fiber orientation. Changes in the surface electrical activation patterns due to anisotropic conduction along fibers were reflected in the V_f^∗ maps. As seen within the difference maps of Fig. 10, g and h, varying depth-resolved fiber orientation altered the optical upstroke distribution and emphasizes the influence of structure on electrophysiological propagation and subsequently optical mapping signal characteristics. These differences appeared to be more significant closer to the stimulus point and particularly as the wave front transitioned from traveling away to traveling toward the tissue surface.

In addition to incorporation of fiber orientation, we were also able to build OCT-derived tissue-specific models of ablation lesions and simulate optical mapping in the models to observe the interaction between the electrical and optical signals and the lesions. The blurring of the optical signal compared to the electrical signal around the boundaries of the lesion was observed. In particular, the minimal, normalized optical signal intensity was higher in the transmural lesion within our simulations. There was a low contribution to the optical mapping signal from the electrical propagation occurring underneath the nontransmural lesion because of the decay of excitation intensity. Thus, the lateral scattering from the regions surrounding the lesion contributed more significantly to the optical mapping signal. Because of the smaller diameter of the transmural lesion, this can explain the higher optical signal intensity within the transmural lesion and emphasizes the need to be aware of the origin of the optical signal when relating lesion depth to optical signal amplitude. Modeling of light propagation in tissue-specific conditions could assist in the development of optical techniques to monitor lesion formation such as those using endogenous nicotinamide adenine dinucleotide fluorescence (50) or near infrared-spectroscopy (47). Tissue-specific ablation models could be used to evaluate and analyze the behavior of the optical techniques in a realistic model containing heterogeneities that would otherwise complicate use of the techniques.

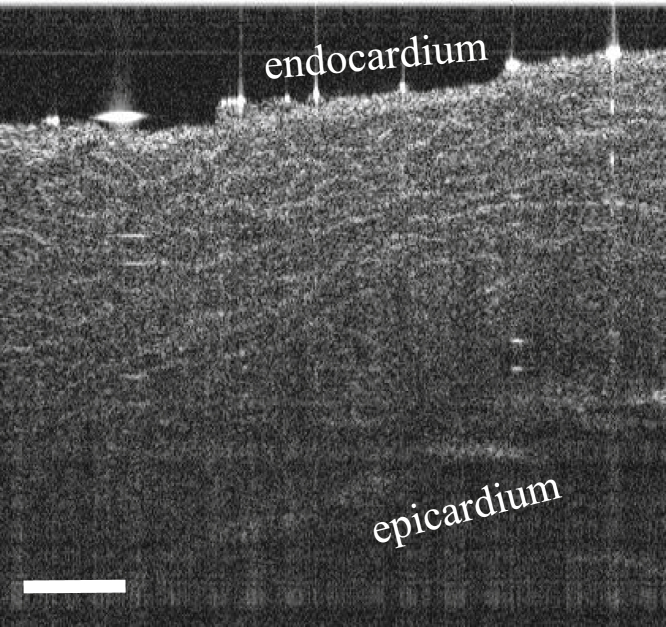
This study demonstrated a framework for developing OCT-derived atrial tissue models and showed influences of OCT-derived structural features on the electrophysiological and optical signals. However, a larger imaged tissue region would be helpful to enable a more thorough investigation of arrhythmia dynamics in large animals or human hearts and the influences on electrical and optical signals with respect to detailed structural information. The lateral field of view can be enlarged by stitching a larger number of OCT volumes, whereas the imaging depth of OCT could be expanded by imaging and stitching both sides of the tissue, imaging thick serial sections of the tissue, or through optical clearing combined with imaging by a swept-source (SS)-OCT system. SS-OCT systems offer higher imaging depths because of the use of longer wavelength light sources. Fig. 12 shows a B-scan of swine left atrial tissue optically cleared by a 2,2’-thiodiethanol-based aqueous solution (51) and imaged by a custom-built SS-OCT system (52), showing tissue contrast throughout the tissue thickness of ∼2 mm. Combined with increased optical depth penetration induced by optical clearing, imaging with an SS-OCT system could enable high-resolution imaging of deeper tissue structure without complications of image registration or potential artifacts from sectioning. However, future work remains in obtaining the best balance between tissue contrast and depth penetration with optical clearing.

Figure 12.

Representative SS-OCT B-scan from a swine left atrial sample optically cleared by a 2,2’-thiodiethanol-based aqueous solution. Scale bar indicates 0.5 mm.

Limitations of this study include lack of experimental validation, which would require registration of optical mapping data from the tissue to its OCT-derived model. Although the optical mapping signal characteristics observed within this study, such as the optical signal blurring and morphology changes, are in line with previous experimental and modeling results, direct experimental comparison would be necessary to fully validate tissue-specific effects and parameters. In this study, the electrophysiological parameters were informed by literature. Additionally, although the optical absorption and scattering parameters were obtained from a swine tissue sample through an inverse Monte Carlo method, the reduced scattering coefficient, as opposed to the scattering coefficient, was obtained. The scattering coefficient was estimated from the reduced scattering coefficient and an approximate value of the anisotropy coefficient, near the range found in previous literature (54), because of the lack of existing information on swine atrial optical properties. The tissue was also not stained with voltage-sensitive dye when the optical parameters were measured. With regards to lesion imaging and modeling, OCT was unable to detect the lesion depth. Furthermore, changes in endocardial and myocardial contrast as the marker for lesion boundaries may vary in alignment between the lesion necrotic core and border zone. Establishing a more accurate framework for electrophysiological and optical modeling of the lesion in detail is a focus for future investigation. Lastly, because of the different algorithms used for generation of the hexahedral and tetrahedral meshes and different simulation approaches of the electrical and light propagation, registration between the two models have slight differences, primarily in the lesion model that has a smoothly transitioning lesion boundary in the electrophysiological model but a sharp boundary within the photon scattering model.

The next steps for OCT-derived optical mapping atrial models include the modeling of larger tissue regions (including the incorporation of varying tissue types, such as collagen, adipose tissue, and fibrosis (53)) and ultimately working toward a comprehensive visualization and model of the whole atria utilizing stitched OCT image volumes. Future studies will also include further study of OCT-derived lesion models, including simulation of electrical propagation with multiple ablation lesions of varying sizes and configurations, and inclusion of transmural myofiber orientation to allow a more detailed understanding of varying electrophysiological conduction and block around ablated areas in different conditions. OCT-derived atrial models have the potential to provide additional, high-resolution, tissue-specific structural detail in simulations of cardiac electrophysiology and optical mapping. In the future, OCT imaging could be registered with MRI or computed tomography-derived data for a multimodality imaging approach. In conclusion, this study has laid the framework for OCT-derived tissue-specific, optical mapping models of the atria, which has the potential to enable a more direct comparison between simulation and experimental results. Optical mapping models of atrial tissue as derived from OCT have the potential to guide further investigation of the relationship between cardiac function and specific tissue structure.

Author Contributions

C.P.H. conceived the research aims and secured funding. T.H.L. designed and performed the study, including model creation, running of simulations, and data processing and analysis. K.P.V. contributed software components and assisted in model creation and simulation. A.D.M. and K.P.V. provided expertise. T.H.L. wrote the manuscript. C.P.H., A.D.M., and K.P.V. provided feedback and edits to the manuscript.

Editor: Raimond Winslow.