Abstract
Cancer cells are usually found to be softer than normal cells, but their stiffness changes when they are in contact with different environments because of mechanosensitivity. For example, they adhere to a given substrate by tuning their cytoskeleton, thus affecting their rheological properties. This mechanism could become efficient when cancer cells invade the surrounding tissues, and they have to remodel their cytoskeleton in order to achieve particular deformations. Here we use an atomic force microscope in force modulation mode to study how local rheological properties of cancer cells are affected by a change of the environment. Cancer cells were plated on functionalized polyacrylamide substrates of different stiffnesses as well as on an endothelium substrate. A new correction of the Hertz model was developed because measurements require one to account for the precise properties of the thin, layered viscoelastic substrates. The main results show the influence of local cell rheology (the nucleus, perinuclear region, and edge locations) and the role of invasiveness. A general mechanosensitive trend is found by which the cell elastic modulus and transition frequency increase with substrate elasticity, but this tendency breaks down with a real endothelium substrate. These effects are investigated further during cell transmigration, when the actin cytoskeleton undergoes a rapid reorganization process necessary to push through the endothelial gap, in agreement with the local viscoelastic changes measured by atomic force microscopy. Taken together, these results introduce a paradigm for a new—to our knowledge—possible extravasation mechanism.
Introduction
The role of cell mechanics has been investigated a lot in recent years, and it is essential in many biological phenomena based on the cell’s ability to modify its shape and cytoskeleton and therefore its rheology. These changes are important during embryogenesis, cell division, cell migration, metastasis, or the epithelial-mesenchymal transition, to mention just a few processes. Therefore the investigation of cell mechanics has become a major issue and has led to the development of specific tools to study cell (visco)elasticity—such as optical tweezers, optical stretchers, microplates, micropipettes, magnetic twisting cytometry, atomic force microscopy (AFM), and microbead tracking with a laser or light—to investigate cell internal microrheological properties (1).
Because of the variety of possible ways to investigate cell mechanics, different cell types have been tested; in particular, metastatic cancer cells have been studied extensively (2) and seem to become softer as they pass from blood through the endothelium (3) to invade new tissues (4). More precisely, E, the elastic Young modulus of cells, seems to decrease when cells become invasive as compared to normal ones (5, 6, 7). This concept is not always recognized because cells may require more stiffness to break through a biological tissue, as shown recently by combining AFM and confocal microscopy (8). One way to answer this question is to study the cytoskeleton, a complex dynamic system involving actomyosin contractile elements, intermediate filaments, and microtubules (9, 10, 11). The cytoskeleton is both locally and mechanically heterogeneous (12). In particular, the region on top of the nucleus of adherent cells, or the perinuclear part, can exhibit significantly different mechanical properties as compared to protrusions or filopodia (13, 14). Finally, the nucleus plays a role in cell elasticity (15), as its deformability is a prerequisite to squeeze through complex confined networks (16). Another important parameter is viscosity, which can be quite relevant (17) because of the viscous components of the cell cytoplasm and could be a potential marker of cancer cells (18).
Recently, studies focusing on the environment revealed important strategies used by cells to remodel their cytoskeleton, a process known as mechanosensing. Indeed cells can adapt their response when the substrate has changing stiffness (19) or migrate toward a more rigid substrate (20), where they spread and reinforce their focal adhesions (21). Cell spreading also increases on thinner gels, since they feel the substrate below (22). Cells also adapt their stiffness according to the substrate elasticity (23). When in contact with substrates of rapidly increasing stiffness, they develop larger forces via remodeling of the actomyosin cortex (24). Regarding the particular case of cancer cells, it has been shown that human breast cancer invasion correlates with a stiffening of the surrounding extracellular matrix (ECM) depending on cell type, matrix, integrins, or collective effects (25, 26). Cancer cell invasiveness seems to be linked with the way cells sense or indent elastic gels, so it could be a good tool to distinguish them (27). Further works showed that the heterogeneity of complex Matrigels mimicking the microenvironment can promote cancer cell invasion (28). In tumors, cells remodel the ECM around them to force progression (29, 30). This change in force generation has been studied using two-dimensional and three-dimensional traction force microscopy (31, 32, 33) but is not yet related so clearly to the cytoskeleton of cancer cells.
To investigate the cell microrheological properties, AFM in force modulation mode (14, 17, 34, 35) is particularly well adapted. Despite the commonly available AFM software programs or homemade systems, few results have focused on the role of the environment on cell viscoelastic properties. Thus, in this work, we considered the effect of an elastic substrate on the mechanical properties of adhering cancer cells and evaluated their mechanosensitivity. This was carried out for three different elastic gels (E ranging from 5 to 28 kPa) and an endothelium substrate. Microrheological properties (36) were obtained in a large frequency range (1–500 Hz). Since substrates are thin and viscoelastic, a three-layer model, inspired from previous work (37), was used to account for substrate effects. Finally, using a viscoelastic model (14), two main parameters were identified that corresponded to the signature of cancer cells—namely, , the elastic plateau modulus, and , the transition frequency from an elastic to a glassy state (38). The evolution of these parameters showed surprising changes in the case of invasive cancer cells on the endothelium substrate. This was confirmed by separate transmigration experiments showing that rapid cytoskeleton reorganization is necessary to cross the endothelial barrier.
Materials and Methods
Cell culture
Cancer cells
Three epithelial bladder cancer cell lines representing increasing malignancy states of metastasis progression were used: RT112, T24, and J82 (American Type Culture Collection, Manassas, VA). RT112 cancer cells are moderately differentiated, whereas T24 and J82 cancer cells are poorly differentiated and have a higher malignancy potential (especially J82 cells). The choice of these bladder cell lines comes from earlier studies by the authors (39, 40, 41). Cell lines are classified according to the corresponding tumor they were taken from using the tumor node metastasis system (Union for International Cancer Control). T stands for the stage and describes how far the primary tumor has grown into the bladder . The majority of bladder cancers are linked to noninvasive papillary tumors of a lower grade . N is the spread to lymph nodes near the bladder , and M is the spread of the tumor to other parts of the body (M0 and M1). This information is combined to give the overall stage . According to these standards, RT112 (luminal molecular subtype, Leibniz Institute DSMZ- German Collection of Microorganisms and Cell Cultures, Braunschweig, Germany) is a − cell type. T24 (ATCC-HTB-4, luminal and/or basal molecular subtype) is a more invasive cell line . J82 (ATCC-HTB-1, luminal and/or basal molecular subtype) is a very invasive cell line . Taken together, this gives a wide variety of invasiveness.
These cells were cultured in RPMI 1640 (Gibco, Saint-Aubin, France) supplemented with fetal calf serum and penicillin-streptomycin. One day before measurements, cells were seeded at a density of cells per well on gels coated with 20 μg/mL fibronectin (PromoCell, Heidelberg, Germany) overnight at in a humidified CO2 atmosphere. Such cells are considered to have a low migrating velocity since the fibronectin concentration is quite high (42). AFM measurements were carried out on isolated cells at . Cancer cells were transfected with the LifeAct plasmid expressing actin-GFP (green fluorescent protein).
Endothelial cells
Human umbilical vascular endothelial cells (HUVECs) purchased from PromoCell were plated in complete culture medium (PromoCell) on glass coverslips coated with fibronectin (10 μg/mL) and left for 3 days at in a humidified CO2 atmosphere to spread and achieve confluence.
Cell transendothelial migration
To verify the results postulated with the atomic force microscope and understand how a change in substrate can affect the cytoskeleton of cancer cells during transmigration, an experiment was carried out using cancer cells in contact with a HUVEC monolayer that was grown on a gel with an elasticity 8 kPa. A stamping procedure was used with a patterned polydimethylsiloxane block functionalized with fibronectin (25 μg/mL). Stamps were put in contact with gels for 1 h and then were gently removed (43). Endothelial cells (HUVECs) were seeded in complete culture medium (PromoCell) overnight to form a monolayer on the circular 80 μm patterns. Finally, invasive cancer cells (J82) were put in solution and left to sediment. As many patterns were used in parallel, cases with one single cancer cell adhering and transmigrating through the HUVEC monolayer could be followed. J82 cells were transfected for actin-GFP so that the actin cytoskeleton could be visualized on the confocal microscope (LSM; Carl Zeiss AG, Jena, Germany). HUVECs were stained with CellTrace Far Red DDAO-SE (Life Technologies, Carlsbad, CA) to observe their shape. The microscope was equipped with multiwave acquisition (green and red) and a chamber to maintain and supply CO2 for the cells. After cancer cells had sedimented, they came in contact with the endothelial cells, found their way through the cell-cell junctions, then passed through and spread below. Fluorescence was used to visualize cancer cells and endothelial cells at the same time.
Gel preparation
Polyacrylamide (PAA) gels were prepared following a previous protocol (43). Three gels containing OH bonds, enabling easy functionalization using fibronectin (20 μg/mL), were prepared by mixing acrylamide ( weight per weight [w/w]), N-hydroxyethyl-acrylamide ( w/w), and N,N-methylene-bisacrylamide (2 w/w) in different amounts (Sigma-Aldrich, St. Louis, MO). Three concentrations of bisacrylamide were used (0.1, 0.3, and 0.6 ), whereas the acrylamide (3.2) and N-hydroxyethyl-acrylamide (1.25) contents were fixed in the final 50 mM HEPES solution. Polymerization was initiated by incorporating N,N,N,N-tetramethylethylene-diamine (Sigma-Aldrich) and ammonium persulfate 10 solution (Sigma-Aldrich). 70-μm-thick gels were prepared on a pretreated glass petri dish for better adhesion. After polymerization, samples were indented using AFM in contact mode or characterized using a rheometer to obtain the plateau modulus (30). Since viscous effects were negligible, one could assume that . Both measurements agreed, with gel moduli 5 1 kPa, 8 1.5 kPa, and 28 3 kPa. Gels were kept under humid conditions before cell seeding.
AFM measurements
Experiments were carried out using a Nanowizard II atomic force microscope (JPK Instruments, Berlin, Germany) mounted on a ZEISS microscope (Observer D1; Carl Zeiss AG). All measurements were conducted in force modulation mode at using a petri dish heater (JPK Instruments). We used triangular silicon nitride cantilevers with four-sided pyramidal tips (MLCT, lever C; Bruker, Billerica, CA) and a nominal spring constant that was calibrated using the thermal noise method (44). Sharp tips are better suited to reach a higher spatial resolution. The applied force was lower than 2 nN in order to deform the substrate within the linear elastic regime where the Hertz indentation model can be used. When the cantilever tip gets into contact with the sample, the force acting on the cantilever increases to a previously chosen set point F, corresponding to an initial indentation δ. The relationship is given by Sneddon’s modification of the Hertzian contact mechanics model (45):
| (1) |
where E is the cell’s Young modulus, ν is its Poisson ratio , is the apparent modulus, and ° is the half pyramid angle.
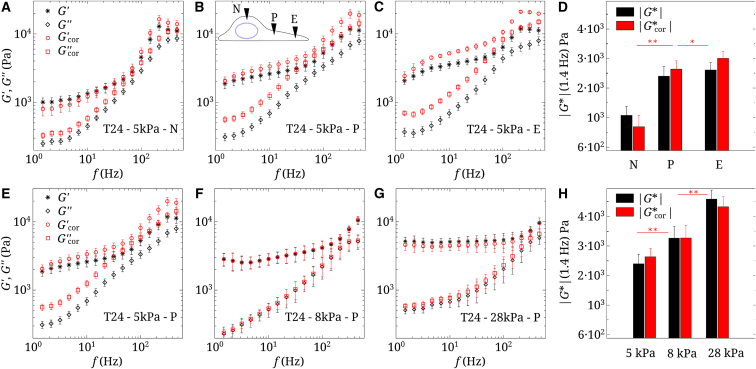
AFM measurements were carried out at different geometrical locations, namely N, P, and E (14). N designates a location on top of the nucleus, but this does not mean that the nucleus is measured, since it is known that the actin cytoskeleton may be present in the thin layer between the nucleus and the cell membrane. P is usually located 10 μm away from the geometrical center of the nucleus. Finally, E represents the edge of the cell, typically 5 μm from the edge. These locations can be seen on the sketch in the inset of Fig. 1 B and in Fig. 2 C.
Figure 1.
Raw and corrected viscoelastic moduli of T24 cells. (A–C) Data on a 5 kPa gel at three locations (nucleus (N), perinuclear region (P), and edge (E)) are shown. (D) Modulus (1.4 Hz) at the three locations (N, P, and E) is shown. (E–G) Data measured in the perinuclear region (P) on three gels are shown ( = 5, 8, and 28 kPa). n = 5, and error bars represent the mean ± SE. (H) Modulus (1.4 Hz) for the three gels is shown ( = 5, 8, and 28 kPa). Statistical relevance is shown for corrected values of . To see this figure in color, go online.
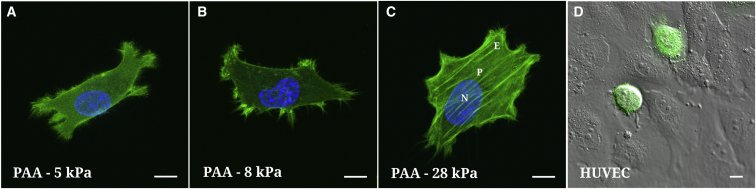
Figure 2.
(A–C) Fluorescence of actin-GFP T24 cells on three PAA substrates ( = 5, 8, and 28 kPa) with respective spreading areas (863, 1025, and 1541 μm2). (D) A differential interference contrast image of a HUVEC monolayer with green fluorescent T24 cells superimposed is shown. Because of the round shape of the cells, it is not possible to define a lamellipodium or edge (E). The scale bar represents . To see this figure in color, go online.
Correction for indentation of a cell on a soft substrate: three-layer model
The precise analysis of the indentation experiment of a cell is highly dependent on its environment, which consists of soft (gel or HUVEC monolayer) and hard substrates (glass dish). The Hertz formula (Eq. 1) is only valid as long as the indentation depth is small compared to the sample thickness. The influence of the substrate grows with increasing indentation depth δ and starts to be nonnegligible at about one-tenth of the substrate thickness h . This induces an overall strain of , which is the accepted limit between small and large strains. More details on specific corrections have been proposed for spherical or pyramidal indenters (13, 36, 46). In the case of indentation on a hard substrate, the cell elastic modulus appears much higher than expected, whereas on a soft gel, the cell modulus seems to be smaller.
The analysis presented here is a generalization of the Hertz formula for indentation of a composite substrate using power law functionals. The numerical model employed is based on the Papkovich-Neuber potential representation of the displacement field and has been verified on various hard and soft combinations of substrates with different axially symmetric indenter shapes (37, 47, 48). In this experimental configuration, a cell (layer 1) is spread on a soft gel or HUVEC monolayer (layer 2) in contact with glass (layer 3). Let us call Ei, νi, and hi the Young modulus, the Poisson ratio, and the thickness, respectively, where the indices i = 1, 2, and 3 denote the layers. Let us further remark that the glass substrate thickness is infinite . This three-layer system is treated using power law functionals as detailed in Appendix A of the Supporting Material (Fig. S1) and has an apparent effective modulus:
| (2) |
where and , , , and denote a series of shape parameters.
The model parameters , , , and were obtained (see Fig. S2) for relevant values of the cell modulus , ranging from 1 to 20 kPa. The gel modulus was given values between 5 and 28 kPa, as in the experiments, and the stiffness of the glass substrate was considered very large ( 70 MPa). , the cell height, was measured experimentally on the nucleus, perinuclear region, and cell edge. equaled for gels and was ∼ 8μm in the case of endothelial cells.
Dynamic AFM measurements: G′ and G″
In order to carry out microrheology measurements, an initial indentation was made, corresponding to the applied force in Eq. 1. A small perturbation at angular frequency ω ( and the frequency f varies from 1 to ) was superposed to the initial indentation . During this procedure the tip remained in contact with the cell. We imposed the indentation and measured the force response (17, 36). Because the perturbation was small, Eq. 1 was linearized around the equilibrium . At first order, the equation is as follows:
| (3) |
where , , and are functions of the reduced indentations , . Parameters and from Eq. 2 are investigated in Appendix B of the Supporting Material:
| (4) |
By the correspondence principle of linear viscoelasticity, one uses a complex indentation and force . The hydrodynamic viscous drag is substracted from as explained previously (14, 17). is estimated from the extrapolation of as a function of the tip-sample separation h to . For the sake of simplicity, it is not written in Eq. 5,which now reads, in complex form, as the following:
| (5) |
where is the required cell complex viscoelastic modulus. Note that and can be complex as well. This is the case with endothelial cells . For the third layer (glass), is real. The initial indentation and heights and are known experimentally. We impose = 500 nm, 10 μm on the nucleus (N); = 400 nm, 1 μm on the perinuclear region (P); and = 100 nm, 200 nm on the edge (E). Functions , , and are calculated using parameters , , , and as explained in Appendix B of the Supporting Material. The procedure requires an initial value of to start iterating (since , , and in Eq. 5 depend on ) to find the new . Convergence is verified when the relative error is smaller than 1%, usually after 20 iterations.
Modeling G′ and G″
After obtaining experimental rheology data using correction formulae, it was found that in most cases is flat at low frequencies, then increases to reach a power law with slope a, in terms of ω. On the other hand, decreases with slope at low frequencies, then increases as a power law with the same exponent a. A simple model (14) was proposed:
| (6) |
| (7) |
where is the so-called plateau modulus (Pa), a is the slope of and at high frequencies, b is the ratio at high frequencies, and and are constants. Note that there exists a transition frequency corresponding to the crossing of and at the higher frequencies, given by . This model is slightly different from previous ones (17, 38) but assumes that universal power law behavior is not always met (49). In particular, at low frequencies, an elastic plateau modulus is found. Parameters and will be used in what follows to quantify differences in cancer cell microrheological properties.
Statistical analysis
Data were analyzed by a two-sample unpaired Student’s t-test. n is the number of cells per condition. Values in Figs. 1, 2, 3, 4, and 5 correspond to ∗∗∗p < 0.001, ∗∗p < 0.01, ∗p < 0.05, and p > 0.05 (not significant). Values were considered statistically significant when p < 0.05. Error bars in all figures represent the standard error (SE) of the mean (mean ± SE).
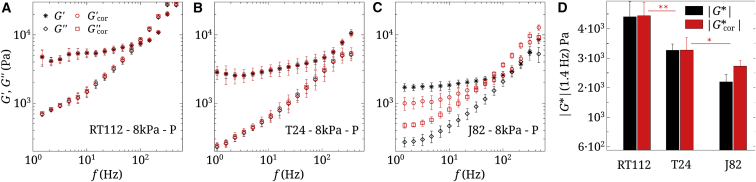
Figure 3.
(A–C) Raw and corrected viscoelastic moduli of three cancer cells (RT112, T24, and J82) on the 8 kPa gel. n = 5, and error bars represent the mean ± SE. (D) Shown are corresponding values of (1.4 Hz) for the three cell types. Statistical relevance is shown for corrected values of . To see this figure in color, go online.
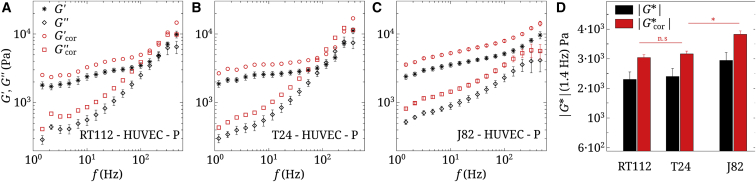
Figure 4.
(A–C) Raw and corrected viscoelastic moduli of three cancer cells (RT112, T24, and J82), measured in the perinuclear region (P), on a HUVEC monolayer. n = 5, and error bars represent the mean ± SE. (D) Shown are corresponding values of (1.4 Hz) for the three cell types. Statistical relevance is shown for corrected values of . To see this figure in color, go online.
Figure 5.
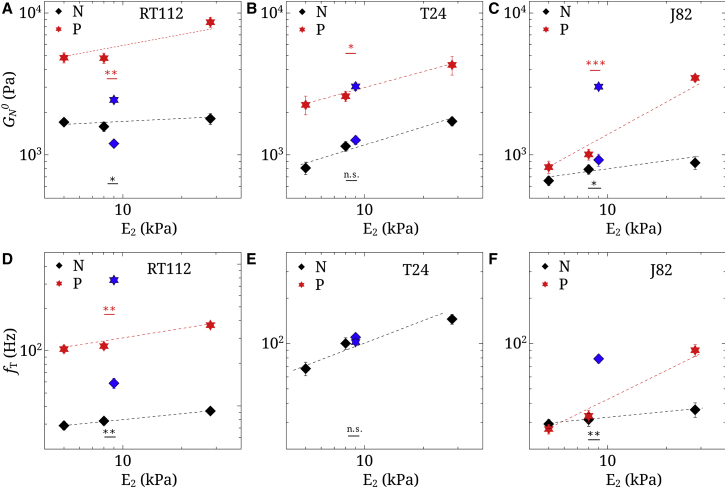
Parameters (A–C) and (D–F) for RT112, T24, and J82 cancer cells, both on rigid substrates ( = 5, 8, and 28 kPa) and a HUVEC monolayer ( 9 kPa). P represents the perinuclear region and N represents the nucleus. n = 5, and error bars represent the mean ± SE. The points at 9 kPa represent data on the HUVEC substrate. The lines are just a guide for the eye. Statistical relevances of and are shown when comparing the HUVEC substrate with the gel of rigidity = 8 kPa. To see this figure in color, go online.
Results
Local microrheology depends on cell location and substrate stiffness
We first present results of the measurements made using T24 cancer cells on a soft gel ( = 5 kPa), and different locations are tested in Fig. 1, A–D. The contribution of the substrate has been taken into account. Both sets of data can be seen, with and without corrections. It is clear that the shear moduli and are affected by the presence of the substrate. Note also that the measurements depend on tip position. To clarify this, Fig. 1 D shows the modulus at 1.4 Hz, increasing as the point of measurement moves from the center (nucleus (N)) to the perinuclear region (P) and toward the lamellipodium (or edge (E)).
We next turn to the evolution of the dynamic moduli when substrate stiffness is increasing. Three gels were used: = 5, 8, and 28 kPa. This is presented in Fig. 1, E–H. At low frequencies, (1.4 Hz) increases when increases, as seen in Fig. 1, H. This can be due to the cell actin microstructure or the spreading of cells on the substrate (14). In Fig. 2, A–C, T24 cells plated on PAA gels (5, 8, and 28 kPa) are shown using confocal microscopy: they spread more, become thinner, and develop more actin fibers on rigid gels. Note that the variation of with (Fig. 1 H), because of the thinning of cells and enhanced substrate effects, is less important after corrections are made. It can be concluded that the increase in cell elasticity comes rather from the cytoskeleton through creation of aligned actin fibers.
Cell microrheological properties are linked to cell invasiveness
The influence of invasiveness was studied next. Three cancer cells of increasing invasiveness (RT112 T24 J82) were plated on the 8 kPa PAA gel. Their viscoelastic properties are shown in Fig. 3, A–C and display a common trend, with lower moduli and as the invasiveness increases. Substrate corrections are shown together with raw data. One can conclude that the microrheological properties of cancer cells depend on their invasiveness (i.e., moduli are lower for the more invasive cells). This is clearly shown for (1.4 Hz) in Fig. 3 D. Such results were previously reported for the global elastic moduli E of cancer cells (5), their local elasticity (6, 7, 50), or viscoelasticity (14, 35). Note here that applying substrate corrections has a significant effect on the results.
Invasive cells exhibit an inverse behavior on the HUVEC substrate
We next characterize the behavior of the same cancer cells in contact with the endothelial monolayer. This layer has similar mechanical properties (51) as the 8 kPa PAA gel studied above. Therefore, one could wonder what effects can be found regarding cell spreading or cell viscoelasticity and whether this could affect transendothelial migration. We find that on the HUVEC monolayer, cells do not spread much and remain round (Fig. 2 D), so it is hard to distinguish a lamellipodium (or edge (E)). Only measurements on the nucleus (N) and perinuclear region (P) were performed. Fig. 4, A–D shows these measurements on the perinuclear region (P). Note that corrections in Fig. 4, A–C use the real viscoelastic properties of endothelial cells, measured separately (51). In this case the viscoelastic properties of cancer cells show a different trend. Fig. 4 D summarizes the evolution of (1.4 Hz), showing that more invasive cells are slightly stiffer in the perinuclear region. Finally, the crossover frequency varies significantly. For J82 cells, cannot be reported because this crossover is out of the range of frequencies used. In the next part we will compare quantitative numbers, such as and .
Parameters and increase with substrate elasticity
In order to quantify the changes highlighted in the previous part, two parameters were studied, namely the plateau modulus (Fig. 5, A–C) and the transition frequency (Fig. 5, D–F). These parameters were defined earlier in Eq. 6. Their evolution is shown at locations N and P for all cell types. To compare results on HUVECs and gels, we assume that 9 kPa for endothelial cells (51). Fig. 5 represents the evolution of and in terms of elasticity , with HUVECs being close to the elastic substrate = 8 kPa. Justification of the model for the endothelial monolayer as a thin substrate can be found in Appendix C of the Supporting Material. and both increase linearly (log-log scale), with substrate rigidity at a higher rate for location P as compared to N. One could expect the HUVEC data to lie along the evolution curve. On the contrary, the values found for and are quite different from the ones expected for an equivalent elastic substrate. is higher in the perinucleus region (P) than on the nucleus (N). With the HUVEC monolayer, is higher than expected for J82, equal for T24, and lower for RT112 cells. Finally, regarding (when defined), differences are also found on the HUVECs: RT112 exhibits larger , a T24 value exists only on HUVECs at the perinucleus (P), and for invasive J82 cells shows a large change on the nucleus (N) but is not defined on the perinucleus (P). The presence of the endothelium (HUVEC) indeed shows differences that could have been expected because of the different nature of the substrates, both in terms of cytoskeleton as well as adhesion molecules. Thus, the next section investigates the dynamic behavior of J82 cancer cells in contact with the endothelium until transmigration is achieved. The actin cytoskeleton organization (52) will be followed and linked with microrheological changes observed above.
Transendothelial migration requires actin reorganization of cancer cells
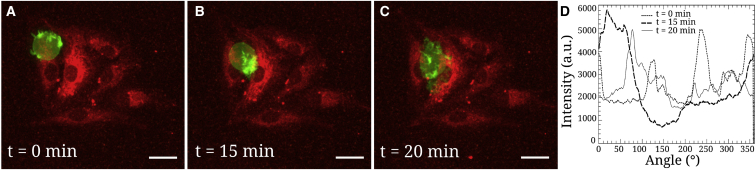
When cancer cells are in contact with the endothelium substrate, they may possibly transmigrate (3), so it is important to understand how they adapt their actin cytoskeleton. This effect could be related to the mechanical features shown previously and to mechanosensitivity. One example of these features is shown in Fig. 6. Cancer cells were allowed to sediment and to adhere to endothelial cell patterns. We selected one pattern with only one cancer cell adhering and followed it when it interacted with the HUVEC monolayer. The cell shape and actin organization could be seen during the course of transmigration. Initially, the cell was round (, Fig. 6 A) and the actin seemed to be concentrated on the sides. This local concentration can be linked to the cell’s mechanical properties, as measured above. Then the cell became ovoid (min, Fig. 6 B) and actin seemed to relocate close to the junction, as if the cell was pushing harder to penetrate. Finally, the cell squeezed through the junction and was found below the endothelial monolayer (min, Fig. 6 C), where it had spread. Fig. 6 D also shows the polar distribution of actin along the cell edge. At time min, there was indeed a very large actin concentration in the (0–70°) angular range, close to the endothelial gap.
Figure 6.
Transmigration of a J82 cancer cell in contact with the endothelium. (A) Initially the cell is round ( min) with actin concentrated at the periphery, (B) followed by an ovoid shape with actin relocation close to the endothelial gap ( min), (C) then it transmigrates and spreads below the endothelium ( min). The scale bar represents . (D) Shown are polar representations of the actin intensity (in arbitrary units) at the cell edge, measured from the center of geometry, at different times. Note in particular the large actin area for min. a.u., arbitrary units. To see this figure in color, go online.
Discussion
The choice of bladder cancer cells comes from previous studies by the authors (39, 40, 41), in which various properties associated with invasiveness, such as adhesion and rheology, were reported. RT112 cancer cells are moderately differentiated, whereas T24 and J82 cancer cells are poorly differentiated and have a higher malignancy potential (especially J82 cells). In addition, these cancer cells were used before as models for molecular classification (53). They exhibited various expression degrees of mTOR-associated genes, which is relevant for chemotherapy. Adhesion molecules or ligands (leukosialin [CD43] and mucin 1 [MUC1]) present at the cancer cell surface have been identified (40, 41, 54) as well as receptors (ICAM-1, VCAM-1) on the HUVEC side (39). Note that CD43 and MUC1 are expressed more on invasive cells, especially T24 and J82 cell lines. When plated on gels functionalized with fibronectin, cancer cell receptors are more likely to be or integrins (55) that interact with the ECM (fibronectin). In addition, the expressions of and are particularly relevant for cancer cells such as T24 (56). Finally, during the process of metastasis, it was shown that the NFκ-B pathway can be involved in the overexpression of adhesion molecules (39).
Rheological data corrections
The effect of a cell adhering on a rigid substrate has been investigated previously and corrections have been proposed (13, 14, 46). But softer substrates with a rigidity close to that of the cell can also play a role; therefore, it is necessary to account for the effect of both substrates—the soft one with elasticity and the rigid one with elasticity (glass, for instance)—to determine (the cell elastic modulus) when the environment has different stiffnesses or thicknesses. Here we used a previous model (48) to investigate these properties numerically, taking into account the exact tip shape (a rounded cone), as considered earlier by other authors (57). An important result is that depending on substrate stiffness, cell modulus can be overestimated (when ) or underestimated (when ). This is illustrated in Figs. S1–S3: the effective modulus can be a decreasing or increasing function of the reduced indentation. The other important parameters are the indentation δ, cell height , and substrate thickness . Note that the spreading of cells on soft gels was studied earlier (22) when gel thickness was varied in the particular case of mesenchymal stem cells. Cells spread more when the thickness decreased, and the cell area leveled out for high thicknesses. This latter statement is in agreement with our model at small indentations (or large heights), as the apparent stiffness also shows a plateau in Fig. S1, corresponding to the expected modulus. Finally, our model was applied to dynamic rheology and linearized in Eq. 5 to obtain the complex dynamic viscoelastic modulus , accounting for substrate effects, including both viscoelasticity and thickness. Validation of the model in simple cases can be found in Appendix B of the Supporting Material.
Cell stiffens away from nucleus
First, rheological measurements were made at different locations. Fig. 1, A–D shows the raw data obtained at positions N, P, and E, indicating respectively the nucleus, perinuclear region, and cell edge (see sketch as an inset in Fig. 1 B and positions indicated in Fig. 2 C). These locations were chosen based on geometry and microstructure considerations. The data were corrected, as explained above, because of the presence of the gel (5 kPa). Corrections were not negligible, as shown by differences in the and moduli of up to . The final corrected value of the cell shear elastic modulus at low frequency was around 1 kPa on the nucleus (N), thus 3 kPa. This means the substrate is stiffer (5 kPa), so we found an overestimated value of in the experiments. Regarding , the effects were more subtle, but increased after correction (see Fig. S4 in Appendix C of the Supporting Material). On the perinuclear region (P) or edge (E), kPa and kPa, so the substrate was softer, and therefore was underestimated.
After making these corrections, we noted (Fig. 1 D) that the cell was stiffer when going from the center (3 kPa) to the edge (9 kPa). It is not so surprising that the center was less rigid because the atomic force microscope tip feels the cytoskeleton as well as the nucleus at position N. Isolated nuclei are known to have a Young modulus 5–8 kPa (15), so 3 kPa is the average of nucleus, cytoplasm, and membrane effects. The edge (E) or perinucleus (P), on the other hand, contain actin bundles, which are quite rigid, as observed earlier (13, 14). Disruption of actin filaments using latrunculin A fluidifies the cytoskeleton, whereas Y27632 (an actomyosin-inhibiting drug) rigidifies the cell edge (14).
increases with substrate stiffness
Interesting results are presented in Fig. 1, E–H, in which the influence of substrate rigidity ( 5–8–28 kPa) is shown. Corrections show an increase of the modulus after correction when 5 kPa, hardly no change for 8 kPa, and an increase for 28 kPa (Fig. 1 H). We find 2.5-3.2-4.3 kPa or 7.5-9.6-12.9 kPa to be compared to 5-8-28 kPa, respectively. We can conclude that cells adapt their rheology (i.e., are mechanosensitive). A global trend is a cell elasticity increase with substrate stiffness, and we have seen that it is related to the development of actin fibers on stiffer substrates (Fig. 2, A–C). This is in agreement with previous works (19, 20, 22, 58) and the development of stress fibers in connection with focal adhesions.
decreases with invasiveness as cells become glassy
The role of invasiveness on cell microrheological properties is shown in Fig. 3 using three cell types (RT112, T24, and J82) by increasing order of invasiveness. When comparing measurements on the perinuclear area (P), a clear decrease in viscoelastic moduli is observed with invasiveness, both for and , and this effect persists after corrections. This confirms common trends found in the literature (5, 6, 7, 50), but more complete data are found here because both and as well as are obtained in Fig. 3. In this respect, the more invasive J82 cell shows a smaller (crossing of and ) around 40 Hz, revealing an earlier transition to the disordered glassy state. This was also observed for other malignant cells, such as MCF-7 and MDA-MB-231 (35).
Most invasive cells stiffen on a HUVEC monolayer
Fig. 4 illustrates measurements carried out with the three cell types on a HUVEC monolayer at position P. This position was chosen in order to compare on HUVECs and PAA substrates. As cancer cells do not spread when in contact with the HUVEC monolayer (Fig. 2), only two locations (N and P) are common between gels and HUVECs. One could argue that the proteins at the surface of the latter two substrates are different in both cases. Here we can assume that bonds are all strong ones because they are receptor-ligand bonds involving integrins and fibronectin on gels and ICAM-1 versus other ligands (CD43 and MUC1) in the case of the HUVEC substrate (41). So the comparison can hold. To correct the data, we assume that the HUVEC monolayer behaves like a thin viscoelastic layer, as explained in Fig. S5 in Appendix C of the Supporting Material. Indeed, in the range of parameters studied, the small indentation (∼500 nm) ensures no differences whatever the height of the soft substrate is, so the uneven HUVEC monolayer (2–8 μm) is only affecting results through its viscoelastic properties, but not its height.
Data on the viscoelastic HUVEC substrate show slightly increasing values of with invasiveness, which is the opposite of the results found previously on gels. increases from 3 kPa (RT112 cells) up to 3.8 kPa (J82 cells) in Fig. 4 D. To investigate these changes more accurately, we use the model described previously.
increases with substrate stiffness, except on HUVECs
The rheological model (14) was used to fit the data in Figs. 1, 2, 3, and 4 to identify , the plateau modulus, and , the transition frequency. The other parameters a, b, , and were also obtained but are not discussed further. To include the effect of the endothelial substrate, we used previous data on HUVECs (51) in which the elasticity was found to be 9 kPa. This value is also included when plotting (Fig. 5, A–C) and (Fig. 5, D–F) at positions N and P. The substrates have been chosen to cover a large range of elasticities (5–28 kPa), and the evolution of in log-log scale displays a power law, with a positive slope for position (P), as observed before when averaging different locations (23). At position (N), seems to increase less with substrate stiffness, in agreement with indentation on the nucleus, where no difference was found (18). Thus, our results reconciliate these two studies (18, 23) by comparing measurements at different locations. When the cells become more invasive (excluding HUVECs), the slope of versus at position (P) seems to increase, suggesting that more invasive cell types are more mechanosensitive to gel stiffness. Finally, increases with , and therefore cells become more elastic and do not switch to the glassy state. Note that in some cases, could not be determined since there is no crossing of and .
Invasive J82 cells stiffen in the perinuclear area on HUVECs
Finally, we show that RT112 cells become less rigid on HUVECs as opposed to invasive J82 cells, especially on the perinucleus P (Fig. 5, A–C). These results are also observed on the nucleus (N) but are less visible. This could be the sign of invasive J82 cells starting to rigidify (P) in order to break through the endothelium and let the softer nucleus (N) collapse through the endothelial gap. This process is not explained yet, although morphology changes may come from activity of the Rho family of GTPases, which may control the cytoskeleton and actomyosin contractility (52). In any case, this suggests a strong reorganization or mechanosensitivity of the cytoskeleton of invasive cancer cells, compatible with the current rheology data. Indeed, the transition frequency changes a lot on the perinucleus (P), from less invasive RT112 cells ( 300 Hz) to invasive T24 cells ( 100 Hz) and finally to J82 cells that show no transition (Fig. 5, D–F). This latter case is a further indication of a new dynamic organization of the cytoskeleton—corresponding to a glassy state and giving rise to the same slopes of and (17, 35, 38)—and could be a signature of invasiveness. Thus, we show for the first time to our knowledge the importance of the transition frequency . This parameter, together with , shows that few changes occur around the nucleus as opposed to the perinuclear region, highlighting possible mechanotransduction pathways between the cytoskeleton and the nucleus associated with linker proteins (59).
J82 stiffening correlates with actin reorganization during transmigration
Finally, to illustrate the change in cancer cell mechanics when in contact with the HUVEC monolayer, transendothelial migration was followed in order to study the relationship with microrheology measured above. Fig. 6 shows a J82 cancer cell transmigrating through a small pattern of HUVECs (6–8 cells). At the onset of transmigration ( min, Fig. 6 A), the GFP–actin J82 cell exhibits reinforcement of its cytoskeleton at the periphery, as shown by high-fluorescence-intensity areas. This seems to go along with our above results and Fig. 5, which shows a higher in the perinuclear region (as compared to the nuclear region). This suggests that the cell edges are required to maintain stress at the periphery. Next, the actin cortex seems to reinforce below the nucleus ( min, Fig. 6 B) to push through the gap. It is not yet possible to measure this with the atomic force microscope from below, but our previous rheology data support the dynamic nature of the cell cytoskeleton in a metastable state. Finally, the cell is able to go through the gap and spread on the gel below ( min, Fig. 6 C) to complete transmigration (see also Movie S1 and Appendix D in the Supporting Material). This actin reinforcement is also notable in Fig. 6 D, in which the intensity indicates a very localized actin structure corresponding to the precise location of the endothelial gap. Of course, such results need to be confirmed further. In any case, this explanation provides an answer to the controversy on softer cells as opposed to rigid ones, indicating that local rheology is essential to understand this pathological mechanism: higher rigidity on the edge is required first, followed by rapid actin reorganization to push through the gap until the nucleus follows.
Conclusions
In this work, we have first explained the need for correcting AFM measurements in order to obtain reliable cell viscoelastic data, which are very sensitive with respect to substrate rigidity and thickness. Our results have shown that cancer cell properties are local, vary with invasiveness, and such cells adapt their rheology depending on substrate elasticity. In the case of an endothelial substrate, mechanosensitive effects were observed. With respect to this behavior and possible transendothelial migration leading to metastasis, invasive cancer cells exhibited locally tuned and highly dynamic mechanical properties. Further experiments are now possible to obtain real-time in vitro cell mechanical properties during transmigration.
Author Contributions
Y.A. performed all experiments and analyzed data. A.C. developed indentation models. V.M.L., V.S.R., R.M., V.L., A.D., and C.V. contributed analytical and experimental tools. A.D, V.M.L., and C.V. designed research. Y.A., A.D., and C.V. wrote the article.
Acknowledgments
We thank the Agence Nationale de la Recherche for grant No. 12-BS09-020-01 (TRANSMIG) and the Nanoscience Foundation for support of the AFM platform. This work has been partially supported by the LabeX Tec 21 (Investissements d’Avenir: grant agreement No. ANR-11-LABX-0030).
Editor: Steven Rosenfeld.
Footnotes
Supporting Materials and Methods, five figures, and one movie are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30070-5.
Supporting Material
References
- 1.Verdier C., Etienne J., Preziosi L. Review: rheological properties of biological materials. C. R. Phys. 2009;10:790–811. [Google Scholar]
- 2.Wirtz D., Konstantopoulos K., Searson P.C. The physics of cancer: the role of physical interactions and mechanical forces in metastasis. Nat. Rev. Cancer. 2011;11:512–522. doi: 10.1038/nrc3080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chotard-Ghodsnia R., Haddad O., Duperray A. Morphological analysis of tumor cell/endothelial cell interactions under shear flow. J. Biomech. 2007;40:335–344. doi: 10.1016/j.jbiomech.2006.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Weder G., Hendriks-Balk M.C., Mariotti A. Increased plasticity of the stiffness of melanoma cells correlates with their acquisition of metastatic properties. Nanomedicine (Lond.) 2014;10:141–148. doi: 10.1016/j.nano.2013.07.007. [DOI] [PubMed] [Google Scholar]
- 5.Gück J., Schinkinger S., Bilby C. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys. J. 2005;88:3689–3698. doi: 10.1529/biophysj.104.045476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cross S.E., Jin Y.-S., Gimzewski J.K. Nanomechanical analysis of cells from cancer patients. Nat. Nanotechnol. 2007;2:780–783. doi: 10.1038/nnano.2007.388. [DOI] [PubMed] [Google Scholar]
- 7.Lekka M. Discrimination between normal and cancerous cells using AFM. Bionanoscience. 2016;6:65–80. doi: 10.1007/s12668-016-0191-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Staunton J.R., Doss B.L., Ros R. Correlating confocal microscopy and atomic force indentation reveals metastatic cancer cells stiffen during invasion into collagen I matrices. Sci. Rep. 2016;6:19686. doi: 10.1038/srep19686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bischofs I.B., Klein F., Schwarz U.S. Filamentous network mechanics and active contractility determine cell and tissue shape. Biophys. J. 2008;95:3488–3496. doi: 10.1529/biophysj.108.134296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Guo M., Ehrlicher A.J., Weitz D.A. The role of vimentin intermediate filaments in cortical and cytoplasmic mechanics. Biophys. J. 2013;105:1562–1568. doi: 10.1016/j.bpj.2013.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Brangwynne C.P., MacKintosh F.C., Weitz D.A. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J. Cell Biol. 2006;173:733–741. doi: 10.1083/jcb.200601060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rigato A., Rico F., Scheuring S. Atomic force microscopy mechanical mapping of micropatterned cells shows adhesion geometry-dependent mechanical response on local and global scales. ACS Nano. 2015;9:5846–5856. doi: 10.1021/acsnano.5b00430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Santos J.A.C., Rebêlo L.M., de Sousa J.S. Thickness-corrected model for nanoindentation of thin films with conical indenters. Soft Matter. 2012;8:4441–4448. [Google Scholar]
- 14.Abidine Y., Laurent V.M., Verdier C. Local mechanical properties of bladder cancer cells measured by AFM as a signature of metastatic potential. Eur. Phys. J. Plus. 2015;130:202. [Google Scholar]
- 15.Caille N., Thoumine O., Meister J.-J. Contribution of the nucleus to the mechanical properties of endothelial cells. J. Biomech. 2002;35:177–187. doi: 10.1016/s0021-9290(01)00201-9. [DOI] [PubMed] [Google Scholar]
- 16.Thiam H.-R., Vargas P., Piel M. Perinuclear Arp2/3-driven actin polymerization enables nuclear deformation to facilitate cell migration through complex environments. Nat. Commun. 2016;7:10997. doi: 10.1038/ncomms10997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Alcaraz J., Buscemi L., Navajas D. Microrheology of human lung epithelial cells measured by atomic force microscopy. Biophys. J. 2003;84:2071–2079. doi: 10.1016/S0006-3495(03)75014-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rianna C., Radmacher M. Comparison of viscoelastic properties of cancer and normal thyroid cells on different stiffness substrates. Eur. Biophys. J. 2017;46:309–324. doi: 10.1007/s00249-016-1168-4. [DOI] [PubMed] [Google Scholar]
- 19.Discher D.E., Janmey P., Wang Y.-L. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 20.Lo C.M., Wang H.B., Wang Y.L. Cell movement is guided by the rigidity of the substrate. Biophys. J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Engler A., Bacakova L., Discher D. Substrate compliance versus ligand density in cell on gel responses. Biophys. J. 2004;86:617–628. doi: 10.1016/S0006-3495(04)74140-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Buxboim A., Rajagopal K., Discher D.E. How deeply cells feel: methods for thin gels. J. Phys. Condens. Matter. 2010;22:194116. doi: 10.1088/0953-8984/22/19/194116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Solon J., Levental I., Janmey P.A. Fibroblast adaptation and stiffness matching to soft elastic substrates. Biophys. J. 2007;93:4453–4461. doi: 10.1529/biophysj.106.101386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Étienne J., Fouchard J., Asnacios A. Cells as liquid motors: mechanosensitivity emerges from collective dynamics of actomyosin cortex. Proc. Natl. Acad. Sci. USA. 2015;112:2740–2745. doi: 10.1073/pnas.1417113112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Acerbi I., Cassereau L., Weaver V.M. Human breast cancer invasion and aggression correlates with ECM stiffening and immune cell infiltration. Integr. Biol. 2015;7:1120–1134. doi: 10.1039/c5ib00040h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.van Helvert S., Friedl P. Strain stiffening of fibrillar collagen during Individual and collective cell migration identified by AFM nanoindentation. ACS Appl. Mater. Interfaces. 2016;8:21946–21955. doi: 10.1021/acsami.6b01755. [DOI] [PubMed] [Google Scholar]
- 27.Alvarez-Elizondo M.B., Weihs D. Cell-gel mechanical interactions as an approach to rapidly and quantitatively reveal invasive subpopulations of metastatic cancer cells. Tissue Eng. Part C Methods. 2017;23:180–187. doi: 10.1089/ten.TEC.2016.0424. [DOI] [PubMed] [Google Scholar]
- 28.Zhu J., Liang L., Liu L., U.S.-China Physical Sciences-Oncology Alliance Enhanced invasion of metastatic cancer cells via extracellular matrix interface. PLoS One. 2015;10:e0118058. doi: 10.1371/journal.pone.0118058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Butcher D.T., Alliston T., Weaver V.M. A tense situation: forcing tumour progression. Nat. Rev. Cancer. 2009;9:108–122. doi: 10.1038/nrc2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Iordan A., Duperray A., Verdier C. Breakdown of cell-collagen networks through collagen remodeling. Biorheology. 2010;47:277–295. doi: 10.3233/BIR-2010-0575. [DOI] [PubMed] [Google Scholar]
- 31.Peschetola V., Laurent V.M., Verdier C. Time-dependent traction force microscopy for cancer cells as a measure of invasiveness. Cytoskeleton (Hoboken) 2013;70:201–214. doi: 10.1002/cm.21100. [DOI] [PubMed] [Google Scholar]
- 32.Mierke C.T., Rösel D., Brábek J. Contractile forces in tumor cell migration. Eur. J. Cell Biol. 2008;87:669–676. doi: 10.1016/j.ejcb.2008.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Koch T.M., Münster S., Fabry B. 3D Traction forces in cancer cell invasion. PLoS One. 2012;7:e33476. doi: 10.1371/journal.pone.0033476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Smith B.A., Tolloczko B., Grütter P. Probing the viscoelastic behavior of cultured airway smooth muscle cells with atomic force microscopy: stiffening induced by contractile agonist. Biophys. J. 2005;88:2994–3007. doi: 10.1529/biophysj.104.046649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rother J., Nöding H., Janshoff A. Atomic force microscopy-based microrheology reveals significant differences in the viscoelastic response between malign and benign cell lines. Open Biol. 2014;4:140046. doi: 10.1098/rsob.140046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Abidine Y., Laurent V.M., Verdier C. Physical properties of polyacrylamide gels probed by AFM and rheology. Europhys. Lett. 2015;109:38003. [Google Scholar]
- 37.Korsunsky A.M., Constantinescu A. The influence of indenter bluntness on the apparent contact stiffness of thin coatings. Thin Solid Films. 2009;517:4835–4844. [Google Scholar]
- 38.Trepat X., Lenormand G., Fredberg J.J. Universality in cell mechanics. Soft Matter. 2008;4:1750–1759. [Google Scholar]
- 39.Haddad O., Chotard-Ghodsnia R., Duperray A. Tumor cell/endothelial cell tight contact upregulates endothelial adhesion molecule expression mediated by NFkappaB: differential role of the shear stress. Exp. Cell Res. 2010;316:615–626. doi: 10.1016/j.yexcr.2009.11.015. [DOI] [PubMed] [Google Scholar]
- 40.Laurent V.M., Duperray A., Verdier C. Atomic force microscopy reveals a role for endothelial cell ICAM-1 expression in bladder cancer cell adherence. PLoS One. 2014;9:e98034. doi: 10.1371/journal.pone.0098034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sundar Rajan V., Laurent V.M., Duperray A. Unraveling the receptor-ligand interactions between bladder cancer cells and the endothelium using AFM. Biophys. J. 2017;112:1246–1257. doi: 10.1016/j.bpj.2017.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Palecek S.P., Loftus J.C., Horwitz A.F. Integrin-ligand binding properties govern cell migration speed through cell-substratum adhesiveness. Nature. 1997;385:537–540. doi: 10.1038/385537a0. [DOI] [PubMed] [Google Scholar]
- 43.Grevesse T., Versaevel M., Gabriele S. A simple route to functionalize polyacrylamide hydrogels for the independent tuning of mechanotransduction cues. Lab Chip. 2013;13:777–780. doi: 10.1039/c2lc41168g. [DOI] [PubMed] [Google Scholar]
- 44.Butt H.-J., Jaschke M. Calculation of thermal noise in atomic force microscopy. Nanotechnology. 1995;6:1–7. [Google Scholar]
- 45.Bilodeau G.G. Regular pyramid punch problem. J. Appl. Mech. 1992;59:519–523. [Google Scholar]
- 46.Dimitriadis E.K., Horkay F., Chadwick R.S. Determination of elastic moduli of thin layers of soft material using the atomic force microscope. Biophys. J. 2002;82:2798–2810. doi: 10.1016/S0006-3495(02)75620-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Korsunsky A.M., Constantinescu A. Work of indentation approach to the analysis of hardness and modulus of thin coatings. Mater. Sci. Eng. A. 2006;423:28–35. [Google Scholar]
- 48.Constantinescu A., Korsunsky A., Oueslati A. Symbolic and numerical solution of the axisymmetric indentation problem for a multilayered elastic coating. Int. J. Solids Struct. 2013;50:2798–2807. [Google Scholar]
- 49.Stamenović D., Rosenblatt N., Ingber D.E. Rheological behavior of living cells is timescale-dependent. Biophys. J. 2007;93:L39–L41. doi: 10.1529/biophysj.107.116582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lekka M., Lekki J., Hrynkiewicz A. Local elastic properties of cells studied by SFM. Appl. Surf. Sci. 1999;141:345–349. [Google Scholar]
- 51.Abidine Y. Université Grenoble Alpes; 2015. Propriétés mécaniques de cellules cancéreuses mesurées par AFM. PhD thesis. [Google Scholar]
- 52.Reymond N., d’Água B.B., Ridley A.J. Crossing the endothelial barrier during metastasis. Nat. Rev. Cancer. 2013;13:858–870. doi: 10.1038/nrc3628. [DOI] [PubMed] [Google Scholar]
- 53.Hau A.M., Nakasaki M., Hansel D.E. Differential mTOR pathway profiles in bladder cancer cell line subtypes to predict sensitivity to mTOR inhibition. Urol. Oncol. 2017;35:593–599. doi: 10.1016/j.urolonc.2017.03.025. [DOI] [PubMed] [Google Scholar]
- 54.Kaur S., Momi N., Batra S.K. Altered expression of transmembrane mucins, MUC1 and MUC4, in bladder cancer: pathological implications in diagnosis. PLoS One. 2014;9:e92742. doi: 10.1371/journal.pone.0092742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kang H.W., Kim W.-J., Yun S.-J. The role of the tumor microenvironment in bladder cancer development and progression. Transl. Cancer Res. 2017;6:744–758. [Google Scholar]
- 56.Saito T., Kimura M., Tomita Y. Correlation between integrin alpha 5 expression and the malignant phenotype of transitional cell carcinoma. Br. J. Cancer. 1996;73:327–331. doi: 10.1038/bjc.1996.57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Rico F., Roca-Cusachs P., Navajas D. Probing mechanical properties of living cells by atomic force microscopy with blunted pyramidal cantilever tips. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:021914. doi: 10.1103/PhysRevE.72.021914. [DOI] [PubMed] [Google Scholar]
- 58.Trichet L., Le Digabel J., Ladoux B. Evidence of a large-scale mechanosensing mechanism for cellular adaptation to substrate stiffness. Proc. Natl. Acad. Sci. USA. 2012;109:6933–6938. doi: 10.1073/pnas.1117810109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Guilluy C., Osborne L.D., Burridge K. Isolated nuclei adapt to force and reveal a mechanotransduction pathway in the nucleus. Nat. Cell Biol. 2014;16:376–381. doi: 10.1038/ncb2927. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.