Mechanism of Mechanosensitive Gating of the TREK-2 Potassium Channel

Abstract

The mechanism of mechanosensitive gating of ion channels underlies many physiological processes, including the sensations of touch, hearing, and pain perception. TREK-2 is the best-studied mechanosensitive member of the two-pore domain potassium channel family. Apart from pressure sensing, it responds to a diverse range of stimuli. Two states, termed “up” and “down,” are known from x-ray structural crystallographic studies and have been suggested to differ in conductance. However, the structural details of the gating behavior are largely unknown. In this work, we used molecular dynamics simulations to study the conductance of the states as well as the effect of mechanical membrane stretch on the channel. We find that the down state is less conductive than the up state. The introduction of membrane stretch in the simulations shifts the state of the channel toward an up configuration, independent of the starting configuration, and also increases its conductance. The correlation of the selectivity filter state and the conductance supports a model in which the selectivity filter gates by a carbonyl flip. This gate is stabilized by the pore helices. We suggest a modulation of these helices by an interface to the transmembrane helices. Membrane pressure changes the conformation of the transmembrane helices directly and consequently also influences the channel conductance.

Introduction

In 1950, Katz first observed the translation of mechanical stress into the depolarization of sensory nerve endings of frog muscles (1). More than half a century later, we still do not fully understand the transition from mechanical stress to a change in conductance of ion channels. However, many important physiological processes, such as touch, hearing, balance, and the sensation of pain, can nowadays be mapped to the function of mechanosensitive ion channels (2, 3).

Most of our structural understanding of mechanogating in ion channels comes from studies of the bacterial ion channels MscL and MscS (4). By computational studies, it was shown that in these channels, the surface tension of the lipid membrane directly induces a structural change (5, 6). This mechanism was suggested before and is known as the force-from-lipid principle (7, 8, 9).

Despite the wealth of knowledge gained from these bacterial channels, it remains unclear to what extent the same principles hold for the structurally unrelated mammalian channels. The mechanogated mammalian ion channels TRAAK, TREK-1, and TREK-2 form the TRAAK/TREK subfamily of two-pore domain potassium (K2P) channels (10). Whereas MscL and MscS channels can gate by opening a direct ion pathway through the cell, K2P channels have a very stable region, known as the selectivity filter, that constricts the ions to a single file. Therefore, the mechanism of these channels is expected to be very different.

K2P channels are present in a variety of cells and generate “leak” or “background” currents to stabilize resting membrane potential and represent important clinical targets for the treatment of cardiovascular diseases and several neurological disorders, including pain and depression (11).

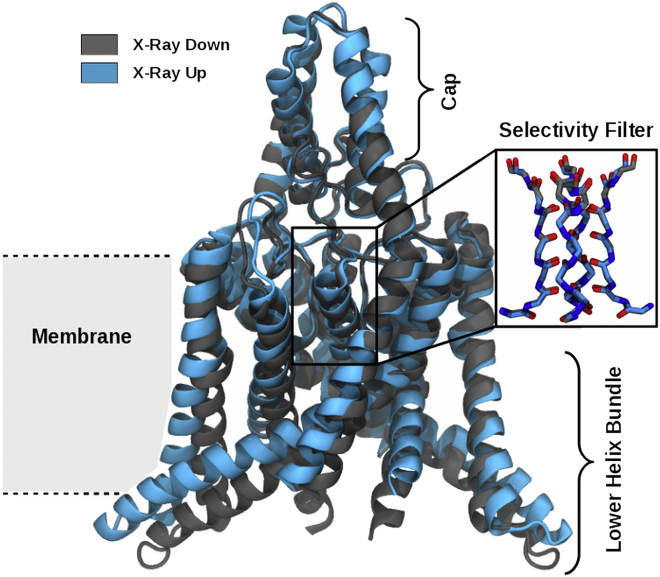
Even before crystal structures of the members of the TRAAK/TREK K2P subfamily were available, studies showed that a gate in these channels had to be located in the selectivity filter and not, as in other ion channels, in the lower helix bundle (12, 13, 14, 15). More recent studies suggest a gating mechanism similar to C-type inactivation, in which the gating takes place via a change in the selectivity filter conformation (16, 17). Crystal structures of the TRAAK and TREK-2 channels, respectively, revealed two different states, which were termed “up” and “down” (18, 19). The difference between these structures can only be found in the lower part of the channel that we termed the lower helix bundle, but not in the selectivity filter (see Fig. 1). This lower helix bundle is more extended in the membrane plane in the up state, whereas it points more into the cytoplasmic side in the down state. Ion occupancies of the selectivity filter have suggested the up state to be conductive and the down state to be nonconductive (18, 20, 21). In contrast, mutational studies on TRAAK reported the down state to be the stretch-activated state and therefore conductive (22).

Figure 1.

Crystallographic difference. Shown is the structural difference of the crystal up (PDB: 4BW5, x-ray up) and down (PDB: 4XDJ, x-ray down) structures of TREK-2 without C-terminus (19). The major difference between the two configurations can be found in the lower helix bundle, whereas the configuration of the selectivity filter is indistinguishable (inset). On the top of the channel, a cap region is located. The membrane in which the channel is embedded is sketched in the background. To see this figure in color, go online.

TREK-2 is the archetype channel of the TRAAK/TREK K2P subfamily on which many of the mechanosensing studies are performed. It was extensively studied and has been crystallized in the up and down states, a prerequisite for accurate molecular dynamics (MD) simulations (19). It is not only known to play a role in thermosensation and pain perception (23, 24) but is also an important pharmacological target (25). Multiple stimuli such as temperature, pH, mechanical force, and several drugs modulate its activation (26, 27, 28, 29). These characteristics make TREK-2 a suitable system with which to study mechanogating in K2P channels.

Recent MD simulations on TREK-2 demonstrated the ability to switch the channel from a down to an up configuration (and vice versa) by applying membrane tension (MT), whereas another nonmechanosensitive K2P channel did not show any response (30). The simulations further suggested the ion occupancy in the selectivity filter to be altered by MT. In addition, extensive simulations with Markov modeling revealed a pinched state of the selectivity filter that is destabilized by MT activation and is exclusively accessed in the down conformation (31).

Despite the insight gained from these studies, all results published so far were obtained without a physiological membrane potential and therefore do not yield insight into the conductance of the channel. We study the effect of MT as well as the difference between the up and down state on the channel conductance. Therefore, we simulated TREK-2 in its up and down state with a membrane potential as well as with applied MT.

Methods

The MD simulations, with a total time of 28 μs, were carried out using the Groningen Machine for Chemical Simulations (GROMACS) software package (version 5.0) (32, 33). The up (Protein Data Bank (PDB): 4BW5) and down (PDB: 4XDJ) crystal structures of the TREK-2 channel missing the C-terminus, which was demonstrated to retain stretch activation (19), were embedded into a 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine lipid membrane, as is common for mechanogating simulations (5, 30), and solvated in water with a K⁺ ion concentration of 1.2 M (as calculated by the number of ions relative to the number of water molecules in the system) and Cl⁻ ions to neutralize the system.

AMBER

MD simulations of MT were performed using the Assisted Model Building with Energy Refinement (AMBER) 99SB force field (34) with an extended simple point charge water model (35), Joung et al. (36) ion parameters, and Berger lipids (37, 38, 39). Velocity rescaling (40) was applied for temperature coupling to a reference temperature of 300 K. Berendsen pressure coupling (41) was applied to keep a constant pressure of 1 bar in the z direction with a time constant of $\tau =2.0$. For the x-y direction (membrane plane), the constant surface-tension coupling (32) was used to keep it at the reference value. Initial velocities were sampled from a Maxwellian distribution at 300 K. The bonds were constrained using the Lincs algorithm (42). By replacing the hydrogen bonds with virtual sites (33, 43), internal vibrational degrees of freedom of the hydrogen atoms were removed, allowing for a 4 fs time step. Short-ranged van der Waals interactions and electrostatic interactions were cut off at 1.0 nm each. The simulations were performed using periodic boundary conditions, allowing treatment of long-range electrostatic interactions by Particle Mesh Ewald summation (44, 45) with a grid spacing of 0.135 nm.

Missing atoms and loops in the crystal structure were modeled using the program LOOPY (46). To integrate the channel into the membrane, the “gmx membed” program was used (47). Subsequently, the system was minimized and equilibrated with restraints on the heavy atoms. For each of the MTs, four simulations of around 700 ns each were performed.

CHARMM

CHARMM (charmm36 ff (48)) simulations were set up using the Chemistry at Harvard Macromolecular Mechanics graphical user interface (CHARMM-GUI) (49) together with the membrane builder (49, 50, 51). The simulations were run using the GROMACS input generated by the CHARMM-GUI (52, 53). The minimization and equilibration were performed using the standard GROMACS inputs of the CHARMM-GUI. For conductance assessments, an external field of 400 mV was applied (54). This field creates a constant electrostatic potential on both sides of the membrane. The potential difference between the compartments thus equals the voltage of 400 mV. For the up and down state, 10 replicas of 600 ns each were run for each state, respectively.

Results and Discussion

The TREK-2 up state is more conductive than the down state

Comparing the up (PDB: 4BW5) and down (PDB: 4XDJ) crystal structures, we only found a difference in the lower helix bundle (Fig. 1). These crystal structures suggest a conductive up state and a nonconductive down state (19), whereas mutational studies suggest a conductive down state (22). Not only the conductance of the different states but also the mechanism by which the gating occurs remain unclear.

To find a functional difference between the crystal structures, we simulated both states in a membrane with an external electric field of 400 mV applied (54). This setup gives us the opportunity to study the current through the channel while observing its motion in atomistic detail. We chose this setup because it more readily allows the application of a membrane pressure as compared to the double-membrane setup utilized in computational electrophysiology (55).

Comparing the current of TREK-2 in simulations starting from the two different crystal structures, we found the channel in simulations starting from the up configuration to have a current of 8.6 $\pm$ 1.8 pA, whereas simulations starting from the down configuration had a current of only 4.0 $\pm$ 1.3 pA (Table 1). From this difference, we conclude that the up state is more conductive than the down state by a factor of two.

Table 1.

Summary of Simulations Results

	Up State	Down State
Simulations with Relaxed Membrane
Total simulation time (μs)	7.4	7.3
Number of ion permeations	396	181
Current (pA)	8.6 $\pm$ 1.8	4.0 $\pm$ 1.3
Current, no flip (pA)	13.6 $\pm$ 1.6	9.5 $\pm$ 2.2
Number of water permeations	19	19
Flips (%)	37 $\pm$ 12	60 $\pm$ 11
Permeations after direct knock-on (%)	90 $\pm$ 7	82 $\pm$ 9
Simulations with Stretched Membrane
Current (pA)	13.4 $\pm$ 1.9	12.9 $\pm$ 1.5
Flips (%)	10 $\pm$ 7	10 $\pm$ 10

How this result compares to that of experiments is hard to address because in experiments the state of the channel cannot be determined while measuring a current. Likewise, the crystal structures do not allow us a direct readout of the difference in conductance. However, previous experimental studies on TREK-2 investigated single-channel electrophysiology traces (27, 56). These studies consistently found multiple states of conductance, a closed state without any current, and multiple open states that were multiples of each other. The nonconductance of the closed state is in agreement with our flipped state in which no ions permeate. Furthermore, the open state of the channel shows a current of 6 pA at an applied voltage of 80 mV. These findings are in agreement with our simulations, resulting in a current of ∼14 pA at 400 mV for the conductive state. Such an agreement is a strong indicator that we have sampled the correct mechanism of permeation. The additional open states could be due to multiple channels being measured simultaneously.

To find an explanation for the observed difference in conductance for the two states, we address the dynamic properties of the channel in the following section.

The up state stabilizes the selectivity filter

Previous studies suggest the ion gate to be located at the selectivity filter (12, 13, 14, 15). However, in the crystal structures, the selectivity filter of the up state is identical to that of the down state. As the crystal structures give a static picture only, we use the advantage of simulations to account for the flexible nature of proteins on short timescales and in atomistic detail. Therefore, we analyzed the behavior of the selectivity filter in relation to ion permeations.

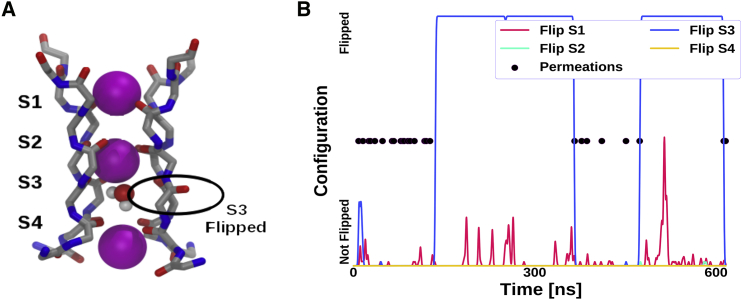
In Fig. 2, the permeation events and the selectivity filter configuration of an example trajectory (up state) are shown. When the selectivity filter is in its crystallographic configuration, ions permeate at an even rate. In this example trajectory, a flip of one of the carbonyl groups (S3 in subfigure A) occurs after 150 ns. At the same time, the ions stop permeating. At around 400 ns, the flip is spontaneously reversed. We see that the ions start permeating again. When a flip occurs, we find a water molecule present in the selectivity filter sitting at the binding site of the flip, as can be seen in Fig. 2 A. In this configuration, the flipped carbonyl and the water are stabilizing each other. The reversion of a flip to a permeating configuration is accompanied by the water permeating and thus leaving the channel. The same behavior is consistent across all simulations and for up and down starting configurations. Because we saw events of water copermeation, we further investigated the permeation mechanism. To analyze the mechanism, we computed the number of permeations after the direct knock-on mechanism (21). A permeation event was assigned to the direct knock-on type if no permeating water could be found in the selectivity filter at the time of permeation. Both states clearly favored the pure, direct knock-on mechanism, which more than 80% of the permeations exhibited (Table 1).

Figure 2.

Permeations and carbonyl flips. (A) The conformation of the selectivity filter is shown on the left. S1–S4 correspond to the carbonyls separating the binding sites rather than to the binding sites themselves. The selectivity filter is filled with potassium ions (spheres). The carbonyl S3 shows a flipped configuration with a water molecule inside the selectivity filter. (B) Dots represent ion permeation events. In relation to this, the selectivity filter configuration is shown as lines (Flip S1–S4 represent the state of the corresponding carbonyl group). If the line is at the bottom, it represents a configuration in which all carbonyls of the corresponding site of the selectivity filter are in their canonical configuration (as seen in Fig. 2A for S2). The top represents a state in which at least one carbonyl of the respective site is steadily flipped (as seen in Fig. 2A for S3). If the line is in the intermediate area, it represents a temporarily flipped state (less than 1 ns), and the height shows its duration. If no flip is present, the channel shows permeation events. When S3 flips after around 150 ns, permeations stop. At around 400 ns, the S3 carbonyl flips back into the canonical configuration, and permeations resume. This behavior is representative for all simulations. To see this figure in color, go online.

These results suggest the probability of flips to be the discriminating factor between simulations starting from the up and down structures. To test this hypothesis, we further analyzed the probability of flips in both states and also the current of the channels where no flip was present (Table 1). Indeed, we found that when only the nonflipped parts are taken into account, a more similar current is found for the up and down state. The difference that is not accounted for is mainly due to a single trajectory displaying a subconductive behavior. Consistently, we found that the probability of being in a flipped state is statistically significantly increased for the down state, as expected. As the water block occurs together with the flip, two possible pathways could explain the difference of flip probability. The first pathway includes a change in the probability of a water molecule to enter the SF, whereas subsequently the probability of the SF to show a flipped state remains the same if a water molecule is present. The second pathway does not change the probability of a water molecule to enter the SF, but rather the probability of a flip to occur if a water molecule is present. To test which pathway is more likely we analyzed the water permeations in our simulations. In all 10 simulations of the up state, 19 water permeations occurred (Table 1). This number is the same as for the simulations of the down state. The same number of water permeations in both states suggests the same probability of water to enter the channel. Consequently, the probability for the carbonyls to flip depends on the state rather than on the water permeation probability.

However, comparison between experiments and our simulations reveal a difference in timescales on which the channel switches between the two states. In our simulations, the switching occurs on a nanosecond-microsecond timescale, whereas in experiments, the gating occurs on a millisecond timescale. The comparison to experimental results makes us believe that the CHARMM force field, as applied in these simulations, samples the protein dynamics faster, leading to reduced time required for selectivity-filter state transitions.

In contrast to our findings of a flip dominantly occurring in S3 (see Fig. 2 A), Aryal et al. (30) found a flip of the selectivity filter occurring in the carbonyl of selectivity filter binding site zero (S0)/S1 binding site when doing comparable simulations. However, these simulations were performed without an external membrane potential. We found that the behavior of the ions in the selectivity filter changes significantly depending on the electric field. Spontaneous leaving of an ion at S0 is very likely with and without an external field. When an external field is applied, ions from the other binding sites tend to move into the void created by an ion that leaves S0, preventing the carbonyls of that binding site to flip.

The probability of flips can explain the difference in conductance between the states. However, how the flip probability is altered by the overall configuration of the channel could not be resolved. TREK activator studies found that the selectivity filter can directly be activated by a ligand binding behind it. This study further suggests a mobility reduction of the interface between the pore helix and transmembrane helix four (TM4) to be the reason for the activation (57). Furthermore, structural analysis of functionally relevant mutations as well as differing wild-type structures also suggest an allosteric transition of the information from the TM2 and/or TM4 helices toward the selectivity filter (22). Together with various studies suggesting a selectivity filter gate, we find our results to be strongly supported (12, 13, 14, 15, 16, 17). Based on these previous results and our own findings, we suggest the relative stability of the flipped versus nonflipped configuration of the selectivity filter to be altered by the state of the channel and to therefore be the discriminating factor between the conductive versus nonconductive state. Possible reasons for the flipped state of the selectivity filter not being observed in crystallographic studies so far could be due to its transient occurrence as well as the high ionic concentration used for crystallization, which likely stabilizes the canonical configuration.

Membrane stretch switches between the up and down state

So far, we identified a possible mechanism by which the conductance of TREK-2 can be linked to the different crystallographic states. To identify the mechanism by which the channel reacts to pressure, we performed further simulations. The majority of these simulations were performed in the AMBER99SB force field (34), and only two MTs were simulated in the standard charmm36 force field (48, 49) as a reference.

When the pressure activation of the channel is measured in an experiment, a suction is applied to the membrane, which leads to a distortion of the membrane, bending and stretching it simultaneously. The pressure activation of the channel is independent of the direction in which the pressure is applied, indicating a stretch activation rather than a membrane bend activation (10). Results from Aryal et al. (30) suggest that stretch activation of TREK-2 occurs by a down-to-up transition. To test this more extensively, we simulated TREK-2 at different MTs and analyzed the effect of the stretch on the current and on the structure of the channel.

The current of the channel increases by MT for both states, and simulations starting from both states reach the same conductance of around 13 pA (Table 1). By comparing the percentage of flips, we find a significant decrease (a Fisher’s test of the number of simulations with and without flips results in $p=0.001$). This decrease is likely the reason for the change in conductance.

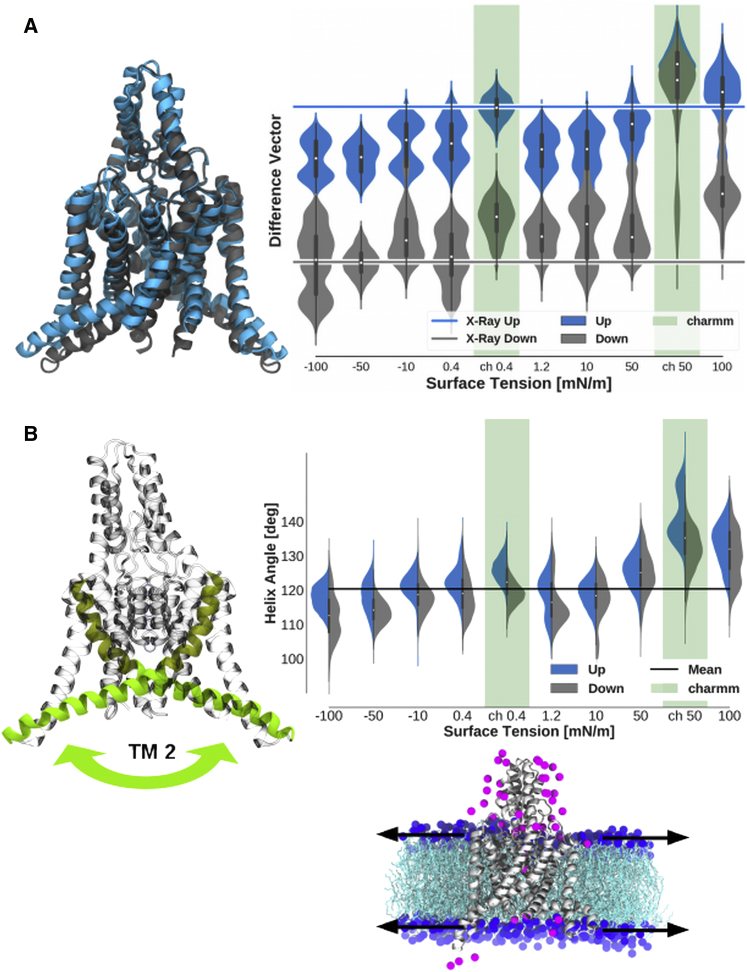
To investigate if the pressure-induced structural changes are related to the structural difference between the up and the down state, we used the crystallographic difference vector of TREK-2 without the cap region and mapped the structure of the different MT simulations after every 1 ns onto it (Fig. 3 A). This transition mode incorporates the relevant motion of the protein.

Figure 3.

Effects of membrane tension on the up-down difference vector and on the TM2 helix angle. (A) Shown is a projection of simulations at different membrane tensions projected onto the difference vector of the crystallographic states (excluding the cap). On the x axis, the membrane tension is shown. The figure at the bottom represents the simulation setup where the channel is located inside the membrane and is shown with some ions surrounding them. The arrows represent the stretch applied to the membrane. The lines in (A) represent the configuration of the crystallographic state (x-ray down, PDB: 4XDJ; x-ray up, PDB: 4BW5). The violins represent the probability of the simulations starting from the up and down structures to be at the position on the difference vector. The dot in the violin represents the average over all simulations, and the bars represent the variance of the data points summarized in the respective violins. MD simulations using the CHARMM force field are highlighted. Going from a negative (compression) to a positive (stretch) tension of the membrane, the configuration of TREK-2 moves along the difference vector from a more down-like configuration to a more up-like configuration. Only the CHARMM simulations are flexible enough to reach the up state. (B) Quantification of the helix angle between the transmembrane helix 2 (TM2) of the two subunits. The violins show the distribution of the helix angle for different membrane tensions. The helix flattens out in the membrane with stretch applied (represented by a larger TM2 angle between the helices), whereas a compression of the membrane results in a steeper position of the helix in the membrane, which is represented by a smaller angle between the TM2 helices of the subunits. Up and down simulations show a minor difference, with the up simulations having a tendency toward a larger helix angle. deg, degree. To see this figure in color, go online.

The projection shows a significant movement toward the up state when the membrane is stretched. In contrast, the trend is toward the down state when there is no stretch or a compressed membrane. However, the simulations seem to be not fully converged yet, as they do not show a Gaussian distribution as expected. Focusing on the CHARMM trajectories, we see a full transition toward the up state. This full transition is compatible with the previously observed faster dynamics of the selectivity filter.

In the simulations with applied membrane pressure, we see a major effect on the transmembrane helix two (TM2). Therefore, we analyzed the reaction of these helices on the MT in more detail. To do so, we used the same simulations as previously mapped on the crystallographic difference vector. In these simulations, we calculated the angle between the TM2 helices of the two subunits. The results are shown in Fig. 3 B. When a membrane stretch is applied, the angle between the TM2 helices is increased. This means the helices move further into the plane of the membrane. The compression of the membrane, in contrast, reduces the angle between the TM2 helices.

As the MT is translated mainly in a change in the TM2 helices, we suggest that in the absence of the C-terminus, which is not resolved in the crystal structures, TM2 is the major force-sensing domain. Looking at the effect of the MT, we see a decrease of membrane thickness by stretch. We suggest the change in membrane thickness to be a major pathway for changing the helix angle. We speculate that the movement of the lower helices, which are directly in contact with the membrane, propagates to the pore helices, which in turn affects the region behind the selectivity filter. As this is the area the carbonyls rotate into upon flipping, we suggest that these changes affect the flip probability and, with that, the channel conductance. Further investigation on this mechanism will be conducted in the future.

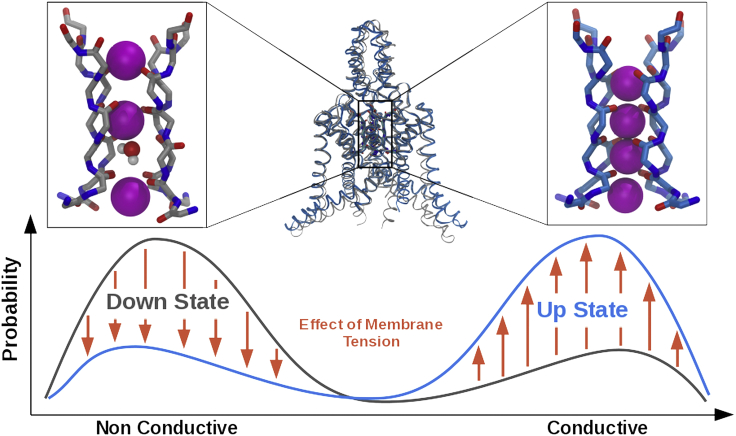
We propose a model of gating that extends the model of McClenaghan et al. (58). This model includes our findings for the difference in conductance determined from the up and down starting configurations as well as the effect of MT on the channel configuration and current (Fig. 4). We suggest that up and down states have different probabilities to be in either the conductive or nonconductive state. When the channel is in the up state, it is more likely to be in the conductive state, whereas the down state increases the probability of being in the nonconductive state. The conductive state is characterized by a canonical selectivity filter configuration, whereas the nonconductive state has a carbonyl flip in the selectivity filter, resulting in the disruption of the current. The effect of the MT is to change the configuration of the channel. Stretch of the membrane moves the channel from a more down-like to a more up-like configuration. Together with the relation of the up and/or down state to conductance of the channel, this model is proposed to explain the observed mechanogating.

Figure 4.

Relation of up- and down state to conductance. Here, we summarize our results into a gating model. The down state is more likely to be in a nonconductive conformation than the up state (lines). The down state is represented by a selectivity filter configuration with a flip and a water molecule in the selectivity filter. In contrast, the up state is more likely to be in a conductive configuration, as represented by a canonical selectivity filter with full ion occupancy. Applying membrane tension (arrows) changes the state of the protein toward a more up-like configuration that is more conductive. To see this figure in color, go online.

Conclusions

To study the mechanogating mechanism of TREK-2 in atomistic detail, we performed MD simulations of the channel in a lipid membrane with applied MT. The simulations revealed a factor of two difference in conductance for simulations that started from the up and the down state. Further investigation of the underlying reason suggests that a difference in the relative stability of the selectivity filter functions as the distinguishing factor for conductance. In the up state, the selectivity filter is less likely to adopt a nonconductive conformation compared to the down state. The nonconductive conformation is characterized by a deviation from the canonical selectivity filter configuration—the flipped conformation—characterized by an outward-pointing carbonyl group. This flipped conformation prevents ions from passing through the filter and is frequently accompanied by a water molecule in the filter.

The results are consistent with a proposed mechanism by which the transmembrane helices TM2 and TM4 change the interface of TM4, with the pore helices behind the selectivity filter (57). We suggest that this change of the interface subsequently alters the relative stability of the selectivity filter states.

Consistent with findings reported by Aryal et al. (30), we found MT to alter the state of the channel, especially of the lower helix bundle, to adopt a more up- or down-like conformation by membrane stretch or compression, respectively. This results in an increase of current by membrane stretch.

Based on these results, we propose the following model of gating, which is illustrated in Fig. 4. In this model, applied membrane stretch makes the channel more likely to adopt the up state compared to the down state. Furthermore, the up state stabilizes the selectivity filter, leading to an (on average) more conductive channel as compared to the down state. This mechanical tension of the membrane can thus translate into a change in conductance of TREK-2.

Author Contributions

J.T.B. and B.L.d.G. developed the concept of the study. J.T.B. prepared and performed the simulations and analysis. J.T.B. and B.L.d.G. wrote the article.

Editor: Jose Faraldo-Gomez.