Prediction of In-hospital Mortality in Emergency Department Patients With Sepsis: A Local Big Data–Driven, Machine Learning Approach

Abstract

Objectives

Predictive analytics in emergency care has mostly been limited to the use of clinical decision rules (CDRs) in the form of simple heuristics and scoring systems. In the development of CDRs, limitations in analytic methods and concerns with usability have generally constrained models to a preselected small set of variables judged to be clinically relevant and to rules that are easily calculated. Furthermore, CDRs frequently suffer from questions of generalizability, take years to develop, and lack the ability to be updated as new information becomes available. Newer analytic and machine learning techniques capable of harnessing the large number of variables that are already available through electronic health records (EHRs) may better predict patient outcomes and facilitate automation and deployment within clinical decision support systems. In this proof-of-concept study, a local, big data–driven, machine learning approach is compared to existing CDRs and traditional analytic methods using the prediction of sepsis in-hospital mortality as the use case.

Methods

This was a retrospective study of adult ED visits admitted to the hospital meeting criteria for sepsis from October 2013 to October 2014. Sepsis was defined as meeting criteria for systemic inflammatory response syndrome with an infectious admitting diagnosis in the ED. ED visits were randomly partitioned into an 80%/20% split for training and validation. A random forest model (machine learning approach) was constructed using over 500 clinical variables from data available within the EHRs of four hospitals to predict in-hospital mortality. The machine learning prediction model was then compared to a classification and regression tree (CART) model, logistic regression model, and previously developed prediction tools on the validation data set using area under the receiver operating characteristic curve (AUC) and chi-square statistics.

Results

There were 5,278 visits among 4,676 unique patients who met criteria for sepsis. Of the 4,222 patients in the training group, 210 (5.0%) died during hospitalization, and of the 1,056 patients in the validation group, 50 (4.7%) died during hospitalization. The AUCs with 95% confidence intervals (CIs) for the different models were as follows: random forest model, 0.86 (95% CI = 0.82 to 0.90); CART model, 0.69 (95% CI = 0.62 to 0.77); logistic regression model, 0.76 (95% CI = 0.69 to 0.82); CURB-65, 0.73 (95% CI = 0.67 to 0.80); MEDS, 0.71 (95% CI = 0.63 to 0.77); and mREMS, 0.72 (95% CI = 0.65 to 0.79). The random forest model AUC was statistically different from all other models (p ≤ 0.003 for all comparisons).

Conclusions

In this proof-of-concept study, a local big data–driven, machine learning approach outperformed existing CDRs as well as traditional analytic techniques for predicting in-hospital mortality of ED patients with sepsis. Future research should prospectively evaluate the effectiveness of this approach and whether it translates into improved clinical outcomes for high-risk sepsis patients. The methods developed serve as an example of a new model for predictive analytics in emergency care that can be automated, applied to other clinical outcomes of interest, and deployed in EHRs to enable locally relevant clinical predictions.

Predictive analytics in emergency care has traditionally been limited to the use of clinical decision rules (CDRs) in the form of simple heuristics and scoring systems focused on appropriate test utilization, risk of serious outcomes, and prognosis.^1,2 In the development of CDRs, constraints in analytic methods and concerns over usability (e.g., manual data entry and/or calculation of scores) have generally confined models to a preselected small set of variables judged to be clinically relevant and to rules that are easily calculated.^3,4 This approach excludes potentially important factors for prediction that might not be identified or known a priori and often sacrifices prediction accuracy for ease of computability and interpretability.⁵ Furthermore, CDRs frequently suffer from questions of generalizability and performance variance when applied to the populations different from the derivation cohort,^6,7 often take years to develop and validate,⁸ and are unlikely to be updated as new information becomes available.⁹

The application of preprocessing, data mining, and machine learning techniques to big data stored in the electronic health records (EHRs) of a hospital or health care system provides an alternative, data-driven approach to predictive analytics in emergency care.^2,10 EHRs enable access to, and the collection of, large volumes of clinical data within emergency department (ED) visits.¹¹ Data pipelines on EHR data can be developed that clean data through preprocessing steps, discover novel relationships through data mining, and ultimately make analytic predictions based on new, more sophisticated techniques.¹² These big data analytic techniques are potentially scalable and transferable to other domains of care.¹³ They also can be updated as new information is acquired and are local, thus eliminating questions of applicability. In essence, they reflect a key component of the push toward a learning health care system.¹⁴ These techniques, however, are not without limitations and issues of interpretability, infrastructure investment, and technical requirements for implementation must be addressed.¹⁵ Yet, nowhere in the health care system is the need more pressing to find methods to reduce uncertainty than in the fast, chaotic environment of the ED.¹⁶

Our objective in this study was to provide a proof-of-concept example of a local, big data–driven, machine learning approach to predictive analytics in emergency care. We chose prediction of sepsis mortality as the use case because of its clinical importance (half of hospital deaths in the United States are related to sepsis)¹⁷ and because early detection and treatment has been shown to improve outcomes.^18,19 In addition, CDRs such as the Mortality in Emergency Department Sepsis score (MEDS);²⁰ the Rapid Emergency Medicine Score (REMS);²¹ and the Confusion, Urea nitrogen, Respiratory Rate, Blood pressure, 65 years of age and older (CURB-65)^22,23 score are well described in the literature and offer a means of comparison. We hypothesized that a data-driven approach using a sophisticated machine learning technique with EHR data for predictive analytics would outperform existing CDRs and traditional analytic techniques (logistic regression and classification and regression tree [CART] analysis).

METHODS

Study Design

This was a retrospective study of ED visits resulting in inpatient admission. This study was approved by the institutional review board and adhered to the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) statement on reporting predictive models.²⁴

Study Setting and Population

Data were obtained from four EDs over a 12-month period (October 2013 to October 2014). All EDs were part of a single health care system: the first ED was an urban, academic, Level I trauma center with an annual census over 85,000 patients; the second ED was an urban community-based, academic Level II trauma center with an annual census over 70,000 patients; the third ED was a community-based center with an annual census over 75,000 patients; and the fourth ED was a suburban, free-standing ED with annual census over 30,000 patients. All three hospital-based EDs had intensive care units capable of providing advanced care for sepsis. All hospitals used the Epic ASAP (Verona, WI) EHR.

We included all visits for adult patients (≥18 years) who met criteria for systemic inflammatory response syndrome (SIRS)¹⁹ at some point during their ED visit and who were admitted with an infection diagnosis from the ED. An admitting infection diagnosis was determined by linking International Classification of Diseases–9th edition (ICD-9) codes with the Agency for Healthcare Research and Quality (AHRQ) Clinical Classification Software (CCS), which categorizes over 14,000 available ICD-9 diagnostic codes into 255 clinically meaningful categories,²⁵ and by performing regular expression searches on the categories (see Data Supplement S1, available as supporting information in the online version of this paper, for list of expression terms). A total of 1,697 ICD-9 codes were included as indicative of infection or sepsis. We chose to use ICD-9 codes linked to the AHRQ Clinical Classification Software and filtered based on regular expression searches for infectious terms, as this approach provided a more inclusive and exhaustive list of patients with infection than metrics previously used (e.g., blood culture being ordered),²⁰ avoided patient inclusion by indications, which is potentially fraught with reliability challenges,²⁶ was closely aligned with previously used definitions of sepsis from claims data,²⁷ and was an almost fully automated process that could be easily extended into other domains. We excluded all visits in which the patient died in the ED or was discharged from the ED.

Study Protocol

Data Set Creation and Definitions

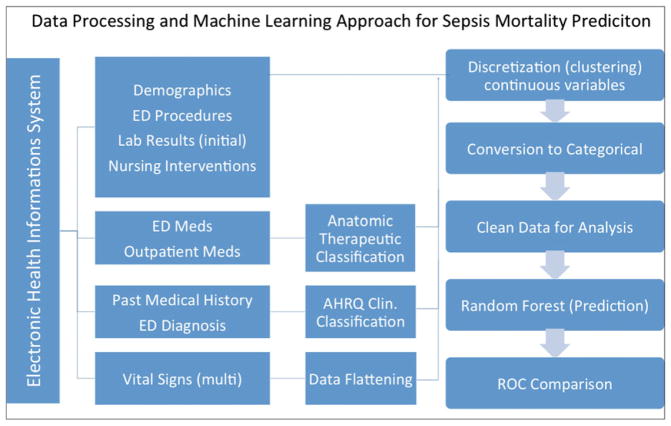
All data elements for each ED visit were obtained from the enterprise data warehouse Clarity (Epic). Only data available or generated during the ED visit until the time of admission were used as prediction variables. Structured Query Language (SQL) queries were written to identify and abstract all demographic information (e.g., age, sex, insurance status, employment, marital status, race), previous health status (e.g., past medical and surgical history, outpatient medications), ED health status (e.g., triage emergency severity index, chief complaint, vital signs, mental status, laboratory result values, code status, ED clinical impression, and hospital discharge diagnosis), ED services rendered (e.g., supplemental oxygen type, EKG performance, ED medications administered, ED procedures), and operational details (e.g., weekend presentation, ED arrival method; see Data Supplement S2, available as supporting information in the online version of this paper, for full variable list). Each data element necessary for the calculation of previously published prediction models was mapped to structured data elements to ensure reliable comparison. ICD-9 codes for past medical history, ED clinical impression, and hospital discharge diagnoses were recoded to AHRQ CCS categories. Prior medication usage, as well as medications administered, was recategorized using a string search into the Anatomical Therapeutic Chemical Classification System (ATC) for medications,²⁸ with 89 possible therapeutic drug classes. Vital sign information collected over time was mapped into first, last, mean, minimum, and maximum values for each patient encounter. All descriptive statistics were calculated using Stata (Version 13.1), and the data processing steps can be found in Figure 1.

Figure 1.

Data processing and machine learning approach for sepsis mortality prediction. All variables were obtained from structured data elements within the electronic health record. Certain data elements were linked to existing classification systems. Vital signs were flattened (first, last, mean, maximum, and minimum values were obtained). Continuous variables were subsequently discretized using kmeans clustering before the random forest model was constructed. ROC = receiver operating characteristic curve.

Data Preprocessing

All continuous variables were placed into five discrete categories using K-means clustering.^29–31 K-means clustering aims to divide data into k clusters in which each data point belongs to the cluster with the closest mean. The selection of five clusters was based on balanced considerations of interpretability versus reductions in clustering variance. We chose k = 5, as it is a small enough number of clusters to map into preconceived clinical and laboratory notions (critically low, low, normal, high, critically high) and represents a reasonable inflection point in which further numbers of clusters do not appreciably change the cluster variance.^32,33 Missing values (e.g., a result of not performing a test) were included and treated as categorical values within the models. In the context of clinical care, missing values often provide additional information about patients (e.g., not ordering a troponin on a patient with abdominal pain) and can improve prediction performance.³⁴ The same approach to clustering was applied to the first laboratory result value if the test was ordered in the ED. Categorical variables (race, arrival method, etc.) were included in the models in their current categorical form.

Outcomes

The primary outcome for all analyses was in-hospital mortality, defined as in-hospital death within 28 days of admission without interval transfer or discharge.^20,21

Model Generation and Comparison

Our primary analysis sought to compare the predictive accuracy of a local big data–driven, machine learning approach to previously developed CDRs and traditional analytic techniques for classification. Three models were developed based on random forest methods, CART analysis, and logistic regression. The random forest model served as the newer machine learning approach and was trained using all available variables. CART and logistic regression models were chosen as traditional models as they have previously been used to develop most CDRs in emergency medicine.³ For CART and logistic regression, we adhered to traditional methods for variable selection, selecting variables a priori based on literature and clinician input.^3,4 Both the CART and the logistic regression models included 20 predictor variables (Data Supplement S3, available as supporting information in the online version of this paper) for which a literature review–based linkage to sepsis outcomes has been established. Twenty variables were chosen to approximate the recommended 10:1 ratio of events to predictors based in the training data.³⁵ Data preprocessing steps (discussed above) were common to all three models and were designed to smooth the data by reducing the effect of outliers and influential data points and to accommodate for missing variables. All three models were trained and tested on a randomly partitioned 80%/20% split of the data. The predictive accuracies of the models were then compared to previously validated prediction tools: a modified REMS (where GCS is recoded into “altered mental status”),³⁶ MEDS, and CURB-65. While the CURB-65 score was originally developed to determine prognosis in sepsis patients with pneumonia, several studies afterward have applied it to a more general sepsis population.^22,36,37 We provide it in addition to the more widely used MEDS score to support the construct validity of our findings. We did not include other frequently used CDRs for sepsis prognostication that require data not routinely collected or available during the ED visit, and have only been applied to narrower intensive care unit populations.^38,39

We report the area under the curve (AUC) and receiver operating characteristic curves (ROC) as the primary measure of model prediction.⁴⁰ Model comparison was performed in STATA using the command roc-comp to evaluate significance via chi-square statistics.⁴¹ A p-value of 0.05 was considered statistically significant.

Logistic Regression Model

We used a multivariate logistic model with mixed effects as the first example of a traditional model (R Statistical Software, lme4 package). We adjusted for clustering at the hospital level and for patients with multiple ED visits. Because the data were smoothed through preprocessing, additional diagnostic checks for outliers and influential data points were not performed. Additionally, as all 20 variables used in the model were thought to contribute to sepsis outcomes, no additional variable selection procedures were performed. The Hosmer-Lemeshow goodness-of-fit test was used to assess model fit.

CART Model

We used CART analysis (R, rpart package) as the second example of a traditional model.^42,43 In a tree-based classifier such as CART, decisions are modeled in a single tree by successive binary splits of the data based on variable values. Decision trees determine on which variable to split using criteria that attempt to maximize the separation of individual classes of the target variable. This process is repeated until a stop criterion is met or the data has been fully separated. Tree-based classifiers have several advantages over parametric techniques like logistic regression in that they are more efficient at dealing with high-dimensional data and complex interactions, handle missing values, and have no distribution or parameter requirements.⁴⁴ However, decision trees are susceptible to small fluctuations in the training set (i.e., have high variance) and are thus prone to overfitting and poor generalizability.⁴⁵ To reduce overfitting, the decision tree was pruned based on cross-validated error results using the complexity parameter associated with minimal error.⁴²

Random Forest Model

Random forest was selected as the modern machine learning based model and can be thought of as an extension to traditional decision tree base classifiers.⁴⁶ Random forest was chosen over other machine learning techniques (e.g., neural networks, support vector machines) due to its similarity to CART and advantages handling EHR data outlined below. Random forest attempts to mitigate the limitations of decision trees through an ensemble-based technique using multiple decision trees (i.e., “forest). Each tree is constructed from a random subset of the original training data. At each node for splitting, a random subset of the total number of variables is analyzed. By taking the mode of the decisions of a large number of these randomly generated trees (making use of the law of large numbers),⁴⁷ random forests are able to minimize the problem of overfitting. Some additional advantages of random forests for EHR data sets include running efficiently on large samples with thousands of input variables, the ability to accommodate different data scales (e.g., lactate and serum sodium have different normal values), and a robustness to the inclusion of irrelevant variables.¹⁹ Random forest methods were generated in R using the party package and the cforest unbiased function, with 500 trees. Twenty-five variables were evaluated as potential splitters at each node, representing approximately the square root of the number of independent variables.⁴⁸ Following the methods of Strobl et al.,⁴⁹ individual conditional inference trees were constructed using bootstrap samples of the full data set. Samples were drawn without replacement, and sample size was selected to represent the percentage (63.2%) of unique data that would be obtained from bootstrap sampling with replacement. Variables of importance in the random forest were calculated based on permutation importance. Importantly, permutation importance does not control for correlated variables.⁵⁰ The result is that multiple similar variables may cluster along the same importance range (e.g., maximum respiratory rate recorded and initial respiratory rate) in variable importance plots.

RESULTS

There were 5,278 visits among 4,676 unique patients who met criteria for SIRS and an infectious admitting diagnosis. Of the 4,222 visits in the derivation group, 210 (5.0%) patients died during hospitalization, and of the 1,056 visits in the validation group, 50 (4.7%) patients died during hospitalization. Patient demographic and clinical characteristics of the derivation and validation groups are presented in Table 1.

Table 1.

Characteristics of the Study Sample

Characteristic	Training, n (%) (N = 4,222)	Validation, n (%) (N = 1,056)
Demographics
Age (yr), mean ± SD	66.1 ± 20.1	64.7 ± 19.3
Sex (n, % female)	2248 (53.2)	603 (57.1)
Race
Asian	32 (0.9)	4 (0.4)
Black or African American	762 (18.1)	186 (17.6)
Other	455 (10.8)	120 (11.3)
Patient refused	52 (1.2)	10 (0.95)
White	2921 (69.2)	735 (69.6)
Ethnicity
Hispanic/Latino	511 (12.1)	142 (13.5)
Not Hispanic/Latino	3667 (86.9)	912 (86.4)
Unknown	37 (0.88)	0 (0.00)
Patient refused	7 (0.17)	2 (0.19)
Primary insurance status
Private/HMO	660 (15.6)	166 (15.7)
Medicaid	712 (16.9)	180 (17.8)
Medicare	2437 (57.7)	578 (54.7)
Self-pay/uninsured	409 (9.7)	123 (11.6)
Other	4 (0.1)	1 (0.1)
Arrival by ambulance	2623 (62.1)	610 (57.8)
Triage acuity (ESI), mean ± SD	2.4 ± 0.6	2.5 ± 0.6
Lactate*	2.0 ± 1.7	1.9 ± 1.6
Vasopressors	126 (3.0)	28 (2.6)
Intubations	58 (1.4)	16 (0.9)
ED disposition
ICU	682 (16.2)	145 (13.7)
Step-down unit	551 (13.1)	137 (13.0)
Floor	2989 (70.8)	774 (73.3)
In-hospital mortality	210 (5.0)	50 (4.7)
Severity scores, median (IQR)
CURB-65	2 (1–3)	2 (1–3)
MEDS	6 (3–8)	5 (3–8)
mREMS	6 (4–8)	6 (4–8)

CURB-65 = Confusion, Urea nitrogen, Respiratory rate, Blood pressure, ≥65 years; ESI = Emergency Severity Index; ICU = intensive care unit; IQR = interquartile range; MEDS = Mortality in ED Sepsis; mREMS = modified Rapid Emergency Medicine Score

^*Lactate only ordered in 38% of training data visits, and 40% of validation data visits

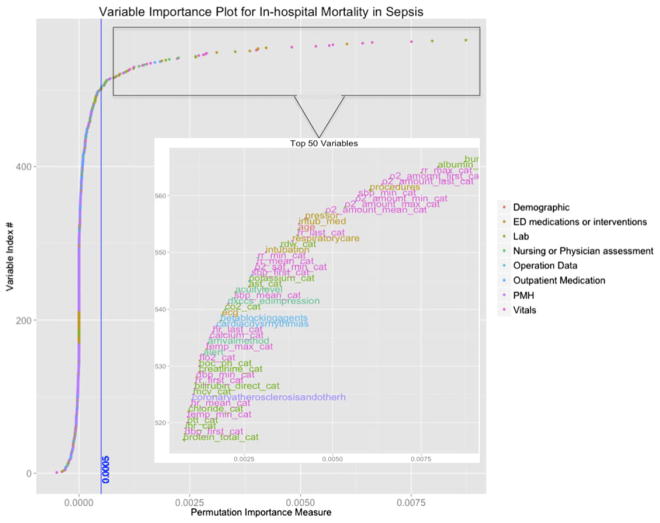
In the random forest model, developed using all the potential predictors (Data Supplement S2), variables of importance were identified and plotted (Figure 2). The 20 variables with highest coefficients of permutation importance for mortality were compared to variables included in the CURB-65, MEDS, and mREMS (Table 2).

Figure 2.

Variable importance plot for in-hospital mortality in sepsis. Variables are plotted according to ascending order of permutation importance (see main text for description). Permutation importance does not factor in variable correlation, and thus similar variables are often clustered together. The vertical blue line is the threshold cutoff point for importance and represents the value beyond which the importance is not attributable to random variation.

Table 2.

Most Important Variables by Permutation Importance in Random Forest Model Compared to Variables in Existing Sepsis Clinical Decision Rules

Variables of Importance*	Random Forest	MEDS	m-REMS	CURB-65
Oxygen saturation†	RF	MEDS‡	mREMS‡	CURB-65‡
Respiratory rate†	RF	MEDS‡	mREMS‡	CURB-65‡
Blood pressure†	RF	MEDS‡	mREMS‡	CURB-65‡
BUN	RF			CURB-65‡
Albumin	RF
Intubation†	RF
Procedures (in ED)	RF
Need for vasopressors	RF
Age	RF	MEDS‡	mREMS‡	CURB-65‡
RN, resp care	RF
RDW	RF
Potassium	RF
AST	RF
Heart rate†	RF		mREMS‡
Acuity level (triage)	RF
ED impression (Dx)	RF
CO2 (Lab)	RF
ECG performed	RF
Beta-blocker (Home Med)	RF
Cardiac dysrhythmia (PMHx)	RF

All four scoring systems presupposed infectious illness and included additional variables not listed.

CURB-65 = Confusion, Urea nitrogen, Respiratory rate, Blood pressure, ≥65 years; MEDS = Mortality in ED Sepsis; mREMS = modified Rapid Emergency Medicine Score.

^*Based on permutation importance.

^†Combination of variable in all dimensions (e.g., RSI drugs administered and intubation procedure done).

^‡Score includes data element in at least one dimension (e.g., O₂ sat) but may not have other dimensions (e.g. max, min).

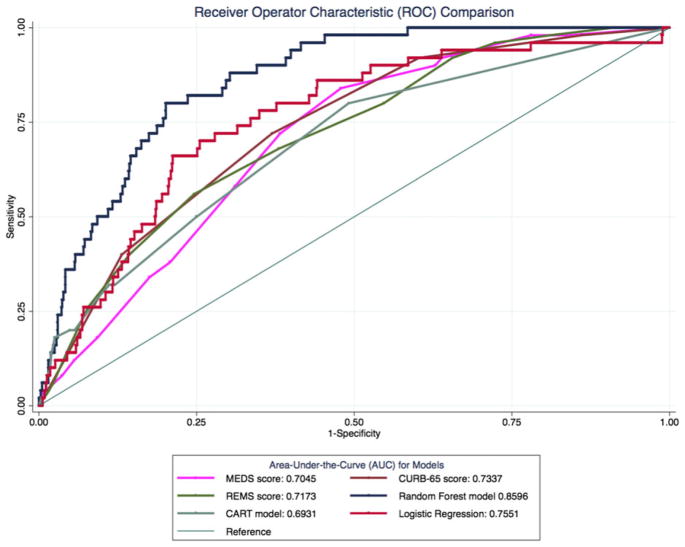
All models were able to predict in-hospital death with an AUC greater than 0.69. Performance of the random forest model was compared with the logistic regression model and the CURB-65, MEDS, and mREMS prediction tools (Figure 3, Table 3). The AUCs with 95% confidence interval (CI) for the random forest model, CART model, logistic regression model, CURB-65, MEDS, and mREMS were 0.86 (0.82–0.90), 0.69 (0.62–0.77), 0.76 (0.69–0.82), 0.73 (0.67–0.80), 0.71 (0.63–0.77), and 0.72 (0.65–0.79), respectively. The differences between AUC for the random forest model and the other models were statistically greater (p ≤ 0.003, for all comparisons; Table 3).

Figure 3.

Receiver operator characteristic (ROC) curves with area-under-the-curve (AUC) values for random forest, traditional models, and existing sepsis clinical decision rules.

Table 3.

AUC Comparison of Random Forest to Other Models

Model	Observations*	AUC	SE	Lower 95% CI	Upper 95% CI	Prob > χ2†
Random forest	1,054	0.860	0.021	0.819	0.900	N/A
Logistic regression	1,054	0.755	0.034	0.689	0.821	0.003
MEDS score	1,052	0.705	0.032	0.634	0.765	<0.0001
CURB-65 score	1,054	0.734	0.032	0.670	0.797	<0.0001
REMS score	1,052	0.717	0.035	0.649	0.785	<0.0001
CART model	1,054	0.693	0.037	0.62	0.766	<0.0001

AUC = area under the curve; CART = classification and regression tree; CURB-65 = Confusion, Urea nitrogen, Respiratory rate, Blood pressure, ≥65 years; MEDS = Mortality in ED Sepsis; REMS = Rapid Emergency Medicine Score.

^*Unable to compute MEDS and REMS score in two patients secondary to missing data

^†Compared to Random forest model.

DISCUSSION

In this proof-of-concept study, we found that a local, big data–driven approach using an advanced machine learning algorithm was superior to traditional analytic models and CDRs for predicting in-hospital mortality for ED patients with sepsis. Our approach to the prediction of a clinically important outcome demonstrates several notable advantages for clinical predictive analytics.

The traditional approach to predictive analytics in emergency care involves the formulation of CDRs, which are typically developed by gathering predetermined cohort data prospectively at one or more centers and deriving and validating a model from a chosen set of predictors. The resulting CDRs are then widely applied, often in settings different from those in the derivation study centers.⁵¹ External validation studies are not common, and when conducted, they tend to show lower predictive accuracy than the original studies.⁵² The approach we detail, however, uses local real-world data to make predictions about the local population, with improved accuracy over traditionally derived models. Our machine learning approach only utilizes structured data available in an EHR without being subject to ambiguous clinical definitions or to the biases of data collection (prospective or retrospective). Furthermore, since this model utilizes local data and can work with different sets of variables, it does not require providers to conform to a prescribed pattern of testing or treatment. It is also robust in dealing with different scales of data as well as missing data. Such an approach has the potential to be integrated into computerized clinical decision support without additional burdensome EHR builds to collect necessary information. In essence, our method conforms to actual clinical practice rather than ideal conditions of epidemiologic research. Integration of these advanced predictive analytics techniques into health care systems can provide clinicians real-time, actionable, prognostic information to assist in decision-making.^2,10,11,14 As big data analytic methods are introduced into clinical practice, future efforts should seek to move from generalizable rules to generalizable methods that utilize the richness of local data.

Our use of an advanced machine learning algorithm allows for evaluation of far more clinical variables than would be present in traditional modeling approaches, with the added benefit of discovering clinical variables not expected to be of predictive value (e.g., aspartate aminotransferase) or which otherwise would have been omitted as a rare predictor (e.g., albumin; see Table 2). Similar to previous work in which a machine learning model substantially improved the prediction of Clostridium difficile test positivity among hospitalized patients,²³ our results demonstrate the strength of machine learning using a large number of variables for prediction

Our results support previous approaches to sepsis mortality prediction, while demonstrating the limitations of generalizing previous CDRs derived in other populations and settings. For example, while the original derivation of the REMS score demonstrated an AUC of 0.85,²⁴ our analysis showed an AUC of 0.72, and other validation studies reported AUCs of 0.74²⁵ to 0.80.²⁶ Similarly, the original derivation of the MEDS prediction aid demonstrated an AUC of 0.76, our analysis showed an AUC of 0.71, and other validation studies reported AUCs 0.75²⁷ to 0.85.²⁶

The incremental improvement in prediction offered by a local, big data–driven machine learning approach may appear small, but translated in the context of our health care system over 1 year (~5,000 patients with sepsis), and setting the model sensitivity and specificity to values at the inflection point of the ROC curve up to 369 additional patients would be correctly classified compared to the best performing traditional model (logistic regression). It is likely that the value of this method would be even greater when applied to clinical scenarios with more frequent or probabilistic outcomes, such as 24-hour deterioration as evidenced by pressor use, patient placement in a higher level of care, or rapid response team activation.

While critics of clinical prediction systems point to the limited generalizability of such approaches between health systems or EDs,⁵¹ we believe that our work demonstrates the importance of distinguishing between a generalizable method and a generalizable predictor model of an outcome. We believe that our conceptual and methodologic method could be replicated in other EHR systems, making using of the fact that each health system is likely to have distinctive phenotypic expressions of disease. While we recognize the challenges and difficulties of implementation, evolving these methods from use by researchers to clinical prediction models integrated in real time with electronic health information systems could be a powerful tool for improving patient care. One can, in our example, envision a simple prompt (similar to the Rothman index for inpatients)⁵³ being incorporated into the EHR that provides valuable information regarding the appropriate disposition of the patient within the hospital (i.e., admission to the floor, step-down, or intensive care unit), facilitates the communication of patient illness severity during care transitions, and focuses the attention of scarce ED and inpatient acute care resources.

On a more general level regarding the interaction of computerized algorithms and physicians, we believe that clinical decision support tools should be just that, something that serves as an aid to physician judgment, and does not aim to supplant it.⁵⁴ In an era where thousands, if not millions, of data points are generated about patients, physicians must be cognizant of their limitations as information processors, yet recognize that there will likely always be contextual and visual information and knowledge obtained through life experience that are unable to be put into a computer algorithm.

LIMITATIONS

Machine learning techniques often suffer from issues of interpretability, and inferences about variables tend to be more difficult than CART and logistic regression techniques.⁵⁵ However, compared to some techniques (e.g., neural networks, support vector machines) we believe that random forests provide for a good deal of interpretability through variable importance plots and the underlying simplicity of the individual trees. Representative trees from the random forest can even be produced to allow the user to see the “inner” workings of the mode similar to the display of CART-based trees.

Newer predictive analytic methods, such as the one we are proposing, are faced with difficult logistic aspects of real-time application.^15,56 However, hospitals are increasingly developing the infrastructure necessary to make real-time predictive analytics a reality. We envision that the random forest model would be initially constructed on large sample of historical data for the hospital (e.g., 6 months). After construction, the model could be periodically updated (every few weeks to months) as new data are accumulated. Real-time processing of patient information would require only preprocessing and prediction based on the previously constructed model. For our validation cohort of greater than 1,000 patients this process took less than 10 minutes on a single desktop computer. Implementation could also be made easier through variable reduction, likely without significant reductions in predictive accuracy.

As this was a retrospective study, data were not available on the individual provider’s predictions of in-hospital mortality. As such we were unable to compare the model to what we believe should be the standard comparison for all predictive analytic methods and models: provider judgment. Further study is warranted to compare our method with provider judgment, to determine whether it would influence physician behavior, and to assess how outcomes may be affected. In addition, while AUC is not the only measure of predictive accuracy it is considered one of the primary means of comparing approaches in the biostatistics and computer science literature and we believe best represents the clinical goal of optimizing sensitivity and specificity given the need to balance early recognition of severe sepsis with treatment and intensive care resources.^28,29

Our approach was limited to data elements available during each ED visit and does not include unstructured data elements, such as features in the patient history or physical examination, that may further improve the predictive accuracy. In addition, our results reflect the predictive possibility of an EHR approximately 1 year after implementation. It is likely that the model’s predictive accuracy could be improved as structured data elements such as past medical history or even bedside ultrasound findings are more comprehensively captured, and elements such as chief complaint are more consistently standardized in more mature EHR data.

The proposed approach to predictive analytics is also limited by local disease prevalence and the rarity of outcomes. Many rare events and diseases will be unable to be modeled until enough data have accumulated within the health care system. These scenarios require larger catchment areas and databases and highlight the need for supplementing local data with interoperable regional or national databases.

CONCLUSIONS

In this proof-of-concept study, a local big data–driven, machine learning approach using random forest methods outperformed existing clinical decision rules and traditional analytic techniques for predicting in-hospital mortality of ED patients with sepsis. The methods developed serve as an example that could be automated, applied to other clinical outcomes of interest, and deployed in electronic health records to enable locally relevant clinical predictions. Future research should evaluate the ability of such methods to prospectively identify patients missed by traditional algorithms and to translate into improved clinical outcomes for high-risk sepsis patients.

Supplementary Material

Data Supplement S1. Regular expression terms* on AHRQ CCS for identification of infectious diagnoses. Data Supplement S1.

Regular expression terms* on AHRQ CCS for identification of infectious diagnoses.

Data Supplement S2. All variables included in random forest model. Data Supplement S2.

All variables included in random forest model.

Data Supplement S3. Twenty hand-selected variables. Data Supplement S3.

Twenty hand-selected variables.