Isotopic evolution of the protoplanetary disk and the building blocks of Earth and Moon

Abstract

Nucleosynthetic isotope variability amongst Solar System objects is commonly used to probe the genetic relationship between meteorite groups and rocky planets, which, in turn, may provide insights into the building blocks of the Earth-Moon system^1–5. Using this approach, it is inferred that no primitive meteorite matches the terrestrial composition such that the nature of the disk material that accreted to form the Earth and Moon is unconstrained⁶. This conclusion, however, is based on the assumption that the observed nucleosynthetic variability amongst inner Solar System objects predominantly reflects spatial heterogeneity. Here, we use the isotopic composition of the refractory element calcium to show that the inner Solar System’s nucleosynthetic variability in the mass-independent ⁴⁸Ca/⁴⁴Ca ratio (μ⁴⁸Ca) primarily represents a rapid change in the μ⁴⁸Ca composition of disk solids associated with early mass accretion to the proto-Sun. In detail, the μ⁴⁸Ca values of samples originating from the ureilite and angrite parent bodies as well as Vesta, Mars and Earth are positively correlated to the masses of the inferred parent asteroids and planets – a proxy of their accretion timescales – implying a secular evolution of the bulk μ⁴⁸Ca disk composition in the terrestrial planet-forming region. Individual chondrules from ordinary chondrites formed within 1 Myr of proto-Sun collapse⁷ record the full range of inner Solar System μ⁴⁸Ca compositions, indicating a rapid change in the composition of the disk material. We infer that this secular evolution reflects admixing of pristine outer Solar System material to the thermally-processed inner protoplanetary disk associated with the accretion of mass to the proto-Sun. The indistinguishable μ⁴⁸Ca composition of the Earth (0.2±3.9 ppm) and Moon (3.7±1.9 ppm) reported here is a prediction of our model if the Moon-forming impact involved protoplanets or precursors that completed their accretion near the end of the disk lifetime.

Protoplanetary disks form as a result of mass accretion from the collapsing envelope onto the star. The rate of mass accretion onto the star via the disk is typically high in the early stages, resulting in elevated temperatures within a few astronomical units (AU) of the star⁸. In the Solar System, mass accretion to the proto-Sun resulted in thermal processing of pristine infalling molecular cloud material, including the selective destruction of presolar carriers of nucleosynthetic isotope anomalies. This process is expressed by correlated variability in the abundance of nuclides of distinct nucleosynthetic origin such as ⁴⁶Ti-⁵⁰Ti and ⁴³Ca-⁴⁶Ca-⁴⁸Ca amongst Solar System reservoirs^2,3. Parent bodies of meteorites formed from inner, thermally-processed, disk material record depletions in these isotopes relative to bodies formed in the outer disk regions. The mass-independent isotopic compositions of various elements can thus fingerprint the source of the precursor material to terrestrial planets. However, this requires understanding the secular evolution of the nucleosynthetic composition of the disk material that accreted to growing planetary bodies. Unlike nucleosynthetic tracers present as trace elements in planets (Ti and Cr) or siderophile elements (Mo and Ru) that track the source of the metal fraction of a body, calcium is a major constituent of rock-forming minerals and, hence, provides robust constraints on the precursor material to rocky planets. To probe the Ca isotope evolution of the protoplanetary disk, we determined the mass-independent ⁴⁸Ca isotope composition of strategically-selected Solar System objects, including ordinary and carbonaceous chondrites, ureilites, eucrites, angrites, martian and lunar meteorites as well as individual chondrules from ordinary and carbonaceous chondrites (Fig. 1).

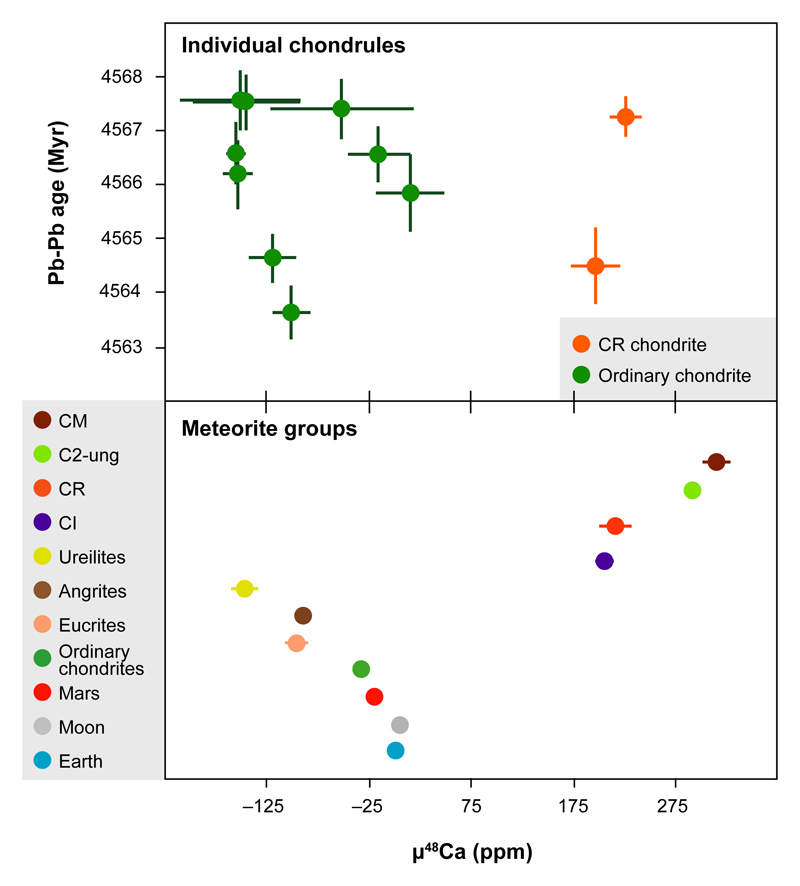
Fig. 1. Mass-independent ⁴⁸Ca data for individual chondrules and bulk meteorites.

Chondrule data are shown versus their Pb-Pb age⁷. Data are reported in the μ-notation where μ⁴⁸Ca = [(⁴⁸Ca/⁴⁴Ca)_sample/(⁴⁸Ca/⁴⁴Ca)_SRM915b − 1] × 10⁶. Uncertainties are 2SE.

The growth of asteroids and Mars-sized embryos can result from the gas-drag-assisted accretion of mm-sized chondrules within ~3 Myr^9,10. The U-corrected Pb-Pb ages and initial Pb isotopes of the chondrules we investigated indicate a primary formation age restricted to the first Myr of disk evolution, although some objects have been remelted at later times⁷. These chondrules provide insights into the spatial and temporal evolution of the μ⁴⁸Ca composition of disk solids at early times (Fig. 1). The CR chondrules record μ⁴⁸Ca compositions comparable to CI chondrites, indicating that their precursor material escaped extensive thermal processing. In contrast, ordinary chondrite chondrules record variable μ⁴⁸Ca compositions ranging from the terrestrial value to deficits of –161±27 ppm. Our bulk meteorite data are consistent with earlier studies^3,11, namely that bodies formed in the inner disk show systematic depletions in μ⁴⁸Ca whereas carbonaceous outer Solar System bodies record excesses relative to Earth (Fig. 1).

Given the analytical uncertainty of the individual chondrule ages, it is difficult to distinguish between a model where the deficits in μ⁴⁸Ca relative to the solar composition reflect spatial heterogeneity or temporal evolution of the bulk composition of inner disk solids. Astronomical observations of young stars and their disks indicate that the main accretion epoch of thermally-unprocessed envelope material occurs over timescales comparable to those of primary chondrule formation, namely during the first Myr of disk evolution¹². Accepting that CI chondrites approximate the average composition of the envelope material, admixing this material to the inner disk will result in a progressive increase in the μ⁴⁸Ca composition of solids and bodies formed during this epoch. To test this hypothesis, we turn to the ⁴⁸Ca composition of differentiated asteroids and planetary bodies, as their μ⁴⁸Ca values reflect the average compositions of their precursors throughout the bodies´ accretion history.

Recent models^9,10 for the formation and growth of asteroidal bodies and planetary embryos suggest a two stage process, where first generation bodies with characteristic sizes of ~100 km form rapidly by streaming instabilities followed by continuous growth that is dominated by the gas-drag assisted accretion of mm-sized particles for bodies with radii larger than ~200 km. This results in the formation of Mars-sized embryos over typical disk lifetimes of less than 5 Myr. Importantly, formation of the first embryos leads to the excitation of the inclinations of the smaller asteroids, which disconnects the asteroids from the chondrules in the mid-plane layer and, hence, terminates their accretion. Assuming a similar rate of accretion in the terrestrial planet forming region, a consequence of these models is that the final mass of a rocky body is a function of its accretion timescale. Whereas the masses of Earth, Mars and Vesta (the howardite-eucrite-diogenite parent body¹³) can be inferred, the parent bodies of ureilites and angrites meteorites are not known. However, the presence of a core dynamo in the angrite parent body¹⁴, a magmatic differentiation and volcanic evolution indicating a similar thermal history to Vesta^15,16 and the retention of basaltic lavas on its surface suggests the angrite parent body may have been comparable in size to Vesta. The mass of the ureilite parent body was calculated using a density of 3.22 g cm^-3 and a radius of 105±25 km^17,18. We note that the absence of basaltic meteorites from the ureilite parent body, possibly indicating loss of basaltic lavas via explosive volcanism, is consistent with a radius ≤100 km for this body¹⁹. Figure 2A shows that the ⁴⁸Ca composition of inner Solar System differentiated bodies systematically increases with their masses, indicating a secular evolution of the time-integrated average ⁴⁸Ca composition of the disk material that accreted to form the terrestrial planets. Thus, the inner disk ⁴⁸Ca nucleosynthetic variations are best understood as predominantly reflecting progressive admixing of pristine, outer Solar System matter to an initially thermally-processed dust reservoir during the early stage of disk evolution. This establishes that the nucleosynthetic variability recorded by inner disk bodies is primarily controlled by the formation timescales of their precursors. This interpretation is also generally consistent with other nucleosynthetic tracers of lithophile affinity when considering the uncertainties of the data (see methods).

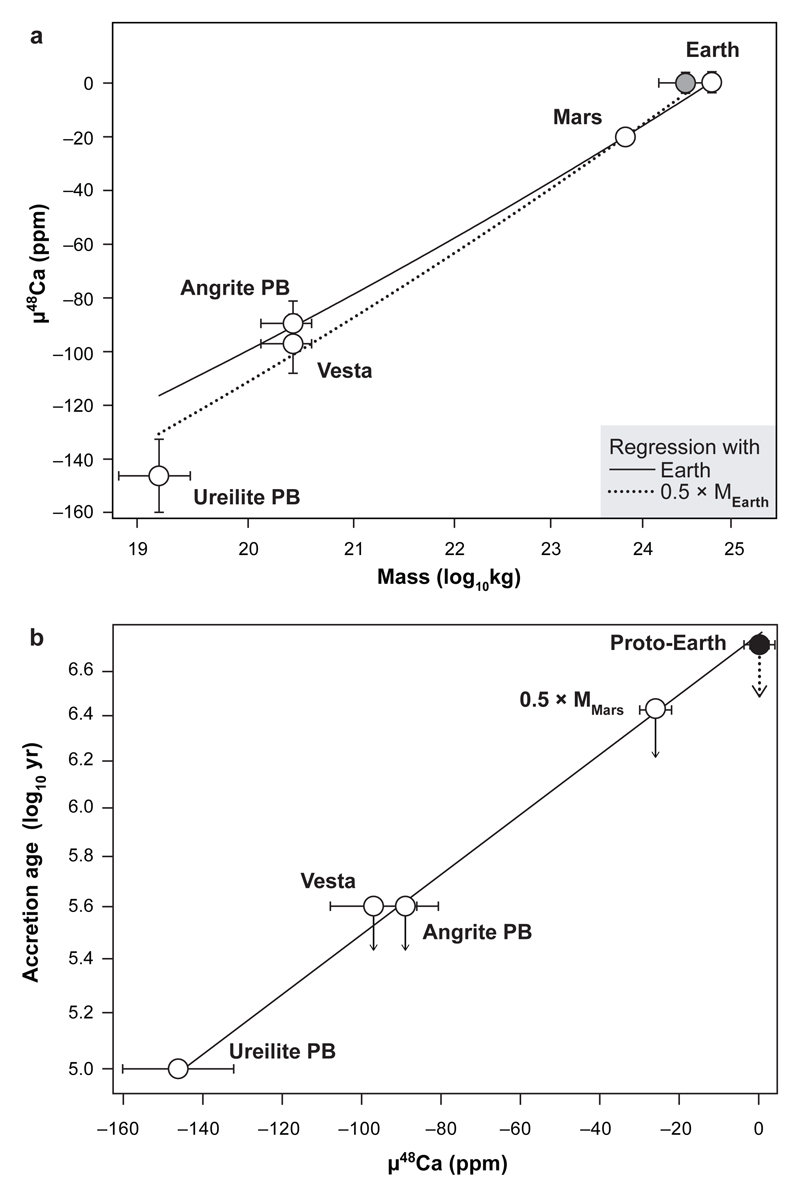
Fig. 2. The μ⁴⁸Ca composition of planetary bodies versus their mass and their maximum accretion age.

(A) Correlation of μ⁴⁸Ca composition of the ureilite parent body, Vesta, angrite parent body, Mars and the Earth with their respective masses on a logarithmic scale. The regression is a linear least-square fit (y = a + b×x), where a = –517.08±0.11 and b = 20.878±0.005 (1SD). We assigned 50% uncertainty to the angrite parent body and the eucrite parent body (namely Vesta) masses. We also show a regression assuming a 0.50±0.25×M_Earth precursor (dash-dotted line). Regressions using alternative masses for the ureilite parent body and Earth (precursors) are shown in the Extended Data Figure 1. (B) Plot of the maximum accretion ages of ureilite parent body, Vesta, angrite parent body and Mars at half of its current mass (see methods and ref. 20,21,23), shown in log₁₀ yr after Solar System formation, versus the parent body μ⁴⁸Ca composition. Downward arrows indicate that accretion ages are upper limits. The linear regression with a = 6.7232 and b = 0.011886 is used to calculate the accretion age of proto-Earth at 5.3 Myr based on its μ⁴⁸Ca value. The accretion age of the proto-Earth likely reflects the accretion age of its precursors, which may include a number of planetary embyos. Thus, Earth’s final accretion occurred after disk dissipation from colliding embryos. Note, however, that formation of a 0.9 Earth-mass object at 1 A.U. within 5 Myr is possible via pebble accretion¹⁰ although early accretion of proto-Earth is inconsistent the present-day W isotope composition of Earth’s mantle³³. However, a better understanding of the W isotope evolution of the proto-Earth in the framework of pebble accretion and a thourough assessment the extent of metal-silicate fractionation during the Moon-forming impact is required to assess this model. PB, parent body.

The inner Solar System chondrules investigated here suggest that the μ⁴⁸Ca of disk solids evolved from an ureilite-like to a terrestrial composition within ~1 Myr of Solar System formation. Whereas these data indicate a rapid isotopic evolution of accreting disk solids, they provide no constraints on the rate of change of the average bulk composition of the inner disk. However, this information can be inferred from the μ⁴⁸Ca of differentiated asteroids and planetary bodies as their composition reflects the time-integrated average of the disk composition at the time of their accretion. Two ordinary chondrite chondrules with U-corrected Pb-Pb ages within ~100,000 years of Solar System formation record μ⁴⁸Ca compositions identical to the most depleted μ⁴⁸Ca value defined by a differentiated asteroid, namely the ureilite parent body. Short-lived radionuclide chronology and thermal modeling indicate that the ureilite parent body completed its accretion <100,000 years of Solar System formation (see methods). Collectively, these observations suggest that the ureilite μ⁴⁸Ca value of –146±14 ppm represents that of the inner disk dust reservoir initially depleted in ⁴⁸Ca through thermal processing. When Vesta and the angrite parent bodies accreted <0.25±0.15 Myr of Solar System formation^20,21, the time-integrated average μ⁴⁸Ca of inner disk rocky bodies had evolved to –93.2±7.1 ppm and, lastly, to –20.0±2.8 and 0.2±3.9 ppm when Mars and Earth’s precursors completed their accretion, respectively.

It is well-established that the protoplanetary disk was dissipated at the time of formation of the impact-generated Gujba CB chondrules at 4562.49±0.21 Ma²², implying cessation of infall of outer Solar System material to the inner disk. Thus, the timing of disk dissipation marks the transition when the μ⁴⁸Ca composition of inner disk bodies can no longer be modified by infall. Given the observed relationship between μ⁴⁸Ca values and planetary masses (Fig. 2A), the timing of accretion of Earth's precursor can be deduced assuming that the accretion timescales of Mars, Vesta as well as angrite and ureilite parent bodies are well understood. The Hf-W systematics of martian meteorites suggest that Mars reached half of its mass by ${1.8}_{-1.0}^{+0.9}$ Myr²³, whereas thermal modelling and ²⁶Al-²⁶Mg data constrain the accretion of Vesta and the angrite parent body <0.4 Myr of CAI formation^20,21. Accretion of the ureilite parent body is believed to have been completed by ~0.1 Myr to ensure partial differentiation from the decay of ²⁶Al (see methods). Using these estimates, we show in Fig. 2B that accretion of the proto-Earth or its precursors, which may include a number of planetary embryos (see Fig. 2 caption), was completed by ~5.3 Myr. Collectively, these observations suggest that the μ⁴⁸Ca value of Earth represents the average bulk inner disk composition prior to its dissipation. The addition rate of outer Solar System material to the inner disk can be evaluated from the secular change in the average μ⁴⁸Ca inner disk composition inferred from differentiated asteroids and planets. Accepting an ureilite-like μ⁴⁸Ca value for the bulk inner disk at 0.1 Myr, we show in Fig. 3A that the rate of addition of outer Solar System material to the inner disk mirrors the typical mass accretion rates of low mass protostars²⁴. Thus, the flux of outer Solar System material to the inner disk appears associated with infall of envelope material and, hence, growth of the proto-Sun.

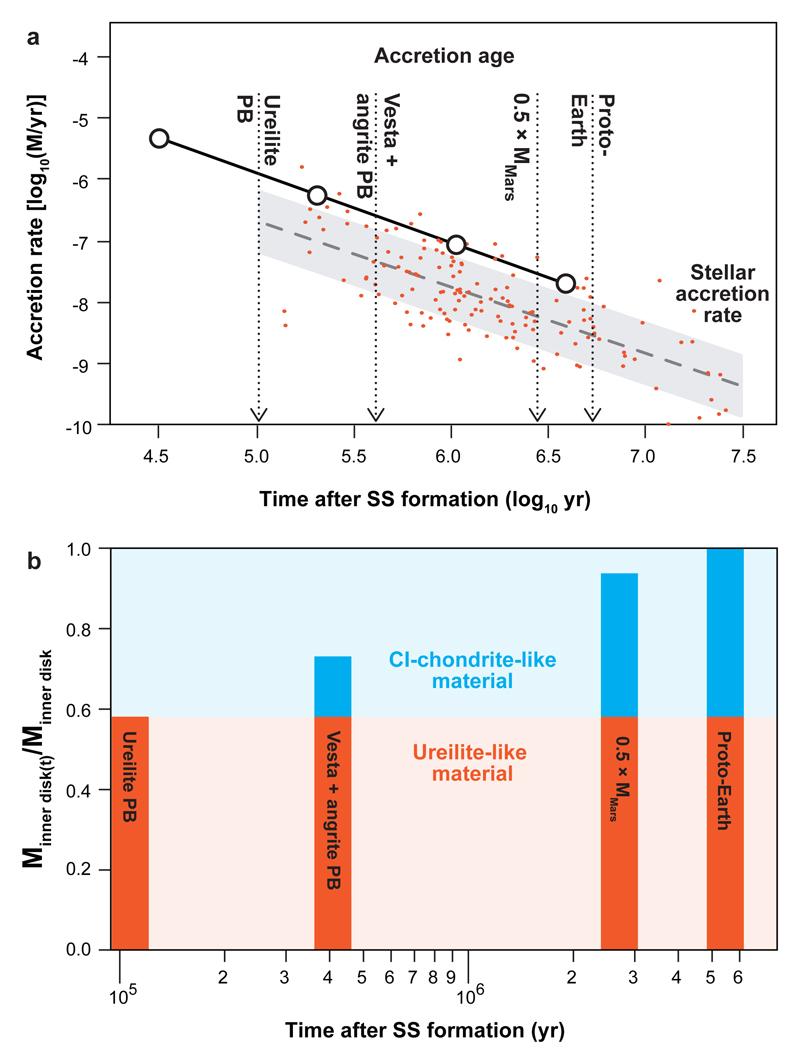
Fig. 3. Accretion rate of inner disk mass versus time.

Shown in (A) are the calculated accretion rates of the inner protoplanetary disk inferred from μ⁴⁸Ca composition and maximum accretion timescales of planetary bodies (white circles), assuming the μ⁴⁸Ca signature is representative of the entire inner disk mass at that time. Thus, the accretion rate of the inner protoplanetary disk reflects the amount of mass locked into bodies at any given time relative to the final disk mass, which is taken as the mass of asteroids, moons and planets located sunward of Jupiter (see methods). Given the apparent power law decline in our calculated accretion rates, we show the calculated values at Δlog(t)/2 of their respective time interval. For comparison, we also show observed stellar accretion rates and the empirical accretion rate scaled to a 0.7 solar mass star versus time²³. In (B), we show the proportion of mass locked into asteroids, embryos and planets at their maximum accretion age assuming that each parent body composition is representative of the bulk disk composition at the time of their accretion. The proportions are calculated as mixtures between a ureilite-like ⁴⁸Ca composition and outer Solar System dust represented by CI chondrites (see methods).

Our model for the secular μ⁴⁸Ca evolution of the inner protoplanetary disk provides insights into the nature of the precursor material to planetesimals and planets. The compositions of Vesta and the angrite parent body requires admixing of 15% of thermally-unprocessed CI-like material to their precursors. For Mars and the proto-Earth, the amount of thermally-unprocessed material needed to account for their bulk μ⁴⁸Ca compositions is 36% and 42%, respectively. If correct, this implies that more than half of the mass of the inner disk was already locked into asteroidal bodies and/or planetary embryos ~100,000 years after proto-Sun collapse (Fig. 3B). Thus, the μ⁴⁸Ca composition of terrestrial planets preserves a record of their accretion history throughout the entire disk lifetime. In contrast, most chondrites represent fragments of late accreted bodies and, as such, can at best only represent a snapshot of a disk composition at the time of their accretion. However, given the small size of their parent bodies, it is unclear if their compositions are representative of that of the average accreting material at the time of their formation, which can be also influenced by variable proportions of chondrule and matrix. For example, the ordinary chondrite chondrules analysed here record a weighted average μ⁴⁸Ca of –129±50 ppm, making the bulk rock composition very sensitive to the chondrule to matrix ratio. Thus, chondrites cannot be used to faithfully assess the nature of the precursor material to rocky planets.

To explain the observed nucleosynthetic dichotomy between inner and outer Solar System bodies, Kruijer et al.²⁵ proposed that transport of outer Solar System material to the inner disk was stopped by the opening of a disk gap related to the formation Jupiter’s core ~1 Myr after formation of the Sun. However, numerical simulations and astronomical observations suggest that opening of a disk gap does not quench mass accretion to the protostar but rather limits the inward transport of large dust grains by filtration^26,27. Coagulation of smaller dust particles sunward of the disk gap will continue to fuel planetary growth by pebble accretion. The apparent lack of this material in ordinary chondrites may reflect the fact that the main growth mechanism of small bodies, namely the streaming instability, is less efficient in accreting smaller particles. Testing this hypothesis, however, requires numerical simulation to better understand size sorting during planetesimal formation by the streaming instability relative to size sorting by pebble accretion. Lastly, our results and interpretations imply that more than half of the mass of the inner disk was already locked into sizeable bodies with a μ⁴⁸Ca composition akin to ureilites ~100,000 years after proto-Sun collapse (Fig. 3B). Mass balance arguments indicate that admixing of pristine outer Solar System CI-like dust to this inner disk reservoir can at most raise the bulk μ⁴⁸Ca disk value to approximately the terrestrial composition, thereby preserving a contrast between rocky planets and carbonaceous asteroidal bodies. Thus, we infer that the nucleosynthetic dichotomy between inner and outer Solar System bodies reflects the rapid accretion of thermally-processed disk material into asteroidal bodies and/or planetary embryos and does not require the early formation of a disk gap.

The giant impact theory for the formation of the Earth-Moon system proposes that a Mars-sized embryo collided with the proto-Earth and ejected material into an Earth-orbiting disk, which subsequently accumulated into the Moon²⁸. Since models predict that most of the Moon’s mass is derived from the impactor, this theory is difficult to reconcile with the near identical isotopic composition of the Earth and Moon for lithophile elements^1,5,29. As such, a number of alternate models have been proposed that allow for disk-planet compositional equilibration to occur^30–32. Our high-precision data define a μ⁴⁸Ca value for the Moon of 3.7±1.9 ppm relative to Earth, requiring the ⁴⁸Ca compositions of the proto-Earth and the impactor in the framework of the canonical model²⁹ to be within 10 ppm. As our results suggest that the bulk ⁴⁸Ca composition of the inner protoplanetary disk evolved to a terrestrial composition within ~5 Myr (Fig. 2B), the isotopic similarity between the Earth and Moon can be easily understood if the giant impact involved bodies or precursors that completed their accretion towards the end of the disk lifetime. The nearly identical isotope signature of the Earth and the Moon is not fortuitous but rather an outcome of the evolving isotopic composition of the disk.

Methods

Sample preparation and isotope analyses

Bulk samples, weighing between 20 and 100 mg, were digested in a HF-HNO₃ media in Parr bombs at 210°C for 2-3 days. Calcium was also separated from sample digestions of nine chondrules extracted from the ordinary chondrite (L3.10) NWA 5697 and two chondrules from the CR2 NWA 6043 that have previously been analysed for Pb isotopes⁷. The individual sample dissolutions typically represent <10 mg of sampled chondrule material, which is significantly smaller than the amount of processed bulk meteorite samples. Following complete dissolution of the samples, Ca was purified in a four-step procedure from the sample matrix by ion exchange chromatography³⁴. Although this procedure normally results in an efficient separation of Ca from the sample matrix, all samples were monitored for the presence of contaminant elements in the purified Ca solution such as Mg, Sr and Ti. Individual chromatography separation steps were repeated for samples where the presence of contaminants was considered to have a potential impact on the analysis (e.g. Sr/Ca > 1 × 10^-6). Isotopic compositions of the purified Ca separates were measured with the Neptune Plus multiple collector – inductively coupled plasma – mass spectrometer (MC-ICPMS) at the Centre for Star and Planet Formation (Natural History Museum of Denmark, University of Copenhagen) following established analytical procedures^3,34. Calcium isotope data were acquired in static mode using six Faraday collectors set-up as follows: ⁴⁸Ca, ⁴⁷Ti, and ⁴⁶Ca in the high-4, high-2 and high-1 collectors, respectively, on the high mass side of the axial Faraday and ⁴²Ca, ⁴³Ca and ⁴⁴Ca in the low-4, low-2, and low-1 collector, respectively on the low mass side of the axial Faraday. The high-2 collector Faraday cup (⁴⁷Ti) was connected to an amplifier with a 10¹² Ω feedback resistor, whereas the remaining collectors were connected to amplifiers with 10¹¹ Ω feedback resistors. Samples were aspirated into the plasma source by means of an Apex sample introduction system with an uptake rate of 20 μL/min and Ca isotopes were measured with a mass resolving power (M/∆M as defined by the peak edge width from 5% to 95% full peak height) that was always greater than 5000. The sensitivity under these analytical conditions was approximately 300 V ppm^-1.

Given the low abundance of the ⁴⁶Ca nuclide as well as the limited μ⁴³Ca variability between bulk inner Solar System reservoirs (<20 ppm) relative to the measurement uncertainty (~2 ppm)^3,34, we focus in this work on the high-precision determination of the mass-independent component of ⁴⁸Ca (μ⁴⁸Ca), which we measure with an external reproducibility of 12 ppm for individual sample analyses³⁴. We also report the mass-dependent ⁴²Ca/⁴⁴Ca (δ^42/44Ca) and ⁴³Ca/⁴⁴Ca (δ^43/44Ca) values with respect to SRM 915b in the delta notation that are obtained alongside the μ⁴⁸Ca data. Single analyses for each sample of sufficient size consist of 15-20 sample measurements comprising a total of 839 s of data acquisition and 340 s of baseline bracketed by measurements of the SRM 915b standard. For individual chondrules both signal intensity and number of repeat analyses were adjusted to achieve the best possible precision given the limited amount of Ca available for these samples. All data reduction was conducted off-line and changes in mass bias with time were interpolated using a smoothed cubic spline. For each analysis the mean and standard error of the measured ratios were calculated using a 3SD threshold to reject outliers. Individual analyses of a sample were combined to produce an average weighted by the propagated uncertainties of individual analyses and reported final uncertainties are 2 times the standard error (2SE) of the mean.

Calculation of disk mass accretion rates

For simplicity, we assume that the mass of the asteroids, moons and planets sunward of Jupiter represents the final mass of the protoplanetary disk and the ⁴⁸Ca signature of Earth, which makes up 50% of this mass, is representative of the final inner disk composition. This assumption is justified as the μ⁴⁸Ca values track the composition of disk solids and not that of the gas. The mass accreted in bodies at any given time is assumed to be traced by the bulk μ⁴⁸Ca signature of planetary bodies, where increase in the ⁴⁸Ca of planetary bodies represents an addition of outer Solar System material to the growing inner disk. In this simple two-component mixing model, the ureilite parent body represents the mean composition of the inner disk at 0.1 Myr after the formation of the Solar System. The ⁴⁸Ca signature of CI chondrites represents the added outer Solar System material during the lifetime of the disk and the ⁴⁸Ca signature of the Earth the final composition of the disk after accretion has ceased. This mixing model requires 58.4% of the material has accreted by the time the ureilite parent body formed (<0.1 Myr). The subsequent increase in bulk ⁴⁸Ca signatures of Vesta and the angrite parent body, Mars at half of its current mass and proto-Earth represent addition of 15.0%, 19.6% and 6.9% outer Solar System material during the time intervals between accretion of the 1) the ureilite parent body and Vesta (between 0.1 Myr to 0.4 Myr), 2) Vesta and Mars at 50% of its mass (between 0.4 to 2.7 Myr) and 3) Mars at 50% of its mass and proto-Earth (between 2.7 to 5.3 Myr), respectively. The amount of early-accreted material only increases if the ⁴⁸Ca signature of other carbonaceous chondrites is assumed rather than that of CI chondrites. The change in accreted mass per time interval relative to the final disk mass (i.e. 0.584, 0.150, 0.196 and 0.069 of the final inner disk mass) allows us to calculate mean inner disk mass accretion rates for each of the four interval’s by dividing the added mass per time interval by its duration (0.1, 0.3, 2.3 and 2.6 Myr). Resulting accretion rates are 5.8×10^-6, 5.0×10^-7, 8.5×10^-8 and 2.6×10^-8 M_{inner disk}/yr, respectively.

Timing of accretion of the ureilite parent body

The energy release from the decay of the short-lived ²⁶Al radionuclide (t_1/2 = 0.73 Myr) is the most important heat source driving differentiation on small planetary bodies accreted during the first few Myr of our Solar System’s formation. Thus, determining the timing of accretion of differentiated bodies can be inferred by estimating the time needed for the parent body to achieve global melting from the energy released by ²⁶Al, which requires knowledge of the timing of differentiation as well as the initial abundance of ²⁶Al the body's precursor material. Recent studies have shown that canonical levels of ²⁶Al found in calcium-aluminum-rich inclusions (CAIs) are not representative for the majority of the matter that made up the terrestrial planet forming region^21,35. Instead, ²⁶Al/²⁷Al values in this region at the time of CAI formation were more likely characterized by values between 1 and 1.6×10^-5 (ref. ^21,35). Based on ²⁶Al-²⁶Mg and ⁵³Mn-⁵³Cr systematics the timing of initial magmatic differentiation on the ureilite parent body took place at 4567.1±1.1. Myr ago^36,37, indistinguishable from the age of our Solar System based on CAIs³⁸. Accepting that the initial abundance of ²⁶Al/²⁷Al in the material from which the ureilite parent body formed was 1.3×10^-5 and the precursor material was ordinary chondrite-like in density and composition, thermal modeling requires that the accretion must have been completed by 0.1 Myr after CAI formation. This is constrained by assuming an ambient temperature of 550 K in the accretion region of the ureilite parent body at ~0.1 Myr³⁹ and requires the parent body to achieve an internal temperature of 1553K equivalent to 30% partial melting¹⁸ within 1.1 Myr after CAI formation, which is the time allowed by the age uncertainty for magmatic differentiation^36,37. We note that this accretion age is consistent with independent estimates of the accretion time of the ureilite parent body⁴⁰.

Stable Ca isotope composition of meteorites and chondrules

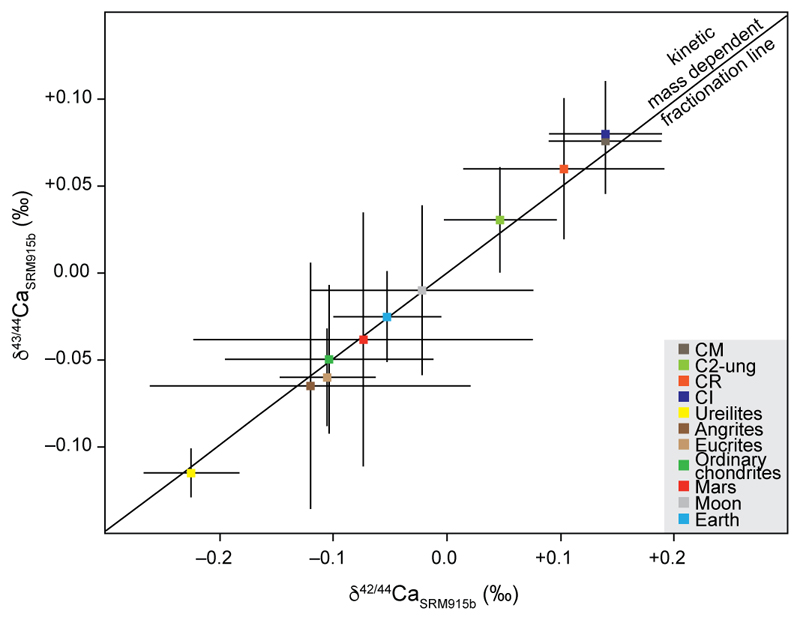
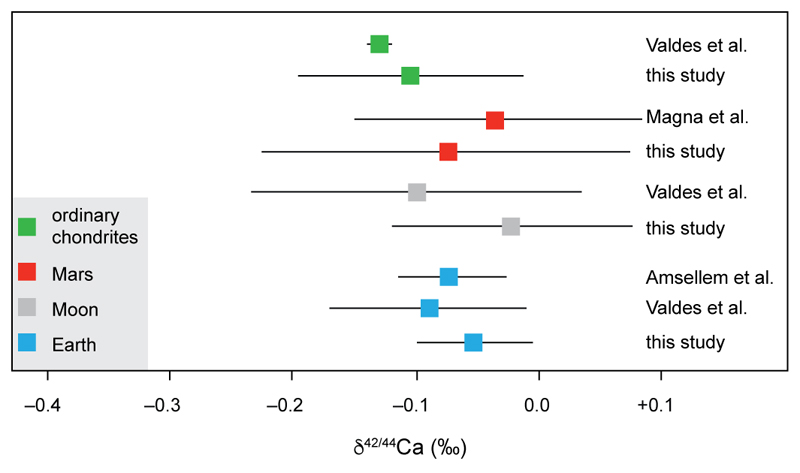
We report δ^42/44Ca and δ^43/44Ca values for each individual sample as the per mil deviations from SRM 915b in the Extended Data Table 1 and Extended Data Figure 2 given that mass-dependent fractionation can, in principle, affect the accuracy of the mass-independent μ⁴⁸Ca data via inappropriate correction for the natural mass fractionation experienced by a sample. For example, correcting the natural mass-dependent fractionation using a kinetic law to retrieve the μ⁴⁸Ca data will result in the introduction of apparent effects (excess or deficit) in μ⁴⁸Ca if the natural fractionation is driven by non-kinetic processes³⁴. Deviation from kinetic mass dependent fractionation can occur during calcite precipitation⁴¹ and during chemical weathering in arid environments⁴². The latter is relevant as a number of our samples are hot desert finds. Potential effects are on the order of up to 12 ppm on the μ⁴⁸Ca for a 0.1‰ effect on the δ^42/44Ca value. The δ^42/44Ca values we report here are in excellent agreement with literature data for the same group of meteorites (Extended Data Figure 3)^43–45, confirming that potential effects from inadequate correction for natural mass-dependent fractionation are well within the uncertainty of our μ⁴⁸Ca measurements. Our δ^42/44Ca data for individual chondrules from ordinary and CR chondrites are also comparable to that reported by for CV chondrites by Amsellem et al.⁴⁴. Moreover, we find no systematics difference in the μ⁴⁸Ca values of hot desert and non-hot desert meteorite as well as falls versus finds in our dataset. In detail, μ⁴⁸Ca values for hot desert and non-hot desert meteorites as well as observed falls and finds from the same differentiated group (i.e. ureilites, angrites and Mars) are indistinguishable within uncertainty (Extended Data Figure 4). Additionally, potential effects on our data from addition of terrestrial Ca for lunar and martian meteorites can also be ruled out based on mass balance arguments. For example, accepting that the pristine martian μ⁴⁸Ca composition is -20±2.8 ppm relative to Earth, addition of 15% of terrestrial Ca, which would clearly be identifiable from hand specimens, would only result in a 3 ppm effect. This effect is well within the external reproducibility of our measurements. Given that the μ⁴⁸Ca composition of the Moon is even closer to Earth, addition of 15% terrestrial Ca to a lunar meteorite would results in even smaller effects relative to martian meteorites. Collectively, these data emphasize that the stable or mass-independent Ca isotope data are not affected by terrestrial processes prior to meteorite recovery within the uncertainty of our measurements.

Other nucleosynthetic isotope data in view of this model

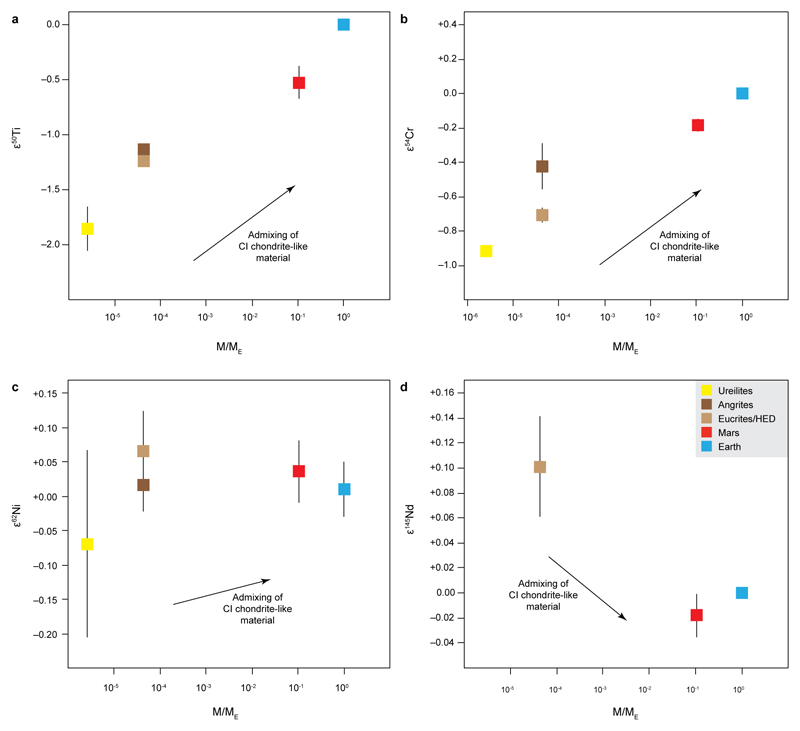
Nucleosynthetic anomalies have been reported for number of elements aside from Ca (i.e. Ti, Cr, Ni, Sr, Nd, Mo, Ru and O)^{1,2,6,46–59} and, as such, we evaluate if our model is consistent with the isotope variability recorded in various Solar System reservoirs for these elements. In this exercise, we simply consider whether it is possible to generate the nucleosynthetic variability amongst inner Solar System bodies by admixing a CI-like composition to a depleted inner Solar System dust composition represented by ureilite (where available) or angrite meteorites (Extended Data Figure 5). Based on published data^{1,2,6,46–54}, we note that our model is compatible with the isotope variability observed for elements with a lithophile behavior such as ⁵⁰Ti, ⁵⁴Cr, ⁶²Ni, and ¹⁴⁵Nd within the uncertainties of the published data (Extended Data Figure 5). Nucleosynthetic anomalous isotopes of other elements either do not show significant variability beyond typical analytical uncertainties (i.e. ⁸⁴Sr)^55–57, do not track the entire accretion history of planetary bodies (siderophile elements such as Mo, Ru)⁴ or are potentially affected by other processes such as gas-water interaction (oxygen). Thus, we conclude that our model is consistent with the nucleosynthetic variability that exists for elements that track the source of the silicate fraction of asteroidal and planetary bodies.

Extended Data

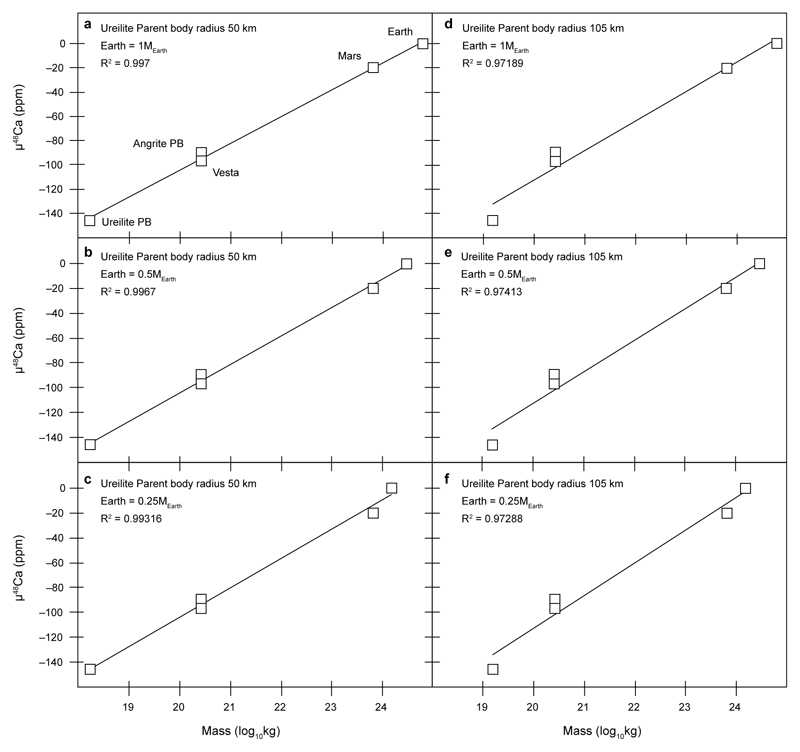
Extended Data Figure 1. The μ⁴⁸Ca composition of planetary bodies versus their mass with variable ureilite parent body and Earth’s precursor masses.

Plots a-c show regressions and their correlation coefficients assuming an ureilite parent body with a radius of 50 km and masses for Earths’ precursors of 1×M_Earth, 0.5×M_Earth and 0.25×M_Earth, respectively. Plots d-f show regressions assuming an ureilite parent body with a radius of 105 km and masses for Earths’ precursors of 1×M_Earth, 0.5×M_Earth and 0.25×M_Earth, respectively. Masses for the angrite parent body, Vesta and Mars are the same as in figure 2A.

Extended Data Figure 2. Three isotope plot of reported average δ^42/44Ca versus δ^43/44Ca for Earth, meteorite parent bodies or chondrite groups relative to SRM 915b.

Shown also is the mass dependent fractionation line predicted by kinetic mass fractionation. Uncertainties are the 2SE of the mean of the analyzed samples per group. Where only a single sample represents the group, the error represents the external reproducibility (0.05 and 0.03 for δ^42/44Ca versus δ^43/44Ca, respectively) or the analytical uncertainty of the measurement, whichever is larger.

Extended Data Figure 3. Comparison of the δ^42/44Ca values reported in the literature for ordinary chondrites, martian basalts, lunar and terrestrial basalts^43–45 with those determined for the same types of samples in this study.

Extended Data Figure 4. Comparison of the μ⁴⁸Ca values determined for desert finds versus non-desert finds or falls.

Individual panels show data for (A) martian meteorites, (B) angrite meteorites and (C) ureilite meteorites. Grey bars indicate the external reproducibility of individual sample analyses.

Extended Data Figure 5. Correlation of parent body mass, shown as mass relative to the mass of Earth (M/M_E), with nucleosynthetic anomalies for ⁵⁰Ti, ⁵⁴Cr, ⁶²Ni and ¹⁴⁵Nd reported in the literature^{1,2,6,46–54}.

Indicated via arrows are the predicted effects of admixing of CI-like matter to the inner disk reservoir on the isotope composition based on measured nucleosynthetic signatures of CI chondrites.

Extended Data Table 1. Mass-independent μ⁴⁸Ca and mass dependent δ^42/44Ca and δ^43/44Ca data reported relative to SRM 915b.

Data marked with * are from ref. 3 and with † from ref. 34.

Sample	μ48Ca ± 2SE	δ42/44Ca ± 2SE	δ43/44Ca ± 2SE
Earth
BIR-1a (n=6)	+0.2 ± 1.7	−0.04 ± 0.02	−0.02 ± 0.01
BIR-1a†	+6.1 ± 5.7	−0.04 ± 0.02	−0.01 ± 0.02
BHVO-2†	+6.3 ± 7.5	−0.04 ± 0.04	−0.02 ± 0.02
BCR-2†	+5.2 ± 3.4	−0.08 ± 0.04	−0.04 ± 0.02
DNC-1†	+1.0 ± 4.0	−0.04 ± 0.03	−0.02 ± 0.01
BHVO-1†	−6.1 ± 8.1	−0.08 ± 0.03	−0.04 ± 0.02
SGR-1†	−4.6 ± 8.7	−0.02 ± 0.02	−0.01 ± 0.01
Sarm 40†	−6.7 ± 9.7	−0.08 ± 0.02	−0.04 ± 0.01
Mean	+0.2 ± 3.9	−0.05 ± 0.02	−0.03 ± 0.01
Moon
NWA4734 (n=7)	+3.4 ± 6.7	−0.08 ± 0.04	−0.04 ± 0.02
Dhofar 026 (n=2)	+6.4 ± 2.5	+0.03 ± 0.00	+0.02 ± 0.00
NWA8632 (n=2)	+3.2 ± 3.3	+0.00 ± 0.13	+0.00 ± 0.06
Dhofar 287	+1.9 ± 4.7	−0.04 ± 0.03	−0.02 ± 0.02
Mean	+3.7 ± 1.9	−0.02 ± 0.05	−0.01 ± 0.02
Mars
NWA6234	−18.8 ± 4.2	−0.03 ± 0.01	−0.01 ± 0.00
NWA 7320	−18.0 ± 4.8	−0.03 ± 0.02	−0.02 ± 0.01
NWA 998	−27.7 ± 5.5	−0.01 ± 0.01	−0.01 ± 0.00
NWA 7032	−16.0 ± 4.7	−0.02 ± 0.01	−0.02 ± 0.01
NWA 1775	−20.3 ± 6.1	−0.08 ± 0.04	−0.04 ± 0.02
Tissint	−18.8 ± 7.0	−0.22 ± 0.04	−0.11 ± 0.02
Zagami	−20.4 ± 4.5	−0.12 ± 0.04	−0.06 ± 0.02
Mean	−20.0 ± 2.8	−0.07 ± 0.06	−0.04 ± 0.03
Ordinary chondrites
Kramer Creek (L4) (n=4)	−34.5 ± 10.7	−0.14 ± 0.07	−0.07 ± 0.03
Bovedy (L3)*	−35.4 ± 2.9	−0.13 ± 0.01	−0.06 ± 0.01
NWA 4910 (LL3)	−44.3 ± 9.3	−0.04 ± 0.01	−0.02 ± 0.01
NWA 5697 (L3) (n=3)	−25.5 ± 8.2	−0.11 ± 0.03	−0.05 ± 0.01
Mean	−34.9 ± 7.7	−0.10 ± 0.05	−0.05 ± 0.02
Eucrites
Juvinas*	−91.5 ± 7.1	−0.12 ± 0.03	−0.07 ± 0.02
Stannern*	−102.4± 4.3	−0.09 ± 0.02	−0.05 ± 0.01
Mean	−97.0 ± 10.9	−0.11 ± 0.03	−0.06 ± 0.02
Angrites
D'Orbigny*	−85.3 ± 7.5	−0.07 ± 0.02	−0.04 ± 0.01
Sahara 99555*	−93.6 ± 6.6	−0.17 ± 0.08	−0.09 ± 0.04
Mean	−89.5 ± 8.3	−0.12 ± 0.10	−0.07 ± 0.05
Ureilites
Kenna*	−153.0 ± 5.0	−0.21 ± 0.01	−0.11 ± 0.01
Sahara 98505*	−139.4 ± 5.5	−0.24 ± 0.03	−0.12 ± 0.02
Mean	−146.2 ± 13.6	−0.23 ± 0.03	−0.12 ± 0.01
Carbonaceous chondrites
Ivuna (CI)*	+206.1 ± 8.5	+0.14 ± 0.04	+0.08 ± 0.02
EET 92161 (CR2)	+222.5 ± 4.0	+0.07 ± 0.02	+0.05 ± 0.01
NWA 1180 (CR2)	+206.6 ± 4.6	+0.13 ± 0.01	+0.07 ± 0.00
Tagish Lake (C2-ung)	+291.3 ± 5.3	+0.05 ± 0.01	+0.03 ± 0.01
Jbilet Winselwan (CM2)	+314 ± 14	+0.14 ± 0.01	+0.08 ± 0.00
Chondrules
NWA 5697 (LL3)
2-C1	−150 ± 59	−0.20 ± 0.01	−0.08 ± 0.02
5-C2	−145 ± 53	−0.31 ± 0.10	−0.11 ± 0.04
5-C10	−51 ± 70	−0.19 ± 0.04	−0.08 ± 0.02
D-C3	−154 ± 10	+0.02 ± 0.05	+0.01 ± 0.03
5-C4	−15 ± 31	−0.33 ± 0.04	−0.15 ± 0.02
3-C5	−151 ± 16	−0.12 ± 0.04	−0.01 ± 0.00
11-C1	+16 ± 33	−0.19 ± 0.03	−0.08 ± 0.02
11-C2	−119 ± 24	−0.13 ± 0.01	−0.05 ± 0.02
3-C2	−101 ± 19	−0.10 ± 0.01	−0.05 ± 0.01
NWA 6043 (CR2)
1-C2	+227 ± 16	−0.10 ± 0.01	−0.04 ± 0.01
2-C4	+198 ± 24	−0.06 ± 0.01	−0.04 ± 0.01