The plumbing of land surface models: is poor performance a result of methodology or data quality?

Abstract

The PALS Land sUrface Model Benchmarking Evaluation pRoject (PLUMBER) illustrated the value of prescribing a priori performance targets in model intercomparisons. It showed that the performance of turbulent energy flux predictions from different land surface models, at a broad range of flux tower sites using common evaluation metrics, was on average worse than relatively simple empirical models. For sensible heat fluxes, all land surface models were outperformed by a linear regression against downward shortwave radiation. For latent heat flux, all land surface models were outperformed by a regression against downward shortwave, surface air temperature and relative humidity. These results are explored here in greater detail and possible causes are investigated. We examine whether particular metrics or sites unduly influence the collated results, whether results change according to time-scale aggregation and whether a lack of energy conservation in flux tower data gives the empirical models an unfair advantage in the intercomparison. We demonstrate that energy conservation in the observational data is not responsible for these results. We also show that the partitioning between sensible and latent heat fluxes in LSMs, rather than the calculation of available energy, is the cause of the original findings. Finally, we present evidence suggesting that the nature of this partitioning problem is likely shared among all contributing LSMs. While we do not find a single candidate explanation for why land surface models perform poorly relative to empirical benchmarks in PLUMBER, we do exclude multiple possible explanations and provide guidance on where future research should focus.

1. Introduction

The assessment and intercomparison of land surface models (LSMs) has evolved from simple, site-based synthetic experiments in the absence of constraining observational data (Henderson-Sellers et al. 1996; Pitman et al. 1999) to targeted comparisons of process representation (e.g. Koster et al. 2006; Guo et al. 2006) and global scale experiments (Dirmeyer et al. 1999; Koster et al. 2004; Seneviratne et al. 2013). This history is detailed in Pitman (2003), van den Hurk et al. (2011), Dirmeyer (2011) and Best et al. (2015). Recently, Best et al. (2015) noted that throughout this history, model performance has been assessed by direct comparison with observational products or other LSMs. They argued that without a mechanism to define appropriate levels of performance in a given metric, simple comparisons of this nature are not sufficient to gauge whether models are performing well or not.

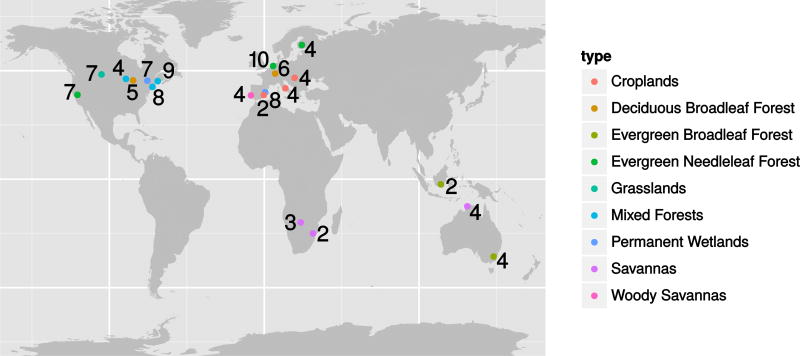
The PALS Land sUrface Model Benchmarking Evaluation pRoject (PLUMBER, Best et al. 2015) was constructed to undertake a multi-model examination of LSMs and focus on defining benchmarks for model performance, rather than simply comparing LSMs and observations. PLUMBER examined the performance of 13 LSMs consisting of variants from 8 distinct models (Table 2) at 20 flux tower sites (Figure 1 and Table 1) covering a wide variety of biomes. Part of the assessment of performance used four common metrics (Table 3), focused on bias, correlation, standard deviation and normalized mean error. Note that the first three metrics provide independent information about model performance, while normalized mean error contains information about all three previous metrics, and is commonly used as a summary metric.

Table 2.

Models used in PLUMBER.

model	developer/custodian	name	version in PLUMBER
CABLE	Commonwealth Scientific and Industrial Research Organisation (CSIRO)	The Community Atmosphere Biosphere Land Exchange model	2.0, 2.0_SLI
CHTESSEL	European Centre for Medium-Range Weather Forecasts	Carbon Hydrology Tiled ECMWF Surface Scheme for Exchange over Land	1.1
COLASSiB	Center for Ocean-Land-Atmosphere Studies (COLA) Centre National de Recherches	COLA-SSiB	2.0
ISBA-SURFEX	Météorologiques - Groupe d’études de l’Atmosphére Météorologique (CNRM-GAME)	Interaction Sol-Biosphére-Atmosphére Surface Externalisee (ISBA-SURFEX)	3l-7.3, dif-7.3
JULES	UK Met Office, Natural Environment Research Council	the Joint UK Land Environment Simulator	3.1,3.1_altP
Mosaic	NASA	Mosaic	1
NOAH	NOAH	The Community Noah Land-Surface Model	2.7.1, 3.3, 3.2
ORCHIDEE	Institut Pierre Simon Laplace (IPSL)	Organising Carbon and Hydrology In Dynamic Ecosystems (ORCHIDEE)	r1401

Fig. 1.

The locations of the 20 flux tower sites in the PLUMBER experiment. The IGBP vegetation type is represented by color and the numbers indicate the of years of data used in the PLUMBER experiment. Site data is given in Table 1.

Table 1.

Fluxnet datasets used in PLUMBER.

	Fluxnet Code	Location	Lat	Lon	IGBP Land Cover Type	Timeframe	Years
Amplero	IT-Amp	Italy	41.9041	13.6052	Croplands	2002–2008	4
Blodgett	US-Blo	California, USA	38.8953	−120.633	Evergreen Needleleaf	1997–2007	7
Bugac	HU-Bug	Hungary	46.6917	19.6017	Croplands	2002–2008	4
ElSaler2	ES-ES2	Spain	39.2756	−0.3153	Croplands	2004–2010	2
ElSaler	ES-ES1	Spain	39.346	−0.3188	Permanent Wetlands	1999–2006	8
Espirra	PT-Esp	Portugal	38.6394	−8.6018	Woody Savannas	2002–2009	4
FortPeck	US-FPe	Montana, USA	48.3077	−105.102	Grasslands	1999–2013	7
Harvard	US-Ha1	Massachusetts, USA	42.5378	−72.1715	Mixed Forests	1991–2013	8
Hesse	FR-Hes	France	48.6742	7.0656	Deciduous Broadleaf	1996–2013	6
Howard	AU-How	Australia	−12.4943	131.152	Savannas	2001–2013	4
Howlandm	US-Ho1	Maine, USA	45.2041	−68.7402	Mixed Forests	1995–2013	9
Hyytiala	FI-Hyy	Finland	61.8474	24.2948	Evergreen Needleleaf	1996–2013	4
Kruger	ZA-Kru	South Africa	−25.0197	31.4969	Savannas	2000–2010	2
Loobos	NL-Loo	Netherlands	52.1679	5.744	Evergreen Needleleaf	1996–2013	10
Merbleue	CA-Mer	Ontario, Canada	45.4094	−75.5187	Permanent Wetlands	1998–2013	7
Mopane	BW-Ma1	Botswana	−19.9165	23.5603	Savannas	1999–2001	3
Palang	ID-Pag	Indonesia	−2.345	114.036	Evergreen Broadleaf	2002–2013	2
Sylvania	US-Syv	US	46.242	−89.3477	Mixed Forests	2001–2009	4
Tumba	AU-Tum	Australia	−35.6557	148.152	Evergreen Broadleaf	2000–2013	4
UniMich	US-UMB	Michigan, USA	45.5598	−84.7138	Deciduous Broadleaf	1998–2013	5

Table 3.

Standard statistical set of metrics used in PLUMBER. All metrics are based on half-hourly values. In formulas, M represents model data, O represents observed flux tower data and n is the number of timesteps.

Metric	Abbr.	Formula
Mean Bias Error	MBE	$\frac{{\sum }_{i=1}^n(M_i-O_i)}{n}$
Normalised Mean Error	NME	$\frac{\sum |M_i-O_i|}{\sum |\overline{O}-O_i|}$
Standard Deviation difference	sd	$|1-\frac{\sqrt{\frac{\sum M_i-{\overline{M}}^2}{n-1}}}{\sqrt{\frac{\sum O_i-{\overline{O}}^2}{n-1}}}|$
Correlation coefficient	r	$\frac{{\sum }_{i=1}^n(M_i-\overline{M})(O_i-\overline{O})}{\sqrt{{\sum }_{i=1}^n{(M_i-\overline{M})}^2}\sqrt{{\sum }_{i=1}^n{(O_i-\overline{O})}^2}}$

The first group of benchmarks in the PLUMBER experiment were two earlier generation physically-based models: the Manabe bucket model (Manabe 1969), a simple soil moisture reservoir model with added surface exchange turbulence; and the Penman-Monteith equation (Monteith and Unsworth 1990), which calculates evapotranspiration based on net irradiance, air temperature, humidity, and wind speed. As anticipated (e.g. Chen et al. 1997), modern LSMs outperform these simpler physically-based models (Best et al. 2015).

The second group of benchmarks investigated in PLUMBER were those used in the Protocol for the Analysis of Land Surface models (PALS; (Abramowitz 2012)), a web-based database of model simulation and observational land surface datasets, with integrated diagnostic analysis tools. This benchmark group consisted of three empirical models: 1lin, a simple linear regression against downward shortwave radiation; 2lin, a 2-dimensional linear regression against downward shortwave and air temperature; and 3km27, a 3-dimensional, k-means clustered piecewise-linear regression against downward shortwave, temperature, and relative humidity. All three empirical models were trained and tested with half-hourly flux tower data. Each empirical model was applied out-of-sample separately at each Fluxnet site, by calibrating on data from the 19 other sites to establish regression parameters, and then using the meteorological data from the testing site to predict flux variables using these parameters.

The two groups of benchmarks were used to quantify expectations of LSM performance. That is, they provide some understanding of how close to observations we should expect a LSM to be, based on the complexity of the processes at each site and how much information is available in meteorological variables about latent and sensible heat fluxes.

In the PLUMBER experiments, LSMs used the appropriate vegetation type, vegetation height and reference height, but otherwise used their default parameter values for the specified vegetation type and selected soil parameter values using their own internal data sets. The LSMs were equilibrated by using the first year of each Fluxnet site repeatedly as a spin-up phase. More detail about the PLUMBER experimental protocol can be found in Best et al. (2015).

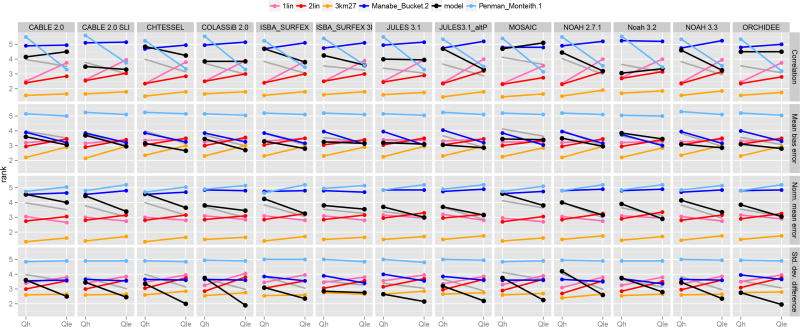
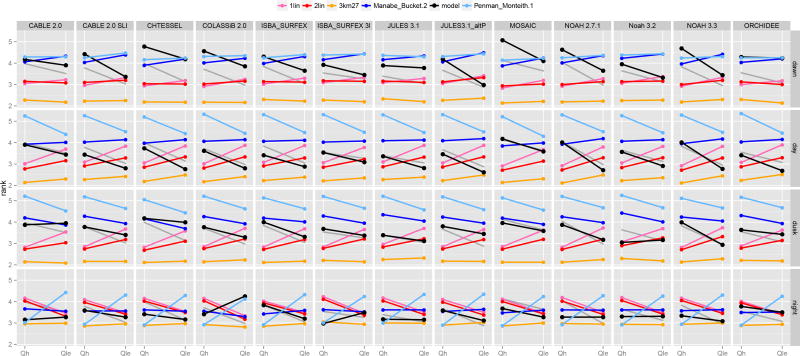
The results of this comparison are reproduced here for reference in Figure 2. Major columns represent different LSMs and the minor columns latent and sensible heat fluxes. The vertical axis represents the rank of each LSM for one of these flux variables, averaged across all four metrics and 20 flux tower sites. Ranks are performed separately for each LSM against the two physically-based approaches and the three empirical models, so that the average rank of any of the benchmark models can be different in each LSM’s panel. Ranks were used as a way of aggregating performance outcomes across the four metrics and 20 sites.

Fig. 2.

Ranks of LSMs relative to benchmarks, averaged over all metrics and sites, after Figure 4 in (Best et al. 2015). Major columns show different land surface models, minor columns show sensible heat (Qh) and latent heat (Qle). In each column, the LSM is shown in black, and various benchmarks are shown in comparison. The vertical axis shows the average performance rank for each model under 4 metrics over the 20 Fluxnet site datasets. In each case, a lower value indicates better relative performance. The 3km27 model clearly outperforms the LSMs for both variables, and the two linear regressions consistently outperform all LSMs for sensible heat.

The key result from PLUMBER, reported by Best et al. (2015), is that LSMs do not perform well in comparison with even simple empirical models for these four common metrics. For sensible heat (Qh), even the simple one-dimensional linear regression against downward shortwave radiation outperforms all of the LSMs (Figure 2). The slightly more complex 3km27 empirical model out-performs all models, for all variables (including net ecosystem exchange of CO₂, not shown here). These results are disturbing, but it is not at all clear from the original experiment what is causing these performance problems, or even if they are particularly meaningful. There are three categories of possible causes of the apparent poor performance by the LSMs:

• The apparent poor performance is due to problems with the PLUMBER methodology;

• The apparent poor performance is due to spurious good performance of the empirical models (e.g. systematic observational error, or empirical models lack of energy conservation constraint); or

• The poor performance is real, and is due to poor representations of physical processes, process order or ability to prescribe appropriate parameter values in LSMs.

Best et al. (2015) did not systematically examine the PLUMBER results in the context of these three categories. Our goal is to either identify the cause of the apparently poor behavior of the LSMs, or - equally usefully - discount possible causes of the problems. Here, we design and execute a number of experiments that target these three categories. As this is a series of discrete experiments, we describe the methods and results together, for each experiment divided into the three categories described above.

2. Methodology and Results

a. Possible cause #1: PLUMBER methodology

There are a number of aspects of the PLUMBER methodology that warrant closer examination. Here we investigate some potentially problematic aspects: the use of ranks instead of metric values; aggregation over sites and metrics; the possibility that PLUMBER was conducted on the wrong time scale; and the simulation initialization procedure.

1) Are ranks representative?

We first confirm that the PLUMBER ranks are a reasonable representation of the underlying relative real performance values for each metric and variable. PLUMBER used ranks in place of metric values because metric values are not comparable or easily normalisable due to their complex distributions. However, ranks do not necessarily capture all of the nuance of the underlying data and they may misrepresent the performance of the LSMs relative to the benchmarks. For example, if empirical models only outperformed LSMs by very small margins, and when LSMs outperformed empirical models the margin were much larger, the average rank diagnostic could be very misleading.

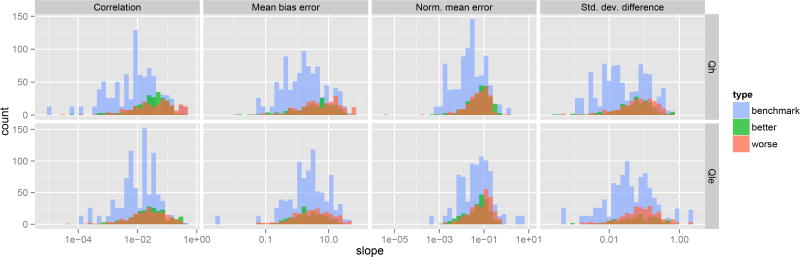
To assess whether this is a problem in the PLUMBER results, we calculated the differences in metric values between each model (benchmark or LSM), and the next best, and next worst model. This measure allows us to make statements about the relative performance of the various models, independent of the distribution of the metrics. If, for example, a model appears equally often at each rank, one might expect that the distribution of metric margins associated with that model (that is, ‘distance’ to the next best or worst model) to be similar to the overall distribution of metric margins across all models. This would not be true, however, if the model was consistently only-just beating other models, relative to other pairs of models in general. In that case one would expect the distribution of ‘next worst’ margins to have a lower mean than overall ‘next worst’ distribution, and the distribution of the ‘next best’ margin to have a higher mean.

Figure 3 shows the distributions of the differences between each model (benchmark or LSM), and the next best and worst model. The red and green data highlight the comparisons between the LSMs and the next worst, and next best of the 5 benchmarks, respectively. In general, the red and green have similar distributions, and those distributions are fairly similar to the differences between benchmark pairs (blue histogram), indicating that the ranks are representing the relative performances reasonably well. In cases where the LSM is the worst performing model, there is no red data, and vice-versa.

Fig. 3.

Histograms of differences between metric values for benchmarks and models with neigh-boring ranks, for all models at all sites. Values are calculated by taking the difference of the metric value for each model (LSM or one of the 5 benchmarks) from the model ranked next-worst for each LSM, Fluxnet site, metric, and variable. The blue data shows the benchmark-to-benchmark metric differences. The red data show the differences between the LSM and the next worst-ranked benchmark (e.g. if the model is ranked 4, the comparison with the 5th-ranked benchmark). The green data show the difference between the LSM and the next best-ranked benchmark. Since the models are ordered, all differences are positive (correlation is inverted before differences are calculated).

The skew to the right that is clearly visible in most of the plots is to be expected. These metrics all have values that converge on 0 (or 1 in the case of correlation, which is inverted), and become more dense as they approach 0. Therefore larger differences are to be expected for worse performing pairs of models. Since LSMs tend to perform worse than the benchmarks on average, this skew is more pronounced. This suggests that it is unlikely that ranks are unrepresentative of the underlying relative performance differences.

2) Is aggregation over sites and metrics problematic?

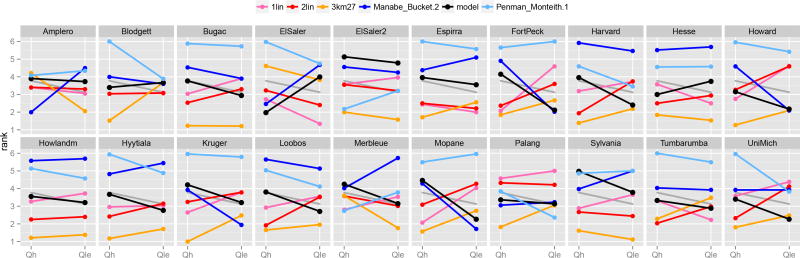
The results presented in PLUMBER are ranks averaged across multiple metrics and across multiple sites for each variable. It is possible that the averaging process is hiding more distinct patterns of performance - perhaps at particular sites, or under particular metrics. To assess whether a particular site or metric was unduly influencing the original PLUMBER results, we reproduce the main PLUMBER plot separately by metric (Fig. 4), and by site (Fig. 5).

Fig. 4.

As for Figure 2, but each row represents an individual metric (see Table 3 for metric definitions). The gray line shows the original LSM mean rank for comparison (as in Figure 2, though note that these data are only comparable with the black line, and not the benchmarks which have also changed).

Fig. 5.

As for Figure 2, but each cell represents the average rank of all LSMs at each individual Fluxnet site. The gray line is identical to that shown in Figure 4.

In both of these plots and in later plots, the original ranks for each LSM from Figure 2 are shown in gray. Note however that the ranks shown in gray are not necessarily ordered with respect to the benchmarks in the same way that they are in Figure 2, and are only comparable to the black line. For example, in Figure 2, most LSMs rank better than 2lin for Qle, but in Figure 4, the gray line might suggest that some these LSMs performed worse than 2lin, but this is only because the relative rank of 2lin has changed.

Figure 4 shows that while there is some variation between metrics, it is not the case that the LSMs are performing much better or worse than empirical models for any particular metric. Performance relative to the benchmarks is generally mediocre across the board. The LSMs do perform better for standard deviation in Qle, out-performing even the 3km27 model in most cases. Best et al. (2015) demonstrated that the LSMs performed better than the empirical benchmarks for the extremes of the distribution of each variable, and our analysis helps confirm that finding. As noted in Best et al. (2015), the empirical models should be expected to produce lower variability since they are regression-based. The normalized mean error and correlation metrics were significantly worse than the original aggregate results in Figure 2. Gupta et al. (2009) showed that RMSE and Correlation contain substantially similar information, however in this study the correlation metric was the least correlated of the four metrics (−0.33 with mean bias; −0.43 with normalized mean error; and −0.20 with standard deviation difference). On the other hand, correlations between the other three metrics were quite high (0.77 mean bias with normalized mean error; 0.75 mean bias with standard deviation difference; and 0.83 normalized mean error with standard deviation bias). The fact that the LSMs appear to be performing best under two of these three highly correlated metrics (mean bias and standard deviation difference), at least relative to the 3km27 benchmark, may indicate that the PLUMBER results overestimate LSM performance.

Figure 5 shows that there is considerable diversity of performance between sites for the LSMs. In this case, results are averaged over all 13 LSMs, and the four metrics in Table 3. For example, the LSMs perform relatively very well for Qh at the ElSaler site. This site is unusual: it is situated on a low-lying narrow spit of land between a small lake and the Mediterranean sea and is likely heavily influenced by horizontal advection. It is possible that rather than the LSMs performing well here, it is actually the empirical models that are performing poorly because they were calibrated on all other sites which do not exhibit behaviors seen at ElSaler. This possibility is supported by the fact that the models that include some measure of humidity (3km27, Penman-Monteith) perform worse than the simpler linear regressions. ElSaler2 is another unusual case - an irrigated crop-land site in Mediterranean Spain. The LSMs and Manabe bucket model, which do not have information about the additional water input to the system, do very poorly. The unconstrained reservoir in the Penman-Monteith equation in this case works very well. There are a number of sites where LSMs consistently perform poorly - Espirra provides an example pattern that we might expect from the original PLUMBER results - LSMs performing worse than empirical models, but much better than early theoretical models. However, there are other sites where LSMs are performing poorly even against the older approaches, especially for Qh, such as Amplero, and Sylvania; and there are no sites where LSMs perform consistently well relative to the benchmarks for both fluxes. While each of these breakdowns - by metric and by site - give us some insight into how LSMs are behaving, they do not explain the cause of the general pattern of apparent poor performance.

3) Do LSMs perform better on longer time scales?

Another possibility is that poor performance in the short time-scale half-hourly responses of LSMs are dominating the performance metrics. While versions of these models are designed for both climate and weather prediction, here we are largely concerned with long term changes in climate and the land surface. In this context, short-time-scale responses may be relatively inconsequential, as long as the longer term result is adequate. It is plausible, for example, that short time lags in various state variables built into LSMs might be adversely affecting the half-hourly model performance, while improving the longer time scale skill of the model. All of the original PLUMBER metrics are calculated on a per time step basis, and so do not take this possibility into account. To examine this, we recalculate the PLUMBER ranks after first averaging the half-hourly data to daily, monthly, and seasonal time steps.

Figure 6 reproduces the PLUMBER plots after averaging data to three different time-scales: daily averages, monthly averages, and seasonal averages. While there are some changes in these plots, there is no major improvement of LSM behavior relative to the empirical benchmarks. On all time-scales, the LSMs are consistently out-performed by the empirical benchmarks suggesting that the problems found in PLUMBER are not related to time-scale.

Fig. 6.

As for Figure 2, but averaged over daily, monthly, and seasonal time periods. The gray line is identical to that shown in Figure 4.

4) Are initial conditions a problem?

It is possible that the initialization procedure used in PLUMBER is inadequate. If the spin-up period was not long enough for state equilibration, or it was not representative of the period immediately preceding the simulation, then we would expect to see a stronger bias in the early parts of the first year of the data for each run. PLUMBER used a spin-up procedure that involved repeatedly simulating the first year at each site 10 times, before running over the whole period and reporting model output. To test whether poor spin-up might be the cause of the poor performance seen in PLUMBER, we calculated a number of new metrics over each simulation, for each variable, based on daily average data. First we calculate the day at which each of these simulation time series first crosses the equivalent observed time series, both as an absolute value, and as a percentage of the length of the dataset, which gives some indication of whether the simulation has converged on the observed data. Next, we calculate the difference in slope parameters of a linear regression over the two time series, and also the significance of this difference (where the null hypothesis is no difference). Lastly, we check if the bias is decreasing - that is, if the simulations have positive mean errors, is the trend slope negative (e.g. mean error is closer to zero in the second half of the time series), or vice-versa.

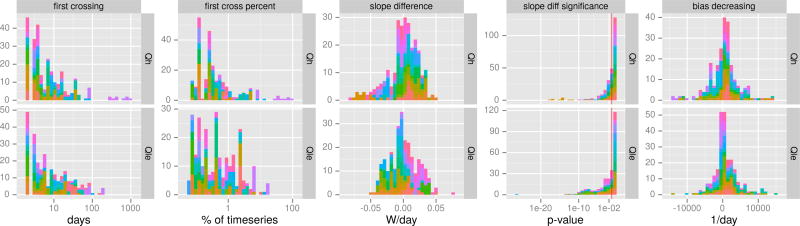
Figure 7 shows the results of the approaches described above. For each of the two fluxes (horizontal rows), using daily average data, it shows: the first day in the time series that the simulated flux is equal to, or crosses, the observed flux (1st column, logarithmic scale); as for the first column, but expressed as a percentage of the time series (2nd column); difference in the slopes of linear regressions of simulated and observed series over time (W/day); significance of the difference in the previous metric - values left of the red line are significant at the α =0.05 level (~44% of all values); and the rate at which the bias is decreasing, measured by means of model error divided by the gradient of model error - negative values indicate the simulations have a trend toward the observations. Each panel is a histogram, with each entry colored by the Fluxnet site it represents.

Fig. 7.

Histograms of model spin-up metrics, based on daily averages, from all LSMs at all sites. From left to right: 1) day at which the simulated series crosses the observed series; 2) as previous, but as a percentage of the time series; 3) difference in the slopes of linear regressions of simulated and observed series over time (W/day); 4) significance of the difference in the previous metric - values left of the red line are significant at the α = 0.05 level (~44% of all values); and 5) the rate at which the bias is decreasing, measured by mean(error)/slope(error) - negative values indicate the simulations have a trend toward the observations. Colors indicate the Fluxnet site at which the simulation is run.

The first two metrics show that in nearly all cases, the simulations’ time series quickly cross the observed time series (76% of simulations cross in the first 1% of the period, and 97% cross in the first 10%), indicating that it is unlikely that lack of equilibration explains the poor behavior of the LSMs relative to the benchmarks. The third and fourth metrics show the differences between the trends in the observations and the simulations, and the significance of those differences. In the majority of cases, effect sizes are quite small, with 61% of absolute trend differences less than 0.02 W/day, or 7.3 W/year (column 3, Figure 7), which is well within the standard error of the time series. 45% of these trend differences are significant at the α = 0.05 level (column 4, Figure 7), but there is no indication of a pattern of trends toward a lower bias - 54% of simulations have a trend that increases rather than decreases the bias (column 5). The colors in the plot specify the Fluxnet sites, and as indicated, aside from the two first-crossing metrics, there is very low correlation between metrics (r << 0.05, see Table 4).

Table 4.

Correlation between model metrics in Figure 7.

	first.crossing	first.cross.percent	slope.difference	slope.diff.significance
bias.decreasing	−0.017	−0.019	−0.025	−0.006
first.crossing		0.990	0.029	0.0386
first.cross.percent			0.015	0.031
slope.difference				0.034

We have therefore not been able to find obvious major systematic flaws in the PLUMBER methodology. The poor performance of the LSMs in PLUMBER, relative to the empirical benchmarks, cannot be dismissed based on any obvious flaw in the methodology.

b. Possible cause #2: Spurious empirical model performance

We next examine the possibility of spurious good performance by the empirical models. While there are a number of possibilities, related to data quality, we focus on one main possibility that has been brought up multiple times by the community in response to the original PLUMBER paper.

1) Lack of energy conservation constraints

The obvious candidate is that the empirical models are able to perform so well relative to the LSMs because they do not have any kind of built in constraint for energy conservation. This allows them to potentially produce results that predict individual flux variables quite well, but are physically inconsistent (e.g. outgoing flux energy is not constrained by net radiation). One way to test this hypothesis is to build empirical models that have additional constraints that ensure that energy is conserved.

Due to the effects of energy storage pools (mainly in the soil), it is not a trivial matter to produce a conservation-constrained empirical model. We therefore approach the problem from the opposite direction: we assume that energy conservation in the LSMs is correct and use the calculated available energy (Qh+Qle) from each LSM to constrain the empirical model output:

$$Q_{\mathit{\text{emp}}}^{\prime }=\frac{Q_{\mathit{\text{emp}}}}{({\mathit{\text{Qh}}}_{\mathit{\text{emp}}}+{\mathit{\text{Qle}}}_{\mathit{\text{emp}}})}\times ({\mathit{\text{Qh}}}_{\mathit{\text{lsm}}}+{\mathit{\text{Qle}}}_{\mathit{\text{lsm}}})$$

where Q_emp can be either Qh_emp or Qle_emp. An alternative approach might be to correct the observations with the LSMs’ total energy, and re-train the empirical models on the corrected data. We have no a priori reason to expect that this approach would provide qualitatively different results, and it would require significantly more computation.

Our approach effectively forces each empirical model to have the same radiation scheme and ground heat flux as the LSM it is being compared to (since available energy, Qle + Qh, is now identical), and preserves only the Bowen ratio from the original empirical model prediction. While this makes the empirical models much more like the LSMs, it informs us whether the empirical models were simply reproducing a systematic lack of energy conservation in the flux tower data. That is, if these modified empirical models perform similarly to their original counterparts, then energy conservation, while no doubt a real data issue, is not the cause of this result. If the reverse is true – that the modified empirical models no longer outperform the LSMs – there are at least two possibilities. Most obviously, the empirical models may indeed be fitting to systematically biased observational data. Alternatively, poor available energy calculations on the part of LSMs might cause the degradation of the modified empirical models, so that energy conservation is less of an issue. There are some difficulties with the transformation shown in the equation above. When the denominator in this equation approaches 0 the conversion could become numerically unstable. Under these conditions we replace all values of Qh and Qle with the values from the LSM whenever |Qh_emp + Qle_emp| < 5 Wm⁻². This effectively means that only day time values are modified.

If the energy conserving empirical models still outperform LSMs, it would indicate that calculation of available energy in LSMs is relatively sound, and that the energy partitioning approach is the likely cause of the poor performance. That is, even when empirical models are forced to have the same available energy as each LSM, performance ranks are essentially unchanged. Alternatively, if the energy conserving empirical models perform poorly, it may either indicate that empirical models are trained to match systematically biased, non-conserving flux tower data, or that the calculation of available energy in LSMs is the main cause of their poor performance.

The results of the energy-conserving empirical model experiment are shown in Figure 8. We wish to reinforce that Figure 8 shows precisely the same LSM, Manabe Bucket and Penman-Monteith simulations as Figure 2, and only the empirical benchmarks have changed (which in turn affects the other models’ ranks).

Fig. 8.

As for Figure 2, with energy conservation constrained empirical models. The gray line is identical to that shown in Figure 4.

It is clear that this change to the empirical models offers some LSMs a relative improvement in their rank. NOAH2.7.1 and ORCHIDEE now beat all empirical models for Qle, for example. This is far from a uniform result, however. Note also that Qle performance from CABLE2.0_SLI, ISBA-SURFEX3l, NOAH 3.2 is now worse than 2lin, which was not the case in Figure 2. The energy constraint has actually improved the empirical model performance in these cases. It is also still the case that all LSMs are outperformed by the energy conserving versions of 1lin for Qh. It therefore appears unlikely that the energy conservation issues in flux tower data are the cause of the empirical models’ good performance.

While some of the changes seen in Figure 8 can be attributed to the forcing of energy conservation on empirical models, there are other possible interpretations. They could be reflecting the effect that each LSM’s available energy calculation had on the empirical models. For example, if a particular LSM had a very poor estimate of instantaneous available energy (that is, Qle + Qh), because of issues in its radiation or soil heat transfer schemes, forcing this estimate on all of the empirical models might degrade their performance in a non-physical way. This would of course appear in Figure 8 as a relative improvement in the LSM’s performance. It is not clear whether this, or accounting for a lack of energy conservation in empirical models, is the cause of the improvements and degradations in performance we see in Figure 8.

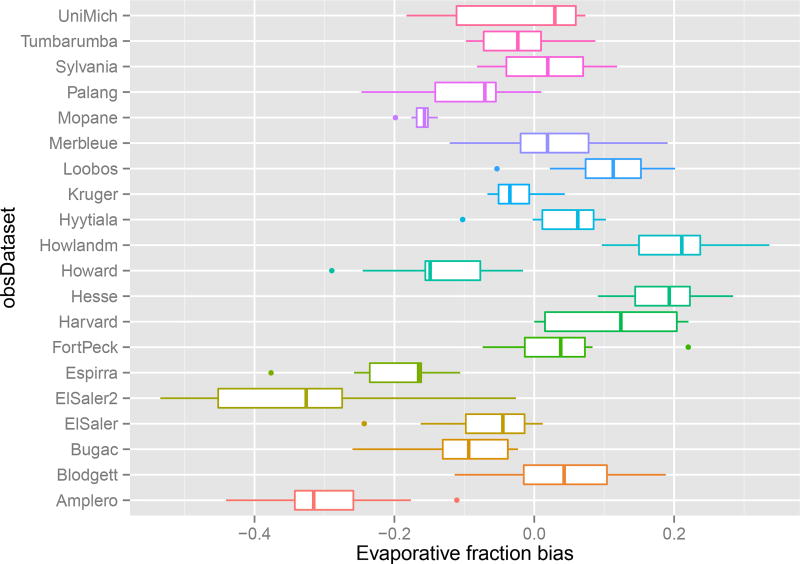
One unavoidable problem with this methodology is that if the flux tower data has a consistent bias in the evaporative fraction, then the LSMs will appear to perform relatively worse due to the empirical models over-fitting that bias. Figure 9 shows the biases in simulated evaporative fraction at each site across all LSMs. This plot consists of standard box-plots showing the mean, first and third quartiles, and outliers. The biases are calculated by taking

$$(\frac{{\mathit{\text{Qle}}}_{\mathit{\text{sim}}}}{{\mathit{\text{Qh}}}_{\mathit{\text{sim}}}+{\mathit{\text{Qle}}}_{\mathit{\text{sim}}}}-\frac{{\mathit{\text{Qle}}}_{\mathit{\text{obs}}}}{{\mathit{\text{Qh}}}_{\mathit{\text{obs}}}+{\mathit{\text{Qle}}}_{\mathit{\text{obs}}}})$$

using daily data, and excluding all cases where |Qh + Qle| < 1 Wm⁻² for either simulations or observations, to avoid numerical instability. It is clear that at some sites the LSMs have an apparent bias in evaporative fraction. It is not possible to be certain whether this bias is in the flux tower data, or due to shared problems between the LSMs. We address this in the discussion.

Fig. 9.

Biases in daily evaporative fraction for each LSM simulation, grouped by site.

This analysis indicates that, while problems with the flux tower data may contribute in a small way, they do not explain the entirety of the poor performance seen in PLUMBER. In general, the LSMs are not only predicting total heat poorly, they are also predicting the partitioning of that heat poorly.

c. Possible cause #3: Poor model performance

Finally, we search for indications that the problem might lie with the LSM simulations themselves. We examine two possibilities: LSM performance over short time scales and performance at different times of the day. We also explore how the LSMs perform as an ensemble, in an attempt to assess whether problems might be shared across models.

1) How do LSMs perform over short time scales?

When investigating the PLUMBER methodology, as outlined above, we examine whether short time scale variability is dominating the PLUMBER metrics by averaging data to different time scales before re-calculating performance measures. The inverse of this possibility is that rather than getting the short time-scale aspects of climate wrong, the LSMs are actually simulating the high-frequency responses well, but failing over the long-term. This would occur, for example, if the magnitude of the soil moisture reservoir were the wrong size, or the input or output to this reservoir caused it to dry too quickly or too slowly. To test this possibility, we remove all of the low frequency variability from the error time series, by first bias-correcting the simulation on a daily basis for each variable ( $Q_{\mathit{\text{sim}}}^{\prime }=Q_{\mathit{\text{sim}}}-\overline{Q_{\mathit{\text{sim}}}}+\overline{Q_{\mathit{\text{obs}}}}$, for each day), and then removing the average daily cycle over the remaining residuals. This gives us a model time series that has the same mean daily temperature and average daily cycle as the observations, but retains all of the modelled high-frequency variability.

The high-frequency only results are shown for each metric in Figure 10. Due to the nature of the bias correction, the bias metric (row 2 in Figure 4) is always zero for the LSMs, resulting in a trivial rank of 1, and so we remove the bias metric from these results. The effect this has can be seen by comparing Figure 10 to row 1, 3 and 4 of Figure 4. In all three metrics there are notable improvements in LSM ranks (averaged over all sites), suggesting that a significant portion of LSM error is likely due to the modulation of instantaneous model responses by the model states (for example soil moisture and temperature). The degree of improvement does vary between models to some degree - CABLE_SLI, COLASSiB, and NOAH3.3 improved in absolute rank in all metrics as a result.

Fig. 10.

As for Figure 2 with high-frequency response only, by metric - for this plot, LSMs are bias-corrected on a daily basis, and then have the daily cycle in the errors removed. The gray line is identical to that shown in Figure 4. The mean bias error metric is not included because it is trivially 0 due to the bias correction process.

2) Do LSMs perform better at different times of the day?

The LSMs appear to be having problems extracting all of the available information from the available meteorological forcings, especially SW down, as evidenced by the 1lin model outperforming each LSM for Qh. It thus seems likely that the LSM performance might vary according to the availability of that information. To test this possibility, we split the analysis over time of day, splitting each time series into night (9pm–3am), dawn (3am–9am), day (9am–3pm), and dusk (3pm–9pm), and repeating the analysis for each sub-series.

The time-of-day analysis is presented in Figure 11. As might be expected, there is clear variation in LSM performance relative to the benchmarks at different times of the day. The LSMs generally outperform the 1lin and 2lin model at night time. This is to be expected, as these two benchmarks, 1lin especially, have essentially no information at this time of day. In general, the LSMs all appear to be having difficulty with both fluxes around sunrise. It is worrying that some of the LSMs appear to be doing worse than a linear regression on sunlight during the night time for latent heat (COLASSiB, ISBA_SURFEX 3l, ORCHIDEE). However, the performance differences are small in those cases, and may be simply an artifact of the data (for example the empirical models fitting noise in Fluxnet). Overall it does not appear to be the case that the LSMs are performing well at any particular times of the day.

Fig. 11.

As for Figure 2, split by daily cycle - the 4 rows represent the 6-hour periods around dawn (3am–9am), noon (9am–3pm), dusk (3pm–9pm), and midnight (9pm–3am). The gray line is identical to that shown in Figure 4.

3) How do the LSMs perform as an ensemble?

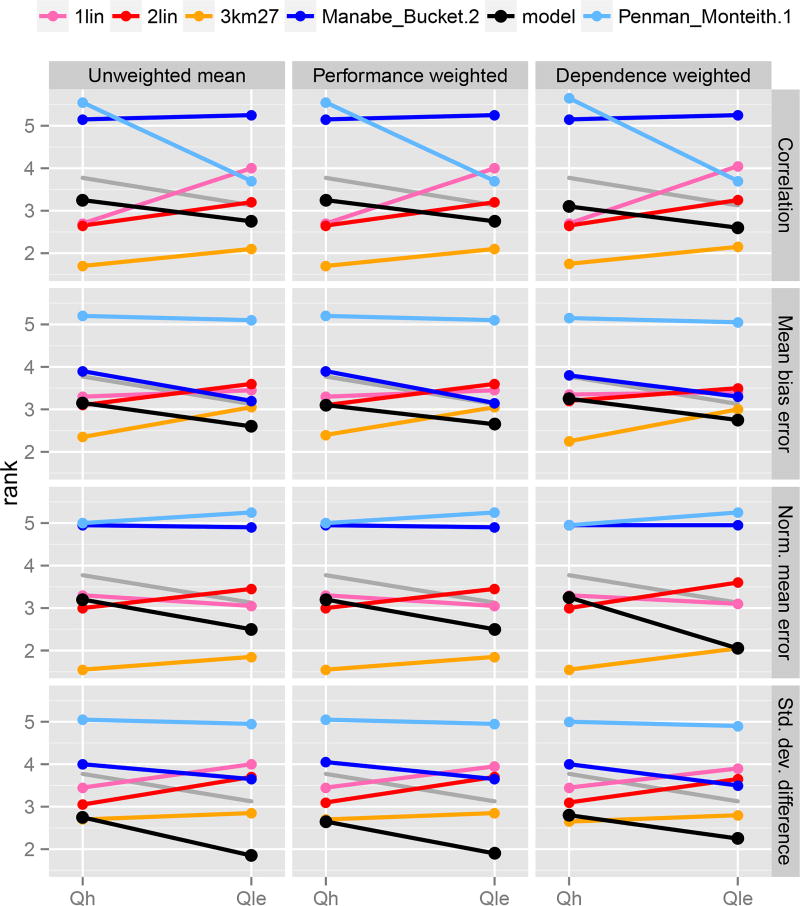
Lastly, we investigate whether the nature of the poor performance is a problem that is shared among models by examining the performance of the LSMs as an ensemble. Model ensemble analysis has a long history in the climate sciences (e.g. the Climate Model Intercomparison Projects, Meehl et al. 2007; Taylor et al. 2012), as well as in the land surface modelling community (Dirmeyer et al. 2006). Ensemble analysis allows us to identify similarities in performance between the LSMs. If each LSM is performing poorly for very different reasons, we might expect that at a given site, the time series of model error (model-observed) between different models would be uncorrelated. If this were the case, the multi-model mean should provide a significantly better estimate of the observed time series, since the eccentricities causing each model’s poor performance will tend to cancel each other. By analogy, the standard deviation of the mean of n random number time series, each with standard deviation 1 and mean 0, is $1/\sqrt{n}$. As an attempt to try to ascertain the degree of shared bias among LSMs, we choose to examine three different ensemble means - the unweighted average, the error-variance based performance-weighted mean, and the error-covariance independence-weighted mean (Bishop and Abramowitz 2013; Haughton et al. 2015). A priori, we should expect these ensemble means to perform differently in different circumstances. First, as mentioned above, if errors from different models have pair-wise low correlations, we should expect the model mean to perform better than individual models. Next, if there are substantial differences in performance of the models, we should expect the performance-weighted mean to out-perform the unweighted mean. If performance across the ensemble is similar but errors are highly correlated in a subset of the LSMs, then we should expect the independence-weighted mean to out-perform both the unweighted mean and performance weighted mean. The corollary is that if the independence-weighted mean does not out-perform the unweighted mean, this likely indicates that problems causing poor performance are shared among LSMs.

The results of the performance of the three ensemble means is shown in Figure 12. The means all perform similarly, or slightly better than the best LSMs under each metric (see Figure 4). However, the means are still out-performed by the empirical models in many cases. It is notable that there is also very little improvement under either of the weighted means. The performance-weighted mean only gives a slight improvement, which confirms that the differences in performance between LSMs relative to the benchmarks are not significant. The independence weighted mean also has little improvement, which gives an indication that problems with performance are shared across LSMs.

Fig. 12.

As for Figure 2, but showing the results for three different means across all LSMs, by metric. The gray line is identical to that shown in Figure 4. In general, we should expect means to perform better under all metrics except the standard deviation metric, as the averaging process acts as a smoother, removing non-correlated noise from the model results.

3. Discussion

The PLUMBER results are worrisome and it seems sensible to approach them with some skepticism. It is tempting to write off the results as an artifact of the PLUMBER methodology, but this does not appear to be the case. Over all LSMs tested, there is a consistent problem of poor performance relative to basic empirical models that is not obviously related to simulation initialization, particular sites or metrics biasing the analysis, or the time scale of the analysis. Despite the very wide range of performance ranks across different flux tower sites, once the obvious, understandable cases are removed (especially the ElSaler, ElSaler2 pair of sites, for different reasons), the aggregated picture of performance in Figure 2 seems broadly representative of our current LSMs.

In our energy-conserving empirical model analysis, we rescaled the total available energy in the empirical models to match that in each LSM, effectively making the total available energy identical in each pair of models, and only comparing the partitioning of that energy into Qh and Qle. We then showed that there are biases between the LSMs and the Fluxnet data, but that across sites there is no consistent bias that might cause the empirical models to perform spuriously well. There are known problems with energy conservation in flux tower data - Rnet = Qle + Qh + Qg is unbalanced by 10–20% at most sites (Wilson et al. 2002). However, this does not tell us anything about any potential bias in the evaporative fraction. Indeed, Wilson et al. (2002) note that the flux biases are independent of the Bowen ratio. Other studies have found that energy balance closure is dependent on stability (Kessomkiat et al. 2013; Stoy et al. 2013). We corrected the empirical model with the evaporative fraction, which is very close but more stable than the Bowen ratio suggested by Wilson et al. (2002). There is, however, discussion in the literature that eddy flux measurements might underestimate sensible heat much more than latent heat (e.g. Ingwersen et al. 2011; Charuchittipan et al. 2014; Mauder and Foken 2006). This would affect the PLUMBER results for sensible heat and might improve LSM ranks. It would not affect the latent heat results however and LSMs would still perform worse than the empirical benchmarks for the normalized mean error and correlation metrics.

So, if there is a problem with the LSMs, as appears to be the case, where does it leave us? There are two broad possibilities to investigate.

The first, and perhaps most confronting, is that there are flaws in the structuring, conception of the physics, or ordering of processes in the models. The results from the three approaches to LSM averaging suggest that such a problem might be largely shared amongst LSMs. LSMs do commonly share some similar conceptualizations of land surface processes, even if they do not share implementation details. Masson and Knutti (2011) showed how inter-related climate models can be. Those results include many of the models used here and it would be interesting to see such an analysis performed on LSMs alone.

Examples of such shared problems might be that all of the LSMs could be missing a major component, a relationship between components, or they may share a flawed representation of one or more components. This part of the modelling process is hard to analyze rigorously, however some analysis of assumptions contained in models and the effects that those assumptions have on model performance has been undertaken (e.g. Clark et al. 2008; De Kauwe et al. 2013; Zaehle et al. 2014). In principle, one could take a single LSM and replace major model components with calibrated linear regressions (if the observational data were available to create these), and compare performance, in order to pinpoint which component is the main cause of the poor performance. This would likely require a quantity of process level data that is not yet available.

While we largely present negative results in our attempts to pinpoint these problems, there are some indications as to where the problem may lie if model physics is the cause of this result. The energy-conserving empirical models give a strong indication that the calculation of available energy for Qle and Qh is not the main problem. That is, since the conserving empirical models effectively have the same Rnet and ground heat flux as the LSMs, and still broadly outperform the LSMs, we assume that the main issue is in the calculation of these fluxes. While there are snow periods in some of these data sets, the majority do not include any significant snow - we can probably safely ignore snow sub-models as a cause of the overall result. It does appear that there are some issues in the available energy calculations that vary across models. Some models, for example, do perform better in a relative sense once the empirical models are forced to match their available energy (compare Figures 2 and 8). Overall, however, this does not make a qualitative difference to LSM ranks against the empirical models. The analysis removing diurnal means (Figure 10) also broadly supports the idea that available energy and partitioning is being adversely affected by storage. That is, when the error in the diurnal average and average diurnal cycle was removed from LSMs, effectively removing any bias from inappropriate soil moisture levels and leaving behind only each LSM’s high frequency responses, there was an improvement in performance. Ideally, we would like to test directly whether, for example, soil moisture is correlated with the accuracy of evaporative fraction prediction. Unfortunately the Fluxnet datasets we used did not all contain soil moisture observations. In the cases that did report soil moisture, major challenges exist in using these data to evaluate LSMs. Observations are taken over different depths, using different measurement strategies, for example. There are also major issues in what soil moisture means in a LSM (Koster et al. 2009) and whether this variable can be compared directly with observed soil moisture. We therefore avoid comparisons of the LSM results with observed soil moisture but note that if the problems of data quality, consistency of measurements and issues of scale can be resolved this would provide a particularly good way forward for resolving why the LSMs perform poorly.

One caveat that must be added here is that these simulations are all run in an offline - uncoupled from an atmosphere model. In climate simulation and numerical weather prediction experiments, the LSM would be coupled to an atmosphere model which provides feedback to the land surface in a way that fixed meteorological forcings can not, and this feedback may provide damping of errors that the LSMs produce. Wei et al. (2010) indicates an effect along these lines in dry regions, by showing that an ensemble of LSMs coupled to an atmosphere model can produce higher variance between the LSMs when they are coupled individually, likely due to the fact that the strength of the coupling feedback is divided among the participating LSMs. Holtslag et al. (2007) also find that coupled models tend to produce less variance in stable boundary layer conditions because the fluctuating surface temperature provides feedback to the heat fluxes. A logical next step is therefore to perform a PLUMBER-like benchmarking evaluation in a coupled environment. Due to the difficulty of coupling many LSMs with one or more atmosphere models, as well as the problem of how to fit the benchmarks, such an experiment would be extremely challenging to undertake.

Calibration is also an ongoing problem, particularly because of the large number of poorly constrained parameters and internal variables, combined with the non-linearity of the models, which leads to problems of equifinality. These results might also reflect the compensating effect of calibration against stream-flow or gridded evapotranspiration products, where model structural and spatial property assumptions form part of the calibration process. Experiment-specific calibration may have improved the performance of the LSMs in PLUMBER. However calibrating LSMs per-site would give them an unfair advantage over the empirical models, which are only calibrated out of sample, and which use no site-characteristic data. The simulations in PLUMBER were run with appropriate reference heights and IGBP vegetation type, using the LSM’s default calibration for that vegetation type. Soil characteristics were selected by individual modelling groups. Clearly, using broad vegetation classes risk losing a lot of site-level specificity, but there is no way to calibrate the LSMs for specific sites while ensuring no over-fitting (e.g. out-of-sample calibration) within the PLUMBER dataset, since there are not multiples of each vegetation class represented. Improved per-vegetation class calibration using other Fluxnet sites may help, but at least some of the LSMs in this study are already calibrated on Fluxnet or similar datasets at multiple sites, and should perform reasonably well over these 20 datasets without re-calibration. While there are advanced methods of multi-criteria calibration available (e.g. Guerrero et al. 2013; Gupta et al. 1999), as well as viable alternatives to performance-based calibration (Schymanski et al. 2007), it would seem sensible to also focus on model parsimony, especially in components which are largely under-constrained. However, even if calibration is part of the problem here, it must be remembered that the empirical models are acting on only 1–3 of the 7 meteorological variables available to the LSMs, and also take no account of spatial or temporal variables. While it is true that adding further forcing variables would not guarantee a better result, for example if those variables have systematic errors, the consistency of performance of the empirical models indicates that that is not the case for at least downward shortwave radiation, air temperature, and relative humidity, and we have no a priori reason to expect it to be the case with the other variables.

It is also worth reflecting on the fact that the core conceptual process representations in LSMs were derived before any high-density data was widely available across different biomes. While the majority of these LSMs are calibrated on some site-level data, there is the possibility that our conceptually consistent LSMs are in some way not physically consistent with observations. An example of this possibility, that may explain the PLUMBER result that the LSMs are almost always worse at simulating Qh compared to Qle, relates to how the models are designed. The formulation of Qh and Qle in LSMs commonly refers to a “within canopy temperature” for example, through which these fluxes are exchanged with the atmosphere above the canopy. Imagine that this “within canopy air temperature” is erroneous. Under these circumstances Qh would systematically be simulated poorly relative to Qle, because it is not limited by available moisture. On top of this, energy-conservation correction formulas may be partitioning the conservation error poorly.

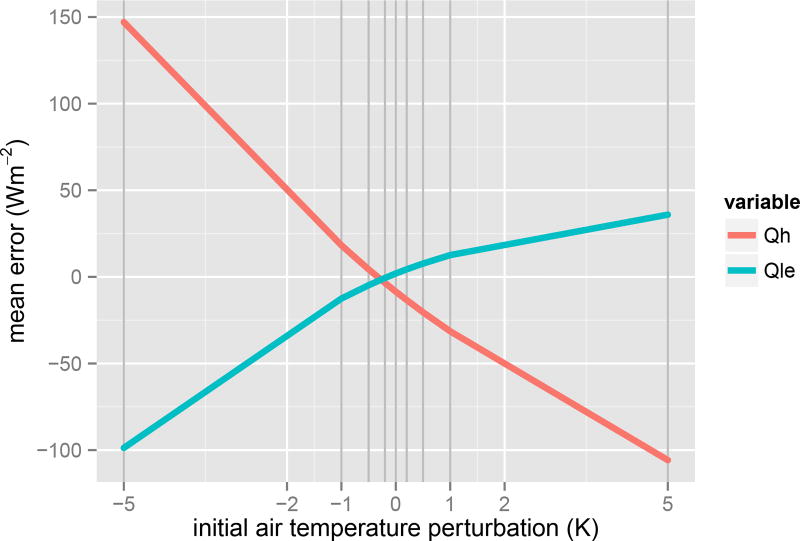
We cannot test this in all models involved in PLUMBER, but we can test this idea using one of the PLUMBER models. We took CABLE and introduced an error in the initial temperature of the canopy air space ranging from −5K to +5K, at the start of each time-step, and we then examined the impact of this error on Qh and Qle. Figure 13 shows how the error in Qh and Qle scales with the error in within canopy air temperature and shows that the error in Qh increases much more quickly than the error in Qle. We are not suggesting here that this is why all LSMs testing in PLUMBER show this behavior but we do suggest that there are key variables, common to LSMs, that act as pivots in the performance of a LSM and that are not resolved by feedbacks. While canopy interception cannot introduce too large an error (because too much evaporation in one hour will be compensated by too little in the next hour), if a systematic error is implicit in the interpolation of a reference air temperature to a canopy air temperature then this may not be compensated by feedbacks and lead to an error that is not resolved on longer time scales. We can demonstrate this for CABLE, and we suggest it is a plausible explanation for other LSMs. We suspect that other similar pivot variables, not ameliorated by feedbacks, might exist and might provide keys to unlocking the PLUMBER results.

Fig. 13.

Mean error in Qh and Qle as a result of perturbing the initial canopy air temperature at each time step, in CABLE at the Tumbarumba site, in south eastern Australia. Temperature was perturbed by ±(5, 2, 1, 0.5, 0.2)K, and a control run is included. All model parameters were left as default values. The response in Qh to negative temperature perturbations is about 50% stronger than in Qle, and about 3 times stronger for positive perturbations.

The second possibility is that the LSMs are conceptually correct, but are too complex for the task at hand. Modern LSMs have around 40 spatially varying parameters. At the scales that they normally operate - globally or regionally - observations rarely adequately constrain these parameters. To get around this issue they are usually calibrated, often using flux tower data, for each vegetation type. This process makes assumptions about landscape homogeneity, and forces the LSM to behave consistently with the time, place and circumstances of the calibration data. Using complex LSMs in this way may be forcing relatively capable models to operate essentially as empirical models, and using them out of sample. If we only use very simple metrics this can appear to be an issue of equifinality in calibration, but in reality the right answer is obtained for the wrong reasons, and as a result poor predictive outcomes are likely.

If true, this suggests that the appropriate level of complexity for a global LSM is a model with a parameter set of approximately the same dimension as the number of independent observable surface properties at the global scale - perhaps an order of magnitude smaller than modern LSMs today. While this is approximately the amount of information we provide LSMs at this scale, by prescribing vegetation and soil types, it is the fixed parameters, or forced co-variation of these parameters, that is potentially more important. Related issues of poor parameter constraint were explored by Mendoza et al. (2015). It should also be noted that regression methods, which are based on maximizing-variance of the variables we attempt to predict, benefit from a simpler method of fitting and can make stronger use of some observed variables that are not pure predictors, such as relative humidity, which is highly correlated with the Bowen ratio (Barros and Hwu 2002), and therefore may have a substantial advantage. However, this only explains the performance of the 3km27 benchmark, and not the fact that the simpler regressions still out-perform the LSMs for Qh.

It is also possible that the problems identified by PLUMBER do not have a single cause, and are simply an agglomeration of small, individually insignificant errors including some of those possibilities identified here. While our results do not explicitly resolve the performance problems shown in the original PLUMBER results, they do help us to rule out a number of possible causes, and in doing so, suggest directions for further investigation.

4. Conclusions

We investigated three broad categories of possible causes for the key result in the original PLUMBER experiment - LSMs being outperformed by simple, out of sample empirical models. These were: the experimental methodology of PLUMBER; spurious good performance of the empirical models in PLUMBER resulting from systematic bias in flux tower data, and; genuine poor performance of LSMs. While not every aspect of PLUMBER methodology was investigated, we did establish that particular sites or metrics were not biasing the result. Analyzing data on different time scales similarly had little effect, and there did not appear to be any systematic drift toward observed values that might be indicative of a systematic failure in the model spin-up protocol. We also repeated the experiment with energy-conserving versions of the original empirical models used in PLUMBER, constrained by the available energy calculations of each LSM, to try to ascertain whether a lack of energy conservation on the part of empirical models was the likely cause. Again, this had little effect on the result.

This leaves only the last of these three causes, the LSMs themselves. The empirical models suggest that there is more information in the input data available to reproduce observed latent and sensible heat than the LSMs are using. The calculations of the heat fluxes and the model states upon which these depend are therefore the most likely candidates for the cause of the large discrepancies observed here. It remains a topic for further investigation whether this is ultimately the result of, for example, over-parameterisation, missing process, problems with calibration, or one of several other possible reasons. Not all models are developed with the same purpose, and some LSM development may have focussed on very different aspects of the model, such as the distribution of natural vegetation, which might lead to models that are conceptually consistent but observationally inconsistent when predicting heat fluxes. We cannot recommend specific LSM improvements but rather provide a framework for model developers against which they can check their developments.

The validity of the benchmarking methodology in Best et al. (2015) was further evaluated in this study. It is worth noting that while PLUMBER may have undiscovered flaws, it is still extremely valuable: the relative poor performance of LSMs would likely have remained hidden under any previous model evaluation or intercomparison methodology.