 Inversion-symmetry separation of electronic state manifolds in RIXS enables identification of transient species in photo-chemical dynamics.
Inversion-symmetry separation of electronic state manifolds in RIXS enables identification of transient species in photo-chemical dynamics.
Abstract
We describe how inversion symmetry separation of electronic state manifolds in resonant inelastic soft X-ray scattering (RIXS) can be applied to probe excited-state dynamics with compelling selectivity. In a case study of Fe L3-edge RIXS in the ferricyanide complex Fe(CN)63–, we demonstrate with multi-configurational restricted active space spectrum simulations how the information content of RIXS spectral fingerprints can be used to unambiguously separate species of different electronic configurations, spin multiplicities, and structures, with possible involvement in the decay dynamics of photo-excited ligand-to-metal charge-transfer. Specifically, we propose that this could be applied to confirm or reject the presence of a hitherto elusive transient Quartet species. Thus, RIXS offers a particular possibility to settle a recent controversy regarding the decay pathway, and we expect the technique to be similarly applicable in other model systems of photo-induced dynamics.
1. Introduction
The intricate interplay of electronic, spin and structural degrees of freedom in excited-state dynamics is the key driver of photo-chemical reactions1,2 and crucially determines the efficiency of, for instance, charge transfer capabilities.3,4 Yet, disentanglement of electronic, spin and structural dynamics through simultaneous observation thereof remains a formidable task, as these different degrees of freedom, for many of our popular probes, often result in overlapping and inseparable spectral responses.
Of interest for biochemical,5 catalytic6,7 and photovoltaic8,9 processes are transition metal (TM) complexes, which accordingly have received decades of attention from several spectroscopic techniques. In particular for the development of light harvesting applications, mechanistic understanding of the formation and stabilization of charge separated states in these complexes constitutes a challenging and essential case of excited-state dynamics to unravel. Charge-transfer occurs through strong optical absorptivity, where e.g. ligand-to-metal charge-transfer (LMCT) and metal-to-ligand charge-transfer (MLCT) electronic excitations can be mapped out with valence state spectroscopy.10–13 Charge separation is facilitated by structural dynamics and symmetry reduction, of which vibrational spectroscopy14–16 and X-ray scattering6,17 prove capable probes. Transient hard X-ray Kβ fluorescence spectroscopy,18,19 sensitive mainly to metal spin states, and hard X-ray absorption near-edge structure (XANES) spectroscopy, sensitive to bond distances,20 have meanwhile demonstrated the importance of intersystem crossings (ISCs) and spin cascades in stabilizing excited states. To gain a more extensive picture of all the involved dynamics, studies have also been made by combination of several probes,19,21,22 as their individual information contents struggle to cover all the relevant degrees of freedom.
1.1. Symmetry enhanced selectivity in RIXS
In this work we describe a spectroscopic principle that enhances selectivity in resonant inelastic soft X-ray scattering (RIXS),23 applicable in general for systems with structural inversion symmetry. As demonstrated by example, the principle can be applied to obtain the necessary spectral fingerprints to disentangle transient species of different electronic configurations, spin multiplicities, and structures in a TM complex with a single probe.
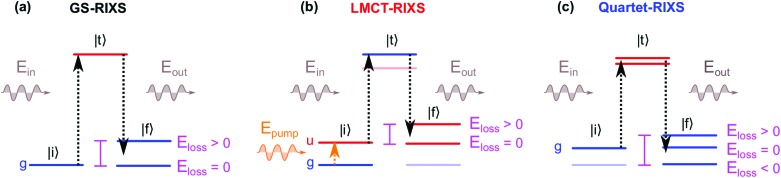
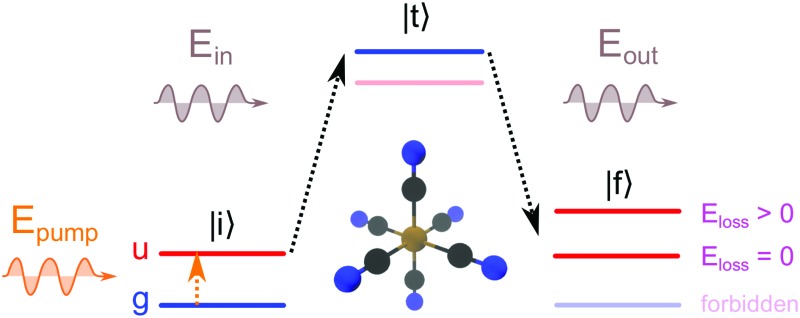
The RIXS process, in a two step picture, is illustrated in Fig. 1a. X-ray absorption coherently followed by X-ray emission takes the system from the initial state |i, through an intermediate core-excited state |t, to a final state |f. The core-excitation in RIXS contains the same rich information content as soft X-ray absorption spectroscopy.24,25 However, the energy difference of the incident and emitted photons additionally defines an energy loss that results from valence-excitations in the final state. The energy loss of inelastic RIXS features thus corresponds to the domain of valence-excited states that are locally probed with the element and chemical selectivity of X-ray pulses.
Fig. 1. Schematic illustrations of the two-step RIXS process |i → |t → |f (for electronic states and soft X-ray regime) in a system with inversion symmetry, with color coded electronic inversion parities g (gerade, blue) and u (ungerade, red). (a) Static RIXS with the electronic GS as initial state (GS-RIXS): only g → u → g RIXS processes are allowed, with zero or positive energy loss. (b) Pump–probe RIXS (LMCT-RIXS for Fe(CN)63–): the optical pump pulse inverts the initial inversion parity from g to u, with u → g → u RIXS process for the pumped species (here the energetically lowest state of u symmetry). The state manifolds for the GS-RIXS and LMCT-RIXS processes are thereby separated, with no possibility for negative energy losses. (c) Excited-state RIXS after excited-state dynamics (Quartet-RIXS after inter-system crossing for Fe(CN)63–): non-adiabatic transition(s) populates an excited state with g parity. Both the unpumped and newly populated excited species have g → u → g RIXS processes, with overlapping state manifolds that allows for negative energy loss, denoted as anti-Stokes RIXS (AS-RIXS).
In time-resolved pump–probe RIXS measurements, electronic and structural degrees of freedom can be efficiently monitored during the evolution of a photo-induced process.26–28 The rich information content of the two-dimensional RIXS spectrum especially aids in the identification of transient species which may not be distinguishable with comparable one-dimensional spectroscopies. When probing optically excited systems, in particular anti-Stokes RIXS (AS-RIXS)27 enables background free identification of even highly dilute excited species and spectroscopically weak but informative transitions. There, the interaction of the optical pump pulse and the X-ray scattering process enables the detection of negative energy loss features characteristic for electronically excited transient species, as illustrated in Fig. 1c.
For systems with structural inversion symmetry, we now propose that the concept of AS-RIXS may be brought one step further by also considering the symmetry separation of different excited species. In the soft X-ray regime of pump–probe RIXS, both the pump and probe transitions obey dipole selection rules, i.e. the involved electronic states can be characterized and separated by their inversion symmetry parities gerade (g, even) and ungerade (u, odd). Assuming a ground state (GS) symmetry of g, the GS-RIXS process is g → u → g. An optically pumped state will then necessarily be of u symmetry with u → g → u RIXS process. As illustrated in Fig. 1b the RIXS pathways of the two different initial states are thereby separated into two disjoint state manifolds, with no possibility for AS-RIXS. Only through subsequent excited-state dynamics, i.e. non-adiabatic transitions or structural symmetry reduction, may AS-RIXS become enabled. The mere presence (or absence) of AS features thereby directly probes the presence of transient species with g electronic symmetry. This, as compared to e.g. comparison of shape and intensity of often spectrally overlapping features, can facilitate the identification and separation of transient species in pump–probe measurements of excited-state dynamics.
1.2. Fingerprints of LMCT dynamics in Fe(CN)63–
While the described principle of symmetry-separation in RIXS applies to any system with structural inversion symmetry, we expect it to find particular usefulness in the study of TM complexes as they typically exhibit both highly symmetrical structures and rich photo-chemistry. For exemplification we therefore now apply the principle in a detailed case study of the excited-state dynamics of the ferricyanide complex Fe(CN)63–. As a model system for pseudo-octahedral complexes it has been studied with both static11,29–39 and time resolved methods.16,21,40,41 Recently, the decay dynamics following 400 nm optically induced LMCT excitation has become a debated topic, as measurements with different probes have given rise to conflicting interpretations.16,21,41 From multi-configurational quantum chemical simulations we show how Fe L3-edge RIXS can provide the necessary fingerprints to unambiguously identify and separate between all the proposed electronic, spin and structural species. This lays a theoretical foundation which, together with current development of new X-ray sources,42,43 may provide the definitive answer to a recently debated question.
The first study of LMCT induced dynamics in ferricyanide below the picosecond (ps) timescale was performed by Zhang et al.16 with transient IR absorption spectroscopy in acetonitrile and di-methyl sulfoxide solutions, where the authors interpreted the absence of transient anisotropy to result from ultrafast (500 femtoseconds (fs) or less) ligand hole delocalization. On the picosecond timescale (4.9 ps and 1.9 ps) the C–N stretch absorption spectrum shows two excited-state absorption peaks, which was originally interpreted to result from a symmetry reduction induced by solvent mediated ligand hole trapping. However, more recent measurements in water, D2O and ethylene glycol solutions by Ojeda et al.41 show that transient population of the C–N stretch mode, upon decay from the LMCT electronic state into a vibrationally hot GS (GS*, in 0.5 ps, 0.6 ps and 1.2 ps), is a likelier explanation for the additional peaks.
In parallel, Engel et al.21 proposed an entirely different mechanism for the LMCT decay. The authors argue that a likely candidate for the second transient species is a state of quartet multiplicity (hereafter referred to as Quartet), which in the region of the LMCT-Quartet intersection may readily be populated through vibronic coupling. This offers a conceptually simple explanation for the additional vibrational peaks through structural symmetry reduction which naturally occurs by a D4h stretch in the Quartet state. From time-dependent density functional theory calculations it is shown that such an interpretation is consistent with their time-resolved extreme ultraviolet (XUV) photo-electron spectroscopy (PES) data measured in water solution, with time constants of 170 fs and 730 fs for population of the Quartet and GS respectively. Ojeda et al.'s41 highly similar measurements (with reported ∼180 fs time-resolution) show no direct evidence for a Quartet state, but the authors also present no alternative mechanistic explanation for the re-population of the electronic GS.
A safe conclusion, uncontested by any of the studies, is that the choice of solvent strongly influences the resulting decay dynamics. In particular, this affects the decay rates of the involved transient species as shown both by Zhang et al.16 and Ojeda et al.,41 and it should in principle not be ruled out that the dynamics may be qualitatively effected. Yet, the divergent interpretations of Ojeda et al.41 and Engel et al.41 are particularly difficult to reconcile, since both were performed in water solution. This calls for a probe capable of unambiguous distinction between all the suggested species.
2. Computational details
Multi-configurational quantum chemical calculations were performed with the second-order perturbation theory restricted active space (RASPT2) method44,45 in the Molcas 8.0 program package.46 All calculations were performed in D2h symmetry, with the electronic symmetries (irreducible representations) ordered as: (ag, b3u, b2u, b1g, b1u, b2g, b3g, au). As in e.g. the work of Engel et al.21 this enforces an electronic wave function that conforms to the nuclear symmetry, i.e. prohibiting localization of molecular orbitals and thereby the LMCT electron–hole to a single ligand. A correspondence between orbital symmetry denotations of the Oh point group (of our discussion) and the D2h point group (of the calculations) is provided in Table S1 (ESI†).
An active space of 16 electrons in 13 RAS2 orbitals (4, 1, 1, 2, 1, 2, 2, 0 per symmetry) was used for geometry optimization and potential energy scans of electronic states 2B1g (GS), 4B1g (Quartet) and 2B3u (LMCT) with the ANO-RCC-VTZP basis set.47,48
An active space of 8 (2, 2, 2, 0, 2, 0, 0, 0 per symmetry) RAS1, 3 (0, 0, 0, 1, 0, 1, 1, 0 per symmetry) RAS2, and 5 (2, 0, 0, 1, 0, 1, 1, 0 per symmetry) RAS3 orbitals, allowing for 2 electron holes in RAS1 and 2 electrons in RAS3 spaces, was used for RIXS simulations with a basis set of TZVP quality. The orbitals were manually reordered in symmetries 2, 3 and 5, to include the Fe2p(t2u) orbitals within the RAS1 space as illustrated in ESI,† Fig. S1. Separate orbital constraints were added in the restricted active space self-consistent field (RASSCF) iterations for the Fe2p(t2u) orbitals (to retain a 2p core-hole character) and to the Lπ(t2u) orbitals (to disallow rotations with the Lπ(t1u) orbitals that fall within the same symmetries in the D2h calculations). 60 doublet + 60 quartet states (no core-excitations) and 60 doublet + 60 quartet (core-excited) states were obtained for each of the 8 electronic symmetries within the state averaging formalism. An imaginary shift of 0.2 Hartree was applied to ensure convergence. Transition dipole moments between the states were obtained with the restricted active space state interaction (RASSI) method.49,50 Scalar relativistic effects were included through a Douglas–Kroll (DK) Hamiltonian51,52 and spin orbit coupling through atomic mean field integrals.53 The electron repulsion integrals were based on a density-fitting approximation.54–56
For comparison to experimental spectra and conditions (as compared to previous publication34), all core-excited states were shifted by –8.5 eV. The transitions were life-time broadened along the absorption energy axis by a Lorentzian function with full-width half-maximum (FWHM) of 0.3 eV. Broadening due to instrumental effects was included through a Gaussian function with FWHM of 0.5 eV along the absorption energy axis, and 1.0 eV along the emission energy axis. Further broadening due to inhomogeneity and dynamical effects (such as fluctuations in structure and solvatization, and Franck–Condon effects) was included through a Gaussian function with FWHM of 0.5 eV along the absorption energy, emission energy and energy loss axes. The spread of the nuclear wave packet due to evolution in the valence-excited and core-excited states is assumed to have limited effects that can be captured in the same treatment. The broadening procedure is motivated by the excellent comparison previously obtained34 to experimental steady-state spectra of room temperature solutions. Relative polarization of incident and emitted X-ray photons was taken into account,57 assuming a horizontal mode of experimental setup. The obtained RIXS spectral intensities were normalized to a maximum intensity of one for each spectrum.
3. Results
We first characterize in detail the electronic states that have been previously proposed to be involved in the LMCT decay dynamics of ferricyanide and their structures as described on our level of theory. We establish the physical origin of RIXS spectral features of the different electronic states in terms of a molecular orbital picture and show by comparison of simulated spectra how fingerprint regions in the RIXS spectra may be chosen to unambiguously distinguish all potentially involved species, electronically excited as well as structurally distorted.
3.1. Electronic states and structures
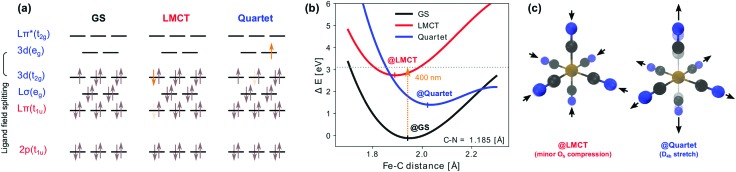
The electronic GS of Fe(CN)63– is a doublet T2g symmetric state, due to a single electron–hole in the 3d(t2g) level, as illustrated in Fig. 2a. As previously pointed out by Engel and coworkers,21 the complex should therefore experience a weak Jahn–Teller distortion away from its often assumed octahedral structural symmetry.11,16,58,59 In their work, the authors find a D3d structure to be most stable. However, the minor angular distortions of ±1.7° in D3d are both (for our purposes) spectroscopically negligible and insignificant in comparison to structural fluctuations in a solution environment.32,33 As our simulations impose D2h symmetry, we instead obtain a D4h structure. This restriction is well motivated by the accuracy of similarly simulated RIXS spectra in a recent comparison to the fully octahedral ferrocyanide complex Fe(CN)64–.34
Fig. 2. Electronic states with possible involvement in the LMCT decay dynamics of Fe(CN)63–. (a) Electronic configurations of the proposed GS, LMCT and Quartet electronic states. The electrons excited with respect to the GS configuration are shown in orange. (b) One-dimensional projections of potential energy surfaces of the considered electronic states, along scans of octahedral symmetry with varied Fe–C distance and frozen C–N bonds. Vertical excitation with 400 nm optical pump from the GS to LMCT surface occurs close to an intersection between the LMCT and Quartet surfaces. (c) Optimized structures (as obtained in D2h symmetry) of the LMCT state (@LMCT) and Quartet state (@Quartet) compared to the shaded GS structure (@GS).
To quantify structural deviation from octahedral symmetry we therefore instead focus on the differences in axial elongation, as described by the ratio q = rmaxFe–C/rminFe–C. For the GS, with q = 1.011, this deviation is apparently too small to be resolved by infrared (IR) spectroscopy16 (at room temperature) and near-edge X-ray absorption fine structure spectroscopy (see ESI,† Fig. S2). This is not surprising as the electron–hole is located in a 3d(t2g) orbital, which is only weakly interacting with the ligands.30,37 The GS structure can thus be labeled as effectively octahedral, and our discussion will be carried out in the nomenclature of the Oh point group. The slightly distorted octahedral symmetry in principle lifts the otherwise six-fold (three-fold spatial and two-fold spin) degeneracy of the GS. In a spin-free picture (before inclusion of spin–orbit coupling) this results (in D4h symmetry) in a non-degenerate (doublet) GS separated from a higher lying pair of degenerate (doublet) states by insignificant 0.0014 eV. The bigger effect instead comes from spin–orbit interactions of the open 3d shell, which splits the states into three spin-degenerate pairs. The two higher pairs are situated at 0.071 eV and 0.072 eV above the true GS, which consequently has a thermal population of roughly 89% at room temperature. Nevertheless, since similar Jahn–Teller and spin–orbit effects apply also for other species considered in the decay pathways, where thermal distributions do not apply in the out-of-equilibrium-dynamics, we will for simplicity only consider the energetically lowest electronic configuration of each species to be populated. This simplification does not qualitatively affect the obtained spectra, but has minor impact on peak extension and intensities.
Upon absorption of 400 nm light the complex is excited to a doublet T1u LMCT state, through an optical absorption feature peaked at 420 nm.11,16 The excitation corresponds to filling of the 3d(t2g) level by nominal promotion of one electron from a ligand based orbital with dominantly π character, Lπ(t1u), as illustrated in Fig. 2a. In a situation similar to the GS, weak Jahn–Teller distortions can be expected. However, due to the binding character of the 3d(t2g) orbital between the metal center and the ligands,30 we find a minor contraction of all metal–ligand Fe–C bonds (on average 0.057 Å) as the main structural response, as illustrated in Fig. 2c. This is accompanied by an even smaller elongation of the intra-ligand C–N bonds (on average 0.028 Å), as the Lπ(t1u) orbital instead has a C–N binding character. With the ratio q = 1.007, the LMCT state deviates even less from structural octahedral symmetry than the GS.
Close to the vertical excitation point, and even closer to the LMCT optimal structure, the LMCT potential energy surface is intersected by that of a quartet T1g state (denoted Quartet), as illustrated in Fig. 2b. Its electronic configuration as shown in Fig. 2a is a ligand-field excited state with a 3d(t2g) electron promoted into the 3d(eg) level. The structural response is a significant expansion of the complex in terms of the Fe–C distances (on average 0.154 Å), with nearly preserved ligand lengths (on average <0.003 Å compression) compared to the GS structure. This is a combined effect resulting from the single electron occupying the strongly anti-bonding 3d(eg) orbital and the additional electron–hole created in the weakly bonding 3d(t2g) orbitals. Further, excitation into the 3dz2 orbital centered along the z-axis also leads to strong Jahn–Teller distortions; the uneven distribution of electrons between different ligand pairs results in Fe–C bonds of 2.291 Å in the z-direction and 1.990 Å in the xy-plane. Thus, with a ratio of q = 1.151, the Quartet state structure implies a significant structural symmetry reduction from Oh to D4h, as illustrated in Fig. 2c.
3.2. LMCT decay pathways
In the following we treat the two proposed decay pathways of optically induced LMCT-excitation in ferricyanide, representative of Ojeda et al.'s41 and Engel et al.'s21 interpretations respectively, as equal possibilities. We describe how the proposed transient species can be represented in terms of electronic configurations, spin multiplicities, and structures, and demonstrate how time-resolved RIXS could provide the necessary fingerprints to distinguish all of the species.
In decay model I
| LMCT → GS* → GS | 1 |
the LMCT state decays directly into the electronic GS. However, the undissipated energy is conserved within vibrational excitations of the GS*, which subsequently decays to the completely relaxed GS through energy dissipation into the solvent. In terms of previously described electronic states and structures this may be represented by transitions between the following species:
| LMCT@LMCT → GS@GS | 2 |
As the GS* has not yet been clearly characterized it can only be dealt with indirectly and is therefore not the main focus of our analysis. However, we consider it qualitatively through two hypothetical scenarios. For this purpose we note that the “hot” C–N vibrations are likely excited as a response to rapid Fe–C bond length change,41 which on a short time scale (sub ∼ 1 ps41) can be expected to be the dominant effect as seen from a Fe centered core-level spectroscopy. The GS@Quartet could then represent a situation of Fe–C bond elongation, consistent with Engel et al.'s21 mechanistic interpretation for electronic re-population of the GS. The opposite possible case, i.e. Fe–C bond contraction, would in fact be qualitatively simpler to detect, as explained in Section 3.5. On a timescale of ∼1 ps and above,41 the intramolecular vibrational redistribution (i.e. population of other vibrational modes via e.g. anharmonic coupling) will lead to an ensemble of hot samples. This can be expected to significantly smear out the signals of most spectroscopies (as seen for both IR and XUV PES by Zhang et al., Engel et al. and Ojeda et al.). Consequently, the species would better be separated in terms of an additional characteristic time scale component (∼10 ps41), than by assignment of characteristic spectral features.
In decay model II
| LMCT → Quartet → GS | 3 |
the LMCT state decays via intersystem crossing to the Quartet state, which then mediates a return to the electronic GS through wave packet propagation on its excited-state potential energy surface. This may be described asLMCT@LMCT → Quartet@LMCT→ Quartet@Quartet → GS@Quartet
| → GS@GS | 4 |
where the presence of four transient species, of differing electronic states (GS vs. LMCT vs. Quartet), spin-multiplicity (doublet GS and LMCT vs. Quartet) and structure (@LMCT vs. @Quartet vs. @GS) poses a clear challenge in terms of identification and analysis, even in the absence of competing models.
In the following sections we demonstrate that all species of model I and II may be distinguished with time-resolved RIXS by their different spectral signatures. Yet, we emphasize that the most essential point lies in the possibility for definite detection (or, alternatively, rejection) of the Quartet species, which spectrally overlaps with both the GS and LMCT states in previously applied XUV PES.21 A RIXS experiment with sufficient time resolution will therefore be able to discriminate between model I and II as they both refer to dominant photo-products on similar time-scales. In general, however, reaction kinetics also determine whether a species is detectable or not: if the decay rate of any species greatly exceeds its rate of formation, then the low population will render the species undetectable, irregardless of time-resolution and spectral separation of distinct fingerprints.
3.3. RIXS – electronic and spin effects
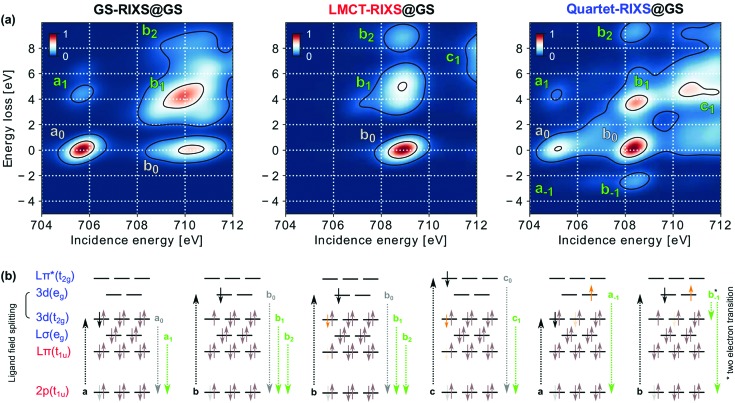
To motivate the choice of spectral fingerprints applicable to the LMCT decay, we first illustrate the influence of electronic and structural excitations on simulated Fe L3-edge RIXS spectra. Fig. 3a shows how electronic configuration and spin multiplicity influences the RIXS spectral features, as seen by a comparison of the three relevant electronic initial states in the GS structure. The features are nominally assigned to their dominant electronic transitions as seen from a molecular orbital picture in Fig. 3b to rationalize their origin. As will be seen, however, such a simplistic one-electron picture is not sufficient to explain all of the spectral trends.
Fig. 3. Electronic and spin effects on RIXS spectral features. (a) RIXS spectra of the three relevant electronic species GS-RIXS, LMCT-RIXS and Quartet-RIXS simulated within the optimized structure of the GS. (b) Molecular orbital type assignments of the dominant electronic transitions for the marked RIXS spectral features. Absorption resonances a, b and c are shown with black arrows. Elastic features, enumerated with subscript 0, are marked with gray text and shown with gray arrows. Inelastic features, enumerated with positive subscripts, are marked with green text and shown with green arrows. Anti-Stokes features (negative energy loss) are instead indexed with negative subscripts (the b–1 transition by a nominal two-electron transition, as indicated by the two green arrows). Core-excited electrons (from the RIXS probe) are shown in black, whereas valence excited electrons (due to the pump and subsequent excited-state dynamics) are shown in orange.
Simulations of GS-RIXS have previously been explained in detail and compared to measured spectra by Kunnus et al.34 In short, the L3 X-ray absorption spectrum, within the displayed range, consist of two resonances a and b due to excitation into the ligand field split 3d orbitals of t2g and eg symmetry, respectively. The compact resonance a exhibits one inelastic feature, a1, due to core-hole decay from the ligand centered Lσ(eg) orbital. Resonance b shows a more extended structure as the simultaneously open 3d(t2g), 3d(eg) and 2p levels in the intermediate state result in strong multiplet interactions. The strong inelastic feature b1 results from core-hole decay from the 3d(t2g) orbital and the weaker feature b2 from Lσ(eg) decay. Importantly, the three features a0, b0 and b1 thereby roughly form an isosceles right triangle in the incidence energy and energy loss plane, with equal side-lengths a0 to b0 and b0 to b1 directly determined by the strength of the ligand field splitting between the 3d(t2g) and 3d(eg) levels. In comparison to Kunnus et al.34 the intensity of elastic features are slightly overestimated in our work, due to the smaller number of allowed electronic excitations between g symmetric orbitals within our active space, which limits the electron correlation and the number of possible absorption and emission channels. The restriction is, however, computationally necessary to afford the inclusion of the Lπ(t1u) orbitals responsible for the LMCT excitation. A third resonance c, due to excitation into Lπ*(t2g), lies just outside the displayed energy range. The resonance will be briefly discussed where applicable; it is otherwise intentionally excluded from present analysis as its shape has been found to strongly depend on the number of included core-excited states in the spectrum simulations.30,37
The LMCT-RIXS spectrum may largely be compared to the RIXS spectrum of ferrocyanide also studied by Kunnus et al.34 As the LMCT excited electron (additional electron in the case of ferrocyanide) fills the 3d(t2g) level, absorption resonance a is completely quenched. Resonance b instead shifts towards lower energy and decreases significantly in width. The latter effect is due to the closing of all multiplet interactions with the 3d(t2g) hole in the LMCT state (as opposed to the GS), leading to much smaller splittings between different intermediate states. The same inelastic features, b1 and b2, are otherwise seen as in GS-RIXS, but with the LMCT excitation present in all three states of the RIXS process. Absorption resonance c, due to excitation into Lπ*(t2g), still lies outside the spectral range. However, the more extensive tail of its inelastic feature c1, due to decay from 3d(t2g), enters the very high energy range of the spectrum.
Unique features of Quartet-RIXS are AS-RIXS features a–1 and b–1, which result from effective decay from Quartet to GS through the RIXS process. The negative energy loss (energy gain) thereby corresponds to vertical de-excitation from Quartet to GS and directly measures their energy separation in a background free region of the RIXS spectrum available only to electronically excited transient species. As these features occur by spin-crossover from quartet to doublet multiplicity through the core-excited intermediate, their intensities are inherently determined by spin–orbit coupling. This results in appreciably higher b–1 than a–1 intensity, despite the nominal two-electron nature of the b–1 decay transition (as indicated by two arrows in Fig. 3b).
For features with zero or positive energy loss, the most pronounced features of the Quartet-RIXS spectrum can nominally be assigned to the same transitions as in GS-RIXS. Similarly to LMCT-RIXS, but with slightly larger magnitude, all observed absorption resonances are shifted towards lower energy, which consequently brings resonance c into the spectral range. The inelastic feature c1 is notably more intense than its elastic correspondence c0, which can be explained by stronger overlap of the Fe centered 3d(t2g) orbital from which inelastic decay occurs, than the ligand centered Lπ*(t2g) orbital of the elastic decay. The relative intensity and extension of features associated with resonances a and b are, however, subject to more complex effects. Notably and in contrast to GS-RIXS, elastic feature b0 here has a higher peak intensity than a0. This is contrary to what might be expected from a simple molecular orbital picture, wherein the opening of a second hole in the 3d(t2g) level should increase the absorption of resonance a. However, as shown in ESI,† Fig. S2 the peak absorption intensity of resonance a is in fact slightly lower in the Quartet than in the GS spectrum. As also explained in the ESI,† this stems both from multiplet interactions between the 3d(t2g) promoted electron and the 2p core-hole which causes a more complex absorption profile by splitting of resonances into multiple sub-features, and multi-configurational mixing in the core-excited state that significantly decreases absorption intensity of several transitions in the Quartet spectrum.
3.4. RIXS – structural effects
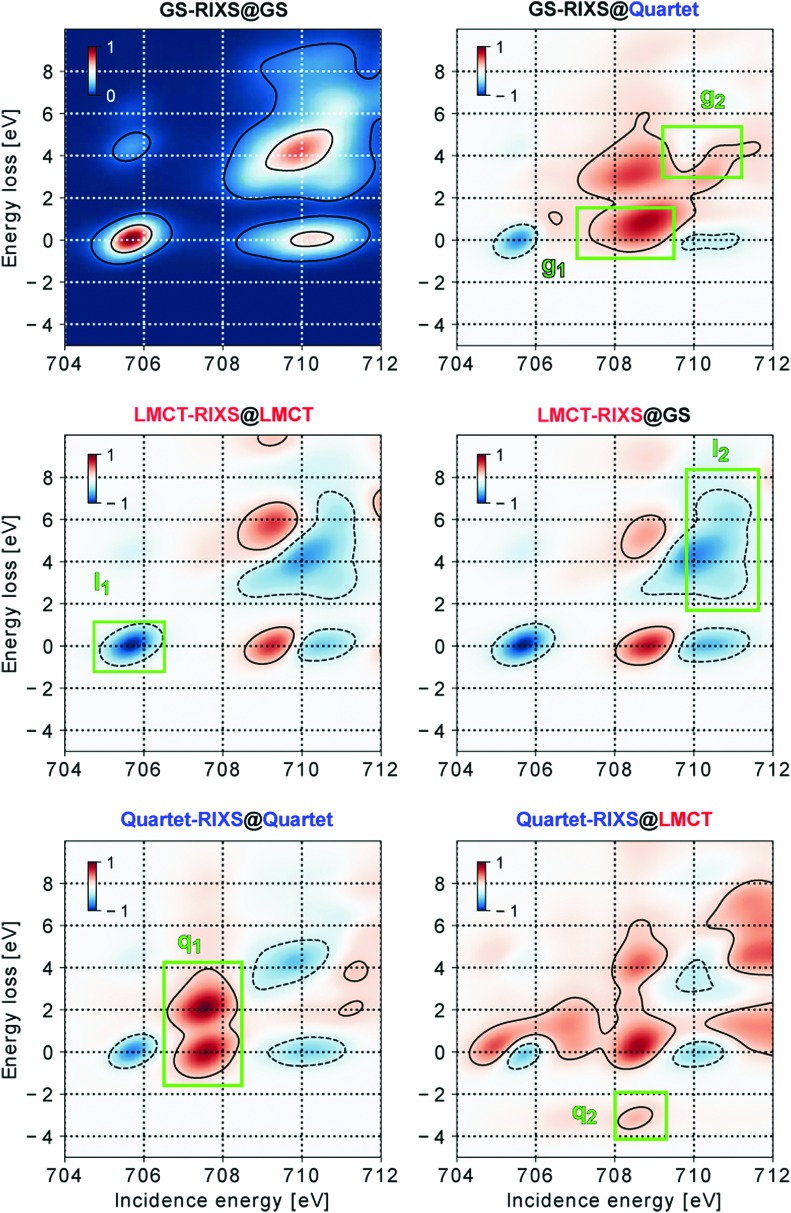
With the RIXS features assigned, we now demonstrate how structural changes influence the spectra of different electronic states. Fig. 4 shows difference maps of RIXS spectral intensities of the three different electronic states in two relevant structures, with GS-RIXS@GS as the reference. The corresponding spectra without subtraction are shown in ESI,† Fig. S3.
Fig. 4. Fingerprints of combined electronic, spin and structural effects on RIXS spectral features for the three relevant electronic states GS-RIXS, LMCT-RIXS and Quartet-RIXS in the three different optimized structures @GS, @LMCT and @Quartet. The left column shows spectra in the natively optimized structure of the electronic state, the right column spectra in the structure from which the state may be populated. GS-RIXS@GS, as a reference spectrum, is subtracted from the other spectra to indicate spectral differences.
The spectral response to structural distortion can to a good degree be explained by how the structural changes affect the ligand field splitting of the 3d(t2g) and 3d(eg) levels. In general, a compressed complex strengthens the ligand influence, increasing the splitting, whereas an expanded complex weakens the influence, thereby decreasing the splitting. Consequently, the “triangle” formed by features a0, b0 and b1 in GS-RIXS@GS is expected to grow at structure @LMCT and shrink at structure @Quartet, with analogous effects in LMCT-RIXS and Quartet-RIXS.
As shown in Fig. 4, the GS-RIXS@Quartet spectrum indeed shows a closing-in of the a0, b0 and b1 features, with a predominant intensity increase of the low incidence energy flank of the original b resonance. Lowered intensity is instead seen mainly on the original position of the a resonance.
In LMCT-RIXS, the spectral differences are highly comparable for the @LMCT and @GS spectra; the structural distortion following the electronic excitation is, as also already indicated in Fig. 2b, simply too small to be spectroscopically significant. Accordingly, the LMCT@GS and LMCT@LMCT species can not, and need not, be separated due to their highly similar properties. This motivates the omission of an initial structural relxation step on the LMCT potential energy surface (i.e. LMCT@GS → LMCT@LMCT) in both of the studied decay models.
Quartet-RIXS shows the strongest difference between the two presented structures. Quartet-RIXS@LMCT is, in accordance with the previous paragraph, highly comparable to Quartet-RIXS@GS from Fig. 3. In its relaxed @Quartet structure, however, the a and b resonances close in by several eV, which strongly shifts intensity into the incidence region of 707 eV to 708.5 eV from nearby spectral regions. Further, as AS feature b–1 measures the energy separation between GS and Quartet for a given structure, it is strongly dependent on the propagation on the Quartet potential energy surface. From the original 3.22 eV separation @LMCT (and 2.49 eV @GS), this is reduced to 0.79 eV in the Quartet structure, which thereby merges the b–1 feature with the (much more intense) elastic feature b0.
3.5. RIXS dynamical fingerprints
Against the background of the necessary spectral sensitivity presented in Section 1, we now turn to the task of separating the species of the proposed decay models by their spectral fingerprints. For an unambiguous identification of species, we wish to minimize their spectral overlap. As the signal trend in transient spectroscopy, i.e. intensity change with respect to a reference spectrum as in Fig. 4, can be either positive or negative (or unchanged) we aim to identify regions where the different species show opposite trends, which thereby uniquely separates the species in a pairwise fashion. Our six suggested fingerprint regions g1, g2, l1, l2, q1 and q2 are marked and labeled in Fig. 4. As shown in Table 1, their combined information content of pairwise separating spectral trends is sufficient to uniquely identify all of the 5 potential species in models I and II. Table 2 further contains a categorization of the fingerprints according to their ability to separate, specifically, electronic configurations, spin multiplicities, and structures. The fingerprints have been chosen according to their ability to uniquely separate at least two of the species, and to encompass as large and clear spectral regions as possible. Their characteristics will be discussed in the following.
Table 1. Pairwise unique separator fingerprints (corresponding to the fingerprints of the five potential species presented in Fig. 4). Each fingerprint represents a single spectral trend (either increased or decreased intensity) for one species, and opposite trend (or no change) for the other species, thereby acting as a unique separator for the two species.
| GS@Quartet | LMCT | Quartet@Quartet | Quartet@LMCT | |
| GS@GS | g1 | l1 & l2 | g2 | q2 |
| GS@Quartet | — | l2 | g2 | q2 |
| LMCT | — | q1 | q1 & q2 | |
| Quartet@Quartet | — | q2 |
Table 2. Fingerprints of electronic, spin and structural species (from Fig. 4 and Table 1), sorted according to their ability to separate specifically electronic configurations (i.e. different electronic states for a fixed spin multiplicity and structure), spin multiplicities (i.e. electronic states of different spin multiplicity for a fixed structure) and structures (i.e. different structures for a fixed electronic state).
| Type | Fingerprint | Separated | Fixed |
| Electronic | l1 | GS vs. LMCT | @GS |
| l2 | GS vs. LMCT | @GS | |
| Spin | g2 | GS vs. Quartet | @Quartet |
| q1 | LMCT vs. Quartet | @LMCT | |
| q2 | LMCT vs. Quartet | @LMCT | |
| Structural | g1 | @GS vs. @Quartet | GS |
| q2 | @Quartet vs. @LMCT | Quartet | |
The completely relaxed GS@GS is best separated from the GS@Quartet by an increased intensity in region g1, due to the reduced ligand field splitting of the expanded complex. Alternatively, in the situation of a GS* described by a compressed complex (as mentioned in Section 3.2), the opposite trend of intensity shift should be expected. In particular, the b0 feature will then instead shift towards higher incidence energy, allowing for a fingerprint region on the high energy flank of its original position to identify a structurally compressed GS, as all other species there show the opposite trend.
The LMCT species (which includes both LMCT@GS and LMCT@LMCT) is readily separated from GS@GS by its characteristic 3d(t2g) shell-closing, which completely quenches the intensity in region l1. However, as the GS@Quartet also shows a decreased intensity in region l1, we also need to introduce region l2 for unambiguous identification. This region relies on the shifted and more compact b1 feature in the LMCT state, which leaves a gap between the b and c resonances.
The q2 fingerprint, i.e. AS feature b–1, is the single most informative fingerprint, as it allows Quartet@LMCT to be separated from all other species. The symmetry separation of electronic states is here essential, as the LMCT and Quartet@LMCT species cannot be separated neither by their resonance b positions, nor in terms of relative energy to the GS potential energy surface. A RIXS process which effectively de-excites from LMCT to GS (i.e. dipole forbidden u → g → g RIXS process) would thus give rise to an AS feature in the same spectral region of roughly 709 eV incidence energy and 3 eV energy loss, if allowed in LMCT-RIXS. As the Quartet@Quartet has no distinct AS feature, it is instead separated from LMCT and GS@GS by fingerprint q1, which relies on the intensity shift caused by the structural expansion of the complex. As GS@Quartet shows a similar trend, we also introduce fingerprint g2 which sees an increased intensity in GS@Quartet, but due to larger total shifts of intensity instead encloses an intensity decrease in the Quartet state. This fingerprint may well be considered the conceptually weakest separator between species. It is not surprising as the electronic structures of the GS@Quartet and Quartet@Quartet species, both with Fe3d5 occupation in a strongly decreased ligand field, should be highly comparable and thereby difficult to separate.
In comparison to one-dimensional spectroscopies we note that fingerprints g1, l1, l2 and q1 should also be detectable with near-edge X-ray absorption fine structure (NEXAFS) spectroscopy. g2, however, would in GS-RIXS@Quartet instead show the opposite trend (decreased intensity) in NEXAFS as detected in transmission mode (the same information content as the elastic RIXS intensities), and mixed trends (overlapped intensity increase and decrease) as detected by fluorescence yield (corresponding to integration of RIXS intensities over the energy loss axis). Similarly, q2 cannot be distinguished from b0 or b1 in either mode. Thus, g2 and the crucial fingerprint q2 are only detectable by spectrally resolved fluorescence (emission spectroscopy). The information content obtainable from non-resonant X-ray emission spectroscopy (as an alternative probe) cannot be directly inferred from the RIXS intensities, but it is clear from Fig. 4 that the separation of features in terms of incidence energy (see e.g.l1vs.q1) greatly helps in distinguishing between the species. Consequently, RIXS (used here as the resonant version of X-ray emission spectroscopy) constitutes a particularly powerful probe in its capability to unambiguously identify all 5 species.
With the importance placed on the q2 fingerprint, we emphasize that b–1 is a low-intensity feature uniquely enabled by L-edge spectroscopy. Its detection is greatly aided by the non-existent spectral overlap with all other features, but it may yet prove experimentally challenging to obtain the statistics necessary for sufficient signal-to-noise ratio, particularly at the time-resolution required to clearly confirm or reject the existence of a Quartet species. This underlines the importance of new and currently developed X-ray sources,42,43 which with their increased brilliance and time-resolution will allow for significant advances in the application of X-ray spectroscopy. Development of more efficient high-level quantum chemical methods60,61 might in parallel enable studies of larger and more complex systems. This could help to answer questions such as how well symmetry based arguments for RIXS intensities can be generalized to systems with weakly to strongly distorted structural symmetry, like pseudo-octahedral bi-pyridine ligated metals and metal centers in biological environments.
4. Conclusion
In this work we have described and employed inversion symmetry separation of electronic state manifolds for enhanced selectivity in resonant inelastic soft X-ray scattering. Particularly in combination with characteristic anti-Stokes features of electronically excited states, this facilitates identification of transient species in excited-state dynamics. In an exemplifying case study of ligand-to-metal charge-transfer induced dynamics in the ferricyanide complex, we have shown from multi-configurational restricted active space simulations how Fe L3 edge RIXS spectroscopy provides the necessary fingerprints to disentangle the possible electronic, spin and structural dynamics. Specifically, this offers the possibility to unambiguously confirm or reject the presence of a hitherto elusive transient Quartet species. Time-resolved RIXS spectroscopy, with inversion symmetry separation, thereby constitutes a promising probe for settling a recent controversy regarding the decay pathway of ligand-to-metal charge-transfer excitation in the complex, and we expect the technique to be similarly applicable, in particular, to other transition metal complexes in high symmetry structures.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
J. N. thanks Faris Gelmukhanov for productive discussions. M. O. acknowledges financial support from the Swedish Research Council (VR) (contract number 2015-03956). We acknowledge financial support of the Helmholtz-Virtual-Institute VI 419 “Dynamic Pathways in Multidimensional Landscapes”. R. M. J., S. E., A. F. acknowledge funding from the ERC-ADG-2014 – Advanced Investigator Grant – no. 669531 EDAX under the Horizon 2020 EU Framework Programme for Research and Innovation. M. L. acknowledges financial support from the Swedish Research Council (VR) and the Knut and Alice Wallenberg Foundation (Grant No. KAW-2013.0020). Work by K. J. G. was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division. We thank Kristjan Kunnus for productive discussions.
Footnotes
†Electronic supplementary information (ESI) available: RASSCF active space, point group denotations, complementary spectrum simulations, and complementary spectral assignments. See DOI: 10.1039/c7cp08326b
References
- Zewail A. H. Science. 1988;242:1645–1653. doi: 10.1126/science.242.4886.1645. [DOI] [PubMed] [Google Scholar]
- Zewail A. H. J. Phys. Chem. A. 2000;104:5660–5694. [Google Scholar]
- Falke S. M., Rozzi C. A., Brida D., Maiuri M., Amato M., Sommer E., De Sio A., Rubio A., Cerullo G., Molinari E., Lienau C. Science. 2014;344:1001–1005. doi: 10.1126/science.1249771. [DOI] [PubMed] [Google Scholar]
- Delor M., Keane T., Scattergood P. A., Sazanovich I. V., Greetham G. M., Towrie M., Meijer A. J., Weinstein J. A. Nat. Chem. 2015;7:689–695. doi: 10.1038/nchem.2327. [DOI] [PubMed] [Google Scholar]
- Bjornsson R., Lima F. A., Spatzal T., Weyhermüller T., Glatzel P., Bill E., Einsle O., Neese F., DeBeer S. Chem. Sci. 2014;5:3096–3103. [Google Scholar]
- van Driel T. B., Kjær K. S., Hartsock R. W., Dohn A. O., Harlang T., Chollet M., Christensen M., Gawelda W., Henriksen N. E., Kim J. G., Haldrup K., Kim K. H., Ihee H., Kim J., Lemke H., Sun Z., Sundström V., Zhang W., Zhu D., Møller K. B., Nielsen M. M., Gaffney K. J. Nat. Commun. 2016:13678. doi: 10.1038/ncomms13678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu D., Teong S. P., Zhang Y. Coord. Chem. Rev. 2015;293:279–291. [Google Scholar]
- Hagfeldt A., Grätzel M. Acc. Chem. Res. 2000;33:269–277. doi: 10.1021/ar980112j. [DOI] [PubMed] [Google Scholar]
- Grätzel M. Inorg. Chem. 2005;44:6841–6851. doi: 10.1021/ic0508371. [DOI] [PubMed] [Google Scholar]
- Parsons R., Drickamer H. J. Chem. Phys. 1958;29:930–937. [Google Scholar]
- Alexander J. J., Gray H. B. J. Am. Chem. Soc. 1968;90:4260–4271. [Google Scholar]
- Naiman C. J. Chem. Phys. 1961;35:323–328. [Google Scholar]
- Gale R., McCaffery A. J. J. Chem. Soc., Dalton Trans. 1973:1344–1351. [Google Scholar]
- Baiz C. R., McRobbie P. L., Anna J. M., Geva E., Kubarych K. J. Acc. Chem. Res. 2009;42:1395–1404. doi: 10.1021/ar9000263. [DOI] [PubMed] [Google Scholar]
- Arrivo S. M., Dougherty T. P., Grubbs W. T., Heilweil E. J. Chem. Phys. Lett. 1995;235:247–254. [Google Scholar]
- Zhang W., Ji M., Sun Z., Gaffney K. J. J. Am. Chem. Soc. 2012;134:2581–2588. doi: 10.1021/ja207306t. [DOI] [PubMed] [Google Scholar]
- Kim K. H., Kim J. G., Nozawa S., Sato T., Oang K. Y., Kim T. W., Ki H., Jo J., Park S., Song C., Sato T., Ogawa K., Togashi T., Tono K., Yabashi M., Ishikawa T., Kim J., Ryoo R., Kim J., Ihee H., Adachi S.-i. Nature. 2015;518:385–389. doi: 10.1038/nature14163. [DOI] [PubMed] [Google Scholar]
- Zhang W., Alonso-Mori R., Bergmann U., Bressler C., Chollet M., Galler A., Gawelda W., Hadt R. G., Hartsock R. W., Kroll T., Kjær K. S., Kubicek K., Lemke H. T., Liang H. W., Meyer D. A., Nielsen M. M., Purser C., Robinson J. S., Solomon E. I., Sun Z., Sokaras D., van Driel T. B., Vankó G., Weng T.-C., Zhu D., Gaffney K. J. Nature. 2014;509:345–348. doi: 10.1038/nature13252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W., Kjaer K. S., Alonso-Mori R., Bergmann U., Chollet M., Fredin L. A., Hadt R. G., Hartsock R. W., Harlang T., Kroll T., Kubicek K., Lemke H. T., Liang H. W., Liu Y., Nielsen M. M., Persson P., Robinson J. S., Solomon E. I., Sun Z., Sokaras D., van Driel T. B., Weng T.-C., Zhu D., Warnmark K., Sundstrom V., Gaffney K. J. Chem. Sci. 2017;8:515–523. doi: 10.1039/c6sc03070j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressler C., Milne C., Pham V.-T., ElNahhas A., van der Veen R. M., Gawelda W., Johnson S., Beaud P., Grolimund D., Kaiser M., Borca C. N., Ingold G., Abela R., Chergui M. Science. 2009;323:489–492. doi: 10.1126/science.1165733. [DOI] [PubMed] [Google Scholar]
- Engel N., Bokarev S. I., Moguilevski A., Raheem A. A., Al-Obaidi R., Mohle T., Grell G., Siefermann K. R., Abel B., Aziz S. G., Kühn O., Borgwardt M., Kiyan I. Y., Aziz E. F. Phys. Chem. Chem. Phys. 2017;19:14248–14255. doi: 10.1039/c7cp01288h. [DOI] [PubMed] [Google Scholar]
- Canton S. E., Kjær K. S., Vankó G., van Driel T. B., Adachi S.-i., Bordage A., Bressler C., Chabera P., Christensen M., Dohn A. O., Galler A., Gawelda W., Gosztola D., Haldrup K., Harlang T., Liu Y., Møller K. B., Németh Z., Nozawa S., Pápai M., Sato T., Sato T., Suarez-Alcantara K., Togashi T., Tono K., Uhlig J., Vithanage D. A., Wärnmark K., Yabashi M., Zhang J., Sundström V., Nielsen M. M. Nat. Commun. 2015;6:6359. doi: 10.1038/ncomms7359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ament L. J. P., van Veenendaal M., Devereaux T. P., Hill J. P., van den Brink J. Rev. Mod. Phys. 2011;83:705–767. [Google Scholar]
- Huse N., Kim T. K., Jamula L., McCusker J. K., de Groot F. M., Schoenlein R. W. J. Am. Chem. Soc. 2010;132:6809–6816. doi: 10.1021/ja101381a. [DOI] [PubMed] [Google Scholar]
- Huse N., Cho H., Hong K., Jamula L., De Groot F. M., Kim T. K., McCusker J. K., Schoenlein R. W. J. Phys. Chem. Lett. 2011;2:880–884. doi: 10.1021/jz200168m. [DOI] [PubMed] [Google Scholar]
- Wernet P., Kunnus K., Josefsson I., Rajkovic I., Quevedo W., Beye M., Schreck S., Grubel S., Scholz M., Nordlund D., Zhang W., Hartsock R. W., Schlotter W. F., Turner J. J., Kennedy B., Hennies F., de Groot F. M. F., Gaffney K. J., Techert S., Odelius M., Föhlisch A. Nature. 2015;520:78–81. doi: 10.1038/nature14296. [DOI] [PubMed] [Google Scholar]
- Kunnus K., Josefsson I., Rajkovic I., Schreck S., Quevedo W., Beye M., Grübel S., Scholz M., Nordlund D., Zhang W., Hartsock R. W., Gaffney K. J., Schlotter W. F., Turner J. J., Kennedy B., Hennies F., Techert S., Wernet P., Odelius M., Föhlisch A. New J. Phys. 2016;18:103011. [Google Scholar]
- Kunnus K., Josefsson I., Rajkovic I., Schreck S., Quevedo W., Beye M., Weniger C., Grübel S., Scholz M., Nordlund D., Zhang W., Hartsock R. W., Gaffney K. J., Schlotter W. F., Turner J. J., Kennedy B., Hennies F., de Groot F. M. F., Techert S., Odelius M., Wernet P., Föhlisch A. Struct. Dyn. 2016;3:043204. doi: 10.1063/1.4941602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones L. H. Inorg. Chem. 1963;2:777–780. [Google Scholar]
- Hocking R. K., Wasinger E. C., de Groot F. M., Hodgson K. O., Hedman B., Solomon E. I. J. Am. Chem. Soc. 2006;128:10442–10451. doi: 10.1021/ja061802i. [DOI] [PubMed] [Google Scholar]
- Lundberg M., Kroll T., DeBeer S., Bergmann U., Wilson S. A., Glatzel P., Nordlund D., Hedman B., Hodgson K. O., Solomon E. I. J. Am. Chem. Soc. 2013;135:17121–17134. doi: 10.1021/ja408072q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penfold T., Reinhard M., Rittmann-Frank M., Tavernelli I., Rothlisberger U., Milne C., Glatzel P., Chergui M. J. Phys. Chem. A. 2014;118:9411–9418. doi: 10.1021/jp5055588. [DOI] [PubMed] [Google Scholar]
- Prampolini G., Yu P., Pizzanelli S., Cacelli I., Yang F., Zhao J., Wang J. J. Phys. Chem. B. 2014;118:14899–14912. doi: 10.1021/jp511391b. [DOI] [PubMed] [Google Scholar]
- Kunnus K., Zhang W., Delcey M. G., Pinjari R. V., Miedema P. S., Schreck S., Quevedo W., Schröder H., Föhlisch A., Gaffney K. J., Lundberg M., Odelius M., Wernet P. J. Phys. Chem. B. 2016;120:7182–7194. doi: 10.1021/acs.jpcb.6b04751. [DOI] [PubMed] [Google Scholar]
- Pinjari R. V., Delcey M. G., Guo M., Odelius M., Lundberg M. J. Chem. Phys. 2014;141:124116. doi: 10.1063/1.4896373. [DOI] [PubMed] [Google Scholar]
- Pinjari R. V., Delcey M. G., Guo M., Odelius M., Lundberg M. J. Comput. Chem. 2016;37:477–486. doi: 10.1002/jcc.24237. [DOI] [PubMed] [Google Scholar]
- Guo M., Sørensen L. K., Delcey M. G., Pinjari R. V., Lundberg M. Phys. Chem. Chem. Phys. 2016;18:3250–3259. doi: 10.1039/c5cp07487h. [DOI] [PubMed] [Google Scholar]
- Guo M., Källman E., Sørensen L. K., Delcey M. G., Pinjari R. V., Lundberg M. J. Phys. Chem. A. 2016;120:5848–5855. doi: 10.1021/acs.jpca.6b05139. [DOI] [PubMed] [Google Scholar]
- Engel N., Bokarev S. I., Suljoti E., Garcia-Diez R., Lange K. M., Atak K., Golnak R., Kothe A., Dantz M., Kühn O., Aziz E. F. J. Phys. Chem. B. 2014;118:1555–1563. doi: 10.1021/jp411782y. [DOI] [PubMed] [Google Scholar]
- Reinhard M., Penfold T., Lima F., Rittmann J., Rittmann-Frank M., Abela R., Tavernelli I., Rothlisberger U., Milne C., Chergui M. Struct. Dyn. 2014;1:024901. doi: 10.1063/1.4871751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ojeda J., Arrell C. A., Longetti L., Chergui M., Helbing J. Phys. Chem. Chem. Phys. 2017;19:17052–17062. doi: 10.1039/c7cp03337k. [DOI] [PubMed] [Google Scholar]
- Altarelli M., Brinkmann R. and Chergui M., The European X-ray free-electron laser Technical design report, 2007.
- Galayda J. N., Proceedings of IPAC 2014, 2014, 935.
- Malmqvist P. A., Rendell A., Roos B. O. J. Phys. Chem. 1990;94:5477–5482. [Google Scholar]
- Malmqvist P. A., Pierloot K., Shahi A. R. M., Cramer C. J., Gagliardi L. J. Chem. Phys. 2008;128:204109. doi: 10.1063/1.2920188. [DOI] [PubMed] [Google Scholar]
- Aquilante F., Autschbach J., Carlson R. K., Chibotaru L. F., Delcey M. G., De Vico L., Fdez. Galván I., Ferré N., Frutos L. M., Gagliardi L., Garavelli M., Giussani A., Hoyer C. E., Li Manni G., Lischka H., Ma D., Malmqvist P. Å., Müller T., Nenov A., Olivucci M., Pedersen T. B., Peng D., Plasser F., Pritchard B., Reiher M., Rivalta I., Schapiro I., Segarra-Martí J., Stenrup M., Truhlar D. G., Ungur L., Valentini A., Vancoillie S., Veryazov V., Vysotskiy V. P., Weingart O., Zapata F., Lindh R. J. Comput. Chem. 2016;37:506–541. doi: 10.1002/jcc.24221. [DOI] [PubMed] [Google Scholar]
- Roos B. O., Lindh R., Malmqvist P. Å., Veryazov V., Widmark P. O. J. Phys. Chem. A. 2004;108:2851–2858. [Google Scholar]
- Roos B. O., Lindh R., Malmqvist P.-Å., Veryazov V., Widmark P.-O. J. Phys. Chem. A. 2005;109:6575–6579. doi: 10.1021/jp0581126. [DOI] [PubMed] [Google Scholar]
- Malmqvist P.-Å., Roos B. O. Chem. Phys. Lett. 1989;155:189–194. [Google Scholar]
- Malmqvist P. Å., Roos B. O., Schimmelpfennig B. Chem. Phys. Lett. 2002;357:230–240. [Google Scholar]
- Douglas M., Kroll N. M. Ann. Phys. 1974;82:89–155. [Google Scholar]
- Hess B. A. Phys. Rev. A: At., Mol., Opt. Phys. 1986;33:3742–3748. doi: 10.1103/physreva.33.3742. [DOI] [PubMed] [Google Scholar]
- Hess B. A., Marian C. M., Wahlgren U., Gropen O. Chem. Phys. Lett. 1996;251:365–371. [Google Scholar]
- Aquilante F., Pedersen T. B., Lindh R. J. Chem. Phys. 2007;126:194106. doi: 10.1063/1.2736701. [DOI] [PubMed] [Google Scholar]
- Aquilante F., Malmqvist P.-Å., Pedersen T. B., Ghosh A., Roos B. O. J. Chem. Theory Comput. 2008;4:694–702. doi: 10.1021/ct700263h. [DOI] [PubMed] [Google Scholar]
- Boström J., Delcey M. G., Aquilante F., Serrano-Andrés L., Pedersen T. B., Lindh R. J. Chem. Theory Comput. 2010;6:747–754. doi: 10.1021/ct900612k. [DOI] [PubMed] [Google Scholar]
- Gel’mukhanov F., Ågren H. Phys. Rev. A: At., Mol., Opt. Phys. 1994;49:4378. doi: 10.1103/physreva.49.4378. [DOI] [PubMed] [Google Scholar]
- Pierloot K., Van Praet E., Vanquickenborne L., Roos B. J. Phys. Chem. 1993;97:12220–12228. [Google Scholar]
- Bolvin H. J. Phys. Chem. A. 1998;102:7525–7534. [Google Scholar]
- White S. R. and Martin R. L., APS March Meeting Abstracts, 1998.
- Ma D., Li Manni G., Gagliardi L. J. Chem. Phys. 2011;135:044128. doi: 10.1063/1.3611401. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.