Neural signatures of spatial statistical learning: Characterizing the extraction of structure from complex visual scenes

Abstract

Behavioral evidence has shown that humans automatically develop internal representations adapted to the temporal and spatial statistics of the environment. Building on prior functional magnetic resonance imaging (fMRI) studies that have focused on statistical learning of temporal sequences, we investigated the neural substrates and mechanisms underlying statistical learning from scenes with a structured spatial layout. Our goals were twofold: (1) to determine discrete brain regions in which degree of learning (i.e., behavioral performance) was a significant predictor of neural activity during acquisition of spatial regularities and (2) to examine how connectivity between this set of areas and the rest of the brain changed over the course of learning. Univariate activity analyses indicated a diffuse set of dorsal striatal and occipito-parietal activations correlated with individual differences in participants’ ability to acquire the underlying spatial structure of the scenes. In addition, bilateral medial temporal activation was linked to participants’ behavioral performance, suggesting that spatial statistical learning recruits additional resources from the limbic system. Connectivity analyses examined, across the time-course of learning, psychophysiological interactions with peak regions defined by the initial univariate analysis. Generally, we find that task-based connectivity with these regions was significantly greater in early relative to later periods of learning. Moreover, in certain cases, decreased task-based connectivity between time points was predicted by overall post-test performance. Results suggest a narrowing mechanism whereby the brain, confronted with a novel structured environment, initially boosts overall functional integration, then reduces interregional coupling over time.

Introduction

Statistical learning is a powerful mechanism that operates by mere exposure to extract structure from the environment in a variety of domains, species, and developmental periods. Although statistical learning was initially directed to studies of the acquisition of various linguistic structures, there is now substantial evidence that statistical learning is domain-general and supports the acquisition of non-linguistic structures (see Aslin & Newport, 2012 for a review). While language contains a high degree of statistical regularity, the visual world is also richly patterned. A host of behavioral studies have demonstrated that human learners exploit not only the regularities embedded in temporally-ordered sequences (Fiser & Aslin, 2002a; Kirkham, Slemmer, & Johnson, 2002), but also those present in spatially structured scenes (Fiser & Aslin, 2001, 2002b, 2005). Since spatial information is abundant in visual input (e.g., characterizing features within objects and objects within scenes), learners must be equipped with neural machinery capable of generating internal representations of its structure. In the present work, we examine the nature of the neural mechanism that supports the learning of configurations of elements in complex spatial arrays. By exploring univariate activity and functional connectivity approaches, we simultaneously probe functional specialization (i.e., discrete regions of the brain that increase in BOLD response during a spatial learning task) and functional integration (i.e., the networks of brain areas that interact throughout this process; Büchel, Coull, & Friston, 1999).

Recently, functional neuroimaging methods have been employed to examine mechanisms of statistical learning in the brain, but most of this work has focused on temporally-ordered (sequential) input (e.g., Plante, Patterson, Gomez, Almyrde, & Asbjornsen, 2015; Tremblay, Baroni, & Hasson, 2013; Karuza et al., 2013; Tobia, Iacovella, Davis, & Hasson, 2012; Tobia, Iacovella, & Hasson, 2012; Gheysen, Van Opstal, Roggeman, Van Waelvelde, & Fias, 2010, 2011; Turk-Browne, Scholl, Johnson, & Chun, 2010; Turk-Browne, Scholl, Chun, & Johnson, 2009; Cunillera et al., 2009; Abla & Okanoya, 2008; Abla, Katahira, & Okanoya, 2008; McNealy, Mazziota, & Dapretto, 2006). While these studies vary widely (e.g., in terms of stimulus modality, complexity of the material to be learned, and duration of exposure), they generally implicate some combination of sensory-specific cortical areas and downstream association areas such as prefrontal cortex (e.g., inferior frontal gyrus, IFG), the basal ganglia (e.g., the dorsal striatum: caudate and putamen), and medial temporal lobe (e.g., the hippocampus). Indicating some degree of sensory-specific involvement, linguistic and non-linguistic auditory learning tasks have been observed to elicit responses in the temporal lobe, including portions of the superior temporal gyrus (Plante et al., 2015; Tremblay, Baroni, & Hasson, 2013; Karuza et al., 2013; Cunillera et al., 2009; McNealy, Mazziota, & Dapretto, 2006), while visual learning studies have been associated with activation in non-primary regions such as the Lateral Occipital Complex (LOC; Turk-Browne et al., 2009) and middle occipital areas (Gheysen et al., 2011; Turk-Browne et al., 2010). Though some have proposed that hippocampus and striatal areas can be dissociated by their timecourses (rapid versus gradual; Gheysen et al., 2010; 2011), another possibility is that they diverge according to their sensitivity to input modality (auditory versus visual). In particular, hippocampal involvement is less commonly observed in auditory sequence learning studies (but see Schapiro, Gregory, Landau, McCloskey, & Turk-Browne, 2014). Importantly, while we are beginning to disentangle patterns of neural activity underlying statistical learning of sequential information, the architecture supporting the acquisition of spatial regularities remains somewhat less defined. The present study addresses this gap by determining whether the prefrontal (particularly left IFG), dorsal striatal, and medial temporal structures that have been implicated in prior studies of sequence learning also support spatial statistical learning, or whether these substrates are instead specialized for regularities that unfold over time.

In addition to using univariate approaches to localize regions involved in learning, we employ functional connectivity measures to ask how these discrete areas interact with the rest of the brain as learning unfolds (we henceforth refer to these interactions as whole-brain connectivity). Specifically, we examine whether interregional coupling changes over the course of exposure to structured stimuli and probe whether these time-dependent shifts in connectivity are correlated with learning outcomes (e.g., overall post-test performance). We also probe shifts in connectivity at the item-specific level, asking whether interregional coupling is modulated by trial-by-trial learning within-subjects. Relatively few studies have simultaneously investigated activity and functional connectivity during the learning phase, and results range from an inverse relationship between activity and connectivity (e.g., Büchel et al., 1999; McIntosh, Rajah, & Lobaugh, 1999), to a complementary relationship (e.g., Yang, Gates, Molenaar, & Li, 2015), to no clear relationship between the two (e.g., Manelis & Reder, 2012; Sun Miller, Rao, & D’Esposito, 2007). By integrating the results of both univariate activity and functional connectivity approaches, we offer insight into the neural mechanisms underlying the learning process during the acquisition of spatial statistics.

Materials and Methods

Participants

A total of 31 participants ages 18−30 were originally tested in this study (all were right handed). Eleven of those participants were excluded on the following grounds: excess head motion (> 4 mm absolute motion, n = 3), incomplete or corrupted data (n = 4), or failure to respond to a minimum of 70% of test trials (n = 4). Because these analyses are built on the relationship between neural response during learning and behavioral performance at test, it was essential to include only those subjects with a complete posttest dataset. Data from the remaining 20 participants (14 female, 6 male) were analyzed. All participants had normal or corrected-to-normal vision and no history of neurological dysfunction. They were recruited from the Dartmouth College community, provided informed consent, and were compensated according to institutional guidelines.

Stimuli

Following the method of the behavioral experiment of Fiser & Aslin (2001), participants were presented with a series of visual displays: 3 × 3 grids each containing three base-pairs drawn from a possible inventory of six. Base-pairs were defined as two shapes consistently positioned in the same relative arrangement (Figure 1). They were created using a total of twelve individual shapes. Note that while the position of a base-pair within the grid changed from trial to trial, the spatial relationship between the items within a pair was perfectly predictable across the course of the experiment. Two of these base-pairs were oriented vertically, two horizontally, and two diagonally. Shapes appeared only within a base-pair and never in isolation. Base-pairs were combined exhaustively such that participants were exposed to the 144 possible scenes that fit within the 3 × 3 grid, each containing a unique arrangement of 3 different pairs, one from each orientation. The only information that participants could use to discern the underlying base-pair structure was the co-variation of the relative position of shapes within a scene.

Figure 1.

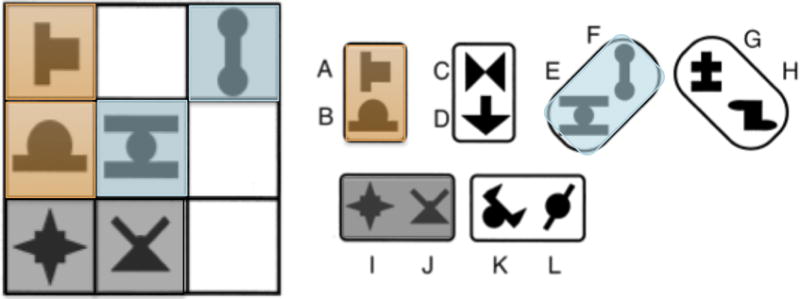
Left panel: Example of a scene viewed by participants during the exposure phase. Each scene contained a variable configuration of 3 base−pairs, where base-pairs were defined as two shapes in a fixed spatial relation. Each pair has been color-coded to illustrate the underlying structure, but this coding was not visible to the participant during exposure. Right panel: the full inventory of base-pairs.

Procedure

Exposure

In an event-related design, each scene was presented for 2.5 s, and the interstimulus interval was jittered so that a baseline fixation cross appeared on the screen for 2.5, 5, or 7.5 seconds. All 144 scenes were distributed across 3 exposure runs so that subjects saw 48 scenes per 6-minute run. Participants were instructed to attend to whichever scene was on the screen and were told that they may notice patterns or regularities within the grids. These instructions represent a slight departure from the canonical passive viewing paradigms used in other visual statistical learning studies. We elected to give participants a slightly more explicit task instruction given the challenges associated with obtaining behavioral evidence of learning in the scanner.

Test

After the exposure phase, participants underwent a testing phase in which they were shown two shapes on each trial: individual base-pairs or non-base-pairs (combinations of familiar shapes they had not seen previously). They were instructed as follows: “The displays that you just saw were made by taking pairs of shapes and combining them in the grid. Now you’ll see the grid with just one pair of shapes in it. Half of the pairs of shapes will have been included in the practice displays, half are new. Decide whether the pair that you see is made up of two shapes that went together, in that arrangement, in the first three runs. Respond when the stimulus is on the screen.” Participants indicated whether or not each pair looked familiar by pressing a button in one hand for “yes” and in the other for “no” (counterbalanced across participants). Responses were recorded during the 2.5 s presentation of each base-pair and non-base-pair. ISI was again jittered at 2.5−7.5 s. Over the course of two randomized testing runs, 6 base-pairs and 6 non-pairs were presented in 4 different positions within the grid, each twice. Base-pairs were presented in configurations that had been seen previously in the exposure phase, while non-pairs were presented in previously unseen configurations. As a result, the testing phase contained 96 items (48 base-pairs and 48 non-base-pairs) and had a total duration of 12 minutes. Neuroimaging data collected at test are not presented here. All stimulus displays were created using one of 2 lists, with order counterbalanced across subjects.

Stimulus presentation and data collection

Visual stimuli were presented using an Apple G3 computer (Apple Computer Inc., Cupertino, CA) interfaced with an Epson (model ELP−7000) LCD projector (Epson America, Inc., Long Beach, CA). Stimuli were projected onto a screen located in the back end of the magnet bore. Participants viewed the screen through a rearview mirror mounted to the head coil. The experiment was programmed using PsyScope 1.0 presentation software (Cohen, MacWhinney, Flatt, & Provost, 1993). Behavioral responses were recorded with hand-held button-boxes.

Images were acquired using a 1.5-T scanner (General Electric Medical Systems Signa CV/Nvi LX8.4, Waukesha, WI), equipped with a one-channel head coil. Anatomical images were obtained with a high-resolution 3D SPGR sequence (124 slices, TR = 25 ms, TE = 6 ms, flip angle = 25°, voxel size = 1.0 × 1.0 × 1.2 mm). Functional data were collected using a gradient spin-echo echo-planar sequence (TR = 2500 ms, TE = 35 ms, flip angle = 90°, voxel size = 3.75mm in-plane resolution). For the 3 functional scans (144 time points each), 25 T2*-weighted slices of 5.5 mm thickness were collected in an interleaved order.

Analysis

Image preprocessing and nuisance regression

Preprocessing was performed using FEAT v. 6.0 (fMRI Expert Analysis Tool) a component of the FSL software package (Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012). To prepare the functional images for analyses, we performed the following steps: skull-stripping with BET (Brain Extraction Tool) to remove non-brain material, motion correction with MCFLIRT (FMRIB’s Linear Image Registration Tool; Jenkinson, Bannister, Brady, & Smith, 2002), slice timing correction (interleaved), spatial smoothing with a 8-mm 3D Gaussian kernel (approximately twice the size of a single voxel), and high pass temporal filtering to reduce low frequency artifacts. Moreover, each participant’s individual anatomical image was segmented into grey matter, white matter, and CSF using the binary segmentation function of FAST v. 4.0 (FMRIB’s Automated Segmentation Tool; Zhang, Brady, & Smith, 2001). The white matter and CSF masks for each participant were then transformed to native functional space and the average timeseries was extracted. These values were included as confound regressors in our statistical modeling along with 6 translation and rotation parameters as estimated by MCFLIRT. Finally, native image transformation to a standard template was completed using FSL’s affine registration tool, FLIRT (Jenkinson et al., 2002). Subject-specific functional images were co-registered to their corresponding high-resolution anatomical images, which were then registered to the standard MNI-152 structural template via a 12-parameter linear transformation.

Within-subject univariate activity analyses: Item-specific learning

We began by performing within-subject analyses for each of the three functional runs (“first-level analysis” carried out using FMRIB’s Improved Linear Model). The waveform corresponding to stimulus presentation was modeled by first specifying, for each timepoint, a value of 1 corresponding to each event. We also included a second, orthogonalized regressor capturing fluctuations in activity related to behavioral performance on a scene-by-scene basis (see description below). Both waveforms underwent gamma-convolution in order to best match it to the measured hemodynamic response function (SD = 3 s; mean lag = 6 s). To reduce unexplained noise, we also added in a fraction of the temporal derivative from the original waveform and applied a temporal filtering process.

Generation of the scene-by-scene learning regressor

Though our task involved a continuous, passive viewing phase, it could be broken into discrete events, or scenes containing a unique combination of 3 base-pairs. In evaluating post-test performance, we observed considerable inter- and intra-participant variability in the acquisition of base-pair structures (i.e., some base-pairs were better learned than others). Therefore, we constructed a scene-by-scene learning regressor to allow us to map behavioral performance as measured after exposure onto each of the scenes presented during exposure (Figure 2). Capitalizing on this variability in base-pair learning, we generated the scene-by-scene regressor by calculating, for each participant, the hit rate for each of the 6 base-pairs (this was possible because each base-pair was presented a total of 8 times during the post-test). For each combination of 3 base-pairs in a given scene during the learning phase, we then computed an average accuracy score time-locked to each one of the 144 scenes displayed throughout exposure. Therefore, despite the absence of a canonical on-line measure of performance (such as reaction time), we could still capture the neural correlates of learning that emerged as scenes were presented during each of the three exposure runs. We were forced to exclude from this particular analysis two subjects with perfect scores on all base-pairs at post-test, as the inclusion of their behavioral performance would have led to a rank-deficient model (because the task and scene-by-scene regressors were perfectly collinear).

Figure 2.

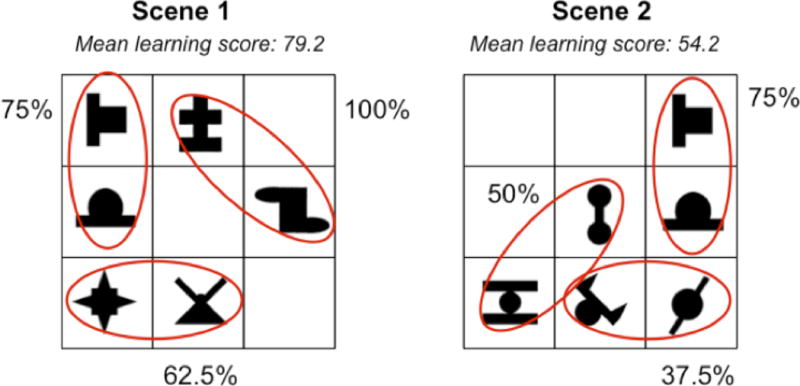
Sample scene scores for a hypothetical participant. Because participants learned base-pairs to varying degrees, it was possible to calculate an average learning score for each scene. Recall that each scene contained 3 base-pairs. In this example, the learning score for scene 1 was calculated by averaging 75%, 100%, and 62.5%, or correct endorsement of base-pairs 1, 4, and 5 at post-test. In our model, the time point for this scene would thus be assigned a value of 79.2. The time point associated with Scene 2, which contains base-pairs, 1, 3, and 6 would be assigned a score of 54.2.

Group-level univariate activity analyses

Next, we performed a series of group-level analyses designed to reveal (1) regions exhibiting an effect of scene-by-scene learning across the entirety of exposure, as well as (2) regions exhibiting a stronger/ weaker effect depending on the phase of exposure. One might, for example, expect behavioral performance to be associated with different patterns of neural activations early in the process of learning (e.g., run 1) compared to later in the learning phase (e.g., run 3). In the first group-level analysis, we combined across all 3 runs within-participant by inputting the first-level parameter estimates of the scene-by-scene learning regressor into a fixed effects Generalized Linear Model (GLM). This analysis was intended to reveal which regions were activated on average, in contrast to subsequent analyses, which were intended to tease apart activity patterns that might differ between runs. After this intermediate step, we combined across participants, modeling the overall group effect via FMRIB’s Local Analysis of Mixed Effects (FLAME). All results presented below were first thresholded at the single voxel level using a Z-statistic of 1.96 (corresponding to an uncorrected two-tailed p-value of 0.05). Resulting clusters’ significance levels, as estimated by Gaussian Random Field theory (Worsley, 2001), were then compared to a cluster-forming probability threshold of 0.05.

To delineate differences in learning-related activity between runs, the intermediate across-run concatenation step was not performed. Instead, we performed a “tripled t-test,” or a Repeated Measures ANOVA containing one fixed and one random factor. In this case, the fixed factor contained three levels corresponding to each of the three exposure runs, plus random subject intercepts. First-level estimates of the scene-by-scene learning effect were entered directly into a FLAME mixed effects model. We specified 6 run-to-run contrasts (run 1–run 3; run 3–run 1, etc.).

Functional connectivity analyses: Psycho-physiological interactions

We next explored whether functional connectivity with learning-related regions changed throughout the course of exposure. There are a variety of approaches to investigating the functional context in which regions of the brain operate. We opted to examine psycho-physiological interactions (PPI); that is, to ask where in the brain correlations between regions strengthen (or weaken) during a specific condition (O’Reilly, Woolrich, Behrens, Smith, & Johansen-Berg, 2012). The benefit of this approach is that it focuses on regions that exhibit a tighter functional association during the task of interest (in this case stimulus exposure relative to baseline) as opposed to those regions that are correlated in general, irrespective of task and, perhaps, due only to robust anatomical connections or close physical proximity.

Generation of the timeseries regressors

We performed a whole-brain PPI analysis using seed regions that showed an effect of learning in the univariate activity analysis (scene-by-scene learning). As we found no significant differences in univariate activity when comparing runs, we chose to define all seeds based on learning-related activation peaks when concatenating across all three exposure runs (Figure 3). From that map, we selected the top two activation peaks from each significant cluster, resulting in 4 seed ROIs (in order of intensity): mid precuneus (x = 0, y = −66, z = 32), right amygdala (x = 22, y = −8, z =−16), right thalamus (x = 8, y = −28, z = 0), and left lingual gyrus (x = −22, y = −56, z = 0). With so few studies examining spatial statistical learning, we selected these seed regions, defined purely functionally and limited to 2 per cluster, in order to offer a general snapshot of connectivity patterns uninfluenced by related literature on temporal statistical learning. In addition to this approach, we also chose peak intensity voxels in the dorsal striatum (left putamen: x = −28, y = −16, z = −4), the lateral occipital complex (left LOC: x = −46, y = −66, z = 18), and the right hippocampus¹ (x = 30, y = –22, z = –10), as these areas have previously been implicated in one or more studies of temporal statistical learning (Karuza et al., 2013; McNealy et al., 2006; Turk-Browne et al., 2009; 2010). Finally, we also generated two “control” seed regions in cortical areas uninvolved in this spatial statistical learning task. As prior work has indicated right hemisphere dominance for visual statistical learning (Roser, Fiser, Aslin, & Gazzaniga, 2011), we focused here on left hemisphere seeds localized to Heschl’s gyrus (x = –42, y = –24, z =12) and primary motor cortex (i.e., precentral gyrus: x = –36, y = –20, z = 48)². Thus, we examined connectivity using 7 functionally defined regions of interest: 4 regions that were found to be most strongly related to the time-course of learning and 3 regions that were active, albeit less so, and were previously observed in statistical learning tasks. In addition, we explored connectivity patterns involving two control regions in presumably unrelated cortical areas.

Figure 3.

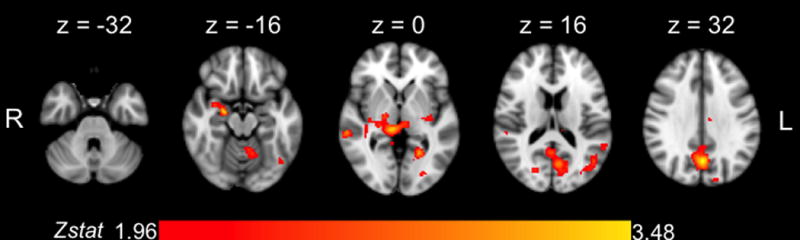
Axial views (z = –32 mm to z = 32 mm) for the univariate scene-by-scene (item-specific) learning analysis, collapsed across all three exposure runs.

Implementation of the PPI models

All seeds were defined in 2-mm MNI space and then transformed back to each subject’s native functional image via their anatomical scan. Peak voxels were dilated using a spherical kernel with a 5 mm radius resulting in a 5-voxel ROI centered on the peak activation. To reduce noise in the signal, the mean time-course within the ROI was extracted from each subject’s filtered functional image after it had been motion-corrected and preprocessed. Separate first-level models were generated for each seed, and preprocessing/ registration steps were performed exactly as previously described.

In the task-based version of the PPI analysis, we input for each of the 20 participants three explanatory variables: (1) a psychological regressor specifying stimulus event timing that was gamma-convolved with a hemodynamic response function. This regressor was centered such that the zero point fell halfway between each event and the baseline period; (2) a physiological regressor consisting of the filtered (pre-processed) time-course of our seed spheres, centered by subtracting the mean intensity across the timeseries from the intensity value at each TR; and (3) an interaction regressor modeling the relationship between the psychological regressor and the physiological regressor. While some approaches to PPI analysis (particularly in the case of event-related designs) recommend deconvolving the physiological timeseries, then reconvolving its interaction with the real-time task regressor (Gitelman, Penny, Ashburner, & Friston; 2003³), we took the approach described in O’Reilly et al. (2012). We first convolved the task regressor, then combined it with the physiological timeseries extracted from the filtered neural data. Neither this physiological regressor nor the resulting interaction term was then convolved, nor did they undergo additional temporal filtering. This approach enabled us to examine broad shifts in task-based connectivity patterns over time while also relating them to between-subject variability in overall learning outcomes.

To make contact with our initial univariate analysis (i.e., where we examined activity associated with learning at the within-subject level), we ran a second, nearly identical version of the PPI analysis that additionally included a scene-by-scene learning regressor. An interaction regressor was then generated by combining this measure of item-specific variability with the physiological timecourse drawn from each participant’s seed spheres. We were again required to exclude two subjects displaying no scene-by-scene differences in behavioral performance. Thus, we investigated here a different type of shift in connectivity, asking whether interregional correlations modulated by item-specific learning changed over the course of exposure.

Group-level connectivity analyses

At group-level, parameter estimates for the PPI effects corresponding were contrasted by run, exactly as in the “tripled t-test” used to compare activity patterns across runs (described above for the univariate analyses). For both PPI model implementations, first-level interaction estimates for each participant were entered into separate FLAME mixed effects models comprised of random subject intercepts and a fixed factor containing three levels corresponding to each of the three exposure runs. We specified 6 run-to-run contrasts (run 1 – run 3; run 3 – run 1, etc.). We focus on the comparisons between the first and last exposure runs, as they represent maximally dissimilar phases of learning (early and late).

Finally, we evaluated whether broad shifts in task-based connectivity represented a potential mechanism of successful knowledge acquisition at the between-subject level. To this end, we investigated whether differences in connectivity between the first run and the last exposure runs might be modulated by individual differences in overall post-test performance. Task-based PPI estimates from run 1 and run 3 were entered into a group-level FLAME model containing a fixed categorical factor with two levels corresponding to each of the two exposure runs, a numeric post-test regressor for each of the 20 participants (scores centered with respect to the group mean), and random subject intercepts. All connectivity maps were thresholded at Z > 1.96 using a cluster probability threshold of 0.05⁴.

Results

Behavioral Results

Participants successfully discriminated structured base-pairs from two-shape combinations lacking statistical coherence (non-base-pairs), replicating the findings of Fiser & Aslin (2001). When categorizing pairs as “familiar” or “unfamiliar,” participants’ overall percentage correct was significantly greater than chance (mean % correct = 68.07%, SD = 19.97; t(19) = 4.05, p = 0.0007). We also calculated a non-parametric sensitivity measure (A; Zhang & Mueller, 2005) to confirm that the hit rate for base-pairs differed significantly from the false alarm rate. Results indicated that A differed significantly from chance (mean A = 0.71, SD = 0.21, t(19) = 4.40, p = 0.0003).

Neuroimaging Results

Univariate activity results: Item-specific learning

In the scene-by-scene analysis we examined brain areas in which signal change during stimulus presentation in the learning phase was modulated by average base-pair learning per scene, as indicated by behavioral performance in the test phase. In this way, we capitalized on within-subject variability in learning of individual base-pairs. When combining across all runs, we observed a significant effect of this scene-by-scene regressor in two clusters: (1) a bilateral occipito-parietal cluster with a peak in the medial precuneus (extent = 3400 voxels; Z-max = 3.48 at x = 0, y = −66, z = 32, p < 0.0001); and (2) a bilateral subcortical cluster with a peak in the right amygdala (extent = 1581 voxels; Z-max = 3.35 at x = 22, y = −8, z = −16, p = 0.0086). For a detailed breakdown of all active regions, refer to Table 1. In line with our hypotheses, we found that learning recruited a network of subcortical and medial temporal structures (Figure 3), with engagement of bilateral hippocampus (R: x = 22, y = −8, z = −20, Z-max = 2.96; L: x = −24, y = −14, z = −14, Z-max = 2.09) and bilateral putamen (R: x = 32, y = −16, z = −6, Z-max = 2.13; L: x = −28, y = −16, z = −4, Z-max = 2.46). Interestingly, however, some of the strongest learning effects in the bilateral medial temporal lobe (including the peak voxels in cluster 2) extended beyond the hippocampus, specifically left and right amygdalae (R: see above; L: x = −24, y = −14, z = −12, Z-max = 2.14). A tripled t-test comparing the runs revealed no significant differences in either learning-related or overall task-based activation between any of the exposure runs.

Table 1.

Detailed break down of activation in all significant cortical and subcortical areas for the univariate scene-by-scene (item-specific) learning analysis, collapsed across all three exposure runs. Activation clusters spanning anatomical boundaries have been parcellated into individual anatomical areas using the Harvard-Oxford atlas, ordered by peak Z-statistic value. These areas are coded to indicate which unique functional cluster they belong to (bolded if adhering to cluster 1, unmarked if adhering to cluster 2).

Region	Extent (mm3)	Voxels	x	y	z	Z stat
LIMBIC
R Amygdala	1032	129	22	−8	−16	3.35
R Hippocampus	272	34	22	−8	−20	2.96
L Posterior cingulate	1512	189	−12	−44	38	2.64
L Insula	288	36	−36	−16	−2	2.31
R Posterior cingulate	696	87	4	−52	30	2.26
R Insula	80	10	36	−16	−2	2.21
L Amygdala	80	10	−24	−14	−12	2.14
L Hippocampus	24	3	−24	−14	−14	2.09
R Parahippocampal gyrus	16	2	16	−32	−6	1.99
OCCIPITAL
L Lingual gyrus	1592	199	−22	−56	0	3.02
L Intracalcarine	1576	197	−8	−70	14	2.86
L Supracalcarine	288	36	−4	−70	16	2.79
R Cuneal	800	100	4	−72	28	2.77
L Lateral occipital complex	3120	390	−46	−66	18	2.67
L Occipital fusiform	296	37	−32	−74	−8	2.43
L Cuneal	304	38	0	−72	22	2.37
L Occipital pole	240	30	−20	−90	38	2.16
R Lingual gyrus	32	4	10	−46	−2	2.1
R Supracalcarine	16	2	2	−68	18	2.03
PARIETAL
L Precuneus	5976	747	0	−66	32	3.48
R Precuneus	3432	429	2	−66	32	3.31
L Angular gyrus	496	62	−56	−52	12	2.35
R Parietal operculum	192	24	56	−30	22	2.24
L Supramarginal gyrus	280	35	−58	−46	18	2.15
R Supramarginal gyrus	32	4	58	−28	26	2.03
SUBCORTICAL
R Thalamus	1872	234	8	−28	0	3.18
L Pallidum	152	19	−24	−16	−4	2.64
L Thalamus	656	82	−4	−24	−2	2.47
L Putamen	304	38	−28	−16	−4	2.46
R Pallidum	24	3	20	−12	−4	2.24
R Putamen	32	4	32	−16	−6	2.13
TEMPORAL
R Superior temporal gyrus	616	77	62	−34	4	2.9
R Middle temporal gyrus	320	40	62	−32	0	2.83
L Middle temporal gyrus	400	50	−56	−52	10	2.42
R Planum temporale	104	13	52	−32	12	2.26
L Temporal occipital fusiform	256	32	−44	−58	−24	2.25
L Inferior temporal gyrus	48	6	−42	−62	−10	2.16
L Planum polare	64	8	−40	−18	−4	2.05

Functional connectivity results: Task-based effects

The first PPI analyses examined how the dynamics of interregional correlations change over the course of learning (i.e., does connectivity with regions associated with learning increase or decrease as a function of exposure to structured stimuli?). The results of the run comparison analysis were largely consistent: for all but two seeds we found significantly greater whole-brain connectivity for the first exposure run relative to the third exposure run (Figure 4 displays this result for each of our functionally defined seeds). That is, the strength of the PPI effect was most robust early in learning, except for the right thalamus and right motor cortex, which showed no changes in connectivity between the first and third runs. As further illustrated in Figure 4, the root of this connectivity difference was a positive PPI effect in run 1 (greater connectivity at task relative to baseline) and a negative PPI effect in run 3 (weaker connectivity at task relative to baseline). In other words, it was not the case that the PPI effects converged to zero over the course of exposure, but rather that the initial positive interaction between task and seed timecourse transitioned to a negative interaction later in learning. Table 2 summarizes all clusters exhibiting this significant decrease in connectivity across runs.

Figure 4.

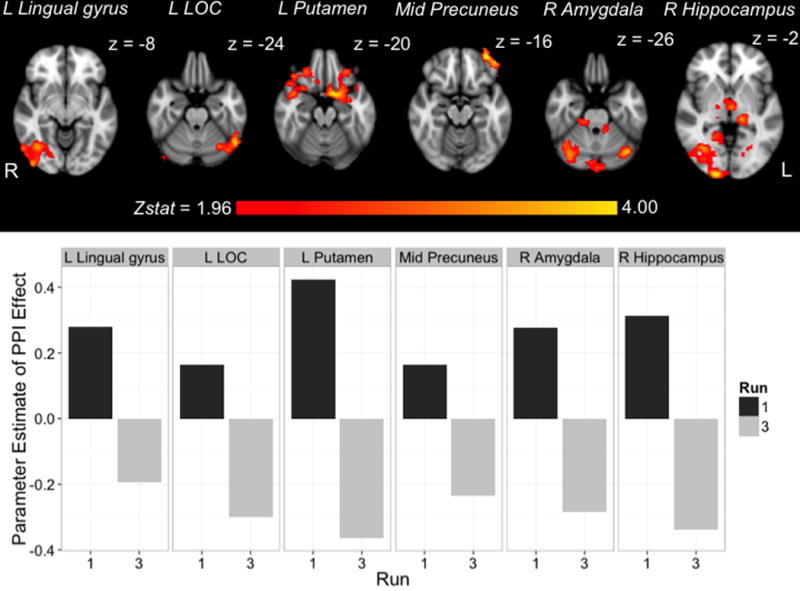
Top panel: For each functionally defined seed region, axial views of areas exhibiting a significant decrease in task- based connectivity over the course of exposure (L LOC = Left lateral occipital complex). Slices were selected to illustrate peak voxels. Bottom panel: Strength of task-based connectivity in individual runs. From the set of regions exhibiting a significant decrease in connectivity over time (i.e., each map above), we extracted for each seed region mean PPI effects for run 1 (dark grey) and run 3 (light grey).

Table 2.

Summary of peak grey matter voxels in clusters that show a significant decrease in general task-based connectivity with each seed region over time. We observed no significant increase in task-based connectivity with this set of seed regions over time.

Seed	Cluster	Peak	Extent (mm3)	Voxels	x	y	z	Cluster P	Z stat
L Lingual gyrus
	1	R LOC	11728	1466	38	−66	−8	0.0363	3.37
L LOC
	1	L Inf. temporal gyrus	25336	3167	−50	−60	−24	0.0004	3.72
	2	L Putamen	13536	1692	−22	10	2	0.0221	3.36
	3	R LOC	14880	1860	42	−66	−2	0.0132	3.13
L Putamen
	1	L Frontal orbital	31624	3953	−10	6	−20	<0.0001	3.94
Mid Precuneus
	1	L Frontal pole	11704	1463	−34	54	−16	0.0457	3.28
R Amygdala
	1	L Cerebellum	47656	5957	−40	−68	−26	<0.0001	3.76
	2	R Thalamus	21112	2639	6	−6	4	0.001	3.38
R Hippocampus
	1	R Occipital pole	30424	3803	18	−100	−2	<0.0001	3.94
	2	L Precuneus	29568	3696	6	−6	4	<0.0001	3.62
L Heschl’s gyrus
	1	L Thalamus	79248	9906	−4	0	6	<0.0001	4.53

We also asked whether differences in connectivity between the earliest and latest exposure runs was modulated by overall accuracy on the base-pair judgment task (i.e., which regions displayed a significant interaction between time and post-test performance). This second analysis enabled us to probe the functional role of connectivity patterns specifically as they relate to between-subject learning outcomes. Of our 7 functionally defined seed ROIs, we found for 2 of them a significant interaction between time (early v. late) and overall post-test performance. For both the precuneus and LOC seeds, a greater drop-off in connectivity from run 1 to run 3 was associated with higher learning outcomes. For the LOC seed, learning-related connectivity decreases were observed in two anterior frontal clusters extending from the frontal pole to the inferior frontal gyrus (right cluster extent = 1615 voxels, Z-max = 3.08 in right frontal pole at x = 38, y = 44, z = 2, cluster p = 0.0204; left cluster extent = 2369 voxels, Z-max = 3.79 in left frontal pole at x = –28, y = 42, z = –16, p = 0.0020; peak coordinates in LIFG: Z-max = 2.71 at x = –48, y = 18, z = 6). For the precuneus seed, this pattern was observed in a single bilateral cluster in anterior frontal cortex (extent = 3808, Z-max = 3.54 in left frontal pole at x = –24, y = 44, z = –14, p < 0.0001). However, with regard to left LOC seed we also found evidence in the anterior cingulate for an additional negative interaction between connectivity decreases and post-test performance (extent = 2611 voxels; Z-max = 3.32 in right anterior cingulate at x = 2, y = 4, z = 34, p = 0.0010).

Finally, we found that decreases in connectivity with our two cortical control areas were also predictive of learning outcomes. For the seed in primary motor cortex, learning-related connectivity decreases were observed in a right fronto-temporal cluster (extent = 2214 voxels, Z-max = 3.41 in right frontal operculum at x = 46, y = 16, z = –4, p = 0.0034). A similar pattern was observed for the left auditory seed (right cluster extent = 2991 voxels, Z-max = 3.55 in right frontal orbital cortex at x = 28, y = 14, z = –22, p = 0.0003; left cluster extent = 2596 voxels, Z-max = 3.62 in left amygdala at x = –18, y = –2, z = –18, cluster p = 0.0010).

Functional connectivity results: Item-specific learning

Unlike the parallel univariate activity analysis, in which we found no significant differences in scene-by-scene learning between runs, we observed varying timecourses of item-specific connectivity dependent upon seed. This result also stands in contrast to our task-based connectivity analysis, which overwhelmingly revealed that connectivity was stronger during stimulus presentation in the first exposure run relative to the final exposure run. Note that the generation of a PPI regressor based on scene-by-scene variability answers a very different sort of question; namely, at what point in exposure is connectivity most strongly modulated by item-specific learning (i.e., within-subject)? Results are summarized in Table 3. Early in learning, we observed stronger item-specific connectivity with functionally defined seeds in left LOC and right amygdala. However, for functionally defined seeds in the left lingual gyrus, mid precuneus, and right thalamus, we found the opposite pattern: stronger item-specific connectivity in the third exposure run relative to the first exposure run. The left putamen seed displayed both trends (i.e., stronger or weaker connectivity for the first relative to the third exposure runs, depending on which regions cohered with the seed). This same bi-directional pattern of connectivity was observed in our left primary motor and auditory cortex control seeds. We found no differences in early/late connectivity for the right hippocampal seed.

Table 3.

Summary of peak grey matter voxels in clusters that show significant differences (either increases or decreases) in item-specific connectivity with each seed region over time.

Seed	Cluster	Peak	Extent (mm3)	Voxels	x	y	z	Cluster P	Z stat
RUN 1 > RUN 3
L LOC
	1	L Insula	13624	1703	−38	−4	0	0.0106	3.91
	2	R Occipital Fusiform	10936	1367	28	−78	−6	0.0348	3.77
L Putamen
	1	L Frontal medial	29664	3708	−8	50	−10	<0.0001	4.55
R Amygdala
	1	L Parahipp. gyrus	30488	3811	−22	−34	−18	<0.0001	3.96
	2	L Lingual gyrus	23744	2968	−6	−64	−6	0.0006	3.15
L Primary motor
	1	L Frontal pole	36544	4568	−34	40	−14	<0.0001	4.16
L Heschl’s gyrus
	1	R Temporal fusiform	46680	5835	22	−12	−42	<0.0001	3.62
	2	L LOC	13736	1717	−38	−74	−8	0.0100	3.40
RUN 3 > RUN 1
L Lingual gyrus
	1	R Cerebellum	19200	2400	34	−56	−32	0.0008	3.61
L Putamen
	1	R Temporal pole	22480	2810	40	10	−38	0.0004	3.91
	2	R Supramarg. gyrus	18264	2283	50	−32	40	0.0021	3.86
	3	L Sup. Parietal lobule	13016	1627	−26	−48	40	0.0168	3.38
	4	L Cerebellum	11696	1462	−36	−74	−38	0.0296	3.17
Mid Precuneus
	1	R LOC	14328	1791	26	−72	28	0.0098	3.64
R Thalamus
	1	R Brain stem	25600	3200	2	−40	−44	0.0002	4.17
	2	L Frontal pole	11616	1452	−18	58	30	0.0313	3.58
L Primary motor
	1	L Supramarginal gyrus	12984	1623	−38	−50	34	0.0295	3.39
L Heschl’s gyrus
	1	R Middle frontal gyrus	21760	2720	28	22	28	0.0004	3.98

Discussion

The results presented here further inform our understanding of the neural basis of statistical learning, specifically for the learning of spatial patterns of shapes that comprise visual scenes. Similar to prior sequence learning studies, we found diffuse activation associated with the learning of base-pair structure that engages the basal ganglia, the medial temporal lobe, as well as sensory-specific cortical areas such as the lateral occipital complex. In contrast to these studies, however, the observed medial temporal activation encompassed bilateral amygdalae in addition to the hippocampus. Second, functional connectivity analyses revealed that whole-brain integration with active regions was significantly reduced over time, and, for some seeds (including our cortical controls), this reduction in task-based connectivity was predictive of overall behavioral performance. Interestingly, this trend did not extend to the timecourse of item-specific connectivity; we instead observed considerable variation across seeds in the pattern of interregional coupling modulated by scene-by-scene learning.

The representation of spatial information

We begin by situating our findings with respect to neurophysiological studies of spatial processing and topographical learning. There has been considerable investigation into the representation of spatial information in the brain (e.g., in natural scenes, faces, or objects). Reports of both monkey physiology and human brain activity have implicated the inferior temporal cortex in processing complex visual objects and scenes (e.g., Sato et al., 2013; Zhang et al., 2011; Li & DiCarlo, 2010; Haxby et al., 2001; Op de Beeck & Vogels, 2000; Miyashita, Kameyama, Hasegawa, & Fukushima, 1998; Miyashita, 1993), and studies of topographical learning have implicated the hippocampal and parahippocampal regions (e.g., Epstein, DeYoe, Press, Rosen, & Kanwisher, 2001; Aguirre, Detre, Alsop, & D’Esposito, 1996). However, less work has been dedicated to understanding how internal spatial representations are acquired, and topographical learning involves navigation through both space and time, making it difficult to disentangle the potential contributions of the system that learns distal spatial patterns from the system that learns temporal changes or associations between egomotion and visual input. Contextual cueing tasks, which measure learners’ ability to predict the location of an element based on its surrounding array, also involve a spatial memory component (Chun & Jiang, 1998). FMRI studies of this type of visual search task tend to implicate hippocampal regions (Giesbrecht, Sy, & Guerin, 2012; Manelis & Reder, 2012; Greene, Gross, Elsinger & Rao, 2007), prefrontal cortex (Pollmann and Manginelli, 2009), and the temporo-parietal junction (Manginelli, Baumgartner, & Pollman, 2013). In sum, despite key differences between the current paradigm and the afore-mentioned approaches, our results are supported by related work on the processing and acquisition of different types of spatial information.

Domain-general learning substrates

Overall, we observed recruitment of regions similar to those engaged in sequential statistical learning tasks, suggesting that attunement to spatial regularities in the environment has a domain-general neural component. Specifically, results of the scene-by-scene univariate analysis revealed activation in the dorsal striatum and hippocampus. Hippocampal and parahippocampal regions are commonly associated with visual statistical learning of temporally structured patterns (e.g., Schapiro et al., 2014; Gheysen et al., 2010, 2011; Turk-Browne et al., 2009, 2010), and evidence suggests that the basal ganglia, in certain cases along with prefrontal cortex, are similarly recruited during sequence segmentation tasks, regardless of the modality of the input (auditory: Plante et al., 2015; Karuza et al., 2013; McNealy et al., 2006; visual: Turk-Browne et al., 2009). However, here we found only weak evidence of left prefrontal recruitment: connectivity patterns indicated that interregional coherence with prefrontal cortex (i.e., LIFG) was predictive of learning, but this region was not revealed by the univariate activity analyses. An examination of whether prefrontal areas would be more strongly activated during recognition of learned test items, as has been demonstrated by McNealy et al. (2006), constitutes an important area of future study. Moreover, the bilateral nature of the univariate activation observed here differs from other accounts, based on split-brain patients, that the earliest stages of statistical learning are mediated by the right hemisphere (Roser et al., 2011). This finding did, however, motivate the choice of hemisphere for our connectivity control seeds.

Closer scrutiny of activation that covaried with learning revealed a final difference between studies of temporal learning and the results of this experiment: bilateral amygdalae activation. In humans, this region has been traditionally associated with emotional processing, typically exhibiting the greatest activity for stimuli with negative valence (e.g., Phelps, 2006; Bechara, Damasio, & Damasio, 2003). However, within the animal literature, the amygdala has been shown to work in concert with hippocampus and prefrontal cortex in spatial tasks requiring exploration of a novel environment, and it shares an anatomical as well as functional relationship with these same brain areas (for a review, see Richter-Levin & Akirav, 2000). In fact, injection of the stimulant amphetamine into rat amygdalae improved their performance on a water maze task (Packard, Cahill, & McGaugh, 1994). Moreover, lesioning the amygdala has the opposite effect, severely impairing the ability of rats to complete spatial learning tasks (Galliot, Levaillant, Beard, Millot, & Pourie, 2010).

Taken together, these results suggest that dorsal striatum and hippocampal areas are recruited regardless of the type of statistical information to be learned (sequential vs. spatial). This observation is consistent with behavioral findings supporting a domain-general statistical learning mechanism, though of course, any domain-general learning substrate must rely on information transmitted from sensory cortex (e.g., the learner recruits early occipital cortex in initially sampling from visual displays). Moreover, we propose a unique contribution of the limbic system, specifically bilateral amygdalae, in supporting spatial statistical learning. To be clear, the absence of an experimental control condition matched for basic perceptual features of the input makes it challenging to disentangle the contributions of cortical and subcortical areas selectively involved in the learning process from areas that might more indirectly support this process. This issue is further highlighted by the observed pattern of connectivity results, discussed below, which revealed a relationship between behavioral performance and changes in interregional coordination with cortical areas apparently unrelated to the present task.

Patterns of functional connectivity in learning

Within the growing literature on task-based functional connectivity, results are beginning to converge on a view that across many different learning tasks, there is reduced interregional connectivity after learning or when encountering well-learned, well-practiced information. Consistent with these observations, we found for 6 of our 7 functionally defined seeds stronger task-based connectivity early relative to later in exposure. From the first to the third exposure runs, a pronounced reduction in connectivity with occipital, precuneal, medial temporal, and subcortical seeds was evident, and this reduction was driven in part by an inverse PPI effect in run 3. Relative to baseline fixation, interregional links became increasingly decoupled as participants viewed the exposure scenes. For 2 posterior seeds, the mid precuneus and left LOC, weakened connectivity with frontal cortex was specifically correlated with learners’ accuracy at discriminating base-pairs from non-base pairs. This result is consistent with findings that the “release” of high-level association areas predicts reaction times on a visuomotor sequence learning task (Bassett, Yang, Wymbs, & Grafton, 2015). However, the opposite effect was found when comparing occipito-cingulate connectivity patterns, suggesting that functional integration with learning systems may operate at different time scales. Further work is needed to tease apart the factors mediating this effect, especially given that learning-related decreases in connectivity were associated with control seeds not recruited during exposure (i.e., primary motor and auditory cortex, though this pattern was not observed for seeds placed in white matter and cerebral spinal fluid). One possible explanation for this finding is related to the proposal that learners decrease sampling from the environment as a function of exposure to structured stimuli (Karuza et al., 2016)– if such a narrowing mechanism indeed subserves the learning process, it might follow that dissociation over time from unneeded sensory-specific areas (i.e., motor and auditory cortex) would relate to increased behavioral performance.

We further suggest that considering the impact of within-subject, item-specific learning (in addition to between-subject variation in composite measures) might prove to be an especially useful method for increasing our understanding of the functional role of interregional communication. Indeed, while the present analyses reveal a consistent decrease in task-based connectivity over time, connectivity modulated by trial-by-trial measures of learning varied across the course of exposure. In particular, item-specific connectivity with LOC and the amygdala was strongest early in the learning phase, while the opposite effect was observed for seeds in the lingual gyrus, precuneus, and thalamus. Importantly, converging evidence from both our within and between-subject measures of spatial statistical learning indicate that changes in functional integration, at least to the extent that they relate to measures of behavioral performance, are a potential mechanism of learning, not solely the by-product of prolonged stimulus exposure or task adaptation.

Previous studies have found similar decreases in task-based connectivity associated with better learning outcomes or the later stages of learning. After a several-day training period, Lewis, Baldassarre, Committeri, Romani and Corbetta (2009) found that visual and frontal cortices became anti-correlated when participants were at rest, and that the extent of this anti-correlation was predictive of behavioral performance on a shape identification task, suggesting a consolidation of network specialization. Coynel et al. (2010) measured functional integration over a 4-week course of motor skill learning and observed a decrease in connectivity between downstream association cortices and premotor areas as participants executed well-practiced sequences. Similarly, Sun, Miller, Rao and D’Esposito (2007) demonstrated greater interregional connectivity when participants were in the earliest phases of learning a novel bimanual motor pattern. Drawing parallels to the current findings, it appears that task-based connectivity bolsters early phases of learning and narrows as learning progresses. More general cognitive processes related to learning also show this pattern. For example, You et al. (2013) noted that functional connectivity in pre-adolescent children narrowed as participants transitioned from resting state to a sustained attention task.

One potential explanation for this decrease in task-based connectivity, a “plumbing model” of learning in the brain, arises from the observation that low levels of activity are sometimes accompanied by a high degree of functional connectivity (e.g., Kelly & Garavan, 2005; Büchel et al., 1999; McIntosh et al., 1999). Here we examined whether the burden of early computation of statistical regularities was shared by a highly integrated network of regions, and whether, after further exposure, these interregional connections were no longer required, resulting in lower levels of connectivity but greater BOLD activity in specialized downstream regions. From our univariate analyses, we do not find strong support for this plumbing hypothesis: run comparisons revealed no significant differences in activity over time. However, the divergence between the present findings and previous findings that do support the plumbing hypothesis might be traced to key differences in the nature of learning. Specifically, those studies that have dissociated activity and connectivity tend to involve learning tasks that resulted in explicit representations of regularities in the environment (Büchel et al., 1999; McIntosh et al., 1999). By contrast, we have shown that while task-based connectivity clearly fluctuated, activity levels in a more implicit learning context (i.e., one that did not result in explicit representations) did not differ. Above all, our results suggest a complex learning process involving mechanisms operating at different timescales: while we did not observe stark differences in the magnitude of learning-related BOLD activity across runs, we did find a unique connectivity relationship that shifted as exposure to patterned visual stimuli progressed, as well as a correlation between changes in connectivity over time and ultimate learning outcomes. In the future, advances from the field of network neuroscience (Bassett & Sporns, 2017), which involve the use of graph theoretical tools to formalize properties of interregional communication, might be leveraged to shed light on the precise mechanisms underlying both the broad-scale and item-specific shifts in connectivity observed here.