Accuracy of Rats in Discriminating Visual Objects Is Explained by the Complexity of Their Perceptual Strategy

Summary

Despite their growing popularity as models of visual functions, it remains unclear whether rodents are capable of deploying advanced shape-processing strategies when engaged in visual object recognition. In rats, for instance, pattern vision has been reported to range from mere detection of overall object luminance to view-invariant processing of discriminative shape features. Here we sought to clarify how refined object vision is in rodents, and how variable the complexity of their visual processing strategy is across individuals. To this aim, we measured how well rats could discriminate a reference object from 11 distractors, which spanned a spectrum of image-level similarity to the reference. We also presented the animals with random variations of the reference, and processed their responses to these stimuli to derive subject-specific models of rat perceptual choices. Our models successfully captured the highly variable discrimination performance observed across subjects and object conditions. In particular, they revealed that the animals that succeeded with the most challenging distractors were those that integrated the wider variety of discriminative features into their perceptual strategies. Critically, these strategies were largely preserved when the rats were required to discriminate outlined and scaled versions of the stimuli, thus showing that rat object vision can be characterized as a transformation-tolerant, feature-based filtering process. Overall, these findings indicate that rats are capable of advanced processing of shape information, and point to the rodents as powerful models for investigating the neuronal underpinnings of visual object recognition and other high-level visual functions.

Graphical Abstract

Highlights

• •The ability of rats to discriminate visual objects varies greatly across subjects
• •Such variability is accounted for by the diversity of rat perceptual strategies
• •Animals building richer perceptual templates achieve higher accuracy
• •Perceptual strategies remain largely invariant across object transformations

Djurdjevic et al. show that the ability of rats to successfully discriminate visual objects depends on the complexity of their perceptual strategy, which remains largely unchanged under variations in object appearance. This implies that rats process visual objects using mechanisms not dissimilar from those of more evolved species, such as primates.

Introduction

Over the past 10 years, substantial effort has been devoted to better understanding visual perception in rats and mice [1, 2, 3, 4, 5, 6, 7, 8]—from the assessment of visual acuity and contrast sensitivity [9, 10] to the study of higher-order functions, such as object recognition [11, 12, 13, 14, 15, 16, 17, 18, 19], perceptual decision making [20, 21, 22, 23], and the ethology of innate visual behaviors [24, 25, 26]. Despite these efforts, it remains unclear whether rodents are able to deploy advanced visual processing strategies when engaged in complex perceptual tasks, such as discrimination of visual objects. In the case of rats, some studies have found them to be capable of only moderately complex perceptual strategies [15, 17, 18]. By contrast, our group has shown that rats can recognize visual objects in spite of major variation in their appearance (a faculty known as “transformation-tolerant” or “invariant” recognition) [11, 13] and extract from visual shapes multiple diagnostic features, which are partially preserved across view changes [12]. At the same time, we found that the complexity of rat perceptual strategy and its tolerance to transformation can be highly variable across subjects and largely dependent on the specific object pairs the animals have to discriminate [12, 14].

Overall, such a diversity of visual processing skills reported across and within studies suggests that the complexity of rat perceptual strategy is partly determined by the difficulty level of the object discrimination task (with more demanding tasks engaging more advanced strategies), and partly dependent on the propensity of each individual to discover the full spectrum of features afforded by the objects. According to this hypothesis, if a group of rats was tested in a recognition task spanning a range of complexity, only some animals would succeed in the most challenging discriminations, and these animals would also display the higher proficiency at retrieving and integrating information across multiple object features. Establishing this link between discrimination performance and complexity of the perceptual strategy would at once reconcile the variety of findings reported in the literature and confirm that (at least some) rats are capable of advanced shape processing. Our study was designed to test this hypothesis and assess, at the same time, the extent to which rat perceptual strategies remain invariant under changes in object appearance.

Results

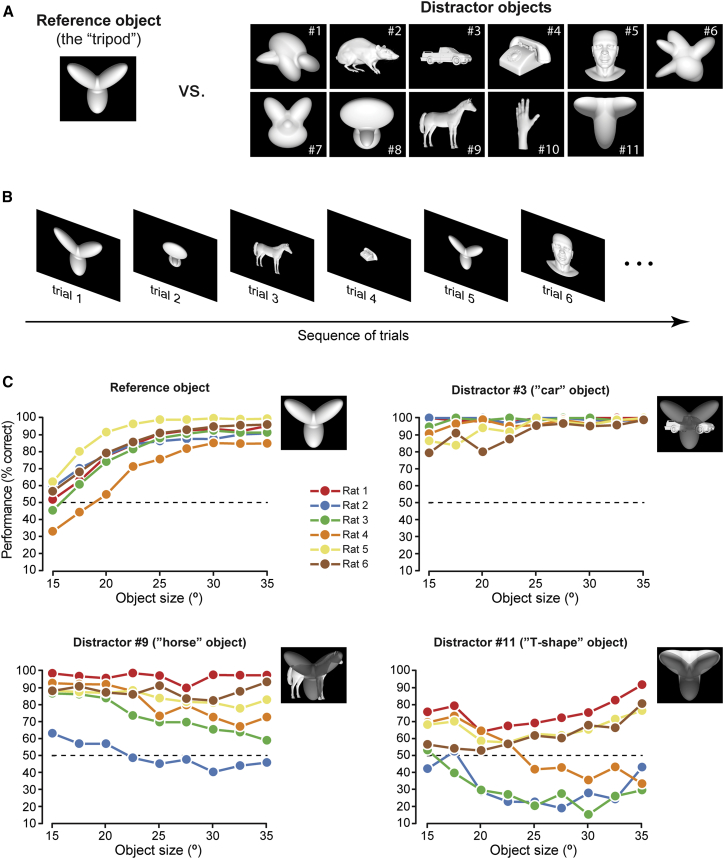
We trained six rats to discriminate a “reference” object from 11 “distractors” (Figure 1A) using the high-throughput rig described in [7] (Figure S1). The reference was an artificial shape made of three lobes, arranged in a tripod-like configuration. The distractors spanned a broad range of image-level similarity with the reference, depending on how much they overlapped with the tripod (insets in Figure 1C). The rationale of this design was to teach the rats a “tripod versus everything else” categorization, thus pushing the animals to develop a tripod recognition strategy that was general enough to allow the classification of any incoming visual stimulus. All objects were presented in randomly interleaved trials (Figure 1B) across a range of sizes (15°–35° visual angle) to induce the rats to deploy a transformation-tolerant processing strategy, thus preventing them from relying on low-level (i.e., screen-centered) discriminatory cues.

Figure 1.

Stimulus Set and Discrimination Performances

(A) The reference and distractor objects that rats were trained to discriminate.

(B) Schematic of the trial structure during training with the reference and distractor objects. Both object identity and size were randomly sampled in each individual trial according to the procedure detailed in STAR Methods. See also Figure S1.

(C) Discrimination performances, as a function of stimulus size, for the reference object and three example distractors. Each curve reports the performance of a rat over the pool of trials recorded across the 32 sessions, during which the random tripods (Figure 2A), in addition to the reference and distractor objects, were also presented (as illustrated in Figure 2B). Insets: overlaid pictures of the reference and each of the three distractors (with the reference rendered in a darker shading to make both objects visible), so as to appreciate to what extent the objects overlapped.

All the animals successfully learned the task, but their performance varied considerably across distractors and was, overall, strongly subject dependent (Figure 1C). At the largest sizes, the reference was identified with high accuracy by all the rats, whereas performance decreased gradually for smaller sizes. Some distractors, such as the “car” object (distractor 3), were correctly classified by all the animals, whereas others, such as the “horse” and the “T” shape (distractors 9 and 11), were correctly classified by only half of the subjects (rats 1, 5, and 6) with high accuracy at the largest size (35°). For the remaining rats (2–4), performance at 35° ranged between 50% and 70% correct for the horse object, whereas it dropped to chance or below for the “T” shape. Such variable proficiency suggests that different rats extracted different combinations of diagnostic features from the objects, and that these features were more or less effective in supporting the discrimination of the more tripod-looking distractors, such as the “T” shape. Interestingly, for the poorer performers, the tendency to choose the distractor category increased at small sizes, thus displaying the opposite trend of that observed for the reference object. This is consistent with the animals learning the “tripod versus everything else” discrimination we intended to teach. In fact, given the poor spatial resolution of rat vision [27, 28], the features that were diagnostic of the tripod identity most likely became poorly defined at sizes lower than 20° [11, 12, 13, 14], thus bringing the animals to choose the “everything else” category more often than at larger sizes.

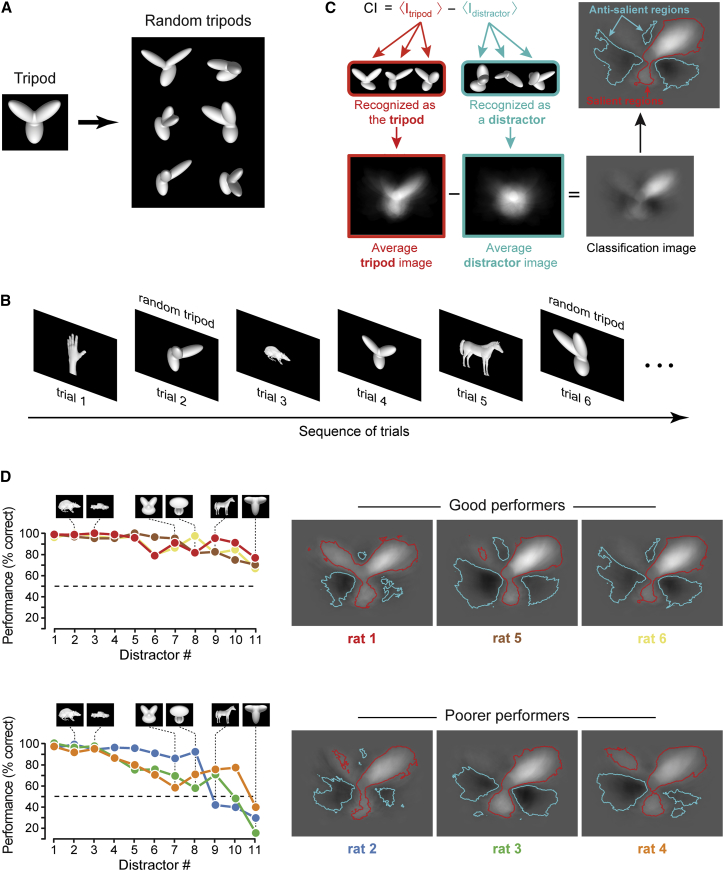
Uncovering Rat Perceptual Strategies

To infer the perceptual strategy employed by the rats in the discrimination task, we took the reference object (at the size of 30° of visual angle) and randomly changed its structural parts to obtain a new set of stimuli, referred to as “random tripods” (examples in Figure 2A). We then presented these stimuli to the rats, randomly interleaved with the reference and the distractors (Figure 2B). By separately averaging the images of the random tripods that were classified as being the tripod and those that were classified as being distractors, and finally subtracting the two average images, we obtained a saliency map, known as the “classification image” [29] (Figure 2C). In the classification image, the bright (positive value) and dark (negative value) areas indicate regions of the image plane that contained the lobes of the random tripods with, respectively, high and low probability, when these stimuli were classified as being the tripod. As such, these regions were labeled as, respectively, salient and anti-salient, with reference to the tripod identity [12, 14]. As shown in Figure 2C (red and cyan boundaries), we also applied a permutation test (STAR Methods), to identify the regions that were significantly (p < 0.01) salient or anti-salient.

Figure 2.

Inferring Rat Perceptual Strategies by Computing Classification Images

(A) Examples of the random variations of the reference object (referred to as “random tripods”) that were used to infer rat perceptual strategy.

(B) Schematic of the trial structure when the random tripods were presented, in randomly interleaved trials, along with the reference and distractor objects (see STAR Methods). See also Table S1.

(C) Illustration of the method to infer rat perceptual strategy by computing a classification image.

(D) The discrimination performances (computed over the same pool of sessions as in Figure 1C) achieved by the rats over the full set of distractors, when presented at 30° of visual angle (left), are shown along with the classification images obtained for all the animals (right). The rats are divided, according to their proficiency in the discrimination task, into a group of good performers (top) and a group of poorer performers (bottom).

The classification images obtained for the six rats shared a common structure, with the salient features matching (fully or partially) the lobes of the tripod and the anti-salient features covering the regions between the lobes (Figure 2D, right). At the same time, the specific combination of features a rat relied upon, as well as their spatial extent, varied across animals. For instance, the animals that better classified the distractors (i.e., the “good performers,” shown in Figure 2D, top) all relied on a small, anti-salient feature (precisely located at the intersection of the tripod’s top lobes), which allowed assigning anti-tripod evidence also to those distractors (as the “T” shape) that more closely resembled the tripod. The lack (in rats 3 and 4) or misplacement (in rat 2) of this feature most likely prevented the “poorer performers” (Figure 2D, bottom) from being just as effective with the more tripod-resembling distractors.

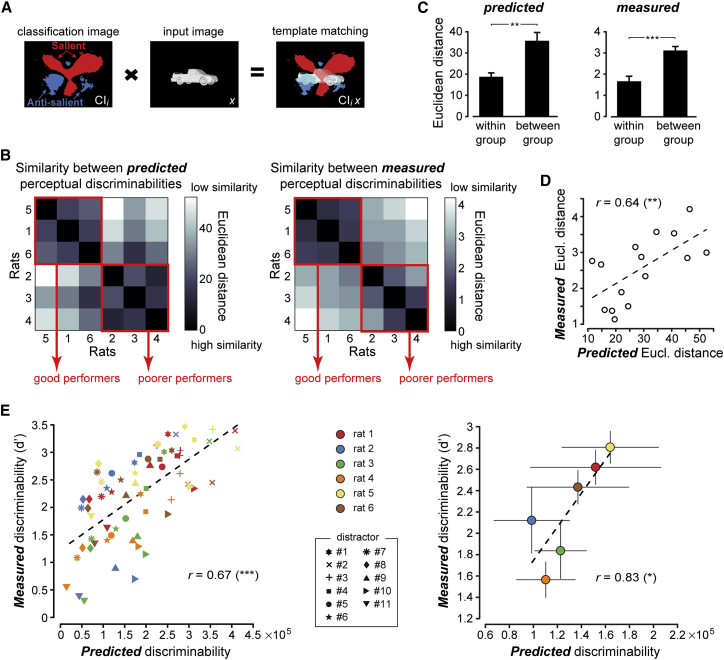
To quantitatively test whether animals achieving similar performance levels relied on similar perceptual strategies, we used the classification images as perceptual filters to predict how discriminable each distractor was from the tripod object. Given a rat i, with classification image $C{I}_i$, we modeled the discriminability of distractor x from the tripod t as $d_i\left(x,t\right)=C{I}_i\cdot t-C{I}_i\cdot x$, where $C{I}_i\cdot t$ and $C{I}_i\cdot x$ are the dot products of the classification image with, respectively, the images of the tripod and the distractor. The dot product computes a weighted sum of the input image (e.g., x), where the weight assigned to each pixel is the corresponding value of the classification image (acting as a spatial filter); e.g., $C{I}_i\cdot x=\sum _{allpixelsj}C{I}_i^j\cdot x^j$. This produces a scalar value that measures how well the input image matches the perceptual template. Graphically, such template-matching computation can be represented as the overlap between the input image and the $C{I}_i$, as depicted in Figure 3A (note that here, for the sake of clarity, a discretized version of the $C{I}_i$ is shown, displaying only the significantly salient and anti-salient regions, whereas the actual dot products were computed using the original, continuous-value classification images shown in Figure 2D).

Figure 3.

Predicting the Perceptual Discriminability of the Distractors Using the Classification Images as Spatial Filters

(A) The overlap between the classification image of rat 1 and an example distractor object (3) provides a graphical intuition of the template-matching computation used to infer the discriminability of the distractors from the reference.

(B) Left: prediction of how similarly each pair of rats would perceive the 11 distractors, if the animals used their classification images to process the stimuli. Similarity was measured as the Euclidean distance between the two sets (vectors) of perceptual discriminabilities of the 11 distractors, as inferred by using the classification images of the rats as perceptual filters. Right: estimate of how similarly each pair of rats actually perceived the distractors, with perceptual discriminability quantified using a d′ sensitivity index. Similarity was measured as the Euclidean distance between the two sets (vectors) of d′ obtained, across the 11 distractors, for the two animals. Rats along the axes of the matrices were sorted according to the magnitude of their d′ vectors (from largest to smallest). The red frames highlight two groups of animals with very similar predicted and measured discriminabilities (corresponding to the “good” and “poorer” performers in Figure 2D).

(C) The Euclidean distances in the cells located above the diagonals of the matrices of (B) were averaged, separately, for the rats inside and outside the red frames. The resulting within- and between-group average distances (±SEM) were significantly different according to a one-tailed t test (^∗∗p < 0.01 and ^∗∗∗p < 0.001, respectively, for the predicted and measured distances).

(D) Relationship between the measured and predicted Euclidean distances corresponding to the cells located above the diagonals of the matrices of (B). The two quantities were significantly correlated according to a two-tailed t test (^∗∗p < 0.01).

(E) Relationship between measured and predicted discriminability of the distractors, as obtained (1) by considering all rats and distractor conditions together (left); and (2) after averaging, separately for each animal, the measured and predicted discriminabilities across the 11 distractors (right) (dots show means ± SEM). Both correlations were significant according to a two-tailed t test (^∗p < 0.05, ^∗∗∗p < 0.001).

Given a rat i, we measured the predicted discriminability $d_i\left(x,t\right)$ from the tripod for each of the 11 distractors, thus obtaining an 11-component discriminability vector ${\overrightarrow{d}}_i$. The vectors obtained for each pair of rats i and j were then compared by computing their Euclidean distance $e_{ij}=\Vert {\overrightarrow{d}}_i-{\overrightarrow{d}}_j\Vert$. This yielded a matrix (Figure 3B, left) showing, for each pair of rats, how similarly the two animals would perceive the distractors, if they processed the stimuli using their classification images as perceptual filters. This matrix was compared to another matrix (Figure 3B, right), reporting how similarly each pair of rats actually perceived the distractors. This matrix was obtained by computing the discriminability of each distractor from the tripod using a d prime sensitivity index $d_i^{\text{'}}\left(x,t\right)$ (STAR Methods), thus obtaining, for each rat i, an 11-component discriminability vector ${\overrightarrow{d}}_i^{\text{'}}$, and, for each pair of rats i and j, the Euclidean distance $e_{ij}^{\text{'}}=\Vert {\overrightarrow{d}}_i^{\text{'}}-{\overrightarrow{d}}_j^{\text{'}}\Vert$.

As shown in Figure 3B, the predicted (left) and measured (right) similarity matrices were similar (note that rats were sorted according to the magnitude of their ${\overrightarrow{d}}_i^{\text{'}}$ vectors, from largest to smallest). Two clusters of rats with similar perceptual behavior (i.e., small Euclidean distances) were visible in the matrices, in the top-left and bottom-right corners (red frames), corresponding to the groups of good (rats 5, 1, and 6) and poorer (rats 2–4) performers of Figure 2D. Such clustering was confirmed by the much lower average distance measured within, rather than between, the two groups (Figure 3C; p < 0.01; one-tailed t test). More importantly, the off-diagonal elements of the two matrices (i.e., the $e_{ij}$ and $e_{ij}^{\text{'}}$, with $i\ne$j) were positively correlated (Figure 3D; r = 0.64; p < 0.01; two-tailed t test). This means that the extent to which two rats showed similar responses to the distractor objects was well predicted by the similarity of their classification images, notwithstanding that the latter had been inferred from responses to a fully independent stimulus set (the random tripods).

These results suggest that the classification images are able to predict the perceptual discriminability of the distractors from the tripod both within and across rats. To verify this, we plotted the measured $d_i^{\text{'}}\left(x,t\right)$ versus the predicted $d_i\left(x,t\right)$ across all rats i and distractors x (Figure 3E, left). The two quantities were significantly correlated (r = 0.67; p < 0.001; two-tailed t test), with the objects that were more dissimilar from the tripod, such as the “car” (distractor 3) and “phone” (distractor 4), yielding larger discriminability (both observed and predicted) than those that were more tripod looking, such as the “T” shape (distractor 11). Among individual rats, the correlation between measured and predicted discriminability was significant in 4 out of 6 cases (p < 0.05), with group average r = 0.71 ± 0.07 (p < 0.005; two-tailed t test). This means that the classification images successfully predicted how similar to the tripod each animal judged the 11 distractors. At the same time, the CI-based models also seemed to explain why different rats achieved different levels of discriminability with the distractors—e.g., the “T” shape was perceived as more discriminable from the tripod by rats 1, 5, and 6 than by rats 2–4, in agreement with the models’ predictions (compare the downward triangles in Figure 3E, left). To statistically assess whether this was the case, for each rat i, we separately averaged the $d_i^{\text{'}}\left(x,t\right)$ and $d_i\left(x,t\right)$ values across the 11 distractors. The resulting scatterplot (Figure 3E, right) showed a strong linear relationship between the measured and predicted discriminability across the six animals (r = 0.83, p < 0.05). This indicates that each rat used a subject-specific perceptual strategy, whose complexity determined the animal’s sensitivity in discriminating the distractors from the reference object.

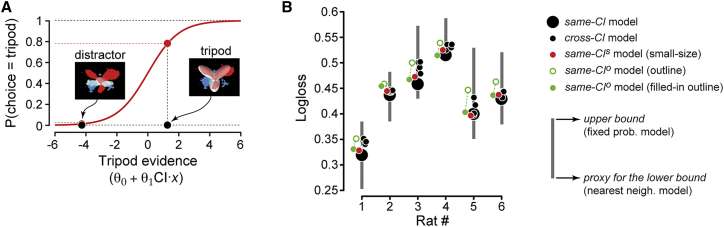
Building Models of Rat Perceptual Choices

The discriminability of an image (e.g., a distractor) from the tripod, as inferred by using the classification image as a filter, can be translated into a prediction of the animal’s perceptual choice by using logistic regression [30], i.e., by modeling the probability of rat i to classify an input image x as being the tripod as

$$p_i\left(y=1|x\right)=\sigma \left({\theta }_0^i+{\theta }_1^{i}C{I}_i\cdot x\right).$$ (Equation 1)

Here, the similarity of the input image to the perceptual template $C{I}_i$ (i.e., the dot product $C{I}_i\cdot x$) is weighted by a gain factor ${\theta }_1^i$ and adjusted by an offset term ${\theta }_0^i$, thus yielding the evidence that the animal has acquired about the presence of the tripod. As illustrated in Figure 4A, the logistic function $\sigma$ translates this evidence into the probability that the choice y of the animal is the tripod category (i.e., y = 1). This model was fit to the responses of the rat to a subset of the random tripods (the “training” set), and then used to predict its responses to the held-out stimuli (the “test” set). Specifically, a 10-fold cross-validation procedure was applied, where prediction performance was quantified by computing the “logloss”—a widely used cost function for measuring the discrepancy between predicted response probabilities and actual responses (STAR Methods).

Figure 4.

Building Predictive Models of Rat Perceptual Choices

(A) Illustration of how the classification image obtained for rat 1 was combined with logistic regression to (1) infer the evidence gathered by the animal about an arbitrary input image being the tripod (abscissa axis); and (2) translate this evidence into a probability of choosing the tripod category (ordinate axis).

(B) The accuracy of various models in predicting rat responses to the full-body, regular-size random tripods is measured using a logloss function (see STAR Methods). Predictions of five different models are shown (see caption on the right), which differed according to the classification images that were plugged into Equation 1 (see Results). The logloss values obtained by constant-probability and nearest-neighborhood response models are also shown, to provide, respectively, an estimate of the logloss’s upper bound and a proxy of its lower bound (gray bars).

See also Figures S2, S3, and S5.

For each rat i, we also fit five alternative models by applying the same procedure, but with a key difference—rather than using the $C{I}_i$ of the rat under consideration, we plugged into Equation 1 the $C{I}_j$ (with $j\ne i$) of the other animals. This allowed testing whether the classification image obtained for a rat (“same-CI” model) was able to predict its perceptual choices better (i.e., with lower logloss) than the classification images obtained for the other subjects (“cross-CI” models). To better quantify the goodness of the same-CI model in predicting rat choices, we also estimated the upper bound of the logloss, by implementing a “constant-probability” response model with $p_i\left(y=1|x\right)=p_{tripod}$, i.e., the overall fraction of tripod choices over the whole stimulus set. Obtaining the logloss’s lower bound would require instead measuring the fraction of tripod responses to repeated presentations of every random tripod, because no model can capture the perceptual decisions of a subject better than the reliability of its responses to every individual stimulus. However, because each random tripod was presented only once, we computed a proxy of the logloss’s lower bound by implementing a “nearest-neighborhood” response model with $p_i\left(y=1|x\right)=p_{nearestneigh.}\left(x\right)$, i.e., the fraction of tripod responses to the 10 stimuli that were more similar (pixel-wise) to the input image x.

As shown in Figure 4B, the upper bound of the logloss (upper end of the gray bars) varied considerably across rats, because it was determined by the overall randomness of rat choices, with more predictable responses (i.e., smaller $p_{tripod}$ values) yielding smaller upper bounds (Figure S2). Critically, the same-CI models (large black dots) reached logloss values that were considerably lower than the upper bounds, and were either halfway toward or close to the losses of the nearest-neighborhood models (lower end of the gray bars). This means that the CI-based models explained rat choices much better than could be achieved by guessing (based on the overall rat propensity to respond “tripod”), and they reached performances not far from those achieved by a “look-up” model based on nearest neighbors. More importantly, for five out of six rats, the same-CI model yielded logloss values that were lower than those returned by all the cross-CI models (small black dots), and this pattern was highly significant (p < 0.0006; binomial test; STAR Methods). This implies that each rat relied on a distinctive perceptual strategy, whose specificity was well captured by the classification image. This conclusion was strengthened by a second analysis, where, for each rat, the logistic regression model (Equation 1) was first fitted to the full set of random tripods and then tested for its ability to predict the responses to the 11 distractors, when presented at 30° of visual angle. The predicted and measured distractor evidences were strongly and significantly correlated (Figure S3), following the same trends already found at the level of perceptual discriminability (Figure 3).

Modeling Rat Invariant Recognition

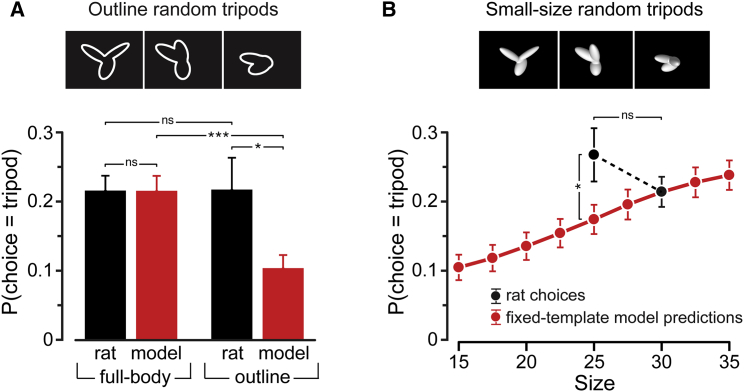
The success of the logistic regression model in predicting rat perceptual choices does not imply that the animals filtered every incoming stimulus using a fixed perceptual template. Such a rigid template-matching computation would prevent the animals from correctly classifying transformed versions of the objects—for instance, those resulting in global luminosity changes, such as size variations. This can be appreciated by considering the argument of Equation 1—the smaller (or dimmer) the object in the input image $x$ becomes, the smaller its dot product with the template $\left(C{I}_i\cdot x\right)$ gets, and the more likely it becomes for the object to be classified as a distractor. This scenario is at odds with the tolerance of rat object vision to identity-preserving transformations [7] (see also Figure 1C). To directly show that a fixed template-matching strategy is not able to account for rat invariant recognition, we measured how well the logistic regression model, derived to account for rat discrimination of full-body stimuli at 30° of visual angle, generalized to outlined and scaled versions of the random tripods (83% of their original size, corresponding to scaling the reference object from 30° to 25° of visual angle). We then compared the performance of the model to the actual performances of the rats with these transformed stimuli.

Reducing an object to its outline leaves its overall shape largely unaltered, while substantially changing the luminance cues that define the object. As expected, a template-matching model, developed to specifically process full-body stimuli, showed little cue invariance, predicting a much lower fraction of tripod responses to the outline than to the full-body random tripods (Figure 5A, red bars; p < 0.001; one-tailed, paired t test). By contrast, rats displayed a fully cue-invariant behavior, with the fraction of tripod responses being virtually identical for outline versus full-body random tripods (black bars; p = 0.97). A similar finding applied to size variations (Figure 5B). The logistic regression model, trained with the random tripods at size 30°, predicted a significant decrease of the probability of tripod responses as the size of the random tripods becomes smaller (red curve; p < 0.001; F_8,40 = 113.488; one-way ANOVA). This trend did not match that observed for the rats, where the fraction of tripod responses was actually slightly larger (although not significantly) for the “small-size” (25°) than for the “regular-size” (30°) random tripods (black dots; p = 0.12; one-tailed, paired t test). In summary, for both the outlines and small-size stimuli, the model significantly underestimated the probability of tripod responses (p = 0.03 and p = 0.02, respectively). This conclusion was confirmed by a similar analysis performed with the reference and distractor objects, where a fixed-size template-matching model failed to account for the modulation of rat responses as a function of size (Figure S4).

Figure 5.

Rat Invariant Recognition Cannot Be Accounted for by a Fixed Template-Matching Strategy

(A) Fraction of random tripods classified as being the tripod by the rats (black) and by models (red) that were based on the classification images obtained from the full-body, regular-size random tripods (i.e., those shown in Figures 2D and 6A). Classification rates are reported for these full-body stimuli (left), as well as for their outlines (right) (examples shown at the top). Bars refer to group averages across the six rats ±SEM. Asterisks indicate a significant difference according to a one-tailed, paired t test (^∗p < 0.05, ^∗∗∗p < 0.001; ns, not significant).

(B) Same as above, but with classification rates referring to the random tripods presented at the default, regular size (30°) and additional sizes—i.e., the whole size range, in the case of model predictions (red curve), and size 25°, in the case of rat responses (black dots). Dots refer to group averages across the six rats ±SEM. Same statistical analysis as in (A).

See also Figure S4.

These findings suggest that the rat visual system most likely achieves invariant recognition by matching the visual input not to a single (fixed) perceptual template but to a bank of perceptual filters with similar shape, iterated across multiple scales, positions, etc.—a process reminiscent of the computations performed by the primate ventral stream [31] and by state-of-the-art machine vision systems [32, 33]. This hypothesis can be tested by computing classification images from stimuli transformed along a variety of dimensions (i.e., luminance-cue and size changes in our study) and then checking the consistency of the resulting perceptual templates in terms of their ability to predict rat choices.

In the case of the outline stimuli, the classification images still displayed salient and anti-salient features (Figure 6B, top) that, although thinner and more scattered, largely matched those obtained for the full-body stimuli (Figure 6A). Such consistency became even more apparent after replacing the outline random tripods with their filled-in versions in the computation of the classification images (Figure 6B, bottom). The rationale was to infer the strategies that the rats would deploy, if they extracted diagnostic information not only from the features that were actually visible (the outlines) but also from the (empty) bodies of the objects, so as to perceptually fill the lobes of the random tripods and process them as solid features.

Figure 6.

Transformation Tolerance of Rat Perceptual Strategies

The classification images obtained, for the six rats, from (A) the regular-size (30°), full-body random tripods; (B) their outlines (top) and the filled-in versions of their outlines (bottom); and (C) the small-size (25°), full-body random tripods. Note that the classification images in (A) are those already shown in Figure 2D. See also Figures S5 and S6.

To quantitatively assess whether the perceptual strategy of rat i was similar when extracted from the full-body or the outline stimuli, we plugged the classification image ${CI}_i^o$ obtained from the outlines into Equation 1 and tested the ability of the logistic regression model to predict the responses of the animal to the full-body stimuli. When this “same-CI^o” model was built using the classification image derived from the actual outlines, it was outperformed by most of the “cross-CI” models (compare the empty green to the small black dots in Figure 4B). By contrast, when the same-CI^o model was based on the classification image derived from the filled-in outlines, it yielded the lowest logloss for 3 out of 6 rats, and the second lowest logloss for another animal (solid green dots). Although this result was only marginally significant (p = 0.06; binomial test), it indicates that, for many rats, the perceptual strategy was largely preserved under variation of the luminance cues that defined the visual stimuli. In addition, the superiority of the model based on the filled-in versions of the outlines over the one based on the actual outlines (p = 0.01; binomial test) suggests that rats did indeed process the outline stimuli by perceptually filling their inside, so as to effectively treat them as solid-body objects.

A similar analysis was carried out for the classification images ${CI}_i^s$ obtained from the small-size random tripods (shown in Figure 6C). These images were rescaled, so as to match the size of the regular-size $C{I}_i$, and were plugged into Equation 1 to test their ability to predict the responses of the animals to the regular-size stimuli. The resulting “same-CI^s” models (red dots in Figure 4B) outperformed the cross-CI models for 4 out of 6 rats, and this pattern was highly significant (p = 0.003; binomial test). This means that the perceptual strategies used by the rats remained largely preserved across size variations. This conclusion was supported by the identical ability of the $C{I}_i$-based and ${CI}_i^s$-based models to predict rat responses to both the small-size and regular-size distractors (Figure S5).

Discussion

Our study was inspired by previous applications of classification image approaches, such as the Bubbles method [34, 35, 36], to uncover rat visual processing strategies [12, 14, 15] but, different from these earlier studies, our experimental design relied on three innovative features. First, we trained rats to discriminate a reference object (the “tripod”) not from a single but from many different distractors (Figure 1A). This allowed ranking the animals on the basis of their classification accuracy (Figure 2D). Second, to infer rat perceptual strategies, we produced altered versions of the reference (the “random tripods”) by randomly varying its structure (Figure 2A), rather than applying additive or multiplicative noise [29]. Such a generative approach, rarely applied in classification image studies [37, 38, 39, 40], allowed sampling a region of the shape space, centered over the reference, in a rather homogeneous way. This yielded a perceptual template (Figure 2C) that could be used as a spatial filter to infer the discriminability of the distractors (Figure 3) and build predictive models of rat perceptual choices [30] (Figure 4). This marks the third difference from previous rat studies—we went beyond an image-level analysis of the classification images, and we explicitly tested their ability to account for rat visual perception. As such, our approach adds to a growing body of studies combining classification images with other computational methods to predict perceptual decisions [30, 41, 42, 43] and infer visual processing mechanisms from behavioral and neurophysiological data [37, 43, 44, 45, 46]. Future behavioral studies could take inspiration from these approaches to investigate aspects of rodent vision that were beyond the scope of our experiments—e.g., the representation of object information in different spatial frequency bands could be explored, by relying on multi-resolution generative or filtering manipulations [34, 44, 47].

Validity and Implications of Our Findings

Our study revealed that rats process visual objects by employing subject-specific perceptual strategies, whose complexity explains the variable proficiency of the animals in the discrimination task (Figures 3, 4, and S3). In addition, we showed that rat ability to recognize objects despite changes in their appearance is consistent with a parallel processing of the visual input through multiple perceptual filters (Figures 4B, 5, S4, and S5), whose shape is largely preserved across transformations (Figure 6) but that are properly reformatted (e.g., rescaled) to deal with the specific transformations the objects undergo.

As is customary in psychophysical studies of object vision, these conclusions were drawn from experiments performed with a specific set of visual objects and a limited number of transformations (variations of size and luminance cues), where we concentrated the statistical power of our analyses (with thousands of behavioral trials collected for each class of stimuli; see Table S1). Nevertheless, we believe that our findings have general implications with regard to the perceptual mechanisms underlying rat invariant recognition. In fact, we have previously shown that the perceptual strategy underlying the recognition of the tripod is well preserved across a large number and variety of identity-preserving transformations (two sizes, two positions, and two in-plane and two in-depth rotations) [12, 14]. In these earlier studies, however, we did not test whether the classification images derived from different transformations could work as spatial filters to account for rat perceptual choices. By now interpreting these earlier findings in the light of our current results, we can infer that rat invariant recognition is consistent with a multi-level filtering process. Because this conclusion was derived in the context of the “tripod versus everything else” categorization, the perceptual templates inferred in our experiments are specific to the tripod stimulus. However, there is no reason to believe that the same processing principles (i.e., the filtering of the input images through multiple salient and anti-salient features) do not apply to the recognition of any other object, as long as it is made of multiple, well-discriminable structural elements (such as the lobes of the tripod)—only, objects with different shapes will be processed using different combinations of visual features, as already shown in one of our previous classification image studies [14].

Another issue deserving discussion is whether the complex (multi-feature) perceptual templates found in our study reflect a systematic extraction of multiple diagnostic features from every stimulus in every trial or, instead, result from pooling together much simpler (single-feature) strategies, independently applied by the rats on a trial-by-trial basis (e.g., because of shifts of attention, gaze, or head position). A classification image, by itself, cannot be used to infer the perceptual strategies deployed in single trials, because it is built using a large statistics of stimulus-response associations [29]. However, when applied as a filter in a logistic regression model (Equation 1), it does predict perceptual choices at the level of individual stimuli/trials. As such, the low logloss values attained by the same-CI models in Figure 4B (relative to the upper bounds) are, by themselves, an indication that a unique, multi-feature strategy was consistently applied by the rats across different trials. A further indication is provided by the even lower logloss values reached by the nearest-neighborhood response models. In fact, if a rat randomly picked its strategy, on a trial-by-trial basis, from a repertoire of simple perceptual templates, one would expect responses to very similar random tripods to be highly variable, bringing the performance of the nearest-neighborhood model close to the logloss’s upper bound. In addition, with the exception of rat 2, the classification images were well preserved over time, yielding stable logloss values and being more similar within than between rats (Figure S6).

With regard to eye movements, rats, when stationary (as in our behavioral rig), maintain fixation for long stretches of time, making only sporadic saccades [26, 48, 49]. Moreover, no evidence of target-oriented saccades has even been reported in rodents. As for head movements, we have checked in a previous study [12] that head position is highly reproducible across trials and very stable during stimulus presentation, until a rat starts its motor response to report its choice. Therefore, eye or head movements are unlikely to explain the variable complexity of perceptual strategies revealed by the classification images.

At the mechanistic level, our study suggests that visual objects are represented by neuronal populations that are capable of coding complex features in a transformation-tolerant way. Interestingly, we have recently found evidence of such cortical processing in rat lateral extrastriate areas [50]. Together, these findings support the existence of a rodent object-processing pathway, and pave the way for the investigation of visual cortical processing using the powerful experimental approaches that rodent species afford [1, 2, 3, 4, 5, 6, 7, 8].

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
Long Evans rat	Charles River Laboratories	RGD_2308852
Software and Algorithms
MATLAB v2012b – 2015b – 2017a	MathWorks	https://www.mathworks.com/
Statistics and Machine Learning Toolbox	MathWorks	https://www.mathworks.com/
MWorks	The MWorks Project MIT	https://mworks.github.io/
POV-Ray	Persistence of Vision Raytracer	http://www.povray.org/
Other
Operant Customized Box	Protocase	N/A
Feeding needle customized	Cadence Science	AFN 14 g X 1” w/4mm
Capacitive sensors	Phidgets	Phidgets 1110
ADC interface	Phidgets	Text LCD 8/8/8 1203
Controlled Syringe Pump	New Era	NE-500
Serial to Ethernet bridge	Startech	NETRS2321E
Monitor LCD 21.5”	SAMSUNG	2243SN

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Davide Zoccolan (zoccolan@sissa.it).

Experimental Model and Subject Details

Subjects

Six adult male Long-Evans rats (Charles River Laboratories) were used for behavioral testing. At the arrival, the animals were around 8 weeks old and weighted approximately 200 g. During the course of the experiment, their weight grew to over 500 g. Rats had free access to food but were water restricted. That is, they received 4-8 mL of pear juice as a reward during the course of a daily behavioral session and, in addition, they had access to water ad libitum for 1 h at the end of each session. Each rat was trained in a single daily session (lasting ∼1.5 hr), 5 days per week, with free access to water in the remaining 2 days of the week. All animal procedures were in agreement with international and institutional standards for the care and use of animals in research and were approved by the Italian Ministry of Health: project N. DGSAF 25271 (submitted on Dec. 1, 2014) was approved on Sep. 4, 2015 (approval N. 940/2015-PR); project N. 933-X/10 (submitted on Feb. 216, 2012) was approved according to the legislative decree 116/ 92, article 7.

Method Details

Behavioral rig

The behavioral rig consisted of two racks, each equipped with three operant boxes, to allow training simultaneously the whole group of animals in daily sessions of about 1.5 h. A picture of the whole rig can be found in [7], while a schematic of the operant box is shown in Figures S1A and S1B. Each box was equipped with: (1) a 21.5” LCD monitor (Samsung; 2243SN) used as the stimulus display, with a mean luminance of 43 cd/mm2 and an approximately linear luminance response curve; (2) an array of three stainless steel feeding needles (Cadence Science), positioned ∼10 mm apart from each other and connected to three capacitive touch sensors (Phidgets; 1110), used for initiation of behavioral trials, collection of responses and delivery of the reward; and (3) two computer-controlled syringe pumps (New Era Pump Systems; NE-500), connected to the left-side and right-side feeding needles, used for automatic liquid reward delivery. Access to the sensors was allowed trough a viewing hole (4 cm in diameter) in the wall facing the monitor (Figures S1A and S1B). This hole enabled the rat to extend his head out of the box and frontally face the stimulus display at approximately 30 cm from its eyes. The location and size of the hole were such that the animal had to reproducibly place its head in the same position with respect to the monitor to trigger stimulus presentation. As a result, head position was reproducible across behavioral trials and very stable during stimulus presentation, as quantified in a previous study using the same apparatus [12]. This allowed a precise control over the retinal size of the stimuli.

Visual stimuli

As described in the Results and in the next section, the rats were trained to discriminate a reference object (with a tripod-looking, Y-shaped structure) from 11 distractors (Figure 1A). These stimuli were a mix of artificial shapes and renderings of computer-graphics models of natural objects, and they have all been previously used in behavioral [11, 12, 13] and neurophysiological [50] studies of rat object vision. The artificial shapes were built using the geometric primitives available with the ray tracer software POV-Ray (http://www.povray.org), while the natural objects were mesh-grid models freely downloadable from the web. All the stimuli were rendered using POV-Ray, as gray scale images against a black background, in such a way to be approximately equal in size (i.e., diameter of a bounding circle) along either the vertical (height) or horizontal (width) dimension. The default size of each object (i.e., the size used for the initial training of the rats; see below) was 35° of visual angle and they were all presented in the center of the stimulus display. By design, the distractors spanned a broad range of image-level similarity with the reference, based on how much they overlapped with the tripod object (see examples of overlaps in the insets of Figure 1C). This allowed differentiating the rats, based on their level of proficiency with the various distractors (see performance curves in Figures 1C and 2D).

In a later phase of the experiment, the animals were also presented with a new battery of stimuli, obtained by randomly altering the reference object (when considered at 30° of visual angle). These stimuli, referred to as random tripods, were used to infer rat perceptual strategy, by applying a classification image method that was appositely designed for this study. As mentioned in the Discussion, one of the key features of this method was precisely the way in which the random tripods were generated. Rather than applying additive noise (as in typical classification image studies [29]) or multiplicative noise (as, for instance, in the Bubbles method [34, 35, 36], recently used to investigate rat visual perception [12, 14, 15]), we randomly changed the 3d structure itself of the geometrical primitives of the tripod (i.e., their orientation, size and aspect ratio; see Figure 2A). This allowed obtaining whole objects (i.e., structurally altered tripods), rather than partially degraded or masked versions of the reference (i.e., noisy tripods). As a consequence, the set of random tripods spanned quite uniformly the stimulus display, and the resulting classification images were not constrained within the boundaries of the reference or distractor objects (as in our previous application of the Bubbles method [12, 14]), but extended over the whole image plane. As explained in the next sections, this was critical to obtain general, predictive models of rat perceptual decisions using logistic regression models. During the course of the experiment, a new set of 120 random tripods was generated for each session used to obtain the classification image data (total of 32 sessions; see next section).

Transformed versions of the random tripods were also produced to obtain the perceptual templates used by the rats to process outline and small size stimuli. Specifically, we took all the original random tripods (i.e., the 120 × 32 full-body objects, generated as variations of the 30° tripod object), we extracted their boundaries using a custom written script in MATLAB (Mathworks), and we generated outline versions of the stimuli, with the borders rendered in full white, with a thickness of 1.2° of visual angle (see examples in Figures 5A and 6B). These stimuli were presented during an additional cycle of 32 sessions. We also produced a third set of random tripods, by taking the original stimuli and scaling them down to ∼83% of their original size, corresponding to scaling the tripod object from 30° to 25° of visual angle (see examples in Figures 5B and 6C). This set of small-size random tripods was presented during an additional cycle of 32 sessions.

Experimental design

The animals were trained to initiate a behavioral trial and trigger stimulus presentation, by inserting their heads through the viewing hole facing the stimulus display (Figures S1A and S1B) and by licking the central sensor (Figure S1C). The rats learned to associate each object identity with a specific reward port – presentation of the reference object required a response to the right-side port, while presentation of a distractor was associated to the left-side port (Figure S1C). A correct response prompted the delivery of the liquid reward through the corresponding port (i.e., feeding needle). A reinforcement tone was also played to signal the successful accomplishment of the task. In case of an incorrect choice, no reward was delivered and a 1–3 s timeout started, during which a failure tone sounded and the monitor flickered from black to middle gray at a rate of 15 Hz. The stimulus presentation time was set to 3 s, during which the rat had to make a response. In the case of a correct choice, the stimulus was kept on the monitor for an additional 4 s from the time of the response (i.e., during the time the animal collected his reward). In the case of an incorrect response, the stimulus disappeared and the timeout sequence started. If an animal did not respond within the 3 s time frame, the trial was classified as ignored. To prevent the rats from making very quick, impulsive responses, a trial was aborted if the animal’s reaction time was lower than 300 ms. In such cases, neither reward or time-out was administered, the stimulus was immediately turned off, and a brief tone was played. Over the course of a session, an animal typically performed between 400 and 500 behavioral trials.

The response-side associated to the tripod object (i.e., the right-side port; Figure S1C) was chosen in such a way to be the opposite of that used in a previous study, where the tripod required a response to the left-side port [12]. This allowed counter-balancing the stimulus/response-side association across the two studies. This was motivated by the fact that, in this earlier study, we found a preference, across all tested rats, for the top-left lobe of the tripod, as the dominant salient feature determining their perceptual choices [12]. We suspected that the asymmetry in the classification images obtained in that study was determined by the fact that rats had to collect the reward form the left-side port after a correct identification of the tripod. Our hypothesis was that the animals, by orienting their head toward the left-side port following a correct response to the tripod, and thus observing the object’s left lobe during collection of the reward, learnt to rely more heavily on that specific lobe as a salient feature of tripod’s identity. Interestingly, also in our current study most classification images were asymmetrical (Figure 6A), but with the opposite preference – the tripod’s right lobe, instead of the left one, was the dominant diagnostic feature of tripod’s identity. Taken together, these opposite asymmetries found in the two studies do support our hypothesis about the stimulus/response-side association influencing the preference of the animals for a specific side of the tripod object.

To ease the acquisition of the task, rats were initially trained to discriminate the reference object from two of the distractors only (#1 and 8). These stimuli were chosen because we knew, from previous studies [11, 12, 13], that rats can be trained to discriminate them from the tripod. During this phase of the training, the tripod was presented in 50% of the trials, while each of the two distractors was presented in 25% of the trials. Once performance with these initial stimuli reached 70% correct discrimination, the remaining 9 distractors were introduced. To gradually habituate the rats to these new stimuli, we initially kept the proportion of the previously presented distractors at 25% of the total (12.5% each) and we equally shared the remaining 25% of the trials among the new distractors (∼2.8% each). Once the rats achieved 70% correct discrimination on at least half of the new distractors, we equated the fraction of presented trials for all the distractors (∼4.55% each). Training then continued until the rats reached a stable overall performance (across all stimulus conditions and over the course of five consecutive sessions) of 70% correct discrimination.

Following the acquisition of this task, we used a staircase procedure to familiarize the rats with size variations of the objects, bringing the animals to tolerate size changes from 15° to 35° of visual angle, in steps of 2.5°. Details about this procedure can be found in [11]. Briefly, each rat started the task with the stimuli being presented across a range of possible sizes (initially, only the default size of 35° of visual angle was allowed). If the animal responded correctly to 7 out of 10 consecutive trials at the smallest allowed size, the complete set of stimuli (reference and distractors) at a size that was smaller of 2.5° was added to the pool of possible stimulus conditions (i.e., the range of possible sizes was extended of 2.5°). We then took the smallest size reached by the rat in a given session, we increased it by 5°, and we used that value as the lower bound of the range of sizes initially presented in the next session. Once the animal consistently reached size 15° for five consecutive sessions, we stopped the staircase procedure, and we assessed its performance across the entire stimulus set (i.e., all combinations of object identities and sizes) in a final cycle of sessions, where all the sizes were equally likely to be presented in each trial (Figure 1B). These sessions allowed assessing the performance of each rat with every object, across the whole size span, yielding curves that were similar to those shown in Figure 1C (which refer to the following phase of the experiment, where the rats were also presented with the random tripods; see next paragraph).

Next, rats were tested in sessions were the stimulus pool included the reference and distractor objects (presented across the whole size range), as well as the random tripods. The latter stimuli were presented, randomly interleaved with the other objects, in 10%–20% of the trials (Figure 2B). Responses of the animals to these trials were treated in a special way. Since none of the random tripods was associated to either the reference or the distractor category, and because we wanted to assess how the rats spontaneously classified these stimuli, no feedback was provided to the rats about the outcome of their choices. Following the response to a random tripod, neither the reward nor the time-out period was administered – the stimulus was removed from the display and the rat was allowed to immediately initiate a new trial. As shown in a previous study [11], the animals were not disturbed by these no-feedback trials, as long as they were sparsely interleaved with the regular trials that gave the rats the possibility to gain the reward. The rats kept performing the task and, more importantly, they did not respond randomly to the random tripods, but automatically classified them according to their perceived similarity with the reference object – this was assessed a posteriori, by having obtained statistically significant classification images from these stimuli (see next section).

As mentioned above, each rat was administered a total of 32 sessions with randomly interleaved random tripods. Afterward, a new cycle of 32 sessions started, where the regular stimuli (i.e., reference and distractors) were randomly interleaved to the outline versions of the random tripods. Finally, a last cycle of 32 sessions was administered, where the regular stimuli were randomly interleaved with the scaled versions of the random tripods. The total amounts of trials administered during these three phases of the experiment are reported in Table S1, separately for the regular stimuli (i.e., the reference and distractor objects presented across the full span of sizes) and the random tripod objects.

All the experimental protocols (i.e., presentation of the visual stimuli, collection and evaluation of the behavioral responses, and administration of reward or time-out period with associated reinforcement sounds) were implemented using the freeware, open-source software package MWorks (http://mworks-project.org/).

Quantification and Statistical Analysis

Data analysis

Our study rests on two synergistic modeling approaches: 1) the computation of classification images, aimed at inferring rat perceptual strategies; and 2) the application of logistic regression, aimed at obtaining predictive models of rat perceptual choices. Both procedures have already been qualitatively described in the Results. Here, we provide a more detailed explanation, with a special emphasis on the statistical assessment of the classification images and the cross-validation procedure to fit and test the logistic regression model.

Classification images and their significance

To build a classification image, we first separately averaged the images of the random tripods that were classified by a rat as being the tripod and those that were classified as belonging to the distractor category. By subtracting the two resulting average images, we obtained a saliency map (the classification image [29]), which revealed what regions of the image plane more heavily influenced the rat to choose the reference (bright areas) or the distractor (dark areas) category (Figure 2C). Following a convention established in previous studies [12, 14], these bright and dark regions were named as, respectively, salient and anti-salient (with reference to the tripod identity). By applying a permutation test, we statistically assessed what portions of these regions were significantly more likely (or less likely) than expected by chance to lead the rat to choose the tripod category, when some part of the random tripods hit them (see Figure 2C).

The test was carried out according to the following procedure. We produced 100 randomly shuffled versions of rat responses to the whole set of random tripods. For each set of permuted responses, we computed a permuted classification image, in the same way as described above. Note that this procedure preserved the proportion of rat responses in the two categories across all permutations, while totally destroying the correct associations between stimuli and responses. We then virtually stacked the 100 permuted classification images on top of each other and, for each pixel in the image plane, we computed the empirical distribution of its intensity values across the 100 images. We thus obtained null distributions of classification image values at each pixel location, under the hypothesis of random responses of the rat to the random tripods. We then obtained smooth versions of such distributions by fitting them with one-dimensional Gaussians. Finally, we compared the actual classification image values to the null distributions obtained at the corresponding image plane (i.e., pixel) locations. A value falling on the right tail of its null distribution, within the 0.01 significance region, was considered as significantly salient. Conversely, a value falling on the left tail of its null distribution, within the 0.01 significance region, was considered as significantly anti-salient. These significantly salient and anti-salient regions were delineated with, respectively, red and cyan boundaries (or patches) in the classification images shown in Figures 2, 3, 4, and 6.

This approach was also applied to obtain classification images and estimate their statistical significance from the outline (Figure 6B, top) and the small-size (Figure 6C) random tripods. In the case of the outline stimuli, classification images were also obtained from their filled-in versions (Figure 6B, bottom). These stimuli were produced by taking the outline random tripods and filling uniformly their inside with white color.

Fit of the logistic regression model

To predict the probability of a rat i to classify an arbitrary input image x as being the tripod, we plugged the classification image $C{I}_i$ obtained for that animal into the logistic regression model defined by Equation 1. The regression parameters ${\theta }_0^i$ and ${\theta }_1^i$ (described in the Results) were obtained by fitting the model to the responses of the rat to either the whole set or a subset of the random tripods. The same applied to the classification image itself, which was always obtained using the same pool of random tripods that were later used to fit the model’s parameters. The entire set of random tripods was used when the predictions of the models had to be compared to the responses of the rats to the regular stimuli (i.e., the reference and the distractor objects), as in Figures S3–S5. Instead, when the models were used to predict rat responses to the random tripods themselves, a 10-fold cross-validation procedure was used, so as to test the true ability of the models to generalize their predictions to an independent set of data (Figure 4B).

The cross-validation procedure worked as follows. For each rat, the set of random tripods was randomly divided into 10 subsets. Iteratively, each of these subsets was left out, so as to be used as the test dataset, while the remaining 9 were used as the training dataset, to obtain the classification image and fit the model’s parameters. The ability of the model to predict rat responses to the random tripods was then measured as the average of the model performance across the 10 left-out test sets. Critically, the same cross-validation procedure was applied any time that the model was used to predict the responses of a rat to the random tripods, no matter whether the classification image plugged into Equation 1 was the one of the animal under consideration (same-CI models; big black dots and small colored dots in Figure 4B) or the classification images of a different rat (cross-CI models; small black dots in Figure 4B). This allowed comparing the goodness of the classification images to predict the choices of a rat, independently of the possible bias of the animal (since the bias term ${\theta }_0^i$, as well as the gain factor ${\theta }_1^i$, were always included in every model and fitted to the animal’s responses).

The fitting procedure was based on the minimization of a cost function, known as the logloss (aka logarithmic loss or cross-entropy loss), using a gradient descent method. The logloss is the normalized negative log-likelihood of the true responses, given the probabilistic outcomes of the model’s predictions on the same input images [51], and is defined by the following equation:

$$l\left({\theta }_0,{\theta }_1\right)=-\frac{1}{N}\sum _{k=1}^N{y}^k\log p\left(y^k=1|x^k\right)+\left(1-y^k\right)\log \left(1-p\left(y^k=1|x^k\right)\right),$$ (Equation 2)

where N is the number of samples used to train the model, k is a running index, and the probabilities $p\left(y^k=1|x^k\right)$ are given by the logistic regression model of Equation 1 (although here, for the sake of brevity, their dependence on ${\theta }_0^i$ and ${\theta }_1^i$ is not made explicit). It can be noticed that this equation is composed of two terms. The first term is positive when the response $y^k$ of the rat is 1 (tripod category) and vanishes when the response is 0 (distractor category). The opposite happens in the second term, so that the two terms take care of the two possible choices of the rat independently. When the model predicts a high probability of responding 1 and the actual response was indeed 1, the first term adds only a small contribution to the loss (it vanishes only if the predicted probability is exactly 1, which does not happen in practice, since the sigmoid function in Equation 1 reaches its extreme values only asymptotically, when its argument grows or decrease indefinitely; see Figure 4A). Conversely, if the model predicts a small probability, the contribution to the loss is high, reflecting the fact that the model’s prediction is poor. The larger is the confidence of the model in a wrong prediction, the higher is the contribution to the total loss. Similar considerations can be done for the second term, when the actual response of the rat was 0 (distractor category).

The logloss was minimized by writing a custom script in MATLAB (Mathworks), using the glmfit function of the Statistics and Machine Learning Toolbox with binomial distribution and logit as the canonical link function (MATLAB version: 2017a).

Assessing the evolution of the classification images over time

To check the stability of each rat’s perceptual strategy over time, we again divided the pool of trials in which the random tripods were presented in two subsets: 10% of the data were left out, to be used as the test set, while the remaining 90% of the trials (the training data, N trials) were sorted according to the time at which they had been presented and then split in 4 consecutive sets of equal size (when the total number of trials N was not divisible by 4, we ceiled N/4 to the lowest integer and left out the remainder). From each of the four sets of trials, we computed the corresponding classification image (see Figure S6A), we plugged it into Equation 1 to fit the logistic regression model, and we estimated the ability of the model to predict the responses of the rat to the trials belonging to the test set, by computing the logloss. The whole procedure was repeated 10 times, by randomly splitting, in each run, the random tripod trials in a test and a training set. The resulting logloss values obtained across the ten runs were then averaged to obtain the curves shown in Figure S6B.

Statistical tests

The statistical tests used to assess the significance of our findings are reported in the Results and in the legends of the figures. Here, we only describe in more details the binomial test used to evaluate the overall significance of the comparisons between same-CI models and cross-CI models in Figure 4B. This test was carried out according to the following logic. We computed the probability of obtaining a number of successes in 6 Bernoulli trials that was equal or higher than the number of times a given model (e.g., the same-CI model) outperformed all other alternative models (e.g., the cross-CI models). In the case of the same-CI model versus cross-CI models comparisons (i.e., large black dots and small colored dots versus small black dots in Figure 4B), the chance of success in each Bernoulli trial was set to 1/6. In the case of the filled-in same-CI^o model versus same-CI^o model comparison (i.e., solid green dots versus empty green dots in Figure 4B), the chance of success in each trial was set to 0.5.

Data and Software Availability

Data and custom MATLAB codes used to generate all analyses are available from the Lead Contact upon request.

Published: March 15, 2018