Abstract
Genome-wide association studies (GWAS) have identified thousands of loci that are robustly associated with complex diseases. The use of linear mixed model (LMM) methodology for GWAS is becoming more prevalent due to its ability to control for population structure and cryptic relatedness and to increase power. The odds ratio (OR) is a common measure of the association of a disease with an exposure (e.g., a genetic variant) and is readably available from logistic regression. However, when the LMM is applied to all-or-none traits it provides estimates of genetic effects on the observed 0–1 scale, a different scale to that in logistic regression. This limits the comparability of results across studies, for example in a meta-analysis, and makes the interpretation of the magnitude of an effect from an LMM GWAS difficult. In this study, we derived transformations from the genetic effects estimated under the LMM to the OR that only rely on summary statistics. To test the proposed transformations, we used real genotypes from two large, publicly available data sets to simulate all-or-none phenotypes for a set of scenarios that differ in underlying model, disease prevalence, and heritability. Furthermore, we applied these transformations to GWAS summary statistics for type 2 diabetes generated from 108,042 individuals in the UK Biobank. In both simulation and real-data application, we observed very high concordance between the transformed OR from the LMM and either the simulated truth or estimates from logistic regression. The transformations derived and validated in this study improve the comparability of results from prospective and already performed LMM GWAS on complex diseases by providing a reliable transformation to a common comparative scale for the genetic effects.
Keywords: complex diseases, genome-wide association studies, summary statistics, OR, linear mixed models
GENOME-WIDE association studies (GWAS) of complex diseases often use a case-control design that requires the analysis of a binary trait that indicates whether an individual has the disease. Typically, association studies of disease traits are conducted under the logistic regression model, where each SNP is tested individually against the phenotype for association. One key concern for GWAS is the control of spurious associations due to population structure (Marchini et al. 2004; Hirschhorn and Daly 2005). Principal component (PC) correction (Price et al. 2006) in combination with logistic regression is a common method for GWAS of disease traits when population stratification is of concern (Lambert et al. 2013; Michailidou et al. 2013; Ripke et al. 2014). Linear mixed model (LMM) methodology is becoming the gold standard for GWAS due to its ability to control for population structure and cryptic relatedness, and has been shown to be more powerful than standard GWAS (Yang et al. 2014). These advantages have led to the recent use of LMMs for large-scale GWAS of dichotomous traits (Fingerlin et al. 2013; Boraska et al. 2014; van Rheenen et al. 2016; Howson et al. 2017).
The odds ratio (OR) is a common measure for the strength of association of a genetic locus and has desirable properties; for example, it is not affected by case ascertainment. The OR is readably available from logistic regression, however, when the LMM is applied to all-or-none traits it provides estimates of genetic effects on the observed 0–1 scale; a different scale to that in logistic regression, which limits the comparability of results across studies (Cook et al. 2017). Given that both methodologies are used with experimental data to estimate genetics effects, it would be convenient to have a reliable transformation between effects estimated using the LMM to that from the generalized linear model. Often only summary association statistics are available and thus such a transformation cannot depend on the genotype data.
Methodologies for making such a transformation have been investigated in the statistics and economics literature, with one avenue relying on the links between logistic regression and the linear discriminant analysis (LDA) method of Fisher (1936) as discussed by Cox and Snell (1989), Efron (1975), and Haggstrom (1983). Although the primary aim of the LDA method was for classification of individuals, Haggstrom (1983) showed that LDA provides a convenient avenue for calculating logistic regression coefficients using readily available summary statistics from the fitting of the linear model to a dichotomous dependent variable via least squares. Another method for estimating the logistic regression coefficients from linear regression is via the “reverse Taylor series approximation” (Press and Wilson 1978), which relies on expanding the logistic link function about the sample mean in a Taylor series. This method was initially developed to provide starting values for the iterative estimation procedure of logistic regression, and has been adapted for summary level data in Chang et al. (2000). The reverse Taylor series approximation is similar to the first order approximation provided in Pirinen et al. (2013) for use in GWAS and is equivalent if the genotypes are mean centered. Pirinen et al. (2013) provided a second transformation with smaller relative error across simulated traits than their first order approximation, which relies on the second and third order terms of the Taylor series coupled with some empirical testing. Zhou et al. (2013) justified the use of the linear model for GWAS of binary traits by also recognizing that the linear model is a first order Taylor approximation to a generalized linear model.
In this study, we derive a set of transformations to the OR under the simple linear regression model that do not rely on the Taylor series approximation and are thus hypothesized to be more robust to the small genetic effect assumption of previous methods. To test the proposed transformations, we use real genotypes from the Genetic Epidemiology Research on Adult Health and Aging (GERA) cohort (60,000 individuals) (Lapham et al. 2015), and the first release of the UK Biobank (150,000 individuals) (Sudlow et al. 2015) to simulate 50 all-or-none phenotypes for each of six scenarios that differ in underlying model (logistic or liability threshold models (Dempster and Lerner 1950; Reich et al. 1972; Wray and Visscher 2015), disease prevalence, heritability, and allele frequency spectrum. We measure the performance of each transformation by estimating the MSE and the slope and adjusted from regression of the OR estimates from the LMM on the simulated truth and compare the results with the transformation of Pirinen et al. (2013). Additionally, we investigate the robustness of the assumptions of the derived transformation through a single variant of large effect simulation under the liability threshold model for a highly ascertained study. We further applied these transformations to GWAS summary statistics for type 2 diabetes generated from 108,042 individuals in the UK Biobank.
Materials and Methods
Derivation of the OR under the linear regression model
Let the random variable Y equal 0 or 1, depending on whether an individual is healthy (control) or diseased (case), and let Z represent an allele set, for example A/T, for a genetic locus, and we arbitrarily set A to be the risk allele or exposure. We can define the as
| (1) |
where the notation denotes probability. This expression best represents the meaning of the in this context, where we compare the odds of the disease when one is exposed or unexposed to the risk allele. However, by the symmetry of the we can equivalently write
| (2) |
Equation 2 contains probabilities that are recognizable as the frequencies of each of the alleles in controls and cases. Letting and represent the frequency of the risk allele (or effect allele) within controls and cases, respectively, we can write the as
| (3) |
If we have individual-level data, then we can estimate and from the sample and calculate the directly using Equation 3, without making any further assumptions. However, if only summary statistics are available, we seek to derive an expression for that potentially depends on summary statistics generated from a linear regression model.
We assume the following simple linear regression model:
| (4) |
where is the response variable for individual of a population, which we assume takes values 0 or 1 for unaffected (controls) and diseased (cases) individuals, respectively. We define K as the lifetime probability that an individual will be affected by the disease in the population (Witte et al. 2014). By definition, where the notation denotes expectation. The independent predictor variable is considered random and models a SNP. The random variable takes values 0, 1, or 2 with the corresponding allele frequency of the risk allele, denoted p, and we assume that each SNP is independent. The random variable is thus binomial distributed for each SNP. In Equation 4, is a random error term such that and , and the unknown parameters and are to be estimated.
It is often the case in GWAS of disease phenotypes that the cases are oversampled relative to the controls. This alters the observed probability that an individual has the disease within this misrepresented sample relative to the true population distribution. To symbolize this differentiation, we let k represent the proportion of cases in the sampled population. This may or may not represent K well, depending on the sampling procedure.
Under the simple linear regression model and the ordinary least squares solutions for the regression coefficients, we have the following expression for the derived in Supplemental Material, File S1:
| (5) |
The broad intuition for this solution is that we use the properties of the ordinary least squares solution for the regression parameter which relies on expressions for and under Equation 4, and an expression for the allele frequency to solve for expressions of and that depend on k, p and We then substitute these expressions into Equation 3 to obtain Equation 5. We cannot observe from summary statistics and thus we must make some assumptions about the form of the variance for the SNP to derive a transformation. Initially, we can assume that the SNP genotype frequencies across cases and controls are in Hardy–Weinberg equilibrium (HWE) and let Equation 5 assumes that is a good approximation of the
We can consider a more complete expression for the variance of the SNP under Equation 4, which can be represented as (see File S1):
| (6) |
The difficulty with Equation 6 is that the within case and control variances, and are unknown. However, if we assume HWE within cases and controls, we can equate and in Equation 6 to obtain
| (7) |
Equation 7 coupled with expressions for the under (4) and allows for a solution that better reflects the form of Equation 7 and can be estimated from summary statistics. The solution for the expression of and under this assumption is more challenging and requires a quadratic in We take the solution to the expression for and solve for using To solve for this transformation under assumption Equation 7, we substitute the derived expressions for and into Equation 3 (see File S1) to obtain
| (8) |
The solution to the quadratic in in Equation 8 can have two, one, or no solution. We showed (see File S1) that will have exactly one solution when
| (9) |
It is possible for the quadratic in to have two or no solution but these are for very extreme ORs. For example, for a grid of values we calculated the effect that would be required to have an (Figure S1 in File S1). For all values the effect was contained in the interval (Equation 9), suggesting that ORs of >50 are required, for all values of k and p, for two or no solutions to Equation 8 to exist. If no solution exists then we expect this to be indicative of a quality control or numerical error. Computationally, because we expect there to be only one solution to the quadratic in , we take the solution that lies within
Equations 5 and 8 present the mathematical relationship between the distribution and model parameters k, p and under the model in Equation 4 with varying assumptions about the representation of Equation 6. We make the distinction between and as estimates of when k, p, and are replaced with their estimates , , and in Equations 5 and 8, once we have observed the data. Practically this corresponds to substituting estimates of k, p, and , which contain sampling variation, from summary statistics generated from the sampled data into Equations 5 and 8. The derivations do not account for this sampling variation but rely on the unbiased estimators used for k, p, and to provide good estimates of the under repeated sampling.
Transformations and require an estimate of the allele frequency (p) in the sample, which is often reported with summary statistics. However, if the sample estimate of p is unavailable then an approximate estimate can be taken from an adequate reference data set. Given many GWAS are performed using oversampled cases relative to the true prevalence in the population, the sample allele frequency may deviate from the reference allele frequency especially for SNPs of large effect. We investigate the robustness of Equations 5 and 8 to this deviation from model assumptions through simulation.
It may be the case that the allele frequency for each SNP is not reported and an adequate reference data set is not obtainable, for example, in an admixed population. If this is the case, then we can use the information contained in the SE of the regression coefficient which is often reported with summary statistics, to derive expressions that are independent of p with equivalent assumptions to and (see File S1). We explore their adequacy relative to the expressions that include p through simulation.
Simulation
Data:
To test the proposed transformations, we simulated case-control phenotypes using real genotype data from the GERA study (Lapham et al. 2015), and the UK Biobank (Sudlow et al. 2015). For the GERA data set, a random subsample of 10,000 individuals was taken from the larger data set (∼60,000 individuals) containing ∼1,100,000 HapMap 3 SNPs. The first 10 PCs of the genotype matrix and the genetic relationship matrix (GRM) were generated from these data using the PLINK 1.9 software (Chang et al. 2015).
The UK Biobank is a prospective cohort study of over 500,000 individuals from across the UK. The interim UK Biobank data release contains genotypes for 152,736 individuals that passed sample quality control (99.9% of total samples). Imputed genotype data are provided as part of the data release, which contains 73,355,667 SNPs, short indels, and large structural variants. Selecting out only SNPs with imputation info score >0.3 and minor allele count ≥5 resulted in 40,000,000 SNPs for the 152,249 individuals. PC analysis and the self-declared ethnicity were used to derive a “White British” subset of samples. In addition, samples were excluded if they had a genetically inferred sex that did not match the self-reported sex and extreme heterozygosity or missing genotype outliers. These filters resulted in a data set with 140,720 samples, which includes related individuals. We then selected out 1,162,900 HapMap3 SNPs and performed a final filter excluding SNPs with MAF and HWE P-value
Logistic regression model simulation:
For the first simulation, a logistic regression model was used to generate simulated phenotypes using the GERA data set. To generate case-control phenotypes, the GERA genotypes were pruned on linkage disequilibrium at 0.01 using the PLINK 1.9 software (Chang et al. 2015). This left ∼15,000 independent SNPs from which to simulate phenotypes. For each replicate, 100 effects were drawn from an distribution and randomly assigned to SNPs from the independent set. A vector of composite genetic and PC values (to simulate population structure) were generated as
| (10) |
where (dimension ) is the centered and scaled genotype matrix for the SNPs that have been assigned an effect, () is the set of sampled genetic effects, and () is the first PC of the full genotype matrix. Probabilities of having the disease, given the genotypes , were generated by the logistic function i.e., for each individual i case-control status was generated from a Bernoulli random variable with success probability where is the ith element of the column vector in Equation 10. This generated case-control data with an expected prevalence of 0.5 for each replicate because , due to the expected value of the effects and PC equaling 0. Under the logistic regression model we also simulated a set of null phenotypes that only contained the effect of PC one and no genetic effects. A total of 50 replicates were generated for the logistic and null simulations under the logistic regression model, which were analyzed with logistic regression implemented in PLINK 1.9 with the first PC fitted as a fixed effect, and an LMM implemented in the GCTA software (Yang et al. 2011). Regression coefficients from the LMM were transformed to ORs using Equations 5 and 8 for comparison with results generated from logistic regression and the true simulated OR. To assess the performance of the transformations we regressed the transformed values from the LMM on the simulated true or estimated OR values from logistic regression. For comparison we calculated the transformed OR using Equation (3.2) of Pirinen et al. (2013). We used the estimated slope and adjusted as measures of the degree of correspondence between the two sets of ORs for each of the methods. The MSE was summarized for OR bins (bin width of one) for each of the transformations along with the number of variants and average allele frequency for each bin.
To investigate the rate of decay of Equation 8 for misspecified values of k and p for the logistic regression model simulation, we substituted for k and for p into Equation 8, using the multiplicative factors for both k and p. The transformed ORs under these misspecified coefficients were compared with the simulated true ORs to quantify the rate of decay.
Liability threshold model simulation:
To vary the underlying model generating the data, we simulated case-control phenotypes under the liability threshold model using the GCTA software and the UK Biobank data set. For polygenic disease traits, the liability threshold model has precedence in the genetics literature and has been shown to model the genetics of disease traits well. Related individuals were left within the UK Biobank genotype set to mimic cryptic relatedness, which is best controlled for using a LMM. Additionally, it is common to oversample cases relative to controls in GWAS on disease traits, which can be achieved in the GCTA software. The number of cases is limited to where n is the number of individuals in the data set used to generate the simulated phenotypes and K is the prevalence of the disease in the population. We simulated four scenarios with varying K, heritability (), and ratio of cases to controls (alters K to k) to provide a range of realistic situations in which to test the transformations. The following scenarios were simulated: (1) and (); (2) and (); (3) and (); and (4) and (). The number of individuals was fixed at 10,000 across scenarios with the ratio of cases to controls limited by the size of the UK Biobank. For each scenario, 50 replicates were simulated each using 100 effects drawn from an distribution and randomly assigned to a subset of the independent set of SNPs. The independent SNP set was generated by pruning the UK Biobank genotypes on linkage disequilibrium using the PLINK 1.9, resulting in 14,284 markers to place effects on. Replicates were again analyzed with logistic regression implemented in PLINK 1.9 with the first 15 PCs fitted as covariates, and an LMM implemented in the GCTA software. Within each replicate a new set of 10,000 individuals from the 140,000 total was used by GCTA to generate the phenotype. Therefore, a new GRM was built for each replicate using PLINK 1.9 and a subset of 300,000 linkage disequilibrium pruned SNPs derived from the 1,100,000 HapMap 3 SNPs.
To investigate the performance of the transformations for rare variants, we took a random subsample of 100 variants from chromosome 20 of the UK Biobank data that had minor allele frequencies between 0.001 and 0.01. Using these variants we simulated 50 replicates with the following parameters: and and (). This larger number of cases was chosen to provide the maximum case ascertainment that the UK Biobank data could generate for this disease prevalence. This heritability was chosen so that large effects would be generated when GCTA randomly samples the 100 effect sizes from the distribution. Within each replicate a new set of 10,000 individuals from the 140,000 total was used by GCTA to generate the phenotype, which again required a new GRM to be built for each replicate as above. Replicates were analyzed with logistic regression implemented in PLINK 1.9 with the first 15 PCs fitted as covariates, and an LMM implemented in the GCTA software.
For each scenario, we compared the results from the transformed LMM effects and the reported OR from logistic regression with the true OR, which was calculated by estimating and from the sampled data within each replicate and Equation 3. To assess the performance of the transformations, we again regressed the transformed values from the LMM on the simulated true OR, and used the estimated slope and adjusted as measures of the degree of correspondence. The MSE was also summarized for OR bins (bin width of one) for each of the transformations along with the number of variants and average allele frequency for each bin. We again calculated the transformed OR using the transformation of Pirinen et al. (2013) for comparison. Transformations and require the SNP allele frequency, which is often unavailable for summary statistics, and thus for each of the simulation scenarios we investigated the robustness of these transformations to the use of allele frequencies from a reference. The reference used was the European subset of the 1000 Genomes Phase 1 Version 3 (1000 Genomes Project Consortium et al. 2012). Furthermore, the robustness of and when the SE of the regression coefficient was used rather than the reference allele frequency, was also investigated.
To investigate the rate of decay of Equation 8 for misspecified values of k and p for the liability threshold model simulation scenarios, we again substituted for k and for p into Equation 8, using the multiplicative factors for k and p. The transformed ORs under these misspecified coefficients were compared with the simulated true ORs to quantify the rate of decay.
The transformations derived rely on the model that the genotypes frequencies across cases and controls or within cases and controls are in HWE. However, the expected marker genotype proportions among diseased cases can deviate from HWE when a true association exits, with the amount of deviation depending on the genetic mechanism. We may expect a deviation from HWE for a variant of large effect when the cases are heavily ascertained relative to the controls.
To investigate the potential bias of the method due to case ascertainment for very large effects, we performed the following simulation in the R programming language (R Core Team 2015). For a hypothetical 10,000 individuals (n), we generated 50 simulated phenotypes per genetic effect size across a grid, which ranged from 0.1 to 1.5 in increments of 0.1 (750 total simulated phenotypes). The population prevalence was set to heritability , and cases were oversampled relative to controls such that For each phenotype a simulated SNP was generated from a binomial distribution and mean standardized, where p was sampled at random from the set of minor allele frequencies (>0.001) from chromosome 20 of the UK Biobank data. The genetic component of the phenotype was simulated as where is an column vector of genetic values, is the simulated genetic effect, is an column vector of mean centered simulated genotypes, and is an column vector of values samples from a normal distribution, which represents the contribution from the polygenic background to the genetic component. The final phenotype was generated by adding a random noise term to with column vector entries sampled from a normal distribution with mean zero and variance equal to so that the total heritability on the liability scale is equal to the desired value (0.5). Case-control phenotypes were generated by assigning a one to those individuals with disease liabilities exceeding the quantile threshold of the normal distribution that coincides with a disease prevalence of and a zero otherwise. To oversample cases relative to controls this simulation process was repeated with equal numbers of cases and controls stored within each repetition until the desired sample size was reached.
For each of the phenotypes, both a linear model and a logistic regression model were used to analyze the data. The effect from the linear model was transformed to the OR using The adjusted from the linear model was stored from the linear model to measure the proportion of phenotypic variance explained by the large effect variant. The chi-squared statistics from a one degree of freedom test for HWE genotype deviation were recorded within cases and controls, and for the whole SNP (across cases and controls) for each of the phenotype–SNP pairs. The estimated ORs from logistic regression and the transformed linear model estimates were compared to the true OR, which was calculated by evaluating and within the simulated data and using Equation 3.
Frequently, a large proportion of case-control phenotypic variation can be explained by a large covariate effect such as age and sex. To investigate whether the inclusion of a large covariate effect induces a bias in the transformation, we repeated the above simulation but included a simulated binary covariate with an effect size of unity. In addition to the statistics stored for the above simulation scenarios the proportion of variance explained by the sex effect was also estimated. The large environmental effect had an adjusted on average across all replicates of 15.2% (SD = 4%). Again, the effect from the linear model was transformed to the OR using Logistic regression and the transformed linear model OR estimates were compared to the true OR calculated from the simulated data. If a large binary or categorical covariate explains a large proportion of the phenotypic variance, it is typical to perform a within covariate group analysis and then combine the within group estimates in a meta-analysis. We investigated this concept by performing logistic regression and the linear regression analysis within covariate group and then calculated a meta analyzed genetic effect using the inverse variance method. The meta analyzed effect was then transformed to the OR and compared with the true OR.
Application to type 2 diabetes
To further assess the efficacy of Equations 5 and 8, we analyzed type 2 diabetes in the UK Biobank. We chose this phenotype because it is a well-studied, common complex disease that is present in the UK Biobank and is moderately heritable relative to other common diseases. For the type 2 diabetes study, we further subsetted the 140,720 samples to exclude individuals that had at least one identified closely related sample. Further exclusion on relatedness was performed with one individual from a pair with an estimated SNP marker relatedness >0.05 removed. This resulted in a final sample of 108,042 samples with age, sex, and case-control status for type 2 diabetes. Related individuals were removed from this analysis so that the ORs from logistic regression with PC correction could be used as a benchmark for the transformed OR, which would not have been a fair comparison if related individuals were left in the analysis. Of this set, 5780 individuals were diagnosed with type 2 diabetes.
We performed a GWAS using the 1,162,900 HapMap3 SNPs for type 2 diabetes using a LMM implemented in the BOLT-LMM (Loh et al. 2015) software and logistic regression using PLINK 1.9. The covariates sex and age were fitted as fixed effects in the LMM association study, whereas age, sex, and 15 PCs (generated by the UK Biobank) were fitted in the PLINK 1.9 logistic regression association study.
Data availability
The PLINK, GCTA, and BOLT-LMM software, source code, installation package, and instructions were downloaded from https://www.cog-genomics.org/plink2, http://cnsgenomics.com/software/gcta/, and https://data.broadinstitute.org/alkesgroup/BOLT-LMM/, respectively. An R Shiny application implementing the methodology can be found at http://cnsgenomics.com/shiny/LMOR/. The source code for the R Shiny application and an R function implementing the method can be downloaded from https://github.com/lukelloydjones/ORShiny.
Results
Simulation results
Under the null model of no genetic effects, we observed very close correspondence between the ORs estimated by logistic regression and that from the LMM (adjusted ) for both and (Figure S2 in File S1 and Table 1). Given no genetic effects were simulated, we chose to randomly sample a set of 10,000 results from the 50,000,000 possible results generated from the 50 simulations for display. This reduced the burden of results, with the hypothesis that this random sample represents the distribution of results generated under the null model well. From this subsample of 10,000 estimated effects, we observed ORs from the null model between 0.5 and 2.0 from logistic regression (Figure S2 in File S1). Over the 50 replicates the average estimated proportion of phenotypic variance explained by the first PC was ∼0.11 (SE = 0.038) on the liability scale.
Table 1. Summary of adjusted and slope coefficients from regression of estimated ORs on true or logistic regression ORs from simulated and real-data analysis of type 2 diabetes.
| Null | Logistic | rare | Type 2 diabetes | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.987 | 0.999 | 0.993 | 0.996 | 0.986 | 0.983 | 0.997 | 0.986 | ||
| Slope | 0.989 | 1.00 | 0.969 | 0.965 | 0.975 | 0.953 | 1.02 | 0.977 | |
| R2* | – | 0.992 | 0.988 | 0.995 | 0.984 | 0.988 | 0.997 | 0.986 | |
| Slope* | – | 1.00 | 0.979 | 0.966 | 0.962 | 0.979 | 1.01 | 0.977 | |
| R2** | – | 0.991 | 0.993 | 0.996 | 0.986 | 0.980 | 0.997 | 0.986 | |
| Slope** | – | 1.02 | 0.970 | 0.965 | 0.975 | 0.956 | 1.02 | 0.977 | |
| 0.987 | 0.991 | 0.989 | 0.994 | 0.984 | 0.983 | 0.997 | 0.986 | ||
| Slope | 0.989 | 1.05 | 0.998 | 0.984 | 1.02 | 0.972 | 1.01 | 0.977 | |
| R2* | – | 0.991 | 0.989 | 0.994 | 0.982 | 0.989 | 0.997 | 0.986 | |
| Slope* | – | 1.05 | 0.998 | 0.984 | 0.995 | 0.998 | 1.01 | 0.977 | |
| R2** | – | 0.985 | 0.989 | 0.994 | 0.984 | 0.979 | 0.997 | 0.986 | |
| Slope** | – | 1.06 | 0.998 | 0.984 | 1.01 | 0.975 | 1.02 | 0.977 | |
Results were generated from regression of transformed ORs from the LMM on estimated ORs from logistic regression for the null and type 2 diabetes results and the true simulated ORs in the logistic and liability threshold simulation scenarios. The * rows correspond to the results from the use of reference allele frequencies for p from the 1000 Genomes Phase 1 Version 3 European sample. The ** rows correspond to the results from the use of the transformations using the SE of the regression coefficient instead of p.
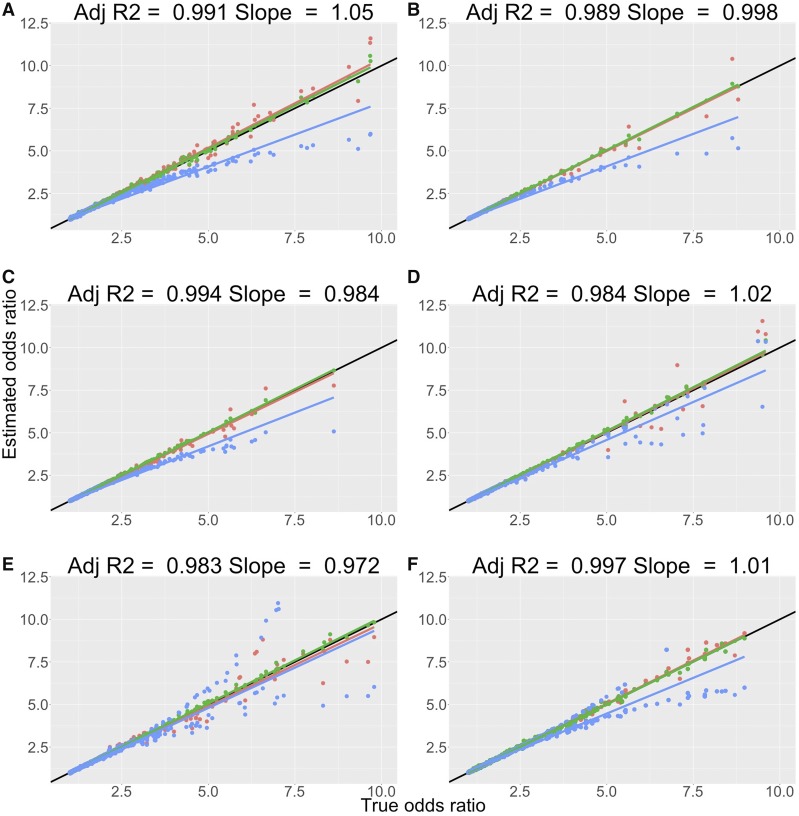
For the data simulated under the logistic model, and performed equally well up to an OR of 10 (Figure 1A and Table 1). Large effects were on average attributed to variants with low minor allele frequency (Table S1 in File S1). The transformation of Pirinen et al. (2013) performed less well with systematic deviations from the true OR occurring after an OR of three (Figure 1A and Figure S3 in File S1). Across OR bins, had a smaller MSE than the transformation of Pirinen et al. (2013) (Figure S3 in File S1). Using an external reference for the allele frequency did not alter the results dramatically for and , with no change in the estimated slope and adjusted when the transformed ORs were compared to the true ORs (Figure S4 in File S1 and Table 1). A similar small deviation in performance was seen when the SE was used to compute the approximate transformations (Figure S4 in File S1 and Table 1). For deviations from the true k of > showed an upward bias, whereas if p was deviated from its true value, no bias was observed (Figures S6A and S7A in File S1).
Figure 1.
Performance of logistic regression and OR transformations from the linear model across simulation scenarios. Comparison of estimated ORs from logistic regression (green), transformed ORs from the LMM using (red), and the transformed ORs from the LMM using the equation from Pirinen et al. (2013) (blue), with true simulated ORs across logistic and liability threshold model simulation scenarios. (A) Results from the logistic model simulation. (B) Results from the simulation scenario with and (). (C) Results for the simulation scenario with and (). (D) Results for the simulation scenario with and (). (E) Results for the simulation scenario with and (). (F) Results from the rare variant simulation scenario with and (). All ORs have been reported for the allele that increases the odds of having the disease such that each point is greater than (1,1). Panels display comparisons from 5000 simulated true effects generated from the 50 replicates. All panels include the fitted linear regression line for each of the sets of points and the line (black) for reference. Key statistics from the regression of the transformed ORs from are displayed at the top of each panel.
Under the liability threshold model, slopes and adjusted values were close to unity across simulation scenarios (Figure 1 and Table 1). Systematic underestimation of the true OR after an OR of 2.5 was again observed when the transformation of Pirinen et al. (2013) was applied (Figure 1 and Figure S3 in File S1). For simulation scenarios one to five, large effects were on average attributed to variants with low minor allele frequency with smaller MSEs observed for relative to Pirinen et al. (2013) as the OR increased (Figure S3 and Table S1 in File S1). There was a small decrease in performance as the sample prevalence decreased with performing marginally better than with respect to slopes and adjusted across scenarios, up to ORs of 10 (Figure 1 and Table 1). We also saw an increase in variance around the fitted line for larger effects and as the prevalence decreased (Figure 1). When the allele frequencies from the 1000 Genomes were used to calculate the transformed ORs, marginal deviations from the slope and statistics were observed relative to those using the sample allele frequency (Figure S4 in File S1 and Table 1). A similar small decrease in performance was seen when using the SE coupled with the regression coefficient to estimate the transformed ORs (Figure S5 in File S1 and Table 1). For deviations from the true k of > showed a substantial bias with an increase in the size of the bias with decreasing true sample prevalence (Figure S6 in File S1). If p was deviated from its true value, no bias was observed for those scenarios in which with an increase in the size of the p dependent bias of when k tended to smaller values (Figure S7 in File S1).
For the large effect variant simulation scenarios under the liability threshold model, we observed an increasing bias in the estimate of the OR for both the transformed effect from the linear model and logistic regression as the effect size of the variant was increased (Figure S8, A and B in File S1). This coincided with a substantial deviation in the HWE assumption across cases and controls and within cases as the proportion of phenotypic variance explained by the single variant of large effect became larger (Figure S8C in File S1). The deviation between the estimated OR from logistic regression and that from was at a maximum when the Hardy–Weinberg disequilibrium within cases was greater than that across cases and controls, which is an assumption in the derivation of (Figure S8D in File S1). Observed maximum average deviations between the estimated OR and the true OR were ∼30% for the transformed OR and 25% for the logistic regression estimates when the true OR exceeded 7.5 (Figure S8D in File S1). The deviations from the true OR for the transformed OR estimates had larger variation than those from logistic regression with maximal deviations of >100%, when the true OR exceeded five, whereas the maximum value for logistic regression was ∼45% (Figure S8D in File S1). When Hardy–Weinberg disequilibrium was larger across cases and controls relative to just within cases, the OR estimates from logistic regression were very similar to those from the transformed linear regression estimate. When a large covariate effect was included in the simulation we observed a further increase in the upward bias of the estimates of the OR from logistic regression (Figure S9, A and B in File S1). Furthermore, when a large covariate effect was included the linear model transformation underestimated the effect (Figure S9, A and D in File S1). The results from the meta-analysis showed an improvement in the bias in the OR estimates from logistic regression and the linear model transformation (Figure S9E in File S1).
Type 2 diabetes results
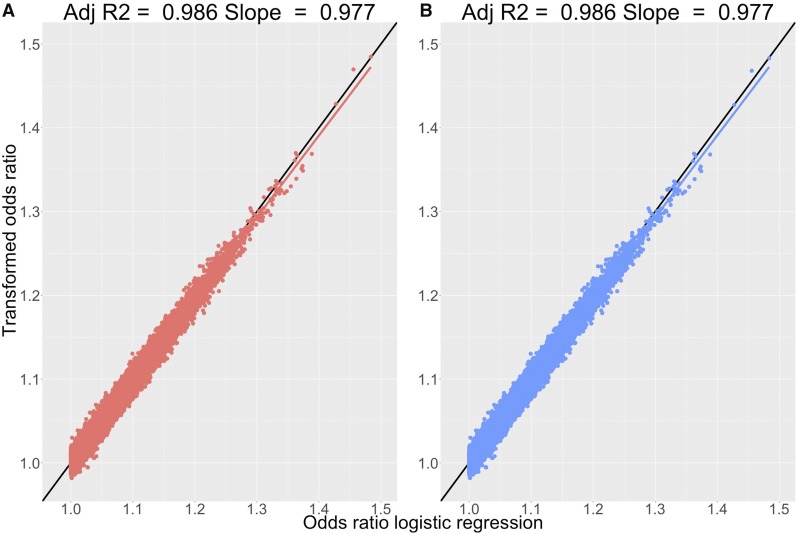
The association results from the analysis of type 2 diabetes showed 12 loci passing genome-wide significance (after clumping with a linkage disequilibrium threshold ) for both the LMM and logistic regression results. Of the set of SNPs passing genome-wide significance, the median OR for the risk allele was 1.14 with a maximum value of 1.30 (P-value = 1.53) from the logistic regression results. Across the full set of association results (1,162,900 SNPs), and performed well, with all regression slopes and adjusted values very close or equal to one (Figure 2A). The results from Pirinen et al. (2013) gave identical slopes and values for the type 2 diabetes results (Figure 2B). The use of a reference for the allele frequencies, or the use of the SE versions of the transformations, did not alter these results (Table 1).
Figure 2.
Performance of OR transformations for type 2 diabetes phenotype in the UK Biobank. Comparison of transformed ORs from and estimated ORs from logistic regression for type 2 diabetes in the UK Biobank. (A) Comparisons from 1,162,900 SNPs generated from logistic regression performed using the PLINK 1.9 software and a LMM implemented in the BOLT-LMM software and transformed using (B) Comparisons for the same set of results as A but with the transformation of Pirinen et al. (2013) used. Panels include the fitted regression line and line (black) for reference with the key statistics of this regression displayed at the top of each panel.
Discussion
We derived and tested transformations to OR under the allelic additive risk model and the assumptions of the simple linear regression model. LMMs are being used for GWAS of dichotomous traits to correct for population structure and cryptic relatedness [Fakiola et al. 2013; International Genetics of Ankylosing Spondylitis Consortium (IGAS) et al. 2013; Jiang et al. 2016; Liu et al. 2017]. Additionally, methods that correct for case-control ascertainment explicitly or through retrospective association analysis have emerged (Golan and Rosset 2014; Hayeck et al. 2015; Jiang et al. 2015; Weissbrod et al. 2015) to overcome the loss in power under case-control ascertainment (Yang et al. 2014). Across simulation scenarios, we showed that the transformed LMM effects from and showed very high concordance with the simulated truth and logistic regression OR estimates. This was again observed for the summary statistics generated for type 2 diabetes in the UK Biobank. Transformation performed the best on average across scenarios, with regression slope and adjusted estimates closest to unity. The transformation of Pirinen et al. (2013) showed systematic deviation as the true OR became larger and had larger MSEs than for OR bins >3. Transformation also showed good robustness across simulation scenarios. Therefore, or are adequate for most complex diseases where the median OR for the risk increasing allele is ∼1.3 (Manolio 2010).
The SE transformations have the added benefit of not relying on the allele frequency, although if an adequate reference is available then and are robust to differences in sample vs. reference allele frequencies, even in ascertained studies. We recommend the use of in all scenarios if allele frequencies are available with the SE transformations a good alternative if one is unsure whether there is a reliable allele frequency reference for the population under study, or if the ancestral background of a set of summary statistics is unknown. Alternatively, if small genetic effects are assumed then we can ignore in Equation 5 and reduce the expression to which is independent of p. Furthermore, if we assume that is small then this equation reduces to which is also equivalent to the first transformation provided in Pirinen et al. (2013) and provides a link to the derivation using the first order Taylor expansion of the logistic link function. These simpler transformations were evaluated but not presented in the simulation results as they showed poor performance for ORs >2 due to the small effect assumption.
Modeling a dichotomous trait using a linear model has a few shortcomings: it implicitly assumes that the error is heteroscedastic because we are equating the mean plus error term to a dichotomous outcome, which induces a dependence between the variance of the error term and the mean (Greene 2003); the predicted values from the linear model are not constrained to lie in the interval (Greene 2003; Wray and Goddard 2010). Chen et al. (2016) showed that the LMM homoscedasticity assumption is violated under some population stratification scenarios, which led to inflated type I error rates in some scenarios. This flaw can be overcome with generalized LMM methods (Chen et al. 2016; Zhou et al. 2017), which are capable of performing association testing in data sets with hundreds of thousands of individuals (Zhou et al. 2017); however, efficient OR estimation is still limited computationally. We found the method of Chen et al. (2016) to be computationally intensive with the estimation of effect sizes for 10 variants from a simulation using 10,000 individuals taking on average 114 hr (SD = 24 hr) across 50 simulations. The score statistic estimation of 14,000 variants in the same simulation scenario took 67 min (SD = 30 min). Zhou et al. (2017) and Dey et al. (2017) showed that the type 1 error rate for the method of Chen et al. (2016) and other LMM approaches is poorly controlled in the presence of unbalanced case-control ratios, which should be considered when performing GWAS using LMM methods. The unrestricted prediction domain of the linear model is not necessarily a severe problem, with the probability estimates potentially being either negative or >1 due to sampling error (Aldrich and Nelson 1984). However, if many predicted values fall outside of [0, 1] then we must question whether the linear probability model is a good fit for the data. The model used to derive the transformations makes assumptions about HWE across cases and controls or within cases and controls. If the genotype frequencies deviate substantially from HWE due to genetic or nongenetic mechanisms, then our transformations may be biased upwards or downward depending on whether the true genotypic variance is greater or smaller than that calculated under HWE. This was observed in the single variant simulation, which showed that for very large effects and high case ascertainment that the HWE assumption breaks down and a bias is induced. However, these scenarios are very extreme relative to those expected in most GWAS.
Logistic LMMs are not free of the problems associated with decreased power when covariates that are independent risk factors for a trait, but not confounders, are included in the model (Mefford and Witte 2012; Pirinen et al. 2012). Stringer et al. (2011) showed that this loss of power may be in part due to the underestimation of the effect (measured with the ORs), which is most severe for diseases influenced by numerous risk variants. In the context of logistic regression, this underestimation effect reduces the efficiency of effect size statistics (Robinson and Jewell 1991), which has links to the nonequivalence of conditional and marginal ORs known as Simpson’s paradox (Simpson 1951; Hernán et al. 2011). In simulation we observed an upward bias in the OR estimate from logistic regression when a binary covariate of very large effect contributed to the simulated phenotype. Stringer et al. (2011) outline that in the context of single variant association testing in GWAS via logistic regression, the conditional (the desired measure) and marginal ORs (the measure estimated in GWAS) are only equivalent if the SNP of interest, or the genetic background, is not associated with disease status. In linear regression, the omitting of covariates has no effect on the precision of the estimated effect size (Robinson and Jewell 1991) but as seen in the large covariate simulation it can alter the estimated transformed OR, which may be improved through a meta-analysis within covariate group.
Given the ever increasing sample sizes and diversity of biobank-based data sets for GWAS, which may include related individuals and population stratification, the application of LMM methods (Yang et al. 2011; Zhou and Stephens 2012; Loh et al. 2015) is likely to remain a reasonable practical choice for most researchers, especially given the promise of increased power (Loh et al. 2017). However, the use of the more correctly specified logistic regression model with adequate control for confounders is likely to remain the method of choice for GWAS of unrelated individuals. The transformations derived and validated in this study improve the comparability of results from prospective and already performed LMM GWAS on complex diseases by providing a common comparative scale for the genetic effects that can be reliably used across a broad range of case-control study scenarios and genetic architectures.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300360/-/DC1.
Acknowledgments
The authors thank Loic Yengo Dimbou and Hien D. Nguyen for helpful discussion and comments on the article. The authors also thank the anonymous reviewers for their insightful comments and excellent suggestions. The authors acknowledge the support from the Australian Research Council (DP160102400), the Australian National Health and Medical Research Council (1113400 and 1078037), the National Institutes of Health (R21 ES025052), and the Sylvia & Charles Viertel Charitable Foundation. The resource for the GERA cohort was accessed via dbGap (accession number: phs000674.v2.p2) and was created by a RC2 Grand Opportunity grant that was awarded to the Kaiser Permanente Research Program on Genes, Environment, and Health (RPGEH) and the University of California, San Francisco Institute for Human Genetics (AG036607; Catherine Schaefer and Neil Risch principal investigators). The RC2 project enabled genome-wide SNP genotyping (GWAS) to be conducted on a cohort of over 100,000 adults who are members of the Kaiser Permanente Medical Care Plan, Northern California Region, and are participating in its RPGEH. The purpose of the RPGEH is to facilitate research on the genetic and environmental factors that affect health and disease by linking together clinical data from electronic health records, survey data on demographic and behavioral factors, and environmental data from various sources with genetic data derived from biospecimens collected from participants. This study has been conducted using the UK Biobank resource under Application Number 12514. UK Biobank was established by the Wellcome Trust medical charity, Medical Research Council, Department of Health, Scottish Government, and the Northwest Regional Development Agency. It has also received funding from the Welsh Assembly Government, British Heart Foundation, and Diabetes UK.
Footnotes
Communicating editor: E. Eskin
Literature Cited
- 1000 Genomes Project Consortium; Abecasis G. R., Auton A., Brooks L. D., DePristo M. A., Durbin R. M., et al. , 2012. An integrated map of genetic variation from 1,092 human genomes. Nature 491: 56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aldrich J. H., Nelson F. D., 1984. Linear Probability, Logit, and Probit Models, Vol. 45 Sage, London. [Google Scholar]
- Boraska V., Franklin C. S., Floyd J. A., Thornton L. M., Huckins L. M., et al. , 2014. A genome-wide association study of anorexia nervosa. Mol. Psychiatry 19: 1085–1094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang B.-H., Lipsitz S., Waternaux C., 2000. Logistic regression in meta-analysis using aggregate data. J. Appl. Stat. 27: 411–424. [Google Scholar]
- Chang C., Chow C., Tellier L., Vattikuti S., Purcell S., et al. , 2015. Second-generation PLINK: rising to the challenge of larger and richer datasets. Gigascience 4: 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H., Wang C., Conomos M. P., Stilp A. M., Li Z., et al. , 2016. Control for population structure and relatedness for binary traits in genetic association studies via logistic mixed models. Am. J. Hum. Genet. 98: 653–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook J. P., Mahajan A., Morris A. P., 2017. Guidance for the utility of linear models in meta-analysis of genetic association studies of binary phenotypes. Eur. J. Hum. Genet. 25: 240–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox D. R., Snell E. J., 1989. Analysis of Binary Data, Vol. 32 CRC Press, Boca Raton, FL. [Google Scholar]
- Dempster E. R., Lerner I. M., 1950. Heritability of threshold characters. Genetics 35: 212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dey R., Schmidt E. M., Abecasis G. R., Lee S., 2017. A fast and accurate algorithm to test for binary phenotypes and its application to PheWAS. Am. J. Hum. Genet. 101: 37–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B., 1975. The efficiency of logistic regression compared to normal discriminant analysis. J. Am. Stat. Assoc. 70: 892–898. [Google Scholar]
- Fakiola M., Strange A., Cordell H. J., Miller E. N., Pirinen M., et al. , 2013. Common variants in the HLA-DRB1-HLA-DQA1 HLA class II region are associated with susceptibility to visceral leishmaniasis. Nat. Genet. 45: 208–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fingerlin T. E., Murphy E., Zhang W., Peljto A. L., Brown K. K., et al. , 2013. Genome-wide association study identifies multiple susceptibility loci for pulmonary fibrosis. Nat. Genet. 45: 613–620 (erratum: Nat Genet. 45: 1409). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher R. A., 1936. The use of multiple measurements in taxonomic problems. Ann. Hum. Genet. 7: 179–188. [Google Scholar]
- Golan D., Rosset S., 2014. Effective genetic-risk prediction using mixed models. Am. J. Hum. Genet. 95: 383–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greene W. H., 2003. Econometric Analysis. Pearson Hall, Upper Saddle River, NJ. [Google Scholar]
- Haggstrom G. W., 1983. Logistic regression and discriminant analysis by ordinary least squares. J. Bus. Econ. Stat. 1: 229–238. [Google Scholar]
- Hayeck T. J., Zaitlen N. A., Loh P.-R., Vilhjalmsson B., Pollack S., et al. , 2015. Mixed model with correction for case-control ascertainment increases association power. Am. J. Hum. Genet. 96: 720–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán M. A., Clayton D., Keiding N., 2011. The Simpson’s paradox unraveled. Int. J. Epidemiol. 40: 780–785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirschhorn J. N., Daly M. J., 2005. Genome-wide association studies for common diseases and complex traits. Nat. Rev. Genet. 6: 95–108. [DOI] [PubMed] [Google Scholar]
- Howson J. M., Zhao W., Barnes D. R., Ho W.-K., Young R., et al. , 2017. Fifteen new risk loci for coronary artery disease highlight arterial-wall-specific mechanisms. Nat. Genet. 49: 1113–1119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Genetics of Ankylosing Spondylitis Consortium (IGAS) Cortes A., Hadler J., Pointon J. P., Robinson P. C., Karaderi T., et al. , 2013. Identification of multiple risk variants for ankylosing spondylitis through high-density genotyping of immune-related loci. Nat. Genet. 45: 730–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang D., Mbatchou J., McPeek M. S., 2015. Retrospective association analysis of binary traits: overcoming some limitations of the additive polygenic model. Hum. Hered. 80: 187–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang D., Zhong S., McPeek M. S., 2016. Retrospective binary-trait association test elucidates genetic architecture of Crohn disease. Am. J. Hum. Genet. 98: 243–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambert J.-C., Ibrahim-Verbaas C. A., Harold D., Naj A. C., Sims R., et al. , 2013. Meta-analysis of 74,046 individuals identifies 11 new susceptibility loci for Alzheimer’s disease. Nat. Genet. 45: 1452–1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lapham K., Kvale M. N., Lin J., Connell S., Croen L. A., et al. , 2015. Automated assay of telomere length measurement and informatics for 100,000 subjects in the genetic epidemiology research on adult health and aging (GERA) cohort. Genetics 200: 1061–1072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J. Z., Erlich Y., Pickrell J. K., 2017. Case-control association mapping by proxy using family history of disease. Nat. Genet. 49: 325–331. [DOI] [PubMed] [Google Scholar]
- Loh P.-R., Tucker G., Bulik-Sullivan B. K., Vilhjalmsson B. J., Finucane H. K., et al. , 2015. Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet. 47: 284–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loh, P.-R., G. Kichaev, S. Gazal, A. P. Schoech, and A. L. Price, 2017 Mixed model association for biobank-scale data sets. bioRxiv. Available at: https://www.biorxiv.org/content/early/2017/09/27/194944. [DOI] [PMC free article] [PubMed]
- Manolio T. A., 2010. Genome-wide association studies and assessment of the risk of disease. N. Engl. J. Med. 363: 166–176. [DOI] [PubMed] [Google Scholar]
- Marchini J., Cardon L. R., Phillips M. S., Donnelly P., 2004. The effects of human population structure on large genetic association studies. Nat. Genet. 36: 512–517. [DOI] [PubMed] [Google Scholar]
- Mefford J., Witte J. S., 2012. The covariate’s dilemma. PLoS Genet. 8: e1003096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michailidou K., Hall P., Gonzalez-Neira A., Ghoussaini M., Dennis J., et al. , 2013. Large-scale genotyping identifies 41 new loci associated with breast cancer risk. Nat. Genet. 45: 353–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pirinen M., Donnelly P., Spencer C. C., 2012. Including known covariates can reduce power to detect genetic effects in case-control studies. Nat. Genet. 44: 848–851. [DOI] [PubMed] [Google Scholar]
- Pirinen M., Donnelly P., Spencer C. C., 2013. Efficient computation with a linear mixed model on large-scale data sets with applications to genetic studies. Ann. Appl. Stat. 7: 369–390. [Google Scholar]
- Press S. J., Wilson S., 1978. Choosing between logistic regression and discriminant analysis. J. Am. Stat. Assoc. 73: 699–705. [Google Scholar]
- Price A. L., Patterson N. J., Plenge R. M., Weinblatt M. E., Shadick N. A., et al. , 2006. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 38: 904–909. [DOI] [PubMed] [Google Scholar]
- R Core Team , 2015. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna. [Google Scholar]
- Reich T., James J., Morris C., 1972. The use of multiple thresholds in determining the mode of transmission of semi-continuous traits. Ann. Hum. Genet. 36: 163–184. [DOI] [PubMed] [Google Scholar]
- Robinson L. D., Jewell N. P., 1991. Some surprising results about covariate adjustment in logistic regression models. Int. Stat. Rev. 59: 227–240. [Google Scholar]
- Schizophrenia Working Group of the Psychiatric Genomics Consortium , 2014. Biological insights from 108 schizophrenia-associated genetic loci. Nature 511: 421–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson E. H., 1951. The interpretation of interaction in contingency tables. J. R. Stat. Soc. B 13: 238–241. [Google Scholar]
- Stringer S., Wray N. R., Kahn R. S., Derks E. M., 2011. Underestimated effect sizes in GWAS: fundamental limitations of single snp analysis for dichotomous phenotypes. PLoS One 6: e27964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sudlow C., Gallacher J., Allen N., Beral V., Burton P., et al. , 2015. UK Biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 12: e1001779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Rheenen W., Shatunov A., Dekker A. M., McLaughlin R. L., Diekstra F. P., et al. , 2016. Genome-wide association analyses identify new risk variants and the genetic architecture of amyotrophic lateral sclerosis. Nat. Genet. 48: 1043–1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weissbrod O., Lippert C., Geiger D., Heckerman D., 2015. Accurate liability estimation improves power in ascertained case-control studies. Nat. Methods 12: 332–334. [DOI] [PubMed] [Google Scholar]
- Witte J. S., Visscher P. M., Wray N. R., 2014. The contribution of genetic variants to disease depends on the ruler. Nat. Rev. Genet. 15: 765–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wray N., Visscher P., 2015. Quantitative genetics of disease traits. J. Anim. Breed. Genet. 132: 198–203. [DOI] [PubMed] [Google Scholar]
- Wray N. R., Goddard M. E., 2010. Multi-locus models of genetic risk of disease. Genome Med. 2: 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Lee S. H., Goddard M. E., Visscher P. M., 2011. GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 88: 76–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Zaitlen N. A., Goddard M. E., Visscher P. M., Price A. L., 2014. Advantages and pitfalls in the application of mixed-model association methods. Nat. Genet. 46: 100–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, W., J. B. Nielsen, L. G. Fritsche, R. Dey, M. B. Elvestad et al., 2017 Efficiently controlling for case-control imbalance and sample relatedness in large-scale genetic association studies. bioRxiv. Available at: https://www.biorxiv.org/content/early/2017/11/15/212357. [DOI] [PMC free article] [PubMed]
- Zhou X., Stephens M., 2012. Genome-wide efficient mixed-model analysis for association studies. Nat. Genet. 44: 821–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X., Carbonetto P., Stephens M., 2013. Polygenic modeling with Bayesian sparse linear mixed models. PLoS Genet. 9: e1003264. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The PLINK, GCTA, and BOLT-LMM software, source code, installation package, and instructions were downloaded from https://www.cog-genomics.org/plink2, http://cnsgenomics.com/software/gcta/, and https://data.broadinstitute.org/alkesgroup/BOLT-LMM/, respectively. An R Shiny application implementing the methodology can be found at http://cnsgenomics.com/shiny/LMOR/. The source code for the R Shiny application and an R function implementing the method can be downloaded from https://github.com/lukelloydjones/ORShiny.